Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.2.1. Static analysis
- A2.5. Software engineering
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.2.6. Optimization
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
Other Research Topics and Application Domains
- B1.1.2. Molecular and cellular biology
- B3.2. Climate and meteorology
- B3.3.2. Water: sea & ocean, lake & river
- B3.3.4. Atmosphere
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B9.6.3. Economy, Finance
1 Team members, visitors, external collaborators
Research Scientists
- Laurent Hascoët [Team leader, Inria, Senior Researcher, HDR]
- Alain Dervieux [Inria, Emeritus, HDR]
- Valérie Pascual [Inria, Researcher]
PhD Student
- Matthieu Gschwend [Inria, from Oct 2020]
Administrative Assistant
- Christine Claux [Inria]
External Collaborator
- Bruno Koobus [Univ Montpellier II (sciences et techniques du Languedoc)]
2 Overall objectives
Team Ecuador studies Algorithmic Differentiation (AD) of computer programs, blending :
- AD theory: We study software engineering techniques, to analyze and transform programs mechanically. Algorithmic Differentiation (AD) transforms a program P that computes a function , into a program P' that computes analytical derivatives of . We put emphasis on the adjoint mode of AD, a sophisticated transformation that yields gradients for optimization at a remarkably low cost.
- AD application to Scientific Computing: We adapt the strategies of Scientific Computing to take full advantage of AD. We validate our work on real-size applications.
We aim to produce AD code that can compete with hand-written sensitivity and adjoint programs used in the industry. We implement our algorithms into the tool Tapenade, one of the most popular AD tools at present.
Our research directions :
- Efficient adjoint AD of frequent dialects e.g. Fixed-Point loops.
- Development of the adjoint AD model towards Dynamic Memory Management.
- Evolution of the adjoint AD model to keep in pace with with modern programming languages constructs.
- Optimal shape design and optimal control for steady and unsteady simulations. Higher-order derivatives for uncertainty quantification.
- Adjoint-driven mesh adaptation.
3 Research program
3.1 Algorithmic Differentiation
Participants: Laurent Hascoët, Valérie Pascual.
- algorithmic differentiation (AD, aka Automatic Differentiation) Transformation of a program, that returns a new program that computes derivatives of the initial program, i.e. some combination of the partial derivatives of the program's outputs with respect to its inputs.
- adjoint Mathematical manipulation of the Partial Differential Equations that define a problem, obtaining new differential equations that define the gradient of the original problem's solution.
- checkpointing General trade-off technique, used in adjoint AD, that trades duplicate execution of a part of the program to save some memory space that was used to save intermediate results.
Algorithmic Differentiation (AD) differentiates programs. The input of AD is a source program that, given some , returns some , for a differentiable . AD generates a new source program that, given , computes some derivatives of 4.
Any execution of amounts to a sequence of instructions, which is identified with a composition of vector functions. Thus, if
where each is the elementary function implemented by instruction . AD applies the chain rule to obtain derivatives of . Calling the values of all variables after instruction , i.e. and , the Jacobian of is
which can be mechanically written as a sequence of instructions . This can be generalized to higher level derivatives, Taylor series, etc. Combining the with the control of yields , and therefore this differentiation is piecewise.
The above computation of , albeit simple and mechanical, can be prohibitively expensive on large codes. In practice, many applications only need cheaper projections of such as:
-
Sensitivities, defined for a given direction in the input space as:
3This expression is easily computed from right to left, interleaved with the original program instructions. This is the tangent mode of AD.
-
Adjoints, defined after transposition (), for a given weighting of the outputs as:
4This expression is most efficiently computed from right to left, because matrixvector products are cheaper than matrixmatrix products. This is the adjoint mode of AD, most effective for optimization, data assimilation 25, adjoint problems 19, or inverse problems.
Adjoint AD builds a very efficient program 21, which computes the gradient in a time independent from the number of parameters . In contrast, computing the same gradient with the tangent mode would require running the tangent differentiated program times.
However, the are required in the inverse of their computation order. If the original program overwrites a part of , the differentiated program must restore before it is used by . Therefore, the central research problem of adjoint AD is to make the available in reverse order at the cheapest cost, using strategies that combine storage, repeated forward computation from available previous values, or even inverted computation from available later values.
Another research issue is to make the AD model cope with the constant evolution of modern language constructs. From the old days of Fortran77, novelties include pointers and dynamic allocation, modularity, structured data types, objects, vectorial notation and parallel programming. We keep developing our models and tools to handle these new constructs.
3.2 Static Analysis and Transformation of programs
Participants: Laurent Hascoët, Valérie Pascual.
- abstract syntax tree Tree representation of a computer program, that keeps only the semantically significant information and abstracts away syntactic sugar such as indentation, parentheses, or separators.
- control flow graph Representation of a procedure body as a directed graph, whose nodes, known as basic blocks, each contain a sequence of instructions and whose arrows represent all possible control jumps that can occur at run-time.
- abstract interpretation Model that describes program static analysis as a special sort of execution, in which all branches of control switches are taken concurrently, and where computed values are replaced by abstract values from a given semantic domain. Each particular analysis gives birth to a specific semantic domain.
- data flow analysis Program analysis that studies how a given property of variables evolves with execution of the program. Data Flow analysis is static, therefore studying all possible run-time behaviors and making conservative approximations. A typical data-flow analysis is to detect, at any location in the source program, whether a variable is initialized or not.
The most obvious example of a program transformation tool is certainly a compiler. Other examples are program translators, that go from one language or formalism to another, or optimizers, that transform a program to make it run better. AD is just one such transformation. These tools share the technological basis that lets them implement the sophisticated analyses 12 required. In particular there are common mathematical models to specify these analyses and analyze their properties.
An important principle is abstraction: the core of a compiler should not bother about syntactic details of the compiled program. The optimization and code generation phases must be independent from the particular input programming language. This is generally achieved using language-specific front-ends, language-independent middle-ends, and target-specific back-ends. In the middle-end, analysis can concentrate on the semantics of a reduced set of constructs. This analysis operates on an abstract representation of programs made of one call graph, whose nodes are themselves flow graphs whose nodes (basic blocks) contain abstract syntax trees for the individual atomic instructions. To each level are attached symbol tables, nested to capture scoping.
Static program analysis can be defined on this internal representation, which is largely language independent. The simplest analyses on trees can be specified with inference rules 15, 22, 13. But many data-flow analyses are more complex, and better defined on graphs than on trees. Since both call graphs and flow graphs may be cyclic, these global analyses will be solved iteratively. Abstract Interpretation 16 is a theoretical framework to study complexity and termination of these analyses.
Data flow analyses must be carefully designed to avoid or control combinatorial explosion. At the call graph level, they can run bottom-up or top-down, and they yield more accurate results when they take into account the different call sites of each procedure, which is called context sensitivity. At the flow graph level, they can run forwards or backwards, and yield more accurate results when they take into account only the possible execution flows resulting from possible control, which is called flow sensitivity.
Even then, data flow analyses are limited, because they are static and thus have very little knowledge of actual run-time values. Far before reaching the very theoretical limit of undecidability, one reaches practical limitations to how much information one can infer from programs that use arrays 28, 17 or pointers. Therefore, conservative over-approximations must be made, leading to derivative code less efficient than ideal.
3.3 Algorithmic Differentiation and Scientific Computing
Participants: Alain Dervieux, Laurent Hascoët, Bruno Koobus, Matthieu Gschwend, Stephen Wornom.
- linearization In Scientific Computing, the mathematical model often consists of Partial Differential Equations, that are discretized and then solved by a computer program. Linearization of these equations, or alternatively linearization of the computer program, predict the behavior of the model when small perturbations are applied. This is useful when the perturbations are effectively small, as in acoustics, or when one wants the sensitivity of the system with respect to one parameter, as in optimization.
- adjoint state Consider a system of Partial Differential Equations that define some characteristics of a system with respect to some parameters. Consider one particular scalar characteristic. Its sensitivity (or gradient) with respect to the parameters can be defined by means of adjoint equations, deduced from the original equations through linearization and transposition. The solution of the adjoint equations is known as the adjoint state.
Scientific Computing provides reliable simulations of complex systems. For example it is possible to simulate the steady or unsteady 3D air flow around a plane that captures the physical phenomena of shocks and turbulence. Next comes optimization, one degree higher in complexity because it repeatedly simulates and applies gradient-based optimization steps until an optimum is reached. The next sophistication is robustness, that detects undesirable solutions which, although maybe optimal, are very sensitive to uncertainty on design parameters or on manufacturing tolerances. This makes second derivatives come into play. Similarly Uncertainty Quantification can use second derivatives to evaluate how uncertainty on the simulation inputs imply uncertainty on its outputs.
To obtain this gradient and possibly higher derivatives, we advocate adjoint AD (cf3.1) of the program that discretizes and solves the direct system. This gives the exact gradient of the discrete function computed by the program, which is quicker and more sound than differentiating the original mathematical equations 19. Theoretical results 18 guarantee convergence of these derivatives when the direct program converges. This approach is highly mechanizable. However, it requires careful study and special developments of the AD model 23, 26 to master possibly heavy memory usage. Among these additional developments, we promote in particular specialized AD models for Fixed-Point iterations 20, 14, efficient adjoints for linear algebra operators such as solvers, or exploitation of parallel properties of the adjoint code.
4 Application domains
4.1 Algorithmic Differentiation
Algorithmic Differentiation of programs gives sensitivities or gradients, useful for instance for :
- optimum shape design under constraints, multidisciplinary optimization, and more generally any algorithm based on local linearization,
- inverse problems, such as parameter estimation and in particular 4Dvar data assimilation in climate sciences (meteorology, oceanography),
- first-order linearization of complex systems, or higher-order simulations, yielding reduced models for simulation of complex systems around a given state,
- adaptation of parameters for classification tools such as Machine Learning systems, in which Adjoint Differentiation is also known as backpropagation.
- mesh adaptation and mesh optimization with gradients or adjoints,
- equation solving with the Newton method,
- sensitivity analysis, propagation of truncation errors.
4.2 Multidisciplinary optimization
A CFD program computes the flow around a shape, starting from a number of inputs that define the shape and other parameters. On this flow one can define optimization criteria e.g. the lift of an aircraft. To optimize a criterion by a gradient descent, one needs the gradient of the criterion with respect to all inputs, and possibly additional gradients when there are constraints. Adjoint AD is the most efficient way to compute these gradients.
4.3 Inverse problems and Data Assimilation
Inverse problems aim at estimating the value of hidden parameters from other measurable values, that depend on the hidden parameters through a system of equations. For example, the hidden parameter might be the shape of the ocean floor, and the measurable values of the altitude and velocities of the surface. Figure 1 shows an example of an inverse problem using the glaciology code ALIF (a pure C version of ISSM 24) and its AD-adjoint produced by Tapenade.
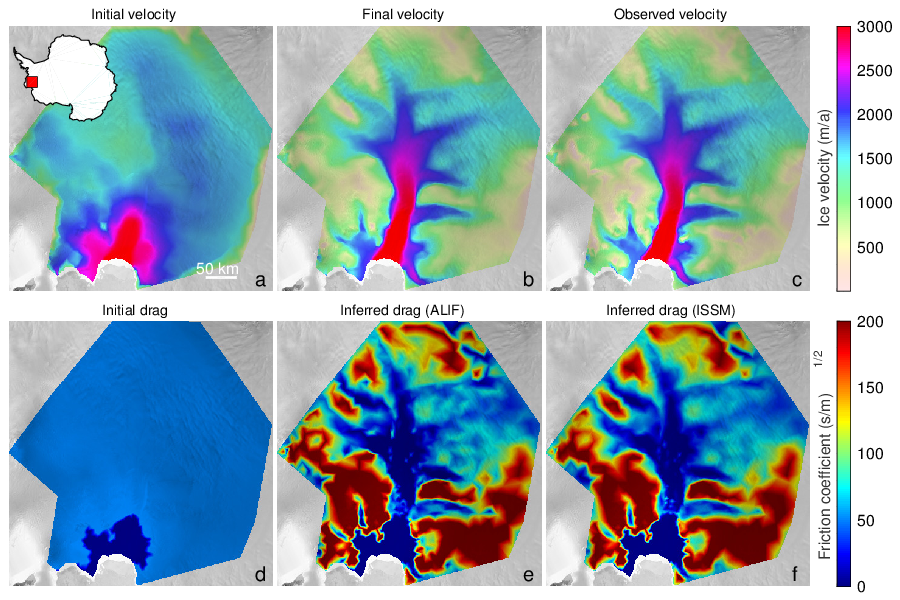
One particular case of inverse problems is data assimilation 25 in weather forecasting or in oceanography. The quality of the initial state of the simulation conditions the quality of the prediction. But this initial state is not well known. Only some measurements at arbitrary places and times are available. A good initial state is found by solving a least squares problem between the measurements and a guessed initial state which itself must verify the equations of meteorology. This boils down to solving an adjoint problem, which can be done though AD 27. The special case of 4Dvar data assimilation is particularly challenging. The 4th dimension in “4D” is time, as available measurements are distributed over a given assimilation period. Therefore the least squares mechanism must be applied to a simulation over time that follows the time evolution model. This process gives a much better estimation of the initial state, because both position and time of measurements are taken into account. On the other hand, the adjoint problem involved is more complex, because it must run (backwards) over many time steps. This demanding application of AD justifies our efforts in reducing the runtime and memory costs of AD adjoint codes.
4.4 Linearization
Simulating a complex system often requires solving a system of Partial Differential Equations. This can be too expensive, in particular for real-time simulations. When one wants to simulate the reaction of this complex system to small perturbations around a fixed set of parameters, there is an efficient approximation: just suppose that the system is linear in a small neighborhood of the current set of parameters. The reaction of the system is thus approximated by a simple product of the variation of the parameters with the Jacobian matrix of the system. This Jacobian matrix can be obtained by AD. This is especially cheap when the Jacobian matrix is sparse. The simulation can be improved further by introducing higher-order derivatives, such as Taylor expansions, which can also be computed through AD. The result is often called a reduced model.
4.5 Mesh adaptation
Some approximation errors can be expressed by an adjoint state. Mesh adaptation can benefit from this. The classical optimization step can give an optimization direction not only for the control parameters, but also for the approximation parameters, and in particular the mesh geometry. The ultimate goal is to obtain optimal control parameters up to a precision prescribed in advance.
5 Social and environmental responsibility
5.1 Impact of research results
Our research has an impact on environmental questions through two of its application domains
- in CFD, we provide gradients that are used for design and shape optimization, and in many cases the optimization criterion is to reduce fuel or energy consumption. This is the case in particular for automotive or aircraft design.
- in Earth sciences, our gradients are used in inverse problems, to determine key properties in oceanography, glaciology, or climate models. For instance they determine basal friction coefficients of glaciers that are necessary to simulate their future evolution. Another example is to locate sources and sinks of CO2 by coupling atmospheric models and remote measurements.
6 New software and platforms
6.1 New software
6.1.1 AIRONUM
- Keywords: Computational Fluid Dynamics, Turbulence
- Functional Description: Aironum is an experimental software that solves the unsteady compressible Navier-Stokes equations with k-epsilon, LES-VMS and hybrid turbulence modelling on parallel platforms, using MPI. The mesh model is unstructured tetrahedrization, with possible mesh motion.
-
URL:
https://
imag. umontpellier. fr/ ~koobus/ norma. html - Contact: Alain Dervieux
- Participant: Alain Dervieux
6.1.2 TAPENADE
- Name: Tapenade Automatic Differentiation Engine
- Keywords: Static analysis, Optimization, Compilation, Gradients
-
Scientific Description:
Tapenade implements the results of our research about models and static analyses for AD. Tapenade can be downloaded and installed on most architectures. Alternatively, it can be used as a web server. Higher-order derivatives can be obtained through repeated application.
Tapenade performs sophisticated data-flow analysis, flow-sensitive and context-sensitive, on the complete source program to produce an efficient differentiated code. Analyses include Type-Checking, Read-Write analysis, and Pointer analysis. AD-specific analyses include the so-called Activity analysis, Adjoint Liveness analysis, and TBR analysis.
- Functional Description: Tapenade is an Algorithmic Differentiation tool that transforms an original program into a new program that computes derivatives of the original program. Algorithmic Differentiation produces analytical derivatives, that are exact up to machine precision. Adjoint-mode AD can compute gradients at a cost which is independent from the number of input variables. Tapenade accepts source programs written in Fortran77, Fortran90, or C. It provides differentiation in the following modes: tangent, vector tangent, adjoint, and vector adjoint.
- News of the Year: - Continued development of multi-language capacity: AD of codes mixing Fortran and C - Extension to a subset of OpenMP, including the most generally used primitives. - Continued refactoring - Open-Source distribution, MIT license
-
URL:
https://
team. inria. fr/ ecuador/ en/ tapenade/ - Authors: Laurent Hascoët, Valérie Pascual
- Contacts: Laurent Hascoët, Valérie Pascual
- Participants: Laurent Hascoët, Valérie Pascual
7 New results
7.1 Algorithmic Differentiation of OpenMP
Participants: Laurent Hascoët, Jan Hueckelheim.
For applications that are parallelized for multi-core CPUs or GPUs using OpenMP, it is desirable to also compute the gradients in parallel. We extended the AD model of Tapenade (source transformation, association by address, storage on tape of intermediate values) towards correct and efficient differentiation of OpenMP parallel worksharing loops, one of the most commonly used OpenMP features, in tangent-linear and adjoint mode. We built a framework to reason about the correctness of the generated derivative code, from which we can justify our OpenMP extension to the adjoint differentiation model. We implemented this model in Tapenade, and ran experiments on a few small to medium-size test cases, testing performance on a multi-core CPU system.An article has been written and is currently under review with ACM TOMS.
7.2 Application to large industrial codes
Participants: Valérie Pascual, Laurent Hascoët, Hervé Guillard, Bruno Maugars, Sébastien Bourasseau, Cédric Content.
We support industrial or academic users with their first experiments of Algorithmic Differentiation of large in-house codes. This year, we continued collaboration with Onera on their Elsa CFD platform, in view of the design of its successor code. This is the continuation of a collaboration started in 2018. Both tangent and adjoint models of the kernel of ElsA were built successfully with Tapenade. It is worth noticing that this application was performed inside ONERA by ONERA engineers (Bruno Maugars, Sébastien Bourasseau, Cédric Content) with no need for installation of ElsA inside INRIA. We take this as a sign of maturity of Tapenade. Our contribution is driven by development meetings, in which we point out some strategies and tool options to improve efficiency. We also help taking into account the constraints of AD for the design of the new CFD platform (Sonice). A collaboration agreement is being finalized.On the academic side, we supported usage of Tapenade for adjoint differentiation of several large codes:
- The plasma code SOLPS-ITER, differentiated by Stefano Carli at KU Leuven.
- The plasma code CTFEM, differentiated by Ali Elarif of the INRIA team Castor (Supervisor Hervé Guillard)
- The glaciology code Sicopolis, differentiated by Shreyas Suni Gaikwad at U. Texas Austin (Supervisor Patrick Heimbach)
7.3 Aeroacoustics
Participants: Alain Dervieux, Matthieu Gschwend, Bruno Koobus, Florian Miralles, Stephen Wornom, Tanya Kozubskaya.
The progress in highly accurate schemes for compressible flows on unstructured meshes (together with advances in massive parallelization of these schemes) allows us to solve problems previously out of reach.The four-year program Norma associating IMAG of Montpellier university (B. Koobus, coordinator), CAALAB of Keldysh Institute of Moscow (T. Kozubskaya) and our team Ecuador, is supported by ANR and Russian Science Foundation.
See https://
Norma is a cooperation on the subject of the extension of these methods to simulate the noise emission of rotating machines (helicopters, future aerial vehicles, unmanned aerial vehicles, wind turbines...).
7.4 Turbulence models
Participants: Alain Dervieux, Bruno Koobus, Florian Miralles, Stephen Wornom, Tanya Kozubskaya.
Modeling turbulence is an essential aspect of CFD. The purpose of our work in hybrid RANS/LES (Reynolds Averaged Navier-Stokes / Large Eddy Simulation) is to develop new approaches for industrial applications of LES-based analyses. In the applications targetted (aeronautics, hydraulics), the Reynolds number can be as high as several tens of millions, far too high for pure LES models. However, certain regions in the flow can be predicted better with LES than with usual statistical RANS (Reynolds averaged Navier-Stokes) models. These are mainly vortical separated regions as assumed in one of the most popular hybrid models, the hybrid Detached Eddy Simulation (DES) model. Here, “hybrid” means that a blending is applied between LES and RANS. An important difference between a real life flow and a wind tunnel or basin is that the turbulence of the flow upstream of each body is not well known.The development of hybrid models, in particular DES in the litterature, has raised the question of the domain of validity of these models. According to theory, these models should not be applied to flow involving laminar boundary layers (BL). But industrial flows are complex flows and often present regions of laminar BL, regions of fully developed turbulent BL and regions of non-equilibrium vortical BL. It is then mandatory for industrial use that the new hybrid models give a reasonable prediction for all these types of flow. We concentrated on evaluating the behavior of hybrid models for laminar BL and for vortical wakes. While less predictive than pure LES on laminar BL, some hybrid models still give reasonable predictions for rather low Reynolds numbers.
During the first phase of Norma, Montpellier and Moscow are computing a series of initial test cases in order to control the consistancy of the results produced by the two platforms of CFD, namely Noisette for Moscow, and Aironum for Montpellier.
7.5 Rotating machines
Participants: Alain Dervieux, Didier Chargy, Matthieu Gschwend, Bruno Koobus, Florian Miralles, Tanya Kozubskaya.
The physical problem addressed by Norma involves a computational domain made of (at least) two components having different rotative motions. The numerical problem of their combination gave birth to many specialized schemes, such as the so-called sliding method, chimera method, immersed boundary method (IBM). In concertation with Moscow, Montpellier is introducing a novel IBM in the CFD code Aironum. The Ecuador team is studying in cooperation with Lemma engineering (Sophia Antipolis) a novel sliding/chimera method.7.6 High order approximations
Participants: Alain Dervieux, Matthieu Gschwend, Bruno Koobus, Stephen Wornom, Tanya Kozubskaya.
High order approximations for compressible flows on unstructured meshes are facing many constraints that increase their complexity i.e. their computational cost. This is clear for the largest class of approximation, the class of -exact schemes, which rely on a local polynomial representation of degree . We are investigating schemes which would solve as efficiently as possible the dilemma of choosing between an approximation with a representation inside macro-elements which finally constrains the mesh, and a representation around each individual cell, as in vertex formulations. For this purpose, we extend the Central Essentially Non Oscillating (CENO) family of schemes. This is a cooperation with the Keldysh Institute of Russian Academy with whom we have already developed several families of superconvergent schemes. T. Kozubskaya, F. Alauzet, A. Loseille and A. Dervieux are coorganizers of a mini-symposium ECCOMAS 2020 MS286 on “High-accuracy Finite-Volume Methods on unstructured meshes for Aviation applications”.7.7 Control of approximation errors
Participants: Alain Dervieux, Matthieu Gschwend, Bruno Koobus, Adrien Loseille, Frédéric Alauzet.
Reducing approximation errors as much as possible is a particular kind of optimal control problem. We formulate it exactly this way when we look for the optimal metric of the mesh, which minimizes a user-specified functional (goal-oriented mesh adaptation). In that case, the usual methods of optimal control apply, using adjoint states that can be produced by Algorithmic Differentiation.This year, a novel a priori estimate has been developed for incompressible flows, in cooperation with Lemma. We are also starting a new analysis for h-p anisotropic mesh adaptation. The monography on mesh adaptation currently being written by Alauzet, Loseille, Koobus and Dervieux now has been extended to 16 chapters.
8 Dissemination
8.1 Promoting scientific activities
8.1.1 Scientific events: organisation
Member of the organizing committees
Laurent Hascoët is on the organizing commitee of the EuroAD Workshops on Algorithmic Differentiation http://
8.1.2 Scientific expertise
Alain Dervieux is Scientific Director for the LEMMA company.
9 Scientific production
9.1 Major publications
- 1 articleReverse automatic differentiation for optimum design: from adjoint state assembly to gradient computationOptimization Methods and Software1852003, 615-627
- 2 inproceedings The Data-Flow Equations of Checkpointing in reverse Automatic Differentiation International Conference on Computational Science, ICCS 2006, Reading, UK 2006
- 3 articleAn optimized treatment for algorithmic differentiation of an important glaciological fixed-point problemGeoscientific Model Development952016, 27
- 4 incollectionAdjoints by Automatic DifferentiationAdvanced data assimilation for geosciencesOxford University Press2014, URL: https://hal.inria.fr/hal-01109881
- 5 article ``To Be Recorded'' Analysis in Reverse-Mode Automatic Differentiation Future Generation Computer Systems 21 8 2004
- 6 articleThe Tapenade Automatic Differentiation tool: Principles, Model, and SpecificationACM Transactions On Mathematical Software3932013, URL: http://dx.doi.org/10.1145/2450153.2450158
- 7 articleCheaper Adjoints by Reversing Address ComputationsScientific Programming1612008, 81--92
- 8 articleProgramming language features, usage patterns, and the efficiency of generated adjoint codeOptimization Methods and Software312016, 885--903
- 9 articleA Framework for Adjoint-based Shape Design and Error ControlComputational Fluid Dynamics Journal1642008, 454-464
- 10 article Algorithmic differentiation of code with multiple context-specific activities ACM Transactions on Mathematical Software 2016
9.2 Publications of the year
International journals
9.3 Cited publications
- 12 book Compilers: Principles, Techniques and Tools Addison-Wesley 1986
- 13 techreportA language and an integrated environment for program transformations3313INRIA1997, URL: http://hal.inria.fr/inria-00073376
- 14 articleReverse accumulation and implicit functionsOptimization Methods and Software941998, 307--322
- 15 articleNatural semantics on the computerProceedings, France-Japan AI and CS Symposium, ICOTAlso, Information Processing Society of Japan, Technical Memorandum PL-86-6. Also INRIA research report # 4161986, 49-89URL: http://hal.inria.fr/inria-00076140
- 16 articleAbstract InterpretationACM Computing Surveys2811996, 324-328
- 17 articleInterprocedural Array Region AnalysesInternational Journal of Parallel Programming2461996, 513--546
- 18 articleAutomatic differentiation and iterative processesOptimization Methods and Software11992, 13--21
- 19 inproceedings Adjoint methods for aeronautical design Proceedings of the ECCOMAS CFD Conference Swansea, U.K. 2001
- 20 articleReduced Gradients and Hessians from Fixed Point Iteration for State EquationsNumerical Algorithms30(2)2002, 113--139
- 21 book Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation SIAM, Other Titles in Applied Mathematics 2008
- 22 phdthesis Transformations automatiques de spécifications sémantiques: application: Un vérificateur de types incremental Université de Nice Sophia-Antipolis 1987
- 23 techreport Automatic Differentiation of Navier-Stokes computations MCS-P687-0997 Argonne National Laboratory 1997
- 24 articleInferred basal friction and surface mass balance of the Northeast Greenland Ice Stream using data assimilation of ICESat (Ice Cloud and land Elevation Satellite) surface altimetry and ISSM (Ice Sheet System Model)Cryosphere862014, 2335-2351URL: http://www.the-cryosphere.net/8/2335/2014/
- 25 articleVariational algorithms for analysis and assimilation of meteorological observations: theoretical aspectsTellus38A1986, 97-110
- 26 article Practical application to fluid flows of automatic differentiation for design problems Von Karman Lecture Series 1997
- 27 phdthesis Différentiation Automatique: application à un problème d'optimisation en météorologie université de Nice Sophia-Antipolis 1993
- 28 inproceedings Symbolic Bounds Analysis of Pointers, Array Indices, and Accessed Memory Regions Proceedings of the ACM SIGPLAN'00 Conference on Programming Language Design and Implementation ACM 2000

