Keywords
Computer Science and Digital Science
- A5.5.1. Geometrical modeling
- A5.10.1. Design
- A7.1. Algorithms
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
- A8.4. Computer Algebra
Other Research Topics and Application Domains
- B1.1.1. Structural biology
- B1.2.3. Computational neurosciences
- B2.6. Biological and medical imaging
- B3.3. Geosciences
- B5.5. Materials
- B5.6. Robotic systems
- B5.7. 3D printing
- B6.2.2. Radio technology
1 Team members, visitors, external collaborators
Research Scientists
- Olivier Devillers [Team leader, Inria, Senior Researcher, HDR]
- Sylvain Lazard [Inria, Senior Researcher, HDR]
- Guillaume Moroz [Inria, Researcher]
- Marc Pouget [Inria, Researcher]
- Monique Teillaud [Inria, Senior Researcher, HDR]
Faculty Members
- Vincent Despré [Univ de Lorraine, Associate Professor]
- Laurent Dupont [Univ de Lorraine, Associate Professor]
- Xavier Goaoc [Univ de Lorraine, Professor, HDR]
- Alba Marina Málaga Sabogal [Univ de Lorraine, Associate Professor, from Sept. 2020]
Post-Doctoral Fellows
- Benedikt Kolbe [Inria]
- Ji Won Park [Inria]
PhD Students
- Charles Duménil [Univ de Lorraine]
- Galatée Hemery Vaglica [Univ de Lorraine, until Aug. 2020]
- Nuwan Herath Mudiyanselage [Inria]
- George Krait [Univ de Lorraine, from Sept. 2020, (INRIA from Oct. 2017 to Aug. 2020)]
- Léo Valque [Univ de Lorraine, from Sept. 2020]
Interns and Apprentices
- Baptiste Brunet De La Charie [Inria, from Jun. 2020 until Sept. 2020]
- Remi Delloque [École Normale Supérieure de Lyon, from Jun. 2020 until Jul. 2020]
- Hippolyte Karakostanoglou [Univ de Lorraine, until Jun. 2020]
- Léo Valque [École Normale Supérieure de Lyon, from Jun. 2020 until Aug. 2020]
Administrative Assistants
- Isabelle Blanchard [Inria]
- Virginie Priester [CNRS]
2 Overall objectives
Starting in the eighties, the emerging computational geometry community has put a lot of effort into designing and analyzing algorithms for geometric problems. The most commonly used framework was to study the worst-case theoretical complexity of geometric problems involving linear objects (points, lines, polyhedra...) in Euclidean spaces. This so-called classical computational geometry has some known limitations:
- Objects: dealing with objects only defined by linear equations.
- Ambient space: considering only Euclidean spaces.
- Complexity: worst-case complexities often do not capture realistic behaviour.
- Dimension: complexities are often exponential in the dimension.
- Robustness: ignoring degeneracies and rounding errors.
Even if these limitations have already got some attention from the community 53, a quick look at the flagship conference SoCG 1 proceedings shows that these topics still need a big effort.
It should be stressed that, in this document, the notion of certified algorithms is to be understood with respect to robustness issues. In other words, certification does not refer to programs that are proven correct with the help of mechanical proof assistants such as Coq, but to algorithms that are proven correct on paper even in the presence of degeneracies and computer-induced numerical rounding errors.
We address several of the above limitations:
Non-linear computational geometry. Curved objects are ubiquitous in the world we live in. However, despite this ubiquity and decades of research in several communities, curved objects are far from being robustly and efficiently manipulated by geometric algorithms. Our work on, for instance, quadric intersections and certified drawing of plane curves has proven that dramatic improvements can be accomplished when the right mathematics and computer science concepts are put into motion. In this direction, many problems are fundamental and solutions have potential industrial impact in Computer Aided Design and Robotics for instance. Intersecting NURBS (Non-uniform rational basis splines) and meshing singular surfaces in a certified manner are important examples of such problems.
Non-Euclidean computational geometry. Triangulations are central geometric data structures in many areas of science and engineering. Traditionally, their study has been limited to the Euclidean setting. Needs for triangulations in non-Euclidean settings have emerged in many areas dealing with objects whose sizes range from the nuclear to the astrophysical scale, and both in academia and in industry. It has become timely to extend the traditional focus on of computational geometry and encompass non-Euclidean spaces.
Probability in computational geometry. The design of efficient algorithms is driven by the analysis of their complexity. Traditionally, worst-case input and sometimes uniform distributions are considered and many results in these settings have had a great influence on the domain. Nowadays, it is necessary to be more subtle and to prove new results in between these two extreme settings. For instance, smoothed analysis, which was introduced for the simplex algorithm and which we applied successfully to convex hulls, proves that such promising alternatives exist.
Discrete geometric structures. Many geometric algorithms work, explicitly or implicitly, over discrete structures such as graphs, hypergraphs, lattices that are induced by the geometric input data. For example, convex hulls or straight-line graph drawing are essentially based on orientation predicates, and therefore operate on the so-called order type of the input point set. Order types are a subclass of oriented matroids that remains poorly understood: for instance, we do not even know how to sample this space with reasonable bias. One of our goals is to contribute to the development of these foundations by better understanding these discrete geometric structures.
3 Research program
3.1 Non-linear computational geometry

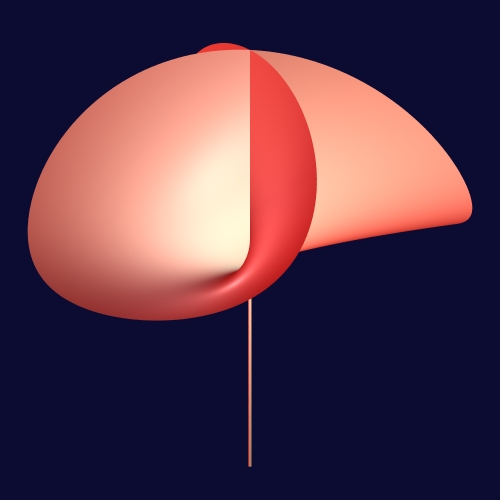
As mentioned above, curved objects are ubiquitous in real world problems and in computer science and, despite this fact, there are very few problems on curved objects that admit robust and efficient algorithmic solutions without first discretizing the curved objects into meshes. Meshing curved objects induces a loss of accuracy which is sometimes not an issue but which can also be most problematic depending on the application. In addition, discretization induces a combinatorial explosion which could cause a loss in efficiency compared to a direct solution on the curved objects (as our work on quadrics has demonstrated with flying colors 60, 61, 59, 63, 67). But it is also crucial to know that even the process of computing meshes that approximate curved objects is far from being resolved. As a matter of fact there is no algorithm capable of computing in practice meshes with certified topology of even rather simple singular 3D surfaces, due to the high constants in the theoretical complexity and the difficulty of handling degenerate cases. Part of the difficulty comes from the unintuitive fact that the structure of an algebraic object can be quite complicated, as depicted in the Whitney umbrella (see Figure 1), surface of the equation on which the origin (the “special” point of the surface) is a vertex of the arrangement induced by the surface while the singular locus is simply the whole -axis. Even in 2D, meshing an algebraic curve with the correct topology, that is in other words producing a correct drawing of the curve (without knowing where the domain of interest is), is a very difficult problem on which we have recently made important contributions 46, 47, 68.
It is thus to be understood that producing practical robust and efficient algorithmic solutions to geometric problems on curved objects is a challenge on all and even the most basic problems. The basicness and fundamentality of two problems we mentioned above on the intersection of 3D quadrics and on the drawing in a topologically certified way of plane algebraic curves show rather well that the domain is still in its infancy. And it should be stressed that these two sets of results were not anecdotal but flagship results produced during the lifetime of the Vegas team (the team preceding Gamble).
There are many problems in this theme that are expected to have high long-term impacts. Intersecting NURBS (Non-uniform rational basis splines) in a certified way is an important problem in computer-aided design and manufacturing. As hinted above, meshing objects in a certified way is important when topology matters. The 2D case, that is essentially drawing plane curves with the correct topology, is a fundamental problem with far-reaching applications in research or R&D. Notice that on such elementary problems it is often difficult to predict the reach of the applications; as an example, we were astonished by the scope of the applications of our software on 3D quadric intersection 2 which was used by researchers in, for instance, photochemistry, computer vision, statistics and mathematics.
3.2 Non-Euclidean computational geometry
Triangulations, in particular Delaunay triangulations, in the Euclidean space have been extensively studied throughout the 20th century and they are still a very active research topic. Their mathematical properties are now well understood, many algorithms to construct them have been proposed and analyzed (see the book of Aurenhammer et al.41). Some members of Gamble have been contributing to these algorithmic advances (see, e.g. 45, 77, 58, 44); they have also contributed robust and efficient triangulation packages through the state-of-the-art Computational Geometry Algorithms Library Cgal whose impact extends far beyond computational geometry. Application fields include particle physics, fluid dynamics, shape matching, image processing, geometry processing, computer graphics, computer vision, shape reconstruction, mesh generation, virtual worlds, geophysics, and medical imaging. 3
It is fair to say that little has been done on non-Euclidean spaces, in spite of the large number of questions raised by application domains. Needs for simulations or modeling in a variety of domains 4 ranging from the infinitely small (nuclear matter, nano-structures, biological data) to the infinitely large (astrophysics) have led us to consider 3D periodic Delaunay triangulations, which can be seen as Delaunay triangulations in the 3D flat torus, quotient of under the action of some group of translations 50. This work has already yielded a fruitful collaboration with astrophysicists 64, 78 and new collaborations with physicists are emerging. To the best of our knowledge, our Cgal package 49 is the only publicly available software that computes Delaunay triangulations of a 3D flat torus, in the special case where the domain is cubic. This case, although restrictive, is already useful. 5 We have also generalized this algorithm to the case of general -dimensional compact flat manifolds 51. As far as non-compact manifolds are concerned, past approaches, limited to the two-dimensional case, have stayed theoretical 69.
Interestingly, even for the simple case of triangulations on the sphere, the software packages that are currently available are far from offering satisfactory solutions in terms of robustness and efficiency 52.
Moreover, while our solution for computing triangulations in hyperbolic spaces can be considered as ultimate 42, the case of hyperbolic manifolds has hardly been explored. Hyperbolic manifolds are quotients of a hyperbolic space by some group of hyperbolic isometries. Their triangulations can be seen as hyperbolic periodic triangulations. Periodic hyperbolic triangulations and meshes appear for instance in geometric modeling 73, neuromathematics 54, or physics 74. Even the case of the Bolza surface (a surface of genus 2, whose fundamental domain is the regular octagon in the hyperbolic plane) shows mathematical difficulties 43, 66.
3.3 Probability in computational geometry
In most computational geometry papers, algorithms are analyzed in the worst-case setting. This often yields too pessimistic complexities that arise only in pathological situations that are unlikely to occur in practice. On the other hand, probabilistic geometry provides analyses with great precision 71, 72, 48, but using hypotheses with much more randomness than in most realistic situations. We are developing new algorithmic designs improving state-of-the-art performance in random settings that are not overly simplified and that can thus reflect many realistic situations.
Sixteen years ago, smooth analysis was introduced by Spielman and Teng analyzing the simplex algorithm by averaging on some noise on the data 76 (and they won the Gödel prize). In essence, this analysis smoothes the complexity around worst-case situations, thus avoiding pathological scenarios but without considering unrealistic randomness. In that sense, this method makes a bridge between full randomness and worst case situations by tuning the noise intensity. The analysis of computational geometry algorithms within this framework is still embryonic. To illustrate the difficulty of the problem, we started working in 2009 on the smooth analysis of the size of the convex hull of a point set, arguably the simplest computational geometry data structure; then, only one very rough result from 2004 existed 55 and we only obtained in 2015 breakthrough results, but still not definitive 57, 56, 62.
Another example of a problem of different flavor concerns Delaunay triangulations, which are rather ubiquitous in computational geometry. When Delaunay triangulations are computed for reconstructing meshes from point clouds coming from 3D scanners, the worst-case scenario is, again, too pessimistic and the full randomness hypothesis is clearly not adapted. Some results exist for “good samplings of generic surfaces” 40 but the big result that everybody wishes for is an analysis for random samples (without the extra assumptions hidden in the “good” sampling) of possibly non-generic surfaces.
Trade-offs between full randomness and worst case may also appear in other forms such as dependent distributions, or random distributions conditioned to be in some special configurations. Simulating these kinds of geometric distributions is currently out of reach for more than a few hundred points 65 although it has practical applications in physics or networks.
3.4 Discrete geometric structures
Our work on discrete geometric structures develops in several directions, each one probing a different type of structure. Although these objects appear unrelated at first sight, they can be tackled by the same set of probabilistic and topological tools.
A first research topic is the study of Order types. Order types are combinatorial encodings of finite (planar) point sets, recording for each triple of points the orientation (clockwise or counterclockwise) of the triangle they form. This already determines properties such as convex hulls or half-space depths, and the behaviour of algorithms based on orientation predicates. These properties for all (infinitely many) -point sets can be studied through the finitely many order types of size . Yet, this finite space is poorly understood: its estimated size leaves an exponential margin of error, no method is known to sample it without concentrating on a vanishingly small corner, the effect of pattern exclusion or VC dimension-type restrictions are unknown. These are all directions we actively investigate.
A second research topic is the study of Embedded graphs and simplicial complexes. Many topological structures can be effectively discretized, for instance combinatorial maps record homotopy classes of embedded graphs and simplicial complexes represent a large class of topological spaces. This raises many structural and algorithmic questions on these discrete structures; for example, given a closed walk in an embedded graph, can we find a cycle of the graph homotopic to that walk? (The complexity status of that problem is unknown.) Going in the other direction, some purely discrete structures can be given an associated topological space that reveals some of their properties (e.g. the Nerve theorem for intersection patterns). An open problem is for instance to obtain fractional Helly theorems for set system of bounded topological complexity.
Another research topic is that of Sparse inclusion-exclusion formulas. For any family of sets , by the principle of inclusion-exclusion we have
where is the indicator function of . This formula is universal (it applies to any family of sets) but its number of summands grows exponentially with the number of sets. When the sets are balls, the formula remains true if the summation is restricted to the regular triangulation; we proved that similar simplifications are possible whenever the Venn diagram of the is sparse. There is much room for improvements, both for general set systems and for specific geometric settings. Another interesting problem (the subject of the PhD thesis of Galatée Hemery) is to combine these simplifications with the inclusion-exclusion algorithms developed, for instance, for graph coloring.
4 Application domains
Many domains of science can benefit from the results developed by Gamble. Curves and surfaces are ubiquitous in all sciences to understand and interpret raw data as well as experimental results. Still, the non-linear problems we address are rather basic and fundamental, and it is often difficult to predict the impact of solutions in that area. The short-term industrial impact is likely to be small because, on basic problems, industries have used ad hoc solutions for decades and have thus got used to it.
The example of our work on quadric intersection is typical: even though we were fully convinced that intersecting 3D quadrics is such an elementary/fundamental problem that it ought to be useful, we were the first to be astonished by the scope of the applications of our software 6 (which was the first and still is the only one —to our knowledge— to compute robustly and efficiently the intersection of 3D quadrics) which has been used by researchers in, for instance, photochemistry, computer vision, statistics, and mathematics. Our work on certified drawing of plane (algebraic) curves falls in the same category. It seems obvious that it is widely useful to be able to draw curves correctly (recall also that part of the problem is to determine where to look in the plane) but it is quite hard to come up with specific examples of fields where this is relevant. A contrario, we know that certified meshing is critical in mechanical-design applications in robotics, which is a non-obvious application field. There, the singularities of a manipulator often have degrees higher than 10 and meshing the singular locus in a certified way is currently out of reach. As a result, researchers in robotics can only build physical prototypes for validating, or not, the approximate solutions given by non-certified numerical algorithms.
The fact that several of our pieces of software for computing non-Euclidean triangulations had already been requested by users long before they become public in Cgal is a good sign for their wide future impact. This will not come as a surprise, since most of the questions that we have been studying followed from discussions with researchers outside computer science and pure mathematics. Such researchers are either users of our algorithms and software, or we meet them in workshops. Let us only mention a few names here. Rien van de Weijgaert 64, 78 (astrophysicist, Groningen, NL) and Michael Schindler 75 (theoretical physicist, ENSPCI, CNRS, France) used our software for 3D periodic weighted triangulations. Stephen Hyde and Vanessa Robins (applied mathematics and physics at Australian National University) used our package for 3D periodic meshing. Olivier Faugeras (neuromathematics, INRIA Sophia Antipolis) had come to us and mentioned his needs for good meshes of the Bolza surface 54 before we started to study them. Such contacts are very important both to get feedback about our research and to help us choose problems that are relevant for applications. These problems are at the same time challenging from the mathematical and algorithmic points of view. Note that our research and our software are generic, i.e., we are studying fundamental geometric questions, which do not depend on any specific application. This recipe has made the sucess of the Cgal library.
Probabilistic models for geometric data are widely used to model various situations ranging from cell phone distribution to quantum mechanics. The impact of our work on probabilistic distributions is twofold. On the one hand, our studies of properties of geometric objects built on such distributions will yield a better understanding of the above phenomena and has potential impact in many scientific domains. On the other hand, our work on simulations of probabilistic distributions will be used by other teams, more maths oriented, to study these distributions.
5 Highlights of the year
5.1 Awards
Xavier Goaoc received the best paper award for his paper at the 36th International Symposium on Computational Geometry coauthored with Emo Welzl (ETH Zurich) 20.
Monique Teillaud received the best paper award at the 28th European Symposium on Algorithms (Track Engineering and Applications) for her paper Generalizing CGAL Periodic Delaunay Triangulations coauthored with Georg Osang (IST Austria) and Mael Rouxel-Labbé (Geometry Factory) 21.
5.2 Keynote talks
Monique Teillaud gave a keynote talk at the 36th European Workshop on Computational Geometry: Triangulations in CGAL - To non-Euclidean spaces and beyond! 26.
5.3 Covid'19 crisis
The major event of the year is of course the corona virus crisis. All ongoing works were slowed down by working remotely most of the time.
6 New software and platforms
6.1 New software
6.1.1 dpp
- Name: Determinantal Point Process
- Keyword: Determinantal point processes
- Functional Description: This program allows to quickly generate a set of random points in the plane according to repulsive laws. The software is based on deterministic point processes, known for their repulsive properties. In particular, the Ginibre law generates with high probability a cloud of points in the disk without clustering.
-
URL:
https://
gitlab. inria. fr/ gmoro/ point_process - Publication: hal-02984323
- Contact: Guillaume Moroz
7 New results
7.1 Non-Linear Computational Geometry
Participants: Laurent Dupont, Nuwan Herath Mudiyanselage, Hippolyte Karakostanoglou, George Krait, Sylvain Lazard, Guillaume Moroz, Marc Pouget.
7.1.1 Clustering Complex Zeros of Triangular Systems of Polynomials
This work, published in the journal of Mathematics in Computer Science, gives the first algorithm for finding a set of natural -clusters of complex zeros of a regular triangular system of polynomials within a given polybox in , for any given . Our algorithm is based on a recent near-optimal algorithm of Becker et al (2016) for clustering the complex roots of a univariate polynomial where the coefficients are represented by number oracles. Our algorithm is based on recursive subdivision. It is local, numeric, certified and handles solutions with multiplicity. Our implementation is compared to well-known homotopy solvers on various triangular systems. Our solver always gives correct answers, is often faster than the homotopy solvers that often give correct answers, and sometimes faster than the ones that give sometimes correct results 17.
In collaboration with R. Imbach and C. Yap (Courant Institute of Mathematical Sciences, New York University, USA).
7.1.2 Isolating the singularities of the plane projection of a generic space curve
Isolating the singularities of a plane curve is the first step towards computing its topology. For this, numerical methods are efficient but not certified in general. We are interested in developing certified numerical algorithms for isolating the singularities. In order to do so, we restrict our attention to the special case of plane curves that are the projections of smooth curves in higher dimensions. This type of curves appears naturally in robotics applications and scientific visualization. In this setting, we show that the singularities can be encoded by a regular square system whose solutions can be isolated with certified numerical methods. Our analysis is conditioned by assumptions that we prove to be generic using transversality theory, and we also provide a semi-algorithm to check their validity 38.
7.2 Non-Euclidean Computational Geometry
Participants: Baptiste Brunet De La Charie, Vincent Despré, Benedikt Kolbe, Alba Marina Málaga Sabogal, Monique Teillaud.
7.2.1 Flipping Geometric Triangulations on Hyperbolic Surfaces
We consider geometric triangulations of surfaces, i.e., triangulations whose edges can be realized by disjoint geodesic segments. We prove that the flip graph of geometric triangulations with fixed vertices of a flat torus or a closed hyperbolic surface is connected. We give upper bounds on the number of edge flips that are necessary to transform any geometric triangulation on such a surface into a Delaunay triangulation 3.
In collaboration with Jean-Marc Schlenker (University of Luxembourg)
7.2.2 Generalizing CGAL Periodic Delaunay Triangulations
Even though Delaunay originally introduced his famous triangulations in the case of infinite point sets with translational periodicity, a software that computes such triangulations in the general case is not yet available, to the best of our knowledge. Combining and generalizing previous work, we present a practical algorithm for computing such triangulations. The algorithm has been implemented and experiments show that its performance is as good as the one of the CGAL package, which is restricted to cubic periodicity 21.
In collaboration with Georg Osang (IST Austria) and Mael Rouxel-Labbé (Geometry Factory).
7.2.3 Delaunay triangulations of generalized Bolza surfaces
Let us consider a regular octagon in the Poincaré disk that is centered at the origin. The hyperbolic isometries identifying its opposite edges pairwise generate a group. The Bolza surface can be seen as the quotient of the hyperbolic plane under the action this group. We consider generalized Bolza surfaces , where the octagon is replaced by the regular 4g-gon, leading to a genus surface. We propose an extension of Bowyer's algorithm to these surfaces. In particular, we compute the value of the systole of ; we also propose algorithms computing sets of points on whose Delaunay triangulation is a simplicial complex 34.
In collaboration with Matthijs Ebbens and Gert Vegter (Bernoulli Institute for Mathematics and Computer Science and Artificial Intelligence, University of Groningen).
7.2.4 Half-minimizers and Delaunay triangulations on closed hyperbolic surfaces
Given a finite point cloud in a Dirichlet fundamental domain with respect to a fundamental group of a closed hyperbolic surface , we derive an explicit way to construct a set of copies of that accounts for all points incident to points of in the Delaunay triangulation of . We also compute precise bounds on the size of this set that only depend on the genus of and are thus independent of the hyperbolic metric under consideration. The results in this paper lay the foundations for a practical algorithm to compute Delaunay triangulations on an arbitrary hyperbolic surface, akin to existing implementations for periodic sets of points in Euclidean space 32.
7.2.5 Testing Balanced Splitting Cycles in Complete Triangulations
Let be a triangulation of an orientable surface of genus . A cycle of is splitting if it cuts into two noncontractible parts and , with respective genus . The splitting cycle is called balanced if . The complexity of computing a balanced splitting cycle in a given triangulation is open, but seems difficult even for complete triangulations. Our main result in this paper is to show that one can rule out in polynomial time the existence of a balanced splitting cycle when the triangulation is -far to have one. Implementing this algorithm, we show that large Ringel and Youngs triangulations (for instance on 22.363 vertices) have no balanced splitting cycle, the only limitation being the size of the input rather than the computation time. 23.
In collaboration with Michaël Rao and Stéphan Thomassé (LIP)
7.2.6 Enumerating tilings of triply-periodic minimal surfaces with rotational symmetries
We present a technique for the enumeration of all isotopically distinct ways of tiling, with disks, a hyperbolic surface of finite genus, possibly nonorientable and with punctures and boundary. This provides a generalization of the enumeration of Delaney-Dress combinatorial tiling theory on the basis of isotopic tiling theory. To accomplish this, we derive representations of the mapping class group of the orbifold associated to the symmetry group of the tiling under consideration as a set of algebraic operations on certain generators of the symmetry group. We derive explicit descriptions of certain subgroups of mapping class groups and of tilings as embedded graphs on orbifolds. We further use this explicit description to present an algorithm that we illustrate by producing an array of examples of isotopically distinct tilings of the hyperbolic plane with symmetries generated by rotations that are commensurate with the prominent Primitive, Diamond and Gyroid triply-periodic minimal surfaces, outlining how the approach yields an unambiguous enumeration. We also present the corresponding 3-periodic graphs on these surfaces 24.
In collaboration with Myfanwy Evans (University of Potsdam)
7.2.7 Isotopic tiling theory for hyperbolic surfaces
In this paper, we develop the mathematical tools needed to explore isotopy classes of tilings on hyperbolic surfaces of finite genus, possibly non-orientable, with boundary, and punctured. More specifically, we generalize results on Delaney-Dress combinatorial tiling theory using an extension of mapping class groups to orbifolds, in turn using this to study tilings of covering spaces of orbifolds. Moreover, we study finite subgroups of these mapping class groups. Our results can be used to extend the Delaney-Dress combinatorial encoding of a tiling to yield a finite symbol encoding the complexity of an isotopy class of tilings. The results of this paper provide the basis for a complete and un-ambiguous enumeration of isotopically distinct tilings of hyperbolic surfaces 18.
In collaboration with Myfanwy Evans (University of Potsdam).
7.2.8 Towards a combinatorial algorithm for the enumeration of isotopy classes of tilings on hyperbolic surfaces
Based on the mathematical theory of isotopic tilings on hyperbolic surfaces and mapping class groups, we present the, to the best of our knowledge, first algorithms for the enumeration of isotopy classes of tilings by compact disks with a given symmetry group on hyperbolic surfaces, which is moreover combinatorial in nature. This enumeration is relevant for crystallography and material science. Using the theory of automatic groups, we give some results on the computational tractability of the presented algorithm. We also extend data structures for combinatorial classes of tilings to isotopy classes and give an implementation of the proposed algorithm for certain classes of tilings and illustrate the enumeration with examples 37.
7.2.9 Tile-transitive tilings of the Euclidean and hyperbolic planes by ribbons
We present a method to enumerate tile-transitive crystallographic tilings of the Euclidean and hyperbolic planes by unbounded ribbon tiles up to equivariant equivalence. The hyperbolic case is relevant to self-assembly of branched polymers. This is achieved by combining and extending known methods for enumerating crystallographic disk-like tilings. We obtain a natural way of describing all possible stabiliser subgroups of tile-transitive tilings using a topological viewpoint of the tile edges as a graph embedded in an orbifold, and a group theoretical one derived from the structure of fundamental domains for discrete groups of planar isometries 36.
In collaboration with Vanessa Robins (Australian National University).
7.3 Probabilistic Analysis of Geometric Data Structures and Algorithms
Participants: Rémi Delloque, Olivier Devillers, Charles Duménil, Xavier Goaoc, Guillaume Moroz.
7.3.1 Expected Complexity of Routing in Theta-6 and Half-Theta-6 Graphs
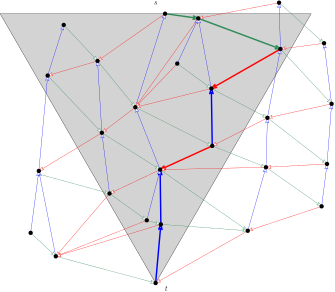
We study online routing algorithms on the 6-graph and the half-6-graph (which is equivalent to a variant of the Delaunay triangulation). Given a source vertex s and a target vertex t in the 6-graph (resp. half-6-graph), there exists a deterministic online routing algorithm that finds a path from s to t whose length is at most 2 st (resp. 2.89 st) which is optimal in the worst case [Bose et al., SIAM J. on Computing, 44(6)]. We propose alternative, slightly simpler routing algorithms that are optimal in the worst case and for which we provide an analysis of the average routing ratio for the 6-graph and half-6-graph defined on a Poisson point process. For the 6-graph, our online routing algorithm has an expected routing ratio of 1.161 (when s and t random) and a maximum expected routing ratio of 1.22 (maximum for fixed s and t where all other points are random), much better than the worst-case routing ratio of 2. For the half-6-graph, our memoryless online routing algorithm has an expected routing ratio of 1.43 and a maximum expected routing ratio of 1.58 (see Figure 3). Our online routing algorithm that uses a constant amount of additional memory has an expected routing ratio of 1.34 and a maximum expected routing ratio of 1.40. The additional memory is only used to remember the coordinates of the starting point of the route. Both of these algorithms have an expected routing ratio that is much better than their worst-case routing ratio of 2.89 13.
In collaboration with Prosenjit Bose (University Carleton) and Jean-Lou De Carufel (University of Ottawa)
7.3.2 Random polytopes and the wet part for arbitrary probability distributions
We examine how the measure and the number of vertices of the convex hull of a random sample of points from an arbitrary probability measure in relates to the wet part of that measure. This extends classical results for the uniform distribution from a convex set [Bárány and Larman 1988]. The lower bound of Bárány and Larman continues to hold in the general setting, but the upper bound must be relaxed by a factor of . We show by an example that this is tight 11.
In collaboration with Imre Barany (Rényi Institute of Mathematics) Matthieu Fradelizi (Laboratoire d'Analyse et de Mathématiques Appliquées) Alfredo Hubard (Laboratoire d'Informatique Gaspard-Monge) Günter Rote (Institut für Informatik, Berlin)
7.3.3 Optimal transport between determinantal point processes and application to fast simulation
We analyze several optimal transportation problems between determinantal point processes. We show how to estimate some of the distances between distributions of DPP they induce. We then apply these results to evaluate the accuracy of a new and fast DPP simulation algorithm. We can now simulate in a reasonable amount of time more than ten thousand points 31 (see also Section 6).
In collaboration with Laurent Decreusefond (Laboratoire Traitement et Communication de l'Information)
7.4 Discrete Geometric structures
Participants: Xavier Goaoc, Galatée Hemery Vaglica.
7.4.1 Convex hulls of random order types
We establish the following two main results on order types of points in general position in the plane (realizable simple planar order types, realizable uniform acyclic oriented matroids of rank 3):
- The number of extreme points in an -point order type, chosen uniformly at random from all such order types, is on average . For labeled order types, this number has average and variance at most 3.
- The (labeled) order types read off a set of n points sampled independently from the uniform measure on a convex planar domain, smooth or polygonal, or from a Gaussian distribution are concentrated, i.e. such sampling typically encounters only a vanishingly small fraction of all order types of the given size.
Result (a) generalizes to arbitrary dimension d for labeled order types with the average number of extreme points and constant variance. We also discuss to what extent our methods generalize to the abstract setting of uniform acyclic oriented matroids. Moreover, our methods allow to show the following relative of the Erdős-Szekeres theorem: for any fixed k, as , a proportion of the n-point simple order types contain a triangle enclosing a convex k-chain over an edge. For the unlabeled case in (a), we prove that for any antipodal, finite subset of the 2-dimensional sphere, the group of orientation preserving bijections is cyclic, dihedral or one of A4, S4 or A5 (and each case is possible). These are the finite subgroups of SO(3) and our proof follows the lines of their characterization by Felix Klein 6.
In collaboration with Emo Welzl (ETH Zürich)
7.4.2 Convexité combinatoire
This chapter (in French) offers an introduction to combinatorial convexity, its algorithmic applications and its extensions in topological combinatorics 28.
7.5 Classical Computational Geometry
Participants: Olivier Devillers, Sylvain Lazard, Ji-won Park, Monique Teillaud, Léo Valque.
7.5.1 Variable-width contouring for additive manufacturing
In most layered additive manufacturing processes, a tool solidifies or deposits material while following pre-planned trajectories to form solid beads. Many interesting problems arise in this context, among which one concerns the planning of trajectories for filling a planar shape as densely as possible. This is the problem we tackle in the present paper. Recent works have shown that allowing the bead width to vary along the trajectories helps increase the filling density. We present a novel technique that, given a deposition width range, constructs a set of closed beads whose width varies within the prescribed range and fills the input shape. The technique outperforms the state of the art in important metrics: filling density (while still guaranteeing the absence of bead overlap) and smoothness of trajectories. We give a detailed geometric description of our algorithm, explore its behavior on example inputs and provide a statistical comparison with the state of the art. We show that it is possible to obtain high quality fabricated layers on commodity FDM printers 16.
In collaboration with Samuel Hornus, Jonàs Martinez, Sylvain Lefebvre (project-team MFX ), Marc Glisse (project-team DataShape ), and Tim Kuipers (Ultimaker).
7.5.2 Covering families of triangles
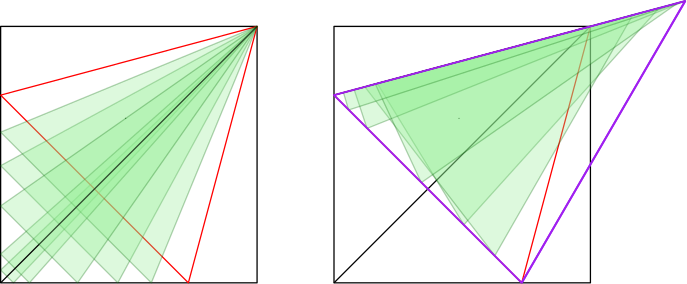
A cover for a family of sets in the plane is a set into which every set in can be isometrically moved. We are interested in the convex cover of smallest area for a given family of triangles. Park and Cheong 25 conjectured that any family of triangles of bounded diameter has a smallest convex cover that is itself a triangle. The conjecture is equivalent to the claim that for every convex set there is a triangle whose area is not larger than the area of , such that covers the family of triangles contained in . We prove this claim for the case where a diameter of lies on its boundary. We also give a complete characterization of the smallest convex cover for the family of triangles contained in a half-disk, and for the family of triangles contained in a square (see Figure 4). In both cases, this cover is a triangle 30.
In collaboration with Otfried Cheong (KAIST) and Marc Glisse (project-team DataShape ).
7.5.3 CovBundled Crossings Revisited
An effective way to reduce clutter in a graph drawing that has (many) crossings is to group edges that travel in parallel into bundles. Each edge can participate in many such bundles. Any crossing in this bundled graph occurs between two bundles, i.e., as a bundled crossing. We consider the problem of bundled crossing minimization: A graph is given and the goal is to find a bundled drawing with at most bundled crossings. We show that the problem is NP-hard when we require a simple drawing. Our main result is an FPT algorithm (in ) for simple circular layouts where vertices must be placed on a circle and edges must be drawn inside the circle. These results make use of the connection between bundled crossings and graph genus. We also consider bundling crossings in a given drawing, in particular for storyline visualizations 14.
In collaboration with Thomas van Dijk, Myroslav Kryven, Alexander Wolff (Universität Würzburg), Steven Chaplick (Maastricht and Würzburg universities), and Alexander Ravsky (Pidstryhach Institute for Applied Problems of Mechanics and Mathematics).
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
-
Company: Waterloo Maple Inc.
Duration: 2 years
Participants: Gamble and Ouragan Inria teams
Abstract: A two-years licence and cooperation agreement was signed on April 1st, 2018 between Waterloo Maple Inc., Ontario, Canada (represented by Laurent Bernardin, its Executive Vice President Products and Solutions) and Inria. On the Inria side, this contract involves the teams Gamble and Ouragan (Paris), and it is coordinated by Fabrice Rouillier (Ouragan).
F. Rouillier and Gamble are the developers of the Isotop software for the computation of topology of curves. The transfer of a version of Isotop to Waterloo Maple Inc. should be done on the long run.
-
Company: GeometryFactory
Duration: permanent
Participants: Inria and GeometryFactory
Abstract: Cgal packages developed in Gamble are commercialized by GeometryFactory.
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Inria Associate Team not involved in an Inria International Lab
TRIP
- Title: Triangulation and Random Incremental Paths
- Duration: 2018 - 2020
- Coordinator: Olivier Devillers
- Partner: CGLab, Carleton University (Canada)
- Inria contact: Olivier Devillers
-
Summary:
The two teams are specialists of the Delaunay triangulation with a focus on computation algorithms on the French side and routing on the Canadian side. The aim was to attack several problems where the two teams are complementary:
- Stretch factor of the Delaunay triangulation in 3D.
- Probabilistic analysis of Theta-graphs and Yao-graphs.
- Smoothed analysis of a walk in Delaunay triangulation.
- Walking in/on surfaces.
- Routing un non-Euclidean spaces.
- Activity of the year: No travels because of Covid'19 crisis. Work about Theta-graphs continued remotely and has been published 13.
- Project website: members.loria.fr/Olivier.Devillers/trip/.
9.1.2 Participation in other international programs
ANR SoS
Project title: Structures on Surfaces
Duration: 4 years + Covid'19 extension
Starting Date: April 1st, 2018
Coordinator: Monique Teillaud
Participants:
- Gamble project-team, Inria.
- LIGM (Laboratoire d'Informatique Gaspard Monge), Université Paris-Est Marne-la-Vallée. Local Coordinator: Éric Colin de Verdière.
- RMATH (Mathematics Research Unit), University of Luxembourg. National Coordinator: Hugo Parlier
SoS is co-funded by ANR (ANR-17-CE40-0033) and FNR (INTER/ANR/16/11554412/SoS) as a PRCI (Projet de Recherche Collaborative Internationale).
The central theme of this project is the study of geometric and combinatorial structures related to surfaces and their moduli. Even though they work on common themes, there is a real gap between communities working in geometric topology and computational geometry and SoS aims to create a long-lasting bridge between them. Beyond a common interest, techniques from both ends are relevant and the potential gain in perspective from long-term collaborations is truly thrilling.
In particular, SoS aims to extend the scope of computational geometry, a field at the interface between mathematics and computer science that develops algorithms for geometric problems, to a variety of unexplored contexts. During the last two decades, research in computational geometry has gained wide impact through CGAL, the Computational Geometry Algorithms Library. In parallel, the needs for non-Euclidean geometries are arising, e.g., in geometric modeling, neuromathematics, or physics. Our goal is to develop computational geometry for some of these non-Euclidean spaces and make these developments readily available for users in academy and industry.
To reach this aim, SoS will follow an interdisciplinary approach, gathering researchers whose expertise cover a large range of mathematics, algorithms and software. A mathematical study of the objects considered will be performed, together with the design of algorithms when applicable. Algorithms will be analyzed both in theory and in practice after prototype implementations, which will be improved whenever it makes sense to target longer-term integration into CGAL.
Our main objects of study will be Delaunay triangulations and circle patterns on surfaces, polyhedral geometry, and systems of disjoint curves and graphs on surfaces.
Project website: members.loria.fr/Monique.Teillaud/collab/SoS/.
9.2 International research visitors
The Covid'19 crisis has forbidden travelling since mid-March.
9.2.1 Visits of international scientists
Otfried Cheong visited Gamble for one week in March.
9.2.2 Visits to international teams
Monique Teillaud visited Gert Vegter's group, Bernoulli Institute for Mathematics, Computer Science and Artificial Intelligence, University of Groningen (two weeks in February).
9.3 National initiatives
9.3.1 ANR PRC
ANR Aspag
Project title: Analyse et Simulation Probabilistes d'Algorithmes Géométriques
Duration: 4 years + Covid'19 extension
Starting date: January 1st, 2018
Coordinator: Olivier Devillers
Participants:
- Gamble project-team, Inria.
- Labri (Laboratoire Bordelais de Recherche en Informatique), Université de Bordeaux. Local Coordinator: Philippe Duchon.
- Laboratoire de Mathématiques Raphaël Salem, Université de Rouen. Local Coordinator: Pierre Calka.
- LAMA (Laboratoire d'Analyse et de Mathématiques Appliquées), Université Paris-Est Marne-la-Vallée. Local Coordinator: Matthieu Fradelizi
Abstract: The ASPAG projet is funded by ANR under number ANR-17-CE40-0017 .
The analysis and processing of geometric data has become routine in a variety of human activities ranging from computer-aided design in manufacturing to the tracking of animal trajectories in ecology or geographic information systems in GPS navigation devices. Geometric algorithms and probabilistic geometric models are crucial to the treatment of all this geometric data, yet the current available knowledge is in various ways much too limited: many models are far from matching real data, and the analyses are not always relevant in practical contexts. One of the reasons for this state of affairs is that the breadth of expertise required is spread among different scientific communities (computational geometry, analysis of algorithms and stochastic geometry) that historically had very little interaction. The Aspag project brings together experts of these communities to address the problem of geometric data. We will more specifically work on the following three interdependent directions.
(1) Dependent point sets: One of the main issues of most models is the core assumption that the data points are independent and follow the same underlying distribution. Although this may be relevant in some contexts, the independence assumption is too strong for many applications.
(2) Simulation of geometric structures: The phenomena studied in (1) involve intricate random geometric structures subject to new models or constraints. A natural first step would be to build up our understanding and identify plausible conjectures through simulation. Perhaps surprisingly, the tools for an effective simulation of such complex geometric systems still need to be developed.
(3) Understanding geometric algorithms: the analysis of algorithms is an essential step in assessing the strengths and weaknesses of algorithmic principles, and is crucial to guide the choices made when designing a complex data processing pipeline. Any analysis must strike a balance between realism and tractability; the current analyses of many geometric algorithms are notoriously unrealistic. Aside from the purely scientific objectives, one of the main goals of Aspag is to bring the communities closer in the long term. As a consequence, the funding of the project is crucial to ensure that the members of the consortium will be able to interact on a very regular basis, a necessary condition for significant progress on the above challenges.
Project website: members.loria.fr/Olivier.Devillers/aspag/.
ANR MinMax
Project title: MIN-MAX
Duration: 4 years
Starting date: 2019
Coordinator: Stéphane Sabourau (Université Paris-Est Créteil)
Participants:
- Université Paris Est Créteil, Laboratoire d'Analyse et de Mathématiques Appliquées (LAMA). Local coordinator: Stéphane Sabourau
- Université de Tours, Institut Denis Poisson. Local coordinator: Laurent Mazet. This node includes two participants from Nancy, Benoît Daniel (IECL) and Xavier Goaoc (Loria, Gamble).
Abstract: The MinMax projet is funded by ANR under number ANR-19-CE40-0014
This collaborative research project aims to bring together researchers from various areas – namely, geometry and topology, minimal surface theory and geometric analysis, and computational geometry and algorithms – to work on a precise theme around min-max constructions and waist estimates.
Project website: bezout.univ-paris-est.fr/anr-project-minmax-accepted/
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
Member of the organizing committees
- Xavier Goaoc co-organized with K. Adiprasito and G. Rote the Oberwolfach Discrete geometry workshop 2020 (1 week hybrid workshop, on invitation).
- Sylvain Lazard organized with S. Whitesides (Victoria University) the 19th Workshop on Computational Geometry at the Bellairs Research Institute of McGill University in February (1 week workshop on invitation).
- Monique Teillaud was a member of the scientific board of the workshop Lost in Translation Surfaces, January 29-31 2020, University of Luxembourg.
10.1.2 Scientific events: selection
Member of the conference program committees
- Guillaume Moroz was a member of the Maple 2020 Conference Program Comittee.
Reviewer
All members of the team are regular reviewers for the conferences of our field, namely Symposium on Computational Geometry (SoCG), European Symposium on Algorithms (ESA), Symposium on Discrete Algorithms (SODA), International Symposium on Symbolic and Algebraic Computation (ISSAC), etc.
10.1.3 Journal
Member of the editorial boards
Monique Teillaud is a managing editor of JoCG, Journal of Computational Geometry. She was a member of the editorial board of IJCGA, International Journal of Computational Geometry and Applications, until December 31st, 2020.
Reviewer - reviewing activities
All members of the team are regular reviewers for the journals of our field, namely Discrete and Computational Geometry (DCG), Journal of Computational Geometry (JoCG), International Journal on Computational Geometry and Applications (IJCGA), Journal on Symbolic Computations (JSC), SIAM Journal on Computing (SICOMP), Mathematics in Computer Science (MCS), etc.
10.1.4 Software Project
Member of the Editorial Boards
Marc Pouget and Monique Teillaud are members of the CGAL editorial board.
10.1.5 Invited talks
- Monique Teillaud gave a keynote talk at the 36th European Workshop on Computational Geometry: Triangulations in CGAL - To non-Euclidean spaces and beyond! 26.
- Xavier Goaoc gave 3h of lectures at the École jeunes chercheurs en informatique mathématique 28.
- Besides these two invited talks, Benedikt Kolbe gave a talk at the workshop on invitation: Structure of Materials.
10.1.6 Leadership within the scientific community
Steering Committees
Monique Teillaud was chairing the Steering Committee of Computational Geometry until June 2020.
Websites
M. Teillaud is maintaining the Computational Geometry Web Pages www.computational-geometry.org/, hosted by Inria Nancy - Grand Est. This site offers general interest information for the computational geometry community, in particular the Web proceedings of the Video Review of Computational Geometry, part of the Annual/International Symposium on Computational Geometry (SoCG).
10.1.7 Scientific expertise
Members of Gamble are occasionally reviewing proposals or applications for foreign research agencies (e.g., FWF, NWO, NSERC, ISF, etc.) or foreign universities. We are not giving more details here to preserve anonymity.
10.1.8 Research administration
Team members are involved in various committees managing the scientific life of the lab or at a national level.
Local:
- Pôle AM2I de l'UL (O. Devillers),
- INRIA Comission Information et Édition Scientifique (L.Dupont),
- Fédération Charles Hermite (X. Goaoc),
- LORIA Conseil scientifique (S. Lazard),
- LORIA department chair (S. Lazard),
- UL Associate Prof hiring committee (chair, S. Lazard),
- INRIA PhD and postdoc hiring committee (chair, S. Lazard),
- École doctorale IAEM (S. Lazard),
- INRIA Comité des utilisateurs des moyens informatiques (chair, G. Moroz),
- INRIA Commission de développement technologique (G. Moroz),
- CLHSCT (G. Moroz),
- INRIA Comité de centre (M. Pouget),
- Agos (M. Pouget),
- INRIA Scientific Advisor for Technologic Development (M. Teillaud),
- LORIA Conseil de laboratoire (M. Teillaud).
National:
- INRIA Mission Jeunes Chercheurs (chair, S. Lazard),
- INRIA BIL work group (M. Teillaud).
10.2 Teaching - Supervision - Juries
10.2.1 Committees
- V. Despré: Head of the Engineer diploma speciality SIR, Systèmes d'Information et Réseaux, Polytech Nancy, Université de Lorraine.
- L. Dupont is the secretary of Commission Pédagogique Nationale Carrières Sociales / Information-Communication / Métiers du Multimédia et de l'Internet (2017-2022).
- L. Dupont represents the Commission Pédagogique Nationale Carrières Sociales / Information-Communication / Métiers du Multimédia et de l'Internet at the national working group on D.U.T/B.U.T reform
- L. Dupont: Co-creator and Head of the Bachelor diploma Licence Professionnelle Animateur, Facilitateur de Tiers-lieux Eco-Responsables, Université de Lorraine.
- L. Dupont: Co-creator of the Bachelor diploma Licence Professionnelle Fabrication additive : Conception, design et réalisation, Université de Lorraine.
- L.Dupont: Responsible of fablab "Charlylab" of I.U.T. Nancy-Charlemagne
10.2.2 Teaching
- Licence: Vincent Despré, Programmation orientée objet, 62h, L2, Polytech Nancy, France.
- Licence: Vincent Despré, Algorithmique, 108h, L3, Polytech Nancy, France.
- Master: Vincent Despré, Programmation réseau, 88h, M1, Polytech Nancy, France.
- Master: Vincent Despré, Architecture Java EE, 50h, M1, Polytech Nancy, France.
- Master: Olivier Devillers, Modèles d'environnements, planification de trajectoires, 18h, M2 AVR, Université de Lorraine (web).
- Licence: Charles Duménil, Algorithmique et programmation avancée, 10h, M2, FST, Université de Lorraine, France.
- Licence: Charles Duménil, Découverte de l'informatique, 104h, L1, Polytech Nancy, Université de Lorraine, France.
- Licence: Laurent Dupont, Web development, 35h, L2, Université de Lorraine, France.
- Licence: Laurent Dupont, Web development, 150h, L2, Université de Lorraine, France.
- Licence: Laurent Dupont Web development and Social networks 100h L3, Université de Lorraine, France.
- Licence : Xavier Goaoc, Operation research, 16 HETD, L3, École des Mines de Nancy, France.
- Master: Xavier Goaoc, Algorithms, 32 HETD, M1, École des Mines de Nancy, France.
- Master: Xavier Goaoc, Computer architecture, 32 HETD, M1, École des Mines de Nancy Nancy, France.
- Master: Xavier Goaoc, machine learning, 12 HETD, M1, École des Mines de Nancy, France.
- Master: Xavier Goaoc, Introduction to blockchains, 42 HETD, M1, École des Mines de Nancy + Polytech Nancy, France.
- Licence: Galatée Hemery, Programmation, 64 HETD, L3, École des Mines de Nancy, France.
- Licence: Benedikt Kolbe, Programmation orientée objet, 22 HETD, L2, Polytech Nancy.
- Licence: George Krait, Python, 24h, L3, Polytech Nancy, Université de Lorraine, France.
- Licence: George Krait, Bases de données, 64h, L3, Polytech Nancy, Université de Lorraine, France.
- Master: Marc Pouget, Introduction to computational geometry, 10.5h, M2, École Nationale Supérieure de Géologie, France.
10.2.3 Supervision
- PhD: Sény Diatta, Topologie de courbes algébriques planes et projection de surfaces analytiques réelles, defended in January 2020, supervised by Daouda Niang Diatta, Marie-Françoise Roy and Guillaume Moroz 29.
- PhD in progress: Charles Duménil, Probabilistic analysis of geometric structures, started in Oct. 2016, supervised by Olivier Devillers.
- PhD in progress: George Krait, Topology of singular curves and surfaces, applications to visualization and robotics, started in Nov. 2017, supervised by Sylvain Lazard, Guillaume Moroz and Marc Pouget.
- PhD in progress: Galatée Hemery, Algorithmic and geometric aspects of inclusion-exclusion, started in Sep. 2018, abandoned Aug. 2020, supervised by Xavier Goaoc and Éric Colin de Verdière (UPEM).
- PhD in progress: Nuwan Herath, Fast algorithm for the visualization of surfaces, started in Nov. 2019, supervised by Sylvain Lazard, Guillaume Moroz and Marc Pouget.
- PhD in progress: Léo Valque, Rounding 3D meshes, started in Sept. 2020, supervised by Sylvain Lazard.
10.2.4 Juries
- M. Teillaud was a reviewer and a member of the PhD committee of Martin Wilhelm (Otto-von-Guericke Universität Magdeburg). She chaired the PhD committee of Simon Masson (Université de Lorraine).
- X. Goaoc was a reviewer and committee member of the habilitation thesis of Arnau Padrol (Sorbonne Université, Paris).
10.3 Popularization
10.3.1 Education
G. Moroz is a member of the Mathematics Olympiads committee of the Nancy-Metz academy.
10.3.2 Interventions
L. Dupont participated to "Day of Science", in Oct. 2020 at "Mines of Neuves-Maisons" : Virtual Reality presentation.
11 Scientific production
11.1 Major publications
- 1 inproceedings Improved Routing on the Delaunay Triangulation ESA 2018 - 26th Annual European Symposium on Algorithms Helsinki, Finland 2018
- 3 inproceedings Flipping Geometric Triangulations on Hyperbolic Surfaces SoCG 2020 - 36th International Symposium on Computational Geometry Zurich, Switzerland 2020
- 4 article Rounding meshes in 3D Discrete and Computational Geometry April 2020
- 5 article Shellability is NP-complete Journal of the ACM (JACM) 66 3 2019
- 6 inproceedingsConvex Hulls of Random Order TypesSoCG 2020 - 36th International Symposium on Computational Geometry16436th International Symposium on Computational Geometry (SoCG 2020)Best paper awardZürich / Virtual, Switzerland2020, 49:1--49:15
- 7 articleReliable Location with Respect to the Projection of a Smooth Space CurveReliable Computing262018, 13-55
- 8 inproceedingsImplementing Delaunay Triangulations of the Bolza Surface33rd International Symposium on Computational Geometry (SoCG 2017)Brisbane, AustraliaJuly 2017, 44:1--44:15
- 9 articleWorkspace, Joint space and Singularities of a family of Delta-Like RobotMechanism and Machine Theory127September 2018, 73-95
- 10 articleBivariate triangular decompositions in the presence of asymptotesJournal of Symbolic Computation822017, 123--133
11.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Scientific book chapters
Doctoral dissertations and habilitation theses
Reports & preprints
11.3 Cited publications
- 40 inproceedingsComplexity of the Delaunay triangulation of points on surfaces: the smooth caseProceedings of the 19th Annual Symposium on Computational Geometry2003, 201--210URL: http://dl.acm.org/citation.cfm?id=777823
- 41 bookVoronoi diagrams and Delaunay triangulationsWorld Scientific2013, URL: http://www.worldscientific.com/worldscibooks/10.1142/8685
- 42 articleHyperbolic Delaunay complexes and Voronoi diagrams made practicalJournal of Computational Geometry52014, 56--85
- 43 inproceedingsDelaunay triangulations on orientable surfaces of low genusProceedings of the 32nd International Symposium on Computational Geometry2016, 20:1--20:15
- 44 inproceedingsIncremental construction of the Delaunay graph in medium dimensionProceedings of the 25th Annual Symposium on Computational Geometry2009, 208--216
- 45 articleApplications of random sampling to on-line algorithms in computational geometryDiscrete and Computational Geometry81992, 51--71
- 46 techreport Improved algorithms for solving bivariate systems via Rational Univariate Representations INRIA February 2015
- 47 articleSeparating linear forms and Rational Univariate Representations of bivariate systemsJournal of Symbolic Computation68May 2015, 84-119
- 48 phdthesis Tessellations, convex hulls and Boolean model: some properties and connections Université René Descartes - Paris V 2009
- 49 incollection3D Periodic TriangulationsCGAL User and Reference Manual3.5CGAL Editorial Board2009, URL: http://doc.cgal.org/latest/Manual/packages.html#PkgPeriodic3Triangulation3Summary
- 50 inproceedingsComputing 3D Periodic TriangulationsProceedings of the 17th European Symposium on Algorithms5757Lecture Notes in Computer Science2009, 59--70
-
51
inproceedingsDelaunay Triangulations of Point Sets in Closed Euclidean
-Manifolds'Proceedings of the 27th Annual Symposium on Computational Geometry2011, 274--282 - 52 inproceedingsRobust and Efficient Delaunay Triangulations of Points on or Close to a SphereProceedings of the 9th International Symposium on Experimental Algorithms6049Lecture Notes in Computer Science2010, 462--473
- 53 incollectionApplication challenges to computational geometry: CG impact task force reportAdvances in Discrete and Computational Geometry223Contemporary MathematicsProvidenceAmerican Mathematical Society1999, 407--463
- 54 articleBifurcation of hyperbolic planformsJournal of Nonlinear Science212011, 465--498URL: http://link.springer.com/article/10.1007/s00332-010-9089-3
- 55 inproceedingsExtreme points under random noiseProceedings of the 12th European Symposium on Algorithms2004, 264--274URL: http://dx.doi.org/10.1007/978-3-540-30140-0_25
- 56 inproceedingsComplexity analysis of random geometric structures made simplerProceedings of the 29th Annual Symposium on Computational GeometryJune 2013, 167-175
- 57 inproceedings On the smoothed complexity of convex hulls Proceedings of the 31st International Symposium on Computational Geometry Lipics 2015
- 58 articleThe Delaunay hierarchyInternational Journal of Foundations of Computer Science132002, 163-180
- 59 articleNear-Optimal Parameterization of the Intersection of Quadrics: III. Parameterizing Singular IntersectionsJournal of Symbolic Computation4332008, 216--232
- 60 articleNear-optimal parameterization of the intersection of quadrics: I. The generic algorithmJournal of Symbolic Computation4332008, 168--191
- 61 articleNear-optimal parameterization of the intersection of quadrics: II. A classification of pencilsJournal of Symbolic Computation4332008, 192--215
- 62 articleSilhouette of a random polytopeJournal of Computational Geometry712016, 14
- 63 articleA complete, exact and efficient implementation for computing the edge-adjacency graph of an arrangement of quadricsJournal of Symbolic Computation4642011, 467-494
- 64 inproceedingsVideo: the sticky geometry of the cosmic webProceedings of the 28th Annual Symposium on Computational Geometry2012, 421--422
- 65 articleDeterminantal processes and independenceProbab. Surv.32006, 206-229
- 66 inproceedingsImplementing Delaunay triangulations of the Bolza surfaceProceedings of the Thirty-third International Symposium on Computational Geometry2017, 44:1--44:15
- 67 articleIntersecting quadrics: an efficient and exact implementationComputational Geometry: Theory and Applications351-22006, 74--99
- 68 techreport Bivariate triangular decompositions in the presence of ssymptotes INRIA September 2015
- 69 articleVoronoi diagrams on orbifoldsComputational Geometry: Therory and Applications81997, 219--230
- 70 misc Periodic meshes for the CGAL library Research Note Londres, United Kingdom 2014
-
71
articleÜber die konvexe Hülle von
zufällig gerwähten Punkten I'Z. Wahrsch. Verw. Gebiete21963, 75--84URL: http://dx.doi.org/10.1007/BF00535300 -
72
articleÜber die konvexe Hülle von
zufällig gerwähten Punkten II'Z. Wahrsch. Verw. Gebiete31964, 138--147URL: http://dx.doi.org/10.1007/BF00535973 - 73 inproceedingsHyperbolic centroidal Voronoi tessellationProceedings of the ACM Symposium on Solid and Physical Modeling2010, 117--126URL: http://dx.doi.org/10.1145/1839778.1839795
- 74 articleTuning the fragility of a glassforming liquid by curving spacePhysical Review Letters1012008, 155701(1)--155701(4)URL: http://dx.doi.org/10.1103/PhysRevLett.101.155701
- 75 articleCavity averages for hard spheres in the presence of polydispersity and incomplete dataThe European Physical Journal E2015, 38--97URL: http://dx.doi.org/10.1103/PhysRevE.88.022315
- 76 articleSmoothed analysis: why the simplex algorithm usually takes polynomial timeJournal of the ACM5132004, 385--463URL: http://dx.doi.org/10.1145/990308.990310
- 77 bookTowards dynamic randomized algorithms in computational geometry758Lecture Notes Comput. Sci.Springer-Verlag1993, URL: http://www.springer.com/gp/book/9783540575030
- 78 inproceedings Alpha, Betti and the megaparsec universe: on the homology and topology of the cosmic web Transactions on Computational Science XIV 6970Lecture Notes in Computer ScienceSpringer-Verlag 2011, 60--101URL: http://dx.doi.org/10.1007/978-3-642-25249-5_3

