Keywords
Computer Science and Digital Science
- A3.4.2. Unsupervised learning
- A3.4.7. Kernel methods
- A3.4.8. Deep learning
- A5.3. Image processing and analysis
- A5.3.2. Sparse modeling and image representation
- A5.3.3. Pattern recognition
- A5.3.5. Computational photography
- A5.7. Audio modeling and processing
- A5.7.3. Speech
- A5.7.4. Analysis
- A5.9. Signal processing
- A5.9.2. Estimation, modeling
- A5.9.3. Reconstruction, enhancement
- A5.9.5. Sparsity-aware processing
Other Research Topics and Application Domains
- B2. Health
- B2.2. Physiology and diseases
- B2.2.1. Cardiovascular and respiratory diseases
- B2.2.6. Neurodegenerative diseases
- B3. Environment and planet
- B3.3. Geosciences
- B3.3.2. Water: sea & ocean, lake & river
- B3.3.4. Atmosphere
1 Team members, visitors, external collaborators
Research Scientists
- Hussein Yahia [Team leader, Inria, Researcher, HDR]
- Nicolas Brodu [Inria, Researcher]
- Khalid Daoudi [Inria, Researcher]
PhD Students
- Biswajit Das [Inria]
- Alexy Decroocq [Inria, until Aug 2020]
- Arash Rashidi [Groupe I2S]
Technical Staff
- Marie Martin [Inria, Engineer, until Jun 2020]
- Chiheb Sakka [Inria, Engineer, until Jul 2020]
- Gabriel Augusto Zebadua Garcia [Inria, Engineer]
Administrative Assistant
- Sabrina Duthil [Inria]
2 Overall objectives
GEOSTAT is a research project which investigates the analysis of some classes of natural complex signals (physiological time series, turbulent universe and earth observation data sets) by determining, in acquired signals, the properties that are predicted by commonly admitted or new physical models best fitting the phenomenon. Consequently, when statistical properties discovered in the signals do not match closely enough those predicted by accepted physical models, we question the validity of existing models or propose, whenever possible, modifications or extensions of existing models. A new direction of research, based on the CONCAUST exploratory action and the newly accepted (in February 2021) associated team COMCAUSA proposed by N. Brodu with USA / UC Davis, Complexity Sciences Center, Physics Department is developped in the team.
An important aspect of the methodological approach is that we don't rely on a predetermined "universal" signal processing model to analyze natural complex signals. Instead, we take into consideration existing approaches in nonlinear signal processing (wavelets, multifractal analysis tools such as log-cumulants or micro-canonical multifractal formalism, time frequency analysis etc.) which are used to determine the micro structures or other micro features inside the acquired signals. Then, statistical analysis of these micro data are determined and compared to expected behaviour from theoretical physical models used to describe the phenomenon from which the data is acquired. From there different possibilities can be contemplated:
- The statistics match behaviour predicted by the model: complexity parameters predicted by the model are extracted from signals to analyze the dynamics of underlying phenomena. Examples: analysis of turbulent data sets in Oceanography and Astronomy.
- The signals displays statistics that cannot be attainable by the common lore of accepted models: how to extend or modify the models according to the behaviour of observed signals ? Example: audio speech signals.
GEOSTAT is a research project in nonlinear signal processing which develops on these considerations: it considers the signals as the realizations of complex extended dynamical systems. The driving approach is to describe the relations between complexity (or information content) and the geometric organization of information in a signal. For instance, for signals which are acquisitions of turbulent fluids, the organization of information may be related to the effective presence of a multiscale hierarchy of coherent structures, of multifractal nature, which is strongly related to intermittency and multiplicative cascade phenomena ; the determination of this geometric organization unlocks key nonlinear parameters and features associated to these signals; it helps understand their dynamical properties and their analysis. We use this approach to derive novel solution methods for super-resolution and data fusion in Universe Sciences acquisitions 12. Specific advances are obtained in GEOSTAT in using this type of statistical/geometric approach to get validated dynamical information of signals acquired in Universe Sciences, e.g. Oceanography or Astronomy. The research in GEOSTAT encompasses nonlinear signal processing and the study of emergence in complex systems, with a strong emphasis on geometric approaches to complexity. Consequently, research in GEOSTAT is oriented towards the determination, in real signals, of quantities or phenomena, usually unattainable through linear methods, that are known to play an important role both in the evolution of dynamical systems whose acquisitions are the signals under study, and in the compact representations of the signals themselves.
Signals studied in GEOSTAT belong to two broad classes:
- Acquisitions in Astronomy and Earth Observation.
- Physiological time series.
3 Research program
3.1 General methodology
- Fully Developed Turbulence (FDT) Turbulence at very high Reynolds numbers; systems in FDT are beyond deterministic chaos, and symmetries are restored in a statistical sense only, and multi-scale correlated structures are landmarks. Generalizing to more random uncorrelated multi-scale structured turbulent fields.
- Compact Representation Reduced representation of a complex signal (dimensionality reduction) from which the whole signal can be reconstructed. The reduced representation can correspond to points randomly chosen, such as in Compressive Sensing, or to geometric localization related to statistical information content (framework of reconstructible systems).
- Sparse representation The representation of a signal as a linear combination of elements taken in a dictionary (frame or Hilbertian basis), with the aim of finding as less as possible non-zero coefficients for a large class of signals.
- Universality class In theoretical physics, the observation of the coincidence of the critical exponents (behaviour near a second order phase transition) in different phenomena and systems is called universality. Universality is explained by the theory of the renormalization group, allowing for the determination of the changes followed by structured fluctuations under rescaling, a physical system is the stage of. The notion is applicable with caution and some differences to generalized out-of-equilibrium or disordered systems. Non-universal exponents (without definite classes) exist in some universal slowing dynamical phenomena like the glass transition and kindred. As a consequence, different macroscopic phenomena displaying multiscale structures (and their acquisition in the form of complex signals) may be grouped into different sets of generalized classes.
Every signal conveys, as a measure experiment, information on the physical system whose signal is an acquisition of. As a consequence, it seems natural that signal analysis or compression should make use of physical modelling of phenomena: the goal is to find new methodologies in signal processing that goes beyond the simple problem of interpretation. Physics of disordered systems, and specifically physics of (spin) glasses is putting forward new algorithmic resolution methods in various domains such as optimization, compressive sensing etc. with significant success notably for NP hard problem heuristics. Similarly, physics of turbulence introduces phenomenological approaches involving multifractality. Energy cascades are indeed closely related to geometrical manifolds defined through random processes. At these structures’ scales, information in the process is lost by dissipation (close to the lower bound of inertial range). However, all the cascade is encoded in the geometric manifolds, through long or short distance correlations depending on cases. How do these geometrical manifold structures organize in space and time, in other words, how does the scale entropy cascades itself ? To unify these two notions, a description in term of free energy of a generic physical model is sometimes possible, such as an elastic interface model in a random nonlinear energy landscape : This is for instance the correspondence between compressible stochastic Burgers equation and directed polymers in a disordered medium. Thus, trying to unlock the fingerprints of cascade-like structures in acquired natural signals becomes a fundamental problem, from both theoretical and applicative viewpoints.
3.2 Turbulence in insterstellar clouds and Earth observation data
The research described in this section is a collaboration effort of GEOSTAT, CNRS LEGOS (Toulouse), CNRS LAM (Marseille Laboratory for Astrophysics), MERCATOR (Toulouse), IIT Roorkee, Moroccan Royal Center for Teledetection (CRST), Moroccan Center for Science CNRST, Rabat University, University of Heidelberg. Researchers involved:
- GEOSTAT: H. Yahia, N. Brodu, K. Daoudi, A. El Aouni, A. Tamim
- CNRS LAB: S. Bontemps, N. Schneider
- CNRS LEGOS: V. Garçon, I. Hernandez-Carrasco, J. Sudre, B. Dewitte
- CNRST, CRTS, Rabat University: D. Aboutajdine, A. Atillah, K. Minaoui
The analysis and modeling of natural phenomena, specially those observed in geophysical sciences and in astronomy, are influenced by statistical and multiscale phenomenological descriptions of turbulence; indeed these descriptions are able to explain the partition of energy within a certain range of scales. A particularly important aspect of the statistical theory of turbulence lies in the discovery that the support of the energy transfer is spatially highly non uniform, in other terms it is intermittent47. Because of the absence of localization of the Fourier transform, linear methods are not successful to unlock the multiscale structures and cascading properties of variables which are of primary importance as stated by the physics of the phenomena. This is the reason why new approaches, such as DFA (Detrented Fluctuation Analysis), Time-frequency analysis, variations on curvelets 45 etc. have appeared during the last decades. Recent advances in dimensionality reduction, and notably in Compressive Sensing, go beyond the Nyquist rate in sampling theory using nonlinear reconstruction, but data reduction occur at random places, independently of geometric localization of information content, which can be very useful for acquisition purposes, but of lower impact in signal analysis. We are successfully making use of a microcanonical formulation of the multifractal theory, based on predictability and reconstruction, to study the turbulent nature of interstellar molecular or atomic clouds. Another important result obtained in GEOSTAT is the effective use of multiresolution analysis associated to optimal inference along the scales of a complex system. The multiresolution analysis is performed on dimensionless quantities given by the singularity exponents which encode properly the geometrical structures associated to multiscale organization. This is applied successfully in the derivation of high resolution ocean dynamics, or the high resolution mapping of gaseous exchanges between the ocean and the atmosphere; the latter is of primary importance for a quantitative evaluation of global warming. Understanding the dynamics of complex systems is recognized as a new discipline, which makes use of theoretical and methodological foundations coming from nonlinear physics, the study of dynamical systems and many aspects of computer science. One of the challenges is related to the question of emergence in complex systems: large-scale effects measurable macroscopically from a system made of huge numbers of interactive agents 26, 42. Some quantities related to nonlinearity, such as Lyapunov exponents, Kolmogorov-Sinai entropy etc. can be computed at least in the phase space 27. Consequently, knowledge from acquisitions of complex systems (which include complex signals) could be obtained from information about the phase space. A result from F. Takens 46 about strange attractors in turbulence has motivated the theoretical determination of nonlinear characteristics associated to complex acquisitions. Emergence phenomena can also be traced inside complex signals themselves, by trying to localize information content geometrically. Fundamentally, in the nonlinear analysis of complex signals there are broadly two approaches: characterization by attractors (embedding and bifurcation) and time-frequency, multiscale/multiresolution approaches. In real situations, the phase space associated to the acquisition of a complex phenomenon is unknown. It is however possible to relate, inside the signal's domain, local predictability to local reconstruction 13 and to deduce relevant information associated to multiscale geophysical signals 14. A multiscale organization is a fundamental feature of a complex system, it can be for example related to the cascading properties in turbulent systems. We make use of this kind of description when analyzing turbulent signals: intermittency is observed within the inertial range and is related to the fact that, in the case of FDT (fully developed turbulence), symmetry is restored only in a statistical sense, a fact that has consequences on the quality of any nonlinear signal representation by frames or dictionaries.

The example of FDT as a standard "template" for developing general methods that apply to a vast class of complex systems and signals is of fundamental interest because, in FDT, the existence of a multiscale hierarchy which is of multifractal nature and geometrically localized can be derived from physical considerations. This geometric hierarchy of sets is responsible for the shape of the computed singularity spectra, which in turn is related to the statistical organization of information content in a signal. It explains scale invariance, a characteristic feature of complex signals. The analogy from statistical physics comes from the fact that singularity exponents are direct generalizations of critical exponents which explain the macroscopic properties of a system around critical points, and the quantitative characterization of universality classes, which allow the definition of methods and algorithms that apply to general complex signals and systems, and not only turbulent signals: signals which belong to a same universality class share common statistical organization. During the past decades, canonical approaches permitted the development of a well-established analogy taken from thermodynamics in the analysis of complex signals: if is the free energy, the temperature measured in energy units, the internal energy per volume unit the entropy and , then the scaling exponents associated to moments of intensive variables corresponds to , corresponds to the singularity exponents values, and to the singularity spectrum 25. The research goal is to be able to determine universality classes associated to acquired signals, independently of microscopic properties in the phase space of various complex systems, and beyond the particular case of turbulent data 40.
We show in figure 1 the result of the computation of singularity exponents on an Herschel astronomical observation map (the Musca galactic cloud) which has been edge-aware filtered using sparse filtering to eliminate the cosmic infrared background (or CIB), a type of noise that can modify the singularity spectrum of a signal.
3.3 Causal modeling
The team is working on a new class of models for modeling physical systems, starting from measured data and accounting for their dynamics 32. The idea is to statistically describe the evolution of a system in terms of causally-equivalent states; states that lead to the same predictions 28. Transitions between these states can be reconstructed from data, leading to a theoretically-optimal predictive model 44. In practice, however, no algorithm is currently able to reconstruct these models from data in a reasonable time and without substantial discrete approximations. Recent progress now allows a continuous formulation of predictive causal models. Within this framework, more efficient algorithms may be found. The broadened class of predictive models promises a new perspective on structural complexity in many applications.
3.4 Speech analysis
Phonetic and sub-phonetic analysis: We developed a novel algorithm for automatic detection of Glottal Closure Instants (GCI) from speech signals using the Microcanonical Multiscale Formalism (MMF). This state of the art algorithm is considered as a reference in this field. We made a Matlab code implementing it available to the community (link). Our approach is based on the Microcanonical Multiscale Formalism. We showed that in the case of clean speech, our algorithm performs almost as well as a recent state-of-the-art method. In presence of different types of noises, we showed that our method is considerably more accurate (particularly for very low SNRs). Moreover, our method has lower computational times does not rely on an estimate of pitch period nor any critical choice of parameters. Using the same MMF, we also developed a method for phonetic segmentation of speech signal. We showed that this method outperforms state of the art ones in term of accuracy and efficiency.
Pathological speech analysis and classification: we made a critical analysis of some widely used methodologies in pathological speech classification. We then introduced some novel methods for extracting some common features used in pathological speech analysis and proposed more robust techniques for classification.
Speech analysis of patients with Parkinsonism: with our collaborators from the Czech Republic, we started preliminary studies of some machine learning issues in the field essentially due the small amount of training data.
3.5 Data-based identification of characteristic scales and automated modeling
Data are often acquired at the highest possible resolution, but that scale is not necessarily the best for modeling and understanding the system from which data was measured. The intrinsic properties of natural processes do not depend on the arbitrary scale at which data is acquired; yet, usual analysis techniques operate at the acquisition resolution. When several processes interact at different scales, the identification of their characteristic scales from empirical data becomes a necessary condition for properly modeling the system. A classical method for identifying characteristic scales is to look at the work done by the physical processes, the energy they dissipate over time. The assumption is that this work matches the most important action of each process on the studied natural system, which is usually a reasonable assumption. In the framework of time-frequency analysis 36, the power of the signal can be easily computed in each frequency band, itself matching a temporal scale.
However, in open and dissipating systems, energy dissipation is a prerequisite and thus not necessarily the most useful metric to investigate. In fact, most natural, physical and industrial systems we deal with fall in this category, while balanced quasi-static assumptions are practical approximation only for scales well below the characteristic scale of the involved processes. Open and dissipative systems are not locally constrained by the inevitable rise in entropy, thus allowing the maintaining through time of mesoscopic ordered structures. And, according to information theory 38, more order and less entropy means that these structures have a higher information content than the rest of the system, which usually gives them a high functional role.
We propose to identify characteristic scales not only with energy dissipation, as usual in signal processing analysis, but most importantly with information content. Information theory can be extended to look at which scales are most informative (e.g. multi-scale entropy 31, -entropy 30). Complexity measures quantify the presence of structures in the signal (e.g. statistical complexity 33, MPR 41 and others 35). With these notions, it is already possible to discriminate between random fluctuations and hidden order, such as in chaotic systems 32, 41. The theory of how information and structures can be defined through scales is not complete yet, but the state of art is promising 34. Current research in the team focuses on how informative scales can be found using collections of random paths, assumed to capture local structures as they reach out 29.
Building on these notions, it should also possible to fully automate the modeling of a natural system. Once characteristic scales are found, causal relationships can be established empirically. They are then clustered together in internal states of a special kind of Markov models called -machines 33. These are known to be the optimal predictors of a system, with the drawback that it is currently quite complicated to build them properly, except for small system 43. Recent extensions with advanced clustering techniques 28, 37, coupled with the physics of the studied system (e.g. fluid dynamics), have proved that -machines are applicable to large systems, such as global wind patterns in the atmosphere 39. Current research in the team focuses on the use of reproducing kernels, coupled possibly with sparse operators, in order to design better algorithms for -machines reconstruction. In order to help with this long-term project, a collaboration is ongoing with J. Crutchfield lab at UC Davis.
4 Application domains
4.1 Sparse signals & optimization
This research topic involves Geostat team and is used to set up an InnovationLab with I2S company
Sparsity can be used in many ways and there exist various sparse models in the literature; for instance minimizing the quasi-norm is known to be an NP-hard problem as one needs to try all the possible combinations of the signal's elements. The norm, which is the convex relation of the quasi-norm results in a tractable optimization problem. The pseudo-norms with are particularly interesting as they give closer approximation of but result in a non-convex minimization problem. Thus, finding a global minimum for this kind of problem is not guaranteed. However, using a non-convex penalty instead of the norm has been shown to improve significantly various sparsity-based applications. Nonconvexity has a lot of statistical implications in signal and image processing. Indeed, natural images tend to have a heavy-tailed (kurtotic) distribution in certain domains such as wavelets and gradients. Using the norm comes to consider a Laplacian distribution. More generally, the hyper-Laplacian distribution is related to the pseudo-norm () where the value of controls how the distribution is heavy-tailed. As the hyper-Laplacian distribution for represents better the empirical distribution of the transformed images, it makes sense to use the pseudo-norms instead of . Other functions that better reflect heavy-tailed distributions of images have been used as well such as Student-t or Gaussian Scale Mixtures. The internal properties of natural images have helped researchers to push the sparsity principle further and develop highly efficient algorithms for restoration, representation and coding. Group sparsity is an extension of the sparsity principle where data is clustered into groups and each group is sparsified differently. More specifically, in many cases, it makes sense to follow a certain structure when sparsifying by forcing similar sets of points to be zeros or non-zeros simultaneously. This is typically true for natural images that represent coherent structures. The concept of group sparsity has been first used for simultaneously shrinking groups of wavelet coefficients because of the relations between wavelet basis elements. Lastly, there is a strong relationship between sparsity, nonpredictability and scale invariance.
We have shown that the two powerful concepts of sparsity and scale invariance can be exploited to design fast and efficient imaging algorithms. A general framework has been set up for using non-convex sparsity by applying a first-order approximation. When using a proximal solver to estimate a solution of a sparsity-based optimization problem, sparse terms are always separated in subproblems that take the form of a proximal operator. Estimating the proximal operator associated to a non-convex term is thus the key component to use efficient solvers for non-convex sparse optimization. Using this strategy, only the shrinkage operator changes and thus the solver has the same complexity for both the convex and non-convex cases. While few previous works have also proposed to use non-convex sparsity, their choice of the sparse penalty is rather limited to functions like the pseudo-norm for certain values of or the Minimax Concave (MC) penalty because they admit an analytical solution. Using a first-order approximation only requires calculating the (super)gradient of the function, which makes it possible to use a wide range of penalties for sparse regularization. This is important in various applications where we need a flexible shrinkage function such as in edge-aware processing. Apart from non-convexity, using a first-order approximation makes it easier to verify the optimality condition of proximal operator-based solvers via fixed-point interpretation. Another problem that arises in various imaging applications but has attracted less works is the problem of multi-sparsity, when the minimization problem includes various sparse terms that can be non-convex. This is typically the case when looking for a sparse solution in a certain domain while rejecting outliers in the data-fitting term. By using one intermediate variable per sparse term, we show that proximal-based solvers can be efficient. We give a detailed study of the Alternating Direction Method of Multipliers (ADMM) solver for multi-sparsity and study its properties. The following subjects are addressed and receive new solutions:
-
Edge aware smoothing: given an input image , one seeks a smooth image "close" to by minimizing:
where is a sparcity-inducing non-convex function and a positive parameter. Splitting and alternate minimization lead to the sub-problems:
We solve sub-problem through deconvolution and efficient estimation via separable filters and warm-start initialization for fast GPU implementation, and sub-problem through non-convex proximal form.
- Structure-texture separation: design of an efficient algorithm using non-convex terms on both the data-fitting and the prior. The resulting problem is solved via a combination of Half-Quadratic (HQ) and Maximization-Minimization (MM) methods. We extract challenging texture layers outperforming existing techniques while maintaining a low computational cost. Using spectral sparsity in the framework of low-rank estimation, we propose to use robust Principal Component Analysis (RPCA) to perform robust separation on multi-channel images such as glare and artifacts removal of flash/no-flash photographs. As in this case, the matrix to decompose has much less columns than lines, we propose to use a QR decomposition trick instead of a direct singular value decomposition (SVD) which makes the decomposition faster.
- Robust integration: in many applications, we need to reconstruct an image from corrupted gradient fields. The corruption can take the form of outliers only when the vector field is the result of transformed gradient fields (low-level vision), or mixed outliers and noise when the field is estimated from corrupted measurements (surface reconstruction, gradient camera, Magnetic Resonance Imaging (MRI) compressed sensing, etc.). We use non-convexity and multi-sparsity to build efficient integrability enforcement algorithms. We present two algorithms : 1) a local algorithm that uses sparsity in the gradient field as a prior together with a sparse data-fitting term, 2) a non-local algorithm that uses sparsity in the spectral domain of non-local patches as a prior together with a sparse data-fitting term. Both methods make use of a multi-sparse version of the Half-Quadratic solver. The proposed methods were the first in the literature to propose a sparse regularization to improve integration. Results produced with these methods significantly outperform previous works that use no regularization or simple minimization. Exact or near-exact recovery of surfaces is possible with the proposed methods from highly corrupted gradient fields with outliers.
- Learning image denoising: deep convolutional networks that consist in extracting features by repeated convolutions with high-pass filters and pooling/downsampling operators have shown to give near-human recognition rates. Training the filters of a multi-layer network is costly and requires powerful machines. However, visualizing the first layers of the filters shows that they resemble wavelet filters, leading to sparse representations in each layer. We propose to use the concept of scale invariance of multifractals to extract invariant features on each sparse representation. We build a bi-Lipschitz invariant descriptor based on the distribution of the singularities of the sparsified images in each layer. Combining the descriptors of each layer in one feature vector leads to a compact representation of a texture image that is invariant to various transformations. Using this descriptor that is efficient to calculate with learning techniques such as classifiers combination and artificially adding training data, we build a powerful texture recognition system that outperforms previous works on 3 challenging datasets. In fact, this system leads to quite close recognition rates compared to latest advanced deep nets while not requiring any filters training.
5 Social and environmental responsibility
5.1 Participation in the Covid-19 Inria mission
GeoStat is participating in the Covid-19 Inria mission: : Vocal biomarkers of respiratory diseases.
6 Highlights of the year
6.1 Price
A. El Aouni, PhD student in Geostat receives the "Prix de thèse Systèmes complexes" CNRS ISC-PIF 2020 for his PhD "Lagrangian coherent structures and physical processes of coastal upwelling" defended September 24, 2019.
7 New software and platforms
7.1 New software
7.1.1 Fluex
- Keywords: Signal, Signal processing
- Scientific Description: Fluex is a package consisting of the Microcanonical Multiscale Formalism for 1D, 2D 3D and 3D+t general signals.
- Functional Description: Fluex is a C++ library developed under Gforge. Fluex is a library in nonlinear signal processing. Fluex is able to analyze turbulent and natural complex signals, Fluex is able to determine low level features in these signals that cannot be determined using standard linear techniques.
-
URL:
http://
fluex. gforge. inria. fr/ - Authors: Hussein Yahia, Denis Arrivault, Rémi Paties, Oriol Pont, Rémi Paties
- Contacts: Rémi Paties, Hussein Yahia
- Participants: Hussein Yahia, Rémi Paties
7.1.2 FluidExponents
- Keywords: Signal processing, Wavelets, Fractal, Spectral method, Complexity
- Functional Description: FluidExponents is a signal processing software dedicated to the analysis of complex signals displaying multiscale properties. It analyzes complex natural signals by use of nonlinear methods. It implements the multifractal formalism and allows various kinds of signal decomposition and reconstruction. One key aspect of the software lies in its ability to evaluate key concepts such as the degree of impredictability around a point in a signal, and provides different kinds of applications. The software can be used for times series or multidimensional signals.
-
URL:
svn+ssh://
fluidexponents@scm. gforge. inria. fr/ svn/ fluidexponents/ FluidExponents - Authors: Antonio Turiel, Hussein Yahia
- Contact: Hussein Yahia
- Participants: Antonio Turiel, Hussein Yahia
7.1.3 ProximalDenoising
- Name: ProximalDenoising
- Keywords: 2D, Image filter, Filtering, Minimizing overall energy, Noise, Signal processing, Image reconstruction, Image processing
- Scientific Description: Image filtering is contemplated in the form of a sparse minimization problem in a non-convex setting. Given an input image I, one seeks to compute a denoised output image u such that u is close to I in the L2 norm. To do so, a minimization term is added which favors sparse gradients for output image u. Imposing sparse gradients lead to a non-convex minimization term: for instance a pseudo-norm Lp with 0 < p < 1 or a Cauchy or Welsh function. Half-quadratic algorithm is used by adding a new variable in the minimization functionnal which leads to two sub-problems, the first sub-problem is non-convex and solved by use of proximal operators. The second sub-problem can be written in variational form, and is best solved in Fourier space: it takes the form of a deconvolution operator whose kernel can be approximated by a finite sum of separable filters. This solution method produces excellent computation times even on big images.
-
Functional Description:
Use of proximal and non quadratic minimization. GPU implementation. If f is an input image, one seeks an output g such that the following functional is minimized:
l/2*(norme2(f-g) + psi(grad(g))) with : l positive constant, norme2 = L2 norm, psi is a Cauchy function used for parcimony.
This functional is also applied for debayerization.
- Release Contributions: This software implements H. Badri PhD thesis results.
-
URL:
https://
gitlab. inria. fr/ marmarti/ i2s_geostat_C - Authors: Marie Martin, Chiheb Sakka, Hussein Yahia, Nicolas Brodu, Gabriel Augusto Zebadua Garcia, Khalid Daoudi
- Contacts: Hussein Yahia, Nicolas Brodu
- Partner: Innovative Imaging Solutions I2S
7.1.4 Manzana
- Name: Manzana
- Keywords: 2D, Image processing, Filtering
- Scientific Description: Software library developed in the framework of I2S-GEOSTAT innovationlab and made of high-level image processing functionalities based on sparsity and non-convex optimization.
- Functional Description: Library of software in image processing: filtering, hdr, inpainting etc.
- Contacts: Hussein Yahia, Marie Martin, Chiheb Sakka, Gabriel Augusto Zebadua Garcia, Nicolas Brodu, Arash Rashidi, Khalid Daoudi, Laure Ait-Ali
- Partner: Innovative Imaging Solutions I2S
8 New results
8.1 CONCAUST Exploratory Action
Participants: N. Brodu, James P. Crutchfield, L. Bourel, P. Rau, A. Rupe, Y. Li.
The exploratory action « TRACME » was renamed « CONCAUST » and is going on with good progress. Collaboration with James P. Crutchfield and its laboratory has lead to a first draft of article, “Discovering Causal Structure with Reproducing-Kernel Hilbert Space -Machines”, available at https://Collaboration has also started on the application of this method for:
-
The analysis of El Niño patterns, with Luc Bourrel and Pedro Rau. An article was already published with Luc Bourrel and collaborators in a another context (satellite image processing). The logical step was to try the new method on related time series data. Indeed, the method is able to both predict time series, but also to extract relevant parameters that give a physical interpretation to the model. In the case of the El Niño patterns, our goal is to search for relevant data and correct time scales, holding sufficient information so that the causal states can correctly identify and predict the Niño patterns. This would give us an intuition on what are the most relevant factors for these catastrophic natural phenomena, together with a model for their evolution. In particular, the model is already able to extract the strong El Niño patterns of 1982, 1997 and 2016 from data, as seen in Fig. 2.
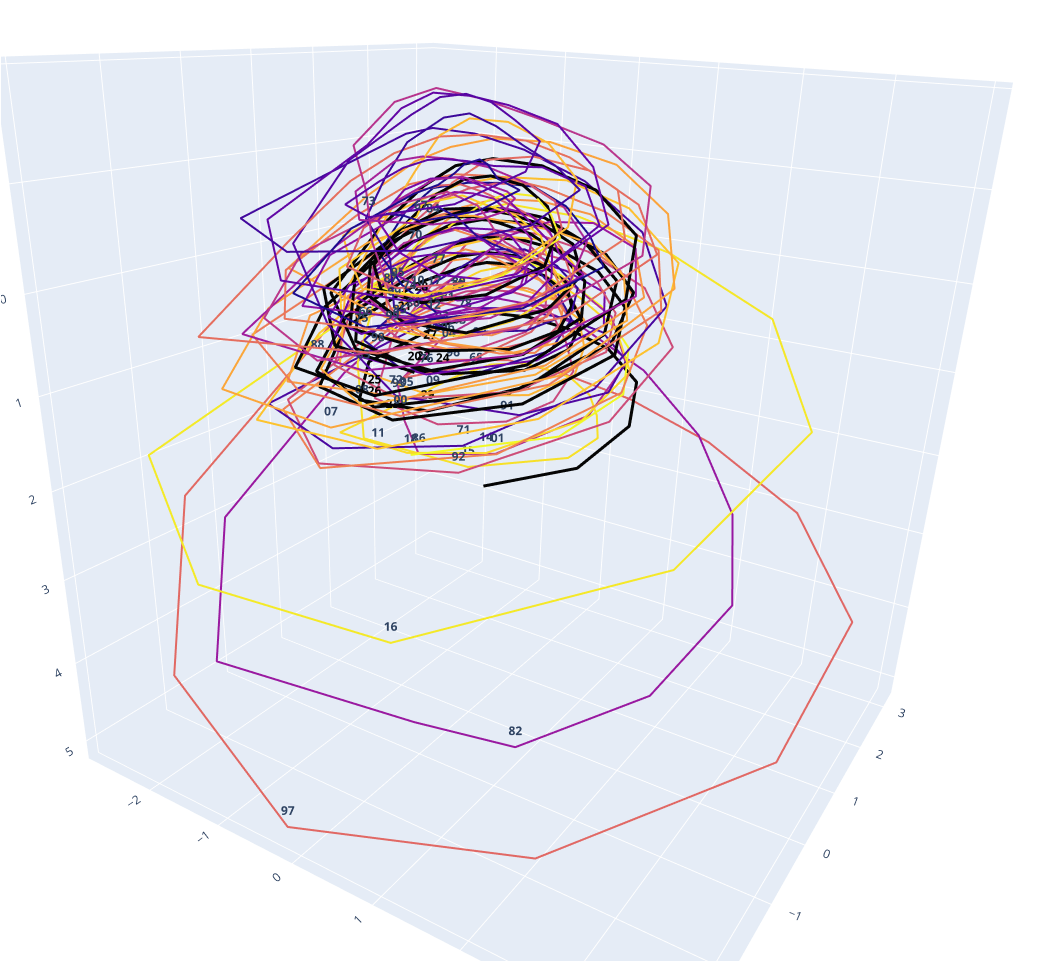
Figure 2: Reconstructed attractor from the El Niño phenomenon. Data from 4 sea surface temperature indicators are combined with precipitations from 9 regions along the south pacific coast. Colors are indexed by time. The yearly seasonal cycle and its phase are captured by the X and Y parameters in this 3D visualization. The signification of the third parameter is under investigation. The strong Niño events of 1982, 1997, and 2016 cleary stand out on the bottom of this figure. This work in progress is likely to change and evolve as we integrate measurements from more variables and more locations, in order to better capture the dynamics of the involved natural processes. -
The analysis of and latent energy exchanges in ecosystems. This collaboration started on the initiative of Adam Rupe, a colleague already involved in the causal states theory, together with Yao Liu, an ecobiology expert. We are answering a call from the Ecoforecast initiative https://
ecoforecast. org, which runs a series of challenges for the prediction and more importantly the analysis and understanding of ecosystems. Our model, by its ability to reconstruct internal states of a physical process from data, is ideally suited for this kind of exploration. Though there is no guarantee we do any better than black box prediction models, this is not our main objective. Our main objective is to better understand how the various biological and physical variables (weather, soil nature, plant types...) interact and extract some of these relations from data. Comparing the output of the CONCAUST theoretical model, a reconstructed model for the physical processes and their interactions, to existing ecobiological models is already instructive. This is a multi-year project and we have just started the collaboration (december 2020) with already interesting results. In particular, we can already reconstruct the system dynamical attractor (Fig. 3), with seasonal cycles, and make realistically looking predictions (Fig. 4). Work is going on for assimilating weather data and improve these predictions, together with making ensemble forecasts. 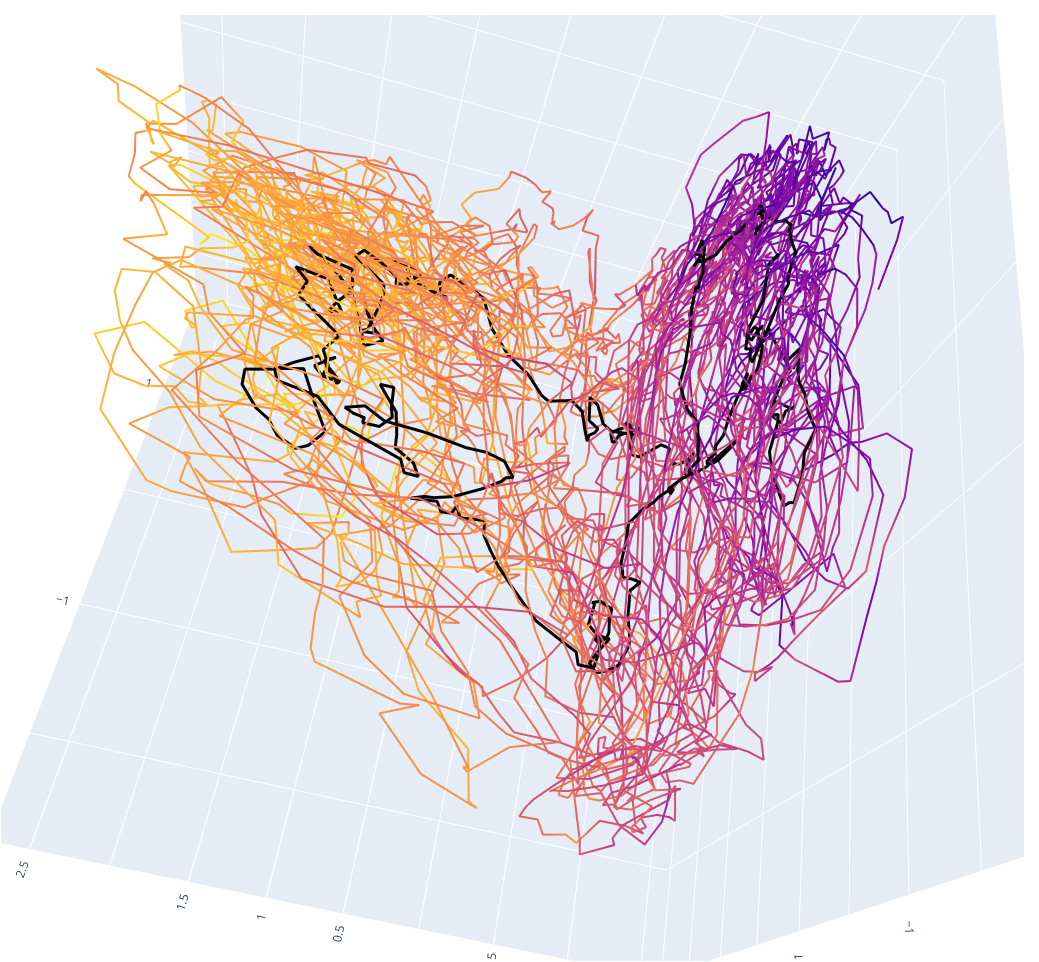
Figure 3: Reconstructed attractor for a forest ecosystem at the Bartlett site, using a combination of Ameriflux data (temperature, solar energy influx, precipitations, soil water content, evapotranspiration, CO2 flux). Colors are indexed by temperature. Again, the seasonal cycle is clearly captured, with 2 distinct lobes for the winter and summer dynamics. The attractor is quite noisy but is well reconstructed by our stochastic model. Predictions for the next causal states are possible by using this model. They are represented as a black line, which evolves on the attractor. 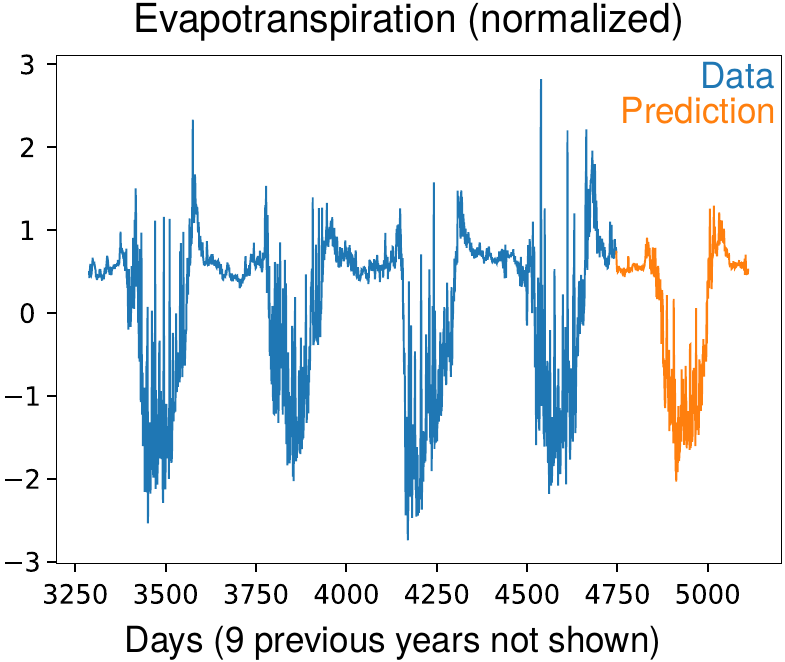
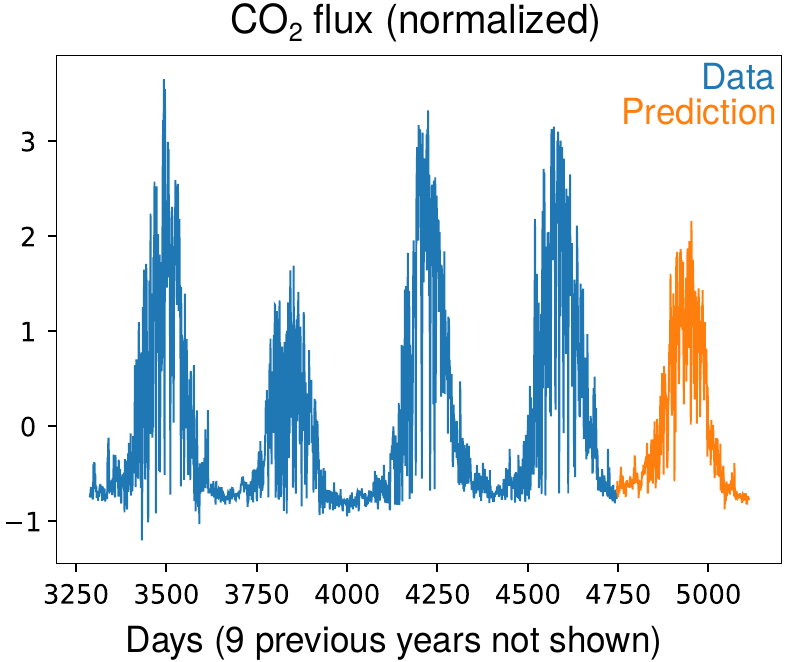
Figure 4: Predictions for the Evaporation and flux. The daily data is collected for 13 years and a causal state model using all measurements (temperature, precipitation, etc) is built. Then, it is possible to extract predictions for specific observables from the causal state evolution (shown in black in Fig 3). Hence, the predictions for the time series shown here use all dependent variables used for building the model.
8.2 Participation in the Covid-19 Inria mission: Vocal biomarkers of respiratory diseases
Participants: K. Daoudi, B. Das, T. Similowski.
GeoStat made a significant contribution to the Covid-19 mission of Inria. Indeed, from the first lockdown, K. Daoudi identified the potential of speech processing for the management of Covid patients in tele-medicine. His proposal aroused the interest of Inria, MESRI and the medical profession and he has since been leading the CovidVoice project. The latter then evolved into the VocaPnée project in partnership with AP-HP and co-directed by K. Daoudi and Thomas Similowski, responsible for the pulmonology and resuscitation service at La Pitié-Salpêtrière hospital and UMR-S 1158. The objective of the VocaPnée project is to bring together all the skills available at Inria to develop and validate a vocal biomarker for the remote monitoring of patients at home suffering from an acute respiratory disease (such as Covid) or chronic (such as asthma) . This biomarker will then be integrated into a telemedicine platform, ORTIF or COVIDOM for Covid, to assist the doctors in assessing the patient's respiratory status. VocaPnée is divided into 2 longitudinal pilot clinical studies, a hospital study and another in tele-medicine.In this context, a voice data collection platform, https://
8.3 Turbulent dynamics in the interstellar medium
Participants: H. Yahia, N. Schneider, S. Bontemps, L. Bonne, et al.
Observations of the interstellar medium (ISM) show a complex density and velocity structure which is in part attributed to turbulence. We here present a self-contained introduction to the multifractal formalism in a microcanonical version which allows us for the first time to compute precise turbulence characteristic parameters from a single observational map without the need for averages in a grand ensemble of statistical observables.Dense molecular filaments are ubiquituous in the interstellar medium, yet their internal physical conditions and the role of gravity, turbulence, the magnetic field, radiation and the ambient cloud during their evolution remain debated. We study the kinematics and physical conditions in the Musca filament, the ambient cloud and the Chamaeleon-Musca complex, to constrain the physics of filament formation.
Publication: Astronomy & Astrophysics, HAL, plus another paper accepted in 2021 in Astronomy & Astrophysics,
8.4 Permuted Spectral and Permuted Spectral-Spatial CNN Models
Participants: G. Phartiyal, N. Brodu, D. Singh, H. Yahia, K. Daoudi.
It is a challenge to develop methods which can process the PolSAR and multispectral (MS) data modalities together without losing information from either for remote sensing applications. This research attempts to introduce novel deep learning based remote sensing data processing frameworks that utilizes convolutional neural networks (CNNs) in both spatial and spectral domains to perform land cover (LC) classification with PolSAR-MS data. Also since earth observation remotely sensed data have usually larger spectral depth than normal camera image data, exploiting the spectral information in remote sensing (RS) data is crucial as well. In fact, convolutions in the sub-spectral space are intuitive and alternative to the process of feature selection.Publication: International Journal of Remote Sensing, HAL
8.5 Robust Detection of the North-West African Upwelling From SST Images
Participants: A. El Aouni, K. Daoudi, K. Minaoui, H. Yahia.
Analysis and study of coastal upwelling using sea surface temperature (SST) satellite images is a common procedure because of its coast effectiveness (economic, time, frequency, and manpower). Developing on the Ekman theory, we propose a robust method to identify the upwelling regions along the northwest African margin. The proposed method comes to overcome the issues encountered in a recent method devoted for the same purpose and for the same upwelling system. Afterward, we show how our method can serve as a framework to study and monitor the spatio-temporal variability of the upwelling phenomenon in the studied region.Publication: IEEE Geoscience and Remote Sensing Letters, HAL
8.6 Defining Lagrangian coherent vortices from their trajectories
Participants: A. El Aouni, K. Daoudi, H. Yahia, H. Kumar Maji, K. Minaoui.
We study the transport properties of mesoscale eddies (i.e. vortices of 100-200 km in diameter) over a finite time duration. While these oceanic structures are well-known to stir and mix surrounding water, they can also carry and transport water properties in a coherent manner. In this paper, we are interested in dynamic transport properties of these coherent structures, despite their chaotic environment. Here, we reveal that such vortices can be identified based a simple decomposition of their Lagrangian trajectories. We identify and extract coherent vortices as material lines along which particles' trajectories share similar polar rotations. The proposed method identifies coherent vortices and their centers in automatic manner. We illustrate our new method by identifying and extracting Lagrangian coherent vortices in different two-dimensional flows.Publication: Physics of Fluids, American Institute of Physics, HAL
8.7 Transparent experiments: releasing data from mechanical tests on three dimensional hydrogel sphere packings
Participants: J. Bares, N. Brodu, H. Zheng, J. A. Dijksman.
We describe here experiments on the mechanics of hydrogel particle packings from the Behringer's lab, performed between 2012 and 2015. These experiments quantify the evolution of all contact forces inside soft particle packings exposed to compression, shear and the intrusion of a large intruder. The experimental set-ups and processes are presented and the data are concomitantly published in a repository.Publication: Granular Matter, HAL
8.8 Structure-preserving denoising of SAR images
Participants: S. Kumar Maji, R. Thakur, H. Yahia.
We propose a speckle removal denois-ing algorithm for synthetic aperture radar (SAR) images. The approach is based on the concept of extracting informative feature (based on the concept of multifractal decomposition of signals) from a speckle-induced SAR image and then estimating a noise-free image from the gradients restricted to those features. The experimental results show that the proposed technique not only improves the visual quality of the SAR images but also effectively preserves their texture. Comparison with the classical and state-of-the-art denoising techniques shows the advantages of the proposed scheme, both visually and quantitatively.Publication: IEEE Geoscience and Remote Sensing Letters, HAL
8.9 LEFE CNRS IMECO Project: Multiscale intermittence in oceanic fields
Participants: F. Schmitt, H. Yahia, V. Garçon, J. Sudre, B. Dewitte, G. Charria.
Oceanic fields display a large variability over large temporal and spatial scales. One way to characterize such variability, borrowed from the field of turbulence, is to consider scaling regimes and multi-scaling properties.The Bay of Biscay and the English Channel, in the Northeastern Atlantic, are considered as a natural laboratory to explore the coastal dynamics at different spatial and temporal scales. In those regions, the coastal circulation is constrained by a complex topography (e.g. varying width of the continental shelf, canyons), river runoffs, strong tides and a seasonally contrasted wind-driven circulation. Based on different numerical model experiments (from 400m to 4km spatial resolution, from 40 to 100 sigma vertical layers using 3D primitive equation ocean models), different features of the Bay of Biscay and English Channel circulation are assessed and explored. Both spatial (submesoscale and mesoscale) and temporal (from hourly to monthly) scales are considered.
8.10 InnovationLab with I2S, sparse signals & optimisation
Participants: A. Zebadua, A. Rashidi, H. Yahia, A. Cherif, J. L. Vallancogne, A. Cailly.
The InnovationLab with I2S is extended one year starting 1st February 2021.In 2020, one main task was to develop image processing algorithms for 3D stereo imaging. Such algorithms improve the quality of noisy and distorted disparity maps that can be used to reconstruct 3D objects. A. Zebadua was responsible for assisting the two research engineers who implemented the algorithms in C++.
A. Zebadua is also responsible for the co-supervision of the Ph.D. of Arash Rashidi worked with him in the development of fast image deconvolution algorithms.
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
InnovationLab with I2S company, starting scheduled after 1st 2019 COPIL in January 2019. This InnovationLab is extended one year starting February 2021.
10 Partnerships and cooperations
10.1 International initiatives
10.1.1 Inria International Labs
The project of associated team COMCAUSA proposed by N. Brodu with USA / UC Davis, Complexity Sciences Center, Physics Department, is accepted, starting Feburary 2021.
10.1.2 Inria international partners
Declared Inria international partners
Jim Crutchfield (Distinguished Prof.) http://
Informal international partners
N. Schneider I. Physik. Institut, University of Cologne, Zülpicher Str. 77, 50937 Cologne, Germany.
10.2 European initiatives
10.2.1 FP7 & H2020 Projects
GENESIS Project (Geostat, Laboratoire d'Astrophysique de Bordeaux, Physics Inst. Köln University).
GENeration et Evolution de la Structure InterStellaire (GENESIS) (GENreration and Evolution of Structure in the ISm).
10.3 National initiatives
- CONCAUST Exploratory Action
The exploratory action « TRACME » was renamed « CONCAUST » and is going on with good progress. Collaboration with James P. Crutchfield and its laboratory has lead to a first draft of article, “Discovering Causal Structure with Reproducing-Kernel Hilbert Space -Machines”, available at https://
arxiv. org/ abs/ 2011. 14821 . That article poses the main theoretical fundations for building a new class of models, able to reconstruct a measured process « causal states » from data. -
Participation in the Covid-19 Inria mission: Vocal biomarkers of respiratory diseases. The CovidVoice project evolved into the VocaPnée project in partnership with AP-HP and co-directed by K. Daoudi and Thomas Similowski, responsible for the pulmonology and resuscitation service at La Pitié-Salpêtrière hospital and UMR-S 1158. The objective of the VocaPnée project is to bring together all the skills available at Inria to develop and validate a vocal biomarker for the remote monitoring of patients at home suffering from an acute respiratory disease (such as Covid) or chronic (such as asthma) . This biomarker will then be integrated into a telemedicine platform, ORTIF or COVIDOM for Covid, to assist the doctors in assessing the patient's respiratory status. VocaPnée is divided into 2 longitudinal pilot clinical studies, a hospital study and another in tele-medicine.
In this context, a voice data collection platform, https://
dream. inria. fr/ vocapnee/, was developed by Inria's SED. This platform is used to collect data from healthy controls. It will then be migrated to the AP-HP servers to collect patient data. - ANR project Voice4PD-MSA, led by K. Daoudi, which targets the differential diagnosis between Parkinson's disease and Multiple System Atrophy. The total amount of the grant is 468555 euros, from which GeoStat has 203078 euros. The duration of the project is 42 months. Partners: CHU Bordeaux (Bordeaux), CHU Toulouse, IRIT, IMT (Toulouse).
- GEOSTAT is a member of ISIS (Information, Image & Vision), AMF (Multifractal Analysis) GDRs.
- GEOSTAT is participating in the CNRS IMECO project Intermittence multi-échelles de champs océaniques : analyse comparative d’images satellitaires et de sorties de modèles numériques. CNRS call AO INSU 2018. PI: F. Schmitt, DR CNRS, UMR LOG 8187. Duration: 2 years.
11 Dissemination
11.1 Reviewer
H. Yahia is reviewer for the IGARSS conference.
11.2 Invited talks
- H. Yahia gave an invited talk "Description of turbulent dynamics in the interstellar medium: multifractal/microcanonical analysis " for the workshop sftools-bigdata : The close structural connection between gas and young stars, focus on current and new tools of data analysis 27-30 Oct 2020 Grenoble. https://
hal. inria. fr/ hal-03002810. - N. Brodu gave a presentation of the concaust method at the “Inference for Dynamical Systems” seminar series, http://
csc. ucdavis. edu/ Inference_for_Dynamical_Systems. html - K. Daoudi gave a talk at Vivhealthtech’2020 (https://
vivhealthtech. events/ FR/), which took place in Bordeaux in November 2020, entitled “Peut-on entendre Parkinson’s ? quid du COVID ?”.
11.3 Supervision
A. Zebadua and H. Yahia are co-supervising A. Rashidi's Phd thesis.
12 Scientific production
12.1 Major publications
- 1 articleMultifractal Desynchronization of the Cardiac Excitable Cell Network During Atrial Fibrillation. II. ModelingFrontiers in Physiology10April 2019, 480 (1-18)
- 2 articleMultifractal desynchronization of the cardiac excitable cell network during atrial fibrillation. I. Multifractal analysis of clinical dataFrontiers in Physiology8March 2018, 1-30
- 3 articleA Non-Local Low-Rank Approach to Enforce IntegrabilityIEEE Transactions on Image ProcessingJune 2016, 10
- 4 inproceedings Fast and Accurate Texture Recognition with Multilayer Convolution and Multifractal Analysis European Conference on Computer Vision ECCV 2014 Zürich, Switzerland September 2014
- 5 articleIncreasing the Resolution of Ocean pCO₂ Maps in the South Eastern Atlantic Ocean Merging Multifractal Satellite-Derived Ocean VariablesIEEE Transactions on Geoscience and Remote SensingJune 2018, 1 - 15
- 6 articleReconstruction of super-resolution ocean pCO 2 and air-sea fluxes of CO 2 from satellite imagery in the Southeastern AtlanticBiogeosciencesSeptember 2015, 20
- 7 article Detection of Glottal Closure Instants based on the Microcanonical Multiscale Formalism IEEE Transactions on Audio, Speech and Language Processing December 2014
- 8 article Efficient and robust detection of Glottal Closure Instants using Most Singular Manifold of speech signals IEEE Transactions on Acoustics Speech and Signal Processing forthcoming 2014
- 9 articleEdges, Transitions and CriticalityPattern RecognitionJanuary 2014, URL: http://hal.inria.fr/hal-00924137
- 10 articleA Multifractal-based Wavefront Phase Estimation Technique for Ground-based Astronomical ObservationsIEEE Transactions on Geoscience and Remote SensingNovember 2015, 11
- 11 articleSingularity analysis in digital signals through the evaluation of their Unpredictable Point ManifoldInternational Journal of Computer Mathematics2012, URL: http://hal.inria.fr/hal-00688715
- 12 articleOcean Turbulent Dynamics at Superresolution From Optimal Multiresolution Analysis and Multiplicative CascadeIEEE Transactions on Geoscience and Remote Sensing5311June 2015, 12
- 13 articleMicrocanonical multifractal formalism: a geometrical approach to multifractal systems. Part I: singularity analysisJournal of Physics A: Math. Theor412008, URL: http://dx.doi.org/10.1088/1751-8113/41/1/015501
- 14 articleMotion analysis in oceanographic satellite images using multiscale methods and the energy cascadePattern Recognition43102010, 3591-3604URL: http://dx.doi.org/10.1016/j.patcog.2010.04.011
12.2 Publications of the year
International journals
International peer-reviewed conferences
Reports & preprints
Other scientific publications
12.3 Cited publications
- 25 book Ondelettes, multifractales et turbulence Paris, France Diderot Editeur 1995
- 26 book Modeling Complex Systems New-York Dordrecht Heidelberg London Springer 2010
- 27 articlePredictability: a way to characterize complexityPhysics Report356arXiv:nlin/0101029v12002, 367--474URL: http://dx.doi.org/10.1016/S0370-1573(01)00025-4
- 28 articleReconstruction of epsilon-machines in predictive frameworks and decisional statesAdvances in Complex Systems14052011, 761-794URL: https://doi.org/10.1142/S0219525911003347
- 29 article Stochastic Texture Difference for Scale-Dependent Data Analysis arXiv preprint arXiv:1503.03278 2015
- 30 book Chaos and coarse graining in statistical mechanics Cambridge University Press Cambridge 2008
- 31 articleMultiscale entropy analysis of complex physiologic time seriesPhysical review letters8962002, 068102
- 32 articleBetween order and chaosNature Physics812012, 17--24
- 33 articleInferring statistical complexityPhysical Review Letters6321989, 105
- 34 articleAbout the role of chaos and coarse graining in statistical mechanicsPhysica A: Statistical Mechanics and its Applications4182015, 94--104
- 35 articleMeasures of statistical complexity: Why?Physics Letters A2384-51998, 244--252
- 36 book Time-frequency/time-scale analysis 10 Academic press 1998
- 37 inproceedingsMixed LICORS: A nonparametric algorithm for predictive state reconstructionArtificial Intelligence and Statistics2013, 289--297
- 38 book Entropy and information theory Springer Science & Business Media 2011
- 39 articleMultifield visualization using local statistical complexityIEEE Transactions on Visualization and Computer Graphics1362007, 1384--1391
- 40 book Statistical physics, statics, dynamics & renormalization World Scie,tific 2000
- 41 articleGeneralized statistical complexity measures: Geometrical and analytical propertiesPhysica A: Statistical Mechanics and its Applications36922006, 439--462
- 42 bookFrom Statistical Physics to Statistical Inference and BackNew York Heidelberg BerlinSpringer1994, URL: http://www.springer.com/physics/complexity/book/978-0-7923-2775-2
- 43 inproceedingsBlind construction of optimal nonlinear recursive predictors for discrete sequencesProceedings of the 20th conference on Uncertainty in artificial intelligenceAUAI Press2004, 504--511
- 44 articleQuantifying Self-Organization with Optimal PredictorsPhys. Rev. Lett.9311Sep 2004, 118701URL: https://link.aps.org/doi/10.1103/PhysRevLett.93.118701
- 45 book Sparse Image and Signal Processing: Wavelets, Curvelets, Morphological Diversity ISBN:9780521119139 Cambridge University Press 2010
- 46 articleDetecting Strange Attractors in TurbulenceNon Linear Optimization8981981, 366--381URL: http://www.springerlink.com/content/b254x77553874745/
- 47 article Revisting multifractality of high resolution temporal rainfall using a wavelet-based formalism Water Resources Research 42 2006

