Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.4. Model reduction
- A6.5.1. Solid mechanics
- A6.5.2. Fluid mechanics
- A9.2. Machine learning
Other Research Topics and Application Domains
- B2.2.1. Cardiovascular and respiratory diseases
- B4.2. Nuclear Energy Production
- B4.3.2. Hydro-energy
- B4.3.3. Wind energy
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Michel Bergmann [Inria, Researcher, HDR]
- Tommaso Taddei [Inria, Researcher]
Faculty Members
- Angelo Iollo [Team leader, Univ de Bordeaux, Professor, HDR]
- Afaf Bouharguane [Univ de Bordeaux, Associate Professor]
Post-Doctoral Fellows
- Gwladys Ravon [Inria, from Mar 2020]
- Lei Zhang [Inria]
PhD Students
- Beatrice Battisti [Ecole Polytechnique de Turin, from May 2020]
- Luis Henrique Benetti Ramos [ONERA, until Sep 2020]
- Michele Giuliano Carlino [Inria]
- Antoine Fondaneche [Univ de Bordeaux]
- Thomas Philibert [Ecole Polytechnique de Turin, from Nov 2020]
- Guillaume Ravel [Univ de Bordeaux]
- Sebastien Riffaud [Univ de Bordeaux, until Nov 2020]
- Ludovica Saccaro [Inria, from Nov 2020]
- Giulia Sambataro [ANDRA]
Technical Staff
- Gwladys Ravon [Inria, Engineer, until Feb 2020]
Interns and Apprentices
- Gloria Bellini [Inria, from Sep 2020 until Nov 2020]
- Matteo Fois [Inria, until Feb 2020]
- Matthieu Nastorg [Inria, from Feb 2020 until Jul 2020]
- Thomas Philibert [Nurea, from Feb 2020 until Jul 2020]
- Alexis Tardieu [Inria, from Jun 2020 until Aug 2020]
Administrative Assistant
- Anne-Laure Gautier [Inria]
Visiting Scientist
- Victor Zucatti Da Silva [Université d'état de Campinas - Brésil, until Apr 2020]
External Collaborator
- Majdi Azaiez [Institut National Polytechnique de Bordeaux, HDR]
2 Overall objectives
2.1 Multi-physics numerical modeling
We aim at a step change in multi-physics numerical modeling by developing two fundamental enablers:
- reduced-order models;
- hierarchical Cartesian schemes.
Reduced-order models (ROMs) are simplified mathematical models derived from the full set of PDEs governing the physics of the phenomenon of interest. ROMs can be obtained exploiting first principles or be data-driven. With ROMs one trades accuracy for speed and scalability, and counteracts the curse of dimensionality of traditional high-fidelity solvers by significantly reducing the computational complexity. ROMs represent an ideal building block for systems with real-time requirements, like interactive decision support systems that offer the possibility to rapidly explore various alternatives.
Hierarchical Cartesian schemes allow the multi-scale solution of PDEs on non body-fitted meshes with a drastic reduction of the computational setup overhead. These methods are easily parallelizable and they can efficiently be mapped to high-performance computer architectures. They avoid dealing with grid generation, a prohibitive task when the boundaries are moving and the topology is complex and unsteady.
3 Research program
3.1 Reduced-order models
Massive parallelization and rethinking of numerical schemes will allow the use of mathematical models for a broader class of physical problems. For industrial applications, there is an increasing need for rapid and reliable numerical simulators to tackle design and control tasks. To provide a concrete example, in the design process of an aircraft, the flight conditions and manoeuvres, which provide the largest aircraft loads, are not known a priori. Therefore, the aerodynamic and inertial forces are calculated for a large number of conditions to give an estimate of the maximum loads, and hence stresses, that the structure of the detailed aircraft design might experience in service. As a result, the number of simulations required for a realistic design problem could easily be in the order of tens of millions. Even with simplistic models of the aircraft behavior this is an unfeasible number of separate simulations. However, engineering experience is used to identify the most likely critical load conditions, meaning that approximately hundreds of thousands simulations are required for conventional aircraft configurations. Furthermore, these analyses have to be repeated every time that there is an update in the aircraft structure.
Compared to existing approaches for ROMs 33, our interest will be focused on two axes. On the one hand, we start from the consideration that small, highly nonlinear scales are typically concentrated in limited spatial regions of the full simulation domain. So for example, in the flow past a wing, the highly non-linear phenomena take place in the proximity of the walls at the scale of a millimeter, for computational domains that are of the order of hundreds of meters. Based on these considerations, we propose in 29 a multi-scale model where the large scales are described by far-field models based on ROMs and the small scales are simulated by high-fidelity models. The whole point for this approach is to optimally decouple the far field from the near field.
A second characterizing feature of our ROM approach is non-linear interpolation. We start from the consideration that dynamical models derived from the projection of the PDE model in the reduced space are neither stable to numerical integration nor robust to parameter variation when hard non-linear multi-scale phenomena are considered.
However, thanks to Proper Orthogonal Decomposition (POD) 39, 45, 28 and 3 we can accurately approximate large solution databases using a low-dimensional base. Recent techniques to investigate the temporal evolution of the POD modes (Koopman modes 40, 26, Dynamic Mode Decomposition 43) and allow a dynamic discrimination of the role played by each of them. This in turn can be exploited to interpolate between modes in parameter space, thanks to ideas relying on optimal transportation 50, 30 that we have started developing in the FP7 project FFAST and H2020 AEROGUST.
3.2 Hierarchical Cartesian schemes
We intend to conceive schemes that will simplify the numerical approximation of problems involving complex unsteady objects together with multi-scale physical phenomena. Rather than using extremely optimized but non-scalable algorithms, we adopt robust alternatives that bypass the difficulties linked to grid generation. Even if the mesh problem can be tackled today thanks to powerful mesh generators, it still represents a severe difficulty, in particular when highly complex unsteady geometries need to be dealt with. Industrial experience and common practice shows that mesh generation accounts for about 20% of overall analysis time, whereas creation of a simulation-specific geometry requires about 60%, and only 20% of overall time is actually devoted to analysis. The methods that we develop bypass the generation of tedious geometrical models by automatic implicit geometry representation and hierarchical Cartesian schemes.
The approach that we plan to develop combines accurate enforcement of unfitted boundary conditions with adaptive octree and overset grids. The core idea is to use an octree/overset mesh for the approximation of the solution fields, while the geometry is captured by level set functions 44, 38 and boundary conditions are imposed using appropriate interpolation methods 25, 49, 42. This eliminates the need for boundary-conforming meshes that require time-consuming and error-prone mesh generation procedures, and opens the door for simulation of very complex geometries. In particular, it will be possible to easily import the industrial geometry and to build the associated level set function used for simulation.
Hierarchical octree grids offer several considerable advantages over classical adaptive mesh refinement for body-fitted meshes, in terms of data management, memory footprint and parallel HPC performance. Typically, when refining unstructured grids, like for example tetrahedral grids, it is necessary to store the whole data tree corresponding to successive subdivisions of the elements and eventually recompute the full connectivity graph. In the linear octree case that we develop, only the tree leaves are stored in a linear array, with a considerable memory advantage. The mapping between the tree leaves and the linear array as well as the connectivity graph is efficiently computed thanks to an appropriate space-filling curve. Concerning parallelization, linear octrees guarantee a natural load balancing thanks to the linear data structure, whereas classical unstructured meshes require sophisticated (and moreover time consuming) tools to achieve proper load distribution (SCOTCH, METIS etc.). Of course, using unfitted hierarchical meshes requires further development and analysis of methods to handle the refinement at level jumps in a consistent and conservative way, accuracy analysis for new finite-volume or finite-difference schemes, efficient reconstructions at the boundaries to recover appropriate accuracy and robustness. These subjects, that are currently virtually absent at Inria, are among the main scientific challenges of our team.
4 Application domains
4.1 Energy conversion
We apply the methods developed in our team to the domain of wind engineering and sea-wave converters. In Figure 1, we show results of a numerical model for a sea-wave energy converter. We here rely on a monolithic model to describe the interaction between the rigid floater, air and water; material properties such as densities, viscosities and rigidity vary across the domain. The appropriate boundary conditions are imposed at interfaces that arbitrarily cross the grid using adapted schemes built thanks to geometrical information computed via level set functions 44. The background method for fluid-structure interface is the volume penalization method 25 where the level set functions is used to improve the degree of accuracy of the method 4 and also to follow the object. The underlined mathematical model is unsteady, and three dimensional; numerical simulations based on a grid with degrees of freedom are executed in parallel using 512 CPUs .



In the context of the Aerogust (Aeroelastic gust modelling) European project, together with Valorem, we investigated the behavior of wind turbine blades under gust loading. The aim of the project was to optimize the design of wind turbine blades to maximize the power extracted. A meteorological mast (Figure 2(a)) has been installed in March 2017 in Brittany to measure wind on-site: data provided by the mast have been exploited to initialize the mathematical model. Due to the large cost of the full-order mathematical model, we relied on a simplified model 36 to optimize the global twist. Then, we validated the optimal configuration using the full-order Cartesian model based on the NaSCar solver. Figure 2(b) shows the flow around the optimized optimized wind turbine rotor.
4.2 Schemes for turbulent flow simulations using Octrees
We have initially developed and tested a 3D first-order Octree code for unsteady incompressible Navier-Stokes equations for full windmill simulations with an LES model and wall laws. We have validated this code on Occigen for complex flows at increasing Reynolds numbers. This step implied identifying stable and feasible schemes compatible with the parallel linear Octree structure. The validation has been conducted with respect to the results of a fully Cartesian code (NaSCAR) that we run on Turing (with significantly more degrees of freedom) and with respect to experimental results.
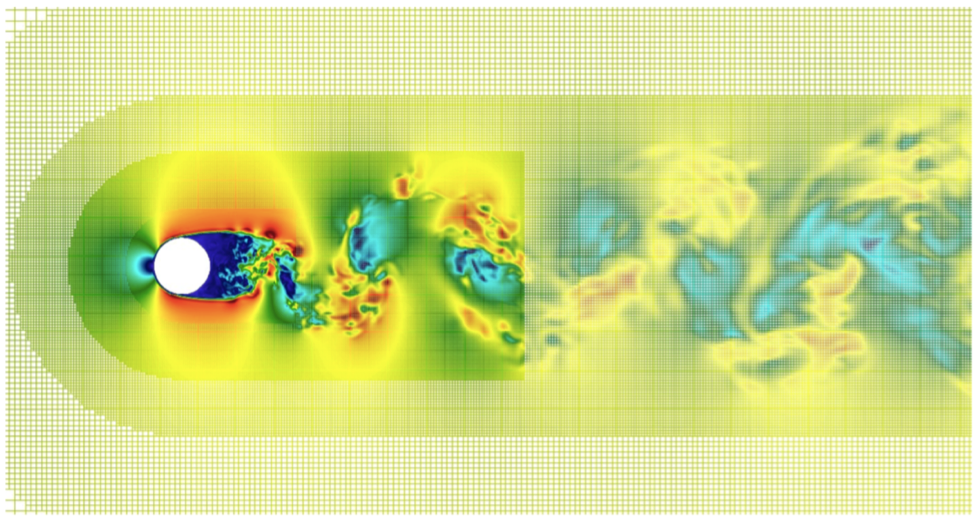
Subsequently, we have developed a second-order Octree scheme that has been validated on Occigen for a sphere at a moderate Reynolds number (), see Table 1. Then, for a cylinder at () (Figures 3(a) and 3(b)), close to real applications, we have preliminary validation results for the second-order scheme with respect to experimental drag coefficient (Table 2). Additional resources will be asked on Occigen to complete the study.
| Mesh | number of cells | (1st-order scheme) | (2nd-order scheme) | |
| 1 | N.A. | |||
| 2 | ||||
| 3 | ||||
| 4 |
| Case | |
| Octree, 1st-order scheme | |
| Octree, 2nd-order scheme | |
| Cartesian | |
| Experimental estimate 32 |

4.3 Vascular flows
A new research direction pursued by the team is the mathematical modelling of vascular blood flows in arteries. Together with the start-up Nurea (http://
4.4 Fluid-structure interactions using Eulerian non-linear elasticity models
Mathematical and numerical modeling of continuum systems undergoing extreme regimes is challenging due to the presence of large deformations and displacements of the solid part, and due to the strongly non-linear behavior of the fluid part. At the same time, proper experiments of impact phenomena are particularly dangerous and require expensive facilities, which make them largely impractical. For this reason, there is a growing interest in the development of predictive models for impact phenomena.
In MEMPHIS, we rely on a fully Eulerian approach based on conservation laws, where the different materials are characterized by their specific constitutive laws, to address these tasks. This approach was introduced in 35 and subsequently pursued and extended in 41, 34, 27, 31 and 9. In Figure 5, we show the results of the numerical simulation of the impact of a copper projectile immersed in air over a copper shield. Results are obtained using a fully parallel monolithic Cartesian method, based on a fixed Cartesian grid. Simulations are performed on a cluster of 512 processors, and benefits from the isomorphism between grid partitioning and processor topology.
In figure 6, we show the results of a three dimensional simulation of a cardiac pump (LVAD, left ventricule assisted device).
Other examples are given in the sections dedicated to the new results.
5 Social and environmental responsibility
One main focus of the team is the renewable energy. We develop mathematical models and numerical methods to study problems related to renewable energies.
5.1 Impact of research results
We are studying two types of green energy extractors.
The first one is around wave energy converters (WECs). For this application, we are working with the PoliTO (Torino, Italy) to model the ISWEC, and we are also starting to work with a Bordeaux-based start-up for another device for extracting the energy from the waves via an Inria-Tech project and a Nouvelle Aquitaine Regional Project submitted by Memphis in collaboration with the CARDAMOM team.
The second one is around wind energy, and in particular wind turbines. In the past, we have supervised two PhD CIFRE thesis with VALOREM-Valeol, and are currently working with them in a European RISE ARIA project led by Memphis. We are also starting to work with IFPEN around the aeroelastic modeling of large wind turbines and the study and optimization of turbines farms in the framework of the joint laboratory Inria-IFPEN with a thesis funded by IFPEN and a post-doc funded by Inria (which will start in October 2021).
In conjunction with these activities we investigate with ANDRA, the national agency for storage of nuclear waste, reduced models allowing efficient and accurate simulations for deep geological storage planning. This activity is concretized with the PhD thesis of Giulia Sambataro.
6 Highlights of the year
2020 was marked by the covid crisis and its impact on the overall society and its activity. The world of research has also been greatly affected:
- Faculty members have seen their teaching load increase significantly.
- PhD students and post-docs have had often to deal with a worsening of their working conditions, as well as of reduced interactions with their supervisors and colleagues.
- Most scientific collaborations have been greatly affected, with several of international activities cancelled or postponed to dates still to be defined.
7 New software and platforms
7.1 New software
7.1.1 COCOFLOW
- Keywords: 3D, Elasticity, MPI, Compressible multimaterial flows
- Functional Description: The code is written in fortran 95 with a MPI parallelization. It solves equations of conservation modeling 3D compressible flows with elastic models as equation of state.
-
URL:
https://
gforge. inria. fr/ projects/ cocoflow - Authors: Alexia De Brauer, Florian Bernard, Yannick Gorsse, Thomas Milcent, Angelo Iollo
- Contact: Florian Bernard
- Partners: CNRS, Université Bordeaux 1
7.1.2 KOPPA
- Name: Kinetic Octree Parallel PolyAtomic
- Keywords: C++, 3D, MPI
- Functional Description: KOPPA is a C++/MPI numerical code solving a large range of rarefied flows from external to internal flows in 1D, 2D or 3D. Different kind of geometries can be treated such as moving geometries coming from CAO files or analytical geometries. The models can be solved on Octree grids with dynamic refinement.
-
URL:
https://
git. math. cnrs. fr/ gitweb/ ?p=plm/ fbernard/ KOPPA. git;a=summary - Authors: Florian Bernard, Angelo Iollo
- Contacts: Florian Bernard, Angelo Iollo
- Participant: Florian Bernard
- Partners: Université de Bordeaux, INP Bordeaux, CNRS
7.1.3 NaSCar
- Name: Navier-Stokes Cartesian
- Keywords: HPC, Numerical analyse, Fluid mechanics, Langage C, PETSc
- Scientific Description: NaSCar can be used to simulate both hydrodynamic bio-locomotion as fish like swimming and aerodynamic flows such wake generated by a wind turbine.
-
Functional Description:
This code is devoted to solve 3D-flows in around moving and deformable bodies. The incompressible Navier-Stokes equations are solved on fixed grids, and the bodies are taken into account thanks to penalization and/or immersed boundary methods. The interface between the fluid and the bodies is tracked with a level set function or in a Lagrangian way. The numerical code is fully second order (time and space). The numerical method is based on projection schemes of Chorin-Temam's type. The code is written in C language and use Petsc library for the resolution of large linear systems in parallel.
NaSCar can be used to simulate both hydrodynamic bio-locomotion as fish like swimming and aerodynamic flows such wake generated by a wind turbine.
-
URL:
https://
gitlab. inria. fr/ memphis/ nascarElast3D - Authors: Michel Bergmann, Angelo Iollo
- Contact: Michel Bergmann
- Participant: Michel Bergmann
- Partner: Université de Bordeaux
7.1.4 NS-penal
- Name: Navier-Stokes-penalization
- Keywords: 3D, Incompressible flows, 2D
- Functional Description: The software can be used as a black box with the help of a data file if the obstacle is already proposed. For new geometries the user has to define them. It can be used with several boundary conditions (Dirichlet, Neumann, periodic) and for a wide range of Reynolds numbers.
- Contact: Charles-Henri Bruneau
- Partner: Université de Bordeaux
7.1.5 HiWind
- Keyword: Simulation
- Functional Description: Hiwind is a software that allows to model in 2D and 3D the effects of air flow on a wind turbine blade (moving solid or elastic structures), and to simulate numerically their interactions. Hiwind also allows to model and characterize the abnormal behavior to warn about a potential weakening of the structure. Hiwind is a "drag and drop" solution (automated meshing phase), massively parallel, and uses adaptive meshing.
- Authors: Claire Taymans, Angelo Iollo, Michel Bergmann
- Contact: Angelo Iollo
- Partner: Valeol
7.1.6 Nemo-Memphis
- Keyword: Octree/Quadtree
- Functional Description: Nemo is a software framework for numerical modeling of multiphysical problems on hierarchical Cartesian meshes (quadtree in 2D and octree in 3D). It is mainly based on the bitpit library (https://optimad.github.io/bitpit/). Nemo provides : - the creation and parallel management of hierarchical Cartesian meshes (2D quadtree or 3D octree) - global or local mesh refinement (based on a distance of levelset or other physical criteria) - the management of several moving geometries in an analytical or explicit form (STL files or others) - the calculation of geometries levelsets at any point of the mesh - 2D/3D differential operators of (gradient, laplacian, hessian, ...) - various 2D/3D interpolators (bilinear, radial basis functions RBF) - an API for solvers (currently with PETSC) - a complete Python3 interface
- Authors: Michel Bergmann, Florian Bernard, Philippe Depouilly, Laurent Facq, Antoine Fondaneche, Antoine Gerard, Matías Hastaran, Angelo Iollo
- Contact: Michel Bergmann
- Partner: CNRS
8 New results
8.1 Fluid-Fluid-Structure interactions
The following results are obtained with the software NaSCar based on our previous works 4, 5, 6, 10. These numerical simulations were performed on the cluster CURTA from the mesocentre MCIA, using 384 CPUs over 48 hours. Periodic boundary conditions are used on the horizontal boundaries. A special treatment is perfomed on the triple line, defined as being the line separeting the three phases, i.e. warter, air and bodies. A model derived form the Cox's model is used. The first example is the sea cruise of a boat. The sea state is artificially generated, but we can see that the waves generated by the boat are realistic (see figure 7).



8.2 Component-based model order reduction for radioactive waste management
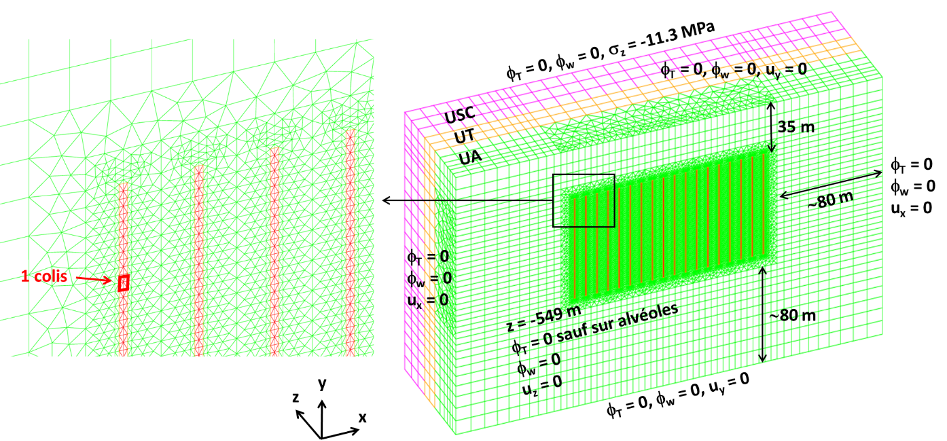
At the end of their cycle, radioactive materials are placed in arrays of cylindrical boreholes (dubbed alveoli) deep underground; due to the large temperatures of the radioactive waste, the thermal flux generated by the alveoli drives a complex time-dependent phenomenon which involves the thermal, hydraulic and mechanical (THM) response of the medium. The role of simulations is to predict the long-term system response and ultimately assess the impact of the repository site to the surrounding areas: Figure 9(a) shows a typical system configuration considered for numerical investigations. Due to the complex nature of the equations (a system of five coupled nonlinear time-dependent three-dimensional equations) and due to the uncertainty in several parameters of the model and on boundary conditions, MOR techniques are important to reduce the computational burden associated with thorough parametric studies.
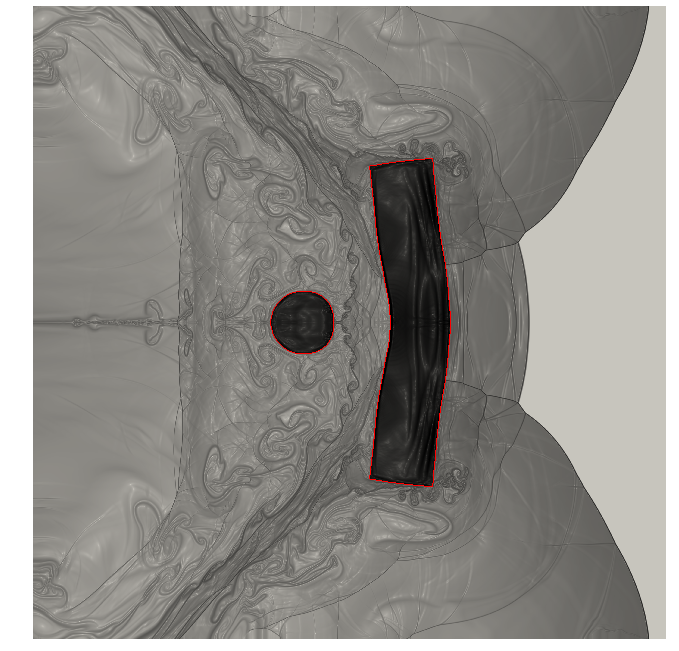
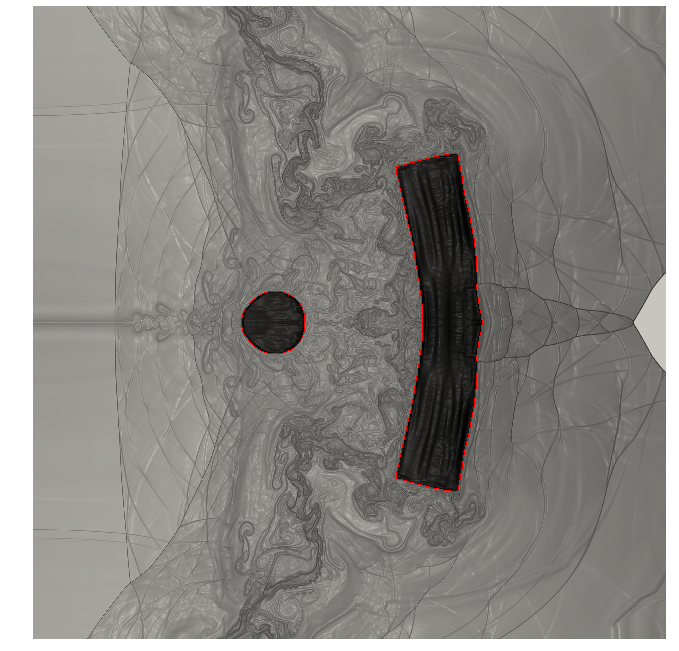
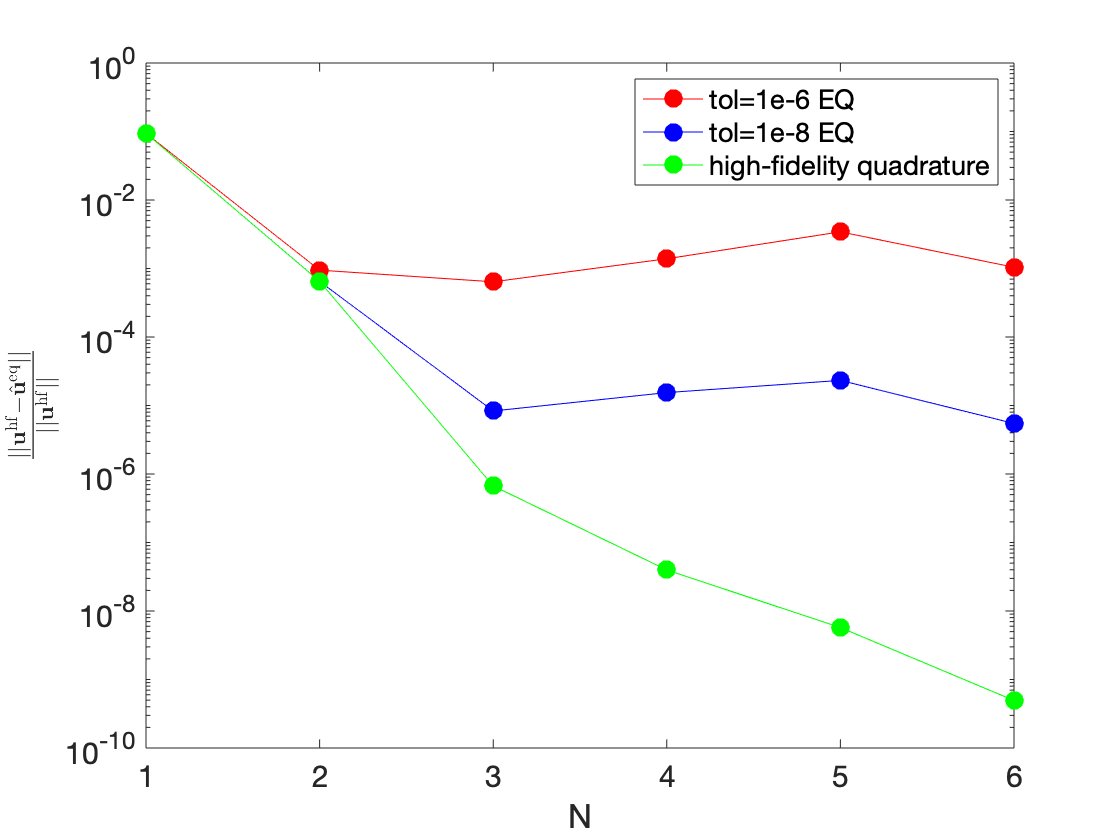
The PhD project of Giulia Sambataro aims to devise a rapid and reliable component-based MOR technique for THM systems, for radioactive waste management applications. Domain decomposition methods are required to deal with varying numbers of alveoli, and also to reduce the training costs of the ROM by avoiding full-scale offline simulations. During the first year of her PhD, Giulia has worked on a two-dimensional hydro-mechanical (HM) model problem and has studied the performance of projection-based hyper-reduced MOR strategies. Figure 9(b) shows the convergence of the relative solution error with respect to the size of the ROM and highlights the impact of hyper-reduction, which reduces the "integration domain" to improve efficiency.
8.3 Registration methods for advection-dominated PDEs
A major issue of state-of-the-art MOR techniques based on linear approximation spaces is the inability to deal with parameter-dependent sharp gradients, which characterize the solutions to advection-dominated problems. To address this issue, we propose a registration technique to align local features in a fixed reference domain. In computer vision and pattern recognition, registration refers to the process of finding a transformation that aligns two datasets; here, registration refers to the process of finding a parametric spatio-temporal transformation that improves the linear compressibility of the solution manifold.
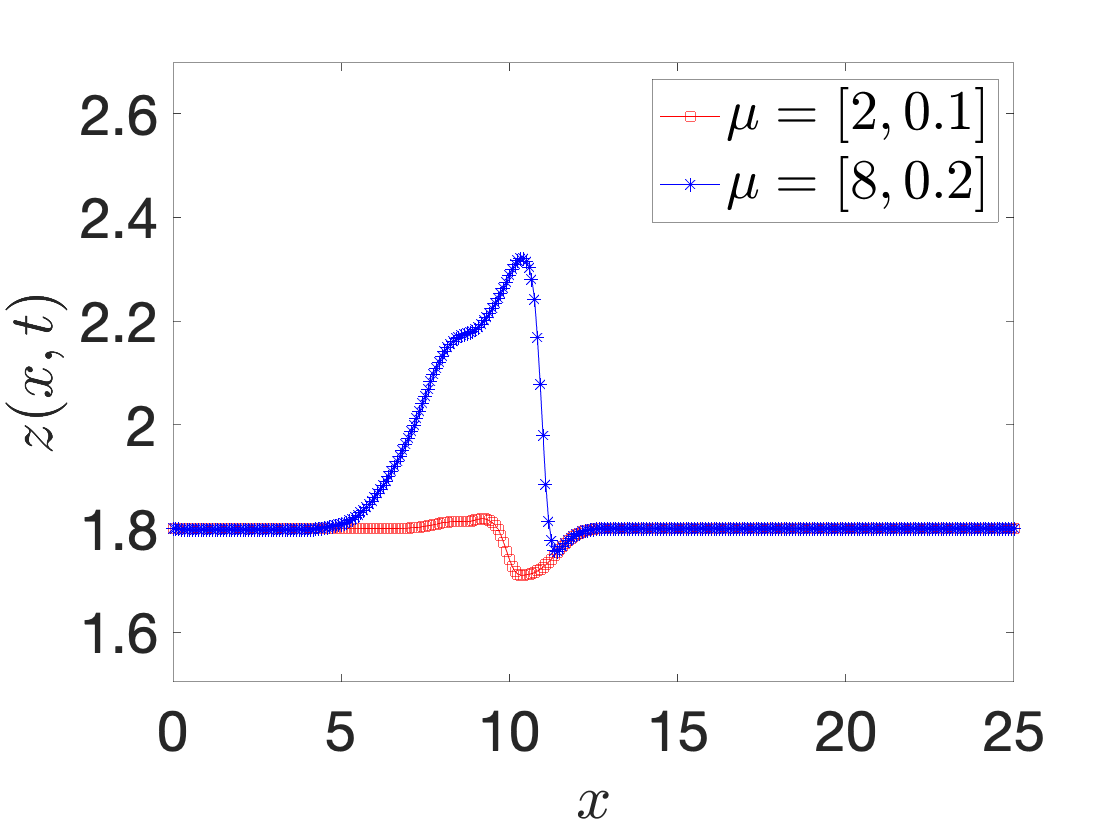
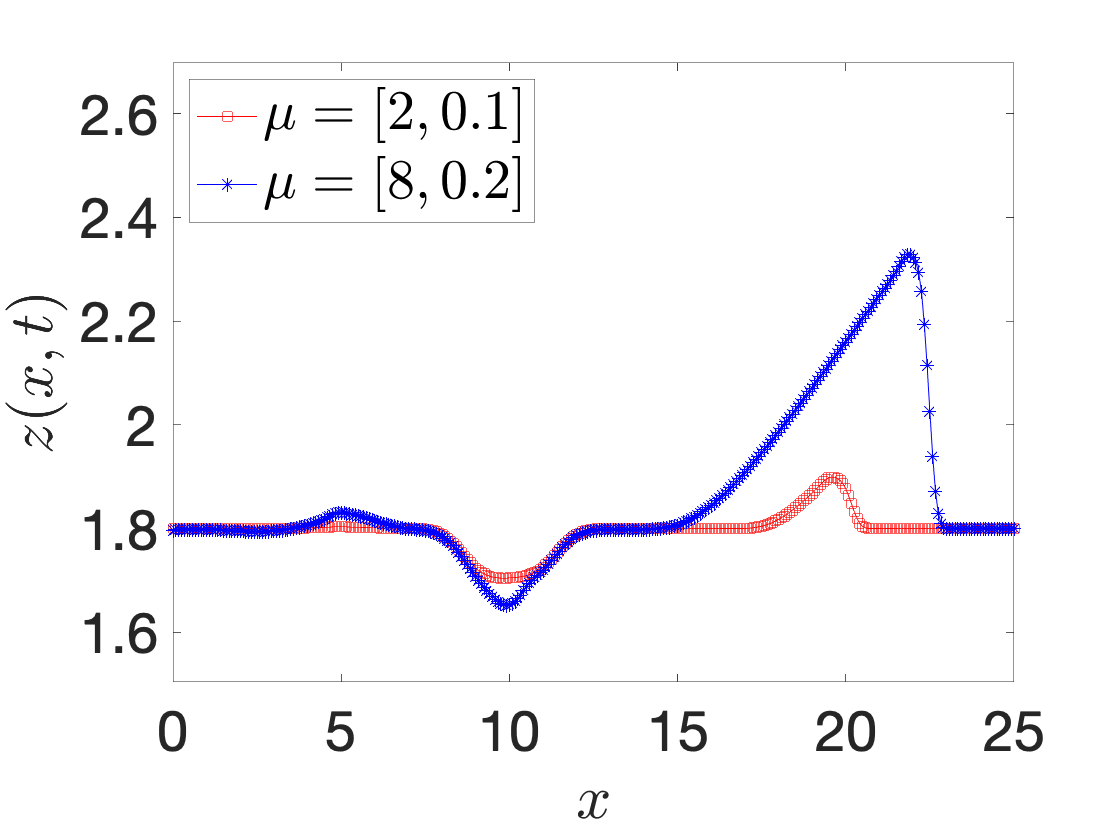
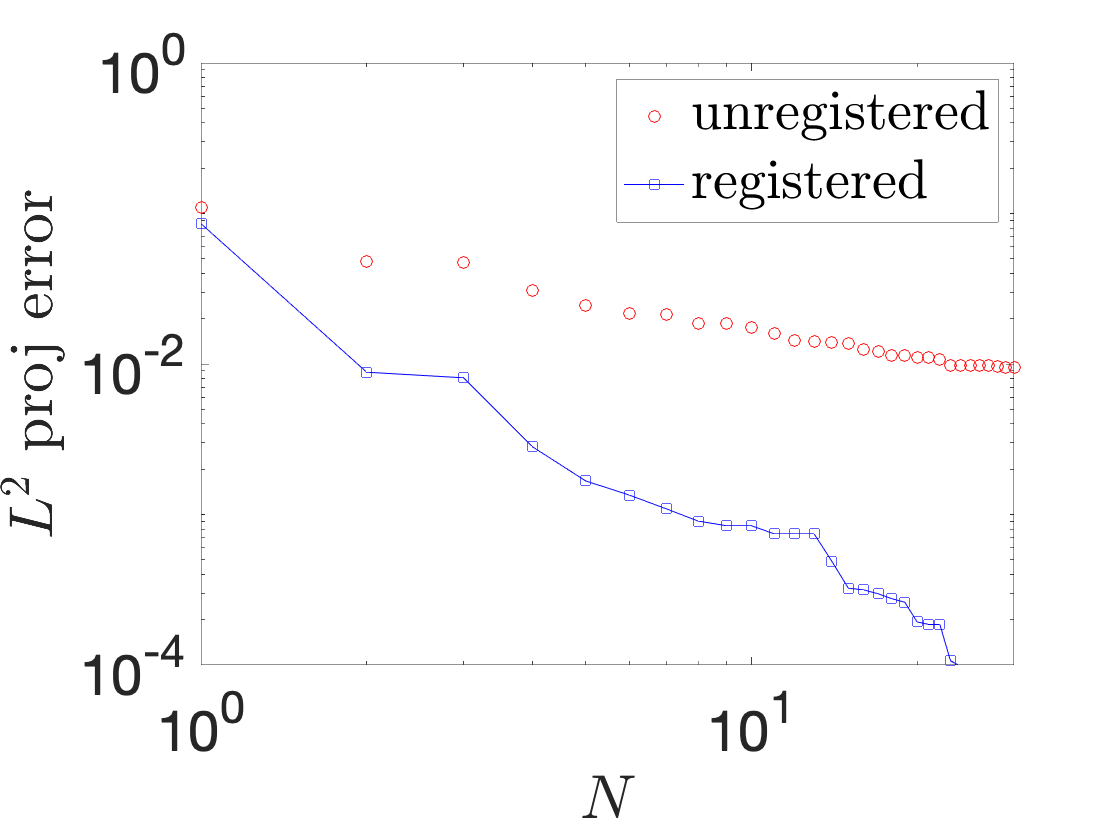
A registration procedure has been proposed in 46, 18 and then further developed in 48, 47. In particular, in 48, we considered the application to one-dimensional applications in hydraulics; in an ongoing collaboration with EDF, we aim to extend the approach to two-dimensional steady and unsteady problems. Figure 10 shows results for a Saint-Venant problem (flow past a bump): Figures 10(a) and 10(b) show the free surface for two different parameters and two time instants, while Figure 10(c) shows the behavior of the out-of-sample projection error associated with a snapshot-based POD space with and without registration. We observe that registration is key to improve performance of linear compression strategies such as POD.
8.4 Numerical modeling of a real zebrafish swimming: an effort test
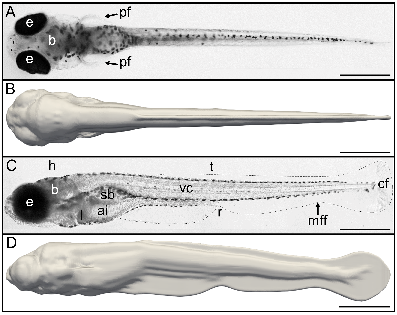
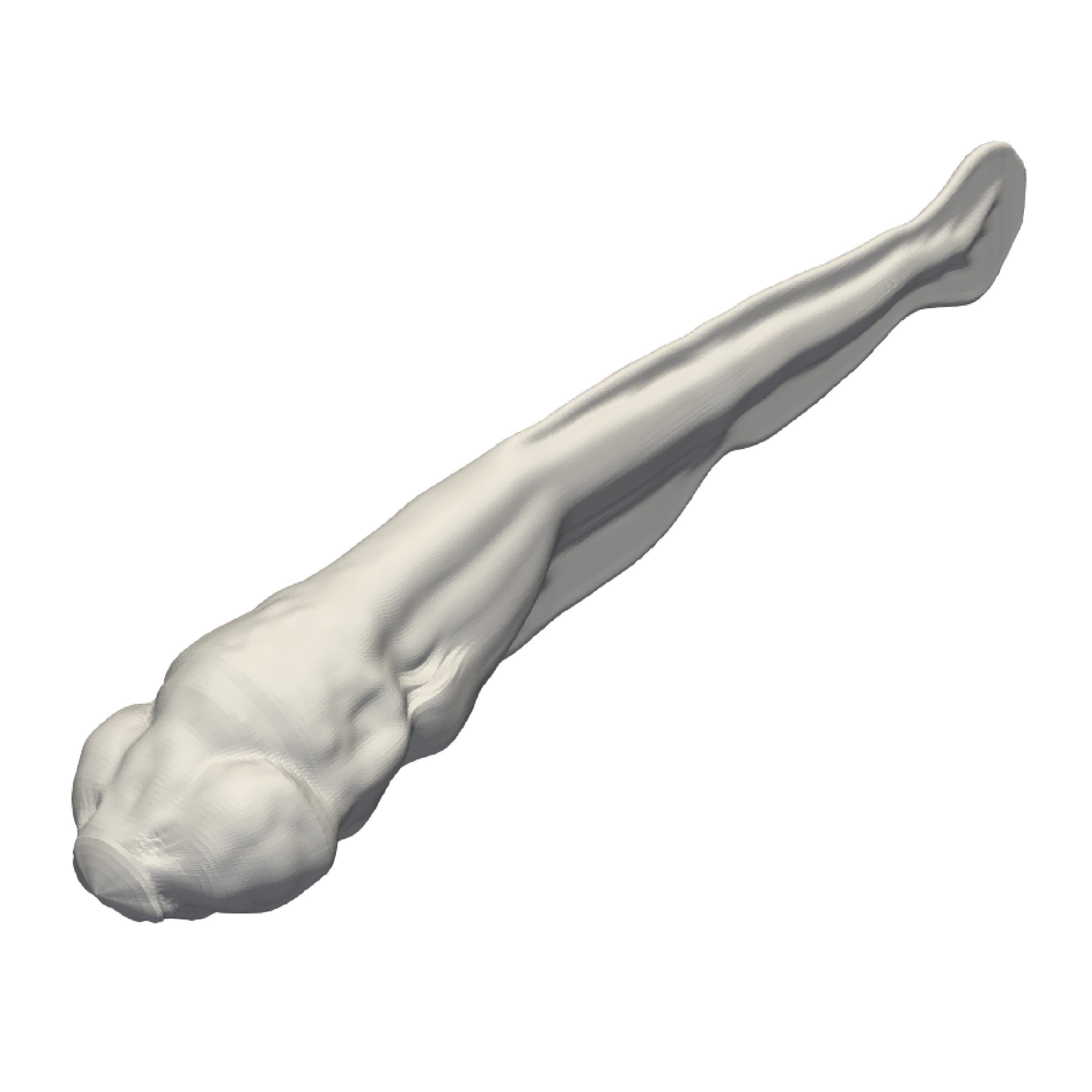
Zebrafish is used by biologists as an animal model to study the effects of neurotoxicants and drugs on locomotion and develop pharmacological treatments. Very few fish swimming simulations have been derived from real body deformations to investigate the complex and stereotyped escape response of zebrafish and support animal experimentation. An experiment-driven numerical approach has been developed to model the body deformations from experimental imaging and perform three-dimensional (3D) numerical simulations to compute the actual energetic performances. To this end, a novel 3D zebrafish shape described by Lagrangian markers, was reconstructed based on 1,600 transverse slices and deformed according to experimental data (see figure 11). As a first application, three escape locomotion were recorded and simulated across six high-viscosity fluids in the range of mPa.s to 15 mPa.s. In addition to kinematic data such as traveled distance, velocity, and bending amplitude, the expended energy and cost of transport were computed based on the power output. Eventually, fictitious simulations were performed by combining body deformations and fluid viscosity, especially for challenging the experimental escape motions. Such simulations have revealed energetic expenditure could be emphasized by increasing fluid viscosity. Therefore, those preliminary results provided new insights for the implementation of an effort test, involving zebrafish experiments, viscous fluids, and energetic performances from numerical simulations. The main goal of effort tests designed by biologists is to highlight zebrafish swimming performances altered by genetics or chemical compounds, by computing the power output expended in higher-viscosity fluids.
8.5 Fluid-structure interactions on AMR enabled quadree grids
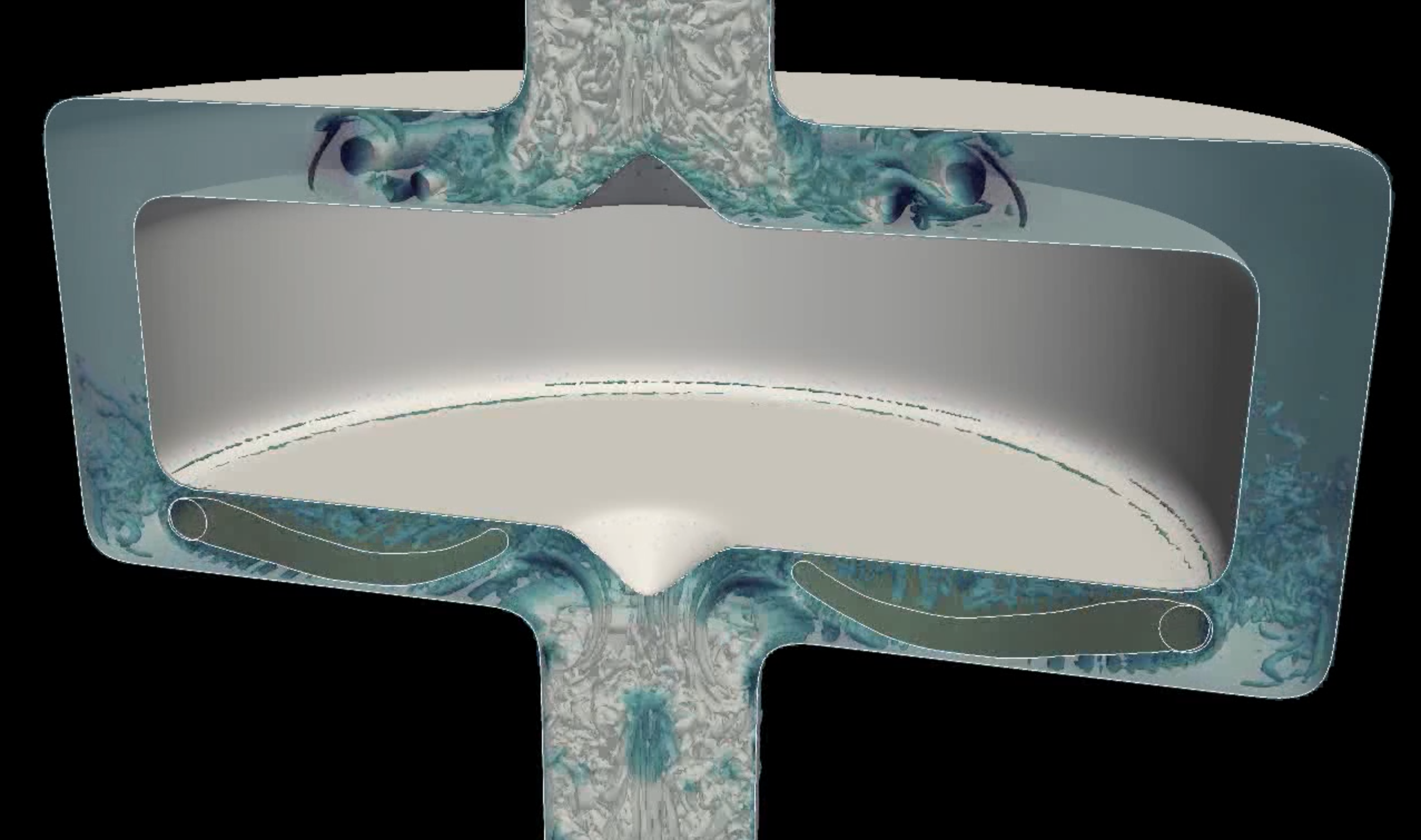
A versatile fully Eulerian method has been developed for the simulation of fluid-structure interaction problems in two dimensions, involving stiff hyper-elastic materials. The unified single continuum model is solved in a monolithic way using a quadtree-based Finite Volume scheme, built on very compact discretizations. In the context of fictitious domain methods, the geometry of a structure is captured through a level-set formalism, which enables to define a diffuse fluid-structure interface. The numerical model has been validated with respect to the literature and an example has been presented in order to compare the computational costs of simulations performed on uniform and dynamic adaptive grids. From the 1D asymptotic analysis of the discretization scheme, recent developments have led to a stabilization of the Finite Volume method, which is needed to take into account very stiff materials. The simulation of a two dimensional axisymmetric flow in a complex cardiac pump geometry is proposed as a biomedical application (see figure 12).
8.6 An ADER approach to advection diffusion equations on Overset Grids
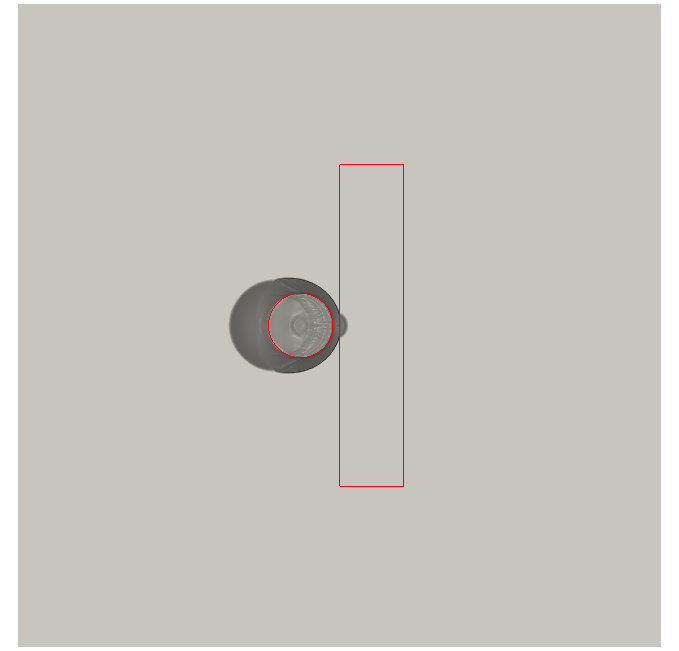
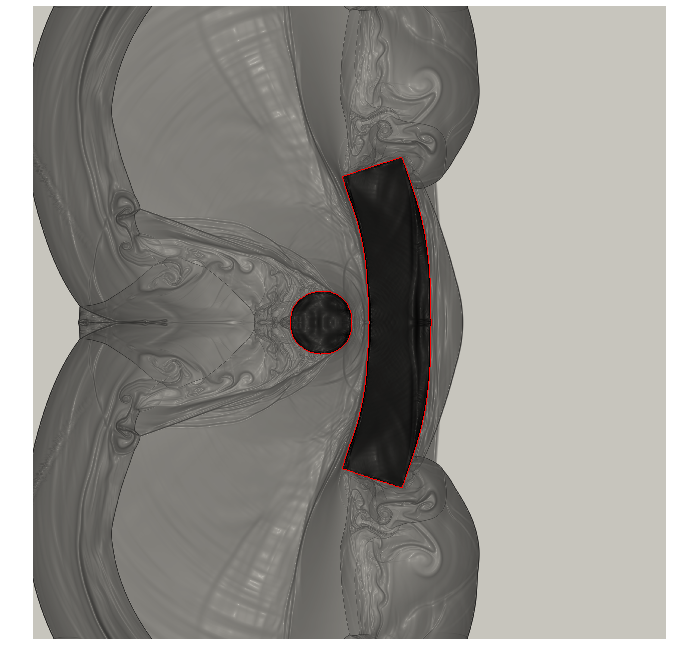
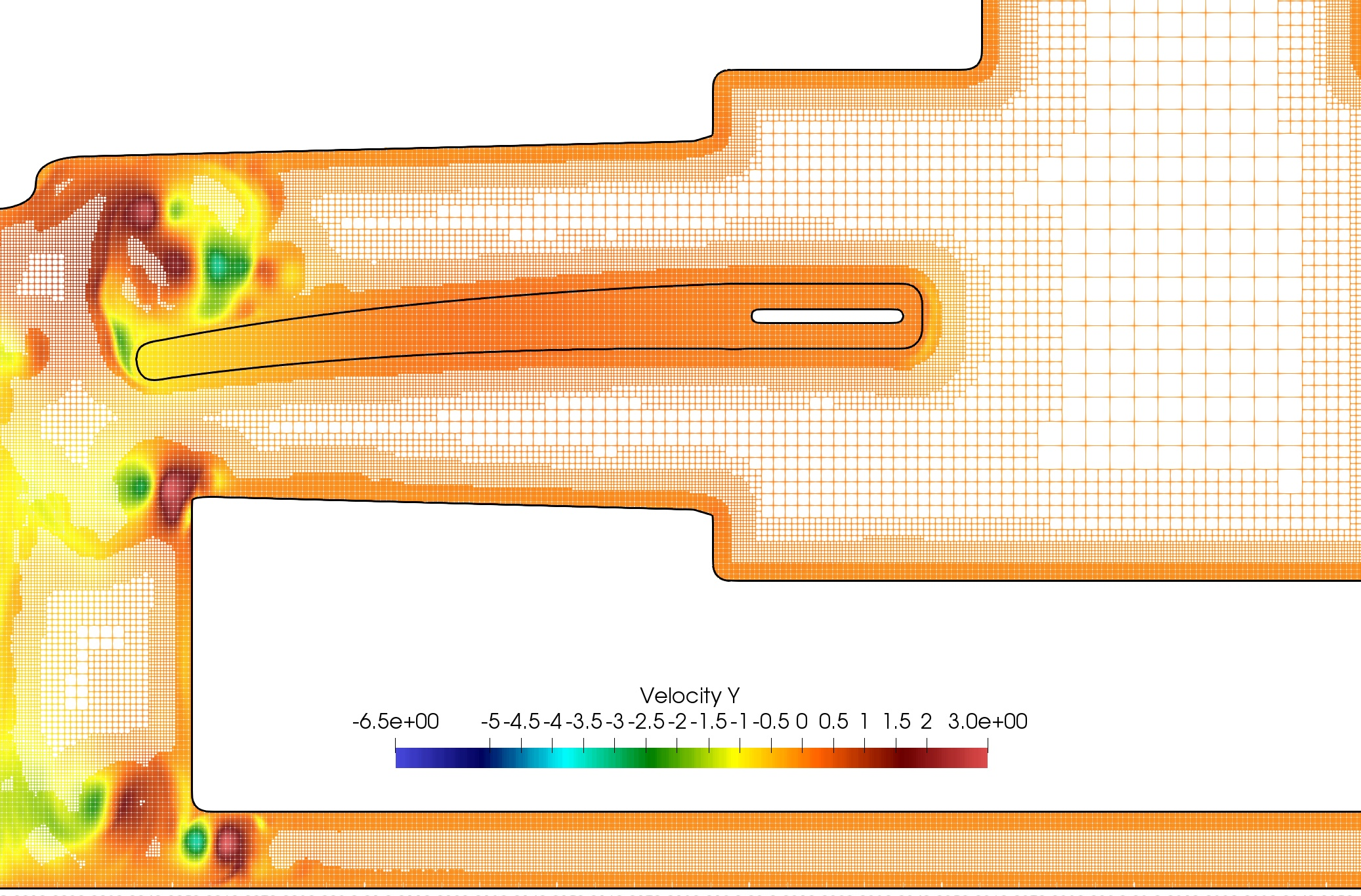
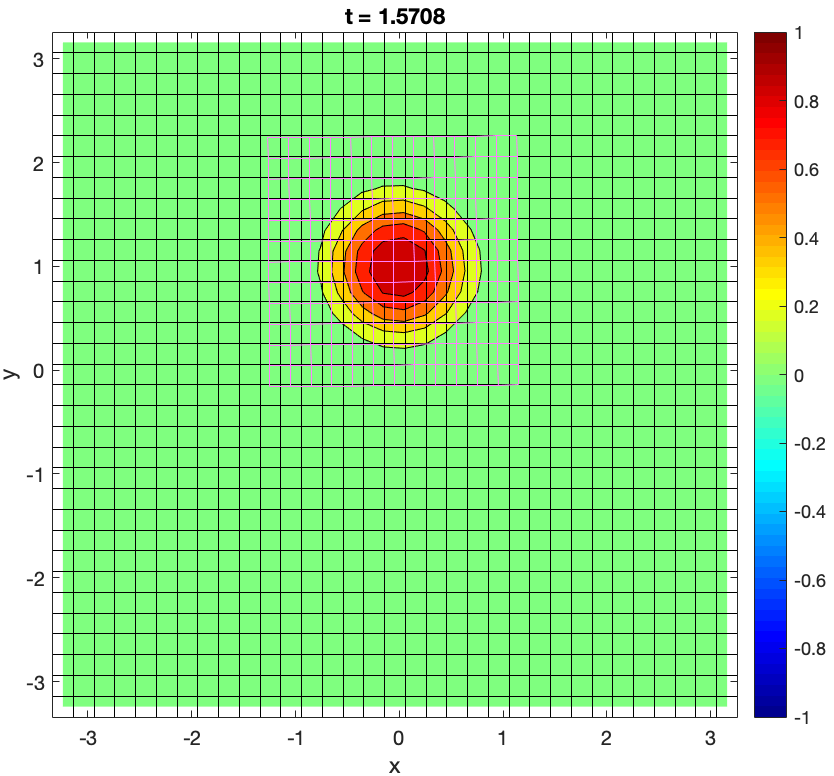
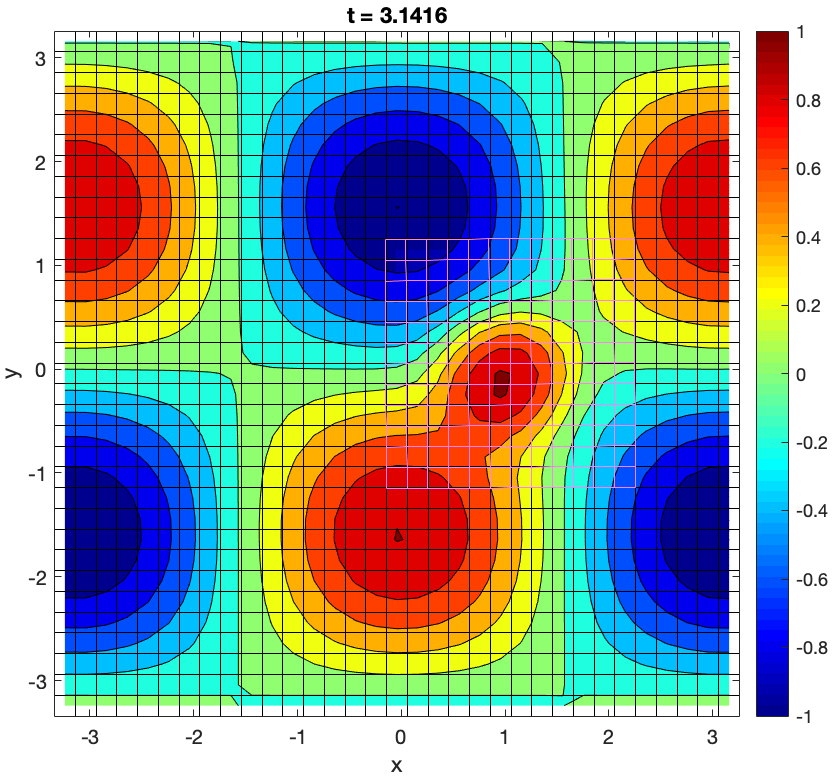
One of the difficulties in the simulation of a fluid flow problem is the representation of the computational domain with a unique block mesh. As a matter of fact, not only the geometry could be particularly complex in itself, but it could change during the simulation and this necessary involves an in itinere geometrical adaptation of the mesh, with consequent high computational costs. One of the ways to overcome this problem is to use multiple overlapping mesh blocks that together define a Chimera or overset grid. Once the different mesh blocks are generated, they are properly composed by the creation of holes and, consequently, an overlapping zone between two overlapping blocks is defined. The overlapping zone is necessary for the the communication and data transfer from one mesh to another through an appropriate definition of local stencils of cells, both within and at the border of the individual blocks. In our simulations, the Chimera grid is composed of a background and a foreground mesh (see Figure 13). In particular, the foreground mesh can move and deform. The Navier-Stokes equations for incompressible fluids are solved through a projection method (Chorin-Temam), thus we propose in the sequel a finite volume (FV) method for the steady diffusion equation and the unsteady advection-diffusion (AD) equation on a Chimera configuration. Both methods are second order accurate 21.
8.7 Modeling and numerical simulation of ellipsoidal particle-laden flows and self propelled swimmers in a porous enclosure
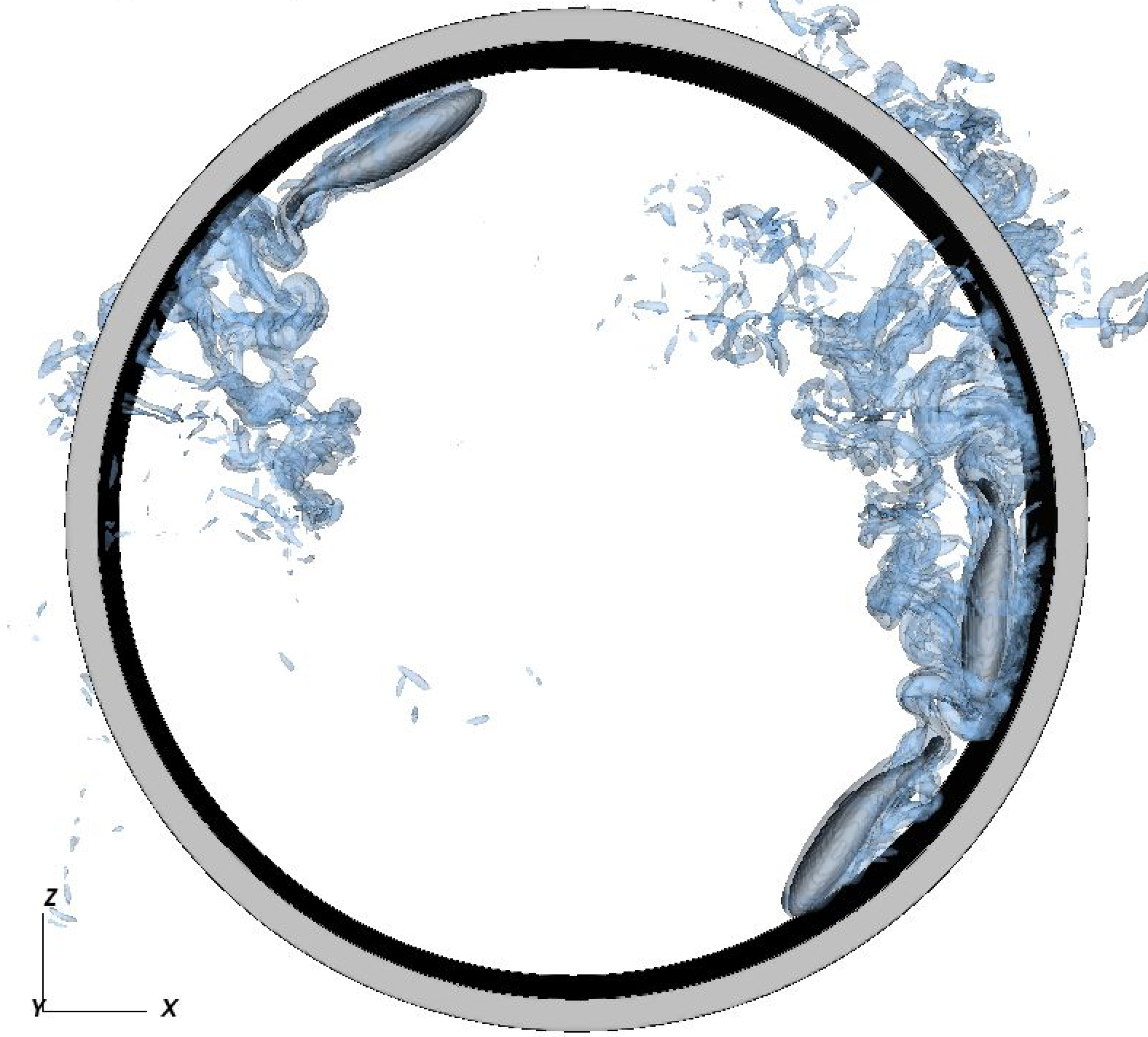
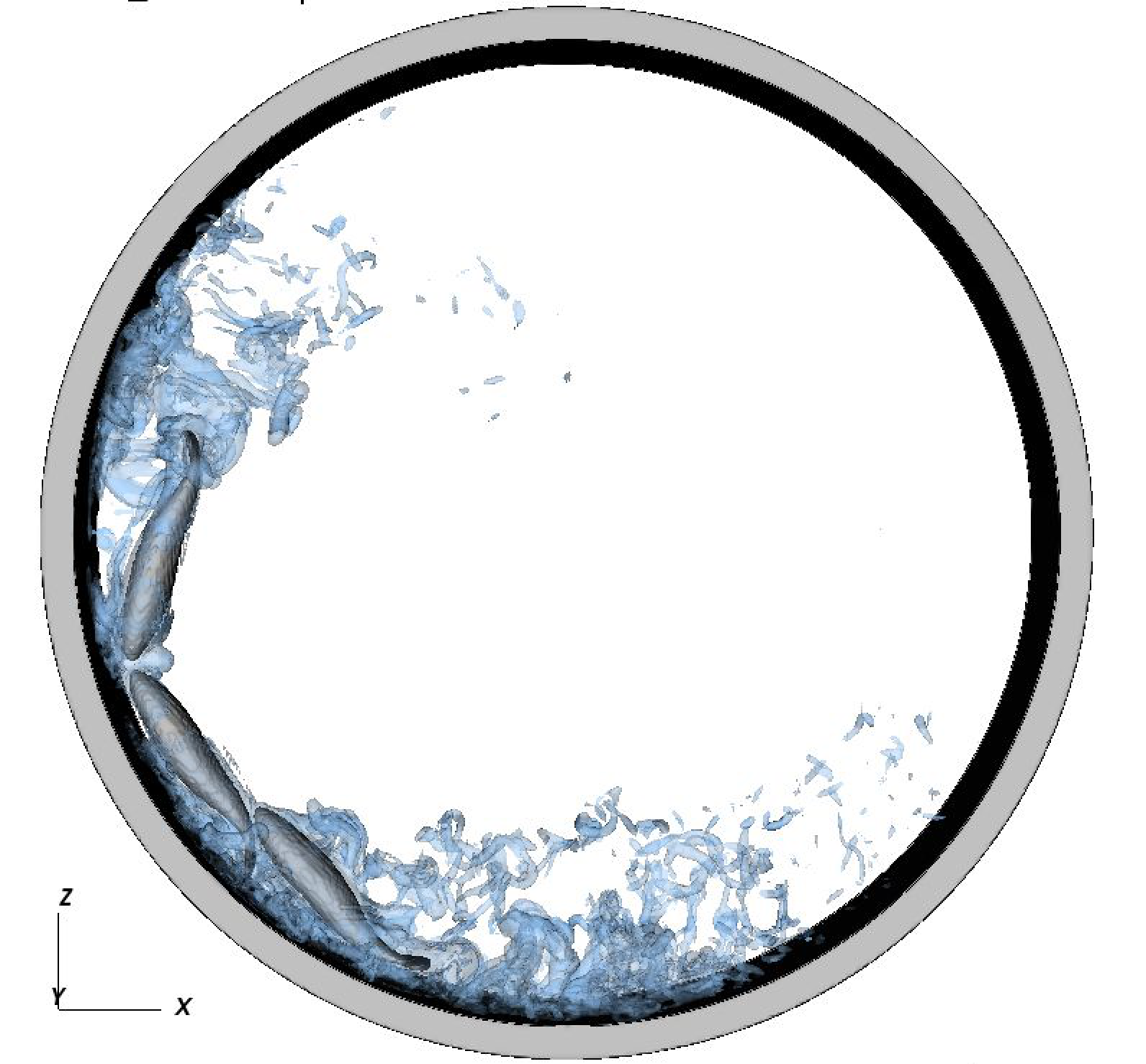
Despite being relevant in many natural and industrial processes, suspensions of non-spherical particles have been largely under-investigated compared to the extensive analyses made on the gravity-driven motions of spherical particles. One of the main reasons for this disparity is the difficulty of accurately correcting the short-range hydrodynamic forces and torques acting on complex particles. These effects, also known as lubrication, are essential to the suspension of the particles and are usually poorly captured by direct numerical simulation of particle-laden flows. We have proposed a partitioned VP-DEM (Volume Penalization method - Discrete Element Method) solver which estimates the unresolved hydrodynamic forces and torques. Corrections are made locally on the surface of the interacting particles without any assumption on the particle global geometry. This is an extension of our previous work 3717. Numerical validations have been made using ellipsoidal particles immersed in an incompressible Navier-Stokes flow.
Self organization of groups of several swimmers is of interest in biological applications. One of the main question is to determine if the possible organization comes from an uncontrolled or a controlled swimming behavior. This work has been motivated by the recent studies of Hamid Kellay (LOMA).
The collision model developed in the previous section has been developed for concave interactions like sphere-sphere or in the limit of sphere-plane wall. For non concave interactions, we have derived a simple approximation considering locally convexity as being a plane wall. Recent 3D results are obtained for a porous and impermeable enclosure (see Fig. 14). The numerical results are similar to those obtained in the experimental ones of Hamid Kellay's group.
8.8 Projection-based reduced-order models for unsteady compressible flows
An analysis of calibration for reduced-order models (ROMs) is done in 19. The Galerkin and least-squares Petrov-Galerkin (LSPG) methods are tested on compressible flows involving a disparity of temporal scales. A novel calibration strategy is proposed for the LSPG method and two test cases are analyzed. The first consists of a subsonic airfoil flow where boundary layer instabilities are responsible for trailing-edge noise generation and the second comprises a supersonic airfoil flow with a transient period where a detached shock wave propagates upstream at the same time that shock-vortex interaction occurs at the trailing edge. Results show that calibration produces stable and long-time accurate Galerkin and LSPG ROMs for both cases investigated. The impact of hyper-reduction is tested on LSPG models via an accelerated greedy missing point estimation (MPE) algorithm. The location for hyper-reduction points is depicted in Figure 15. For the first case investigated, LSPG solutions obtained with hyper-reduction show good comparison with those obtained by the full order model. However, for the supersonic case the transient features of the flow need to be properly captured by the sampled points of the accelerated greedy MPE method. Otherwise, the dynamics of the moving shock wave are not fully recovered. The impact of different time-marching schemes is also assessed and, differently than reported in literature, Galerkin models are shown to be more accurate than those computed by LSPG when the non-conservative form of the Navier-Stokes equations is solved. For the supersonic case, the Galerkin and LSPG models (without hyper-reduction) capture the overall dynamics of the detached and oblique shock waves along the airfoil. However, when shock-vortex interaction occurs at the trailing-edge, the Galerkin ROM is able to capture the high-frequency fluctuations from vortex shedding while the LSPG presents a more dissipative solution, not being able to recover the flow dynamics.

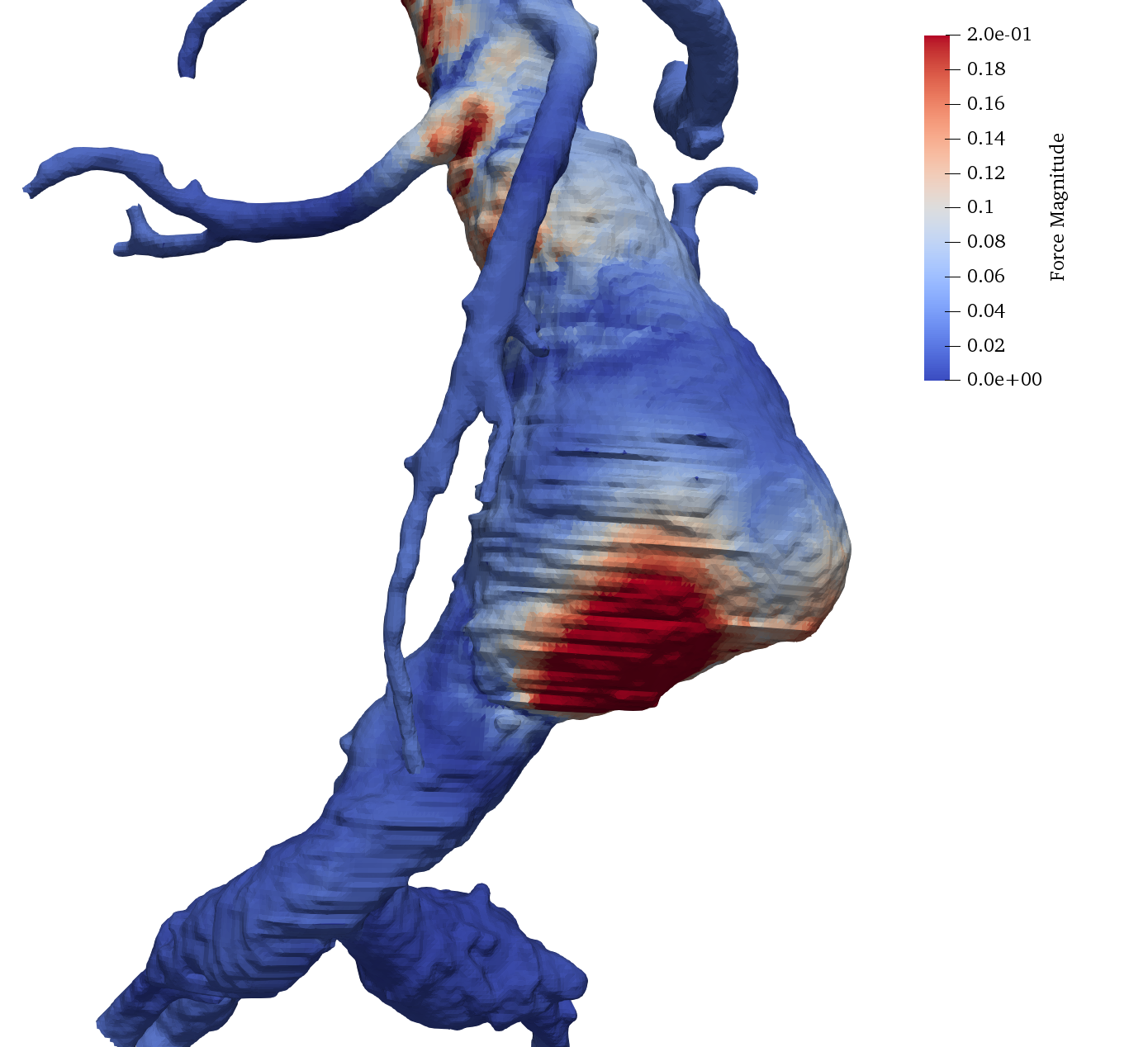
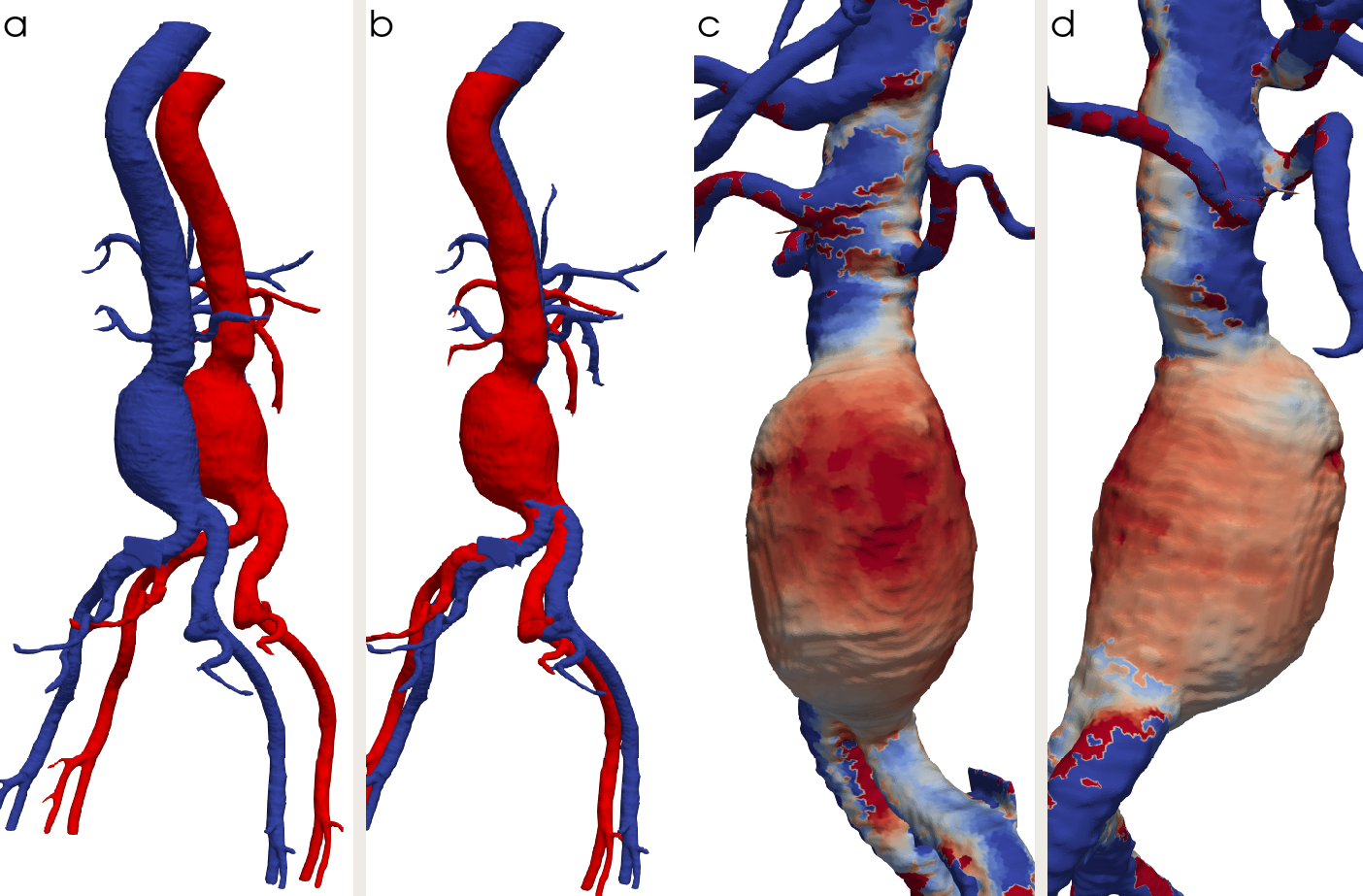
8.9 Aortic aneurysms: automatic segmentation and registration
We developed a new artificial neural network to automatically segment aortic aneurysm. The main idea with this approach was to consider each pixel of the image individually and to see if a model could learn how to categorize it as lumen only from its own intensity and the intensity of its 26 neighbors. We tested different types of input (values, means, variances...) and architecture: a sequential model was retained. For the input, each sample is a vector of 27 intensity values. Only pixels whose intensity is between 100 and 700 are kept for training and prediction.
The second axis of development concerned registration. When a patient have several scans taken at different times, the segmentations are not in the same frame so any comparison would be complicated. The objective was to bring the second segmentation in the frame of the first one. We tested different points-based approaches: register the centerline of the segmentation or the geometry; consider only the lumen or the entire aneurysm. The best results were obtained with the surface of the aneurysm and the iterative closest point algorithm. Once the registration is performed (Figure 16) we can visualize how the aneurysm has evolved.
9 Bilateral contracts and grants with industry
9.1 Bilateral Contracts with Industry
EDF ROM HYDRAU dates: 15/08/2020 au 15/12/2021
10 Partnerships and cooperations
10.1 International Initiatives
10.1.1 Inria International Labs
MARE
- Title: Multiscale Accurate Reduced-order model Enablers
- Duration: 2019 - 2022
- Coordinator: Angelo Iollo
- Partners: VNU University of Engineering and Technology, Stanford (United States)
- Inria contact: Angelo Iollo
- Summary: Reduced-order models (ROMs) are simplified mathematical models derived from the full set of partial differential equations governing the physics of the phenomenon of interest. We focus on ROMs that are data-driven as they are based on relevant solution data previously obtained. In particular we will focus on multiscale adaptive models where the large scales are governed by a PDE and the small scales are described by data driven models. To do that we will leverage on tools from data geometry, numerical PDEs and machine learning.
10.1.2 Inria International Partners
Declared Inria International Partners
Politecnico di Torino (Giovanni Bracco, Francesco Larocca), with two co-tutelle PhDs:
Beatrice BATTISTI (Sujet : Multi-fidelity Multi-scale numerical modelling og wave energy converters farms)
Thomas PHILIBERT (Sujet : Data-driven models for aerospace propulsion)
Informal International Partners
La Sapienza Universita' di Roma (Gabriella Puppo, Dipartimento di Matematica)
Università di Pisa (UNIPI) (Simone Camarri, Department of Civil and Industrial Engineering)
10.2 International Research Visitors
10.2.1 Visits of International Scientists
Victor Zucatti Da Silva, Master Student (equivalent to first years PhD) from Campinas University, Brazil. Six-month visit from November 2019 to May 2020.
10.2.2 Visits to International Teams
Research Stays Abroad
Sébastien Riffaud (Stanford, MARE Associated Team): 26/01/20 - 05/04/20
Antoine Fondanèche (Torino, ARIA project): 29/02/20 - 14/03/20
Michele Giuliano Carlino (Torino, ARIA project): 31/01/20 - 27/07/20 and 01/09/20 - 01/02/21
Lei Zhang (Turin, ARIA project): 01/02/20 - 02/03/20
Angelo Iollo (Torino, ARIA project): 29/02/20 - 07/03/20 and 14/07/20 - 27/07/20
Tommaso Taddei (Torino, ARIA project): 12/07/20 - 24/07/20
10.3 European Initiatives
10.3.1 FP7 & H2020 Projects
ARIA
- Title: Accurate Roms for Industrial Applications
- Duration: 01 December 2019 - 30 November 2023
- Coordinator: Angelo Iollo
-
Partners:
- STANFORD: Aeronautics & Astronautics Department (United States)
- ESTECO SpA: Department of Research and Development (Italy)
- Politecnico di Milano: Laboratory for Modeling and Scientific Computing (MOX) (Italy)
- Politecnico di Torino: Department of Science and Mathematics (Italy)
- Scuola Internazionale Superiore di Studi Avanzati di Trieste: Mathematics Area/mathLab (Italy)
- Universidad de Sevilla: Instituto de Matemáticas de la Universidad de Sevilla (IMUS) (Spain)
- University of South Carolina: Department of Mathematics (United States)
- VALOREM SAS: R&D Department (France)
- Virginia Tech - Department of Mathematics (United States)
- Virtualmechanics, S.L. (Spain)
- Optimad: R&D Department (Italy)
- Volkswagen AG: Group Research, Vehicle Technology (Germany)
- Inria contact: contact@rise-aria.eu
- Summary: The project Accurate Roms for Industrial Applications aims at developing an array of mathematical methods for constructing predictive reduced-order models (ROMs) with guaranteed accuracy, robustness, reliability and efficiency for applications involving complex physical phenomena. New approaches to this challenge are proposed here with a focus on the Euler and Navier–Stokes equations of fluid flow, two of the most challenging continuum models with an extraordinary rich range of industrial applications. The mathematical modeling and solution of the Euler and Navier-Stokes equations is sometimes cited as the greatest challenge in continuum modeling of physical phenomena. This topic is selected as our principal focus because of its intrinsic importance, but also because the mathematical methods developed in addressing this very challenging task may well have an impact on other fields of knowledge. We plan to tackle these challenging objectives in this staff exchange program by combining the unique expertise of our extended research team whose members have made significant progress in ROM research during the past decade. This academic expertise is cross-fertilized by the exchange with knowledge intensive SMEs ans start up and well established industrial partners that will benefit from the scientific and technological results of the team and will challenge the solutions found with applications in real world problems.
10.3.2 Collaborations with Major European Organizations
EDF ROM HYDRAU : dates: 15/08/2020 au 15/12/2021
10.4 National Initiatives
We are part of the GDR AMORE on ROMs.
PEPS DYNAMO : dates : 01/03/2019 au 30/04/2020
10.5 Regional Initiatives
RNA 19 MDPAA (Post-doc of Gwladys Ravon, ) : dates : 14/01/2019 au 13/01/2024
Projet IDEX EMERGENCE : dates : 01/12/2019 au 31/12/2021
11 Dissemination
11.1 Promoting Scientific Activities
Angelo Iollo: Responsible of the Applied Mathematics Master of the University of Bordeaux. From september 2016 up septembre 2020.
Angelo Iollo: 2019-. Nominated at the council of "Département de Sciences du Numérique et Ingénierie" of the université de Bordeaux.
11.1.1 Scientific Events: Organisation
Workshop "Reduced-order models at work: Industry and Medicine" (This workshop has been canceled due to the COVID-19), organized by Bergmann M., Iollo A. and Taddei T.
Member of the Editorial Boards
Michel Bergmann : topic Editors in FLUIDS, guest Editor in FLUIDS (special issue Scientific Computing in Fluids), guest Editor in Frontiers in Physics (special issue related to multi-fidelity models)
Reviewer - Reviewing Activities
The members of the team were reviewers for:
Journal of Computational Physics, International Journal of CFD, Journal of Non-linear Analysis B, ASME Journal of Computational and Nonlinear Dynamics, Journal of Fluid Mechanics, Acta Mechanica, AIAA Journal, International Journal Numerical Methods in Fluids, Computers & Fluids, Journal of Engineering Mathematics, European Journal of Mechanics / B Fluids, Journal Européen de Systèmes Automatisés, Applied Mathematics and Computation. Nuclear Science and Engineering, Computer Methods in Applied Mechanics and Engineering, Journal of Theoretical Biology, Computational Optimization and Applications, Applied science, Meccanica, SIAM journal on scientific computing, SIAM journal on uncertainty quantification, Advances in Computational Mathematics.
11.1.2 Invited Talks
Angelo Iollo: February 5th 2020, Conference in Honor of 60 years of Gabriella Puppo. University of Rome. Conférencier invité. http://
11.1.3 Scientific Expertise
Angelo Iollo was expert for the EU, FET open program.
11.1.4 Teaching
Four members of the team are Professors or Assistant Professors at Bordeaux University and have teaching duties, which consist in courses and practical exercises in numerical analysis and scientific computing. Michel Bergmann (CR) also teaches around 64 hours per year (practical exercises in programming for scientific computing). Tommaso Taddei (CR) also teaches around 50 hours per year (practical exercises in numerical analysis and scientific computing).
11.1.5 Supervision
- 2020-2023. Ludovica Saccaro. Inria Scholarship. Identification of mechanical biomarkers for assessing the risk of rupture of abdominal aortic aneurysms. Advisor: Angelo Iollo.
- 2020-2023. Thomas Philibert. Bourse cotuelle PoliTO (Turin, Italie). Convergence between models and data for the simulation of turbulent flows in aeronautical propulsion. Advisors: Angelo Iollo, Francesco Larocca.
- 2020-2023. Beatrice Battisti. Bourse cotuelle PoliTO (Turin, Italie). Multi-fidelity multi-scale numerical modelling of wave energy converters farms. Advisors: Michel Bergmann, Giovanni Bracco.
- 2019-2022. Giulia Sambataro. Bourse ANDRA. Component-based reduction strategies for THM equations. Advisors: Angelo Iollo, Tommaso Taddei.
- 2018-2021. Michele Giuliano Carlino. Bourse Inria. Fluid-structure Interactions models on Chimera grids. Advisors: Michel Bergmann, Angelo Iollo.
- 2018-2021. Antoine Fondanèche. Bourse UB. Interaction fluide-structure dans les endoprothèses et autres dispositifs vasculaires actifs. Advisors: Michel Bergmann, Angelo Iollo.
- 2017-2020. Sebastien Riffaud. Convergence between data and numerical models. Advisor: Angelo Iollo.
- 2017-2020. Luis Ramos Benetti. Bourse ERC Aeroflex (O. Marquet, ONERA). Auto-propulsion et interaction hydrodynamique d'ailes battantes dans des écoulements visqueux. Advisors: Michel Bergmann, Angelo Iollo.
- 2017-2020. Guillaume Ravel. Bourse Univ. Bordeaux. Modélisation tridimensionnelle et simulation numérique basée sur une approche expérimentale de la nage de fuite du poisson-zèbre pour des applications biologiques. Advisors: Afaf Bouharguane, Patrick Babin.
11.1.6 Juries
Angeo Iollo: reviewer of 3 PhD theses, president of one PhD jury, member of one PhD jury, in France and abroad.
Angelo Iollo. 2020 juin. Recruitement jury of a Professor position « Traitement du signal et mathématiques appliquées en santé », Université de Bordeaux.
Angelo Iollo. 2020 mai. Rapport d’évaluation pour une candidature à assistant professor au Technion, Israel.
Michel Bergmann: comité de selection, Maître de conférences, Strasbourg.
12 Scientific production
12.1 Major publications
- 1 articleAn all-speed relaxation scheme for gases and compressible materialsJournal of Computational Physics3512017, 1-24
- 2 articleFluid--solid Floquet stability analysis of self-propelled heaving foilsJournal of Fluid Mechanics9102021, A28
- 3 articleEnablers for robust POD modelsJournal of Computational Physics22822009, 516--538
- 4 articleAn accurate cartesian method for incompressible flows with moving boundariesCommunications in Computational Physics1552014, 1266--1290
- 5 articleBioinspired swimming simulationsJournal of Computational Physics3232016, 310 - 321
- 6 articleModeling and simulation of fish-like swimmingJournal of Computational Physics23022011, 329 - 348
- 7 articleAccurate Asymptotic Preserving Boundary Conditions for Kinetic Equations on Cartesian GridsJournal of Scientific Computing2015, 34
- 8 article Numerical solution of the Monge--Kantorovich problem by density lift-up continuation ESAIM: Mathematical Modelling and Numerical Analysis 49 6 1577 November 2015
- 9 articleA Cartesian Scheme for Compressible Multimaterial Models in 3DJournal of Computational Physics3132016, 121-143
- 10 articleEnablers for high-order level set methods in fluid mechanicsInternational Journal for Numerical Methods in Fluids79December 2015, 654-675
12.2 Publications of the year
International journals
Scientific book chapters
Reports & preprints
12.3 Cited publications
- 25 articleA penalization method to take into account obstacles in a incompressible flowNumerische Mathematik8141999, 497-520
- 26 article Koopman-mode decomposition of the cylinder wake Journal of Fluid Mechanics 2013
- 27 articleExact and approximate solutions of Riemann problems in non-linear elasticityJournal of Computational Physics228182009, 7046-7068
- 28 articleEnablers for robust POD modelsJournal of Computational Physics22822009, 516--538
- 29 articleA zonal Galerkin-free POD model for incompressible flowsJournal of Computational Physics3522018, 301--325
- 30 articleNumerical solution of the Monge-Kantorovich problem by density lift-up continuationESAIM: M2AN4962015, 1577-1592
- 31 articleA Cartesian scheme for compressible multimaterial models in 3DJournal of Computational Physics3132016, 121-143URL: http://www.sciencedirect.com/science/article/pii/S0021999116000966
- 32 articleAn experimental study of entrainment and transport in the turbulent near wake of a circular cylinderJournal of fluid mechanics1361983, 321--374
- 33 incollection Two typical applications of POD: coherent structures eduction and reduced order modelling Lecture series 2002-04 on post-processing of experimental and numerical data Von Kármán Institute for Fluid Dynamics 2002
- 34 articleModelling wave dynamics of compressible elastic materialsJournal of Computational Physics22752008, 2941-2969
- 35 book Elements of continuum mechanics Nauka Moscow 1978
- 36 phdthesis Construction d'une chaîne d'outils numériques pour la conception aérodynamique de pales d'éoliennes Université de Bordeaux 2014
- 37 articleLocal lubrication model for spherical particles within incompressible Navier-Stokes flowsPhys. Rev. E973Mar 2018, 033313URL: https://link.aps.org/doi/10.1103/PhysRevE.97.033313
- 38 articleEnablers for high-order level set methods in fluid mechanicsInternational Journal for Numerical Methods in Fluids79December 2015, 654-675
- 39 articleAtmospheric turbulence and wave propagationThe structure of inhomogeneous turbulence, AM Yaglom & VI Tatarski1967, 166--178
- 40 article Spectral Properties of Dynamical Systems, Model Reduction and Decompositions Nonlinear Dynamics 41 1 2005
- 41 articleA Conservative Three-Dimensional Eulerian Method for Coupled Solid-Fluid Shock CapturingJournal of Computational Physics18312002, 26-82
- 42 articleImmersed boundary methodsAnnu. Rev. Fluid Mech.372005, 239-261
- 43 articleDynamic mode decomposition of numerical and experimental dataJournal of Fluid Mechanics656008 2010, 5-28
- 44 book Level Set Methods and Fast Marching Methods Cambridge University Press, Cambridge, UK 1999
- 45 articleTurbulence and the dynamics of coherent structuresQuarterly of Applied MathematicsXLV31987, 561-590
- 46 articleA registration method for model order reduction: data compression and geometry reductionSIAM Journal on Scientific Computing4222020, A997--A1027
- 47 article Registration-based model reduction in complex two-dimensional geometries submitted to Journal of Scientific Computing 2021
- 48 article Space-time registration-based model reduction of parameterized one-dimensional hyperbolic PDEs ESAIM: Mathematical Modelling and Numerical Analysis (accepted) 2020
- 49 articleThe immersed boundary method: a projection approachJournal of Computational Physics22522007, 2118-2137
- 50 book Topics in optimal transportation American Mathematical Society 2003

