Keywords
Computer Science and Digital Science
- A5.3. Image processing and analysis
- A5.9. Signal processing
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.6. Optimization
Other Research Topics and Application Domains
- B1.2. Neuroscience and cognitive science
- B9.5.2. Mathematics
- B9.5.3. Physics
- B9.5.4. Chemistry
- B9.6.3. Economy, Finance
1 Team members, visitors, external collaborators
Research Scientists
- Jean-David Benamou [Team leader, Inria, Senior Researcher, HDR]
- Vincent Duval [Inria, Senior Researcher]
- Thomas Gallouèt [Inria, Researcher]
- Irene Waldspurger [Université Paris Sciences et Lettres, Researcher]
Faculty Members
- Guillaume Carlier [Université Paris Sciences et Lettres, Professor, HDR]
- Bruno Nazaret [Université Panthéon Sorbonne, Professor, until Aug 2020]
- Paul Pegon [Université Paris Sciences et Lettres, Professor]
Post-Doctoral Fellows
- Guillaume Mijoule [Inria, until Jun 2020]
- Vincent Reverdy [Ecole normale supérieure Paris-Saclay]
- Luca Tamanini [Université Paris Sciences et Lettres]
PhD Students
- Paul Catala [Ecole normale supérieure Paris-Saclay, until Jun 2020]
- Katharina Eichinger [Université Paris Sciences et Lettres]
- Lucas Martinet [Université Paris Sciences et Lettres, until Oct 2020]
- Romain Petit [Université Paris Sciences et Lettres]
- Quentin Ismael Petit [Université Paris Sciences et Lettres]
- Giorgi Rukhaia [Inria]
- Gabriele Todeschi [Université Paris Sciences et Lettres]
- Adrien Vacher [Université Paris-Est Marne La Vallée, from Jul 2020]
Technical Staff
- Guillaume Chazareix [Inria, Engineer, from Oct 2020]
- Robert Tovey [Inria, Engineer, from Oct 2020]
Interns and Apprentices
- Guillaume Chazareix [Inria, from Mar 2020 until Aug 2020]
- Jean Jacques Godeme [CNRS, from Apr 2020 until Sep 2020]
Administrative Assistant
- Derya Gök [Inria]
Visiting Scientist
- Max Fathi [CNRS, until Mar 2020]
External Collaborators
- Xavier Bacon [Université Panthéon Sorbonne]
- Yann Brenier [CNRS]
- Paul Catala [École Normale Supérieure de Paris, from Jul 2020]
- Yohann De Castro [École centrale de Lyon]
- Quentin Merigot [Université Paris-Saclay]
- Guillaume Mijoule [Ministère de l'Education Nationale, from Jul 2020]
- Andrea Natale [Université Paris-Saclay, until Oct 2020]
- Bruno Nazaret [Université Panthéon Sorbonne, from Sep 2020]
- Gabriel Peyré [CNRS, HDR]
- François-Xavier Vialard [Université Paris-Est Marne La Vallée]
- Miao Yu [Université Denis Diderot]
- Shuangjian Zhang [Ecole normale supérieure Paris-Saclay]
- Gwendoline de Bie [Ecole normale supérieure Paris-Saclay]
2 Overall objectives
2.1 Introduction
vvvv The last decade has witnessed a remarkable convergence between several sub-domains of the calculus of variations, namely optimal transport (and its many generalizations), infinite dimensional geometry of diffeomorphisms groups and inverse problems in imaging (in particular sparsity-based regularization). This convergence is due to (i) the mathematical objects manipulated in these problems, namely sparse measures (e.g. coupling in transport, edge location in imaging, displacement fields for diffeomorphisms) and (ii) the use of similar numerical tools from non-smooth optimization and geometric discretization schemes. Optimal Transportation, diffeomorphisms and sparsity-based methods are powerful modeling tools, that impact a rapidly expanding list of scientific applications and call for efficient numerical strategies. Our research program shows the important part played by the team members in the development of these numerical methods and their application to challenging problems.
2.2 Static Optimal Transport and Generalizations
Optimal Transport, Old and New.
Optimal Mass Transportation is a mathematical research topic which started two centuries ago with Monge's work on the “Théorie des déblais et des remblais" (see 95). This engineering problem consists in minimizing the transport cost between two given mass densities. In the 40's, Kantorovich 102 introduced a powerful linear relaxation and introduced its dual formulation. The Monge-Kantorovich problem became a specialized research topic in optimization and Kantorovich obtained the 1975 Nobel prize in economics for his contributions to resource allocations problems. Since the seminal discoveries of Brenier in the 90's 48, Optimal Transportation has received renewed attention from mathematical analysts and the Fields Medal awarded in 2010 to C. Villani, who gave important contributions to Optimal Transportation and wrote the modern reference monographs 141, 142, arrived at a culminating moment for this theory. Optimal Mass Transportation is today a mature area of mathematical analysis with a constantly growing range of applications. Optimal Transportation has also received a lot of attention from probabilists (see for instance the recent survey 107 for an overview of the Schrödinger problem which is a stochastic variant of the Benamou-Brenier dynamical formulation of optimal transport). The development of numerical methods for Optimal Transportation and Optimal Transportation related problems is a difficult topic and comparatively underdeveloped. This research field has experienced a surge of activity in the last five years, with important contributions of the Mokaplan group (see the list of important publications of the team). We describe below a few of recent and less recent Optimal Transportation concepts and methods which are connected to the future activities of Mokaplan :
Brenier's theorem 51 characterizes the unique optimal map as the gradient of a convex potential. As such Optimal Transportation may be interpreted as an infinite dimensional optimisation problem under “convexity constraint": i.e. the solution of this infinite dimensional optimisation problem is a convex potential. This connects Optimal Transportation to “convexity constrained" non-linear variational problems such as, for instance, Newton's problem of the body of minimal resistance. The value function of the optimal transport problem is also known to define a distance between source and target densities called the Wasserstein distance which plays a key role in many applications such as image processing.
Monge-Ampère Methods.
A formal substitution of the optimal transport map as the gradient of a convex potential in the mass conservation constraint (a Jacobian equation) gives a non-linear Monge-Ampère equation. Caffarelli 59 used this result to extend the regularity theory for the Monge-Ampère equation. In the last ten years, it also motivated new research on numerical solvers for non-linear degenerate Elliptic equations 8311136 35 and the references therein. Geometric approaches based on Laguerre diagrams and discrete data 116 have also been developed. Monge-Ampère based Optimal Transportation solvers have recently given the first linear cost computations of Optimal Transportation (smooth) maps.
Generalizations of OT.
In recent years, the classical Optimal Transportation problem has been extended in several directions. First, different ground costs measuring the “physical" displacement have been considered. In particular, well posedness for a large class of convex and concave costs has been established by McCann and Gangbo 94. Optimal Transportation techniques have been applied for example to a Coulomb ground cost in Quantum chemistry in relation with Density Functional theory 79. Given the densities of electrons Optimal Transportation models the potential energy and their relative positions. For more than more than 2 electrons (and therefore more than 2 densities) the natural extension of Optimal Transportation is the so called Multi-marginal Optimal Transport (see 123 and the references therein). Another instance of multi-marginal Optimal Transportation arises in the so-called Wasserstein barycenter problem between an arbitrary number of densities 20. An interesting overview of this emerging new field of optimal transport and its applications can be found in the recent survey of Ghoussoub and Pass 122.

Example of color transfer between two images, computed using the method developed in 32, see also 135. The image framed in red and blue are the input images. Top and middle row: adjusted image where the color of the transported histogram has been imposed. Bottom row: geodesic (displacement) interpolation between the histogram of the chrominance of the image.
Numerical Applications of Optimal Transportation.
Optimal transport has found many applications, starting from its relation with several physical models such as the semi-geostrophic equations in meteorology 99, 81, 80, 29, 110, mesh adaptation 109, the reconstruction of the early mass distribution of the Universe 91, 49 in Astrophysics, and the numerical optimisation of reflectors following the Optimal Transportation interpretation of Oliker 58 and Wang 143. Extensions of OT such as multi-marginal transport has potential applications in Density Functional Theory , Generalized solution of Euler equations 50 (DFT) and in statistics and finance 26, 93 .... Recently, there has been a spread of interest in applications of OT methods in imaging sciences 43, statistics 40 and machine learning 82. This is largely due to the emergence of fast numerical schemes to approximate the transportation distance and its generalizations, see for instance 32. Figure 1 shows an example of application of OT to color transfer. Figure 9 shows an example of application in computer graphics to interpolate between input shapes.
2.3 Diffeomorphisms and Dynamical Transport
Dynamical transport.
While the optimal transport problem, in its original formulation, is a static problem (no time evolution is considered), it makes sense in many applications to rather consider time evolution. This is relevant for instance in applications to fluid dynamics or in medical images to perform registration of organs and model tumor growth.
In this perspective, the optimal transport in Euclidean space corresponds to an evolution where each particule of mass evolves in straight line. This interpretation corresponds to the Computational Fluid Dynamic (CFD) formulation proposed by Brenier and Benamou in 28. These solutions are time curves in the space of densities and geodesics for the Wasserstein distance. The CFD formulation relaxes the non-linear mass conservation constraint into a time dependent continuity equation, the cost function remains convex but is highly non smooth. A remarkable feature of this dynamical formulation is that it can be re-cast as a convex but non smooth optimization problem. This convex dynamical formulation finds many non-trivial extensions and applications, see for instance 30. The CFD formulation also appears to be a limit case of Mean Fields games (MFGs), a large class of economic models introduced by Lasry and Lions 104 leading to a system coupling an Hamilton-Jacobi with a Fokker-Planck equation. In contrast, the Monge case where the ground cost is the euclidan distance leads to a static system of PDEs 45.
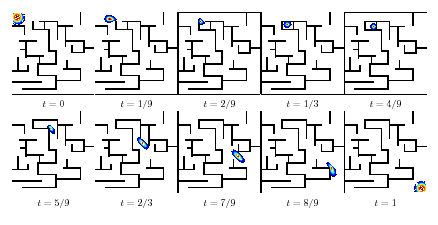
Examples of displacement interpolation (geodesic for optimal transport) according to a non-Euclidean Riemannian metric (the mass is constrained to move inside a maze) between to input Gaussian distributions. Note that the maze is dynamic: its topology change over time, the mass being “trapped” at time .
Gradient Flows for the Wasserstein Distance.
Another extension is, instead of considering geodesic for transportation metric (i.e. minimizing the Wasserstein distance to a target measure), to make the density evolve in order to minimize some functional. Computing the steepest descent direction with respect to the Wasserstein distance defines a so-called Wasserstein gradient flow, also known as JKO gradient flows after its authors 101. This is a popular tool to study a large class of non-linear diffusion equations. Two interesting examples are the Keller-Segel system for chemotaxis 100, 74 and a model of congested crowd motion proposed by Maury, Santambrogio and Roudneff-Chupin 115. From the numerical point of view, these schemes are understood to be the natural analogue of implicit scheme for linear parabolic equations. The resolution is however costly as it involves taking the derivative in the Wasserstein sense of the relevant energy, which in turn requires the resolution of a large scale convex but non-smooth minimization.
Geodesic on infinite dimensional Riemannian spaces.
To tackle more complicated warping problems, such as those encountered in medical image analysis, one unfortunately has to drop the convexity of the functional involved in defining the gradient flow. This gradient flow can either be understood as defining a geodesic on the (infinite dimensional) group of diffeomorphisms 25, or on a (infinite dimensional) space of curves or surfaces 144. The de-facto standard to define, analyze and compute these geodesics is the “Large Deformation Diffeomorphic Metric Mapping” (LDDMM) framework of Trouvé, Younes, Holm and co-authors 25, 98. While in the CFD formulation of optimal transport, the metric on infinitesimal deformations is just the norm (measure according to the density being transported), in LDDMM, one needs to use a stronger regularizing metric, such as Sobolev-like norms or reproducing kernel Hilbert spaces (RKHS). This enables a control over the smoothness of the deformation which is crucial for many applications. The price to pay is the need to solve a non-convex optimization problem through geodesic shooting method 118, which requires to integrate backward and forward the geodesic ODE. The resulting strong Riemannian geodesic structure on spaces of diffeomorphisms or shapes is also pivotal to allow us to perform statistical analysis on the tangent space, to define mean shapes and perform dimensionality reduction when analyzing large collection of input shapes (e.g. to study evolution of a diseases in time or the variation across patients) 60.
2.4 Sparsity in Imaging
Sparse regularization.
Beside image warping and registration in medical image analysis, a key problem in nearly all imaging applications is the reconstruction of high quality data from low resolution observations. This field, commonly referred to as “inverse problems”, is very often concerned with the precise location of features such as point sources (modeled as Dirac masses) or sharp contours of objects (modeled as gradients being Dirac masses along curves). The underlying intuition behind these ideas is the so-called sparsity model (either of the data itself, its gradient, or other more complicated representations such as wavelets, curvelets, bandlets 114 and learned representation 145).
The huge interest in these ideas started mostly from the introduction of convex methods to serve as proxy for these sparse regularizations. The most well known is the norm introduced independently in imaging by Donoho and co-workers under the name “Basis Pursuit” 77 and in statistics by Tibshirani 136 under the name “Lasso”. A more recent resurgence of this interest dates back to 10 years ago with the introduction of the so-called “compressed sensing” acquisition techniques 63, which make use of randomized forward operators and -type reconstruction.
Regularization over measure spaces.
However, the theoretical analysis of sparse reconstructions involving real-life acquisition operators (such as those found in seismic imaging, neuro-imaging, astro-physical imaging, etc.) is still mostly an open problem. A recent research direction, triggered by a paper of Candès and Fernandez-Granda 62, is to study directly the infinite dimensional problem of reconstruction of sparse measures (i.e. sum of Dirac masses) using the total variation of measures (not to be mistaken for the total variation of 2-D functions). Several works 61, 87, 84 have used this framework to provide theoretical performance guarantees by basically studying how the distance between neighboring spikes impacts noise stability.

|

|

|

|
| Segmentation input | output | Zooming input | output |
Two example of application of the total variation regularization of functions. Left: image segmentation into homogeneous color regions. Right: image zooming (increasing the number of pixels while keeping the edges sharp).
Low complexity regularization and partial smoothness.
In image processing, one of the most popular methods is the total variation regularization 131, 55. It favors low-complexity images that are piecewise constant, see Figure 3 for some examples on how to solve some image processing problems. Beside applications in image processing, sparsity-related ideas also had a deep impact in statistics 136 and machine learning 23. As a typical example, for applications to recommendation systems, it makes sense to consider sparsity of the singular values of matrices, which can be relaxed using the so-called nuclear norm (a.k.a. trace norm) 22. The underlying methodology is to make use of low-complexity regularization models, which turns out to be equivalent to the use of partly-smooth regularization functionals 108, 138 enforcing the solution to belong to a low-dimensional manifold.
2.5 Mokaplan unified point of view
The dynamical formulation of optimal transport creates a link between optimal transport and geodesics on diffeomorphisms groups. This formal link has at least two strong implications that Mokaplan will elaborate on: (i) the development of novel models that bridge the gap between these two fields ; (ii) the introduction of novel fast numerical solvers based on ideas from both non-smooth optimization techniques and Bregman metrics, as highlighted in Section 3.2.3.
In a similar line of ideas, we believe a unified approach is needed to tackle both sparse regularization in imaging and various generalized OT problems. Both require to solve related non-smooth and large scale optimization problems. Ideas from proximal optimization has proved crucial to address problems in both fields (see for instance 28, 129). Transportation metrics are also the correct way to compare and regularize variational problems that arise in image processing (see for instance the Radon inversion method proposed in 32) and machine learning (see 82). This unity in term of numerical methods is once again at the core of Section 3.2.3.
3 Research program
3.1 Modeling and Analysis
The first layer of methodological tools developed by our team is a set of theoretical continuous models that aim at formalizing the problems studied in the applications. These theoretical findings will also pave the way to efficient numerical solvers that are detailed in Section 3.2.
3.1.1 Static Optimal Transport and Generalizations
Convexity constraint and Principal Agent problem in Economics.
(Participants: G. Carlier, J-D. Benamou, V. Duval, Xavier Dupuis (LUISS Guido Carli University, Roma)) The principal agent problem plays a distinguished role in the literature on asymmetric information and contract theory (with important contributions from several Nobel prizes such as Mirrlees, Myerson or Spence) and it has many important applications in optimal taxation, insurance, nonlinear pricing. The typical problem consists in finding a cost minimizing strategy for a monopolist facing a population of agents who have an unobservable characteristic, the principal therefore has to take into account the so-called incentive compatibilty constraint which is very similar to the cyclical monotonicity condition which characterizes optimal transport plans. In a special case, Rochet and Choné 130 reformulated the problem as a variational problem subject to a convexity constraint. For more general models, and using ideas from Optimal Transportation, Carlier 65 considered the more general -convexity constraint and proved a general existence result. Using the formulation of 65 McCann, Figalli and Kim 88 gave conditions under which the principal agent problem can be written as an infinite dimensional convex variational problem. The important results of 88 are intimately connected to the regularity theory for optimal transport and showed that there is some hope to numerically solve the principal-agent problem for general utility functions.
Our expertise: We have already contributed to the numerical resolution of the Principal Agent problem in the case of the convexity constraint, see 70, 117, 119.
Goals: So far, the mathematical PA model can be numerically solved for simple utility functions. A Bregman approach inspired by 32 is currently being developed 68 for more general functions. It would be extremely useful as a complement to the theoretical analysis. A new semi-Discrete Geometric approach is also investigated where the method reduces to non-convex polynomial optimization.
Optimal transport and conditional constraints in statistics and finance.
(Participants: G. Carlier, J-D. Benamou, G. Peyré) A challenging branch of emerging generalizations of Optimal Transportation arising in economics, statistics and finance concerns Optimal Transportation with conditional constraints. The martingale optimal transport 26, 93 which appears naturally in mathematical finance aims at computing robust bounds on option prices as the value of an optimal transport problem where not only the marginals are fixed but the coupling should be the law of a martingale, since it represents the prices of the underlying asset under the risk-neutral probability at the different dates. Note that as soon as more than two dates are involved, we are facing a multimarginal problem.
Our expertise: Our team has a deep expertise on the topic of OT and its generalization, including many already existing collaboration between its members, see for instance 32, 37, 30 for some representative recent collaborative publications.
Goals: This is a non trivial extension of Optimal Transportation theory and Mokaplan will develop numerical methods (in the spirit of entropic regularization) to address it. A popular problem in statistics is the so-called quantile regression problem, recently Carlier, Chernozhukov and Galichon 66 used an Optimal Transportation approach to extend quantile regression to several dimensions. In this approach again, not only fixed marginals constraints are present but also constraints on conditional means. As in the martingale Optimal Transportation problem, one has to deal with an extra conditional constraint. The duality approach usually breaks down under such constraints and characterization of optimal couplings is a challenging task both from a theoretical and numerical viewpoint.
JKO gradient flows.
(Participants: G. Carlier, J-D. Benamou, M. Laborde, Q. Mérigot, V. Duval) The connection between the static and dynamic transportation problems (see Section 2.3) opens the door to many extensions, most notably by leveraging the use of gradient flows in metric spaces. The flow with respect to the transportation distance has been introduced by Jordan-Kindelherer-Otto (JKO) 101 and provides a variational formulation of many linear and non-linear diffusion equations. The prototypical example is the Fokker Planck equation. We will explore this formalism to study new variational problems over probability spaces, and also to derive innovative numerical solvers. The JKO scheme has been very successfully used to study evolution equations that have the structure of a gradient flow in the Wasserstein space. Indeed many important PDEs have this structure: the Fokker-Planck equation (as was first considered by 101), the porous medium equations, the granular media equation, just to give a few examples. It also finds application in image processing 54. Figure 4 shows examples of gradient flows.
Our expertise: There is an ongoing collaboration between the team members on the theoretical and numerical analysis of gradient flows.
Goals: We apply and extend our research on JKO numerical methods to treat various extensions:
- Wasserstein gradient flows with a non displacement convex energy (as in the parabolic-elliptic Keller-Segel chemotaxis model 72)
- systems of evolution equations which can be written as gradient flows of some energy on a product space (possibly mixing the Wasserstein and structures) : multi-species models or the parabolic-parabolic Keller-Segel model 41
- perturbation of gradient flows: multi-species or kinetic models are not gradient flows, but may be viewed as a perturbation of Wasserstein gradient flows, we shall therefore investigate convergence of splitting methods for such equations or systems.
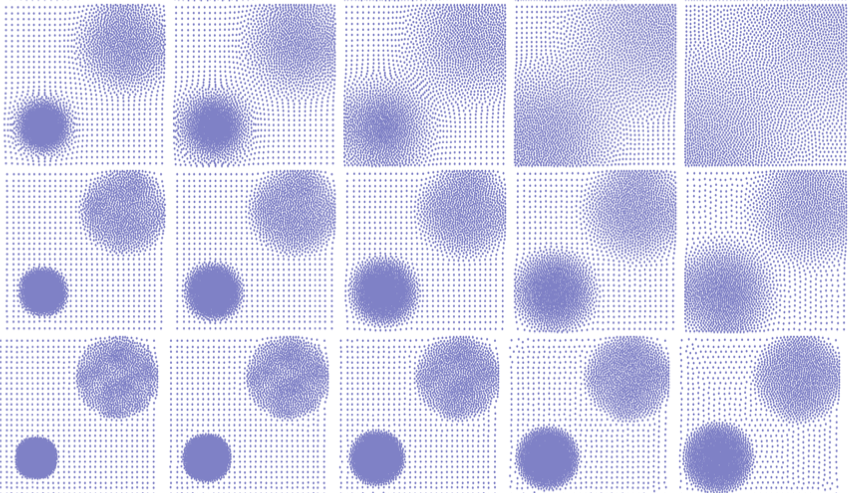
Example of non-linear diffusion equations solved with a JKO flow 33. The horizontal axis shows the time evolution minimizing the functional on the density (discretized here using point clouds, i.e. sum of Diracs' with equal mass). Each row shows a different value of
From networks to continuum congestion models.
(Participants: G. Carlier, J-D. Benamou, G. Peyré) Congested transport theory in the discrete framework of networks has received a lot of attention since the 50's starting with the seminal work of Wardrop. A few years later, Beckmann proved that equilibria are characterized as solution of a convex minimization problem. However, this minimization problem involves one flow variable per path on the network, its dimension thus quickly becomes too large in practice. An alternative, is to consider continuous in space models of congested optimal transport as was done in 69 which leads to very degenerate PDEs 46.
Our expertise: MOKAPLAN members have contributed a lot to the analysis of congested transport problems and to optimization problems with respect to a metric which can be attacked numerically by fast marching methods 37.
Goals: The case of general networks/anisotropies is still not well understood, general -convergence results will be investigated as well as a detailed analysis of the corresponding PDEs and numerical methods to solve them. Benamou and Carlier already studied numerically some of these PDEs by an augmented Lagrangian method see figure 5. Note that these class of problems share important similarities with metric learning problem in machine learning, detailed below.
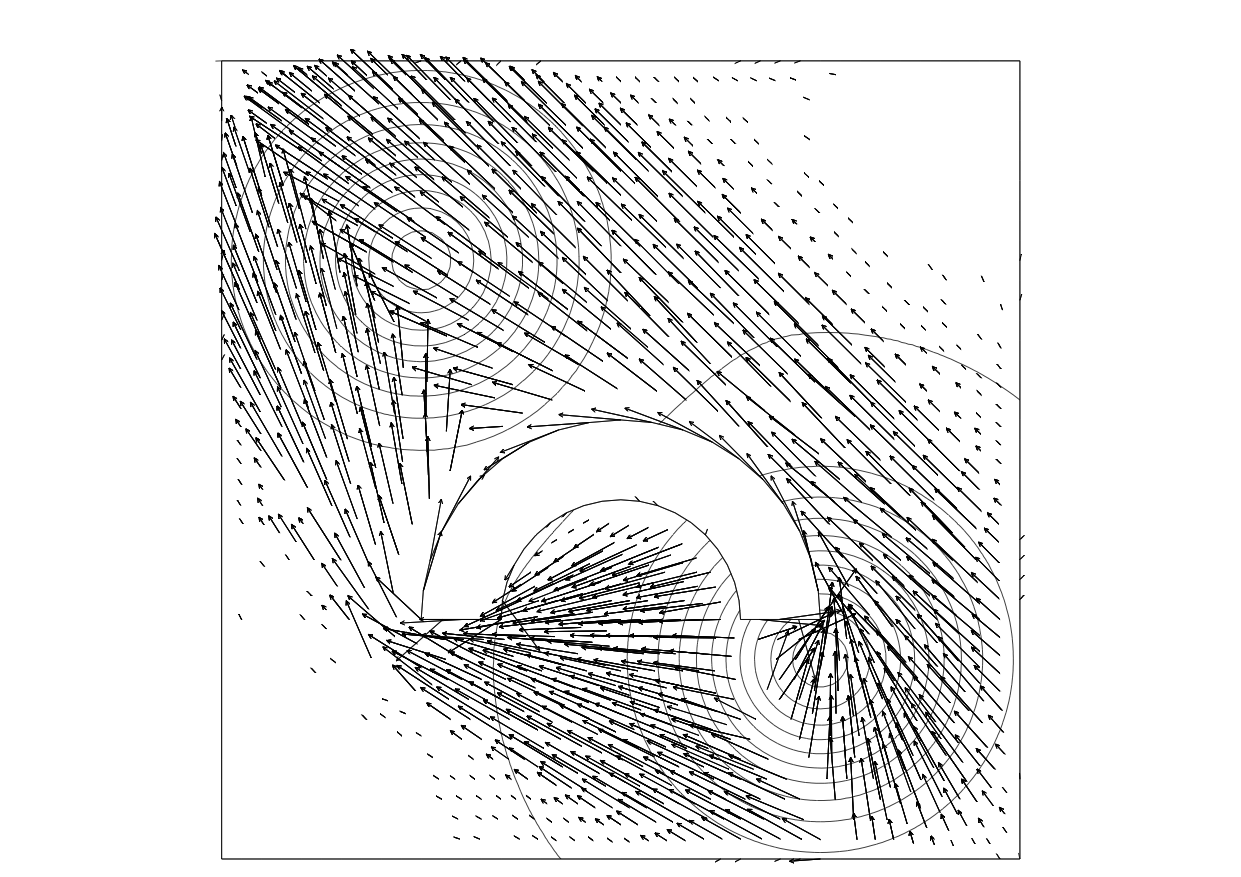
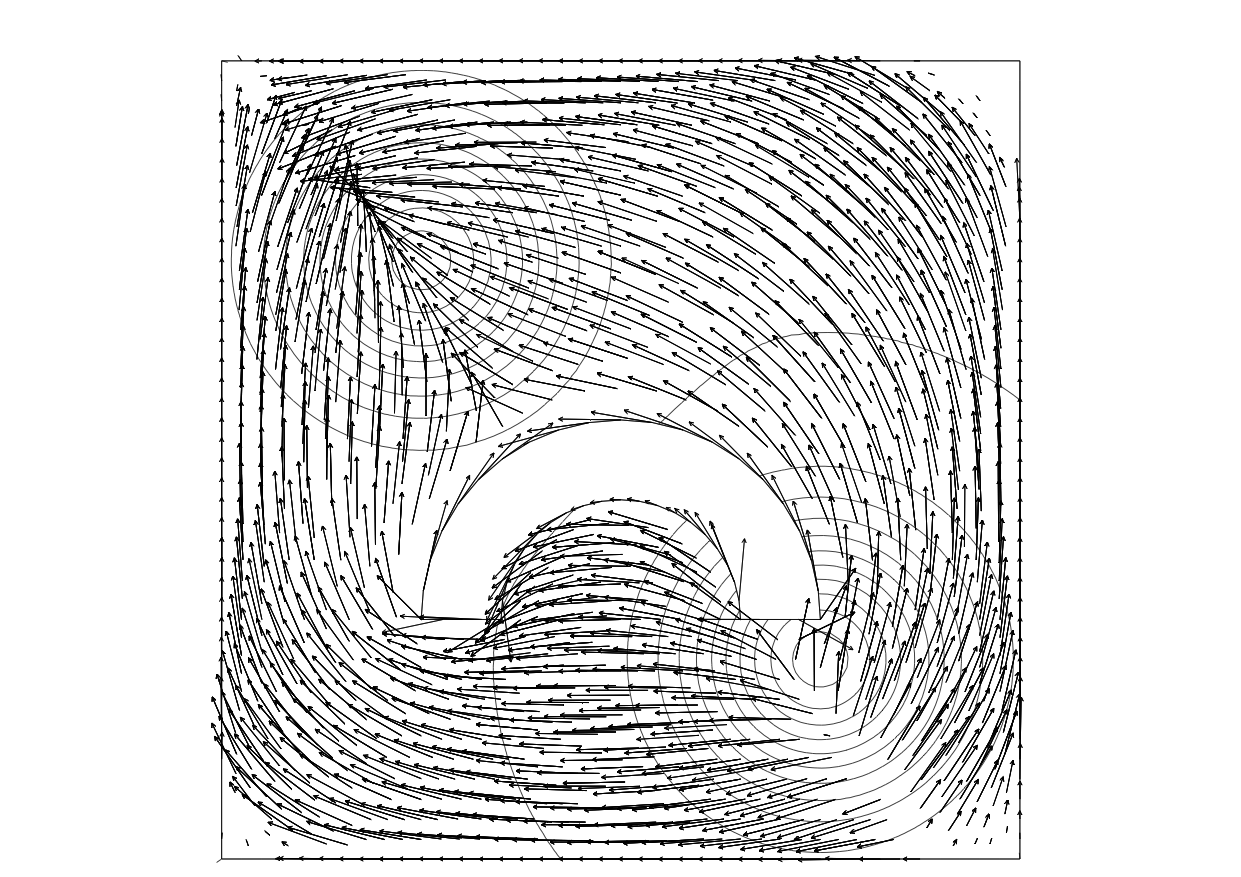
Monge and Wardrop flows of mass around an obstacle 30. the source/target mass is represented by the level curves. Left : no congestion, Right : congestion.
3.1.2 Diffeomorphisms and Dynamical Transport
Growth Models for Dynamical Optimal Transport.
(Participants: F-X. Vialard, J-D. Benamou, G. Peyré, L. Chizat) A major issue with the standard dynamical formulation of OT is that it does not allow for variation of mass during the evolution, which is required when tackling medical imaging applications such as tumor growth modeling 57 or tracking elastic organ movements 133. Previous attempts 112, 127 to introduce a source term in the evolution typically lead to mass teleportation (propagation of mass with infinite speed), which is not always satisfactory.
Our expertise: Our team has already established key contributions both to connect OT to fluid dynamics 28 and to define geodesic metrics on the space of shapes and diffeomorphisms 76.
Goals: Lenaic Chizat's PhD thesis aims at bridging the gap between dynamical OT formulation, and LDDDM diffeomorphisms models (see Section 2.3). This will lead to biologically-plausible evolution models that are both more tractable numerically than LDDM competitors, and benefit from strong theoretical guarantees associated to properties of OT.
Mean-field games.
(Participants: G. Carlier, J-D. Benamou) The Optimal Transportation Computational Fluid Dynamics (CFD) formulation is a limit case of variational Mean-Field Games (MFGs), a new branch of game theory recently developed by J-M. Lasry and P-L. Lions 104 with an extremely wide range of potential applications 96. Non-smooth proximal optimization methods used successfully for the Optimal Transportation can be used in the case of deterministic MFGs with singular data and/or potentials 31. They provide a robust treatment of the positivity constraint on the density of players.
Our expertise: J.-D. Benamou has pioneered with Brenier the CFD approach to Optimal Transportation. Regarding MFGs, on the numerical side, our team has already worked on the use of augmented Lagrangian methods in MFGs 30 and on the analytical side 64 has explored rigorously the optimality system for a singular CFD problem similar to the MFG system.
Goals: We will work on the extension to stochastic MFGs. It leads to non-trivial numerical difficulties already pointed out in 19.
Macroscopic Crowd motion, congestion and equilibria.
(Participants: G. Carlier, J-D. Benamou, Q. Mérigot, F. Santambrogio (U. Paris-Sud), Y. Achdou (Univ. Paris 7), R. Andreev (Univ. Paris 7)) Many models from PDEs and fluid mechanics have been used to give a description of people or vehicles moving in a congested environment. These models have to be classified according to the dimension (1D model are mostly used for cars on traffic networks, while 2-D models are most suitable for pedestrians), to the congestion effects (“soft” congestion standing for the phenomenon where high densities slow down the movement, “hard” congestion for the sudden effects when contacts occur, or a certain threshold is attained), and to the possible rationality of the agents Maury et al 115 recently developed a theory for 2D hard congestion models without rationality, first in a discrete and then in a continuous framework. This model produces a PDE that is difficult to attack with usual PDE methods, but has been successfully studied via Optimal Transportation techniques again related to the JKO gradient flow paradigm. Another possibility to model crowd motion is to use the mean field game approach of Lions and Lasry which limits of Nash equilibria when the number of players is large. This also gives macroscopic models where congestion may appear but this time a global equilibrium strategy is modelled rather than local optimisation by players like in the JKO approach. Numerical methods are starting to be available, see for instance 19, 53.
Our expertise: We have developed numerical methods to tackle both the JKO approach and the MFG approach. The Augmented Lagrangian (proximal) numerical method can actually be applied to both models 30, JKO and deterministic MFGs.
Goals: We want to extend our numerical approach to more realistic congestion model where the speed of agents depends on the density, see Figure 6 for preliminary results. Comparison with different numerical approaches will also be performed inside the ANR ISOTACE. Extension of the Augmented Lagrangian approach to Stochastic MFG will be studied.
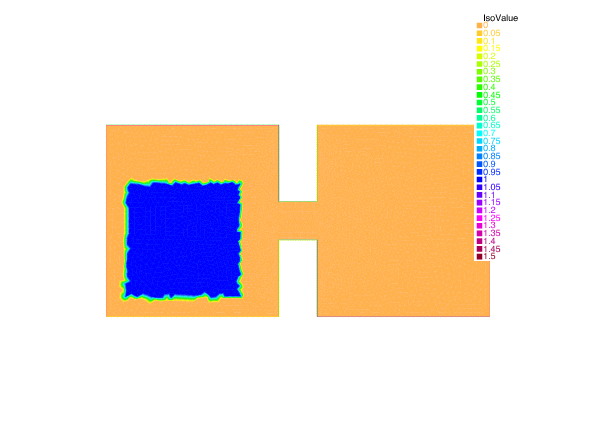
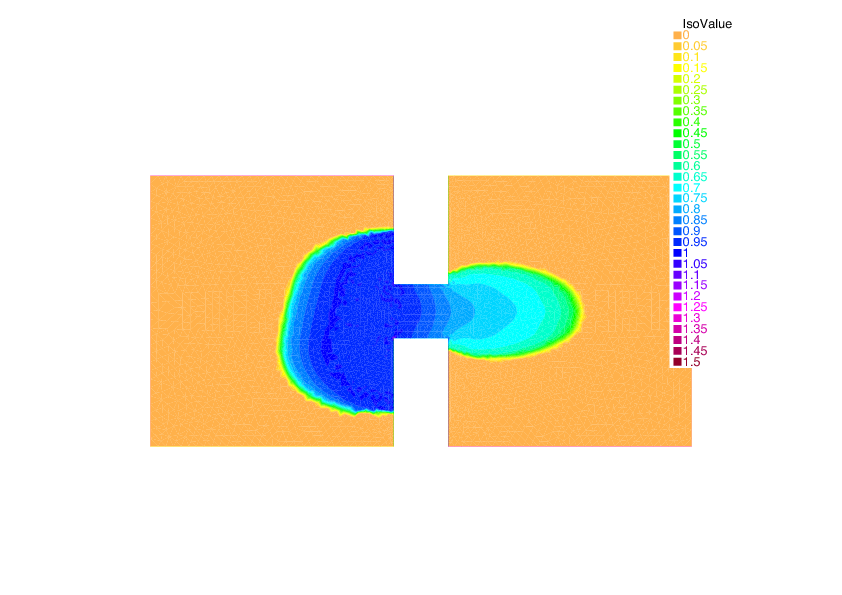
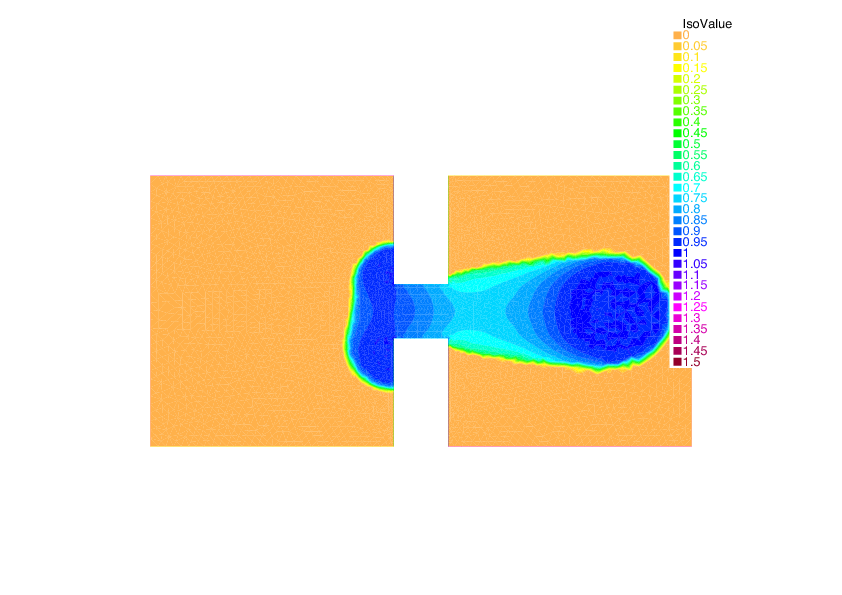
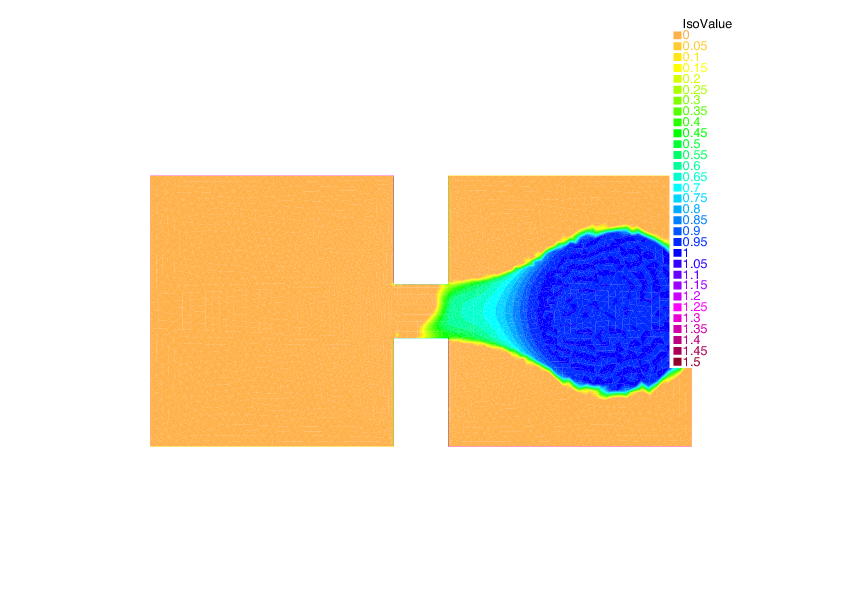
Example of crowd congestion with density dependent speed. The macroscopic density, at 4 different times, of people forced to exit from one room towards a meeting point in a second room.
Diffeomorphic image matching.
(Participants: F-X. Vialard, G. Peyré, B. Schmitzer, L. Chizat) Diffeomorphic image registration is widely used in medical image analysis. This class of problems can be seen as the computation of a generalized optimal transport, where the optimal path is a geodesic on a group of diffeomorphisms. The major difference between the two approaches being that optimal transport leads to non smooth optimal maps in general, which is however compulsory in diffeomorphic image matching. In contrast, optimal transport enjoys a convex variational formulation whereas in LDDMM the minimization problem is non convex.
Our expertise: F-X. Vialard is an expert of diffeomorphic image matching (LDDMM) 139, 52, 137. Our team has already studied flows and geodesics over non-Riemannian shape spaces, which allows for piecewise smooth deformations 76.
Goals: Our aim consists in bridging the gap between standard optimal transport and diffeomorphic methods by building new diffeomorphic matching variational formulations that are convex (geometric obstructions might however appear). A related perspective is the development of new registration/transport models in a Lagrangian framework, in the spirit of 134, 133 to obtain more meaningful statistics on longitudinal studies.
Diffeomorphic matching consists in the minimization of a functional that is a sum of a deformation cost and a similarity measure. The choice of the similarity measure is as important as the deformation cost. It is often chosen as a norm on a Hilbert space such as functions, currents or varifolds. From a Bayesian perspective, these similarity measures are related to the noise model on the observed data which is of geometric nature and it is not taken into account when using Hilbert norms. Optimal transport fidelity have been used in the context of signal and image denoising 106, and it is an important question to extends these approach to registration problems. Therefore, we propose to develop similarity measures that are geometric and computationally very efficient using entropic regularization of optimal transport.
Our approach is to use a regularized optimal transport to design new similarity measures on all of those Hilbert spaces. Understanding the precise connections between the evolution of shapes and probability distributions will be investigated to cross-fertilize both fields by developing novel transportation metrics and diffeomorphic shape flows.
The corresponding numerical schemes are however computationally very costly. Leveraging our understanding of the dynamic optimal transport problem and its numerical resolution, we propose to develop new algorithms. These algorithms will use the smoothness of the Riemannian metric to improve both accuracy and speed, using for instance higher order minimization algorithm on (infinite dimensional) manifolds.
Metric learning and parallel transport for statistical applications.
(Participants: F-X. Vialard, G. Peyré, B. Schmitzer, L. Chizat) The LDDMM framework has been advocated to enable statistics on the space of shapes or images that benefit from the estimation of the deformation. The statistical results of it strongly depend on the choice of the Riemannian metric. A possible direction consists in learning the right invariant Riemannian metric as done in 140 where a correlation matrix (Figure 7) is learnt which represents the covariance matrix of the deformation fields for a given population of shapes. In the same direction, a question of emerging interest in medical imaging is the analysis of time sequence of shapes (called longitudinal analysis) for early diagnosis of disease, for instance 89. A key question is the inter subject comparison of the organ evolution which is usually done by transport of the time evolution in a common coordinate system via parallel transport or other more basic methods. Once again, the statistical results (Figure 8) strongly depend on the choice of the metric or more generally on the connection that defines parallel transport.
Our expertise: Our team has already studied statistics on longitudinal evolutions in 89, 90.
Goals: Developing higher order numerical schemes for parallel transport (only low order schemes are available at the moment) and developing variational models to learn the metric or the connections for improving statistical results.
| Axial | Coronal | Sagittal |

|
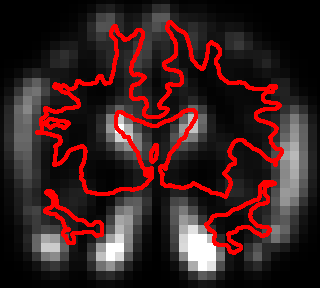
|

|
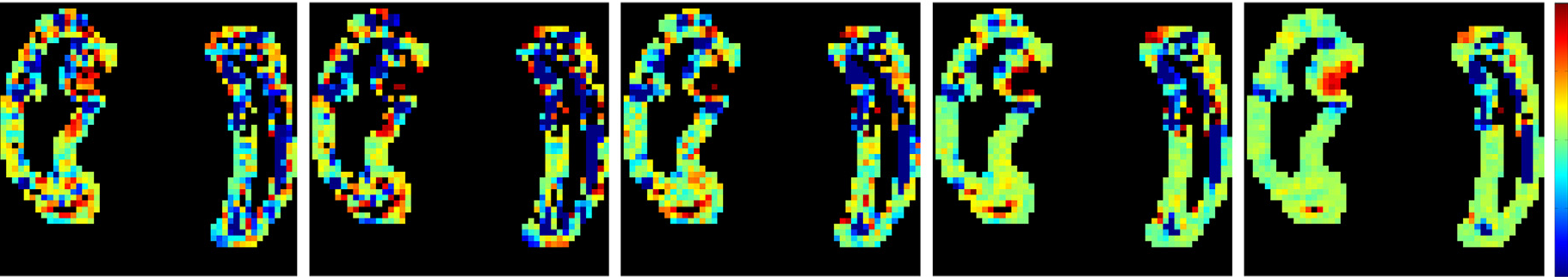
Statistics on initial momenta: In 89, we compared several intersubject transport methodologies to perform statistics on longitudinal evolutions. These longitudinal evolutions are represented by an initial velocity field on the shapes boundaries and these velocity fields are then compared using logistic regression methods that are regularized. The four pictures represent different regularization methods such as , and regularization including a sparsity prior such as Lasso, Fused Lasso and .
3.1.3 Sparsity in Imaging
Inverse problems over measures spaces.
(Participants: G. Peyré, V. Duval, C. Poon, Q. Denoyelle) As detailed in Section 2.4, popular methods for regularizing inverse problems in imaging make use of variational analysis over infinite-dimensional (typically non-reflexive) Banach spaces, such as Radon measures or bounded variation functions.
Our expertise: We have recently shown in 138 how – in the finite dimensional case – the non-smoothness of the functionals at stake is crucial to enforce the emergence of geometrical structures (edges in images or fractures in physical materials 42) for discrete (finite dimensional) problems. We extended this result in a simple infinite dimensional setting, namely sparse regularization of Radon measures for deconvolution 84. A deep understanding of those continuous inverse problems is crucial to analyze the behavior of their discrete counterparts, and in 85 we have taken advantage of this understanding to develop a fine analysis of the artifacts induced by discrete (i.e. which involve grids) deconvolution models. These works are also closely related to the problem of limit analysis and yield design in mechanical plasticity, see 67, 42 for an existing collaboration between Mokaplan's team members.
Goals: A current major front of research in the mathematical analysis of inverse problems is to extend these results for more complicated infinite dimensional signal and image models, such as for instance the set of piecewise regular functions. The key bottleneck is that, contrary to sparse measures (which are finite sums of Dirac masses), here the objects to recover (smooth edge curves) are not parameterized by a finite number of degrees of freedom. The relevant previous work in this direction are the fundamental results of Chambolle, Caselles and co-workers 27, 21, 73. They however only deal with the specific case where there is no degradation operator and no noise in the observations. We believe that adapting these approaches using our construction of vanishing derivative pre-certificate 84 could lead to a solution to these theoretical questions.
Sub-Riemannian diffusions.
(Participants: G. Peyré, J-M. Mirebeau, D. Prandi) Modeling and processing natural images require to take into account their geometry through anisotropic diffusion operators, in order to denoise and enhance directional features such as edges and textures 126, 86. This requirement is also at the heart of recently proposed models of cortical processing 125. A mathematical model for these processing is diffusion on sub-Riemanian manifold. These methods assume a fixed, usually linear, mapping from the 2-D image to a lifted function defined on the product of space and orientation (which in turn is equipped with a sub-Riemannian manifold structure).
Our expertise: J-M. Mirebeau is an expert in the discretization of highly anisotropic diffusions through the use of locally adaptive computational stencils 120, 86. G. Peyré has done several contributions on the definition of geometric wavelets transform and directional texture models, see for instance 126. Dario Prandi has recently applied methods from sub-Riemannian geometry to image restoration 44.
Goals: A first aspect of this work is to study non-linear, data-adaptive, lifting from the image to the space/orientation domain. This mapping will be implicitly defined as the solution of a convex variational problem. This will open both theoretical questions (existence of a solution and its geometrical properties, when the image to recover is piecewise regular) and numerical ones (how to provide a faithful discretization and fast second order Newton-like solvers). A second aspect of this task is to study the implication of these models for biological vision, in a collaboration with the UNIC Laboratory (directed by Yves Fregnac), located in Gif-sur-Yvette. In particular, the study of the geometry of singular vectors (or “ground states” using the terminology of 38) of the non-linear sub-Riemannian diffusion operators is highly relevant from a biological modeling point of view.
Sparse reconstruction from scanner data.
(Participants: G. Peyré, V. Duval, C. Poon) Scanner data acquisition is mathematically modeled as a (sub-sampled) Radon transform 97. It is a difficult inverse problem because the Radon transform is ill-posed and the set of observations is often aggressively sub-sampled and noisy 132. Typical approaches 103 try to recover piecewise smooth solutions in order to recover precisely the position of the organ being imaged. There is however a very poor understanding of the actual performance of these methods, and little is known on how to enhance the recovery.
Our expertise: We have obtained a good understanding of the performance of inverse problem regularization on compact domains for pointwise sources localization 84.
Goals: We aim at extending the theoretical performance analysis obtained for sparse measures 84 to the set of piecewise regular 2-D and 3-D functions. Some interesting previous work of C. Poon et al 128 (C. Poon is currently a postdoc in Mokaplan) have tackled related questions in the field of variable Fourier sampling for compressed sensing application (which is a toy model for fMRI imaging). These approaches are however not directly applicable to Radon sampling, and require some non-trivial adaptations. We also aim at better exploring the connection of these methods with optimal-transport based fidelity terms such as those introduced in 18.
Tumor growth modeling in medical image analysis.
(Participants: G. Peyré, F-X. Vialard, J-D. Benamou, L. Chizat) Some applications in medical image analysis require to track shapes whose evolution is governed by a growth process. A typical example is tumor growth, where the evolution depends on some typically unknown but meaningful parameters that need to be estimated. There exist well-established mathematical models 57, 124 of non-linear diffusions that take into account recently biologically observed property of tumors. Some related optimal transport models with mass variations have also recently been proposed 113, which are connected to so-called metamorphoses models in the LDDMM framework 39.
Our expertise: Our team has a strong experience on both dynamical optimal transport models and diffeomorphic matching methods (see Section 3.1.2).
Goals: The close connection between tumor growth models 57, 124 and gradient flows for (possibly non-Euclidean) Wasserstein metrics (see Section 3.1.2) makes the application of the numerical methods we develop particularly appealing to tackle large scale forward tumor evolution simulation. A significant departure from the classical OT-based convex models is however required. The final problem we wish to solve is the backward (inverse) problem of estimating tumor parameters from noisy and partial observations. This also requires to set-up a meaningful and robust data fidelity term, which can be for instance a generalized optimal transport metric.
3.2 Numerical Tools
The above continuous models require a careful discretization, so that the fundamental properties of the models are transferred to the discrete setting. Our team aims at developing innovative discretization schemes as well as associated fast numerical solvers, that can deal with the geometric complexity of the variational problems studied in the applications. This will ensure that the discrete solution is correct and converges to the solution of the continuous model within a guaranteed precision. We give below examples for which a careful mathematical analysis of the continuous to discrete model is essential, and where dedicated non-smooth optimization solvers are required.
3.2.1 Geometric Discretization Schemes
Discretizing the cone of convex constraints.
(Participants: J-D. Benamou, G. Carlier, J-M. Mirebeau, Q. Mérigot) Optimal transportation models as well as continuous models in economics can be formulated as infinite dimensional convex variational problems with the constraint that the solution belongs to the cone of convex functions. Discretizing this constraint is however a tricky problem, and usual finite element discretizations fail to converge.
Our expertise: Our team is currently investigating new discretizations, see in particular the recent proposal 35 for the Monge-Ampère equation and 119 for general non-linear variational problems. Both offer convergence guarantees and are amenable to fast numerical resolution techniques such as Newton solvers. Since 35 explaining how to treat efficiently and in full generality Transport Boundary Conditions for Monge-Ampère, this is a promising fast and new approach to compute Optimal Transportation viscosity solutions. A monotone scheme is needed. One is based on Froese Oberman work 92, a new different and more accurate approach has been proposed by Mirebeau, Benamou and Collino 34. As shown in 78, discretizing the constraint for a continuous function to be convex is not trivial. Our group has largely contributed to solve this problem with G. Carlier 70, Quentin Mérigot 117 and J-M. Mirebeau 119. This problem is connected to the construction of monotone schemes for the Monge-Ampère equation.
Goals: The current available methods are 2-D. They need to be optimized and parallelized. A non-trivial extension to 3-D is necessary for many applications. The notion of -convexity appears in optimal transport for generalized displacement costs. How to construct an adapted discretization with “good” numerical properties is however an open problem.
Numerical JKO gradient flows.
(Participants: J-D. Benamou, G. Carlier, J-M. Mirebeau, G. Peyré, Q. Mérigot) As detailed in Section 2.3, gradient Flows for the Wasserstein metric (aka JKO gradient flows 101) provides a variational formulation of many non-linear diffusion equations. They also open the way to novel discretization schemes. From a computational point, although the JKO scheme is constructive (it is based on the implicit Euler scheme), it has not been very much used in practice numerically because the Wasserstein term is difficult to handle (except in dimension one).
Our expertise:
Solving one step of a JKO gradient flow is similar to solving an Optimal transport problem. A geometrical a discretization of the Monge-Ampère operator approach has been proposed by Mérigot, Carlier, Oudet and Benamou in 33 see Figure 4. The Gamma convergence of the discretisation (in space) has been proved.
Goals: We are also investigating the application of other numerical approaches to Optimal Transport to JKO gradient flows either based on the CFD formulation or on the entropic regularization of the Monge-Kantorovich problem (see section 3.2.3). An in-depth study and comparison of all these methods will be necessary.
3.2.2 Sparse Discretization and Optimization
From discrete to continuous sparse regularization and transport.
(Participants: V. Duval, G. Peyré, G. Carlier, Jalal Fadili (ENSICaen), Jérôme Malick (CNRS, Univ. Grenoble)) While pervasive in the numerical analysis community, the problem of discretization and -convergence from discrete to continuous is surprisingly over-looked in imaging sciences. To the best of our knowledge, our recent work 84, 85 is the first to give a rigorous answer to the transition from discrete to continuous in the case of the spike deconvolution problem. Similar problems of -convergence are progressively being investigated in the optimal transport community, see in particular 71.
Our expertise: We have provided the first results on the discrete-to-continous convergence in both sparse regularization variational problems 84, 85 and the static formulation of OT and Wasserstein barycenters 71
Goals: In a collaboration with Jérôme Malick (INRIA Grenoble), our first goal is to generalize the result of 84 to generic partly-smooth convex regularizers routinely used in imaging science and machine learning, a prototypal example being the nuclear norm (see 138 for a review of this class of functionals). Our second goal is to extend the results of 71 to the novel class of entropic discretization schemes we have proposed 32, to lay out the theoretical foundation of these ground-breaking numerical schemes.
Polynomial optimization for grid-free regularization.
(Participants: G. Peyré, V. Duval, I. Waldspurger) There has been a recent spark of attention of the imaging community on so-called “grid free” methods, where one tries to directly tackle the infinite dimensional recovery problem over the space of measures, see for instance 62, 84. The general idea is that if the range of the imaging operator is finite dimensional, the associated dual optimization problem is also finite dimensional (for deconvolution, it corresponds to optimization over the set of trigonometric polynomials).
Our expertise: We have provided in 84 a sharp analysis of the support recovery property of this class of methods for the case of sparse spikes deconvolution.
Goals: A key bottleneck of these approaches is that, while being finite dimensional, the dual problem necessitates to handle a constraint of polynomial positivity, which is notoriously difficult to manipulate (except in the very particular case of 1-D problems, which is the one exposed in 62). A possible, but very costly, methodology is to ressort to Lasserre's SDP representation hierarchy 105. We will make use of these approaches and study how restricting the level of the hierarchy (to obtain fast algorithms) impacts the recovery performances (since this corresponds to only computing approximate solutions). We will pay a particular attention to the recovery of 2-D piecewise constant functions (the so-called total variation of functions regularization 131), see Figure 3 for some illustrative applications of this method.
3.2.3 First Order Proximal Schemes
proximal methods.
(Participants: G. Peyré, J-D. Benamou, G. Carlier, Jalal Fadili (ENSICaen)) Both sparse regularization problems in imaging (see Section 2.4) and dynamical optimal transport (see Section 2.3) are instances of large scale, highly structured, non-smooth convex optimization problems. First order proximal splitting optimization algorithms have recently gained lots of interest for these applications because they are the only ones capable of scaling to giga-pixel discretizations of images and volumes and at the same time handling non-smooth objective functions. They have been successfully applied to optimal transport 28, 121, congested optimal transport 56 and to sparse regularizations (see for instance 129 and the references therein).
Our expertise: The pioneering work of our team has shown how these proximal solvers can be used to tackle the dynamical optimal transport problem 28, see also 121. We have also recently developed new proximal schemes that can cope with non-smooth composite objectives functions 129.
Goals: We aim at extending these solvers to a wider class of variational problems, most notably optimization under divergence constraints 30. Another subject we are investigating is the extension of these solvers to both non-smooth and non-convex objective functionals, which are mandatory to handle more general transportation problems and novel imaging regularization penalties.

Example of barycenter between shapes computed using optimal transport barycenters of the uniform densities inside the 3 extremal shapes, computed as detailed in 135. Note that the barycenters are not in general uniform distributions, and we display them as the surface defined by a suitable level-set of the density.
Bregman proximal methods.
(Participants: G. Peyré G. Carlier, L. Nenna, J-D. Benamou, L. Nenna, Marco Cuturi (Kyoto Univ.)) The entropic regularization of the Kantorovich linear program for OT has been shown to be surprisingly simple and efficient, in particular for applications in machine learning 82. As shown in 32, this is a special instance of the general method of Bregman iterations, which is also a particular instance of first order proximal schemes according to the Kullback-Leibler divergence.
Our expertise: We have recently 32 shown how Bregman projections 47 and Dykstra algorithm 24 offer a generic optimization framework to solve a variety of generalized OT problems. Carlier and Dupuis 68 have designed a new method based on alternate Dykstra projections and applied it to the principal-agent problem in microeconomics. We have applied this method in computer graphics in a paper accepted in SIGGRAPH 2015 135. Figure 9 shows the potential of our approach to handle giga-voxel datasets: the input volumetric densities are discretized on a computational grid.
Goals: Following some recent works (see in particular 75) we first aim at studying primal-dual optimization schemes according to Bregman divergences (that would go much beyond gradient descent and iterative projections), in order to offer a versatile and very effective framework to solve variational problems involving OT terms. We then also aim at extending the scope of usage of this method to applications in quantum mechanics (Density Functional Theory, see 79) and fluid dynamics (Brenier's weak solutions of the incompressible Euler equation, see 50). The computational challenge is that realistic physical examples are of a huge size not only because of the space discretization of one marginal but also because of the large number of marginals involved (for incompressible Euler the number of marginals equals the number of time steps).
4 Application domains
4.1 Natural Sciences
FreeForm Optics, Fluid Mechanics (Incompressible Euler, Semi-Geostrophic equations), Quantum Chemistry (Density Functional Theory), Statistical Physics (Schroedinger problem), Porous Media.
4.2 Signal Processing and inverse problems
Full Waveform Inversion (Geophysics), Super-resolution microscopy (Biology), Satellite imaging (Meteorology)
4.3 Social Sciences
Mean-field games, spatial economics, principal-agent models, taxation, nonlinear pricing.
5 Highlights of the year
5.1 Awards
I. Waldspurger received the Bronze medal from CNRS.
I. Waldspurger is the laureate of the “cours Peccot du collège de France”.
6 New results
6.1 An Entropic Optimal Transport Numerical Approach to the Reflector Problem
Benamou, Jean-David and Rukhaia, Giorgi and IJzerman, Wilbert. In 6 : The point source far field reflector design problem is one of the main classic optimal transport problems with a non-euclidean displacement cost [Wang, 2004] [Glimm and Oliker, 2003]. This work describes the use of Entropic Optimal Transport and the associated Sinkhorn algorithm [Cuturi, 2013] to solve it numerically. As the reflector modelling is based on the Kantorovich potentials , several questions arise. First, on the convergence of the discrete entropic approximation and here we follow the recent work of [Berman, 2017] and in particular the imposed discretization requirements therein. Secondly, the correction of the Entropic bias induced by the Entropic OT, as discussed in particular in [Ramdas et al., 2017] [Genevay et al., 2018] [Feydy et al., 2018], is another important tool to achieve reasonable results. The paper reviews the necessary mathematical and numerical tools needed to produce and discuss the obtained numerical results. We find that Sinkhorn algorithm may be adapted, at least in simple academic cases, to the resolution of the far field reflector problem. Sinkhorn canonical extension to continuous potentials is needed to generate continuous reflector approximations. The use of Sinkhorn divergences [Feydy et al., 2018] is useful to mitigate the entropic bias.
In collaboration with G. Chazareix, We are currently applying this technique to a more realistic “finite source” extension of the point source reflector problem.
6.2 Capacity Constrained Entropic Optimal Transport, Sinkhorn Saturated Domain Out-Summation and Vanishing Temperature
Benamou, Jean-David and Martinet, Mélanie. In 7 : We propose a new method to reduce the computational cost of the Entropic Optimal Transport in the vanishing temperature (ε) limit. As in [Schmitzer, 2016], the method relies on a Sinkhorn continuation "ε-scaling" approach; but instead of truncating out the small values of the Kernel, we rely on the exact "out-summation" of saturated domains for a modified constrained Entropic Optimal problem. The constraint depends on an additional parameter λ. In pratice λ = ε also vanishes and the constraint disappear. Using [Berman, 2017], the convergence of the (ε, λ) continuation method based on this modified problem is established. We then show that the saturated domain can be over estimated from the previous larger (ε, λ). On the saturated zone the solution is constant and known and the domain can be "out-summed" (removed) from Sinkhorn algorithm. The computational cost and memory foot print is shown to be almost linear thanks again to an estimate given by [Berman, 2017]. This is confirmed on 1-D numerical experiments.
6.3 Stability of optimal traffic plans in the irrigation problem
Colombo, Maria and De Rosa, Antonio and Marchese, Andrea and Pegon, Paul and Prouff, Antoine. In 12 : We prove the stability of optimal traffic plans in the irrigation problem, namely the optimality of weak limits P of sequences of traffic plans which are optimal for marginals which weakly converge. This is achieved under a uniform bound on the α-energy of branched transport for any exponent α strictly between 0 and 1. The proof builds upon the Eulerian counterpart of this statement which has been recently established in [Colombo, De Rosa, Marchese, 2019], showing that the limit plan does not produce cancellations in the induced current, as a limit of optimal traffic plans. As a consequence, we prove that P is a good decomposition of its induced current and we deduce the optimality of P.
6.4 Rank optimality for the Burer-Monteiro formulation
Waldspurger, Irène and Waters, Alden. In 4 : When solving large scale semidefinite programs that admit a low-rank solution, a very efficient heuristic is the Burer-Monteiro factorization: Instead of optimizing over the full matrix, one optimizes over its low-rank factors. This strongly reduces the number of variables to optimize, but destroys the convexity of the problem, thus possibly introducing spurious second-order critical points which can prevent local optimization algorithms from finding the solution. Boumal, Voroninski, and Bandeira [2018] have recently shown that, when the size of the factors is of the order of the square root of the number of linear constraints, this does not happen: For almost any cost matrix, second-order critical points are global solutions. In this article, we show that this result is essentially tight: For smaller values of the size, second-order critical points are not generically optimal, even when considering only semidefinite programs with a rank 1 solution.
6.5 A mean field game model for the evolution of cities
Barilla, César and Carlier, Guillaume and Lasry, Jean-Michel In 5 : We propose a (toy) MFG model for the evolution of residents and firms densities, coupled both by labour market equilibrium conditions and competition for land use (congestion). This results in a system of two Hamilton-Jacobi-Bellman and two Fokker-Planck equations with a new form of coupling related to optimal transport. This MFG has a convex potential which enables us to find weak solutions by a variational approach. In the case of quadratic Hamiltonians, the problem can be reformulated in Lagrangian terms and solved numerically by an IPFP/Sinkhorn-like scheme. We present numerical results based on this approach, these simulations exhibit different behaviours with either agglomeration or segregation dominating depending on the initial conditions and parameters.
6.6 Explicit constants in Harnack inequalities and regularity estimates, with an application to the fast diffusion equation
Bonforte, Matteo and Dolbeault, Jean and Nazaret, Bruno and Simonov, Nikita In 8 : This paper is devoted to the computation of various explicit constants in functional inequalities and regularity estimates for solutions of parabolic equations, which are not available from the literature. We provide new expressions and simplified proofs of the Harnack inequality and the corresponding Hölder continuity of the solution of a linear parabolic equation. We apply these results to the computation of a constructive estimate of a threshold time for the uniform convergence in relative error of the solution of the fast diffusion equation.
6.7 Stability in Gagliardo-Nirenberg inequalities
Bonforte, Matteo and Dolbeault, Jean and Nazaret, Bruno and Simonov In 9 : The purpose of this paper is to establish a quantitative and constructive stability result for a class of subcritical Gagliardo-Nirenberg inequalities. We develop a new strategy, in which the flow of the fast diffusion equation is used as a tool: a stability result in the inequality is equivalent to an improved rate of convergence to equilibrium for the flow. In both cases, the tail behaviour plays a key role. The regularity properties of the parabolic flow allow us to connect an improved entropy-entropy production inequality during the initial time layer to spectral properties of a suitable linearized problem which is relevant for the asymptotic time layer. Altogether, the stability in the inequalities is measured by a deficit which controls in strong norms the distance to the manifold of optimal functions.
6.8 Entropic-Wasserstein barycenters: PDE characterization, regularity and CLT
Carlier, Guillaume and Eichinger, Katharina and Kroshnin, Alexey In 10 : In this paper, we investigate properties of entropy-penalized Wasserstein barycenters introduced in [5] as a regularization of Wasserstein barycenters [1]. After characterizing these barycenters in terms of a system of Monge-Ampère equations, we prove some global moment and Sobolev bounds as well as higher regularity properties. We finally establish a central limit theorem for entropic-Wasserstein barycenters.
6.9 An Epigraphical Approach to the Representer Theorem
Duval, Vincent In 13 : Describing the solutions of inverse problems arising in signal or image processing is an important issue both for theoretical and numerical purposes. We propose a principle which describes the solutions to convex variational problems involving a finite number of measurements. We discuss its optimality on various problems concerning the recovery of Radon measures.
6.10 A mixed finite element discretization of dynamical optimal transport
Natale, Andrea and Todeschi, Gabriele In 14 :
In this paper we introduce a new class of finite element discretizations of the quadratic optimal transport problem based on its dynamical formulation. These generalize to the finite element setting the finite difference scheme proposed by 121. We solve the discrete problem using a proximal-splitting approach and we show how to modify this in the presence of regularization terms which are relevant for imaging applications.
6.11 TPFA Finite Volume Approximation of Wasserstein Gradient Flows
Natale, Andrea and Todeschi, Gabriele In 16 : Numerous infinite dimensional dynamical systems arising in different fields have been shown to exhibit a gradient flow structure in the Wasserstein space. We construct Two Point Flux Approximation Finite Volume schemes discretizing such problems which preserve the variational structure and have second order accuracy in space. We propose an interior point method to solve the discrete variational problem, providing an efficient and robust algorithm. We present two applications to test the scheme and show its order of convergence.
7 Partnerships and cooperations
7.1 European Initiatives
7.1.1 FP7 & H2020 Projects
ROMSOC
- Title: Reduced Order Modelling, Simulation and Optimization of Coupled systems
- Duration: 18/01 - 21/12
- Coordinator: Mehrmann Volker
-
Partners:
- ABB SCHWEIZ AG (Switzerland)
- ARCELORMITTAL INNOVACION INVESTIGACION E INVERSION SL (Spain)
- BERGISCHE UNIVERSITAET WUPPERTAL (Germany)
- CorWave (France)
- DB Schenker Rail Polska S.A. (Poland)
- FRIEDRICH-ALEXANDER-UNIVERSITAET ERLANGEN-NUERNBERG (Germany)
- MATHCONSULT GMBH (Austria)
- MICROFLOWN TECHNOLOGIES BV (Netherlands)
- Math.Tec GmbH (Austria)
- POLITECNICO DI MILANO (Italy)
- SAGIV TECH LTD (Israel)
- SCUOLA INTERNAZIONALE SUPERIORE DI STUDI AVANZATI DI TRIESTE (Italy)
- SIGNIFY NETHERLANDS BV (Netherlands)
- STICHTING EUROPEAN SERVICE NETWORK OF MATHEMATICS FOR INDUSTRY AND INNOVATION (Netherlands)
- TECHNISCHE UNIVERSITAT BERLIN (Germany)
- UNIVERSITAET BREMEN (Germany)
- UNIVERSITAT LINZ (Austria)
- Inria contact: Odabas, Serkan
-
Summary:
Product development today is increasingly based on simulation and optimization of virtual products and processes. Mathematical models serve as digital twins of the real products and processes and are the basis for optimization and control of design and functionality. The models have to meet very different requirements: Deeply refined mathematical models are required to understand and simulate the true physical processes, while less refined models are the prerequisites to handle the complexity of control and optimization. To achieve best performance of mathematical modeling, simulation and optimization techniques (MSO), in particular in the industrial environment, it would be ideal to create a complete model hierarchy.
The currently most favoured way in industrial applications to achieve such a model of hierarchy is to use a sufficiently fine parameterized model and then apply model order reduction (MOR) techniques to tune this fine level to the accuracy, complexity and computational speed needed in simulation and parameter optimization.
Although the mathematical models differ strongly in different applications and industrial sectors, there is a common framework via an appropriate representation of the physical model.
The main objective of the ROMSOC project is to further develop this common framework and, driven by industrial applications as optical and electronic systems, material engineering, or economic processes, to lift mathematical MSO and MOR to a new level of quality. The development of high dimensional and coupled systems presents a major challenge for simulation and optimization and requires new MOR techniques.
ROMSOC is a European Industrial Doctorate (EID) project that will run for four years bringing together 15 international academic institutions and 11 industry partners. It supports the recruitment of eleven Early Stage Researchers (ESRs) working on individual research projects. In order to train the eleven young researchers for the challenges of multi-disciplinary and international co-operation, their scientific work is embedded in a jointly organized doctoral program, in which lectures and workshops address both scientific content and soft skills. The researchers are supervised by expert tandems, each consisting of an academic and an industrial representative. They spend at least half the time in a company, the rest in a research facility.
7.2 National Initiatives
ANR
V. Duval is the PI of the CIPRESSI (ANR JCJC) project. Its aim is to develop novel numerical schemes which respect the continuous nature of the variational problems in image or signal processing.
J-D. Benamou and G. Carlier are members of the ANR MFG (ANR-16-CE40-0015-01). Scientific topics of the project: Mean field analysis Analysis of the MFG systems and of the Master equation Numerical analysis Models and applications
J-D. Benamou G. Carlier F-X. Vialard and T. O. Gallouët are members of ANR MAGA (ANR-13-JS01-0007-01) which has been extended to 2021. The Monge-Ampère equation is a fully nonlinear elliptic equation, which plays a central role in geometry and in the theory of optimal transport. However, the singular and non-linear nature of the equation is a serious obstruction to its efficient numerical resolution. The first aim of the MAGA project is to study and to implement discretizations of optimal transport and Monge-Ampère equations which rely on tools from computational geometry (Laguerre diagrams). In a second step, these solvers will be applied to concrete problems from various fields involving optimal transport or Monge-Ampère equations such as computational physics: early universe reconstruction problem, congestion/incompressibility constraints economics: principal agent problems, geometry: variational problems over convex bodies, reflector and refractor design for non-imaging optics
T. O. Gallouët is member of the ANR GEOPOR (JCJC of C. Cancès) Scientific topic: geometrical approach, based on Wasserstein gradient flow, for multiphase flows in porous media. Theory and Numerics.
T. O. Gallouët is member of the ANR MESA (JCJC of M. Fathi) Scientific topic: Stein methods.
I. Waldspurger is a springboard PRAIRIE chair holder.
8 Dissemination
8.0.1 Journal
Member of the Editorial Boards
G. Carlier is in the Editorial Board of Journal de l'Ecole Polytechnique, Applied Math and Opt., Journal of Mathematical Analysis and Applications, Mathematics and financial economics and Journal of dynamics and games. I. Waldspurger is associate editor for the IEEE Transactions on Signal Processing
Reviewer - Reviewing Activities
V. Duval has reviewed contributions to Acta Applicandae Mathematicae, Bulletin of the Math. London Society, JOTA (Journal of Optimization, Theory and Applications), Information and Inference: a Journal of the IMA, Journal of Math. Stat. Learning, IEEE Transactions on Signal Processing. P. Pegon has reviewed contributions to Calculs of Variations & PDEs and Journal of Convex Analysis. I. Waldspurger has reviewed contributions to IEEE Transactions on Information Theory, ICML (International Conference on Machine Learning), JFAA (Journal of Fourier Analysis and Applications), SIOPT (SIAM Journal on Optimization), Acta Applicandae Mathematicae and NeurIPS (Neural Information Procesing Systems).
8.0.2 Invited Talks
- J-D. Benamou at Variational Methods for Evolution, MF Oberwolfach workshop 2038, September 13-19th.
- J-D. Benamou at INS colloquium at Shanghai Jiao Tong University, China. May 15th.
- V. Duval at One World Seminar Mathematical Methods for Arbitrary Data Sources (MADS), June 8th, online.
- V. Duval at International Traveling Workshop on Interactions between low complexity data models and Sensing techniques (iTwist), Decembert 2-4, online.
- G. Carlier: séminaire EDP du Collège de France, workshop ICODE à Paris 7, séminaire (en ligne) sur les MFGs, séminaire (en ligne) Erlangen, workshop Optimal Transport: Regularization and Applications (Columbia, NY, en ligne), Heriot-Watt stat. seminar (en ligne).
- I. Waldspurger at the Optimization for Machine Learning workshop, March 10th, in CIRM (Marseille).
- I. Waldspurger at the PDE and inverse problems machine learning workshop, April 22nd, organized online by the University of California, Los Angeles.
- I. Waldspurger at the séminaire signal-apprentissage of I2M / LIS in Marseille, June 19th, online.
- I. Waldspurger at the Virtual Maxwell Analysis Seminar of Edinburgh, October 23nd.
- I. Waldspurger at International Traveling Workshop on Interactions between low complexity data models and Sensing techniques (iTwist), Decembert 2-4, online.
8.0.3 Research Administration
V. Duval is a member of the Comité de Suivi Doctoral (CSD) and the Comité des Emplois Scientifiques (CES) of the Inria Paris research center.
8.1 Teaching - Supervision - Juries
8.1.1 Teaching
- Licence : J-D. Benamou, Méthodes Numériques , 39 H. équivalent TD, niveau (L2), université Paris Dauphine , FR
- Master : V. Duval, Problèmes Inverses, 20 h équivalent TD, niveau M1, Université PSL/Mines ParisTech, FR
- Master : V. Duval, Optimization for Machine Learning, 9h, niveau M2, Université PSL/ENS, FR
- Licence : I. Waldspurger, Pré-rentrée calcul, 31,2 h équivalent TD, niveau L1, Université Paris-Dauphine, FR
- Licence : I. Waldspurger, Analyse 2, 50,7 h équivalent TD, niveau L1, Université Paris-Dauphine, FR
- Master : I. Waldspurger, Optimization for Machine Learning, 6h, niveau M2, Université PSL/ENS, FR
- Licence : G. Carlier, algebre 1, L1 78h, Dauphine, FR
- Master : G. Carlier Variational and transport methods in economics, M2 Masef, 27h, Dauphine, FR
- Licence : A. Natale, Python, 44 h équivalent TD, niveau L2, Université Paris-Sud , FR
- Licence : P. Pegon, Analyse 2 & 3, 102 H. équivalent TD, TD niveau L1-L2, Université Paris-Dauphine, FR
- Licence : P. Pegon, Intégrale de Lebesgue et probabilités, 44 H. équivalent TD, TD niveau L3, Université Paris-Dauphine, FR
- Master : P. Pegon, Pré-rentrée d'analyse, 16 H. équivalent TD, cours/TD niveau M1, Université Paris-Dauphine, FR
- Licence : T. O. Gallouët, Optimisation, 24h équivalent TD, niveau L3, Université d'Orsay), FR
- G. Carlier: Licence Algèbre 1, Dauphine 70h, M2 Masef: Variatioanl and transport problems in economics, 18h
8.1.2 Supervision
- PhD completed : Paul Catala, Optimisation polynomiale pour les problèmes inverses en imagerie, defended on 01/10/2020, V. Duval
- PhD in progress : Romain Petit, Méthodes sans grille pour l'imagerie, 01/10/2019, V. Duval
- PhD stopped before completion : Lucas Martinet 1/10/2020. Supervised by J-D. Benamou.
- PhD in progress : Adrien Vacher 1/10/2020. Co-supervised by F-X. Vialard and J-D. Benamou.
- PhD in progress : Giorgi Rukhaia , An Optimal Transportation computational approach of inverse free-form optical surfaces design for extended sources, 1/05/2018. Supervised by J-D. Benamou
- PhD in progress: Quentin Petit, mean-field games for cities modeling, co-supervision by G. Carlier Y. Achdou and D. Tonon, 1/09/2018
- PhD in progress: G. Carlier, Katharina Eichinger, Systems of Monge-Ampere equations: a variational approach 1/09/2019. Supervised by G. Carlier.
- PhD in progress: T. O. Gallouët, Gabriele Todeschi, Optimal transport and finite volume schemes, 1/09/2018
- G. Carlier is supervising the postdoc of Luca Tamanini.
- G. Carlier supervised the M2 internship of Jules Candau-Tilh, Enis-Chenchene
8.1.3 Juries
- J-D. Benamou, PhD Defense of Jean Feydy.
- G. Carlier coordinator for the HDR of Virginie Ehrlacher, PhD committee of Gwendoline de Bie, Hamza Ennaji
8.2 Popularization
8.2.1 Interventions
- I. Waldspurger: talk at the Séminaire des mathématiques, ENS Paris, on the minimization of functions with Lipschitz gradient.
9 Scientific production
9.1 Publications of the year
International journals
Reports & preprints
9.2 Other
Educational activities
9.3 Cited publications
- 18 article Tomographic reconstruction from a few views: a multi-marginal optimal transport approach Preprint Hal-01065981 2014
- 19 articleIterative strategies for solving linearized discrete mean field games systemsNetw. Heterog. Media722012, 197--217URL: http://dx.doi.org/10.3934/nhm.2012.7.197
- 20 articleBarycenters in the Wasserstein spaceSIAM J. Math. Anal.4322011, 904--924
- 21 articleEvolution of Convex Sets in the Plane by Minimizing the Total Variation FlowInterfaces and Free Boundaries3322005, 329--366
- 22 articleConsistency of Trace Norm MinimizationJ. Mach. Learn. Res.9June 2008, 1019--1048URL: http://dl.acm.org/citation.cfm?id=1390681.1390716
- 23 articleConsistency of the Group Lasso and Multiple Kernel LearningJ. Mach. Learn. Res.9June 2008, 1179--1225URL: http://dl.acm.org/citation.cfm?id=1390681.1390721
- 24 articleA Dykstra-like algorithm for two monotone operatorsPacific Journal of Optimization432008, 383--391
- 25 articleComputing Large Deformation Metric Mappings via Geodesic Flows of DiffeomorphismsInternational Journal of Computer Vision612February 2005, 139--157URL: http://dx.doi.org/10.1023/B:VISI.0000043755.93987.aa
- 26 articleModel-independent bounds for option prices mass transport approachFinance and Stochastics1732013, 477-501URL: http://dx.doi.org/10.1007/s00780-013-0205-8
-
27
articleThe Total Variation Flow in
'J. Differential Equations18422002, 475--525 - 28 articleA computational fluid mechanics solution to the Monge-Kantorovich mass transfer problemNumer. Math.8432000, 375--393URL: http://dx.doi.org/10.1007/s002110050002
- 29 articleWeak existence for the semigeostrophic equations formulated as a coupled Monge-Ampère/transport problemSIAM J. Appl. Math.5851998, 1450--1461
- 30 article Augmented Lagrangian algorithms for variational problems with divergence constraints JOTA 2015
- 31 techreportAn Augmented Lagrangian Numerical approach to solving Mean-Fields GamesINRIADecember 2013, 30
- 32 article Iterative Bregman Projections for Regularized Transportation Problems SIAM J. Sci. Comp. to appear 2015
- 33 techreport Discretization of functionals involving the Monge-Ampère operator HAL July 2014
- 34 article Monotone and Consistent discretization of the Monge-Ampère operator arXiv preprint arXiv:1409.6694 to appear in Math of Comp 2014
- 35 articleNumerical solution of the optimal transportation problem using the Monge--Ampere equationJournal of Computational Physics2602014, 107--126
- 36 articleTwo numerical methods for the elliptic Monge-Ampère equationM2AN Math. Model. Numer. Anal.4442010, 737--758
- 37 articleNumerical approximation of continuous traffic congestion equilibriaNetw. Heterog. Media432009, 605--623
- 38 articleGround states and singular vectors of convex variational regularization methodsMeth. Appl. Analysis202013, 295--334
- 39 article Time discrete geodesic paths in the space of images Arxiv preprint 2014
- 40 article Consistent estimation of a population barycenter in the Wasserstein space Preprint arXiv:1212.2562 2012
-
41
articleThe parabolic-parabolic Keller-Segel system with critical diffusion as a gradient flow in
'Comm. Partial Differential Equations3842013, 658--686URL: http://dx.doi.org/10.1080/03605302.2012.757705 -
42
articleA
Convergence Result for the Upper Bound Limit Analysis of Plates'ESAIM: Mathematical Modelling and Numerical Analysis501January 2016, 215--235URL: https://www.esaim-m2an.org/articles/m2an/abs/2016/01/m2an141087/m2an141087.html - 43 articleSliced and Radon Wasserstein Barycenters of MeasuresJournal of Mathematical Imaging and Vision5112015, 22--45URL: http://hal.archives-ouvertes.fr/hal-00881872/
- 44 techreportHighly corrupted image inpainting through hypoelliptic diffusionPreprint CMAP2014, URL: http://hal.archives-ouvertes.fr/hal-00842603/
- 45 articleCharacterization of optimal shapes and masses through Monge-Kantorovich equationJ. Eur. Math. Soc. (JEMS)322001, 139--168URL: http://dx.doi.org/10.1007/s100970000027
- 46 articleCongested traffic dynamics, weak flows and very degenerate elliptic equationsJ. Math. Pures Appl. (9)9362010, 652--671
- 47 articleThe relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programmingUSSR computational mathematics and mathematical physics731967, 200--217
- 48 articleDécomposition polaire et réarrangement monotone des champs de vecteursC. R. Acad. Sci. Paris Sér. I Math.305191987, 805--808
- 49 article Reconstruction of the early universe as a convex optimization problem Mon. Not. Roy. Astron. Soc.3462003, 501--524URL: http://arxiv.org/pdf/astro-ph/0304214.pdf
- 50 articleGeneralized solutions and hydrostatic approximation of the Euler equationsPhys. D23714-172008, 1982--1988URL: http://dx.doi.org/10.1016/j.physd.2008.02.026
- 51 articlePolar factorization and monotone rearrangement of vector-valued functionsComm. Pure Appl. Math.4441991, 375--417URL: http://dx.doi.org/10.1002/cpa.3160440402
- 52 articleMixture of Kernels and Iterated Semidirect Product of Diffeomorphisms GroupsMultiscale Modeling & Simulation1042012, 1344-1368
- 53 article Mean field games with nonlinear mobilities in pedestrian dynamics DCDS B 19 2014
- 54 articleRegularized regression and density estimation based on optimal transportAppl. Math. Res. Expr.22012, 209--253
- 55 article A guide to the TV zoo Level-Set and PDE-based Reconstruction Methods, Springer 2013
- 56 articleAn optimization problem for mass transportation with congested dynamicsSIAM J. Control Optim.4832009, 1961--1976
- 57 articleIndividual-based and continuum models of growing cell populations: a comparisonJournal of Mathematical Biology584-52009, 657-687
- 58 incollectionOn the numerical solution of the problem of reflector design with given far-field scattering dataMonge Ampère equation: applications to geometry and optimization (Deerfield Beach, FL, 1997)226Contemp. Math.Providence, RIAmer. Math. Soc.1999, 13--32URL: http://dx.doi.org/10.1090/conm/226/03233
- 59 articleThe regularity of mappings with a convex potentialJ. Amer. Math. Soc.511992, 99--104URL: http://dx.doi.org/10.2307/2152752
- 60 article Computational Analysis of LDDMM for Brain Mapping Frontiers in Neuroscience 7 2013
- 61 articleSuper-Resolution from Noisy DataJournal of Fourier Analysis and Applications1962013, 1229--1254
- 62 articleTowards a Mathematical Theory of Super-ResolutionCommunications on Pure and Applied Mathematics6762014, 906--956
- 63 articleAn Introduction to Compressive SensingIEEE Signal Processing Magazine2522008, 21--30
- 64 articleGeodesics for a class of distances in the space of probability measuresCalc. Var. Partial Differential Equations483-42013, 395--420
- 65 articleA general existence result for the principal-agent problem with adverse selectionJ. Math. Econom.3512001, 129--150
- 66 techreport Vector Quantile Regression Arxiv 1406.4643 2014
- 67 articleA Projection Approach to the Numerical Analysis of Limit Load ProblemsMathematical Models and Methods in Applied Sciences2162011, 1291--1316URL: http://hal.archives-ouvertes.fr/hal-00450000/
- 68 techreport An iterated projection approach to variational problems under generalized convexity constraints and applications In preparation 2015
- 69 articleOptimal Transportation with Traffic Congestion and Wardrop EquilibriaSIAM Journal on Control and Optimization4732008, 1330-1350
- 70 articleA numerical approach to variational problems subject to convexity constraintNumer. Math.8822001, 299--318URL: http://dx.doi.org/10.1007/PL00005446
- 71 article Numerical methods for matching for teams and Wasserstein barycenters M2AN to appear 2015
- 72 articleUniqueness for Keller-Segel-type chemotaxis modelsDiscrete Contin. Dyn. Syst.3442014, 1319--1338URL: http://dx.doi.org/10.3934/dcds.2014.34.1319
- 73 articleThe discontinuity set of solutions of the TV denoising problem and some extensionsMultiscale Modeling and Simulation632007, 879--894
- 74 articleKinetic models for chemotaxis and their drift-diffusion limitsMonatsh. Math.1421-22004, 123--141URL: http://dx.doi.org/10.1007/s00605-004-0234-7
- 75 article On the ergodic convergence rates of a first-order primal-dual algorithm Preprint OO/2014/09/4532 2014
- 76 techreportFinsler Steepest Descent with Applications to Piecewise-regular Curve EvolutionPreprint hal-008498852013, URL: http://hal.archives-ouvertes.fr/hal-00849885/
- 77 articleAtomic decomposition by basis pursuitSIAM journal on scientific computing2011999, 33--61
- 78 articleNon-convergence result for conformal approximation of variational problems subject to a convexity constraintNumer. Funct. Anal. Optim.225-62001, 529--547URL: http://dx.doi.org/10.1081/NFA-100105306
- 79 articleDensity Functional Theory and Optimal Transportation with Coulomb CostCommunications on Pure and Applied Mathematics6642013, 548--599URL: http://dx.doi.org/10.1002/cpa.21437
- 80 articleThe semigeostrophic equations discretized in reference and dual variablesArch. Ration. Mech. Anal.18522007, 341--363URL: http://dx.doi.org/10.1007/s00205-006-0040-6
- 81 articleGeneralised Lagrangian solutions for atmospheric and oceanic flowsSIAM J. Appl. Math.5111991, 20--31
- 82 inproceedingsSinkhorn Distances: Lightspeed Computation of Optimal TransportProc. NIPS2013, 2292--2300
- 83 articleNumerical methods for fully nonlinear elliptic equations of the Monge-Ampère typeComput. Methods Appl. Mech. Engrg.19513-162006, 1344--1386
- 84 articleExact Support Recovery for Sparse Spikes DeconvolutionFoundations of Computational Mathematics2014, 1-41URL: http://dx.doi.org/10.1007/s10208-014-9228-6
- 85 articleSparse regularization on thin grids I: the L assoInverse Problems3352017, 055008URL: http://stacks.iop.org/0266-5611/33/i=5/a=055008
- 86 articleSparse Non-negative Stencils for Anisotropic DiffusionJournal of Mathematical Imaging and Vision4912014, 123-147URL: http://dx.doi.org/10.1007/s10851-013-0446-3
- 87 articleSupport detection in super-resolutionProc. Proceedings of the 10th International Conference on Sampling Theory and Applications2013, 145--148
- 88 article When is multi-dimensional screening a convex program? Journal of Economic Theory 2011
- 89 articleLongitudinal deformation models, spatial regularizations and learning strategies to quantify Alzheimer's disease progressionNeuroImage: Clinical402014, 718 - 729URL: http://www.sciencedirect.com/science/article/pii/S2213158214000205
- 90 incollectionLocal vs Global Descriptors of Hippocampus Shape Evolution for Alzheimer's Longitudinal Population AnalysisSpatio-temporal Image Analysis for Longitudinal and Time-Series Image Data7570Lecture Notes in Computer ScienceSpringer Berlin Heidelberg2012, 13-24URL: http://dx.doi.org/10.1007/978-3-642-33555-6_2
- 91 article Monge-Ampère-Kantorovitch (MAK) reconstruction of the eary universe Nature 417 260 2002
- 92 articleConvergent filtered schemes for the Monge-Ampère partial differential equationSIAM J. Numer. Anal.5112013, 423--444
- 93 article A stochastic control approach to No-Arbitrage bounds given marginals, with an application to Loopback options submitted to Annals of Applied Probability 2011
- 94 articleThe geometry of optimal transportationActa Math.17721996, 113--161URL: http://dx.doi.org/10.1007/BF02392620
- 95 articleGaspard Monge, Le mémoire sur les déblais et les remblaisImage des mathématiques, CNRS2012, URL: http://images.math.cnrs.fr/Gaspard-Monge,1094.html
- 96 incollectionMean field games and applicationsParis-Princeton Lectures on Mathematical Finance 20102003Lecture Notes in Math.BerlinSpringer2011, 205--266URL: http://dx.doi.org/10.1007/978-3-642-14660-2_3
- 97 book Image reconstruction from projections: the fundamentals of computerized tomography Academic Press 1980
- 98 articleSoliton dynamics in computational anatomyNeuroImage232004, S170--S178
- 99 incollectionThe mathematical theory of frontogenesisAnnual review of fluid mechanics, Vol. 14Palo Alto, CAAnnual Reviews1982, 131--151
- 100 articleOn explosions of solutions to a system of partial differential equations modelling chemotaxisTrans. Amer. Math. Soc.32921992, 819--824URL: http://dx.doi.org/10.2307/2153966
- 101 articleThe variational formulation of the Fokker-Planck equationSIAM J. Math. Anal.2911998, 1--17
- 102 articleOn the translocation of massesC. R. (Doklady) Acad. Sci. URSS (N.S.)371942, 199--201
- 103 articleA Mumford-Shah-Like Method for Limited Data Tomography with an Application to Electron TomographySIAM J. Imaging Sciences442011, 1029--1048
- 104 articleMean field gamesJpn. J. Math.212007, 229--260URL: http://dx.doi.org/10.1007/s11537-007-0657-8
- 105 articleGlobal Optimization with Polynomials and the Problem of MomentsSIAM Journal on Optimization1132001, 796-817
- 106 articleImaging with Kantorovich-Rubinstein DiscrepancySIAM J. Imaging Sciences742014, 2833--2859
- 107 articleA survey of the Schrödinger problem and some of its connections with optimal transportDiscrete Contin. Dyn. Syst.3442014, 1533--1574URL: http://dx.doi.org/10.3934/dcds.2014.34.1533
- 108 articleActive sets, nonsmoothness, and sensitivitySIAM Journal on Optimization1332003, 702--725
- 109 articleOptimal transportation meshfree approximation schemes for Fluid and plastic FlowsInt. J. Numer. Meth. Engng 83:1541--579832010, 1541--1579
- 110 articleA fully nonlinear version of the incompressible Euler equations: the semigeostrophic systemSIAM J. Math. Anal.3832006, 795--823 (electronic)
- 111 articleNumerical solution of the Monge-Ampére equation by a Newton's algorithmC. R. Math. Acad. Sci. Paris34042005, 319--324
- 112 article Eulerian models and algorithms for unbalanced optimal transport Preprint hal-00976501 2013
- 113 article A generalized model for optimal transport of images including dissipation and density modulation Arxiv preprint 2014
- 114 book A wavelet tour of signal processing Elsevier/Academic Press, Amsterdam 2009
- 115 articleA macroscopic crowd motion model of gradient flow typeMath. Models Methods Appl. Sci.20102010, 1787--1821URL: http://dx.doi.org/10.1142/S0218202510004799
- 116 articleA multiscale approach to optimal transportComputer Graphics Forum3052011, 1583--1592
- 117 articleHandling Convexity-Like Constraints in Variational ProblemsSIAM J. Numer. Anal.5252014, 2466--2487
- 118 articleGeodesic Shooting for Computational AnatomyJournal of Mathematical Imaging and Vision242March 2006, 209--228URL: http://dx.doi.org/10.1007/s10851-005-3624-0
- 119 article Adaptive, Anisotropic and Hierarchical cones of Discrete Convex functions Preprint 2014
- 120 articleAnisotropic Fast-Marching on Cartesian Grids Using Lattice Basis ReductionSIAM Journal on Numerical Analysis5242014, 1573-1599
- 121 articleOptimal Transport with Proximal SplittingSIAM Journal on Imaging Sciences712014, 212--238URL: http://hal.archives-ouvertes.fr/hal-00816211/
- 122 articleOptimal transport: From moving soil to same-sex marriageCMS Notes452013, 14--15
- 123 articleUniqueness and Monge Solutions in the Multimarginal Optimal Transportation ProblemSIAM Journal on Mathematical Analysis4362011, 2758-2775
- 124 articleThe Hele-Shaw Asymptotics for Mechanical Models of Tumor GrowthArchive for Rational Mechanics and Analysis21212014, 93-127URL: http://dx.doi.org/10.1007/s00205-013-0704-y
- 125 articleThe neurogeometry of pinwheels as a sub-riemannian contact structureJournal of Physiology-Paris97232003, 265--309
- 126 articleTexture Synthesis with GroupletsPattern Analysis and Machine Intelligence, IEEE Transactions on324April 2010, 733--746
- 127 articleGeneralized Wasserstein distance and its application to transport equations with sourceArchive for Rational Mechanics and Analysis21112014, 335--358
- 128 article Structure dependent sampling in compressed sensing: theoretical guarantees for tight frames Applied and Computational Harmonic Analysis 2015
- 129 articleA Generalized Forward-Backward SplittingSIAM Journal on Imaging Sciences632013, 1199--1226URL: http://hal.archives-ouvertes.fr/hal-00613637/
- 130 article Ironing, Sweeping and multi-dimensional screening Econometrica 1998
- 131 articleNonlinear total variation based noise removal algorithmsPhysica D: Nonlinear Phenomena6011992, 259--268URL: http://dx.doi.org/10.1016/0167-2789(92)90242-F
- 132 book Variational Methods in Imaging Springer 2008
- 133 article Diffeomorphic image matching with left-invariant metrics Fields Institute Communications series, special volume in memory of Jerrold E. Marsden January 2014
- 134 inproceedingsLeft-Invariant Metrics for Diffeomorphic Image Registration with Spatially-Varying RegularisationMICCAI (1)2013, 203-210
- 135 article Convolutional Wasserstein Distances: Efficient Optimal Transportation on Geometric Domains ACM Transaction on Graphics, Proc. SIGGRAPH'15 to appear 2015
- 136 articleRegression shrinkage and selection via the LassoJournal of the Royal Statistical Society. Series B. Methodological5811996, 267--288
- 137 article Shape splines and stochastic shape evolutions: A second order point of view Quarterly of Applied Mathematics 2012
- 138 articleModel Selection with Piecewise Regular GaugesInformation and Inferenceto appear2015, URL: http://hal.archives-ouvertes.fr/hal-00842603/
- 139 articleDiffeomorphic 3D Image Registration via Geodesic Shooting Using an Efficient Adjoint CalculationInternational Journal of Computer Vision9722012, 229-241URL: http://dx.doi.org/10.1007/s11263-011-0481-8
- 140 incollectionSpatially-Varying Metric Learning for Diffeomorphic Image Registration: A Variational FrameworkMedical Image Computing and Computer-Assisted Intervention MICCAI 20148673Lecture Notes in Computer ScienceSpringer International Publishing2014, 227-234
- 141 bookOptimal transport338Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]Old and newBerlinSpringer-Verlag2009, xxii+973URL: http://dx.doi.org/10.1007/978-3-540-71050-9
- 142 bookTopics in optimal transportation58Graduate Studies in MathematicsAmerican Mathematical Society, Providence, RI2003, xvi+370
- 143 articleOn the design of a reflector antenna. IICalc. Var. Partial Differential Equations2032004, 329--341URL: http://dx.doi.org/10.1007/s00526-003-0239-4
- 144 articleA continuum mechanical approach to geodesics in shape spaceInternational Journal of Computer Vision9332011, 293--318
- 145 articleSparse representation for computer vision and pattern recognitionProceedings of the IEEE9862010, 1031--1044

