Keywords
Computer Science and Digital Science
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.4. Statistical methods
- A6.2.6. Optimization
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.3. Data processing
- A6.3.4. Model reduction
Other Research Topics and Application Domains
- B1.1.7. Bioinformatics
- B1.1.8. Mathematical biology
- B1.1.10. Systems and synthetic biology
- B2.2.3. Cancer
- B2.4.2. Drug resistance
- B2.6.1. Brain imaging
- B2.6.3. Biological Imaging
1 Team members, visitors, external collaborators
Research Scientists
- Olivier Saut [Team leader, CNRS, Senior Researcher, HDR]
- Sebastien Benzekry [Inria, Researcher, HDR]
- Baudouin Denis De Senneville [CNRS, Senior Researcher, HDR]
- Christele Etchegaray [Inria, Researcher]
- Clair Poignard [Inria, Senior Researcher, HDR]
Faculty Member
- Annabelle Collin [Institut National Polytechnique de Bordeaux, Associate Professor]
Post-Doctoral Fellows
- Arturo Alvarez - Arenas Alcami [Inria, until Nov 2020]
- Anne Sophie Giacobbi [Inria]
- Van Linh Le [Inria, from Mar 2020]
- Oceane Saincir [Inria]
PhD Students
- Celestin Bigarre [Inria, from Dec 2020]
- Sergio Corridore [Univ de Bordeaux, until Jul 2020]
- Pedro Jaramillo Aguayo [Univ de Bordeaux]
- Cristina Vaghi [Inria]
Technical Staff
- Cedrick Copol [Inria, Engineer]
- Luc Lafitte [Inria, Engineer, from Mar 2020 until Sep 2020]
- Costanza Simoncini [Inria, Engineer, until Feb 2020]
Interns and Apprentices
- Celestin Bigarre [Inria, from Apr 2020 until Aug 2020]
- Benedicte Buy [Inria, from Jun 2020 until Aug 2020]
- Nicolas Giraud [Univ de Bordeaux, from Feb 2020 until Jul 2020]
- Robin Hanriot [Institut National Polytechnique de Bordeaux, from Apr 2020 until Jun 2020]
- Remi Hernandez [Inria, from Mar 2020 until Sep 2020]
- Quentin Horn [Inria, from Feb 2020 until Jul 2020]
- Yann Le Coz [Ynov Informatique Ingésup Bordeaux, from Jun 2020 until Jul 2020]
- Agathe Minaro [Inria, Jul 2020]
Administrative Assistant
- Sylvie Embolla [Inria]
External Collaborators
- Thierry Colin [Sophia Genetics, HDR]
- Francois Cornelis [Assistance publique/Hôpitaux de Paris]
- Amandine Crombe [Institut Bergonié]
- Charles Mesguich [Centre hospitalier universitaire de Bordeaux]
- Benjamin Taton [Centre hospitalier universitaire de Bordeaux]
- Damien Voyer [Ecole d'ingénieurs en génie des systèmes industriels]
2 Overall objectives
2.1 Objectives
The MONC project-team aims at developing new mathematical models from partial differential equations and statistical methods and based on biological and medical knowledge. Our goal is ultimately to be able to help clinicians and/or biologists to better understand, predict or control the evolution of the disease and possibly evaluate the therapeutic response, in a clinical context or for pre-clinical studies. We develop patient-specific approaches (mainly based on medical images) as well as population-type approaches in order to take advantage of large databases.
In vivo modeling of tumors is limited by the amount of information available. However, recently, there have been dramatic increases in the scope and quality of patient-specific data from non-invasive imaging methods, so that several potentially valuable measurements are now available to quantitatively measure tumor evolution, assess tumor status as well as anatomical or functional details. Using different techniques from biology or imaging - such as CT scan, magnetic resonance imaging (MRI), or positron emission tomography (PET) - it is now possible to evaluate and define tumor status at different levels or scales: physiological, molecular and cellular.
In the meantime, the understanding of the biological mechanisms of tumor growth, including the influence of the micro-environment, has greatly increased. Medical doctors now have access to a wide spectrum of therapies (surgery, mini-invasive techniques, radiotherapies, chemotherapies, targeted therapies, immunotherapies...).
Our project aims at helping oncologists in their followup of patients via the development of novel quantitative methods for evaluation cancer progression. The idea is to build phenomenological mathematical models based on data obtained in the clinical imaging routine like CT scans, MRIs and PET scans. We therefore want to offer medical doctors patient-specific tumor evolution models, which are able to evaluate – on the basis of previously collected data and within the limits of phenomenological models – the time evolution of the pathology at subsequent times and the response to therapies. More precisely, our goal is to help clinicians answer the following questions thanks to our numerical tools:
- When is it necessary to start a treatment?
- What is the best time to change a treatment?
- When to stop a treatment?
We also intend to incorporate real-time model information for improving the accuracy and efficacy of non invasive or micro-invasive tumor ablation techniques like acoustic hyperthermia, electroporation, radio-frequency, cryo-ablation and of course radiotherapies.
There is therefore a dire need of integrating biological knowledge into mathematical models based on clinical or experimental data. A major purpose of our project is also to create new mathematical models and new paradigms for data assimilation that are adapted to the biological nature of the disease and to the amount of multi-modal data available.
2.2 General strategy
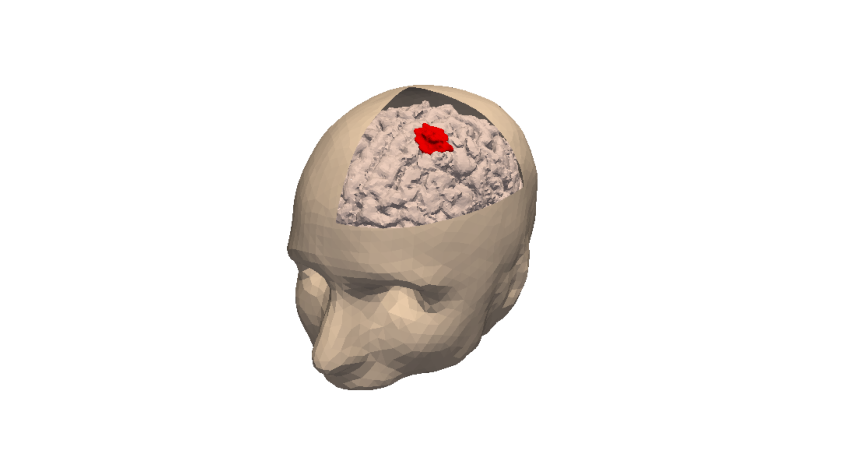
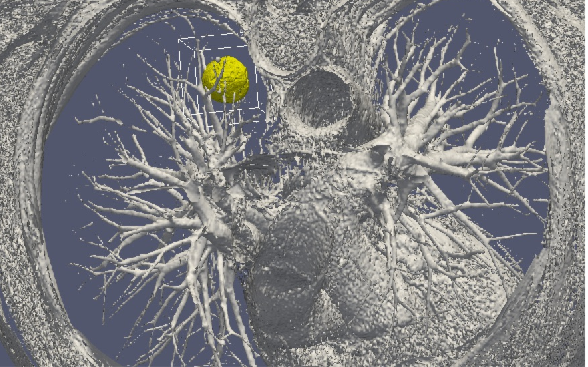
Our general strategy may be described with the following sequence:
- Stage 1: Derivation of mechanistic models based on the biological knowledge and the available observations. The construction of such models relies on the up-to-date biological knowledge at the cellular level including description of the cell-cycle, interaction with the microenvironement (angiogenesis, interaction with the stroma). Such models also include a "macroscopic" description of specific molecular pathways that are known to have a critical role in carcinogenesis or that are targeted by new drugs. We emphasize that for this purpose, close interactions with biologists are crucial. Lots of works devoted to modeling at the cellular level are available in the literature. However, in order to be able to use these models in a clinical context, the tumor is also to be described at the tissue level. The in vitro mechanical characterization of tumor tissues has been widely studied. Yet no description that could be patient specific or even tumor specific is available. It is therefore necessary to build adapted phenomenological models, according to the biological and clinical reality.
-
Stage 2: Data collection. In the clinical context, data may come from medical imaging (MRI, CT-Scan, PET scan) at different time points. We need longitudinal data in time in order to be able to understand or describe the evolution of the disease. Data may also be obtained from analyses of blood samples, biopsies or other quantitative biomarkers. A close collaboration with clinicians is required for selecting the specific cases to focus on, the understanding of the key points and data, the classification of the grades of the tumors, the understanding of the treatment,...In the preclinical context, data may for instance be macroscopic measurements of the tumor volume for subcutaneous cases, green fluorescence protein (GFP) quantifications for total number of living cells, non-invasive bioluminescence signals or even imaging obtained with devices adapted to small animals.
- Data processing: Besides selection of representative cases by our collaborators, most of the time, data has to be processed before being used in our models. We develop novel methods for semi-automatic (implemented in SegmentIt) as well as supervized approaches (machine learning or deep learning) for segmentation, non-rigid registration and extraction of image texture information (radiomics, deep learning).
- Stage 3: Adaptation of the model to data. The model has to be adapted to data: it is useless to have a model considering many biological features of the disease if it cannot be reliably parameterized with available data. For example, very detailed descriptions of the angiogenesis process found in the literature cannot be used, as they have too much parameters to determine for the information available. A pragmatic approach has to be developed for this purpose. On the other hand, one has to try to model any element that can be useful to exploit the image. Parameterizing must be performed carefully in order to achieve an optimal trade-off between the accuracy of the model, its complexity, identifiability and predictive power. Parameter estimation is a critical issue in mathematical biology: if there are too many parameters, it will be impossible to estimate them but if the model is too simple, it will be too far from reality.
-
Stage 4: Data assimilation. Because of data complexity and scarcity - for example multimodal, longitudinal medical imaging - data assimilation is a major challenge. Such a process is a combination of methods for solving inverse problems and statistical methods including machine learning strategies.
- Personalized models: Currently, most of the inverse problems developed in the team are solved using a gradient method coupled with some MCMC type algorithm. We are now trying to use more efficient methods as Kalman type filters or so-called Luenberger filter (nudging). Using sequential methods could also simplify Stage 3 because they can be used even with complex models. Of course, the strategy used by the team depends on the quantity and the quality of data. It is not the same if we have an homogeneous population of cases or if it is a very specific isolated case.
- Statistical learning: In some clinical cases, there is no longitudinal data available to build a mathematical model describing the evolution of the disease. In these cases (e.g. in our collaboration with Humanitas Research Hospital on low grade gliomas or Institut Bergonié on soft-tissue sarcoma), we use machine learning techniques to correlate clinical and imaging features with clinical outcome of patients (radiomics). When longitudinal data and a sufficient number of patients are available, we combine this approach and mathematical modeling by adding the personalized model parameters for each patient as features in the statistical algorithm. Our goal is then to have a better description of the evolution of the disease over time (as compared to only taking temporal variations of features into account as in delta-radiomics approaches). We also plan to use statistical algorithms to build reduced-order models, more efficient to run or calibrate than the original models.
- Data assimilation of gene expression. "Omics" data become more and more important in oncology and we aim at developing our models using this information as well. For example, in our work on GIST, we have taken the effect of a Ckit mutation on resistance to treatment into account. However, it is still not clear how to use in general gene expression data in our macroscopic models, and particularly how to connect the genotype to the phenotype and the macroscopic growth. We expect to use statistical learning techniques on populations of patients in order to move towards this direction, but we emphasize that this task is very prospective and is a scientific challenge in itself.
- Stage 5: Patient-specific Simulation and prediction, Stratification. Once the mechanistic models have been parametrized, they can be used to run patient-specific simulations and predictions. The statistical models offer new stratifications of patients (i.t. an algorithm that tells from images and clinical information wheter a patient with soft-tissue sarcoma is more likely to be a good or bad responder to neoadjuvant chemotherapy). Building robust algorithms (e.g. that can be deployed over multiple clinical centers) also requires working on quantifying uncertainties.
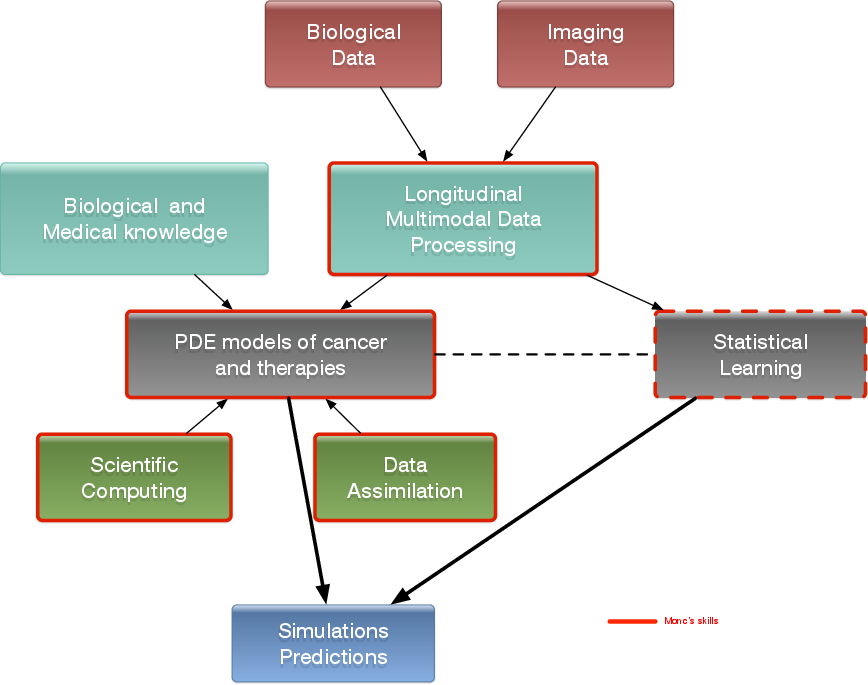
3 Research program
3.1 Introduction
We are working in the context of data-driven medicine against cancer. We aim at coupling mathematical models with data to address relevant challenges for biologists and clinicians in order for instance to improve our understanding in cancer biology and pharmacology, assist the development of novel therapeutic approaches or develop personalized decision-helping tools for monitoring the disease and evaluating therapies.
More precisely, our research on mathematical oncology is three-fold:
- Axis 1: Tumor modeling for patient-specific simulations: Clinical monitoring. Numerical markers from imaging data. Radiomics.
- Axis 2: Bio-physical modeling for personalized therapies: Electroporation from cells to tissue. Radiotherapy.
- Axis 3: Quantitative cancer modeling for biological, clinical and preclinical studies: Biological mechanisms. Metastatic dissemination. Pharmacometrics.
In the first axis, we aim at producing patient-specific simulations of the growth of a tumor or its response to treatment starting from a series of images. We hope to be able to offer a valuable insight on the disease to the clinicians in order to improve the decision process. This would be particularly useful in the cases of relapses or for metastatic diseases.
The second axis aims at modeling biophysical therapies like electroporation, but also radiotherapy, thermo-ablations, radio-frequency ablations or electroporation that play a crucial role for a local treatment of the disease if possible limiting the metastatic dissemination, which is precisely the clinical context where the techniques of axis 1 will be applied.
The third axis is essential since it is a way to better understand and model the biological reality of cancer growth and the (possibly complex) effects of therapeutic intervention. Modeling in this case also helps to interpret the experimental results and improve the accuracy of the models used in Axis 1. Technically speaking, some of the computing tools are similar to those of Axis 1.
3.2 Axis 1: Tumor modeling for patient-specific simulations
The gold standard treatment for most cancers is surgery. In the case where total resection of the tumor is possible, the patient often benefits from an adjuvant therapy (radiotherapy, chemotherapy, targeted therapy or a combination of them) in order to eliminate the potentially remaining cells that may not be visible. In this case personalized modeling of tumor growth is useless and statistical modeling will be able to quantify the risk of relapse, the mean progression-free survival time...However if total resection is not possible or if metastases emerge from distant sites, clinicians will try to control the disease for as long as possible. A wide set of tools are available. Clinicians may treat the disease by physical interventions (radiofrequency ablation, cryoablation, radiotherapy, electroporation, focalized ultrasound,...) or chemical agents (chemotherapies, targeted therapies, antiangiogenic drugs, immunotherapies, hormonotherapies). One can also decide to monitor the patient without any treatment (this is the case for slowly growing tumors like some metastases to the lung, some lymphomas or for some low grade glioma). A reliable patient-specific model of tumor evolution with or without therapy may have different uses:
- Case without treatment: the evaluation of the growth of the tumor would offer a useful indication for the time at which the tumor may reach a critical size. For example, radiofrequency ablation of pulmonary lesion is very efficient as long as the diameter of the lesion is smaller than 3 cm. Thus, the prediction can help the clinician plan the intervention. For slowly growing tumors, quantitative modeling can also help to decide at what time interval the patient has to undergo a CT-scan. CT-scans are irradiative exams and there is a challenge for decreasing their occurrence for each patient. It has also an economical impact. And if the disease evolution starts to differ from the prediction, this might mean that some events have occurred at the biological level. For instance, it could be the rise of an aggressive phenotype or cells that leave a dormancy state. This kind of events cannot be predicted, but some mismatch with respect to the prediction can be an indirect proof of their existence. It could be an indication for the clinician to start a treatment.
- Case with treatment: a model can help to understand and to quantify the final outcome of a treatment using the early response. It can help for a redefinition of the treatment planning. Modeling can also help to anticipate the relapse by analyzing some functional aspects of the tumor. Again, a deviation with respect to reference curves can mean a lack of efficiency of the therapy or a relapse. Moreover, for a long time, the response to a treatment has been quantified by the RECIST criteria which consists in (roughly speaking) measuring the diameters of the largest tumor of the patient, as it is seen on a CT-scan. This criteria is still widely used and was quite efficient for chemotherapies and radiotherapies that induce a decrease of the size of the lesion. However, with the systematic use of targeted therapies and anti-angiogenic drugs that modify the physiology of the tumor, the size may remain unchanged even if the drug is efficient and deeply modifies the tumor behavior. One better way to estimate this effect could be to use functional imaging (Pet-scan, perfusion or diffusion MRI, ...), a model can then be used to exploit the data and to understand in what extent the therapy is efficient.
- Optimization: currently, we do not believe that we can optimize a particular treatment in terms of distribution of doses, number, planning with the model that we will develop in a medium term perspective.
The scientific challenge is therefore as follows: given the history of the patient, the nature of the primitive tumor, its histopathology, knowing the treatments that patients have undergone, some biological facts on the tumor and having a sequence of images (CT-scan, MRI, PET or a mix of them), are we able to provide a numerical simulation of the extension of the tumor and of its metabolism that fits as best as possible with the data (CT-scans or functional data) and that is predictive in order to address the clinical cases described above?
Our approach relies on the elaboration of PDE models and their parametrization with images by coupling deterministic and stochastic methods. The PDE models rely on the description of the dynamics of cell populations. The number of populations depends on the pathology. For example, for glioblastoma, one needs to use proliferative cells, invasive cells, quiescent cells as well as necrotic tissues to be able to reproduce realistic behaviors of the disease. In order to describe the relapse for hepatic metastases of gastro-intestinal stromal tumor (gist), one needs three cell populations: proliferative cells, healthy tissue and necrotic tissue.
The law of proliferation is often coupled with a model for the angiogenesis. However such models of angiogenesis involve too many non measurable parameters to be used with real clinical data and therefore one has to use simplified or even simplistic versions. The law of proliferation often mimics the existence of an hypoxia threshold, it consists of an ODE. or a PDE that describes the evolution of the growth rate as a combination of sigmoid functions of nutrients or roughly speaking oxygen concentration. Usually, several laws are available for a given pathology since at this level, there are no quantitative argument to choose a particular one.
The velocity of the tumor growth differs depending on the nature of the tumor. For metastases, we will derive the velocity thanks to Darcy's law in order to express that the extension of the tumor is basically due to the increase of volume. This gives a sharp interface between the metastasis and the surrounding healthy tissues, as observed by anatomopathologists. For primitive tumors like glioma or lung cancer, we use reaction-diffusion equations in order to describe the invasive aspects of such primitive tumors.
The modeling of the drugs depends on the nature of the drug: for chemotherapies, a death term can be added into the equations of the population of cells, while antiangiogenic drugs have to be introduced in a angiogenic model. Resistance to treatment can be described either by several populations of cells or with non-constant growth or death rates. As said before, it is still currently difficult to model the changes of phenotype or mutations, we therefore propose to investigate this kind of phenomena by looking at deviations of the numerical simulations compared to the medical observations.
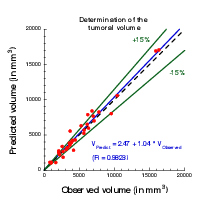
The calibration of the model is achieved by using a series (at least 2) of images of the same patient and by minimizing a cost function. The cost function contains at least the difference between the volume of the tumor that is measured on the images with the computed one. It also contains elements on the geometry, on the necrosis and any information that can be obtained through the medical images. We will pay special attention to functional imaging (PET, perfusion and diffusion MRI). The inverse problem is solved using a gradient method coupled with some Monte-Carlo type algorithm. If a large number of similar cases is available, one can imagine to use statistical algorithms like random forests to use some non quantitative data like the gender, the age, the origin of the primitive tumor...for example for choosing the model for the growth rate for a patient using this population knowledge (and then to fully adapt the model to the patient by calibrating this particular model on patient data) or for having a better initial estimation of the modeling parameters. We have obtained several preliminary results concerning lung metastases including treatments and for metastases to the liver.
3.3 Axis 2: Bio-physical modeling for personalized therapies
In this axis, we investigate locoregional therapies such as radiotherapy, irreversible electroporation. Electroporation consists in increasing the membrane permeability of cells by the delivery of high voltage pulses. This non-thermal phenomenon can be transient (reversible) or irreversible (IRE). IRE or electro-chemotherapy – which is a combination of reversible electroporation with a cytotoxic drug – are essential tools for the treatment of a metastatic disease. Numerical modeling of these therapies is a clear scientific challenge. Clinical applications of the modeling are the main target, which thus drives the scientific approach, even though theoretical studies in order to improve the knowledge of the biological phenomena, in particular for electroporation, should also be addressed. However, this subject is quite wide and we focus on two particular approaches: some aspects of radiotherapies and electro-chemotherapy. This choice is motivated partly by pragmatic reasons: we already have collaborations with physicians on these therapies. Other treatments could be probably treated with the same approach, but we do not plan to work on this subject on a medium term.
-
Radiotherapy (RT) is a common therapy for cancer. Typically, using a CT scan of the patient with the structures of interest (tumor, organs at risk) delineated, the clinicians optimize the dose delivery to treat the tumor while preserving healthy tissues. The RT is then delivered every day using low resolution scans (CBCT) to position the beams. Under treatment the patient may lose weight and the tumor shrinks. These changes may affect the propagation of the beams and subsequently change the dose that is effectively delivered. It could be harmful for the patient especially if sensitive organs are concerned. In such cases, a replanification of the RT could be done to adjust the therapeutical protocol. Unfortunately, this process takes too much time to be performed routinely. The challenges faced by clinicians are numerous, we focus on two of them:
- Detecting the need of replanification: we are using the positioning scans to evaluate the movement and deformation of the various structures of interest. Thus we can detect whether or not a structure has moved out of the safe margins (fixed by clinicians) and thus if a replanification may be necessary. In a retrospective study, our work can also be used to determine RT margins when there are no standard ones. A collaboration with the RT department of Institut Bergonié is underway on the treatment of retroperitoneal sarcoma and ENT tumors (head and neck cancers). A retrospective study was performed on 11 patients with retro-peritoneal sarcoma. The results have shown that the safety margins (on the RT) that clinicians are currently using are probably not large enough. The tool used in this study was developed by an engineer funded by INRIA (Cynthia Périer, ADT Sesar). We used well validated methods from a level-set approach and segmentation / registration methods. The originality and difficulty lie in the fact that we are dealing with real data in a clinical setup. Clinicians have currently no way to perform complex measurements with their clinical tools. This prevents them from investigating the replanification. Our work and the tools developed pave the way for easier studies on evaluation of RT plans in collaboration with Institut Bergonié. There was no modeling involved in this work that arose during discussions with our collaborators. The main purpose of the team is to have meaningful outcomes of our research for clinicians, sometimes it implies leaving a bit our area of expertise.
- Evaluating RT efficacy and finding correlation between the radiological responses and the clinical outcome: our goal is to help doctors to identify correlation between the response to RT (as seen on images) and the longer term clinical outcome of the patient. Typically, we aim at helping them to decide when to plan the next exam after the RT. For patients whose response has been linked to worse prognosis, this exam would have to be planned earlier. This is the subject of collaborations with Institut Bergonié and CHU Bordeaux on different cancers (head and neck, pancreas). The response is evaluated from image markers (e.g. using texture information) or with a mathematical model developed in Axis 1. The other challenges are either out of reach or not in the domain of expertise of the team. Yet our works may tackle some important issues for adaptive radiotherapy.
-
Both IRE and electrochemotherapy are anticancerous treatments based on the same phenomenon: the electroporation of cell membranes. This phenomenon is known for a few decades but it is still not well understood, therefore our interest is two fold:
- We want to use mathematical models in order to better understand the biological behavior and the effect of the treatment. We work in tight collaboration with biologists and bioeletromagneticians to derive precise models of cell and tissue electroporation, in the continuity of the research program of the Inria team-project MC2. These studies lead to complex non-linear mathematical models involving some parameters (as less as possible). Numerical methods to compute precisely such models and the calibration of the parameters with the experimental data are then addressed. Tight collaborations with the Vectorology and Anticancerous Therapies (VAT) of IGR at Villejuif, Laboratoire Ampère of Ecole Centrale Lyon and the Karlsruhe Institute of technology will continue, and we aim at developing new collaborations with Institute of Pharmacology and Structural Biology (IPBS) of Toulouse and the Laboratory of Molecular Pathology and Experimental Oncology (LMPEO) at CNR Rome, in order to understand differences of the electroporation of healthy cells and cancer cells in spheroids and tissues.
- This basic research aims at providing new understanding of electroporation, however it is necessary to address, particular questions raised by radio-oncologists that apply such treatments. One crucial question is "What pulse or what train of pulses should I apply to electroporate the tumor if the electrodes are located as given by the medical images"? Even if the real-time optimization of the placement of the electrodes for deep tumors may seem quite utopian since the clinicians face too many medical constraints that cannot be taken into account (like the position of some organs, arteries, nerves...), one can expect to produce real-time information of the validity of the placement done by the clinician. Indeed, once the placement is performed by the radiologists, medical images are usually used to visualize the localization of the electrodes. Using these medical data, a crucial goal is to provide a tool in order to compute in real-time and visualize the electric field and the electroporated region directly on theses medical images, to give the doctors a precise knowledge of the region affected by the electric field. In the long run, this research will benefit from the knowledge of the theoretical electroporation modeling, but it seems important to use the current knowledge of tissue electroporation – even quite rough –, in order to rapidly address the specific difficulty of such a goal (real-time computing of non-linear model, image segmentation and visualization). Tight collaborations with CHU Pellegrin at Bordeaux, and CHU J. Verdier at Bondy are crucial.
- Radiofrequency ablation. In a collaboration with Hopital Haut Leveque, CHU Bordeaux we are trying to determine the efficacy and risk of relapse of hepatocellular carcinoma treated by radiofrequency ablation. For this matter we are using geometrical measurements on images (margins of the RFA, distance to the boundary of the organ) as well as texture information to statistically evaluate the clinical outcome of patients.
- Intensity focused ultrasound. In collaboration with Utrecht Medical center, we aim at tackling several challenges in clinical applications of IFU: target tracking, dose delivery...
3.4 Axis 3: Quantitative cancer modeling for biological and preclinical studies
With the emergence and improvement of a plethora of experimental techniques, the molecular, cellular and tissue biology has operated a shift toward a more quantitative science, in particular in the domain of cancer biology. These quantitative assays generate a large amount of data that call for theoretical formalism in order to better understand and predict the complex phenomena involved. Indeed, due to the huge complexity underlying the development of a cancer disease that involves multiple scales (from the genetic, intra-cellular scale to the scale of the whole organism), and a large number of interacting physiological processes (see the so-called "hallmarks of cancer"), several questions are not fully understood. Among these, we want to focus on the most clinically relevant ones, such as the general laws governing tumor growth and the development of metastases (secondary tumors, responsible of 90% of the deaths from a solid cancer). In this context, it is thus challenging to exploit the diversity of the data available in experimental settings (such as in vitro tumor spheroids or in vivo mice experiments) in order to improve our understanding of the disease and its dynamics, which in turn lead to validation, refinement and better tuning of the macroscopic models used in the axes 1 and 2 for clinical applications.
In recent years, several new findings challenged the classical vision of the metastatic development biology, in particular by the discovery of organism-scale phenomena that are amenable to a dynamical description in terms of mathematical models based on differential equations. These include the angiogenesis-mediated distant inhibition of secondary tumors by a primary tumor the pre-metastatic niche or the self-seeding phenomenon Building a general, cancer type specific, comprehensive theory that would integrate these dynamical processes remains an open challenge. On the therapeutic side, recent studies demonstrated that some drugs (such as the Sunitinib), while having a positive effect on the primary tumor (reduction of the growth), could accelerate the growth of the metastases. Moreover, this effect was found to be scheduling-dependent. Designing better ways to use this drug in order to control these phenomena is another challenge. In the context of combination therapies, the question of the sequence of administration between the two drugs is also particularly relevant.
One of the technical challenge that we need to overcome when dealing with biological data is the presence of potentially very large inter-animal (or inter-individual) variability.
Starting from the available multi-modal data and relevant biological or therapeutic questions, our purpose is to develop adapted mathematical models (i.e. identifiable from the data) that recapitulate the existing knowledge and reduce it to its more fundamental components, with two main purposes:
- to generate quantitative and empirically testable predictions that allow to assess biological hypotheses or
- to investigate the therapeutic management of the disease and assist preclinical studies of anti-cancerous drug development.
We believe that the feedback loop between theoretical modeling and experimental studies can help to generate new knowledge and improve our predictive abilities for clinical diagnosis, prognosis, and therapeutic decision. Let us note that the first point is in direct link with the axes 1 and 2 of the team since it allows us to experimentally validate the models at the biological scale (in vitro and in vivo experiments) for further clinical applications.
More precisely, we first base ourselves on a thorough exploration of the biological literature of the biological phenomena we want to model: growth of tumor spheroids, in vivo tumor growth in mice, initiation and development of the metastases, effect of anti-cancerous drugs. Then we investigate, using basic statistical tools, the data we dispose, which can range from: spatial distribution of heterogeneous cell population within tumor spheroids, expression of cell markers (such as green fluorescent protein for cancer cells or specific antibodies for other cell types), bioluminescence, direct volume measurement or even intra-vital images obtained with specific imaging devices. According to the data type, we further build dedicated mathematical models that are based either on PDEs (when spatial data is available, or when time evolution of a structured density can be inferred from the data, for instance for a population of tumors) or ODEs (for scalar longitudinal data). These models are confronted to the data by two principal means:
- when possible, experimental assays can give a direct measurement of some parameters (such as the proliferation rate or the migration speed) or
- statistical tools to infer the parameters from observables of the model.
This last point is of particular relevance to tackle the problem of the large inter-animal variability and we use adapted statistical tools such as the mixed-effects modeling framework.
Once the models are shown able to describe the data and are properly calibrated, we use them to test or simulate biological hypotheses. Based on our simulations, we then aim at proposing to our biological collaborators new experiments to confirm or infirm newly generated hypotheses, or to test different administration protocols of the drugs. For instance, in a collaboration with the team of the professor Andreas Bikfalvi (Laboratoire de l'Angiogénèse et du Micro-environnement des Cancers, Inserm, Bordeaux), based on confrontation of a mathematical model to multi-modal biological data (total number of cells in the primary and distant sites and MRI), we could demonstrate that the classical view of metastatic dissemination and development (one metastasis is born from one cell) was probably inaccurate, in mice grafted with metastatic kidney tumors. We then proposed that metastatic germs could merge or attract circulating cells. Experiments involving cells tagged with two different colors are currently performed in order to confirm or infirm this hypothesis.
Eventually, we use the large amount of temporal data generated in preclinical experiments for the effect of anti-cancerous drugs in order to design and validate mathematical formalisms translating the biological mechanisms of action of these drugs for application to clinical cases, in direct connection with the axis 1. We have a special focus on targeted therapies (designed to specifically attack the cancer cells while sparing the healthy tissue) such as the Sunitinib. This drug is indeed indicated as a first line treatment for metastatic renal cancer and we plan to conduct a translational study coupled between A. Bikfalvi's laboratory and medical doctors, F. Cornelis (radiologist) and A. Ravaud (head of the medical oncology department).
4 Application domains
4.1 Tumor growth monitoring and therapeutic evaluation
Each type of cancer is different and requires an adequate model. More specifically, we are currently working on the following diseases:
- Glioma (brain tumors) of various grades,
- Metastases to the lung, liver and brain from various organs,
- Soft-tissue sarcoma,
- Kidney cancer and its metastases,
- non small cell lung carcinoma.
In this context our application domains are:
- Image-driven patient-specific simulations of tumor growth and treatments,
- Parameter estimation and data assimilation of medical images,
- Machine and deep learning methods for delineating the lesions and stratifying patients according to their responses to treatment or risks of relapse.
4.2 Biophysical therapies
- Modeling of electrochemotherapy on biological and clinical scales.
- Evaluation of radiotherapy and radiofrequency ablation.
4.3 In-vitro and animals experimentations in oncology
- Theoretical biology of the metastatic process: dynamics of a population of tumors in mutual interactions, dormancy, pre-metastatic and metastatic niche, quantification of metastatic potential and differential effects of anti-angiogenic therapies on primary tumor and metastases.
- Mathematical models for preclinical cancer research: description and prediction of tumor growth and metastatic development, effect of anti-cancerous therapies.
5 Social and environmental responsibility
5.1 Footprint of research activities
Numerical computations on (GPU) clusters like Plafrim (https://
5.2 Impact of research results
In the long run, our research could yield interesting outcomes for cancer patients. Yet we are mostly building proofs of concept that would have to be taken over by an industrial partner for any transfer towards clinics (like we did with Sophia Genetics in the past).
6 Highlights of the year
The year 2020 was marked by the covid crisis and its impact on society and its overall activity. The world of research was also greatly affected: Faculty members have seen their teaching load increase significantly; PhD students and post-docs have often had to deal with a worsening of their working conditions, as well as with reduced interactions with their supervisors and colleagues; most scientific collaborations have been greatly affected, with many international activities cancelled or postponed to dates still to be defined.
6.1 Covid projects
From the first lockdown, several members of the team have been involved in scientific projects related to the Covid-19.
All faculty members and some post-docs of the team have participated in the RadioCovid project (https://
In addition to her work on RadioCovid, A. Collin has also participated in the GestEpid project (https://
7 New software and platforms
7.1 New software
7.1.1 August
- Name: Antibody Drug Uptake Simulator
- Keyword: Mechanistic modeling
- Functional Description: Numerical code to compute the uptake of an antibody drug at the scale of an histopathology blade. The computation domain (reconstructed from segmented images) is completely meshed and sub-divided accross computational nodes to distribute the load efficiently. The model (based on reaction-diffusion equations) is then solved in parallel using a domain decomposition method. C ++
- Contact: Olivier Saut
8 New results
8.1 Joint state-parameter estimation for tumor growth model
Authors: Annabelle Collin, Thibaut Kritter, Clair Poignard, Olivier Saut
Abstract : We present a shape-oriented data assimilation strategy suitable for front-tracking tumor growth problems. A general hyperbolic/elliptic tumor growth model is presented as well as the available observations corresponding to the location of the tumor front over time extracted from medical imaging as MRI or CT scans. We provide sufficient conditions allowing to design a state observer by proving the convergence of the observer model to the target solution, for exact parameters. In particular, the similarity measure chosen to compare observations and simulation of tumor contour is presented. A specific joint state-parameter correction with a Luenberger observer correcting the state and a reduced-order Kalman filter correcting the parameters is introduced and studied. We then illustrate and assess our proposed observer method with synthetic problems. Our numerical trials show that state estimation is very effective with the proposed Luenberger observer, but specific strategies are needed to accurately perform parameter estimation in a clinical context. We then propose strategies to deal with the fact that data is very sparse in time and that the initial distribution of the proliferation rate is unknown. The results on synthetic data are very promising and work is ongoing to apply our strategy on clinical cases.
8.2 Intensity Harmonization Techniques Influence Radiomics Features and Radiomics-based Predictions in Sarcoma Patients
Authors: Amandine Crombé, Michèle Kind, David Fadli, François Le Loarer, Antoine Italiano, Xavier Buy, Olivier Saut
Intensity harmonization techniques (IHT) are mandatory to homogenize multicentric MRIs before any quantitative analysis because signal intensities (SI) do not have standardized units. Radiomics combine quantification of tumors’ radiological phenotype with machine-learning to improve predictive models, such as metastastic-relapse-free survival (MFS) for sarcoma patients. We post-processed the initial T2-weighted-imaging of 70 sarcoma patients by using 5 IHTs and extracting 45 radiomics features (RFs), namely: classical standardization (IHTstd), standardization per adipose tissue SIs (IHTfat), histogram-matching with a patient histogram (IHTHM.1), with the average histogram of the population (IHTHM.All) and plus ComBat method (IHTHM.All.C), which provided 5 radiomics datasets in addition to the original radiomics dataset without IHT (No-IHT). We found that using IHTs significantly influenced all RFs values (p-values: <0.0001-0.02). Unsupervised clustering performed on each radiomics dataset showed that only clusters from the No-IHT, IHTstd, IHTHM. All, and IHTHM.All.Cdatasets significantly correlated with MFS in multivariate Cox models (p=0.02, 0.007, 0.004 and0.02, respectively). We built radiomics-based supervised models to predict metastatic relapse at 2-years with a training set of 50 patients. The models performances varied markedly depending on the IHT in the validation set (range of AUROCfrom 0.688withIHTstdto 0.823withIHTHM.1). Hence, the use of intensity harmonization and the related technique should be carefully detailed in radiomics post-processing pipelines as it can profoundly affect the reproducibility of analyses.
8.3 Spatial mechanistic modeling for prediction of the growth of asymptomatic meningioma
Authors: Annabelle Collin, Cédrick Copol, Vivien Pianet, Thierry Colin, Julien Engelhardt, Guy Kantor, Hugues Loiseau, Olivier Saut, Benjamin Taton
Background and Objective: Mathematical modeling of tumor growth draws interest from the medical community as they have the potential to improve patients’ care and the use of public health resources. The main objectives of this work are to model the growth of meningiomas – slow-growing benign tumors requiring extended imaging follow-up – and to predict tumor volume and shape at a later desired time using only two times examinations.
Methods: We develop two variants of a 3D partial differential system of equations (PDE) which yield after a spatial integration systems of ordinary differential equations (ODE) that relate tumor volume with time. Estimation of models parameters is a crucial step to obtain a personalized model for a patient that can be used for descriptive or predictive purposes. As PDE and ODE systems share the same parameters, they are both estimated by fitting the ODE systems to the tumor volumes obtained from MRI examinations acquired at different times. A population approach allows to compensate for sparse sampling times and measurement uncertainties by constraining the variability of the parameters in the population.
Results: Description capabilities of the models are investigated in 39 patients with benign asymptomatic meningiomas who had had at least three surveillance MRI examinations. The two models can fit to the data accurately and more realistically than a naive linear regression.Prediction performances are validated for 33 patients using a population approach. Mean relative errors in volume predictions are less than 10% with ODE systems versus 12.5% with the naive linear model using only two times examinations. Concerning the shape, the meanSørensen-Dice coefficients are 85% with the PDE systems in a subset of 10 representativepatients. Conclusions: Our strategy – based on personalization of mathematical model – provides a good insight on meningioma growth and may help decide whether to extend the follow-up or to treat the tumor.
8.4 Systematic review of sarcomas radiomics studies: Bridging the gap between concepts and clinical applications?
Authors: Amandine Crombé, David Fadli, Antoine Italiano, Olivier Saut, Xavier Buy, Michèle Kind.
Objectives: Sarcomas are a model for intra- and inter-tumoral heterogeneities making them particularly suitable for radiomics analyses. Our purposes were to review the aims, methods and results of radiomics studies involving sarcomas METHODS: Pubmed and Web of Sciences databases were searched for radiomics or textural studies involving bone, soft-tissues and visceral sarcomas until June 2020. Two radiologists evaluated their objectives, results and quality of their methods, imaging pre-processing and machine-learning workflow helped by the items of the Quality Assessment of Diagnostic Accuracy Studies (QUADAS-2), Image Biomarker Standardization Initiative (IBSI) and 'Radiomics Quality Score' (RQS). Statistical analyses included inter-reader agreements, correlations between methodological assessments, scientometrics indices, and their changes over years, and between RQS, number of patients and models performance.
Results: Fifty-two studies were included involving: soft-tissue sarcomas (29/52, 55.8%), bone sarcomas (15/52, 28.8%), gynecological sarcomas (6/52, 11.5%) and mixed sarcomas (2/52, 3.8%), mostly imaged with MRI (36/52, 69.2%), for a total of distinct patients. Median RQS was 4.5 (28.4% of the maximum, range: -7 - 17). Performances of predictive models and number of patients negatively correlated (p = 0.027). None of the studies detailed all the items from the IBSI guidelines. There was a significant increase in studies' impact factors since the establishing of the RQS in 2017 (p = 0.038).
Conclusion: Although showing promising results, further efforts are needed to make sarcoma radiomics studies reproducible with an acceptable level of evidence. A better knowledge of the RQS and IBSI reporting guidelines could improve the quality of sarcoma radiomics studies and accelerate clinical applications.
8.5 High-Grade Soft-Tissue Sarcomas: Can Optimizing Dynamic Contrast-Enhanced MRI Postprocessing Improve Prognostic Radiomics Models?
Authors: Amandine Crombé, David Fadli, Xavier Buy, Antoine Italiano, Olivier Saut, Michèle Kind
Background: Heterogeneity on pretreatment dynamic contrast-enhanced (DCE)-MRI of sarcomas may be prognostic, but the best technique to capture this characteristic remains unknown.
Purpose: To investigate the best method to extract prognostic data from baseline DCE-MRI.
Population: Fifty consecutive uniformly-treated adults with nonmetastatic high-grade sarcomas.
Assessment: Ninety-two radiomics features (RFs) were extracted at each DCE-MRI phase (11, from t = 0-88 sec). Relative changes in RFs (rRFs) since the acquisition baseline were calculated (11 × 92 rRFs). Curves of rRF as function of time postinjection were integrated (92 integrated-rRFs [irRFs]). Ktrans and area under the time-intensity curve at 88-sec parametric maps were computed and 2 × 92 parametric-RFs (pRFs) were extracted. Five DCE-MRI-based radiomics models were built on: an RFs subset (32 sec, 64 sec, 88 sec); all rRFs; all irRFs; and all pRFs. Two models were elaborated as reference, on: conventional radiological features; and T2 -WI RFs.
Statistical tests: A common machine-learning approach was applied to radiomics models. Features with P < 0.05 at univariate analysis were entered in a LASSO-penalized Cox regression including bootstrapped 10-fold cross-validation. The resulting radiomics scores (RScores) were dichotomized per their median and entered in multivariate Cox models for predicting metastatic relapse-free survival. Models were compared with integrative area under the curve (AUC) and concordance index.
Results: Only dichotomized RScores from models based on rRFs subset, all rRFS and irRFS correlated with prognostic (P = 0.0107-0.0377). The models including all rRFs and irRFs had the highest c-index (0.83), followed by the radiological model. The radiological model had the highest integrative AUC (0.87), followed by models including all rRFs and irRFs. The radiological and full rRFs models were significantly better than the T2 -based radiomics model (P = 0.02).
Data conclusion: The initial DCE-MRI of STS contains prognostic information. It seems more relevant to make predictions on rRFs instead of pRFs.
8.6 MRI-Based Radiomics Input for Prediction of 2-Year Disease Recurrence in Anal Squamous Cell Carcinoma
Authors: Nicolas Giraud, Olivier Saut, Thomas Aparicio, Philippe Ronchin, Louis-Arnaud Bazire, Emilie Barbier, Claire Lemanski, Xavier Mirabel, Pierre-Luc Etienne, Astrid Lièvre, Wulfran Cacheux, Ariane Darut-Jouve, Christelle De la Fouchardière, Arnaud Hocquelet, Hervé Trillaud, Thomas Charleux, Gilles Breysacher, Delphine Argo-Leignel, Alexandre Tessier, Nicolas Magné, Meher Ben Abdelghani, Côme Lepage, Véronique Vendrely
Purpose: Chemo-radiotherapy (CRT) is the standard treatment for non-metastatic anal squamous cell carcinomas (ASCC). Despite excellent results for T1-2 stages, relapses still occur in around 35% of locally advanced tumors. Recent strategies focus on treatment intensification, but could benefit from a better patient selection. Our goal was to assess the prognostic value of pre-therapeutic MRI radiomics on 2-year disease control (DC).
Methods: We retrospectively selected patients with non-metastatic ASCC treated at the CHU Bordeaux and in the French FFCD0904 multicentric trial. Radiomic features were extracted from T2-weighted pre-therapeutic MRI delineated sequences. After random division between training and testing sets on a 2:1 ratio, univariate and multivariate analysis were performed on the training cohort to select optimal features. The correlation with 2-year DC was assessed using logistic regression models, with AUC and accuracy as performance gauges, and the prediction of disease-free survival using Cox regression and Kaplan-Meier analysis.
Results: A total of 82 patients were randomized in the training (n = 54) and testing sets (n = 28). At 2 years, 24 patients (29%) presented relapse. In the training set, two clinical (tumor size and CRT length) and two radiomic features (FirstOrder_Entropy and GLCM_JointEnergy) were associated with disease control in univariate analysis and included in the model. The clinical model was outperformed by the mixed (clinical and radiomic) model in both the training (AUC 0.758 versus 0.825, accuracy of 75.9% versus 87%) and testing (AUC 0.714 versus 0.898, accuracy of 78.6% versus 85.7%) sets, which led to distinctive high and low risk of disease relapse groups (HR 8.60, p = 0.005).
Conclusion: A mixed model with two clinical and two radiomic features was predictive of 2-year disease control after CRT and could contribute to identify high risk patients amenable to treatment intensification with view of personalized medicine.
8.7 Machine learning and mechanistic modeling for prediction of metastatic relapse in early-stage breast cancer
Authors: C. Nicolò; C. Périer; M. Prague; C. Bellera; G. MacGrogan; O.Saut; S. Benzekry. Published in the Journal of Clinical Oncology: Clinical Cancer Informatics. https://
Purpose: For patients with early-stage breast cancer, prediction of the risk of metastatic relapse is of crucial importance. Existing predictive models rely on agnostic survival analysis statistical tools (e.g. Cox regression). Here we define and evaluate the predictive ability of a mechanistic model for the time to metastatic relapse.
Methods: The data consisted of 642 patients with 21 clinicopathological variables. A mechanistic model was developed on the basis of two intrinsic mechanisms of metastatic progression: growth (parameter ) and dissemination (parameter ). Population statistical distributions of the parameters were inferred using mixed-effects modeling. A random survival forest analysis was used to select a minimal set of 5 covariates with best predictive power. These were further considered to individually predict the model parameters, by using a backward selection approach. Predictive performances were compared to classical Cox regression and machine learning algorithms.
Results: The mechanistic model was able to accurately fit the data. Covariate analysis revealed statistically significant association of Ki67 expression with (p=0.001) and EGFR with (p=0.009). Achieving a c-index of 0.65 (0.60-0.71), the model had similar predictive performance as the random survival forest (c-index 0.66-0.69) and Cox regression (c-index 0.62 - 0.67), as well as machine learning classification algorithms.
Conclusion: By providing informative estimates of the invisible metastatic burden at the time of diagnosis and forward simulations of metastatic growth, the proposed model could be used as a personalized prediction tool of help for routine management of breast cancer patients.
8.8 Numerical workflow for clinical electroporation ablation
Authors: Olivier Gallinato, Baudouin Denis de Senneville, Olivier Seror, Clair Poignard. Published in Physics in Medicine and Biology. https://
The paper describes a numerical workflow, based on the “real-life” clinical workflow ofirreversible electroporation (IRE) performed for the treatment of deep-seated liver tumors. Thanksto a combination of numerical modeling, image registration algorithm and clinical data, our numerical workflow enables to provide the distribution of the electric field as effectively delivered by theclinical IRE procedure. As a proof of concept, we show on a specific clinical case of IRE ablation of liver tumor that clinical data could be advantageously combined to numerical simulations in a nearfuture , in order to give to the interventional radiologists information on the effective IRE ablation. We also corroborate the simulated treated region with the post-treatment MRI performed 3 days after treatment.
8.9 A reduced Gompertz model for predicting tumor age using a population approach
Authors: C. Vaghi, A. Rodallec, R. Fanciullino, J. Ciccolini, J. Mochel, M. Mastri, C. Poignard, J. ML Ebos, S. Benzekry. Published in PLoS Computational Biology. https://
Tumor growth curves are classically modeled by means of ordinary differential equations. In analyzing the Gompertz model several studies have reported a striking correlation between the two parameters of the model, which could be used to reduce the dimensionality and improve predictive power.
We analyzed tumor growth kinetics within the statistical framework of nonlinear mixed-effects (population approach). This allowed the simultaneous modeling of tumor dynamics and inter-animal variability. Experimental data comprised three animal models of breast and lung cancers, with 833 measurements in 94 animals. Candidate models of tumor growth included the exponential, logistic and Gompertz. The exponential and – more notably – logistic models failed to describe the experimental data whereas the Gompertz model generated very good fits. The previously reported population-level correlation between the Gompertz parameters was further confirmed in our analysis (R > 0.92 in all groups). Combining this structural correlation with rigorous population parameter estimation, we propose a reduced Gompertz function consisting of a single individual parameter (and one population parameter). Leveraging the population approach using Bayesian inference, we estimated times of tumor initiation using three late measurement timepoints. The reduced Gompertz model was found to exhibit the best results, with drastic improvements when using Bayesian inference as compared to likelihood maximization alone, for both accuracy and precision. Specifically, mean accuracy was 12.2% versus 78% and mean precision was 15.6 days versus 210 days, for the breast cancer cell line.
These results offer promising clinical perspectives for the personalized prediction of tumor age from limited data at diagnosis. In turn, such predictions could be helpful for assessing the extent of invisible metastasis at the time of diagnosis.
The code and the data used in our analysis are available at https://
8.10 Optimizing 4D abdominal MRI: Image denoising using an iterative back-projection approach
Authors: B Denis de Senneville, C R Cardiet, A J Trotier, E J Ribot, L Lafitte, L Facq, S Miraux. Published in Physics in Medicine and Biology. https://
4D-MRI is a promising tool for organ exploration, target delineation and treatment planning. Intra-scan motion artifacts may be greatly reduced by increasing the imaging frame rate. However, poor signal-to-noise ratios (SNR) are observed when increasing spatial and/or frame number per physiological cycle, in particular in the abdomen. In the current work, the proposed 4D-MRI method favored spatial resolution, frame number, isotropic voxels and large field-of-view (FOV) during MR-acquisition. The consequential SNR penalty in the reconstructed data is addressed retrospectively using an iterative back-projection (IBP) algorithm. Practically, after computing individual spatial 3D deformations present in the images using a deformable image registration (DIR) algorithm, each 3D image is individually enhanced by fusing several successive frames in its local temporal neighborood, these latter being likely to cover common independent informations. A tuning parameter allows one to freely readjust the balance between temporal resolution and precision of the 4D-MRI. The benefit of the method was quantitatively evaluated on the thorax of 6 miceunder free breathing using a clinically acceptable duration. Improved 4D cardiac imaging was also shown in the heart of 1 mice. Obtained results are compared to theoretical expectations and discussed. The proposed implementation is easily parallelizable and optimized 4D-MRI could thereby be obtained with a clinically acceptable duration.
8.11 Development and Validation of a Prediction Model of Overall Survival in High-Risk Neuroblastoma Using Mechanistic Modeling of Metastasis
Authors: S. Benzekry, C. Sentis, C. Coze, L. Tessonnier, N. André. Published in JCO: Clinical Cancer Informatics. https://
Prognosis of high-risk neuroblastoma (HRNB) remains poor despite multimodal therapies. Better prediction of survival could help to refine patient stratification and better tailor treatments. We established a mechanistic model of metastasis in HRNB relying on two processes: growth and dissemination relying on two patient-specific parameters: the dissemination rate μ and the minimal visible lesion size Svis. This model was calibrated using diagnosis values of primary tumor size, lactate dehydrogenase circulating levels, and the meta-iodobenzylguanidine International Society for Paediatric Oncology European (SIOPEN) score from nuclear imaging, using data from 49 metastatic patients. It was able to describe the data of total tumor mass (lactate dehydrogenase, R2 > 0.99) and number of visible metastases (SIOPEN, R2 = 0.96). A prediction model of overall survival (OS) was then developed using Cox regression. Clinical variables alone were not able to generate a model with sufficient OS prognosis ability (P = .507). The parameter μ was found to be independent of the clinical variables and positively associated with OS (P = .0739 in multivariable analysis). Critically, addition of this computational biomarker significantly improved prediction of OS with a concordance index increasing from 0.675 (95% CI, 0.663 to 0.688) to 0.733 (95% CI, 0.722 to 0.744, P < .0001), resulting in significant OS prognosis ability (P = .0422).
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
- Research contract between Roche and the MONC team.
- Collaboration contract with Sophia Genetics in the context of the Pimiento project.
9.2 Bilateral grants with industry
Pimiento project from MSDAvenir (http://
10 Partnerships and cooperations
10.1 National initiatives
10.1.1 Plan Cancer
Moglimaging
- Project acronym - Moglimaging: Modeling of Glioblastoma treatment-induced resistance and heterogeneity by multi-modal imaging.
- Partners - INRIA Monc, IUCT, Institut Pasteur, Univ. Grenoble, INSERM, INRIA Mamba.
- Duration - from Nov. 2016 to May 2020.
- Coordinator - E. Cohen-Jonathan Moyal, Institut Universitaire du Cancer Toulouse / Local coordinator - O. Saut.
- Team participants - S. Benzekry, A. Collin, C. Poignard, O. Saut.
Systems Biology of Renal Carcinoma
- Title: Plan Cancer Systems Biology of Renal Carcinoma using a Mouse RCC model
- Partners : LAMC, INSERM-Univ. Bordeaux.
- Duration - June 2018 to June 2021
- Team participants: O. Saut, S. Benzekry (co-PI)
- Funding: 116.64k€
QUANTIC
- Plan Cancer QUANTIC: 2020–2022. QUANTitative modeling combined to statistical learning to understand and predict resistance to Immune-checkpoint inhibition in non-small cell lung Cancer.
- Funding: 338 k€
- Partners: Inria Team MONC, SMARTc (Centre de Recherche sur le Cancer de Marseille, Inserm, CNRS), Assistance Publique Hôpitaux de Marseille
- Duration: Décembre 2019 — Décembre 2022
- Project leader: S. Benzekry
- Co-PI: D. Barbolosi (SMARTc), F. Barlési (AP-HM)
10.1.2 Transnation call: INCA/ARC
- Title: Minimally and non-invasive methods for early detection and/or progression of low grade glioma
- Partners: INRIA Monc, INRIA SISTM, INSERM, Humanitas Research Hostital, Univ. Bergen
- Acronym: Glioma PRD
- Team participants: A. Collin, C. Etchegaray, C. Poignard, O. Saut (local PI)
- Total funds: 1M150, Monc's share 275k€.
11 Dissemination
11.1 Promoting scientific activities
11.1.1 Scientific events: selection
Reviewer
- O. Saut: MICCAI 2020 conference.
11.1.2 Journal
Member of the editorial boards
- S. Benzekry, Mathematical Biosciences
Reviewer - reviewing activities
- S. Benzekry: AAPS J, Computational and Applied Mathematics, Clinical Pharmacology and Therapeutics, Frontiers in Physiology, Scientific Reports.
- C. Etchegaray, Technology in Cancer Research Treatment, Royal Society Open Science.
- O. Saut: Scientific Reports, European Radiology, EBioMedicine, Medical Image Analysis, MMNP, Precision Oncology.
11.1.3 Invited talks
- S. Benzekry: "Second philosophy of cancer workshop." Quantitative modeling of metastasis: cancer at the organism scale. Bordeaux, France.
- S. Benzekry: "Workshop on Mathematical modelling in the machine learning era". Göteborg, Sweden (online conference).
- C. Etchegaray, at "Interplay between Oncology, Mathematics and Numerics: focus on pre-treatment studies" online conference
- C. Etchegaray, at "Fusion of Mathematics and Biology" online conference (JSPS Core-to-Core Program)
11.1.4 Leadership within the scientific community
- O. Saut: Member of the Steering Committee of Labex TRAIL (https://
trail. labex. u-bordeaux. fr/). - O. Saut: Member of the steering committee of the Oncosphere project (aiming at organizing cancer research in Nouvelle Aquitaine).
11.1.5 Scientific expertise
- S. Benzekry is an expert of the national multi-thematic institute (ITMO) Cancer of Aviesan
- O. Saut: expert for the ANR.
- O. Saut: expert for the Plan Cancer.
- O. Saut: expert for the French Ministry of Research and Innovation (PHC Program)
- O. Saut: expert for international grants (DFG, Allemagne, National Science Center, Pologne) and french hiring committees.
11.1.6 Research administration
- A. Collin: member, Conseil National des Universités,
- O. Saut: in charge of translational and interdisciplinary research at INSMI (http://
www. cnrs. fr/ insmi), Math. Institute of the CNRS.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Master : S. Benzekry, Cours "Modélisation de la croissance tumorale", 3h, niveau M2, Université de Tours, France.
- Master : S. Benzekry, Cours "Mathematical tools for pharmacometrics", 20h, niveau M2, Aix-Marseille Université, France.
- Ecole doctorale : S. Benzekry, "Introduction to modeling and data science in oncology", 12h.
- Master: A. Collin, Pratical C++ programming, 96h, niveau M1, INP Bordeaux, France.
- Master: A. Collin, Mesh theory, 36h, niveau M2, INP Bordeaux, France.
- Master: A. Collin, Machine Learning, niveau M2, INP Bordeaux, France.
- PHD: A. Collin, Modeling Life Science Module, Digital Public Health, Graduate Program.
- Licence : C. Etchegaray, Undergraduate teaching in Harmonic analysis, 32h, niveau L2, Univ. Bordeaux, France.
- Licence : C. Etchegaray, Undergraduate teaching in Linear Algebra (TD+TP Python), 40h, niveau L2, Univ. Bordeaux, France.
- Licence : C. Poignard, Undergraduate teaching in Numerical and Applied Mathematics, 80h, L3-M1, INP Bordeaux, ENSAM, France.
11.2.2 Supervision
- PhD: C. Vaghi, Improving intra-tumor drug distribution of anti-cancer nanoparticles by data-informed mathematical modeling, Nov 2017 - Nov 2020, supervision S. Benzekry and C. Poignard.
- PhD: Sergio Corridore, 2016-2020, supervision A. Collin and C. Poignard
- PhD in progress: Pedro Jaramillo-Aguayo, 2019-..., supervision A. Collin and C. Poignard
- PhD: A. Crombé, October 2017- June 2020, supervision O. Saut
- PhD in progress: C. Bigarré, 2020-..., supervision S. Benzekry
11.2.3 Juries
- S. Benzekry: Reviewer of the PhD thesis of M. Zulian (Ecole Polytechnique, Paris)
- S. Benzekry: Reviewer of the PhD thesis of L. Deyme (Aix-Marseille University)
- S. Benzekry: Reviewer of the PhD thesis of B. Schneider (Iowa State University)
- S. Benzekry: Reviewer of the PhD thesis of J. Goya-Outi (Paris Saclay University)
- A. Collin, Jury member, agrégation de Mathématiques
- O. Saut: Reviewer of the HdR thesis of A. Leclerc, Univ. Paris France.
- O. Saut: Reviewer of the PhD thesis of L. Adenis, Univ. Paris, France.
- O. Saut: Reviewer of the PhD thesis of AS Dirand, Univ. Paris-Saclay, France.
- O. Saut: PhD defense committee, president, C. Mesguich, Univ. Bordeaux, France
11.3 Popularization
11.3.1 Interventions
- C. Etchegaray, "1 scientifique, 1 classe, Chiche !" initiative, 4 interventions (Fête de la Science).
- O. Saut: Asperon patient association (https://
patients-siric-brio. com/ asperon-co/).
12 Scientific production
12.1 Major publications
- 1 article Mathematical modeling of tumor-tumor distant interactions supports a systemic control of tumor growth Cancer Research 2017
- 2 articleClassical Mathematical Models for Description and Forecast of Experimental Tumor GrowthPLoS Computational Biology108August 2014, e1003800
- 3 articleModeling Spontaneous Metastasis following Surgery: An In Vivo-In Silico ApproachCancer Research763February 2016, 535 - 547
- 4 articleComputational Modeling Of Solid Tumor Growth: The Avascular StageSIAM Journal on Scientific Computing324August 2010, 2321--2344
- 5 articlePatient specific simulation of tumor growth, response to the treatment and relapse of a lung metastasis: a clinical caseJournal of Computational Surgery2015, 18
- 6 articleSuperconvergent second order Cartesian method for solving free boundary problem for invadopodia formationJournal of Computational Physics339June 2017, 412 - 431
- 7 articleRevisiting bevacizumab + cytotoxics scheduling using mathematical modeling: proof of concept study in experimental non-small cell lung carcinomaCPT: Pharmacometrics and Systems Pharmacology2018, 1-9
- 8 articleSpatial modelling of tumour drug resistance: the case of GIST liver metastases Mathematical Medicine and Biology AdvanceMathematical Medicine and Biology002016, 1 - 26
- 9 articleConducting and permeable states of cell membrane submitted to high voltage pulses: Mathematical and numerical studies validated by the experimentsJournal of Theoretical Biology360November 2014, 83-94
- 10 article Computational Trials: Unraveling Motility Phenotypes, Progression Patterns, and Treatment Options for Glioblastoma Multiforme PLoS ONE 11 1 January 2016
12.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
Reports & preprints

