2.1 Overall objectives

The research activities of QUANTIC team lie at the border between theoretical and experimental efforts in the emerging field of quantum systems engineering. Our research topics are in direct continuation of a historic research theme of INRIA, classical automatic control, while opening completely new perspectives toward quantum control: by developing a new mathematical system theory for quantum circuits, we will realize the components of a future quantum information processing unit.

One of the unique features of our team concerns the large spectrum of our subjects going from the mathematical analysis of the physical systems (development of systematic mathematical methods for control and estimation of quantum systems), and the numerical analysis of the proposed solutions, to the experimental implementation of the quantum circuits based on these solutions. This is made possible by the constant and profound interaction between the applied mathematicians and the physicists in the group. Indeed, this close collaboration has already brought a significant acceleration in our research efforts. In a long run, this synergy should lead to a deeper understanding of the physical phenomena behind these emerging technologies and the development of new research directions within the field of quantum information processing.

Towards this ultimate task of practical quantum digital systems, the approach of the QUANTIC team is complementary to the one taken by teams with expertise in quantum algorithms. Indeed, we start from the specific controls that can be realistically applied on physical systems, to propose designs which combine them into hardware shortcuts implementing robust behaviors useful for quantum information processing. Whenever a significant new element of quantum engineering architecture is developed, the initial motivation is to prove an enabling technology with major impact for the groups working one abstraction layer higher: on quantum algorithms but also on e.g. secure communication and metrology applications.

3.1 Hardware-efficient quantum information processing

In this scientific program, we will explore various theoretical and experimental issues concerning protection and manipulation of quantum information. Indeed, the next, critical stage in the development of Quantum Information Processing (QIP) is most certainly the active quantum error correction (QEC). Through this stage one designs, possibly using many physical qubits, an encoded logical qubit which is protected against major decoherence channels and hence admits a significantly longer effective coherence time than a physical qubit. Reliable (fault-tolerant) computation with protected logical qubits usually comes at the expense of a significant overhead in the hardware (up to thousands of physical qubits per logical qubit). Each of the involved physical qubits still needs to satisfy the best achievable properties (coherence times, coupling strengths and tunability). More remarkably, one needs to avoid undesired interactions between various subsystems. This is going to be a major difficulty for qubits on a single chip.

The usual approach for the realization of QEC is to use many qubits to obtain a larger Hilbert space of the qubit register  87, 90. By redundantly encoding quantum information in this Hilbert space of larger dimension one make the QEC tractable: different error channels lead to distinguishable error syndromes. There are two major drawbacks in using multi-qubit registers. The first, fundamental, drawback is that with each added physical qubit, several new decoherence channels are added. Because of the exponential increase of the Hilbert's space dimension versus the linear increase in the number of decay channels, using enough qubits, one is able to eventually protect quantum information against decoherence. However, multiplying the number of possible errors, this requires measuring more error syndromes. Note furthermore that, in general, some of these new decoherence channels can lead to correlated action on many qubits and this needs to be taken into account with extra care: in particular, such kind of non-local error channels are problematic for surface codes. The second, more practical, drawback is that it is still extremely challenging to build a register of more than on the order of 10 qubits where each of the qubits is required to satisfy near the best achieved properties: these properties include the coherence time, the coupling strengths and the tunability. Indeed, building such a register is not merely only a fabrication task but rather, one requirers to look for architectures such that, each individual qubit can be addressed and controlled independently from the others. One is also required to make sure that all the noise channels are well-controlled and uncorrelated for the QEC to be effective.

We have recently introduced a new paradigm for encoding and protecting quantum information in a quantum harmonic oscillator (e.g. a high-Q mode of a 3D superconducting cavity) instead of a multi-qubit register  64. The infinite dimensional Hilbert space of such a system can be used to redundantly encode quantum information. The power of this idea lies in the fact that the dominant decoherence channel in a cavity is photon damping, and no more decay channels are added if we increase the number of photons we insert in the cavity. Hence, only a single error syndrome needs to be measured to identify if an error has occurred or not. Indeed, we are convinced that most early proposals on continuous variable QIP  61, 55 could be revisited taking into account the design flexibilities of Quantum Superconducting Circuits (QSC) and the new coupling regimes that are provided by these systems. In particular, we have illustrated that coupling a qubit to the cavity mode in the strong dispersive regime provides an important controllability over the Hilbert space of the cavity mode  63. Through a recent experimental work  95, we benefit from this controllability to prepare superpositions of quasi-orthogonal coherent states, also known as Schrödinger cat states.

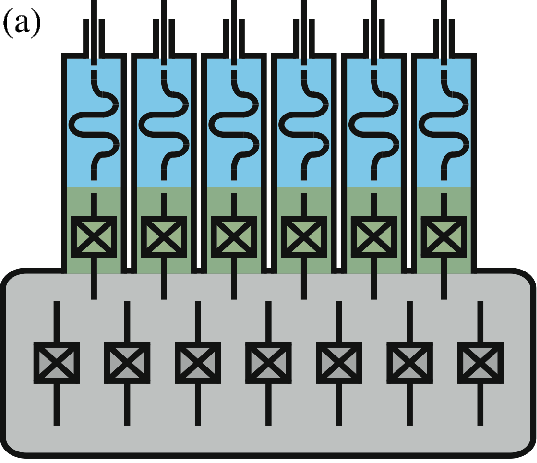
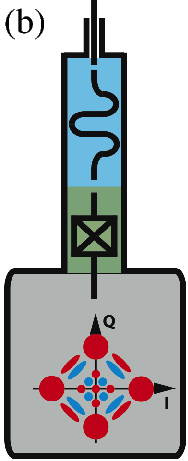
In this Scheme, the logical qubit is encoded in a four-component Schrödinger cat state. Continuous quantum non-demolition (QND) monitoring of a single physical observable, consisting of photon number parity, enables then the tractability of single photon jumps. We obtain therefore a first-order quantum error correcting code using only a single high-Q cavity mode (for the storage of quantum information), a single qubit (providing the non-linearity needed for controllability) and a single low-Q cavity mode (for reading out the error syndrome). An earlier experiment on such QND photon-number parity measurements  91 has recently led to a first experimental realization of a full quantum error correcting code improving the coherence time of quantum information 8. As shown in Figure 1, this leads to a significant hardware economy for realization of a protected logical qubit. Our goal here is to push these ideas towards a reliable and hardware-efficient paradigm for universal quantum computation.

$$

3.2 Reservoir (dissipation) engineering and autonomous stabilization of quantum systems

Being at the heart of any QEC protocol, the concept of feedback is central for the protection of quantum information, enabling many-qubit quantum computation or long-distance quantum communication. However, such a closed-loop control which requires a real-time and continuous measurement of the quantum system has been for long considered as counter-intuitive or even impossible. This thought was mainly caused by properties of quantum measurements: any measurement implies an instantaneous strong perturbation to the system's state. The concept of quantum non-demolition (QND) measurement has played a crucial role in understanding and resolving this difficulty   37. In the context of cavity quantum electro-dynamics (cavity QED) with Rydberg atoms  57, a first experiment on continuous QND measurements of the number of microwave photons was performed by the group at Laboratoire Kastler-Brossel (ENS)  56. Later on, this ability of performing continuous measurements allowed the same group to realize the first continuous quantum feedback protocol stabilizing highly non-classical states of the microwave field in the cavity, the so-called photon number states 10 (this ground-breaking work was mentioned in the Nobel prize attributed to Serge Haroche). The QUANTIC team contributed to the theoretical work behind this experiment  47, 27, 89, 29. These contributions include the development and optimization of the quantum filters taking into account the quantum measurement back-action and various measurement noises and uncertainties, the development of a feedback law based on control Lyapunov techniques, and the compensation of the feedback delay.

In the context of circuit quantum electrodynamics (circuit QED)  45, recent advances in quantum-limited amplifiers  80, 93 have opened doors to high-fidelity non-demolition measurements and real-time feedback for superconducting qubits  58. This ability to perform high-fidelity non-demolition measurements of a quantum signal has very recently led to quantum feedback experiments with quantum superconducting circuits  93, 79, 39. Here again, the QUANTIC team has participated to one of the first experiments in the field where the control objective is to track a dynamical trajectory of a single qubit rather than stabilizing a stationary state. Such quantum trajectory tracking could be further explored to achieve metrological goals such as the stabilization of the amplitude of a microwave drive  71.

While all this progress has led to a strong optimism about the possibility to perform active protection of quantum information against decoherence, the rather short dynamical time scales of these systems limit, to a great amount, the complexity of the feedback strategies that could be employed. Indeed, in such measurement-based feedback protocols, the time-consuming data acquisition and post-treatment of the output signal leads to an important latency in the feedback procedure.

The reservoir (dissipation) engineering  77 and the closely related coherent feedback  69 are considered as alternative approaches circumventing the necessity of a real-time data acquisition, signal processing and feedback calculations. In the context of quantum information, the decoherence, caused by the coupling of a system to uncontrolled external degrees of freedom, is generally considered as the main obstacle to synthesize quantum states and to observe quantum effects. Paradoxically, it is possible to intentionally engineer a particular coupling to a reservoir in the aim of maintaining the coherence of some particular quantum states. In a general viewpoint, these approaches could be understood in the following manner: by coupling the quantum system to be stabilized to a strongly dissipative ancillary quantum system, one evacuates the entropy of the main system through the dissipation of the ancillary one. By building the feedback loop into the Hamiltonian, this type of autonomous feedback obviates the need for a complicated external control loop to correct errors. On the experimental side, such autonomous feedback techniques have been used for qubit reset  54, single-qubit state stabilization  72, and the creation  32 and stabilization  62, 68, 86 of states of multipartite quantum systems.

Such reservoir engineering techniques could be widely revisited exploring the flexibility in the Hamiltonian design for QSC. We have recently developed theoretical proposals leading to extremely efficient, and simple to implement, stabilization schemes for systems consisting of a single, two or three qubits  54, 66, 43, 46. The experimental results based on these protocols have illustrated the efficiency of the approach  54, 86. Through these experiments, we exploit the strong dispersive interaction  84 between superconducting qubits and a single low-Q cavity mode playing the role of a dissipative reservoir. Applying continuous-wave (cw) microwave drives with well-chosen fixed frequencies, amplitudes, and phases, we engineer an effective interaction Hamiltonian which evacuates the entropy of the system interacting with a noisy environment: by driving the qubits and cavity with continuous-wave drives, we induce an autonomous feedback loop which corrects the state of the qubits every time it decays out of the desired target state. The schemes are robust against small variations of the control parameters (drives amplitudes and phase) and require only some basic calibration. Finally, by avoiding resonant interactions between the qubits and the low-Q cavity mode, the qubits remain protected against the Purcell effect, which would reduce the coherence times. We have also investigated both theoretically and experimentally the autonomous stabilization of non-classical states (such as Schrodinger cat states and Fock states) of microwave field confined in a high-Q cavity mode  82, 597, 5.

3.3 System theory for quantum information processing

In parallel and in strong interactions with the above experimental goals, we develop systematic mathematical methods for dynamical analysis, control and estimation of composite and open quantum systems. These systems are built with several quantum subsystems whose irreversible dynamics results from measurements and/or decoherence. A special attention is given to spin/spring systems made with qubits and harmonic oscillators. These developments are done in the spirit of our recent contributions  81, 27, 88, 83, 89, 299 resulting from collaborations with the cavity quantum electrodynamics group of Laboratoire Kastler Brossel.

3.4 Stabilization by measurement-based feedback

The protection of quantum information via efficient QEC is a combination of (i) tailored dynamics of a quantum system in order to protect an informational qubit from certain decoherence channels, and (ii) controlled reaction to measurements that efficiently detect and correct the dominating disturbances that are not rejected by the tailored quantum dynamics.

In such feedback scheme, the system and its measurement are quantum objects whereas the controller and the control input are classical. The stabilizing control law is based on the past values of the measurement outcomes. During our work on the LKB photon box, we have developed, for single input systems subject to quantum non-demolition measurement, a systematic stabilization method  29: it is based on a discrete-time formulation of the dynamics, on the construction of a strict control Lyapunov function and on an explicit compensation of the feedback-loop delay. Keeping the QND measurement assumptions, extensions of such stabilization schemes will be investigated in the following directions: finite set of values for the control input with application to the convergence analysis of the atomic feedback scheme experimentally tested in  96; multi-input case where the construction by inversion of a Metzler matrix of the strict Lyapunov function is not straightforward; continuous-time systems governed by diffusive master equations; stabilization towards a set of density operators included in a target subspace; adaptive measurement by feedback to accelerate the convergence towards a stationary state as experimentally tested in  75. Without the QND measurement assumptions, we will also address the stabilization of non-stationary states and trajectory tracking, with applications to systems similar to those considered in  58, 39.

3.5 Filtering, quantum state and parameter estimations

The performance of every feedback controller crucially depends on its online estimation of the current situation. This becomes even more important for quantum systems, where full state measurements are physically impossible. Therefore the ultimate performance of feedback correction depends on fast, efficient and optimally accurate state and parameter estimations.

A quantum filter takes into account imperfection and decoherence and provides the quantum state at time $t\ge 0$ from an initial value at $t=0$ and the measurement outcomes between 0 and $t$. Quantum filtering goes back to the work of Belavkin   33 and is related to quantum trajectories  40, 44. A modern and mathematical exposure of the diffusive models is given in  31. In  97 a first convergence analysis of diffusive filters is proposed. Nevertheless the convergence characterization and estimation of convergence rate remain open and difficult problems. For discrete time filters, a general stability result based on fidelity is proven in  81, 88. This stability result is extended to a large class of continuous-time filters in  28. Further efforts are required to characterize asymptotic and exponential stability. Estimations of convergence rates are available only for quantum non-demolition measurements  34. Parameter estimations based on measurement data of quantum trajectories can be formulated within such quantum filtering framework  49, 73.

We will continue to investigate stability and convergence of quantum filtering. We will also exploit our fidelity-based stability result to justify maximum likelihood estimation and to propose, for open quantum system, parameter estimation algorithms inspired of existing estimation algorithms for classical systems. We will also investigate a more specific quantum approach: it is noticed in  38 that post-selection statistics and “past quantum” state analysis  50 enhance sensitivity to parameters and could be interesting towards increasing the precision of an estimation.

3.6 Stabilization by interconnections

In such stabilization schemes, the controller is also a quantum object: it is coupled to the system of interest and is subject to decoherence and thus admits an irreversible evolution. These stabilization schemes are closely related to reservoir engineering and coherent feedback   77, 69. The closed-loop system is then a composite system built with the original system and its controller. In fact, and given our particular recent expertise in this domain 986, 54, this subsection is dedicated to further developing such stabilization techniques, both experimentally and theoretically.

The main analysis issues are to prove the closed-loop convergence and to estimate the convergence rates. Since these systems are governed by Lindblad differential equations (continuous-time case) or Kraus maps (discrete-time case), their stability is automatically guaranteed: such dynamics are contractions for a large set of metrics (see  76). Convergence and asymptotic stability is less well understood. In particular most of the convergence results consider the case where the target steady-state is a density operator of maximum rank (see, e.g., 30[chapter 4, section 6]). When the goal steady-state is not full rank very few convergence results are available.

We will focus on this geometric situation where the goal steady-state is on the boundary of the cone of positive Hermitian operators of finite trace. A specific attention will be given to adapt standard tools (Lyapunov function, passivity, contraction and Lasalle's invariance principle) for infinite dimensional systems to spin/spring structures inspired of 9, 786, 54 and their associated Fokker-Planck equations for the Wigner functions.

We will also explore the Heisenberg point of view in connection with recent results of the INRIA project-team MAXPLUS (algorithms and applications of algebras of max-plus type) relative to Perron-Frobenius theory  53, 52. We will start with  85 and  78 where, based on a theorem due to Birkhoff  35, dual Lindblad equations and dual Kraus maps governing the Heisenberg evolution of any operator are shown to be contractions on the cone of Hermitian operators equipped with Hilbert's projective metric. As the Heisenberg picture is characterized by convergence of all operators to a multiple of the identity, it might provide a mean to circumvent the rank issues. We hope that such contraction tools will be especially well adapted to analyzing quantum systems composed of multiple components, motivated by the facts that the same geometry describes the contraction of classical systems undergoing synchronizing interactions 92 and by our recent generalized extension of the latter synchronizing interactions to quantum systems 70.

Besides these analysis tasks, the major challenge in stabilization by interconnections is to provide systematic methods for the design, from typical building blocks, of control systems that stabilize a specific quantum goal (state, set of states, operation) when coupled to the target system. While constructions exist for so-called linear quantum systems 74, this does not cover the states that are more interesting for quantum applications. Various strategies have been proposed that concatenate iterative control steps for open-loop steering 94, 67 with experimental limitations. The characterization of Kraus maps to stabilize any types of states has also been established 36, but without considering experimental implementations. A viable stabilization by interaction has to combine the capabilities of these various approaches, and this is a missing piece that we want to address.

4.1 Quantum engineering

A new field of quantum systems engineering has emerged during the last few decades. This field englobes a wide range of applications including nano-electromechanical devices, nuclear magnetic resonance applications, quantum chemical synthesis, high resolution measurement devices and finally quantum information processing devices for implementing quantum computation and quantum communication. Recent theoretical and experimental achievements have shown that the quantum dynamics can be studied within the framework of estimation and control theory, but give rise to new models that have not been fully explored yet.

The QUANTIC team's activities are defined at the border between theoretical and experimental efforts of this emerging field with an emphasis on the applications in quantum information, computation and communication. The main objective of this interdisciplinary team is to develop quantum devices ensuring a robust processing of quantum information.

On the theory side, this is done by following a system theory approach: we develop estimation and control tools adapted to particular features of quantum systems. The most important features, requiring the development of new engineering methods, are related to the concept of measurement and feedback for composite quantum systems. The destructive and partial 1 nature of measurements for quantum systems lead to major difficulties in extending classical control theory tools. Indeed, design of appropriate measurement protocols and, in the sequel, the corresponding quantum filters estimating the state of the system from the partial measurement record, are themselves building blocks of the quantum system theory to be developed.

On the experimental side, we develop new quantum information processing devices based on quantum superconducting circuits. Indeed, by realizing superconducting circuits at low temperatures and using microwave measurement techniques, the macroscopic and collective degrees of freedom such as the voltage and the current are forced to behave according to the laws of quantum mechanics. Our quantum devices are aimed to protect and process quantum information through these integrated circuits.

6.1 Exponential suppression of bit-flips in a qubit encoded in an oscillator

Participants: R. Lescanne, M. Villiers, A. Sarlette, M. Mirrahimi, Z. Leghtas.

A quantum system interacts with its environment—if ever so slightly—no matter how much care is put into isolating it. Therefore, quantum bits undergo errors, putting dauntingly difficult constraints on the hardware suitable for quantum computation. New strategies are emerging to circumvent this problem by encoding a quantum bit non-locally across the phase space of a physical system. Because most sources of decoherence result from local fluctuations, the foundational promise is to exponentially suppress errors by increasing a measure of this non-locality. Prominent examples are topological quantum bits, which delocalize information over real space and where spatial extent measures non-locality. Here, we encode a quantum bit in the field quadrature space of a superconducting resonator endowed with a special mechanism that dissipates photons in pairs. This process pins down two computational states to separate locations in phase space. By increasing this separation, we measure an exponential decrease of the bit-flip rate while only linearly increasing the phase-flip rate. Because bit-flips are autonomously corrected, only phase-flips remain to be corrected via a one-dimensional quantum error correction code. This exponential scaling demonstrates that resonators with nonlinear dissipation are promising building blocks for quantum computation with drastically reduced hardware overhead. This experimental work was published in 16.

6.2 Irreversible Qubit-Photon Coupling for the Detection of Itinerant Microwave Photons

Participants: R. Lescanne, Z. Leghtas

Single photon detection is a key resource for sensing at the quantum limit and the enabling technology for measurement-based quantum computing. Photon detection at optical frequencies relies on irreversible photoassisted ionization of various natural materials. However, microwave photons have energies 5 orders of magnitude lower than optical photons, and are therefore ineffective at triggering measurable phenomena at macroscopic scales. Here, we report the observation of a new type of interaction between a single two-level system (qubit) and a microwave resonator. These two quantum systems do not interact coherently; instead, they share a common dissipative mechanism to a cold bath: the qubit irreversibly switches to its excited state if and only if a photon enters the resonator. We have used this highly correlated dissipation mechanism to detect itinerant photons impinging on the resonator. This scheme does not require any prior knowledge of the photon waveform nor its arrival time, and dominant decoherence mechanisms do not trigger spurious detection events (dark counts). We demonstrate a detection efficiency of $58\%$ and a record low dark count rate of 1.4 per millisecond. This work establishes engineered nonlinear dissipation as a key enabling resource for a new class of low-noise nonlinear microwave detectors. This experimental work was published in 15.

6.3 Theory of interactions between cavity photons induced by a mesoscopic circuit

Participants: Z. Leghtas

We use a quantum path-integral approach to describe the behavior of a microwave cavity coupled to a dissipative mesoscopic circuit. We integrate out the mesoscopic electronic degrees of freedom to obtain a cavity effective action at fourth order in the light/matter coupling. By studying the structure of this action, we establish sufficient conditions in which the cavity dynamics can be described with a Lindblad equation. This equation depends on effective parameters set by electronic correlation functions. It reveals that the mesoscopic circuit induces an effective Kerr interaction and two-photon dissipative processes. We use our method to study the effective dynamics of a cavity coupled to a double quantum dot with normal metal reservoirs. If the cavity is driven at twice its frequency, the double-dot circuit generates photonic squeezing and nonclassicalities visible in the cavity Wigner function. In particular, we find a counterintuitive situation where mesoscopic dissipation enables the production of photonic Schrödinger cats. These effects can occur for realistic circuit parameters. Our method can be generalized straightforwardly to more complex circuit geometries with, for instance, multiple quantum dots and other types of fermionic reservoirs such as superconductors and ferromagnets. This theoretical work was published in 12.

6.4 Quantum error correction of a qubit encoded in grid states of an oscillator

Participants: Philippe Campagne-Ibarcq and Mazyar Mirrahimi

Quantum Error Correction (QEC) derives from the reasonable assumption that noise is local, that is, it does not act in a coordinated way on different parts of the physical system. Therefore, if a logical qubit is encoded non-locally, we can detect and correct noise-induced evolution before it corrupts the encoded information . In 2001, Gottesman, Kitaev and Preskill (GKP) proposed a hardware-efficient instance of such a non-local qubit: a superposition of position eigenstates that forms grid states of a single oscillator.

In this work in collaboration with the group of Michel Devoret at Yale university, we experimentally prepare square and hexagonal GKP code states through a feedback protocol that incorporates non-destructive measurements that are implemented with a superconducting microwave cavity having the role of the oscillator. We demonstrate QEC of an encoded qubit with suppression of all logical errors, in quantitative agreement with a theoretical estimate based on the measured imperfections of the experiment. This protocol is applicable to other continuous-variable systems and, in contrast to previous implementations of QEC , can mitigate all logical errors generated by a wide variety of noise processes and facilitate fault-tolerant quantum computation.

This work was published in 11.

6.5 Scaling up reservoir engineering for error-correcting codes

Participants: Alain Sarlette and Vincent Martin

Error-correcting codes are usually envisioned to counter errors by operating unitary corrections depending on the projective measurement results of some syndrome observables. We here propose a way to use them in a more integrated way, where the error correction is applied continuously and autonomously by an engineered environment. We focus on a proposal for the repetition code that counters bit-flip errors, and how to scale up the network encoding a logical quantum bit, towards stronger information protection. This proposal is motivated by the cat-qubits, which are strongly protected against one type of error and only need a repetition-code type protection against the other type. The challenge has been to devise a network architecture which allows to autonomously correct higher-order errors, while remaining realistic towards experimental realization by avoiding all-to-all or all-to-one coupling. This work 22 submitted to MTNS 2020 (pandemic postponed as MTNS 2021) was proposing a first architecture and analysis tools.

6.6 Number-resolved photocounter for propagating microwave mode

Participants: Pierre Rouchon

Detectors of propagating microwave photons have recently been realized using superconducting circuits. However a number-resolved photocounter is still missing. In this work, we demonstrate a single-shot counter for propagating microwave photons that can resolve up to 3 photons. It is based on a pumped Josephson Ring Modulator that can catch an arbitrary propagating mode by frequency conversion and store its quantum state in a stationary memory mode. A transmon qubit then counts the number of photons in the memory mode using a series of binary questions. Using measurement based feedback, the number of questions is minimal and scales logarithmically with the maximal number of photons. The detector features a detection efficiency of $0.96\pm 0.04$, and a dark count probability of $0.030\pm 0.002$ for an average dead time of $4.5\mu$s. To maximize its performance, the device is first used as an in situ waveform detector from which an optimal pump is computed and applied. Depending on the number of incoming photons, the detector succeeds with a probability that ranges from $(54\pm 2)\%$ to $99\%$. This experimental result in collaboration with the team of Benjamin Huard at ENS Lyon was published in 13.

6.7 Stabilization and operation of a Kerr-cat qubit

Participants: Mazyar Mirrahimi

Quantum superpositions of macroscopically distinct classical states, so-called Schrödinger cat states, are a resource for quantum metrology, quantum communication, and quantum computation. In particular, the superpositions of two opposite-phase coherent states in an oscillator encode a qubit protected against phase-flip errors. However, several challenges have to be overcome in order for this concept to become a practical way to encode and manipulate error-protected quantum information. The protection must be maintained by stabilizing these highly excited states and, at the same time, the system has to be compatible with fast gates on the encoded qubit and a quantum non-demolition readout of the encoded information. Here, we experimentally demonstrate a novel method for the generation and stabilization of Schrödinger cat states based on the interplay between Kerr nonlinearity and single-mode squeezing in a superconducting microwave resonator. We show an increase in transverse relaxation time of the stabilized, error-protected qubit over the single-photon Fock-state encoding by more than one order of magnitude. We perform all single-qubit gate operations on time-scales more than sixty times faster than the shortest coherence time and demonstrate single-shot readout of the protected qubit under stabilization. Our results showcase the combination of fast quantum control with the robustness against errors intrinsic to stabilized macroscopic states and open up the possibility of using these states as resources in quantum information processing. This experiment performed by the group of Michel Devoret at Yale university was published in 14.

7.1 Bilateral contracts with industry

• New contracts with the start-up Alice and Bob, funding the PhD thesis of François-Marie Le Regent and Vincent Martin.

8.1 International initiatives

8.2 European initiatives

8.3 National initiatives

• ANR project HAMROQS: In the framework of the ANR program JCJC, Alain Sarlette has received a funding for his research program "High-accuracy model reduction for open quantum systems". This grant of 212k euros started on april 2019 and will run for 4 years.
• ANR project SYNCAMIL: In the framework of the ANR program JCJC, Philippe Campagne-Ibarcq has received a funding for his research program "Synthetic Non-Local Hamiltonians for the protection of quantum information". This grant of 380k euros has allowed us to purchase the experimental equipment to perform an experiment on stabilization of GKP grid states at ENS Paris, and to hire a postdoctoral associate, Vincent Lienhard, for 2 years. The project started in December 2020 for 48 months.

8.4 Regional initiatives

• DIM SIRTEQ In the framework of the DIM program AAP PME, the DIM Sirteq is co-financing for 50 keuros the purchase of a high-sampling rate Arbitrary Waveform Generator which will be used for experiments in the project SYNCAMIL.
• DIM SIRTEQ PhD fellowship: We have received in 2017 a funding from DIM SIRTEQ to cover half of the PhD of Jérémie Guillaud under supervision of Mazyar Mirrahimi.
• DIM SIRTEQ project SCOOP:Half a PhD grant for Marius Villiers, supervised by Zaki Leghtas and Audrey Cottet (ENS Paris). The project is to use quantum circuits to detect the entanglement of a single Cooper pair.
• EDPIF PhD fellowship: Ecole Doctorale de Physique en Ile de France has funded half a PhD grant for Marius Villiers.
• DGA PhD fellowship: Direction Générale de l'Armement has funded half a PhD grant for Camille Berdou supervised by Zaki Leghtas. The project is to build a repetition code of cat-qubits.
• Mines Paristech PhD Fellowship: Ecole des Mines Paristech has funded half a PhD grant for Camille Berdou.

9.1 Promoting scientific activities

9.2 Teaching - Supervision - Juries

9.3 Popularization

10.1 Major publications

• 1 article SimonS. Apers and AlainA. Sarlette. Quantum Fast-Forwarding: Markov chains and graph property testing Quantum Information & Computation April 2019
  HAL
• 2 article PhilippeP. Campagne-Ibarcq, AlecA. Eickbusch, StevenS. Touzard, EvanE. Zalys-Geller, Nicholas E.N. Frattini, Volodymyr V.V. Sivak, PhilipP. Reinhold, ShrutiS. Puri, ShyamS. Shankar, Robert J.R. Schoelkopf, LuigiL. Frunzio, MazyarM. Mirrahimi and Michel H.M. Devoret. Quantum error correction of a qubit encoded in grid states of an oscillator Nature 584 Text and figures edited for clarity. The claims of the paper remain the same. Author list fixed August 2020
  HAL
• 3 article GerardoG. Cardona, AlainA. Sarlette and PierreP. Rouchon. Exponential stabilization of quantum systems under continuous non-demolition measurements Automatica December 2019
  HAL
• 4 article JérémieJ. Guillaud and MazyarM. Mirrahimi. Repetition Cat Qubits for Fault-Tolerant Quantum Computation Physical Review X https://arxiv.org/abs/1904.09474 - 22 pages, 11 figures December 2019
  HAL DOI
• 5 articleZakiZ. Leghtas, StevenS. Touzard, Ioan M.I. Pop, AngelaA. Kou, BrianB. Vlastakis, AndreiA. Petrenko, Katrina M.K. Sliwa, AnirudhA. Narla, ShyamS. Shankar, Michael J.M. Hatridge, MatthewM. Reagor, LuigiL. Frunzio, Robert J.R. Schoelkopf, MazyarM. Mirrahimi and Michel H.M. Devoret. Confining the state of light to a quantum manifold by engineered two-photon lossScience3476224February 2015, 853-857
  HALDOIback to text
• 6 article RaphaëlR. Lescanne, MariusM. Villiers, ThéauT. Peronnin, AlainA. Sarlette, MatthieuM. Delbecq, BenjaminB. Huard, TakisT. Kontos, MazyarM. Mirrahimi and ZakiZ. Leghtas. Exponential suppression of bit-flips in a qubit encoded in an oscillator Nature Physics March 2020
  HAL DOI
• 7 articleMazyarM. Mirrahimi, ZakiZ. Leghtas, Victor VV. Albert, StevenS. Touzard, Robert JR. Schoelkopf, LiangL. Jiang and Michel HM. Devoret. Dynamically protected cat-qubits: a new paradigm for universal quantum computationNew Journal of Physics164apr 2014, 045014
  back to textback to text
• 8 articleN. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S.M.S. Girvin, L. Jiang, M. Mirrahimi, M. H.M. Devoret and R. J.R. Schoelkopf. Extending the lifetime of a quantum bit with error correction in superconducting circuitsNature5362016, 5
  back to text
• 9 article A. Sarlette, J.-M. Raimond, M. Brune and P. Rouchon. Stabilization of nonclassical states of the radiation field in a cavity by reservoir engineering Phys. Rev. Lett. 107 010402 2011
  back to text back to text back to text
• 10 articleC. Sayrin, I. Dotsenko, X. Zhou, B. Peaudecerf, T. Rybarczyk, S. Gleyzes, P. Rouchon, M. Mirrahimi, H. Amini, M. Brune, J.-M. Raimond and S. Haroche. Real-time quantum feedback prepares and stabilizes photon number statesNature4772011, 73--77
  back to text

10.2 Publications of the year

10.3 Cited publications

• 27 articleH. Amini, M. Mirrahimi and P. Rouchon. Stabilization of a delayed quantum system: the Photon Box case-studyIEEE Trans. Automatic Control5782012, 1918--1930
  back to textback to text
• 28 articleHH. Amini, C. Pellegrini and P. Rouchon. Stability of continuous-time quantum filters with measurement imperfectionsRussian Journal of Mathematical Physics212014, 297--315
  back to text
• 29 articleH. Amini, A. Somaraju, I. Dotsenko, C. Sayrin, M. Mirrahimi and P. Rouchon. Feedback stabilization of discrete-time quantum systems subject to non-demolition measurements with imperfections and delaysAutomatica4992013, 2683--2692
  back to textback to textback to text
• 30 book S. Attal A. Joye C.-A. Pillet Open Quantum Systems III: Recent Developments Springer, Lecture notes in Mathematics 1880 2006
  back to text
• 31 book A. Barchielli and M. Gregoratti. Quantum Trajectories and Measurements in Continuous Time: the Diffusive Case Springer Verlag 2009
  back to text
• 32 article J.T.J. Barreiro, M. Muller, P. Schindler, D. Nigg, T. Monz, M. Chwalla, M. Hennrich, C.F.C. Roos, P. Zoller and R. Blatt. An open-system quantum simulator with trapped ions Nature 470 486 2011
  back to text
• 33 articleV.P.V. Belavkin. Quantum stochastic calculus and quantum nonlinear filteringJournal of Multivariate Analysis4221992, 171--201
  back to text
• 34 articleT. Benoist and C. Pellegrini. Large Time Behavior and Convergence Rate for Quantum Filters Under Standard Non Demolition ConditionsCommunications in Mathematical Physics2014, 1-21URL: http://dx.doi.org/10.1007/s00220-014-2029-6
  back to text
• 35 articleG. Birkhoff. Extensions of Jentzch's theoremTrans. Amer. Math. Soc.851957, 219--227
  back to text
• 36 article S. Bolognani and F. Ticozzi. Engineering stable discrete-time quantum dynamics via a canonical QR decomposition IEEE Trans. Autom. Control 55 2010
  back to text
• 37 book V. Braginski and F. Khalili. Quantum Measurements Cambridge University Press 1992
  back to text
• 38 articleP. Campagne-Ibarcq, L. Bretheau, E. Flurin, A. Auffèves, F. Mallet and B. Huard. Observing Interferences between Past and Future Quantum States in Resonance FluorescencePhys. Rev. Lett.11218040218May 2014, URL: http://link.aps.org/doi/10.1103/PhysRevLett.112.180402
  DOIback to text
• 39 article P. Campagne-Ibarcq, E. Flurin, N. Roch, D. Darson, P. Morfin, M. Mirrahimi, M. H.M. Devoret, F. Mallet and B. Huard. Persistent Control of a Superconducting Qubit by Stroboscopic Measurement Feedback Phys. Rev. X 3 021008 2013
  back to text back to text
• 40 book H. Carmichael. An Open Systems Approach to Quantum Optics Springer-Verlag 1993
  back to text
• 41 book H. Carmichael. Statistical Methods in Quantum Optics 2: Non-Classical Fields Spinger 2007
  back to text
• 42 book J. Carr. Application of Center Manifold Theory Springer 1981
  back to text
• 43 articleJ. Cohen and M. Mirrahimi. Dissipation-induced continuous quantum error correction for superconducting circuitsPhys. Rev. A902014, 062344
  back to text
• 44 articleJ. Dalibard, Y. Castin and K. Mölmer. Wave-function approach to dissipative processes in quantum opticsPhys. Rev. Lett.6851992, 580--583
  back to text
• 45 misc M. H.M. Devoret, A. Wallraff and J.M.J. Martinis. Superconducting Qubits: A Short Review arXiv:cond-mat/0411174 2004
  back to text
• 46 article NicolasN. Didier, JérémieJ. Guillaud, ShyamS. Shankar and MazyarM. Mirrahimi. Remote entanglement stabilization and concentration by quantum reservoir engineering Physical Review A https://arxiv.org/abs/1703.03379 - 5 pages, 4 figures July 2018
  HAL DOI back to text
• 47 article I. Dotsenko, M. Mirrahimi, M. Brune, S. Haroche, J.-M. Raimond and P. Rouchon. Quantum feedback by discrete quantum non-demolition measurements: towards on-demand generation of photon-number states Physical Review A 80: 013805-013813 2009
  back to text
• 48 articleN. Fenichel. Geometric singular perturbation theory for ordinary differential equationsJ. Diff. Equations311979, 53--98
  back to text
• 49 articleJ. Gambetta and H. M.H. Wiseman. State and dynamical parameter estimation for open quantum systemsPhys. Rev. A644042105September 2001, URL: http://link.aps.org/doi/10.1103/PhysRevA.64.042105
  back to text
• 50 articleS. Gammelmark, B. Julsgaard and K. Mölmer. Past Quantum States of a Monitored SystemPhys. Rev. Lett.11116160401October 2013, URL: http://link.aps.org/doi/10.1103/PhysRevLett.111.160401
  back to text
• 51 book C.W.C. Gardiner and P. Zoller. Quantum Noise Springer 2010
  back to text
• 52 article S. Gaubert and Z. Qu. Checking the strict positivity of Kraus maps is NP-hard arXiv:1402.1429 2014
  back to text
• 53 articleS. Gaubert and Z. Qu. The contraction rate in Thompson's part metric of order-preserving flows on a cone - Application to generalized Riccati equationsJournal of Differential Equations2568April 2014, 2902--2948URL: http://www.sciencedirect.com/science/article/pii/S0022039614000424
  back to text
• 54 article K. Geerlings, Z. Leghtas, I.M.I. Pop, S. Shankar, L. Frunzio, R.J.R. Schoelkopf, M. Mirrahimi and M. H.M. Devoret. Demonstrating a Driven Reset Protocol of a Superconducting Qubit Phys. Rev. Lett. 110 120501 2013
  back to text back to text back to text back to text back to text back to text
• 55 article D. Gottesman, A. Kitaev and J. Preskill. Encoding a qubit in an oscillator Phys. Rev. A 64 012310 2001
  back to text
• 56 articleC. Guerlin, J. Bernu, S. Deléglise, C. Sayrin, S. Gleyzes, S. Kuhr, M. Brune, J.-M. Raimond and S. Haroche. Progressive field-state collapse and quantum non-demolition photon countingNature4482007, 889-893
  back to text
• 57 book S. Haroche and J.-M. Raimond. Exploring the Quantum: Atoms, Cavities and Photons Oxford University Press 2006
  back to text back to text
• 58 articleM. Hatridge, S. Shankar, M. Mirrahimi, F. Schackert, K. Geerlings, T. Brecht, K.M.K. Sliwa, B. Abdo, L. Frunzio, S.M.S. Girvin, R.J.R. Schoelkopf and M. H.M. Devoret. Quantum back-action of an individual variable-strength measurementScience3392013, 178--181
  back to textback to text
• 59 articleE.T.E. Holland, B. Vlastakis, R.W.R. Heeres, M. J.M. Reagor, U. Vool, Z. Leghtas, L. Frunzio, G. Kirchmair, M. H.M. Devoret, M. Mirrahimi and R.J.R. Schoelkopf. Single-photon-resolved cross-Kerr interaction for autonomous stabilization of photon-number statesPhys. Rev. Lett.1152015, 180501
  back to text
• 60 book T. Kato. Perturbation Theory for Linear Operators Springer 1966
  back to text
• 61 article E. Knill, R. Laflamme and G.J.G. Milburn. A scheme for efficient quantum computation with linear optics Nature 409 46 2001
  back to text
• 62 article H. Krauter, C.A.C. Muschik, K. Jensen, W. Wasilewski, J.M.J. Petersen, J.I.J. Cirac and E.S.E. Polzik. Entanglement Generated by Dissipation and Steady State Entanglement of Two Macroscopic Objects Phys. Rev. Lett. 107 080503 2011
  back to text
• 63 article Z. Leghtas, G. Kirchmair, B. Vlastakis, M. H.M. Devoret, R. J.R. Schoelkopf and M. Mirrahimi. Deterministic protocol for mapping a qubit to coherent state superpositions in a cavity Phys. Rev. A 87 042315 2013
  back to text
• 64 article Z. Leghtas, G. Kirchmair, B. Vlastakis, R. JR. Schoelkopf, M. H.M. Devoret and M. Mirrahimi. Hardware-efficient autonomous quantum memory protection Phys. Rev. Lett. 111 120501 2013
  back to text
• 65 article Z. Leghtas, A. Sarlette and P. Rouchon. Adiabatic passage and ensemble control of quantum systems J. Phys. B 44 154017 2011
  back to text
• 66 article Z. Leghtas, U. Vool, S. Shankar, M. Hatridge, S.M.S. Girvin, M. H.M. Devoret and M. Mirrahimi. Stabilizing a Bell state of two superconducting qubits by dissipation engineering Phys. Rev. A 88 023849 2013
  back to text back to text
• 67 articleJr-ShinJ.-S. Li and N. Khaneja. Ensemble control of Bloch equationsIEEE Trans. Autom. Control542009, 528--536
  back to text
• 68 articleY. Lin, J.P.J. Gaebler, F. Reiter, T.R.T. Tan, R. Bowler, A.S.A. Sorensen, D. Leibfried and D.J.D. Wineland. Dissipative production of a maximally entangled steady state of two quantum bitsNature5042013, 415--418
  back to text
• 69 article S. Lloyd. Coherent quantum feedback Phys. Rev. A 62 022108 2000
  back to text back to text
• 70 article L. Mazzarella, A. Sarlette and F. Ticozzi. Consensus for quantum networks: from symmetry to gossip iterations IEEE Trans. Automat. Control in press 2014
  back to text
• 71 conference M. Mirrahimi, B. Huard and M. H.M. Devoret. Strong measurement and quantum feedback for persistent Rabi oscillations in circuit QED experiments IEEE Conference on Decision and Control IEEE Conference on Decision and Control 2012
  back to text
• 72 article K.W.K. Murch, U. Vool, D. Zhou, S.J.S. Weber, S.M.S. Girvin and I. Siddiqi. Cavity-assisted quantum bath engineering Phys. Rev. Lett. 109 183602 2012
  back to text
• 73 articleAA. Negretti and KK. Mölmer. Estimation of classical parameters via continuous probing of complementary quantum observablesNew Journal of Physics15121250022013, URL: http://stacks.iop.org/1367-2630/15/i=12/a=125002
  back to text
• 74 articleH.I.H. Nurdin, M.R.M. James and I.R.I. Petersen. Coherent quantum LQG controlAutomatica452009, 1837--1846
  back to text
• 75 articleB. Peaudecerf, T. Rybarczyk, S. Gerlich, S. Gleyzes, J.-M. Raimond, S. Haroche, I. Dotsenko and M. Brune. Adaptive Quantum Nondemolition Measurement of a Photon NumberPhys. Rev. Lett.1128080401Feb 2014, URL: http://link.aps.org/doi/10.1103/PhysRevLett.112.080401
  DOIback to text
• 76 articleD. Petz. Monotone Metrics on matrix spacesLinear Algebra and its Applications2441996, 81--96
  back to text
• 77 articleJ.F.J. Poyatos, J.I.J. Cirac and P. Zoller. Quantum Reservoir Engineering with Laser Cooled Trapped IonsPhys. Rev. Lett.77231996, 4728--4731
  back to textback to text
• 78 articleD. Reeb, M.~J.M. Kastoryano and M.~M.M. Wolf. Hilbert's projective metric in quantum information theoryJournal of Mathematical Physics528082201August 2011, URL: http://dx.doi.org/10.1063/1.3615729
  back to text
• 79 article D. Ristè, J.V.J. Leeuwen, H.-S. Ku, K. Lehnert and L. Dicarlo. Initialization by measurement of a superconducting quantum bit circuit Phys. Rev. Lett. 109 050507 2012
  back to text
• 80 article N. Roch, E. Flurin, F. Nguyen, P. Morfin, P. Campagne-Ibarcq, M. H.M. Devoret and B. Huard. Widely tunable, non-degenerate three-wave mixing microwave device operating near the quantum limit Phys. Rev. Lett. 108 147701 2012
  back to text
• 81 articleP. Rouchon. Fidelity is a Sub-Martingale for Discrete-Time Quantum FiltersIEEE Transactions on Automatic Control56112011, 2743--2747
  back to textback to text
• 82 articleA. Roy, Z. Leghtas, A.D.A. Stone, M.H.M. Devoret and M. Mirrahimi. Continuous generation and stabilization of mesoscopic field superposition states in a quantum circuitPhys. Rev. A912015, 013810
  back to text
• 83 article A. Sarlette, Z. Leghtas, M. Brune, J.-M. Raimond and P. Rouchon. Stabilization of nonclassical states of one- and two-mode radiation fields by reservoir engineering Phys. Rev. A 86 012114 2012
  back to text
• 84 articleD.I.D. Schuster, A.A.A. Houck, J.AJ. Schreier, A. Wallraff, J.M.J. Gambetta, A. Blais, L. Frunzio, J. Majer, B. Johnson, M. H.M. Devoret, S.M.S. Girvin and R. J.R. Schoelkopf. Resolving photon number states in a superconducting circuitNature4452007, 515--518
  back to text
• 85 inproceedingsR. Sepulchre, A. Sarlette and P. Rouchon. Consensus in non-commutative spacesDecision and Control (CDC), 2010 49th IEEE Conference on2010, 6596--6601
  back to text
• 86 articleS. Shankar, M. Hatridge, Z. Leghtas, K.M.K. Sliwa, A. Narla, U. Vool, S.M.S. Girvin, L. Frunzio, M. Mirrahimi and M. H.M. Devoret. Autonomously stabilized entanglement between two superconducting quantum bitsNature5042013, 419--422
  back to textback to textback to textback to textback to text
• 87 articleP. Shor. Scheme for reducing decoherence in quantum memoryPhys. Rev. A521995, 2493--2496
  back to text
• 88 inproceedingsA. Somaraju, I. Dotsenko, C. Sayrin and P. Rouchon. Design and Stability of Discrete-Time Quantum Filters with Measurement ImperfectionsAmerican Control Conference2012, 5084--5089
  back to textback to text
• 89 article A. Somaraju, M. Mirrahimi and P. Rouchon. Approximate stabilization of infinite dimensional quantum stochastic system Reviews in Mathematical Physics 25 1350001 2013
  back to text back to text
• 90 article A. Steane. Error Correcting Codes in Quantum Theory Phys. Rev. Lett 77 5 1996
  back to text back to text
• 91 articleL. Sun, A. Petrenko, Z. Leghtas, B. Vlastakis, G. Kirchmair, K.M.K. Sliwa, A. Narla, M. Hatridge, S. Shankar, J. Blumoff, L. Frunzio, M. Mirrahimi, M. H.M. Devoret and R. J.R. Schoelkopf. Tracking photon jumps with repeated quantum non-demolition parity measurementsNature5112014, 444--448
  back to text
• 92 article J.N.J. Tsitsiklis. Problems in decentralized decision making and computation PhD Thesis, MIT 1984
  back to text
• 93 articleR. Vijay, C. Macklin, D.H.D. Slichter, S.J.S. Weber, K.W.K. Murch, R. Naik, A.N.A. Korotkov and I. Siddiqi. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedbackNature4902012, 77--80
  back to textback to text
• 94 articleL. Viola, E. Knill and S. Lloyd. Dynamical decoupling of open quantum systemPhys. Rev. Lett.821999, 2417-2421
  back to text
• 95 articleB. Vlastakis, G. Kirchmair, Z. Leghtas, S.E.S. Nigg, L. Frunzio, S.M.S. Girvin, M. Mirrahimi, M. H.M. Devoret and R. J.R. Schoelkopf. Deterministically encoding quantum information using 100-photon Schrödinger cat statesScience3422013, 607--610
  back to text
• 96 article X. Zhou, I. Dotsenko, B. Peaudecerf, T. Rybarczyk, C. Sayrin, S. Gleyzes, J.-M. Raimond, M. Brune and S. Haroche. Field locked to Fock state by quantum feedback with single photon corrections Physical Review Letter 108 243602 2012
  back to text
• 97 articleR. van Handel. The stability of quantum Markov filtersInfin. Dimens. Anal. Quantum Probab. Relat. Top.122009, 153--172
  back to text