Keywords
Computer Science and Digital Science
- A3.1.8. Big data (production, storage, transfer)
- A3.4.1. Supervised learning
- A3.4.2. Unsupervised learning
- A3.4.5. Bayesian methods
- A3.4.7. Kernel methods
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.4. Statistical methods
- A6.2.6. Optimization
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.4. Model reduction
- A6.3.5. Uncertainty Quantification
- A6.5.2. Fluid mechanics
- A6.5.4. Waves
Other Research Topics and Application Domains
- B3.2. Climate and meteorology
- B3.3.2. Water: sea & ocean, lake & river
- B3.3.4. Atmosphere
- B3.4.1. Natural risks
- B4.3.2. Hydro-energy
- B4.3.3. Wind energy
- B9.11.1. Environmental risks
1 Team members, visitors, external collaborators
Research Scientists
- Laurent Debreu [Team leader, Inria, Senior Researcher, HDR]
- Eugene Kazantsev [Inria, Researcher]
- Florian Lemarié [Inria, Researcher]
- Gurvan Madec [CNRS, Senior Researcher, HDR]
- Patrick Vidard [Inria, Researcher]
- Olivier Zahm [Inria, Researcher]
Faculty Members
- Elise Arnaud [Univ Grenoble Alpes, Associate Professor]
- Eric Blayo-Nogret [Univ Grenoble Alpes, Professor, HDR]
- Christine Kazantsev [Univ Grenoble Alpes, Associate Professor]
- Clémentine Prieur [Univ Grenoble Alpes, Professor, HDR]
- Martin Schreiber [Univ Grenoble Alpes, Professor, from Sep 2021]
Post-Doctoral Fellows
- Anass El Aouni [Inria, until Sep 2021]
- Sanal Parameswaran [Inria, from Nov 2021]
PhD Students
- Rishabh Bhatt [Inria]
- Qiao Chen [Univ Grenoble Alpes, from Oct 2021]
- Simon Clement [Univ Grenoble Alpes]
- Clement Duhamel [Inria]
- Emilie Duval [Inria]
- Rafael Floch [Technical University of Denmark, from Oct. 2020]
- Adrien Hirvoas [IFPEN, until Mar 2021]
- Henri Mermoz Kouye [Institut national de recherche pour l'agriculture, l'alimentation et l'environnement]
- Arthur Macherey [École centrale de Nantes, until Jun 2021]
- Antoine Alexis Nasser [Inria]
- Manolis Perrot [Univ Grenoble Alpes, from Oct 2021]
- Katarina Radisic [Univ. Grenoble Alpes, from Dec.2021]
- Emilie Rouzies [Institut national de recherche pour l'agriculture, l'alimentation et l'environnement]
- Sophie Thery [Univ Grenoble Alpes, until Aug 2021]
- Victor Trappler [Univ Grenoble Alpes, until Jun 2021]
- Robin Vaudry [CNRS, from Oct 2021]
Technical Staff
- Celine Acary Robert [Univ Grenoble Alpes, Engineer]
- Joel Andrepont [Inria, Engineer, Oct 2021]
- Maurice Bremond [Inria, Engineer]
- Nicolas Ducousso [Inria, Engineer, until Mar 2021]
- Laurent Gilquin [Inria, Engineer]
- Joris Pianezze [Inria, Engineer, from Apr 2021]
- Aurelien Prat [Univ de La Réunion, Engineer, from Jul 2021]
Interns and Apprentices
- Joel Andrepont [Inria, from Mar 2021 until Aug 2021]
- Alisa Barkar [Inria, from May 2021 until Jul 2021]
- Thomas Xavier Ledoux [Inria, from Mar 2021 until Jul 2021]
- Jules Maurel-Barros [Inria, from May 2021 until Aug 2021]
- Matthieu Oliver [Inria, from Apr 2021 until Sep 2021]
- Manolis Perrot [École Normale Supérieure de Paris, until Sep 2021]
- Katarina Radisic [Inria, from Apr 2021 until Sep 2021]
Administrative Assistant
- Annie Simon [Inria]
2 Overall objectives
The general scope of the AIRSEA project-team is to develop mathematical and computational methods for the modeling of oceanic and atmospheric flows. The mathematical tools used involve both deterministic and statistical approaches. The main research topics cover a) modeling and coupling b) model reduction for sensitivity analysis, coupling and multiscale optimizations c) sensitivity analysis, parameter estimation and risk assessment d) algorithms for high performance computing. The range of application is from climate modeling to the prediction of extreme events.
3 Research program
Recent events have raised questions regarding the social and economic implications of anthropic alterations of the Earth system, i.e. climate change and the associated risks of increasing extreme events. Ocean and atmosphere, coupled with other components (continent and ice) are the building blocks of the Earth system. A better understanding of the ocean atmosphere system is a key ingredient for improving prediction of such events. Numerical models are essential tools to understand processes, and simulate and forecast events at various space and time scales. Geophysical flows generally have a number of characteristics that make it difficult to model them. This justifies the development of specifically adapted mathematical methods:
- Geophysical flows are strongly non-linear. Therefore, they exhibit interactions between different scales, and unresolved small scales (smaller than mesh size) of the flows have to be parameterized in the equations.
- Geophysical fluids are non closed systems. They are open-ended in their scope for including and dynamically coupling different physical processes (e.g., atmosphere, ocean, continental water, etc). Coupling algorithms are thus of primary importance to account for potentially significant feedback.
- Numerical models contain parameters which cannot be estimated accurately either because they are difficult to measure or because they represent some poorly known subgrid phenomena. There is thus a need for dealing with uncertainties. This is further complicated by the turbulent nature of geophysical fluids.
- The computational cost of geophysical flow simulations is huge, thus requiring the use of reduced models, multiscale methods and the design of algorithms ready for high performance computing platforms.
Our scientific objectives are divided into four major points. The first objective focuses on developing advanced mathematical methods for both the ocean and atmosphere, and the coupling of these two components. The second objective is to investigate the derivation and use of model reduction to face problems associated with the numerical cost of our applications. The third objective is directed toward the management of uncertainty in numerical simulations. The last objective deals with efficient numerical algorithms for new computing platforms. As mentioned above, the targeted applications cover oceanic and atmospheric modeling and related extreme events using a hierarchy of models of increasing complexity.
3.1 Modeling for oceanic and atmospheric flows
Current numerical oceanic and atmospheric models suffer from a number of well-identified problems. These problems are mainly related to lack of horizontal and vertical resolution, thus requiring the parameterization of unresolved (subgrid scale) processes and control of discretization errors in order to fulfill criteria related to the particular underlying physics of rotating and strongly stratified flows. Oceanic and atmospheric coupled models are increasingly used in a wide range of applications from global to regional scales. Assessment of the reliability of those coupled models is an emerging topic as the spread among the solutions of existing models (e.g., for climate change predictions) has not been reduced with the new generation models when compared to the older ones.
Advanced methods for modeling 3D rotating and stratified flows The continuous increase of computational power and the resulting finer grid resolutions have triggered a recent regain of interest in numerical methods and their relation to physical processes. Going beyond present knowledge requires a better understanding of numerical dispersion/dissipation ranges and their connection to model fine scales. Removing the leading order truncation error of numerical schemes is thus an active topic of research and each mathematical tool has to adapt to the characteristics of three dimensional stratified and rotating flows. Studying the link between discretization errors and subgrid scale parameterizations is also arguably one of the main challenges.
Complexity of the geometry, boundary layers, strong stratification and lack of resolution are the main sources of discretization errors in the numerical simulation of geophysical flows. This emphasizes the importance of the definition of the computational grids (and coordinate systems) both in horizontal and vertical directions, and the necessity of truly multi resolution approaches. At the same time, the role of the small scale dynamics on large scale circulation has to be taken into account. Such parameterizations may be of deterministic as well as stochastic nature and both approaches are taken by the AIRSEA team. The design of numerical schemes consistent with the parameterizations is also arguably one of the main challenges for the coming years. This work is complementary and linked to that on parameters estimation described in 3.3.
Ocean Atmosphere interactions and formulation of coupled models State-of-the-art climate models (CMs) are complex systems under continuous development. A fundamental aspect of climate modeling is the representation of air-sea interactions. This covers a large range of issues: parameterizations of atmospheric and oceanic boundary layers, estimation of air-sea fluxes, time-space numerical schemes, non conforming grids, coupling algorithms ...Many developments related to these different aspects were performed over the last 10-15 years, but were in general conducted independently of each other.
The aim of our work is to revisit and enrich several aspects of the representation of air-sea interactions in CMs, paying special attention to their overall consistency with appropriate mathematical tools. We intend to work consistently on the physics and numerics. Using the theoretical framework of global-in-time Schwarz methods, our aim is to analyze the mathematical formulation of the parameterizations in a coupling perspective. From this study, we expect improved predictability in coupled models (this aspect will be studied using techniques described in 3.3). Complementary work on space-time nonconformities and acceleration of convergence of Schwarz-like iterative methods (see 8.1.2) are also conducted.
3.2 Model reduction / multiscale algorithms
The high computational cost of the applications is a common and major concern to have in mind when deriving new methodological approaches. This cost increases dramatically with the use of sensitivity analysis or parameter estimation methods, and more generally with methods that require a potentially large number of model integrations.
A dimension reduction, using either stochastic or deterministic methods, is a way to reduce significantly the number of degrees of freedom, and therefore the calculation time, of a numerical model.
Model reduction Reduction methods can be deterministic (proper orthogonal decomposition, other reduced bases) or stochastic (polynomial chaos, Gaussian processes, kriging), and both fields of research are very active. Choosing one method over another strongly depends on the targeted application, which can be as varied as real-time computation, sensitivity analysis (see e.g., section 8.5) or optimisation for parameter estimation (see below).
Our goals are multiple, but they share a common need for certified error bounds on the output. Our team has a 4-year history of working on certified reduction methods and has a unique positioning at the interface between deterministic and stochastic approaches. Thus, it seems interesting to conduct a thorough comparison of the two alternatives in the context of sensitivity analysis. Efforts will also be directed toward the development of efficient greedy algorithms for the reduction, and the derivation of goal-oriented sharp error bounds for non linear models and/or non linear outputs of interest. This will be complementary to our work on the deterministic reduction of parametrized viscous Burgers and Shallow Water equations where the objective is to obtain sharp error bounds to provide confidence intervals for the estimation of sensitivity indices.
Reduced models for coupling applications Global and regional high-resolution oceanic models are either coupled to an atmospheric model or forced at the air-sea interface by fluxes computed empirically preventing proper physical feedback between the two media. Thanks to high-resolution observational studies, the existence of air-sea interactions at oceanic mesoscales (i.e., at scales) have been unambiguously shown. Those interactions can be represented in coupled models only if the oceanic and atmospheric models are run on the same high-resolution computational grid, and are absent in a forced mode. Fully coupled models at high-resolution are seldom used because of their prohibitive computational cost. The derivation of a reduced model as an alternative between a forced mode and the use of a full atmospheric model is an open problem.
Multiphysics coupling often requires iterative methods to obtain a mathematically correct numerical solution. To mitigate the cost of the iterations, we will investigate the possibility of using reduced-order models for the iterative process. We will consider different ways of deriving a reduced model: coarsening of the resolution, degradation of the physics and/or numerical schemes, or simplification of the governing equations. At a mathematical level, we will strive to study the well-posedness and the convergence properties when reduced models are used. Indeed, running an atmospheric model at the same resolution as the ocean model is generally too expensive to be manageable, even for moderate resolution applications. To account for important fine-scale interactions in the computation of the air-sea boundary condition, the objective is to derive a simplified boundary layer model that is able to represent important 3D turbulent features in the marine atmospheric boundary layer.
Reduced models for multiscale optimization The field of multigrid methods for optimisation has known a tremendous development over the past few decades. However, it has not been applied to oceanic and atmospheric problems apart from some crude (non-converging) approximations or applications to simplified and low dimensional models. This is mainly due to the high complexity of such models and to the difficulty in handling several grids at the same time. Moreover, due to complex boundaries and physical phenomena, the grid interactions and transfer operators are not trivial to define.
Multigrid solvers (or multigrid preconditioners) are efficient methods for the solution of variational data assimilation problems. We would like to take advantage of these methods to tackle the optimization problem in high dimensional space. High dimensional control space is obtained when dealing with parameter fields estimation, or with control of the full 4D (space time) trajectory. It is important since it enables us to take into account model errors. In that case, multigrid methods can be used to solve the large scales of the problem at a lower cost, this being potentially coupled with a scale decomposition of the variables themselves.
3.3 Dealing with uncertainties
There are many sources of uncertainties in numerical models. They are due to imperfect external forcing, poorly known parameters, missing physics and discretization errors. Studying these uncertainties and their impact on the simulations is a challenge, mostly because of the high dimensionality and non-linear nature of the systems. To deal with these uncertainties we work on three axes of research, which are linked: sensitivity analysis, parameter estimation and risk assessment. They are based on either stochastic or deterministic methods.
Sensitivity analysis Sensitivity analysis (SA), which links uncertainty in the model inputs to uncertainty in the model outputs, is a powerful tool for model design and validation. First, it can be a pre-stage for parameter estimation (see 3.3), allowing for the selection of the more significant parameters. Second, SA permits understanding and quantifying (possibly non-linear) interactions induced by the different processes defining e.g., realistic ocean atmosphere models. Finally SA allows for validation of models, checking that the estimated sensitivities are consistent with what is expected by the theory. On ocean, atmosphere and coupled systems, only first order deterministic SA are performed, neglecting the initialization process (data assimilation). AIRSEA members and collaborators proposed to use second order information to provide consistent sensitivity measures, but so far it has only been applied to simple academic systems. Metamodels are now commonly used, due to the cost induced by each evaluation of complex numerical models: mostly Gaussian processes, whose probabilistic framework allows for the development of specific adaptive designs, and polynomial chaos not only in the context of intrusive Galerkin approaches but also in a black-box approach. Until recently, global SA was based primarily on a set of engineering practices. New mathematical and methodological developments have led to the numerical computation of Sobol' indices, with confidence intervals assessing for both metamodel and estimation errors. Approaches have also been extended to the case of dependent entries, functional inputs and/or output and stochastic numerical codes. Other types of indices and generalizations of Sobol' indices have also been introduced.
Concerning the stochastic approach to SA we plan to work with parameters that show spatio-temporal dependencies and to continue toward more realistic applications where the input space is of huge dimension with highly correlated components. Sensitivity analysis for dependent inputs also introduces new challenges. In our applicative context, it would seem prudent to carefully learn the spatio-temporal dependences before running a global SA. In the deterministic framework we focus on second order approaches where the sought sensitivities are related to the optimality system rather than to the model; i.e., we consider the whole forecasting system (model plus initialization through data assimilation).
All these methods allow for computing sensitivities and more importantly a posteriori error statistics.
Parameter estimation Advanced parameter estimation methods are barely used in ocean, atmosphere and coupled systems, mostly due to a difficulty of deriving adequate response functions, a lack of knowledge of these methods in the ocean-atmosphere community, and also to the huge associated computing costs. In the presence of strong uncertainties on the model but also on parameter values, simulation and inference are closely associated. Filtering for data assimilation and Approximate Bayesian Computation (ABC) are two examples of such association.
Stochastic approach can be compared with the deterministic approach, which allows to determine the sensitivity of the flow to parameters and optimize their values relying on data assimilation. This approach is already shown to be capable of selecting a reduced space of the most influent parameters in the local parameter space and to adapt their values in view of correcting errors committed by the numerical approximation. This approach assumes the use of automatic differentiation of the source code with respect to the model parameters, and optimization of the obtained raw code.
AIRSEA assembles all the required expertise to tackle these difficulties. As mentioned previously, the choice of parameterization schemes and their tuning has a significant impact on the result of model simulations. Our research will focus on parameter estimation for parameterized Partial Differential Equations (PDEs) and also for parameterized Stochastic Differential Equations (SDEs). Deterministic approaches are based on optimal control methods and are local in the parameter space (i.e., the result depends on the starting point of the estimation) but thanks to adjoint methods they can cope with a large number of unknowns that can also vary in space and time. Multiscale optimization techniques as described in 8.3 will be one of the tools used. This in turn can be used either to propose a better (and smaller) parameter set or as a criterion for discriminating parameterization schemes. Statistical methods are global in the parameter state but may suffer from the curse of dimensionality. However, the notion of parameter can also be extended to functional parameters. We may consider as parameter a functional entity such as a boundary condition on time, or a probability density function in a stationary regime. For these purposes, non-parametric estimation will also be considered as an alternative.
Risk assessment Risk assessment in the multivariate setting suffers from a lack of consensus on the choice of indicators. Moreover, once the indicators are designed, it still remains to develop estimation procedures, efficient even for high risk levels. Recent developments for the assessment of financial risk have to be considered with caution as methods may differ pertaining to general financial decisions or environmental risk assessment. Modeling and quantifying uncertainties related to extreme events is of central interest in environmental sciences. In relation to our scientific targets, risk assessment is very important in several areas: hydrological extreme events, cyclone intensity, storm surges...Environmental risks most of the time involve several aspects which are often correlated. Moreover, even in the ideal case where the focus is on a single risk source, we have to face the temporal and spatial nature of environmental extreme events. The study of extremes within a spatio-temporal framework remains an emerging field where the development of adapted statistical methods could lead to major progress in terms of geophysical understanding and risk assessment thus coupling data and model information for risk assessment.
Based on the above considerations we aim to answer the following scientific questions: how to measure risk in a multivariate/spatial framework? How to estimate risk in a non stationary context? How to reduce dimension (see 3.2) for a better estimation of spatial risk?
Extreme events are rare, which means there is little data available to make inferences of risk measures. Risk assessment based on observation therefore relies on multivariate extreme value theory. Interacting particle systems for the analysis of rare events is commonly used in the community of computer experiments. An open question is the pertinence of such tools for the evaluation of environmental risk.
Most numerical models are unable to accurately reproduce extreme events. There is therefore a real need to develop efficient assimilation methods for the coupling of numerical models and extreme data.
3.4 High performance computing
Methods for sensitivity analysis, parameter estimation and risk assessment are extremely costly due to the necessary number of model evaluations. This number of simulations require considerable computational resources, depends on the complexity of the application, the number of input variables and desired quality of approximations. To this aim, the AIRSEA team is an intensive user of HPC computing platforms, particularly grid computing platforms. The associated grid deployment has to take into account the scheduling of a huge number of computational requests and the links with data-management between these requests, all of these as automatically as possible. In addition, there is an increasing need to propose efficient numerical algorithms specifically designed for new (or future) computing architectures and this is part of our scientific objectives. According to the computational cost of our applications, the evolution of high performance computing platforms has to be taken into account for several reasons. While our applications are able to exploit space parallelism to its full extent (oceanic and atmospheric models are traditionally based on a spatial domain decomposition method), the spatial discretization step size limits the efficiency of traditional parallel methods. Thus the inherent parallelism is modest, particularly for the case of relative coarse resolution but with very long integration time (e.g., climate modeling). Paths toward new programming paradigms are thus needed. As a step in that direction, we plan to focus our research on parallel in time methods.
New numerical algorithms for high performance computing Parallel in time methods can be classified into three main groups. In the first group, we find methods using parallelism across the method, such as parallel integrators for ordinary differential equations. The second group considers parallelism across the problem. Falling into this category are methods such as waveform relaxation where the space-time system is decomposed into a set of subsystems which can then be solved independently using some form of relaxation techniques or multigrid reduction in time. The third group of methods focuses on parallelism across the steps. One of the best known algorithms in this family is parareal. Other methods combining the strengths of those listed above (e.g., PFASST) are currently under investigation in the community.
Parallel in time methods are iterative methods that may require a large number of iteration before convergence. Our first focus will be on the convergence analysis of parallel in time (Parareal / Schwarz) methods for the equation systems of oceanic and atmospheric models. Our second objective will be on the construction of fast (approximate) integrators for these systems. This part is naturally linked to the model reduction methods of section (8.3.1). Fast approximate integrators are required both in the Schwarz algorithm (where a first guess of the boundary conditions is required) and in the Parareal algorithm (where the fast integrator is used to connect the different time windows). Our main application of these methods will be on climate (i.e., very long time) simulations. Our second application of parallel in time methods will be in the context of optimization methods. In fact, one of the major drawbacks of the optimal control techniques used in 3.3 is a lack of intrinsic parallelism in comparison with ensemble methods. Here, parallel in time methods also offer ways to better efficiency. The mathematical key point is centered on how to efficiently couple two iterative methods (i.e., parallel in time and optimization methods).
4 Application domains
4.1 The Ocean-Atmosphere System
The evolution of natural systems, in the short, mid, or long term, has extremely important consequences for both the global Earth system and humanity. Forecasting this evolution is thus a major challenge from the scientific, economic, and human viewpoints.
Humanity has to face the problem of global warming, brought on by the emission of greenhouse gases from human activities. This warming will probably cause huge changes at global and regional scales, in terms of climate, vegetation and biodiversity, with major consequences for local populations. Research has therefore been conducted over the past 15 to 20 years in an effort to model the Earth's climate and forecast its evolution in the 21st century in response to anthropic action.
With regard to short-term forecasts, the best and oldest example is of course weather forecasting. Meteorological services have been providing daily short-term forecasts for several decades which are of crucial importance for numerous human activities.
Numerous other problems can also be mentioned, like seasonal weather forecasting (to enable powerful phenomena like an El Nio event or a drought period to be anticipated a few months in advance), operational oceanography (short-term forecasts of the evolution of the ocean system to provide services for the fishing industry, ship routing, defense, or the fight against marine pollution) or the prediction of floods.
As mentioned previously, mathematical and numerical tools are omnipresent and play a fundamental role in these areas of research. In this context, the vocation of AIRSEA is not to carry out numerical prediction, but to address mathematical issues raised by the development of prediction systems for these application fields, in close collaboration with geophysicists.
5 Social and environmental responsibility
5.1 Impact of research results
Most of the research activities of the AIRSEA team are directed towards the improvement of numerical systems of the ocean and the atmosphere. This includes the development of appropriated numerical methods, model/parameter calibration using observational data and uncertainty quantification for decision making. The AIRSEA team members work in close collaboration with the researchers in the field of geophyscial fluid and are partners of several interdisciplinary projects. They also strongly contribute to the development of state of the art numerical systems, like NEMO and CROCO in the ocean community.
6 Highlights of the year
Clémentine Prieur was selected as one of ambassadors for La Science taille XX elles in Grenoble xxlgrenoble.sciencesconf.org
7 New software and platforms
7.1 New software
7.1.1 AGRIF
-
Name:
Adaptive Grid Refinement In Fortran
-
Keyword:
Mesh refinement
-
Scientific Description:
AGRIF is a Fortran 90 package for the integration of full adaptive mesh refinement (AMR) features within a multidimensional finite difference model written in Fortran. Its main objective is to simplify the integration of AMR potentialities within an existing model with minimal changes. Capabilities of this package include the management of an arbitrary number of grids, horizontal and/or vertical refinements, dynamic regridding, parallelization of the grids interactions on distributed memory computers. AGRIF requires the model to be discretized on a structured grid, like it is typically done in ocean or atmosphere modelling.
-
Functional Description:
AGRIF is a Fortran 90 package for the integration of full adaptive mesh refinement (AMR) features within a multidimensional finite difference model written in Fortran. Its main objective is to simplify the integration of AMR potentialities within an existing model with minimal changes. Capabilities of this package include the management of an arbitrary number of grids, horizontal and/or vertical refinements, dynamic regridding, parallelization of the grids interactions on distributed memory computers. AGRIF requires the model to be discretized on a structured grid, like it is typically done in ocean or atmosphere modelling.
-
News of the Year:
In 2020, the development of the AGRIF software received the support of 6 months of ATOS-BULL engineer through the European project ESIWACE2. The developments focused on optimizations in the interpolation phases.
- URL:
- Publications:
-
Contact:
Laurent Debreu
-
Participants:
Roland Patoum, Laurent Debreu
7.1.2 BALAISE
-
Name:
Bilbliothèque d’Assimilation Lagrangienne Adaptée aux Images Séquencées en Environnement
-
Keywords:
Multi-scale analysis, Data assimilation, Optimal control
-
Functional Description:
BALAISE (Bilbliothèque d’Assimilation Lagrangienne Adaptée aux Images Séquencées en Environnement) is a test bed for image data assimilation. It includes a shallow water model, a multi-scale decomposition library and an assimilation suite.
-
Contact:
Patrick Vidard
7.1.3 NEMOVAR
-
Name:
Variational data assimilation for NEMO
-
Keywords:
Oceanography, Data assimilation, Adjoint method, Optimal control
-
Functional Description:
NEMOVAR is a state-of-the-art multi-incremental variational data assimilation system with both 3D and 4D var capabilities, and which is designed to work with NEMO on the native ORCA grids. The background error covariance matrix is modelled using balance operators for the multivariate component and a diffusion operator for the univariate component. It can also be formulated as a linear combination of covariance models to take into account multiple correlation length scales associated with ocean variability on different scales. NEMOVAR has recently been enhanced with the addition of ensemble data assimilation and multi-grid assimilation capabilities. It is used operationnaly in both ECMWF and the Met Office (UK)
-
Contact:
Patrick Vidard
-
Partners:
CERFACS, ECMWF, Met Office
7.1.4 Sensitivity
-
Functional Description:
This package is useful for conducting sensitivity analysis of complex computer codes.
- URL:
-
Contact:
Laurent Gilquin
8 New results
8.1 Modeling for Oceanic and Atmospheric flows
8.1.1 Numerical Schemes for Ocean Modelling
Participants: Eric Blayo, Laurent Debreu, Emilie Duval, Florian Lemarié, Gurvan Madec, Antoine Nasser.
With the increase of resolution, the hydrostatic assumption becomes less valid and the AIRSEA group also works on the development of non-hydrostatic ocean models. The treatment of non-hydrostatic incompressible flows leads to a 3D elliptic system for pressure that can be ill conditioned in particular with non geopotential vertical coordinates. That is why we favour the use of the non-hydrostatic compressible equations that removes the need for a 3D resolution at the price of reincluding acoustic waves 69.
A comparison between 2D and 3D simulations of non hydrostatic surface waves has been performed in 13.
In addition, Emilie Duval started her PhD in September 2018 on the coupling between the hydrostatic incompressible and non-hydrostatic compressible equations. In 2021, a detailed analysis of acoustic-gravity waves in a free-surface compressible and stratified ocean has been published in Ocean Modelling2.
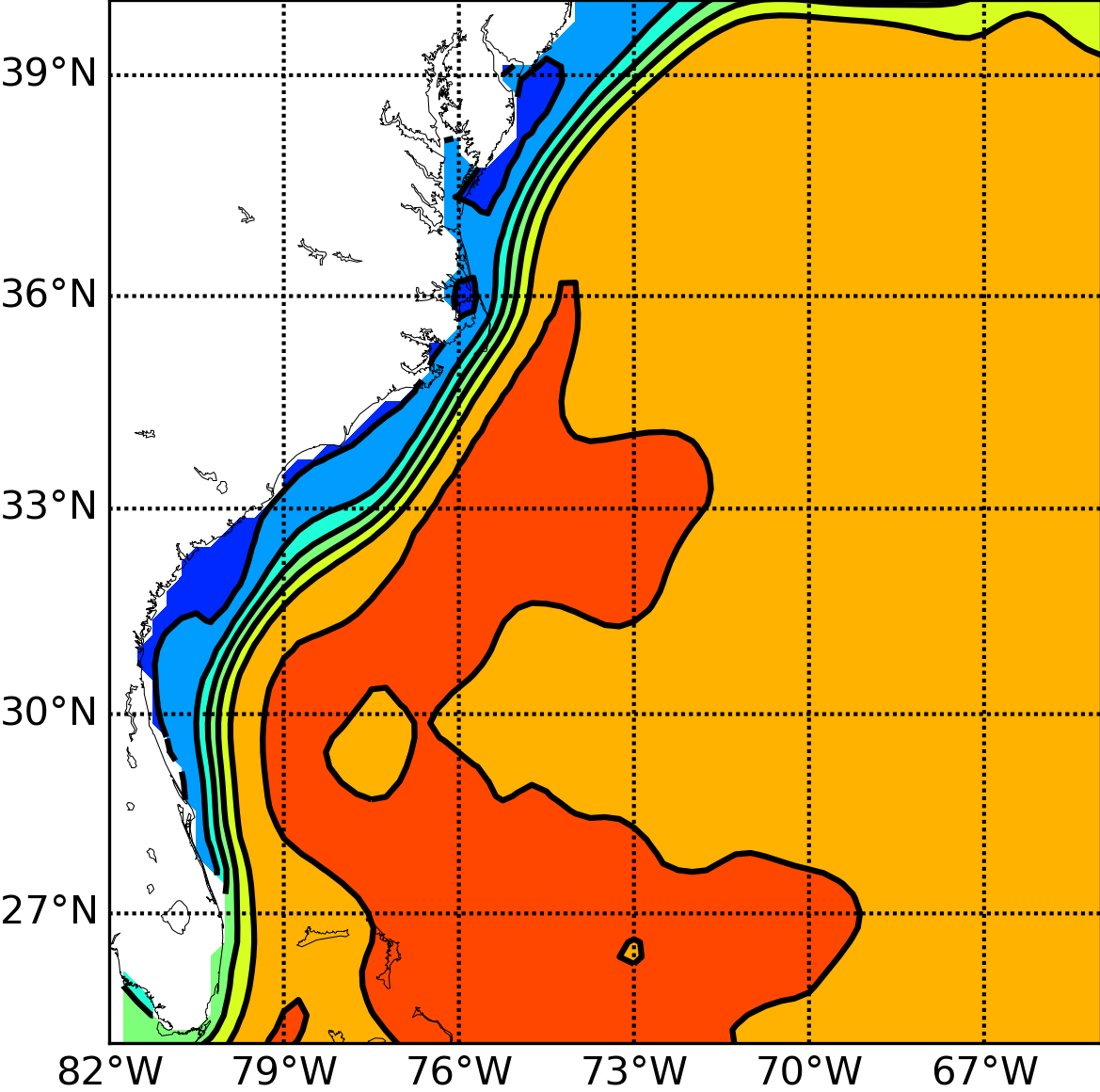
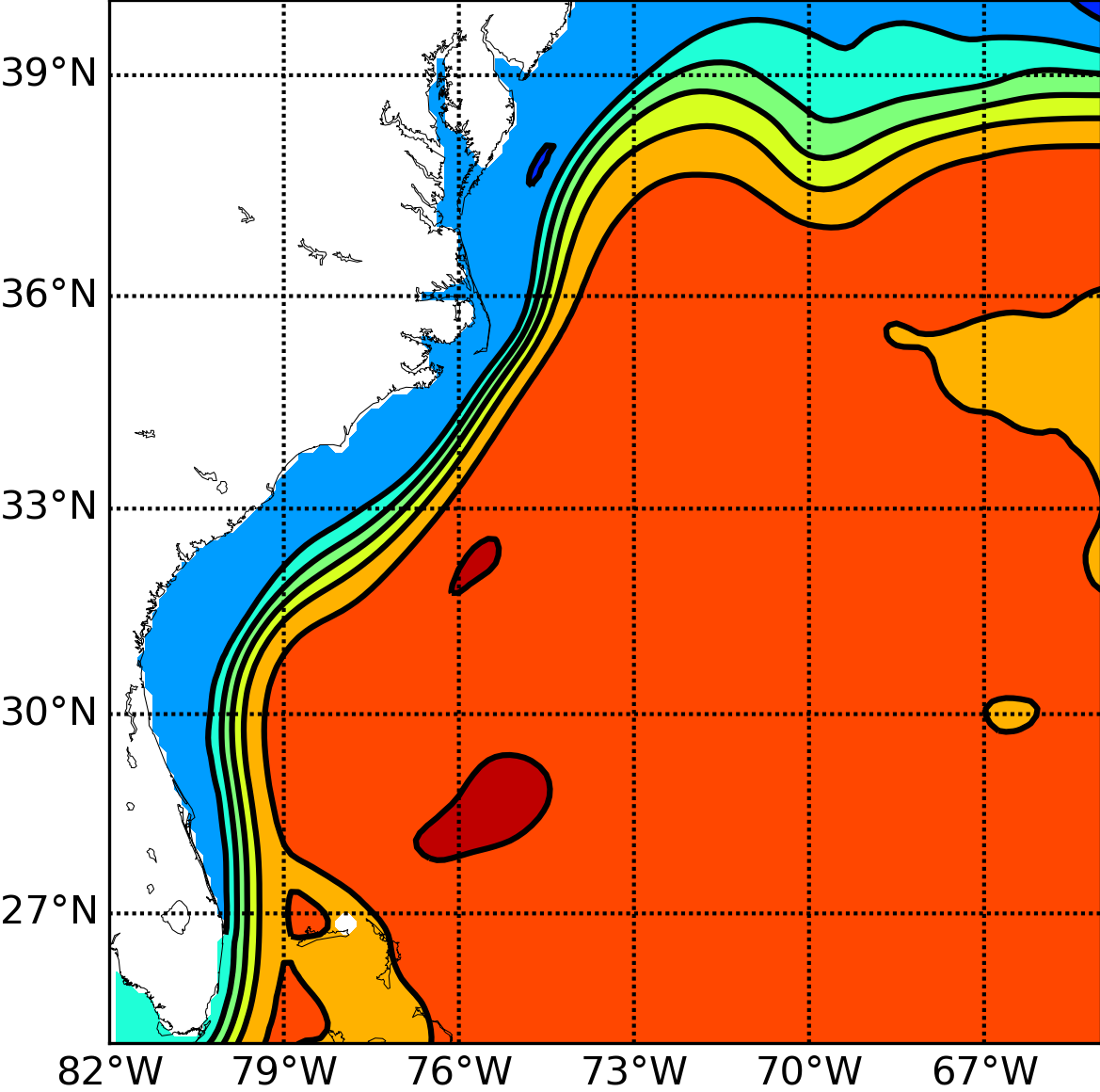
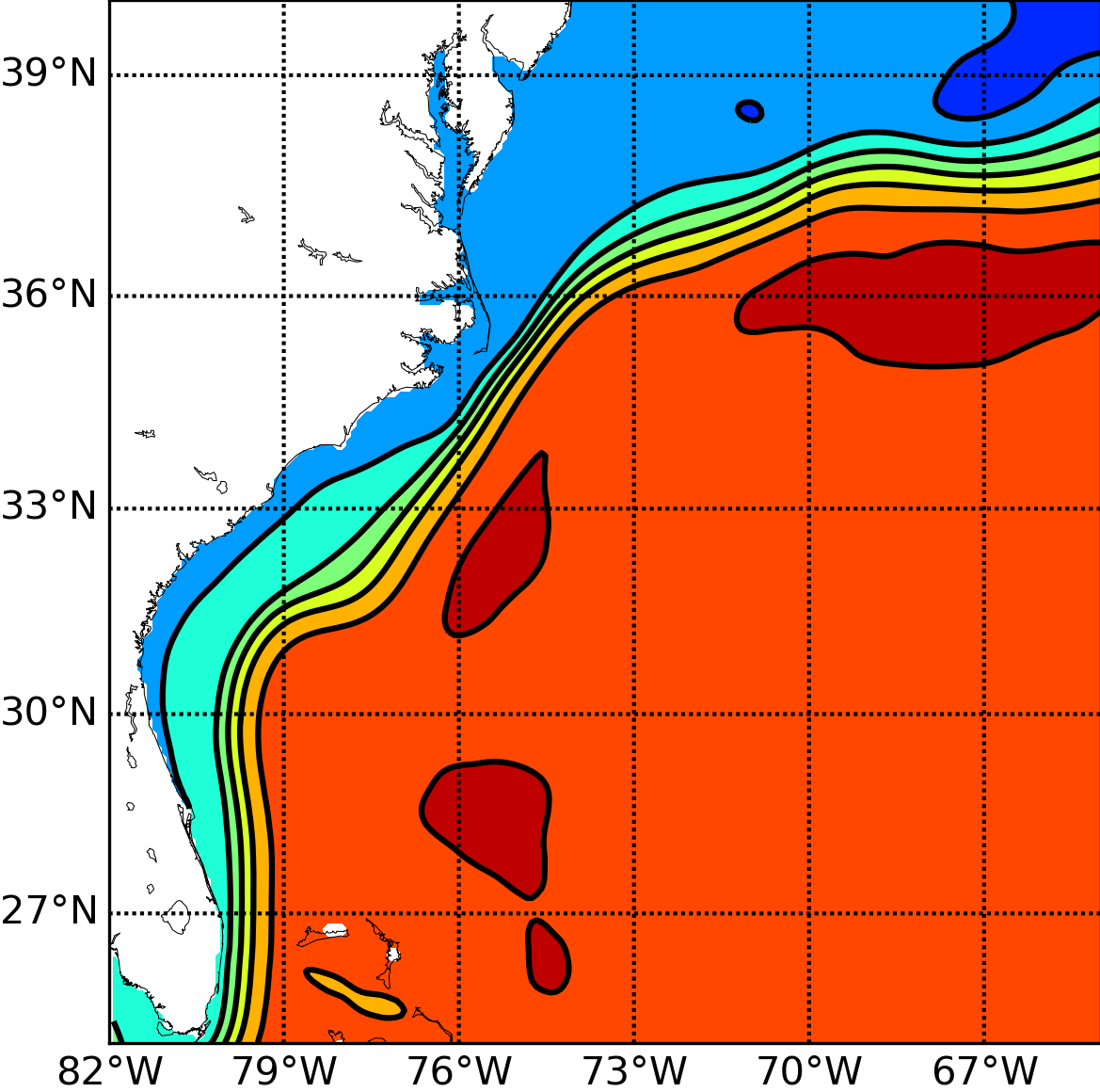
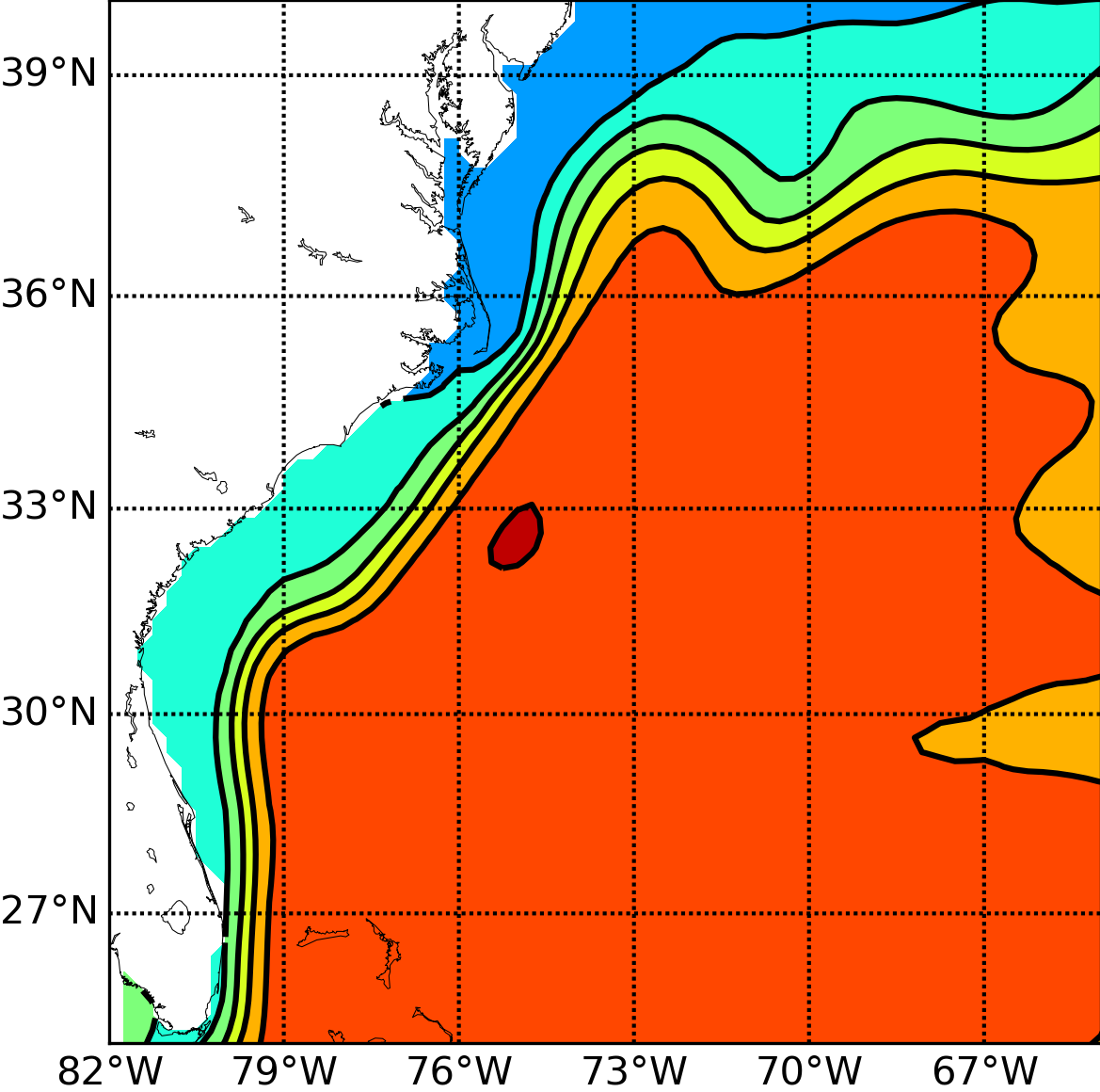
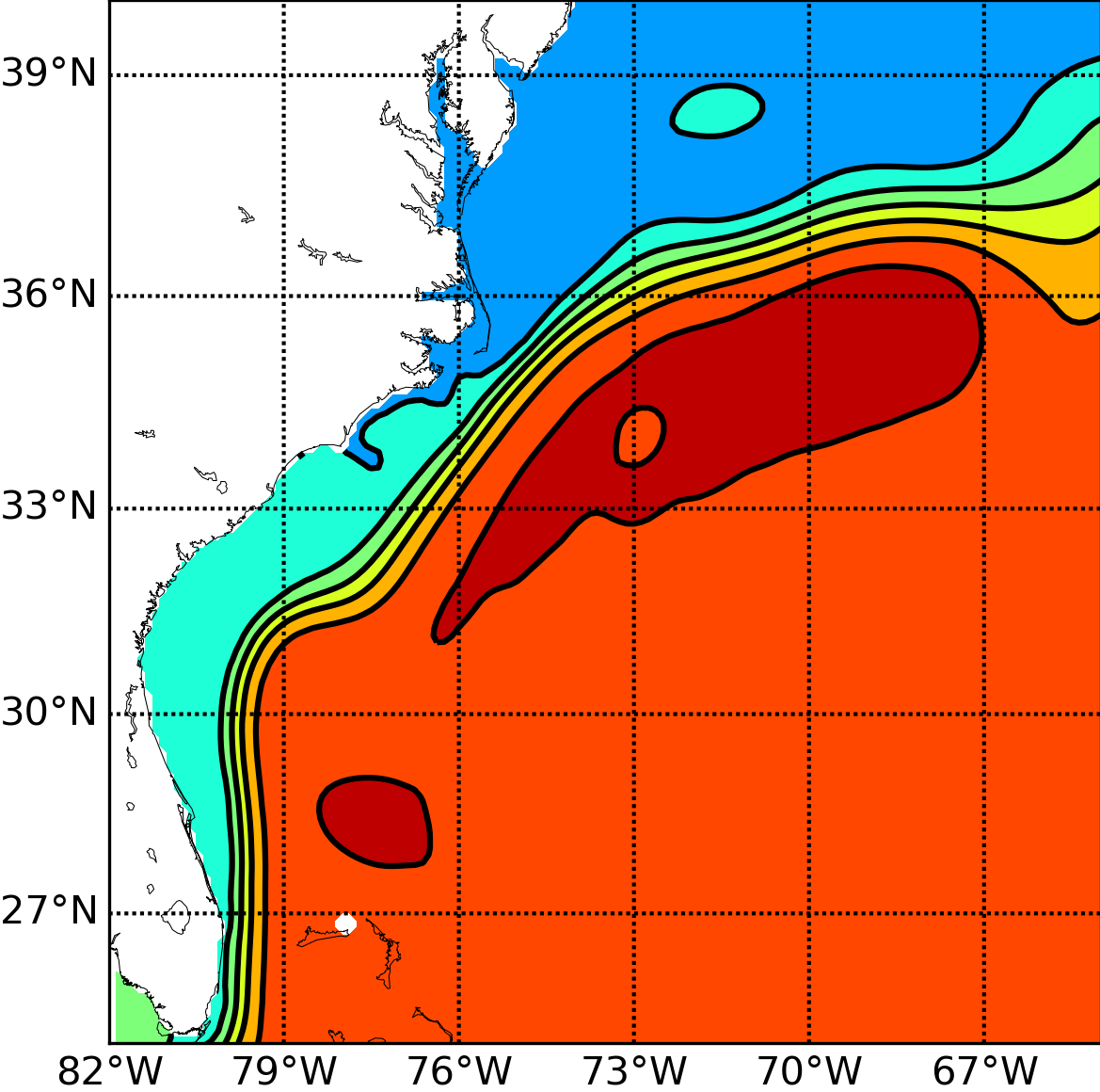
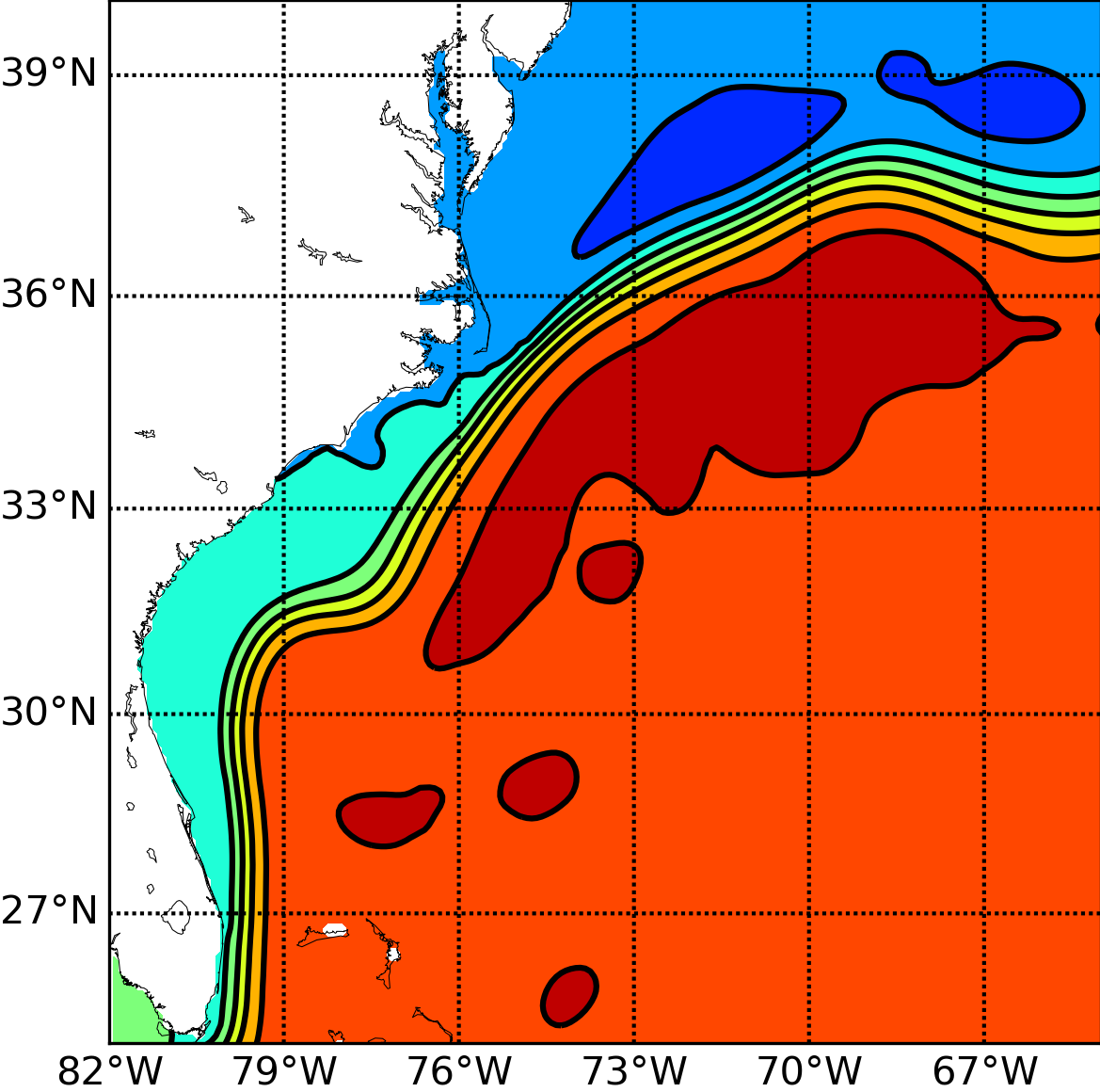
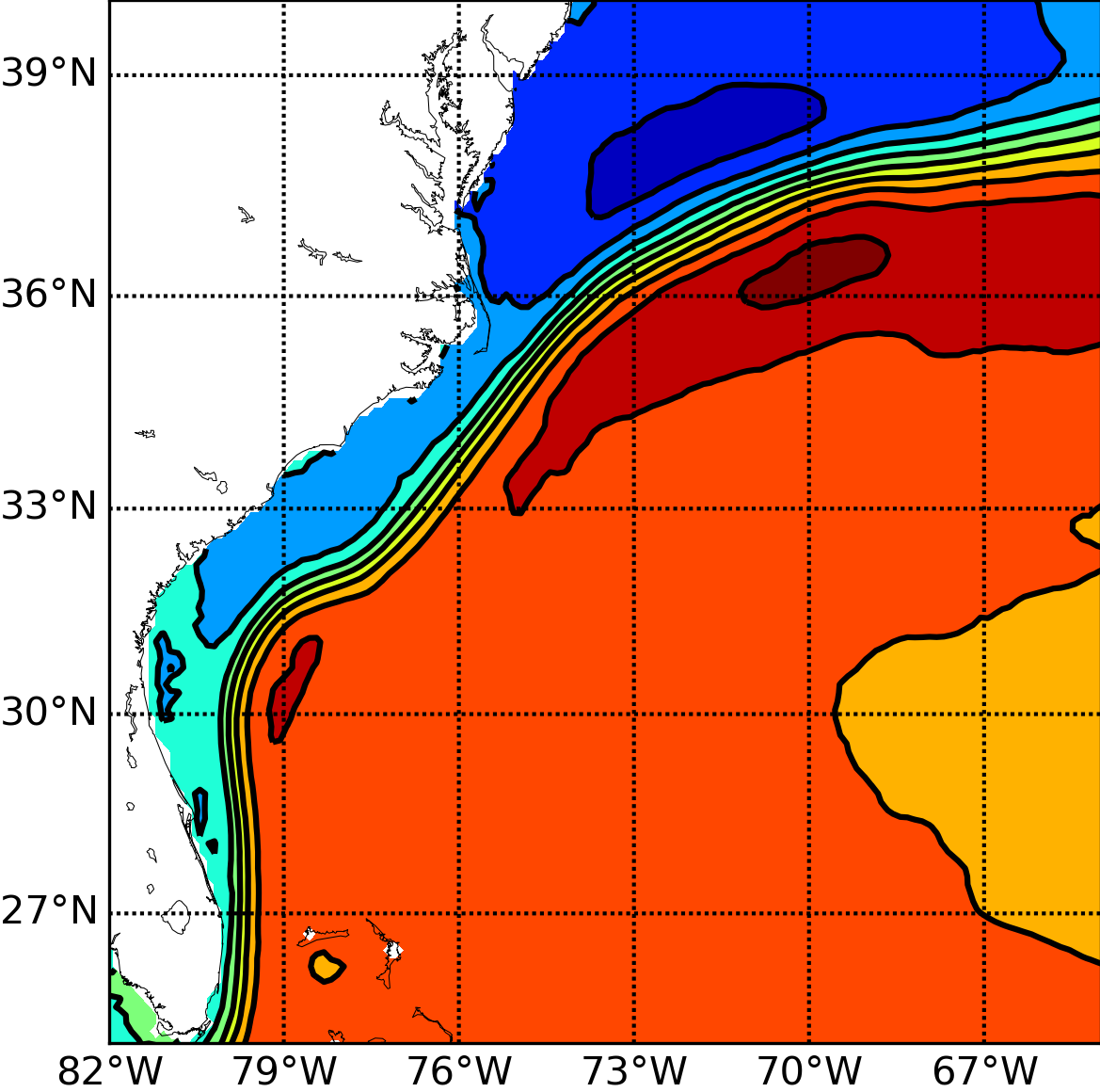
Accurate and stable implementation of bathymetry boundary conditions in ocean models remains a challenging problem. The dynamics of ocean flow often depend sensitively on satisfying bathymetry boundary conditions and correctly representing their complex geometry. Generalized (e.g. ) terrain-following coordinates are often used in ocean models, but they require smoothing the bathymetry to reduce pressure gradient errors. Geopotential -coordinates are a common alternative that avoid pressure gradient and numerical diapycnal diffusion errors, but they generate spurious flow due to their “staircase” geometry. In 61, we introduce a new Brinkman volume penalization to approximate the no-slip boundary condition and complex geometry of bathymetry in ocean models. This approach corrects the staircase effect of -coordinates, does not introduce any new stability constraints on the geometry of the bathymetry and is easy to implement in an existing ocean model. The porosity parameter allows modelling subgrid scale details of the geometry. We illustrate the penalization and confirm its accuracy by applying it to three standard test flows: upwelling over a sloping bottom, resting state over a seamount and internal tides over highly peaked bathymetry features. New results on realistic applications will be submitted soon. In the context of the Gulf Stream simulation, Figure (1) shows very significant improvements brought by the use of penalization methods. Through the use of penalty methods, the Gulf Stream detachment is correctly represented in a 1/8 degree simulation. This opens the door to a clear improvement of climate models in which a good representation of this mechanism is essential. Following this work, Antoine Nasser started his PhD in October 2019 on penalization methods. One of the objectives is to study the representation of overflows in global ocean model. The NEMO ocean model will be used for the applications.
In the context of the H2020 IMMERSE project, the AIRSEA team is in charge of the development of a new time stepping strategy for the NEMO ocean model. The team also studies the use of exponential time integrators (54 (submitted to Applied Numerical Mathematics) and 4) for ocean models.
|
|
|
|
| penalized |
|
|
|
| AVISO |
|
8.1.2 Coupling Methods for Oceanic and Atmospheric Models and Representation of the Air-Sea Interface
Participants: Eric Blayo, Florian Lemarié, Sophie Thery, Simon Clément.
The Airsea team is involved in the modeling and algorithmic aspects of ocean-atmosphere (OA) coupling. For the last few years we have been actively working on the analysis of such coupling both in terms of its continuous and numerical formulation 74, 23. Our activities can be divided into three general topics-
Continuous and discrete analysis of Schwarz algorithms for OA coupling: we have been developing coupling approaches for several years, based on so-called Schwarz algorithms. Schwarz-like domain decomposition methods are very popular in mathematics, computational sciences and engineering notably for the implementation of coupling strategies. However, for complex applications (like in OA coupling) it is challenging to have an a priori knowledge of the convergence properties of such methods. Indeed coupled problems arising in Earth system modeling often exhibit sharp turbulent boundary layers whose parameterizations lead to peculiar transmission conditions and diffusion coefficients. In the framework of S. Thery PhD (defended in February 2021) the well-posedness of the non-linear coupling problem including parameterizations has been addressed and a detailed continuous analysis of the convergence properties of the Schwarz methods has been pursued to entangle the impact of the different parameters at play in such coupling problem 30, 18. In S. Clement PhD, a general framework has been proposed to study the convergence properties at a (semi)-discrete level to allow a systematic comparison with the results obtained from the continuous problem 36. Such framework allows to study more complex coupling problems whose formulation is representative of the discretization used in realistic coupled models 60.
Within the COCOA project, a Schwarz-like iterative method has been applied in a state-of-the-art Earth-System model to evaluate the consequences of inaccuracies in the usual ad-hoc ocean-atmosphere coupling algorithms used in realistic models 14, 43. Numerical results obtained with an iterative process show large differences at sunrise and sunset compared to usual ad-hoc algorithms thus showing that synchrony errors inherent to ad-hoc coupling methods can be significant. The objective now is to reduce the computational cost of Schwarz algorithms using deep learning techniques.
-
Representation of the air-sea interface in coupled models: During the PhD-thesis of Charles Pelletier the scope was on including the formulation of physical parameterizations in the theoretical analysis of the coupling, in particular the parameterization schemes to compute air-sea fluxes. Following this work, a novel and rigorous framework for a consistent two-sided modeling of the surface boundary layer has been proposed 15. This framework allows for a more general representation of the vertical physics at the air-sea interface while improving the mathematical regularity of the numerical solutions. Moreover, it is flexible enough to include additional physical parameters for example to account for the effect of surface waves in the turbulent flux computation. This work is the first step toward more adequate discretization methods for the parameterization of surface and planetary boundary layers in coupled models.
At a more fundamental level, in collaboration with A. Wirth, we have studied turbulent fluctuations in a coupled Ekman layer problem with randomized drag coefficient 20.
- A simplified atmospheric boundary layer model for oceanic purposes: Part of our activities within the IMMERSE and SHOM 19CP07 projects is dedicated to the development of a simplified model of the marine atmospheric boundary layer (called ABL1d) of intermediate complexity between a bulk parameterization and a full three-dimensional atmospheric model and to its integration to the NEMO general circulation model 11. A constraint in the conception of such a simplified model is to allow an apt representation of the downward momentum mixing mechanism and partial re-energization of the ocean by the atmosphere while keeping the computational efficiency and flexibility inherent to ocean only modeling. Realistic applications of the coupled NEMO-ABL1d modeling system have been carried out 5. The next step is to find adequate ways to fill some gaps in the 1D approach either using multiple scales asymptotic techniques or by casting the equations in terms of perturbations around an ambient state given by a large-scale dataset.
These topics are addressed through strong collaborations between the applied mathematicians and the climate and operational community (Meteo-France, Ifremer, SHOM, Mercator-Ocean, LMD, and LOCEAN). Our work on ocean-atmosphere coupling has steadily matured over the last few years and has reached a point where it triggers interest from the physicists. Through the funding of the projects ANR COCOA (2017-2021, PI: E. Blayo) and SHOM 19CP07 (2020-2024, PI: F. Lemarié), Airsea team members play a major role in the structuration of a multi-disciplinary scientific community working on ocean-atmosphere coupling spanning a broad range from mathematical theory to practical implementations in climate and operational models.
8.1.3 Physics-Dynamics coupling: Consistent subgrid-scale modeling
Participants: Florian Lemarié, Manolis Perrot, Simon Clement.
During the year 2021, the AIRSEA team has started to work on new topics around physics-dynamics coupling 66. Schematically, numerical models consist of two blocks generally identified as “physics” and “dynamics” which are often developed separately. The “Physics” represents unresolved or under-resolved processes with typical scales below model resolution while the “dynamics” corresponds to a discrete representation in space and time of resolved processes. Unresolved processes cannot be ignored because they directly influence the resolved part of the flow since energy is continuously transferred between scales. The interplay between resolved and unresolved scales is a large, incomplete and complex topic for which there is still much to do within the Earth system modeling community 24.In current models, the scale separation between the resolved part of the flow and the unresolved part is carried out via the Reynolds decomposition which corresponds to a filtering of the Navier-Stokes equations. Such a filtering leads to an evolution equation for the large-scale flow containing unknown terms (often called Reynolds stress terms) which represent the average contribution of the small-scale processes. The system is closed by so-called parameterizations that arbitrarily relate the contribution of small-scale processes to large-scale variables. In this context, the AIRSEA team has started work on two aspects:
- Energetically consistent discretization of boundary layer parameterizations Part of S. Clement's thesis is about the discretization of boundary layer parameterizations. The problem of interest takes the form of an nonstationary nonlinear parabolic equation. The objective is to derive a discretization for which we could prove nonlinear stability criteria and show robustness to large variations in parabolic Courant number while being consistent with our knowledge of the underlying physical principles (e.g. the Monin-Obukhov theory in the surface layer).
- Representation of penetrative convection in oceanic models Accounting for the mean effect of subgrid scale intermittent coherent structures like convective plumes is very challenging. Currently this is done very crudely in ocean models (vertical diffusion is locally increased to ’mix’ unstable density profiles). A difficulty is that in convective conditions, turbulent fluxes are dominated by processes unrelated to local gradients thus invalidating the usual downgradient approach (a.k.a. Boussinesq Hypothesis). In the framework of the PhD of Manolis Perrot a first step is to study the derivation of mass-flux convection schemes, popular in atmospheric models, to extend them specifically to the oceanic context. This extension to the oceanic context will be carried out under certain "consistency" constraints: energetic considerations, scale-awareness and well-posedness of the resulting model. In a second step, reference LES simulations will be developed to guide the formulation of unknown/uncertain terms in the extended mass-flux scheme.
Those topics are addressed through collaborations with the climate and operational community (Meteo-France, SHOM, Mercator-Ocean, and IGE). Two projects are currently funded, one on the energetically consistent discretization aspect (SHOM 19CP07, 2020-2024, PI: F. Lemarié) and one on the convection parameterization (Institut des Mathématiques pour la Planètre Terre, 2021-2024, PIs: F. Lemarié and G. Madec).
8.1.4 Nonhydrostatic Modeling
Participant: Eric Blayo, Laurent Debreu, Emilie Duval.
In the context of the French initiative CROCO (Coastal and Regional Ocean COmmunity model, www.croco-ocean.org) for the development of a new oceanic modeling system, Emilie Duval is working on the design of methods to couple local nonhydrostatic models to larger scale hydrostatic ones (PhD started in Oct. 2018). Such a coupling is quite delicate from a mathematical point of view, due to the different nature of hydrostatic and nonhydrostatic equations (where the vertical velocity is either a diagnostic or a prognostic variable). A thorough analysis of the different families of waves that can be present in these equations was performed. Moreover a decomposition of the solutions into vertical modes, which is quite usual in the hydrostatic case, has been generalized in the nonhydrostatic case, which could be an interesting lead for coupling algorithms. A prototype has been implemented, which allows for analytical solutions in simplified configurations and makes it possible to test different numerical approaches.
8.1.5 Machine learning for reconstruction of model parameters.
Participants: Laurent Debreu, Eugene Kazantsev, Arthur Vidard, Olivier Zahm.
Artificial intelligence and machine learning may be considered as a potential way to address unresolved model scales and to approximate poorly known processes such as dissipation that occurs essentially at small scales. In order to understand the possibility to combine numerical model and neural network learned with the aid of external data, we develop a network generation and learning algorithm and use it to approximate nonlinear model operators.
A potential way to reconstruct subgrid scales consists in application the Image Super-Resolution methods that refer to the process of recovering high-resolution images from low-resolution image in computer vision and image processing. Recent years have shown remarkable progress of image super-resolution using machine learning techniques 84. We try to use this methodology in order to identify fine structure of the chaotic turbulent solution of a simple barotropic ocean model. After the learning the flow patterns obtained by the high resolution model, the neuron net can identify fine structure in the low-resolution model solution with better precision than bicubic interpolation.
Different techniques of neuron net construction have been analyzed. Full-connected networks, basic convolutional and encoder-decoder processes 72 as well as mixed architectures were compared with each other and with the classical interpolation of model solution on a low-resolution grid.
8.2 Assimilation of spatially dense observations
Participant: Elise Arnaud, Arthur Vidard, Emilie Rouzies.
8.2.1 Direct assimilation of image sequences
At the present time the observation of Earth from space is done by more than thirty satellites. These platforms provide two kinds of observational information:
- Eulerian information as radiance measurements: the radiative properties of the earth and its fluid envelops. These data can be plugged into numerical models by solving some inverse problems.
- Lagrangian information: the movement of fronts and vortices give information on the dynamics of the fluid. Presently this information is scarcely used in meteorology by following small cumulus clouds and using them as Lagrangian tracers, but the selection of these clouds must be done by hand and the altitude of the selected clouds must be known. This is done by using the temperature of the top of the cloud.
Our current developments are targeted at the use of learning methods methods to describe the evolution of the images. This approach is being applied to the tracking of oceanic oil spills in the framework of a Long Li's Phd in co-supervision with Jianwei Ma. It led to the publication of 12 . In parallel, we investigated the same problem in the framework of pesticide transfer 27
8.2.2 Observation error representation
Accounting for realistic observations errors is a known bottleneck in data assimilation, because dealing with error correlations is complex. Following a previous study on this subject, we propose to use multiscale modelling, more precisely wavelet transform, to address this question. In 59 we investigate the problem further by addressing two issues arising in real-life data assimilation: how to deal with partially missing data (e.g., concealed by an obstacle between the sensor and the observed system); how to solve convergence issues associated to complex observation error covariance matrices? Two adjustments relying on wavelets modelling are proposed to deal with those, and offer significant improvements. The first one consists in adjusting the variance coefficients in the frequency domain to account for masked information. The second one consists in a gradual assimilation of frequencies. Both of these fully rely on the multiscale properties associated with wavelet covariance modelling.
This kind of work was put to application in a collaboration with colleagues of LGGE and led to the publication of 10
In the meantime, STORM, a new collaborative project with Université de La Réunion started this year 53. Our role is to prepare for the assimilation of data collected by sea turtles., and in particular work on the description of observation error statistics.
8.3 Model reduction / multiscale algorithms
8.3.1 Parameter space dimension reduction and Model order reduction
Participants: Arthur Macherey, Youssef Marzouk, Clémentine Prieur, Alessio Spantini, Ricardo Baptista, Daniele Bigoni, Olivier Zahm.
Numerical models describing the evolution of the system (ocean + atmosphere) or any numerical models describing the evolution of a complex dynamical system (e.g., the evolution of a pandemic) contain a large number of parameters which are generally poorly known. The reliability of the numerical simulations strongly depends on the identification and calibration of these parameters from observed data. In this context, it seems important to understand the kinds of low-dimensional structure that may be present in geophysical models and to exploit this low-dimensional structure with appropriate algorithms. We focus in the team, on parameter space dimension reduction techniques, reduced bases, low-rank structures and transport maps techniques for probability measure approximation.
In 34 we introduce a method for the nonlinear dimension reduction of a high-dimensional function , . Our objective is to identify a nonlinear feature map , with a prescribed intermediate dimension , so that can be well approximated by for some profile function . We propose to build the feature map by aligning the Jacobian with the gradient , and we theoretically analyze the properties of the resulting . Once is built, we construct by solving a gradient-enhanced least squares problem. Our practical algorithm makes use of a sample and builds both and on adaptive downward-closed polynomial spaces, using cross validation to avoid overfitting. We numerically evaluate the performance of our algorithm across different benchmarks, and explore the impact of the intermediate dimension . We show that building a nonlinear feature map can permit more accurate approximation of than a linear , for the same input data set. This work was conducted in the framework of the Inria associate team UNQUESTIONABLE, in collaboration with Youssef Marzouk (MIT, US).
In 37 we present a novel offline-online method to mitigate the computational burden of the characterization of conditional beliefs in statistical learning. In the offline phase, the proposed method learns the joint law of the belief random variables and the observational random variables in the tensor-train (TT) format. In the online phase, it utilizes the resulting order-preserving conditional transport map to issue real-time characterization of the conditional beliefs given new observed information. Compared with the state-of-the-art normalizing flows techniques from machine learning, the proposed method relies on function approximation and is equipped with thorough performance analysis. This also allows us to further extend the capability of transport maps in challenging problems with high-dimensional observations and high-dimensional belief variables. On the one hand, we present novel heuristics to reorder and/or reparametrize the variables to enhance the approximation power of TT. On the other, we integrate the TT-based transport maps and the parameter reordering/reparametrization into layered compositions to further improve the performance of the resulting transport maps. We demonstrate the efficiency of the proposed method on various statistical learning tasks in ordinary differential equations (ODEs) and partial differential equations (PDEs).
Undirected probabilistic graphical models represent the conditional dependencies, or Markov properties, of a collection of random variables. Knowing the sparsity of such a graphical model is valuable for modeling multivariate distributions and for efficiently performing inference. While the problem of learning graph structure from data has been studied extensively for certain parametric families of distributions, most existing methods fail to consistently recover the graph structure for non-Gaussian data. In 32, we propose an algorithm for learning the Markov structure of continuous and non-Gaussian distributions. To characterize conditional independence, we introduce a score based on integrated Hessian information from the joint log-density, and we prove that this score upper bounds the conditional mutual information for a general class of distributions. To compute the score, our algorithm SING estimates the density using a deterministic coupling, induced by a triangular transport map, and iteratively exploits sparse structure in the map to reveal sparsity in the graph. For certain non-Gaussian datasets, we show that our algorithm recovers the graph structure even with a biased approximation to the density. Among other examples, we apply sing to learn the dependencies between the states of a chaotic dynamical system with local interactions.
In a joint work 44 with Didier Georges (GIPSA Lab, Grenoble) and Mathieu Oliver (internship student), we proposed a spatialized extension of a SIR model that accounts for undetected infections and recoveries as well as the load on hospital services. The spatialized compartmental model we introduced is governed by a set of partial differential equations (PDEs) defined on a spatial domain with complex boundary. We proposed to solve the set of PDEs defining our model by using a meshless numerical method based on a finite difference scheme in which the spatial operators were approximated by using radial basis functions. Then we calibrated our model on the French department of Isère during the first period of lockdown, using daily reports of hospital occupancy in France. Our methodology allowed to simulate the spread of Covid-19 pandemic at a departmental level, and for each compartment. However, the simulation cost prevented from online short-term forecast. Therefore, we proposed to rely on reduced order modeling tools to compute short-term forecasts of infection number. The strategy consisted in learning a time-dependent reduced order model with few compartments from a collection of evaluations of our spatialized detailed model, varying initial conditions and parameter values. A set of reduced bases was learnt in an offline phase while the projection on each reduced basis and the selection of the best projection was performed online, allowing short-term forecast of the global number of infected individuals in the department.
In the framework of Arthur Macherey’s PhD (defended in June 2021), in collaboration with Anthony Nouy and Marie Billaud-Friess (Ecole Centrale Nantes), we have proposed algorithms for solving high-dimensional Partial Differential Equations (PDEs) that combine a probabilistic interpretation of PDEs, through Feynman-Kac representation, with sparse interpolation 52. Monte-Carlo methods and time-integration schemes are used to estimate pointwise evaluations of the solution of a PDE. We use a sequential control variates algorithm, where control variates are constructed based on successive approximations of the solution of the PDE. We are now interested in solving parametrized PDE with stochastic algorithms in the framework of potentially high dimensional parameter space. A preliminary step was the development of a PAC algorithm in relative precision for bandit problem with costly sampling 35.
Reduced models are also developed In the framework of robust inversion. In 62, we have combined a new greedy algorithm for functional quantization with a Stepwise Uncertainty Reduction strategy to solve a robust inversion problem under functional uncertainties. In a more recent work, we further reduced the number of simulations required to solve the same robust inversion problem, based on Gaussian process meta-modeling on the joint input space of deterministic control parameters and functional uncertain variable 39. These results are applied to automotive depollution. This research axis was conducted in the framework of the Chair OQUAIDO. This research axis is till active in the team through Clément Duhamel’s PhD, in collaboration with Céline Helbert (Ecole Centrale Lyon) and Miguel Munoz Zuniga, Delphine Sinoquet (IFPEN, Rueil Malmaison).
8.4 High performance computing
8.4.1 Variational data assimilation and parallel in time methods
Participants: Rishabh Bhatt, Laurent Debreu, Arthur Vidard.
Rishabh Bhatt started his PhD in December 2019. Under the supervision of Laurent Debreu and Arthur Vidard, he studies the application of time parallelization algorithms to variational data assimilation methods. Thus, at each step of the optimization algorithm, the direct model is integrated by a time-parallel method (here the Parareal algorithm 76). One of the main difficulties lies in the choice of the stopping criterion of the Parareal algorithm. To do so, we rely on theoretical results on the convergence of conjugate gradient methods in the presence of approximate gradient calculations 65. The first results are encouraging and show the possibility to optimally tune the stopping criterion of the Parareal algorithm (and thus the number of iterations) without affecting the convergence of the conjugate gradient. These results are reported in (33). We are now working on taking better advantage of the coupling of these two iterative methods (conjugate gradient and Parareal), in particular by optimally reusing the Krylov bases of the Krylov Enhanced version of the Parareal algorithm.
8.5 Sensitivity analysis
Participants: Elise Arnaud, Eric Blayo, Laurent Gilquin, Maria Belén Heredia, Adrien Hirvoas, François-Xavier Le Dimet, Henri Mermoz Kouye, Clémentine Prieur, Laurence Viry.
Scientific context
Forecasting geophysical systems require complex models, which sometimes need to be coupled, and which make use of data assimilation. The objective of this project is, for a given output of such a system, to identify the most influential parameters, and to evaluate the effect of uncertainty in input parameters on model output. Existing stochastic tools are not well suited for high dimension problems (in particular time-dependent problems), while deterministic tools are fully applicable but only provide limited information. So the challenge is to gather expertise on one hand on numerical approximation and control of Partial Differential Equations, and on the other hand on stochastic methods for sensitivity analysis, in order to develop and design innovative stochastic solutions to study high dimension models and to propose new hybrid approaches combining the stochastic and deterministic methods. We took part to the writing of a position paper on the futur of sensitivity analysis 17.
8.5.1 Global sensitivity analysis
Participants: Elise Arnaud, Eric Blayo, Laurent Gilquin, Maria Belén Heredia, Adrien Hirvoas, Alexandre Janon, Henri Mermoz Kouye, Clémentine Prieur, Laurence Viry, Arthur Vidard, Emilie Rouzies.
8.5.2 Global sensitivity analysis with dependent inputs
An important challenge for stochastic sensitivity analysis is to develop methodologies which work for dependent inputs. Recently, the Shapley value, from econometrics, was proposed as an alternative to quantify the importance of random input variables to a function. Owen 79 derived Shapley value importance for independent inputs and showed that it is bracketed between two different Sobol' indices. Song et al. 82 recently advocated the use of Shapley value for the case of dependent inputs. In a recent work 78, in collaboration with Art Owen (Standford's University), we showed that Shapley value removes the conceptual problems of functional ANOVA for dependent inputs. We also investigated further the properties of Shapley effects in 71. By the end of 2021, Clémentine Prieur started a collaboration with Elmar Plischke (TU Clausthal, Germany) and Emanuele Borgonovo (Bocconi University, Milan, Italy) to estimate total Sobol’ indices as a measure for variable selection even in the framework of dependent inputs. In particular, it allows to estimate total Sobol’ indices for inputs defined on a non rectangular domain. This setting is of particular interest for applications where the input space is reduced due to physical constraints on the quantity of interest. This last setting was encountered, e.g., in Maria Belén Heredia’s PhD thesis (defended in december, 2020), and analyzed by estimating Shapley effects with a nonparametric procedure based on nearest neighbors 50 (see Section 8.5.4 for more details). In October 2021, Ri Wang has started a PhD, cosupervised by Clémentine Prieur and Véronique Maume-Deschamps (ICJ, Lyon 1) on the estimation of quantile oriented sensitivity indices in the framework of dependent inputs, by means of random forests or other machine learning tools. Ri Wang has received a funding from the Chinese Scientific Council.
8.5.3 Iterative estimation of Sobol’ indices
Participants: Elise Arnaud, Laurent Gilquin, Clémentine Prieur.
In the field of sensitivity analysis, Sobol’ indices are widely used to assess the importance of the inputs of a model to its output. Among the methods that estimate these indices, the replication procedure is noteworthy for its efficient cost. A practical problem is how many model evaluations must be performed to guarantee a sufficient precision on the Sobol’ estimates. We proposed to tackle this issue by rendering the replication procedure iterative 7. The idea is to enable the addition of new model evaluations to progressively increase the accuracy of the estimates. These evaluations are done at points located in under-explored regions of the experimental designs, but preserving their characteristics. The key feature of this approach is the construction of nested space-filling designs. For the estimation of first-order indices, a nested Latin hypercube design is used. For the estimation of closed second-order indices, two constructions of a nested orthogonal array design are proposed. Regularity and uniformity properties of the nested designs are studied.
8.5.4 Green sensitivity for multivariate and functional outputs
Participants: María Belén Heredia, Clémentine Prieur.
Another research direction for global SA algorithm starts with the report that most of the algorithms to compute sensitivity measures require special sampling schemes or additional model evaluations so that available data from previous model runs (e.g., from an uncertainty analysis based on Latin Hypercube Sampling) cannot be reused. One challenging task for estimating global sensitivity measures consists in recycling an available finite set of input/output data. Green sensitivity, by recycling, avoids wasting. These given data have been discussed, e.g., in 80, 81. Most of the given data procedures depend on parameters (number of bins, truncation argument…) not easy to calibrate with a bias-variance compromise perspective. Adaptive selection of these parameters remains a challenging issue for most of these given-data algorithms. In the context of María Belén Heredia’s PhD thesis, we have proposed 3 a non-parametric given data estimator for aggregated Sobol’ indices, introduced in 73 and further developed in 64 for multivariate or functional outputs. We also introduced aggregated Shapley effects and we have extended a nearest neighbor estimation procedure to estimate these indices 50. We also started a collaboration with Sébastien Da Veiga (Safran Tech), Agnès Lagnoux, Thierry Klein and Fabrice Gamboa (Institut de Mathématiques de Toulouse) on a new nonparametric estimation procedure for closed Sobol’ indices of any order based on degenerate U-statistics.
8.5.5 Global sensitivity analysis for parametrized stochastic differential equations
Participants: Henri Mermoz Kouye, Clémentine Prieur.
Many models are stochastic in nature, and some of them may be driven by parametrized stochastic differential equations (SDE). It is important for applications to propose a strategy to perform global sensitivity analysis (GSA) for such models, in presence of uncertainties on the parameters. In collaboration with Pierre Etoré (DATA department in Grenoble), Clémentine Prieur proposed an approach based on Feynman-Kac formulas 63. The research on GSA for stochastic simulators is still ongoing, first in the context of the MATH-AmSud project FANTASTIC (Statistical inFerence and sensitivity ANalysis for models described by sTochASTIC differential equations) with Chile and Uruguay, secondly through the PhD thesis of Henri Mermoz Kouye, co-supervised by Clémentine Prieur, in collaboration with Gildas Mazo and Eliza Vergu (INRAE, département MIA, Jouy). Note that our recent developments with P. Etoré on GSA for parametrized SDEs and are strongly related to reduced order modeling (see Section 8.3), as GSA requires jose leon intensive computations of the quantity of interest. In collaboration with Pierre Etoré and Joël Andrepont (master internship started in spring 2021), Clémentine Prieur is working on GSA for parametrized SDEs based on Fokker-Planck equation and kernel based sensitivity indices. Note that a joint work between Pierre Etoré, Clémentine Prieur and Jose R. Leon has been submitted, related to exact or approximated computation of Kolmogorov hypoelliptic equations (KHE). Even if not dealing with GSA, it could be a starting point for analyzing sensitivity for models described by a parametrized version of KHE. Concerning Henri Mermoz Kouye’s PhD thesis, the approach is different. We are interested in GSA for compartmental stochastic models. Our methodology relies on a deterministic representation of continuous time Markov chains stochastic compartmental models.
8.5.6 Sensitivity analysis in pesticide transfer models
Participants: Arthur Vidard, Emilie Rouzies, Katarina Radisic.
Pesticide transfer models are valuable tools to predict and prevent pollution of water bodies. However, using such models in operational contexts requires a strong knowledge of their structure including influential parameters. This project aims at performing global sensitivity analysis (GSA) of the PESHMELBA model (pesticide and hydrology: modelling at the catchment scale). This work is made hard due to the modular, complex structure of the model that couples different physical processes. It results in a large input space dimension and a high computational cost that limits the number of available runs. Using classical GSA tools such as Sobol' indices is thus not feasible. In order to circumvent those limitations, we also explored alternative techniques such as HSIC dependence measure or Random Forest metamodel. The use of such methods in the specific context of spatially distributed output was presented in 28 and submitted in a journal paper 46. We extended this work to spatiotemporal output, as presented in 25.
To conclude Section 8.5, let us mention that Clémentine Prieur took part to the writing on a monography on recent trends in sensitivity analysis, which appeared by the end of 2021 29.
8.6 Model calibration and statistical inference
Participants: Maria Belén Heredia, Adrien Hirvoas, Clémentine Prieur, Victor Trappler, Arthur Vidard, Elise Arnaud, Laurent Debreu.
8.6.1 Bayesian calibration
Physically-based avalanche propagation models must still be locally calibrated to provide robust predictions, e.g. in long-term forecasting and subsequent risk assessment. Friction parameters cannot be measured directly and need to be estimated from observations. Rich and diverse data is now increasingly available from test-sites, but for measurements made along ow propagation, potential autocorrelation should be explicitly accounted for. In the context of María Belén Heredia’s PhD, in collaboration with IRSTEA Grenoble, we have proposed in 68 a comprehensive Bayesian calibration and statistical model selection framework with application to an avalanche sliding block model with the standard Voellmy friction law and high rate photogrammetric images. An avalanche released at the Lautaret test-site and a synthetic data set based on the avalanche were used to test the approach. Results have demonstrated i) the efficiency of the proposed calibration scheme, and ii) that including autocorrelation in the statistical modelling definitely improves the accuracy of both parameter estimation and velocity predictions. In the context of the energy transition, wind power generation is developing rapidly in France and worldwide. Research and innovation on wind resource characterisation, turbin control, coupled mechanical modelling of wind systems or technological development of offshore wind turbines floaters are current research topics. In particular, the monitoring and the maintenance of wind turbine is becoming a major issue. Current solutions do not take full advantage of the large amount of data provided by sensors placed on modern wind turbines in production. These data could be advantageously used in order to refine the predictions of production, the life of the structure, the control strategies and the planning of maintenance. In this context, it is interesting to optimally combine production data and numerical models in order to obtain highly reliable models of wind turbines. This process is of interest to many industrial and academic groups and is known in many fields of the industry, including the wind industry, as "digital twin”. The objective of Adrien Hirvoas's PhD work is to develop of data assimilation methodology to build the "digital twin" of an onshore wind turbine. Based on measurements, the data assimilation should allow to reduce the uncertainties of the physical parameters of the numerical model developed during the design phase to obtain a highly reliable model. Various ensemble data assimilation approches are currently under consideration to address the problem. In the context of this work, it is necessary to develop algorithms of identification quantifying and ranking all the uncertainty sources. This work in done in collaboration with IFPEN. A first paper has been accepted for publication 8.
8.6.2 Simulation & Estimation of EPIdemics with Algorithms
Participants: Clémentine Prieur.
Due to the sanitary context, Clémentine Prieur decided to join a working group, SEEPIA Simulation & Estimation of EPIdemics with Algorithms, animated by Didier Georges (Gipsa-lab). A first work has been published 67. An extension of the classical pandemic SIRD model was considered for the regional spread of COVID-19 in France under lockdown strategies. This compartment model divides the infected and the recovered individuals into undetected and detected compartments respectively. By fitting the extended model to the real detected data during the lockdown, an optimization algorithm was used to derive the optimal parameters, the initial condition and the epidemics start date of regions in France. Considering all the age classes together, a network model of the pandemic transport between regions in France was presented on the basis of the regional extended model and was simulated to reveal the transport effect of COVID-19 pandemic after lockdown. Using the the measured values of displacement of people mobilizing between each city, the pandemic network of all cities in France was simulated by using the same model and method as the pandemic network of regions. Finally, a discussion on an integro-differential equation was given and a new model for the network pandemic model of each age was provided. As already mentioned in Section 8.3, Clémentine Prieur went on working on the pandemic, in collaboration with Didier Georges (GIPSA Lab, Grenoble). Both of them supervised the internship of Matthieu Oliver, submitting a work proposing time-dependent reduced order modeling for short-term forecast from a spatialized SIR model 44. Robin Vaudry started in October 2021 a PhD, funded by the CNR research platform MODCOV19, and cosupervised by Clémentine Prieur and Didier Georges. The objective of this PhD is to solve inverse problems related to spatialized and ages structured commpartmental models of COVID19 pandemic.
8.6.3 Non-Parametric statistical inference for Kinetic Diffusions
Participants: Clémentine Prieur, Jose Raphael Leon Ramos.
This research is the subject of a collaboration with Chile and Uruguay. More precisely, we started working with Venezuela. Due to the crisis in Venezuela, our main collaborator on that topic moved to Uruguay.
We are focusing our attention on models derived from the linear Fokker-Planck equation. From a probabilistic viewpoint, these models have received particular attention in recent years, since they are a basic example for hypercoercivity. In fact, even though completely degenerated, these models are hypoelliptic and still verify some properties of coercivity, in a broad sense of the word. Such models often appear in the fields of mechanics, finance and even biology. For such models we believe it appropriate to build statistical non-parametric estimation tools. Initial results have been obtained for the estimation of invariant density, in conditions guaranteeing its existence and unicity 56 and when only partial observational data are available. A paper on the non parametric estimation of the drift has been accepted recently 57 (see Samson et al., 2012, for results for parametric models). As far as the estimation of the diffusion term is concerned, a paper has been accepted 57, in collaboration with J.R. Leon (Montevideo, Uruguay) and P. Cattiaux (Toulouse). Recursive estimators have been also proposed by the same authors in 58, also recently accepted. In a recent collaboration with Adeline Samson from the statistics department in the Lab, we considered adaptive estimation, that is we proposed a data-driven procedure for the choice of the bandwidth parameters.
In 55, we focused on damping Hamiltonian systems under the so-called fluctuation-dissipation condition. Idea in that paper were re-used with applications to neuroscience in 75.
Note that Professor Jose R. Leon (Caracas, Venezuela, Montevideo, Uruguay) was funded by an international Inria Chair, allowing to collaborate further on parameter estimation.
We recently proposed a paper on the use of the Euler scheme for inference purposes, considering reflected diffusions. This paper could be extended to the hypoelliptic framework.
We also have a collaboration with Karine Bertin (Valparaiso, Chile), Nicolas Klutchnikoff (Université Rennes) and Jose R. León (Montevideo, Uruguay) funded by a MATHAMSUD project (2016-2017) and by the LIA/CNRS (2018). We are interested in new adaptive estimators for invariant densities on bounded domains 51, and would like to extend that results to hypo-elliptic diffusions. More recently, in relation with her work on GSA for parametrized SDEs (see Section 8.5.5), Clémentine Prieur is interested in proposing and analyzing theoretical properties of reduced order modeling (see Section 8.3) based on weak formulations of stationary Fokker Planck equations related to hypoelliptic SDEs. This is a collaboration with Pierre Etoré (LJK, département DATA).
8.6.4 Parameter control in presence of uncertainties: robust estimation of bottom friction
Participants: Victor Trappler, Arthur Vidard, Elise Arnaud, Laurent Debreu.
Many physical phenomena are modelled numerically in order to better understand and/or to predict their behaviour. However, some complex and small scale phenomena can not be fully represented in the models. The introduction of ad-hoc correcting terms, can represent these unresolved processes, but they need to be properly estimated.
A good example of this type of problem is the estimation of bottom friction parameters of the ocean floor. This is important because it affects the general circulation. This is particularly the case in coastal areas, especially for its influence on wave breaking. Because of its strong spatial disparity, it is impossible to estimate the bottom friction by direct observation, so it requires to do so indirectly by observing its effects on surface movement. This task is further complicated by the presence of uncertainty in certain other characteristics linking the bottom and the surface (eg boundary conditions). The techniques currently used to adjust these settings are very basic and do not take into account these uncertainties, thereby increasing the error in this estimate.
Classical methods of parameter estimation usually imply the minimisation of an objective function, that measures the error between some observations and the results obtained by a numerical model. In the presence of uncertainties, the minimisation is not straightforward, as the output of the model depends on those uncontrolled inputs and on the control parameter as well. That is why we will aim at minimising the objective function, to get an estimation of the control parameter that is robust to the uncertainties.
The definition of robustness differs depending of the context in which it is used. In this work, two different notions of robustness are considered: robustness by minimising the mean and variance, and robustness based on the distribution of the minimisers of the function. This information on the location of the minimisers is not a novel idea, as it had been applied as a criterion in sequential Bayesian optimisation. However, the constraint of optimality is here relaxed to define a new estimate. To evaluate this estimation, a toy model of a coastal area has been implemented. The control parameter is the bottom friction, upon which classical methods of estimation are applied in a simulation-estimation experiment. The model is then modified to include uncertainties on the boundary conditions in order to apply robust control methods. This was the topic of Victor Trappler's PhD 31.
This work will be continued in two different actions : On the application side, in the framework of an Inrae/Inria collaboration for dealing with pesticide transfer parameterisation, and on the methodological side, in the framework of the joint-lab with ATOS, in order to explore the use of Machine Learning techniques for such problem.
8.7 Modeling and inference for extremes
Participants: Philomène Le Gall, Clémentine Prieur, Patricia Tencaliec.
In 83, we are considering the modeling of precipitation amount with semi-parametric models, modeling both the bulk of the distribution and the tails, but avoiding the arbitrary choice of a threshold. We work in collaboration with Anne-Catherine Favre (LGGE-Lab in Grenoble) and Philippe Naveau (LSCE, Paris).
In the context of Philomène Le Gall’s PhD thesis, we are applying the aforementioned modeling of extreme precipitation with the aim of regionalizing extreme precipitation.
9 Bilateral contracts and grants with industry
Participants: Elise Arnaud, Clément Duhamel, Adrien Hirvoas, Florian Lemarié, Clémentine Prieur.
9.1 Bilateral contracts with industry
- A 5-year contract (started in January 2020) 19CP07 with the Oceanographic and Hydrographic Service of the French Navy (SHOM) on the topic « Analyse numérique pour la réconciliation en espace et en temps des discrétisations des échanges air-mer et leur paramétrisation. Application à des cas simplifiés et réalistes couplés.» (PI: F. Lemarié).
- ATOS. In the context of the French recovery plan, a collaboration with the ATOS group has been launched late 2021. This collaboration will allow to have a total of 5 people working full time over the next two years on topics related to the application of learning methods for ocean atmosphere problems.
- Contract with IFPEN (Institut Français du pétrole et des énergies nouvelles), for the supervision of a PhD (Adrien Hirvoas). Research subject: Development of a data assimilation method for the calibration and continuous update of wind turbines digital twins
- Contract with IFPEN (Institut Français du pétrole et des énergies nouvelles), for the supervision of a PhD (Clément Duhamel) within the framework of IFPEN and Inria strategic partnership. PhD subject: Robust inversion of a computer code under functional uncertainties. Application to the design of floating wind turbines.
- Consortium CIROQUO – Consortium Industrie Recherche pour l’Optimisation et la QUantification d’incertitude pour les données Onéreuses – gathers academical and technological partners to work on problems related to the exploitation of numerical simulators. This Consortium, created in January 2021, is the continuation of the projects DICE, ReDICE and OQUAIDO which respectively covered the periods 2006-2009, 2011-2015 and 2015-2020.
10 Partnerships and cooperations
10.1 International initiatives
Participants: Elise Arnaud, Florian Lemarié, Clémentine Prieur, Patrick Vidard, Olivier Zahm.
10.1.1 Inria associate team not involved in an IIL or an international program
UNQUESTIONABLE
-
Title:
UNQUESTIONABLE
-
Duration:
2018 - 2020 (due to COVID 19 pandemic, the duration was extended at least one year 2018 - 2021)
-
Coordinator:
Clémentine Prieur
-
Partners:
- Aerospace Computational Design Laboratory, Massachusetts Institute of Technology (United States)
-
Inria contact:
Clémentine Prieur
-
Summary:
The ability to understand and predict the behavior of geophysical flows is of greatest importance, due to its strong societal impact. Numerical models are essential to describe the evolution of the system (ocean + atmosphere), and involve a large number of parameters, whose knowledge is sometimes really poor. The reliability of the numerical predictions thus requires a step of parameter identification. The Inria-AIRSEA team has a strong expertise in variational approaches for inverse problems. An alternative is the use of particle filters, whose main advantage is their ability to tackle non-gaussian frameworks. However, particle filters suffer from the curse of dimensionality. The main objective of the collaboration we propose between the Inria-AIRSEA team and the MIT UQ group is the understanding of potential low-dimensional structure underlying geophysical applications, then the exploitation of such structures to extend particle filter to high-dimensional applications. See also team.inria.fr/unquestionable/
10.1.2 Informal International Partners
Clémentine Prieur is PI of MATH-AmSud project 2020-2021 FANTASTIC (Statistical inFerence and sensitivity ANalysis for models described by sTochASTIC differential equations). This project involves Chile (local head Karine Bertin, Universidad de Valparaíso) and Uruguay (local head Jose R. Leon, Universdad de la república de Uruguay, Montevideo).
10.2 European initiatives
10.2.1 FP7 & H2020 projects
IMMERSE
-
Title:
Improving Models for Marine EnviRonment SErvices
-
Duration:
December 2018 - Novembre 2022.
-
Coordinator:
CNRS
-
Partners:
- Alma Mater Studiorum - Universita Di Bologna (Italy)
- Barcelona Supercomputing Center - Centro Nacional de Supercomputacion (Spain)
- Centre National De La Recherche Scientifique Cnrs (France)
- Cerfacs Centre Europeen De Recherche et de Formation Avancee En Calcul Scientifique Societe Civile (France)
- Fondazione Centro Euro-Mediterraneosui Cambiamenti Climatici (Italy)
- Helmholtz Zentrum Fur Ozeanforschung Kiel (Germany)
- Institut De Recherche pour le Developpement (France)
- Plymouth Marine Laboratory Limited (UK)
- Puertos del Estado (Spain)
- United Kingdom Research And Innovation (UK)
- Universiteit Utrecht (Netherlands)
-
Inria contact:
F. Lemarié
-
Summary:
The overarching goal of IMMERSE project is to ensure that the Copernicus Marine Environment Monitoring Service (CMEMS) will have continuing access to world-class marine modelling tools for its next generation systems while leveraging advances in space and information technologies, therefore allowing it to address the ever-increasing and evolving demands for marine monitoring and prediction in the 2020s and beyond.
10.2.2 Other european programs/initiatives
- Program: C3S
- Project acronym: ERGO
- Project title: Enabling an Ensemble of Data Assimilation for the Ocean
- Duration: Février 2019 - juillet 2021
- Coordinator: Arthur Vidard
- Other partners: Cerfacs (France), Met Office (U.K.), CMRE (int, Italie)
- Abstract: The scope of this contract is to improve ocean data assimilation capabilities at ECMWF, used in both initialization of seasonal forecasts and generation of coupled Earth System reanalyses. In particular it shall focus on i) improving ensemble capabilities in NEMO and NEMOVAR and the use of their information to represent background error statistics; ii) extend NEMOVAR capabilities to allow for multiple resolution in multi-incremental 3D-Var; iii) make better use of ocean surface observations. It shall also involve performing scout experiments and providing relevant diagnostics to evaluate the benefit coming from the proposed developments.
10.3 Collaborations with Major European Organizations
- Partner: European Center for Medium Range Weather Forecast. Reading (UK)
- World leading Numerical Weather Center, that include an ocean analysis section in order to provide ocean initial condition for the coupled ocean atmosphere forecast. They play a significant role in the NEMOVAR project in which we are also partner.
- Partner: Met Office (U.K) National British Numerical Weather and Oceanographic service. Exeter (UK).
- We do have a strong collaboration with their ocean initialization team through both our NEMO, NEMO-ASSIM and NEMOVAR activities. They also are our partner in the NEMOVAR consortium.
- Partner : SAMO board
-
SAMO board is in charge of the organization of the SAMO (sensitivity analysis of model outputs) conferences, every three years. It is strongly supported by the Joint Research Center of the European Commission.
In 2019, Clémentine Prieur, which is part of this board, as also co-chair of a satellite event on the future of sensitivity analysis. A position paper 16 has been published in 2021, as a synthesis of the discussions hold in Barcelona (autumn 2019).
10.4 National initiatives
10.4.1 ANR
- A 4.5-year contract: ANR COCOA (COmprehensive Coupling approach for the Ocean and the Atmosphere). PI: E. Blayo. (Jan. 2017 - Sep. 2021). Other partners: Laboratoire des Sciences du Climat et de l'Environnement (UMR8212, Gif-sur-Yvette), Laboratoire de Météorologie Dynamique (UMR8539, Paris), Laboratoire d'Océanographie Physique et Spatiale (UMR6523, Brest), Centre National de Recherche Météorologique (UMR3589, Toulouse), Cerfacs (Toulouse). This project aims at revisiting the overall representation of air-sea interactions in coupled ocean-atmosphere models, and particularly in climate models, by coherently considering physical, mathematical, numerical and algorithmic aspects.
- A 4-year contract: ANR ADOM (Asynchronous Domain decomposition methods) anr.fr/Projet-ANR-18-CE46-0008
- A 5-year contract: ANR MELODY (Bridging geophysics and MachinE Learning for the modeling, simulation and reconstruction of Ocean DYnamic) anr.fr/Projet-ANR-19-CE46-0011
-
A 4-year contract: ANR MODENA, "Model and data reduction for efficient assimilation", PI: Olivier ZAHM The reliability of numerical predictions strongly rely on our ability to calibrate the unknown model parameters using observable data. Data assimilation is a particularly challenging task in ocean modelling because of the complexity of the computational models and because of the high-dimension of both the parameters and the data. The objective of this project is to explore novel methodologies to improve the probabilistic description of the Bayesian solution to inverse problem while, at the same time, taking into consideration the computational limitations imposed by large scale applications. This project relies on three building blocks and on their interplay:
- transport maps as a novel approximation tool of complex probability densities,
- reduced order models to alleviate the computational burden of expensive models and
- dimension reduction to concentrate the computational efforts onto the most relevant directions.
In addition, the proposed methodology addresses key challenges present in many real-world applications and therefore we expect that they can find applications in other domains.
- A 5-year contract with the French Navy (SHOM) on the improvment of the CROCO ocean model www.croco-ocean.org.
- C. Prieur and E. Arnaud are involved as experts in project High-Tune www.agence-nationale-recherche.fr/Projet-ANR-16-CE01-0010 funded by ANR.
10.4.2 Inria Challenge
- Sea Uncertainty Representation and Forecast (SURF),
- Coord : Airsea (A. Vidard),
- Partenaires Inria : Ange, Cardamom, Fluminance, Lemon, Mingus, Defi
- Partenaires extérieurs: BRGM, Ifremer, SHOM
10.4.3 Other Initiatives
- C. Prieur is co-advising the PhD thesis of Henri Mermoz Kouye, in the framework of the Inria-INRA partnership.
- C. Prieur chaired GdR MASCOT NUM 2010-2017, in which are also involved M. Nodet, E. Blayo, C. Helbert, E. Arnaud, L. Viry, S. Nanty, L. Gilquin. She is still strong involved in the group (co-chair). In particular, she will co-chair next GdR annual meeting in Aussois (May 2020, reported to April 2021). www.gdr-mascotnum.fr/doku.php.
- A 3-year contract (started in Sept 2021) funded by the Institut des Mathématiques pour la Planète Terre (IMPT) on the topic « Modélisation cohérente des échelles sous-maille pour les modèles océaniques de climat » (PI: F. Lemarié).
11 Dissemination
Participants: Elise Arnaud, Eric Blayo, Laurent Debreu, Christine Kazantsev, Florian Lemarié, Clémentine Prieur.
11.1 Promoting scientific activities
11.1.1 Scientific events: selection
Member of the conference program committees
- Clémentine Prieur is a member of the scientific committee of the next international SAMO conference (to be held in 2022 in Florida).
- Clémentine Prieur is a member of the scientific committee of the next international MASCOT NUM conference (to be held in Clermont-Ferrand).
Reviewer
- E. Blayo: reviewer for ANR
11.1.2 Journal
Member of the editorial boards
- Clémentine Prieur is associate editor for Computational and Applied Mathematics journal.
- Clémentine Prieur is associate editor for SIAM/ASA Journal of Uncertainty Quantification journal.
- Clémentine Prieur is a member of the reading committee of Annales Mathématiques Blaise Pascal.
- F. Lemarié is associate editor of the Journal of Advances in Modeling Earth Systems (JAMES)
Reviewer - reviewing activities
- E. Blayo: reviewer for Ocean Modelling, Journal of Scientific Computing
11.1.3 Invited talks
- Clémentine Prieur was invited as plenary speaker of NASPDE 2020, Numerical Analysis of Stochastic PDEs, CIRM, Luminy (France), November, 5-6, 2020 (reported to November, 4-5, 2021).
- Clémentine Prieur was invited as plenary speaker of the 3th International Workshop on Rare-Event Simulation, Paris (France), May, 26-29, 2020 (reported to May, 18-21, 2021)
- Clémentine Prieur was invited as plenary speaker of the 18th International Workshop on Quality Improvements Methods, Dortmund (Germany), June 26-27, 2020 (cancelled).
- Clémentine Prieur was invited as plenary speaker of the SWGEN 2020 Conference on Stochastic Weather Generators, Lyon (France), June 17-19, 2020 (cancelled).
- F. Lemarié: école IMPT impacts morphologiques du changement climatique, Lyon, Nov. 2021 24
- F. Lemarié: 16th U.S. National Congress on Computational Mechanics, Chicago, Jul. 2021 23
11.1.4 Leadership within the scientific community
- L. Debreu is the chair of the CNRS-INSU research program LEFE-MANU on mathematical and numerical methods for ocean and atmosphere insu.cnrs.fr/fr/methodes-mathematiques-et-numeriques-manu since April 2018.
- F. Lemarié is the co-leader with Mike Bell (UK Met Office) of the NEMO (www.nemo-ocean.eu) Working Group on numerical kernel development.
11.1.5 Scientific expertise
- L. Debreu is a member of the steering committee of the CROCO ocean model www.croco-ocean.org
- F. Lemarié is a member of the CROCO (www.croco-ocean.org) scientific committee in charge of the « numerical methods » topic.
11.1.6 Research administration
- E. Blayo is a deputy director of the Jean Kuntzmann Lab.
- C. Prieur is local correspondant in Grenoble for the Mathematical Society of France (SMF).
- C. Prieur is a member of the MSTIC pole council of UGA.
- C. Prieur is responsible for the applied math speciality for doctoral school MSTII edmstii.univ-grenoble-alpes.fr/
- E. Arnaud is in charge of the AMAC (Algorithmes, Modeles, Analyses, Calcul) department of the Jean Kuntzmann Lab.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Licence (ou équivalent) : E. Arnaud, Mathematics for engineers, 20h, L2, UGA, France
- Licence (ou équivalent) : E. Blayo, Mathematical analysis, 105h, L1, University Grenoble Alpes, France
- Licence (ou équivalent) : C. Kazantsev, Mathématiques approfondies pour l'ingénieur, 72h, L2, UGA, France
- Licence (ou équivalent) : C. Kazantsev, Mathématiques pour les sciences de l'ingénieur, 81h, L2, UGA, France
- Master (ou équivalent) : E. Arnaud, Statistics, 30h, M1, UGA, France
- Master (ou équivalent) : E. Arnaud, Supervision of student in apprenticeship, 30h, M2, UGA, France
- Master (ou équivalent) : E. Blayo, Partial Differential Equations, 45h, M1, University Grenoble Alpes, France
- E-learning : Mooc Inria Impacts environnementaux du numérique : E. Blayo, "La modélisation numérique, un outil devenu central pour l'environnement"
- E-learning : E. Arnaud is in charge of the pedagogic platform math@uga : implementation of a collaborative moodle platform math.u-ga.fr to share pedagogical resources within teachers and towards students.
11.2.2 Supervision
- PhD: Victor Trappler, Parameter control in presence of uncertainties, Université Grenoble-Alpes, defended June 11th 2021, E. Arnaud, L. Debreu and A. Vidard. 31
- PhD: Sophie Théry, Numerical study of ocean-atmosphere coupling algorithms with boundary layer parameterizations, Université Grenoble Alpes, 10 February 2021, E. Blayo and F. Lemarié.30
- PhD: Arthur Macherey, Uncertainty quantification methods for models described by stochastic differential equations or partial differential equations with a probabilistic interpretation, June, 2021, M. Billaud-Friess, A. Nouy (Ecole Centrale Nantes), C. Prieur 77
- PhD: Adrien Hirvoas, Development of a data assimilation method for the calibration and continuous update of wind turbines digital twins, March, 2021, E. Arnaud, C. Prieur, promoted by F. Caleyron (IFPEN) 70
- PhD in progress : Emilie Duval, Coupling hydrostatic and nonhydrostatic ocean circulation models. October 2018, L. Debreu and E. Blayo.
- PhD in progress : Antoine Nasser, Volume penalization methods for the representation of flows along topography in 3D ocean models, October 2019, L. Debreu and G. Madec.
- PhD in progress : Rishabh Bhatt, Asynchronousparallel in time schemes for data assimilation, December 2019, L. Debreu and A. Vidard.
- PhD in progress: Emilie Rouziès, Assimilation of multi-source data in a pesticide transfer model in a small agricultural watershed, Université Grenoble-Alpes, December 2019, C. Lauvernet (Inrae) and A. Vidard.
- PhD in progress: Katarina Radisic, Prise en compte d'incertitudes externes dans l'estimation de paramètres d'un modèle de transfert d'eau et de pesticides à l'échelle du bassin versant, Université Grenoble-Alpes December 2021, C. Lauvernet (Inrae) and A. Vidard.
- PhD in progress: Simon Clément, Numerical analysis for reconciling in space and time the air-sea exchanges and their parameterization. October 2019, E. Blayo and F. Lemarié.
- PhD in progress: Manolis Perrot, Consistent subgrid scale modeling for oceanic climate models. October 2021, E. Blayo and F. Lemarié.
- PhD in progress : Ri Wang, Apprentissage statistique pour l'analyse de sensibilité globale avec entrées dépendantes, October 2021, V. Maume-Deschamps (Université Lyon 1), C. Prieur.
- PhD in progress : Robin Vaudry, Analyse de Sensibilité, quantification d'incerTitudes et calibRAtion pour des modèles épidémioloGiques structurés, October 2021, D. Georges (Grenoble INP), C. Prieur.
- PhD in progress : Clément Duhamel, Inversion robuste d'un code de calcul prenant en entrées des données de nature fonctionnelle. Application à la conception d'éoliennes, October 2020, C. Helbert (Ecole Centrale Lyon), C. Prieur, promoted by M. Munoz Zuniga, D. Sinoquet (IFPEN)
- PhD in progress : Henri Mermoz Kouye, Analyse de sensibilité basée sur les indices de Sobol' pour modèles à sorties stochastiques et fonctionnelles, Octobre 2019, G. Mazo, E. Vergu (INRAE, MIA, Jouy), C. Prieur
- PhD in progress : Qiao CHEN, Low-dimensional structure of ocean data assimilation problems via gradient information, Octobre 2020 (encadrement : Olivier ZAHM et Élise Arnaud)
- PhD in progress : Rafael Floch, Dimension reduction of large-scale linear Bayesian inverse problems, Octobre 2020 (encadrement : Olivier ZAHM et Yiqiu DONG)
- Post Doc : Anass El Aouni, Multi-resolution techniques for ocean data assimilation, October 2019, October 2021, A. Vidard
11.2.3 Juries
- E. Blayo:
- Jan. 12, 2021: PhD thesis of Dimitri Mottet, Institut National Polytechnique de Toulouse (reporter)
- Mar. 30, 2021: PhD thesis of Adrien Hirvoas, University Grenoble Alpes (president)
- May 4, 2021: HDR thesis of Julien Le Sommer, University Grenoble Alpes (examiner)
- Jun. 22, 2021: PhD thesis of Cyril Bozonnet, University Grenoble Alpes (president)
- Dec. 7, 2021: PhD thesis of Meryl Wimmer, Université Toulouse III Paul Sabatier (reporter)
- Dec. 13, 2021: PhD thesis of Camille Besombes, Institut National Polytechnique de Toulouse (reporter)
- C. Prieur is the president of the jury of Prix de thèse AMIES (2020-…).
- E. Arnaud : participation to the PhD committee of Emilie Rouziès, UGA INRAE.
11.3 Popularization
11.3.1 Internal or external Inria responsibilities
- F. Lemarié is a member of the local "comité des emplois scientifiques" (CES) (since Sept 2019)
- F. Lemarié is the local scientific correspondent for national calls for projects (since July 2020)
- E. Arnaud : member of Inria PhD recruitment committee CORDI-S
- E. Arnaud : in charge of ATER recruitment committee in computer science of UFR IM2AG, UGA
- E. Arnaud : in charge of the parity commission at Jean Kuntzmann Lab
- E.Kazantsev is a member of the Local Commission for Permanent Formation of Inria Grenoble - Rhône-Alpes.
- F. Lemarié gave a talk at the "Parlons Europe s01e07" internal meeting.
11.3.2 Articles and contents
- Clémentine Prieur took part to a webcast on The Future of Sensitivity Analysis for Systems Modelling and Policy Support www.youtube.com
- Clémentine Prieur gave interviews as a CNRS expert (Figaro, Hoffpost, RCF) on the evolution of COVID19 pandemic.
- C. Prieur was placed on a list of experts who could answer questions on various aspects of the news related to the ongoing Covid-19 epidemic by the CNRS press office. This list is made available to journalists in order to direct them to the appropriate interlocutors according to the angle of their questions.
11.3.3 Education
- C. Kazantsev and E. Blayo are strongly involved in the creation and dissemination of pedagogic suitcases with mathematical activities designed for primary and secondary schools used by about 4,000 pupils in 2020-2021, despite the sanatory crisis. This is done in collaboration with the Rectorat de Grenoble.
- C. Kazantsev is a member of an IREM group for creation of scientific activities for professional development of secondary schools teachers.
- C. Kazantsev is a member of an International Inter-IREM commission, which work on the multi-languages problem for children in the mathematical learning. Three meetings take place in Paris during the year, the first was on October 2. Last year, most of them were on visioconference.
11.3.4 Creation of media or tools for science outreach
- C. Kazantsev participated in the edition of the Teachers notebooks which explain and advise how to use the "La Grange Suitcases" (sets of mathematical games, problems and animations) destined for primary and secondary schools teachers as well as for the general public.
- C. Kazantsev participated in the creation of mathematical activities that can be autonomously used by schoolchildren of primary and secondary schools and by the general public.
- C. Kazantsev participated in the creation of a mathematical serious game that can be played by schoolchildren of secondary schools and by the general public. See www.la-grange-des-maths.fr/mission-exoplanetes/
- C. Kazantsev participated in the creation of a mathematical exposition on Johannes Kepler : "Kepler, les maths pour décrire le monde", in colaboration with Jean-Louis Hodeau, a cristallograph of the Neel Institut and CNRS (Grenoble, France). This exposition was visited on the fête de la science by schoolchildren of secondary schools and by the general public.
- C. Kazantsev had encadred a group of seven students of Télécom SudParis high school for a project named "Learn By Play". They created a game "Math'Venture" with ten mathematical challenges. See www.la-grange-des-maths.fr/mathventure
11.3.5 Interventions
- E. Blayo gave several outreach talks, in particular for middle school and high school students, and for more general audiences.
- Clémentine Prieur was invited to give a training at Ecole Thématique sur les Incertitudes en Calcul Scientifique (ETICS) 2021, Sept. 12-17, 2021, Erdeven (France).
- Clémentine Prieur was invited to give a training at the 8th edition of the research school organized by the CNRS research group EGRIN (Ecoulements Gravitaires et RIsques Naturels), June 29-July 02, 2020, Nouan-le-Fuzelier (reported to May, 27-28, 2021 as a virtual event).
- C. Kazantsev and E. Blayo are strongly involved in the creation of "La Grange des maths", a science popularization center that will be located in Varces (south of Grenoble), which will offer a huge variety of mathematical hands-on exhibits. See www.la-grange-des-maths.fr
- C. Kazantsev participated to the Fête de la Science with a mathematical exposition on Johannes Kepler : "Kepler, les maths pour décrire le monde" presented in the CNRS - Neel Institut.
- C. Kazantsev participated to the Fête de la Science with a presentation of the activities created by the association "La Grange des Maths".
- E. Arnaud participated to a training day for primary school teachers on critical thinking, oct. 2021
- E. Arnaud has given a seminar "(se) tromper avec les chiffres", at La fête de la sciences, oct. 2021
12 Scientific production
12.1 Publications of the year
International journals
Conferences without proceedings
Scientific books
Doctoral dissertations and habilitation theses
Reports & preprints
Other scientific publications
12.2 Cited publications
- 50 unpublishedAggregated Shapley effects: nearest-neighbor estimation procedure and confidence intervals. Application to snow avalanche modeling.July 2020, working paper or preprint
- 51 articleAdaptive density estimation on bounded domains under mixing conditions.Electronic Journal of Statistics 1412020, 2198-2237
- 52 inproceedingsStochastic methods for solving high-dimensional partial differential equations.International Conference on Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing - MCQMC 2018324Springer Proceedings in Mathematics & StatisticsRennes, FranceSpringerJuly 2018, 125-141
- 53 articleSea Turtles for Ocean Research and Monitoring: Overview and Initial Results of the STORM Project in the Southwest Indian Ocean.Frontiers in Marine Science7October 2020, 594080:1-19
- 54 unpublishedComparaison of Exponential integrators and traditional time integration schemes for the Shallow Water equations.April 2020, working paper or preprint
- 55 articleAn overlook on statistical inference issues for stochastic damping Hamiltonian systems under the fluctuation-dissipation condition.Statistics5112017, 11-29
- 56 articleEstimation for Stochastic Damping Hamiltonian Systems under Partial Observation. I. Invariant density.Stochastic Processes and their Applications1243March 2014, 1236-1260
- 57 articleEstimation for Stochastic Damping Hamiltonian Systems under Partial Observation. II Drift term.ALEA (Latin American Journal of Probability and Statistics)1112014, 359-384
- 58 articleRecursive Estimation for Stochastic Damping Hamiltonian Systems.Journal of Nonparametric Statistics2732015, 401-424
- 59 articleMultiscale Representation of Observation Error Statistics in Data Assimilation.Sensors205March 2020, 1-20
- 60 inproceedingsDiscrete analysis of Schwarz Waveform Relaxation for a simplified air-sea coupling problem with nonlinear transmission conditions.DD26 - 26th International Domain Decomposition ConferenceHong Kong, Hong Kong SAR ChinaDecember 2020
- 61 articleBrinkman volume penalization for bathymetry in three-dimensional ocean models.Ocean Modelling145January 2020, 1-13
- 62 articleData-driven Stochastic Inversion via Functional Quantization.Statistics and Computing303May 2020, 525-541
- 63 articleGlobal sensitivity analysis for models described by stochastic differential equations.Methodology and Computing in Applied Probability22June 2020, 803-831
- 64 articleSensitivity analysis for multidimensional and functional outputs.Electronic Journal of Statistics812014, 575--603
- 65 articleMinimizing convex quadratics with variable precision conjugate gradients.Numerical Linear Algebra with Applications2812021, e2337URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/nla.2337
- 66 articlePhysics--Dynamics Coupling in Weather, Climate, and Earth System Models: Challenges and Recent Progress.Monthly Weather Review14611November 2018, 3505--3544
- 67 articleTransport effect of COVID-19 pandemic in France.Annual Reviews in Control502020, 394-408
- 68 inproceedingsCalibration of the Voellmy avalanche friction parameters using a Bayesian approach from an high rate positioning avalanche.EGU 2018 - European Geosciences Union General AssemblyVienna, AustriaApril 2018
- 69 articleNumerical modeling of hydraulic control, solitary waves and primary instabilities in the Strait of Gibraltar.Ocean Modelling155July 2020, 101642
- 70 phdthesisDevelopment of a data assimilation method for the calibration and continuous update of wind turbines digital twins..Université Grenoble Alpes [2020-....]March 2021
- 71 articleShapley effects for sensitivity analysis with correlated inputs: comparisons with Sobol' indices, numerical estimation and applications.International Journal for Uncertainty Quantification952019, 493-514
-
72
articleMachine learning
computational fluid dynamics.Proceedings of the National Academy of Sciences118212021 - 73 articleMultivariate sensitivity analysis to measure global contribution of input factors in dynamic models.Reliability Engineering & System Safety9642011, 450--459
- 74 inproceedingsAn overview of the ocean-atmosphere coupling.2019 - Physics-Dynamics Coupling in Earth System ModelsBanff, CanadaOctober 2019
- 75 articleHypoelliptic stochastic FitzHugh-Nagumo neuronal model: mixing, up-crossing and estimation of the spike rate.Annals of Applied Probability2017
- 76 articleA "parareal" in time discretization of PDE's.Comptes Rendus de l'Académie des Sciences - Series I - Mathematics3322001, 661--668URL: http://dx.doi.org/10.1016/S0764-4442(00)01793-6
- 77 phdthesisApproximation and model reduction for partial differential equations with probabilistic interpretation.École centrale de NantesJune 2021
- 78 articleOn Shapley value for measuring importance of dependent inputs.SIAM/ASA Journal on Uncertainty Quantification511September 2017, 986--1002
- 79 articleSobol' indices and Shapley value.Journal on Uncertainty Quantification22014, 245--251
- 80 articleAn effective algorithm for computing global sensitivity indices (EASI).Reliability Engineering & System Safety9542010, 354--360
- 81 articleGlobal sensitivity measures from given data.European Journal of Operational Research22632013, 536--550
- 82 techreportShapley Effects for Global Sensitivity Analysis: Theory and Computation.Northwestern University2015
- 83 articleFlexible semiparametric Generalized Pareto modeling of the entire range of rainfall amount.Environmetrics312June 2019, e2582:1-28
- 84 miscDeep Learning for Image Super-resolution: A Survey.2020

