Keywords
Computer Science and Digital Science
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.5. Mathematical modeling for physical sciences
- A6.5.1. Solid mechanics
- A6.5.4. Waves
Other Research Topics and Application Domains
- B3. Environment and planet
- B3.3. Geosciences
- B3.3.1. Earth and subsoil
- B4. Energy
- B5.2. Design and manufacturing
- B5.5. Materials
- B5.7. 3D printing
- B9.2.1. Music, sound
- B9.5.2. Mathematics
- B9.5.3. Physics
1 Team members, visitors, external collaborators
Research Scientists
- Hélène Barucq [Team leader, Inria, Senior Researcher, from Feb 2021, HDR]
- Juliette Chabassier [Inria, Researcher, from Feb 2021]
- Julien Diaz [Inria, Senior Researcher, from Feb 2021, HDR]
- Augustin Ernoult [Inria, Researcher, from Feb 2021]
- Florian Faucher [Inria, Researcher, from Oct 2021]
- Ha Howard Faucher [Inria, Researcher, from Feb 2021]
Faculty Members
- Marc Duruflé [Institut National Polytechnique de Bordeaux, Associate Professor, from Feb 2021]
- Sébastien Tordeux [Univ de Pau et des pays de l'Adour, Associate Professor, from Feb 2021, HDR]
Post-Doctoral Fellows
- Titly Farhana Faisal [Inria, from Feb 2021]
- Pierre Jacquet [Univ de Pau et des pays de l'Adour, from Mar 2021]
- Tobias Van Baarsel [Inria, from Feb 2021]
PhD Students
- Guillaume Castera [Inria, from Feb 2021]
- Ibrahima Djiba [Inria, from Oct 2021]
- Stefano Frambati [TOTAL-Pau, from Feb 2021]
- Arjeta Heta [Univ de Pau et des pays de l'Adour, from Sep 2021]
- Pierre Jacquet [Inria, Feb 2021]
- Augustin Leclerc [INSA Rouen, from Oct 2021]
- Victor Martins Gomes [Univ de Pau et des pays de l'Adour, from Feb 2021]
- Rose Cloe Meyer [Univ de Pau et des pays de l'Adour, from Feb 2021]
- Nathan Rouxelin [Univ de Pau et des pays de l'Adour, from Feb 2021]
- Margot Sirdey [ONERA, from Feb 2021 until May 2021]
- Margot Sirdey [Inria, from Jun 2021]
- Alexis Thibault [Univ de Pau et des pays de l'Adour, from Feb 2021]
- Vinduja Vasanthan [Inria, from Feb 2021]
- Nicolas Victorion [Inria, from Oct 2021]
Technical Staff
- Julien Besset [Inria, Engineer, from Feb 2021]
- Aurelien Citrain [Inria, Engineer, from Feb 2021]
- Olivier Geber [Inria, Engineer, from Feb 2021]
- Mamadou N'Diaye [Inria, Engineer, from Feb 2021 until Aug 2021]
- Chengyi Shen [Inria, Engineer, from Feb 2021]
Interns and Apprentices
- Ibrahima Djiba [Univ de Pau et des pays de l'Adour, from Mar 2021 until Jul 2021]
- Johan Hedman [Inria, from Sep 2021]
- Augustin Leclerc [Inria, from Mar 2021 until Aug 2021]
- Nadezhda Serdiuk [Univ de Pau et des pays de l'Adour, from Mar 2021 until Aug 2021]
Administrative Assistant
- Sylvie Embolla [Inria, from Feb 2021]
External Collaborator
- Florian Faucher [Université de Vienne - Autriche, from Feb 2021 until Sep 2021]
2 Overall objectives
Numerical geosciences encompass a large variety of scientific activities tackling societal challenges like water resources, energy supply, climate change, etc. They are based upon observations, physical modeling and accurate mathematical formulations. The tremendous progresses of scientific computing have allowed the addition of extensive numerical simulations which provide tools based on wave measurements to study and possibly monitor complex environments that are otherwise difficult to probe and even fathomless e.g. the subsurface or the interior of stars. Bridging the gap between experimental measurements and numerical simulations is an important objective of Makutu, which will pursue a balance between accuracy and efficiency depending on the application domains in consideration. A common strategy will be to develop frugal models using mathematical methods (asymptotic methods, artificial boundary conditions, reduction methods…), and efficient numerical schemes (in time and harmonic domains, with analytical and high order numerical methods). Makutu proposes a research program to develop numerical software packages for retrieving shapes and/or physical properties of complex media with a particular focus on the Earth and its natural reservoirs. For this, the team is collaborating with experimental geophysicists from the LFCR (Laboratory of Complex Fluids and their Reservoirs, UPPA) who help to assess the impact of parameters on the wave propagation. In addition to geophysical setting, Makutu's research program includes two other topics: solar imaging and musical acoustics. For solar imaging, modeling is of great importance and the team is working with different equations in a new mathematical formalism. New simulation codes are under development with a long-term view to solve inverse problems. Given the similarities that exist between seismic and solar imaging methods, software development is carried out in-house using many of the skills acquired by the team in geophysical imaging. Regarding modeling of musical instruments, the size of the objects and the wavelengths considered are different from geophysical or solar contexts, but similar physical principles and theoretical aspects of models and numerical methods are applicable. Last but not least, parameter reduction and great precision required in the simulation and the possibility to easily compare numerical and experimental data make them an ideal topic to develop new research related to modeling and simulating wave propagation. To address the above research agenda, the team gathers applied mathematicians and acousticians who have long working experience in wave propagation. The team is jointly shared by the University of Pau and Pays de l’Adour (UPPA) and Inria. The majority of Makutu's members are located in Pau. The team is therefore attached to LMAP (Mathematics and Applications Laboratory in Pau, UMR CNRS 5142). However, some members of the team are located in Talence, in the Inria building of the Bordeaux campus. The choice of Makutu's principal location in Pau is fully justified by the long-term involvement of the city of Pau in Geosciences, which offers an important network of companies working in the geo-resources sector. In particular, the company Total is our main industrial partner with whom we aim at developing activities on energy transition.
3 Research program
Makutu organizes its research program from in-house accurate solution methodologies for simulating wave propagation in realistic scenarios to various applications involving transdisciplinary efforts. Performing simulations of real-world phenomena is an ultimate endeavor by all numerical scientists. To achieve this, one needs real data and advanced mathematical models and high-order numerical schemes that are compatible with high-performance computing architectures.
To obtain real data, in addition to its current collaborations with scientists both from Academia and Industry, Makutu is developing a new branch of research activities by carrying out its own laboratory measurements. The desire to carry out its own measurements is motivated by the need to solve problems whose increasing complexity involves a large number of physical parameters that need to be calibrated. For instance, in order to take into account porosity, parameters such as viscosity, attenuation, thermodynamic effects, etc., must be integrated, and their impact must be properly analyzed before considering using them to characterize the propagation media. This constitutes a clear step ahead for Makutu, and opens up new prospects of contributing to the characterization of very complex media based on wave field measurements.
Regarding the development of numerical schemes, Makutu is developing high-order Discontinuous Galerkin (DG) methods and high-order time schemes. Recently, the team has launched a new research project on space-time integration for seismic waves, in partnership with Total. The coupling of DG methods with other techniques of discretization is also under consideration. Trefftz-DG and Hybridizable DG methods are currently developed both for poro-elastic waves and electromagnetic waves. HDG and HDG+ formulations are also under study for helioseismology.
The research activities of members of Makutu share a common theme of using numerically computed wavefield measurements to reconstruct the propagation medium they passed through before recording. The medium can be reconstructed by identifying either the physical parameters or the geometrical parameters that characterize it. In each case, the next step is to solve an inverse problem that is non-linear and ill-posed. To solve it, Makutu is focusing on the Full Waveform Inversion (FWI), which is a high-definition imaging method widely used in the field of geophysics.
4 Application domains
Makutu research program is organized around three principal domains of applications: geophysical exploration, solar imaging, and music. Each of them requires a relevant panel of significant contributions requiring achievements in laboratory measurements, modeling, mathematical analysis, advanced numerical schemes and massively parallel software development. Experimental research is a new activity that will ensure the team to have its own set of real data in addition to those provided by its partners. Makutu's application domains can be regrouped into a long-standing activity dedicated to subsurface imaging, and two more recent activities dedicated to solar imaging and the development of numerical wind instruments. Each field of application is not compartmentalized in the methodological sense of the term: equations, numerical schemes and programming practices can be shared and then adapted to the application in question.
4.1 Geophysical exploration
Geophysical exploration is a historical field for the team (see e.g 52, 56, 57, 61.Geophysical exploration has been driven for a very long time by the goal of finding hydrocarbons. Today, it is evolving towards a very proactive direction in favor of renewable energies and Makutu commits part of its research activities in this direction. As a powerful tool for mapping the subsurface, seismic imaging is very useful in many applications like geothermal energy and injection of CO2.
These applications share the Full Waveform Inversion (FWI) as a solution methodology for reconstructing quantitatively the physical parameters from observed data. FWI can be carried out in time-domain 55, 84, 95, 96 or in frequency domain 89, 88, 87. Its main feature is to avoid the formation of the large Jacobian matrix by computing the gradient of the misfit functional using the adjoint-state method 64. A detailed review of FWI for geophysical applications can be found in 86.
4.1.1 Deep geothermal energy
Obtaining accurate images of natural reservoirs is still critical for their management and exploitation and seismic imaging is an efficient tool (see 83, 81 and their references therein. One example is with deep geothermal energy which requires precise imaging of deep fractured reservoirs filled with geothermal fluids. Standard seismic imaging is based upon inverting mechanical waves which have difficulties to detect them, whereas electromagnetic waves are more sensitive. We see here a clear interest of coupling seismic with electromagnetic methods and this is what Makutu is developing with the CHICkPEA project. This is a multidisciplinary project involving experimental geophysicists from UPPA, members of the LFCR (Laboratory of Complex Fluids and their Reservoirs) and Steve Pride, professor at the University of Berkeley, who developed the theory describing the coupling between seismic waves and electromagnetic waves called seismoelectric effects 90. CHICkPEA started in 2018 and it was scheduled to be completed at the end of 2021. However, beginning of 2021, the team will be involved in a new project SEE4GEO funded by ADEME, in the framework of Geothermica call. Hence CHICkPEA project will continue as long as SEE4GEO, i.e. until the end of 2023. The project belongs with E2S (Energy Environment Solutions) program of UPPA which steers the actions of the University labeled I-Site within the framework of the Investment Plan for the Future.
4.1.2 Shallow geothermal energy
Regarding shallow geothermal energy, Makutu has started a collaboration with RealTimeSeismic SME in the framework of the FEDER-Poctefa Pixil project in order to use surface waves for a better imaging of shallow reservoirs. This project goes further in the work carried out on the inversion of seismic waves. Surface waves have long been considered as noise in seismograms because they were used to study the subsurface at depths. In shallow geothermal energy, surface waves contain interesting information on the first layers of the subsurface. Inverting them is a real problem because the surface waves are of high amplitude while propagating slowly. They therefore pose difficulties for multi-frequency optimization methods. The analysis of surface wave properties derives from the analysis of elastic wave propagation in horizontally stratified media 97, 79, 82. Consequently, current surface inversion derives 1D property profiles from dispersion curves picked in the frequency-wavenumber domain 94. Most of the available methods are limited to only inverting the fundamental modes, while lateral variations are difficult to handle with this approach. To overcome these limitations, the academia community has recently started to apply Full Waveform Inversion to this specific problem 92, 85.
4.1.3 CO2 injection
The reduction of greenhouse gases in the atmosphere is a societal topic of the utmost importance, with the Paris Agreement setting ambitious goals for many countries. One fundamental pillar of greenhouse emission management is Carbon Capture Utilisation and Storage (CCUS) 98. With this strategy, carbon dioxide produced on- or off-site is sequestered and injected into depleted reservoirs, thus offsetting an important portion of current CO2 emissions. The successful and safe implementation of this strategy requires the prediction, monitoring and surveillance of stored CO2 over long periods, which presents significant challenges in terms of seismic acquisition, seismic inversion and numerical simulation. These tools, coupled with state-of-the-art flow simulations, are vital in order to support the injection operations with vital real-time and long-term information. Moreover, specific challenges related to the physics of injected CO2, such as viscosity, temperature and multi-phase fluid conditions push to the limits our current numerical models, and require ambitious new multi-physics simulations to support safe and cost-effective CO2 injection operations. For example, some recent publications like 93, 101 have shown that the combination of CO2-brine flow with wave propagation provides efficient simulations for the monitoring of sequestered CO2. Makutu proposes to develop numerical methods for this new application, in collaboration with Total, in the framework of the research agreement DIP (Depth Imaging Partnership).
4.2 Solar imaging
The Sun sustains various types of waves which are driven by near-surface turbulent convection. These movements can be observed at the surface by the Dopplergrams given by ground-based or satellite-borne observatories. In recent years, methods for understanding Earth subsurfaces have opened up new ways to study the interior of the Sun as in the case with helioseismology and the interior of stars with aesteroseismology from oscillation observed at their surface. Techniques in helioseisomolgy is generally divided into global and local helioseismology. The first approach studies frequencies of oscillations modes, cf. 59, 65. This is also the current strategy of asteroseismology, cf 80, 50, 51. On the other hand, local helioseimology, which adapts techniques of geophysical seismic interferometry studies, measures local wave propagation and works with the full 3D observed wavefield, and is thus more adapted to study additional features such large-scale flows in active region, sun spots and plage, cf. 76, 75.
With its long-run expertise in numerical tools for imaging Earth subsurfaces, Makutu is extending its activity on terrestrial seismology to studying the Sun, for the latter offers a vast wealth of problems to be explored both for direct modeling as well as inversion. In this development, associated team ANTS (Advance Numerical meThods for helioSeismology was created in 2019 to formalize a collaboration with MPS (Max Planck institute for Solar research). In a first step, one can study acoustic waves which are identified with p-modes on the power spectrum, and acoustic waves at low frequencies can be adequately described by a scalar equation which allows for convection. The stochastic nature is described by random right-hand source term, and in using statistical analysis, under appropriate assumptions (e.g. the convenient source assumption), power spectrums and time-distance diagrams can obtained from the deterministic Green kernel of modelling wave equation, cf. 74. In this approach, the Green kernel becomes a crucial object in local helioseismology, and its accurate and efficient computation is the main goal of forward modelling.
As a first result of the collaboration of Magique-3D, with MPS, in 74, a new computational framework based on the scalar equation was developed and produces solar-like power spectra and time-distance diagrams under appropriate assumption of source excitation. A second topic under active research is boundary conditions that allow waves to propagate. This also plays a crucial point in forward modeling as well as inversion. There are two on-going directions to proceed.
- In a goal to create power spectrum and time-distance diagram that are closer to real observable, we need to include important physical effects such as gravity, magnetic and rotation forces. This requires extending the computation framework for scalar equation to vector equation. In including the effect of gravity, one hopes to find g-modes on simulated power spectrum (currently missing from that associated with the scalar equation). These above physics are also needed in order to study active regions of the sun such as Sunspots. Shallow layers of the Sun will be probed with more accuracy, which will be useful for the study of supergranulation. For this topic, Makutu can benefit from discussion and collaboration with Inria teams such as TONUS team with their experience in simulating tokamak plasma for thermonuclear reaction (SCHNAPS).
- On the other hand, with the current established framework for the scalar equation, the next step is to the inverse problem, in particular with time-distance helioseismology 62, 72 and holography 102, 77. Current state-of-the art tools in these references is linear inversion using Born approximation. In additional they are carried out in 1D or 2D. It is thus interesting to apply nonlinear inversion such as Full Waveform Inversion cf. 69 to these problems.
4.3 Musical acoustics
This field of application is a subject of study for which the team is willing to take risks. We propose using a mix of experimental and numerical approach in order to study and design musical instruments. Makers have designed wind musical instruments (as flutes, trumpets, clarinets, bassoons...) in the past through “trial and error” procedures by performing a geometrical calibration of musical instruments in order to improve their accuracy, tone, homogeneity and even their sound volume, ergonomics, and robustness. During the past few decades, musical acoustics has been in a process of rationalizing the empiric understanding of instrument makers in order to formulate a scientific approach to future evolution. Our research proposal is along this axis of research by proposing new mathematical models based on our solid experience in terms of wave propagation in media with interfaces that can significantly change the sound. As was done in geophysical exploration, we propose to assist the modelling process with laboratory experiments. Direct comparison between simulations and experiments will allow to assess the model error. For this purpose, an experimental device has been developed in collaboration with I2M, Mechanics Laboratory of the University of Bordeaux and Humeau Factory, Montpon- Ménestérol, and is currently in use.
4.3.1 Modeling
Although the playing context should always be the final reference, some aspects of the behavior of a wind instrument can be firstly characterized by its entry impedance which quantifies the Dirichlet-to-Neumann map of the wave propagation in the pipe in the harmonic domain. This impedance can be both measured 73, 66 and computed with simulations based on accurate and concise models of the pipe 91, 6099, 67. A more realistic approach accounts for the embouchure 78, 60, 53, 54, 100, which is modeled as a nonlinear oscillator coupled with the pressure and acoustic velocity at the entry of the pipe, allowing to predict the sound qualities. Mathematical properties of the underlying models are not yet totally understood, and adequate models still need to be developed. This is particularly true when accounting for dissipation phenomena, junctions of pipes, pipe porosity and rugosity, embouchures...
To reproduce the sound of instruments, time-dependent models are more suitable. Here, nonlinear lumped elements induce an “auto-oscillatory” behavior of the instrument. The models currently available in the literature are meant to reproduce viscothermal effects, pipe junctions, pipe radiation, lips oscillation, etc. They do not necessarily possess adequate mathematical properties to ensure stable simulations and they should be improved using asymptotic analysis methods or Lagrangian formalism.
4.3.2 Numerical methods
As far as numerical developments are concerned, the accuracy of the calculations is essential. Indeed, for some aspects like the sounding frequency, a deviation of 1% between the predictions and the observations is unacceptable. Moreover, contrary to what the team is used to do for geophysics or astrophysics thanks to HPC, numerical methods for acoustical musics must be frugal to be run on personal computers by acousticians and makers. Makutu has a wide range of numerical methods that have been implemented in its codes for linear problems. New numerical schemes will have to be implemented to take into account the non-linearities of time-dependent models.
4.3.3 Virtual workshop
Beyond the idea of mathematically modeling musical instruments, Makutu wishes to develop a virtual workshop whose vocation will be twofold: (i) support the manufacturers to design new instruments; (ii) recreate the sound of old and historical instruments. To implement this idea, we propose to elaborate optimization techniques that are well-known in the team to define optimal geometries to meet given specifications. This can be used to reconstruct existing instruments from acoustic measurement or to design new instruments by fixing relevant quantitative objective which is a research activity by its own 68. Behind the idea of the virtual workshop is also the intention to hear the instruments, from the knowledge of their shape and playing regime. For that purpose, time-domain models are essential.
5 Highlights of the year
5.1 New project with industry
In January, we have launched a new project with TotalEnergies on the development of an advanced numerical framework dedicated to seismic for CCUS (Carbon Capture, Utilization and Storage) which is a priority technology for the Group. This project is developed in collaboration with Stanford University and Lawrence Livermore National Laboratory in the US. Both universities are with TotalEnergies (FC Maelstrom project) a consortium around the Open Source Multi-physics computational platform GEOSX. We have hired to research engineers (Julien Besset and Mamadou N'diaye) who have had in charge with Aurélien Citrain to initiate a new branch in GEOSX for seismic. This project is paving the way for Makutu's ambitious new CCUS technology research activity.
5.2 New application in Electromagnetism
KRAKEN SUBSEA SOLUTIONS is an engineering company entirely specialised in the Marine Renewable Energies (MRE). We have launched a collaboration with this SME located in Bidart, 64. For the time being, the collaboration consists in knowledge exchange in the framework of an internship in the first semester of 2021. The objective was to develop a precise calculation method to restore the electrical and magnetic radiation of submarine cables that transport the energy produced by offshore wind farms. First results obtained for a straight cable are very promising, and we decided to continue the project in the framework of a thesis in collaboration with the INSA of Rouen. This project is an opportunity for Montjoie software to be used by Kraken Subsea Solutions and for Makutu to work on a new application in Electromagnetism.
5.3 New collaboration for extra-terrestrial imaging
We have started a collaboration with Anton Ermakov (Space Sciences Laboratory, UC Berkeley) and Burkhard Militzer (UC Berkeley) regarding the imaging of Saturn's interior structure. The Cassini spacecraft opens up new perspectives of measurements and waves were recently detected in Saturn's rings, caused by resonances between ring particles and normal modes excited in the planet's interior. Hence it provides us with new possibilities to infer Saturn's interior. In our collaboration, both physical, mathematical and numerical aspects are discussed and the expertise that Makutu acquired in the context of helioseismology proves to be particularly useful. We first expect to develop the robust numerical framework to compute the normal modes of giant gas planets, including gravity in the wave equations and avoiding Cowling approximation. The software Hawen, developed in Makutu, will be used for the implementation. It offers an opportunity for the Makutu team to diversify its activities and enrich its experience in exrta-terrestrial imaging.
Florian Faucher, who was recruited this year as a Chargé de Recherche in the team Makutu is in charge of monitoring the collaboration.
6 New software and platforms
6.1 New software
6.1.1 OpenWind
-
Name:
Open Wind Instrument Design
-
Keywords:
Wave propagation, Inverse problem, Experimental mechanics, Time Domain, Physical simulation
-
Scientific Description:
Implementation of first order finite elements for wind musical instrument simulation. Implementation of the Full Waveform inversion method for wind musical instrument inversion. Implementation of energy consistent numerical schemes for time domain simulation of reed-type wind musical instrument.
-
Functional Description:
Simulation and inversion of wind musical instruments using one-dimensional finite element method with tonholes or valves and fingering chart. The software has three functionnalities. First, the software takes the shape of a wind instrument and computes the acoustical response (answer to a given frequential excitation). Second, the software takes the instrument shape and the control parameters of a musician, and computes the produced sound and the time evolution of many acoustical quantities. Last, the software takes a measured acoustical response and computes the corresponding instrument geometry (inner bore and tone holes parameters).
-
Release Contributions:
Addition of valves (pistons) for brass instruments and their activations with a fingering chart. New thermo-viscous losses model within conical parts.
- URL:
- Publications:
-
Contact:
Juliette Chabassier
-
Participants:
Juliette Chabassier, Augustin Ernoult, Alexis Thibault, Robin Tournemenne, Olivier Geber, Guillaume Castera, Tobias Van Baarsel
6.1.2 Hou10ni
-
Keywords:
2D, 3D, Elastodynamic equations, Acoustic equation, Elastoacoustic, Frequency Domain, Time Domain, Discontinuous Galerkin
-
Scientific Description:
Hou10ni simulates acoustic and elastic wave propagation in time domain and in harmonic domain, in 2D and in 3D. It is also able to model elasto acoustic coupling. It is based on the second order formulation of the wave equation and the space discretization is achieved using Interior Penalty Discontinuous Galerkin Method. Recently, the harmonic domain solver has been extended to handle Hybridizable Discontinuous Galerkin Methods.
-
Functional Description:
This software simulates the propagation of waves in heterogeneous 2D and 3D media in time-domain and in frequency domain. It is based on an Interior Penalty Discontinuous Galerkin Method (IPDGM) and allows for the use of meshes composed of cells of various order (p-adaptivity in space).
-
News of the Year:
In 2021, we have implemented the 3D seismoelectomagnetic equations (poroelastic+electromagnetic) for the HDG formulation and started comparison with laboratory experiments.
- URL:
-
Publications:
hal-01513597, hal-01957131, hal-01388195, hal-01972134, hal-01957147, hal-02152117, hal-02486942, hal-02408315, hal-02911686, hal-03464413v1, tel-03442300v1, tel-03014772, hal-01656440, hal-01662677, hal-01623953, hal-01623952, hal-01513597, hal-01519168, hal-01254194, hal-01400663, hal-01400656, hal-01400643, hal-01313013, hal-01303391, hal-01408981, tel-01304349, hal-01184090, hal-01223344, hal-01207897, hal-01184111, hal-01184110, hal-01184107, hal-01207906, hal-01184104, hal-01207886, hal-01176854, hal-01408705, hal-01408700, tel-01292824, hal-01656440, hal-00931852, hal-01096390, hal-01096392, hal-01096385, hal-01096324, hal-01096318, tel-01133713, tel-00880628
-
Contact:
Julien Diaz
-
Participants:
Conrad Hillairet, Elodie Estecahandy, Julien Diaz, Lionel Boillot, Marie Bonnasse, Marc Fuentes, Rose-Cloé Meyer, Vinduja Vasanthan
6.1.3 haven
-
Name:
time-HArmonic waVe modEling and INversion using Hybridizable Discontinuous Galerkin Discretization
-
Keywords:
Inverse problem, Wave Equations, Geophysics, Helioseismology, Discontinuous Galerkin, MPI, Large scale, Wave propagation, 3D, 2D
-
Scientific Description:
Many applications such as seismic and medical imaging, material sciences, or helioseismology and planetary science, aim to reconstruct properties of a non directly accessible or non-visible interior. For this purpose, they rely on waves whose propagation through a medium interrelates with the physical properties (density, sound speed, etc.) of this medium. Haven is a software designed to perform imaging with waves, following an algorithm that comprises of two main stages: In the data acquisition stage, the medium response to probing waves is recorded (e.g., seismic waves from Earthquakes recorded by ground network). In the second stage, we rely on a reconstruction procedure which iteratively updates an initial model of physical parameters, so that numerical simulations approach the measurements. This procedure is employed, for instance, for seismic (reconstruction of subsurface layers) and medical (disease diagnostic) imaging.
-
Functional Description:
The software solves time-harmonic forward and inverse wave problems for acoustic and elastic media using the Hybridizable Discontinuous Galerkin method for discretization. It combines MPI and OpenMP parallelism to solve large-scale applications such as Earth's imaging and helioseismology.
-
News of the Year:
- Several choices of visco-acoustic and visco-elastic models have been added for the propagation, - New propagators dedicated to helioseismology have been implemented
- URL:
- Publications:
-
Contact:
Florian Faucher
-
Participant:
Florian Faucher
6.1.4 MONTJOIE
-
Keywords:
High order finite elements, Edge elements, Aeroacoustics, High order time schemes
-
Scientific Description:
Montjoie is designed for the efficient solution of time-domain and time-harmonic linear partial differential equations using high-order finite element methods. This code is mainly written for quadrilateral/hexahedral finite elements, partial implementations of triangular/tetrahedral elements are provided. The equations solved by this code, come from the ”wave propagation” problems, particularly acoustic, electromagnetic, aeroacoustic, elastodynamic problems.
-
Functional Description:
Montjoie is a code that provides a C++ framework for solving partial differential equations on unstructured meshes with finite element-like methods (continuous finite element, discontinuous Galerkin formulation, edge elements and facet elements). The handling of mixed elements (tetrahedra, prisms, pyramids and hexahedra) has been implemented for these different types of finite elements methods. Several applications are currently available : wave equation, elastodynamics, aeroacoustics, Maxwell's equations.
- URL:
-
Contact:
Marc Durufle
-
Participants:
Juliette Chabassier, Marc Durufle, Morgane Bergot
6.1.5 GEOSX
-
Keywords:
Physical simulation, Multiphysics modelling
-
Functional Description:
GEOSX is an open-source, multiphysics simulator developed cooperatively by Lawrence Livermore National Laboratory, Stanford University, and TotalEnergies. Its goal is to open up new horizons in modeling carbon storage and other subsurface energy systems. This includes: - taking advantage of the ongoing revolution in high-performance computing hardware, which is enabling orders-of-magnitude gains in performance, but also forcing a fundamental rethink of our software designs, - enriching the physics used in industrial simulations, allowing complex fluid flow, thermal, and geomechanical effects to be handled in a seamless manner, - developing highly-scalable algorithms for solving these coupled systems, - and improving workflows for modeling faults, fractures, and complex geologic formations. Inria contributes to the seismic wave propagators of GEOSX, and to its python interface. Inria also contributes advanced workflows for seismic inversion, and CO2 storage an monitoring.
-
News of the Year:
Project-team Makutu has contributed to the integration of seismic propagators based on Q1 SEM (spectral element method), and to the development of the python interface (pyGEOSX), with the goal of later using it to integrate a complete seismic inversion workflow via full waveform inversion (FWI). These developments will carry on and expand in 2022.
- URL:
-
Contact:
Randolph Settgast
6.1.6 Gar6more2D
-
Keywords:
Validation, Wave propagation
-
Functional Description:
This code computes the analytical solution of problems of waves propagation in two layered 3D media such as- acoustic/acoustic- acoustic/elastodynamic- acoustic/porous- porous/porous,based on the Cagniard-de Hoop method.
-
News of the Year:
In the framework of collaboration with Peter Moczo (Comenius University Bratislava and Slovak Academy of Sciences), David Gregor, Josef Kriztek, Miriam Kristekova (Comenius University Bratislava), Arnaud Mesgouez, Gaëlle Lefeuve-Mesgouez (Inrae, Avignon University) and Christina Morency (Laurence Livermore National Laboratory) and we have implemented the coupling between elastic and poroelastic media. The obtained results are presented in an article of Geophysical Journal Internation 16.
- URL:
- Publications:
-
Contact:
Julien Diaz
-
Participants:
Abdelaâziz Ezziani, Julien Diaz
-
Partner:
Université de Pau et des Pays de l'Adour
7 New results
7.1 Analytical and experimental solutions for validation
7.1.1 Comparative study of French and German bassoons
Participants: Augustin Ernoult.
The bassoon is a woodwind instrument with side holes, and it is played with a double cane reed. Today, the French and German models coexist in the orchestra, with a predominance of the German model. They differ mainly by the number and the location of the holes and by the shape of the reed. The resulting timbre is slightly different, the sound of the French bassoon being often described as more “nasal” than the one of its German cousin. The aim of this work is to understand the relation between the geometric differences and the sound differences by comparing these two instruments through a series of measurements and simulations. The main part of this study as been carried out with Timo Grothe in the Erich Thienhaus Institute (ETI) in the “Hochscule für Musik” of Detmold in Germany during the research stay of Augustin Ernoult 9.2.1.
To begin, the internal geometries of one bassoon of each type have been measured with split probes (main bore and side holes). Thanks to this knowledge, the acoustic response of these instruments have been computed with the software Openwind 6.1.1. The results of these simulations and in particular their input impedance for each fingering have been compared with acoustic measurement to validate both geometric measurements and the acoustic models. To compare their sound, the two instruments have been played by the same professional player and recorded with a high quality set-up from ETI. A second set of sound recording have been carried out with an artificial mouth designed by T. Grothe allowing the fine control and the measurement of all the “player's parameters”. This knowledge has been used to compute the sound by using the temporal simulation of Openwind and compare the predicted and measured sounds.
The sound from the different measurement have been then processed to highlight the difference between the two instruments. This supposes to define specific sound descriptors. The simulations give us the possibility to vary independently each geometric parameters and observe which sound characteristic is modified. We developed phenomenological models acoustically informed to relate some geometric parameters (such has the chimney height of side holes) to the timbre signature.
The results of this study will be presented in two conference in 2022 (German and French Acoustic Congress) and should lead to the publication of two papers currently in redaction.
7.1.2 Benchmark study on wind instrument models
Participants: Juliette Chabassier, Augustin Ernoult.
In the musical acoustic community, the wave propagation within the body of the instrument and the radiation at the openings are generally computed by using light models (1D for the propagation and equivalent boundary condition at the opening). These models are obtained with a large variety of process (asymptotic studies, phenomenological models from measurement or more complex numerical simulations, etc.). For some geometric configurations, no consensus exist on which solution which must be used to correctly model a given wind instrument.
In the aim of developing a numerical tool to support the manufacture of wind instrument, a collaborative study has been started in June 2021. About thirty benchmark cases have been designed to cover the most of the geometric configurations encountered within the existing wind instruments. Each participant compute the acoustic response of these configurations with its own model, then the data are shared to be analyzed together. In parrallel of this numerical work, an experimental work has been started in December. Some of these benchmark geometries are build by the Itemm (Institut Technique Européen des Métiers de la Musique) and their acoustic characteristic s will be measured by several participants to be compared to the numeric data.
This work is done in collaboration with about ten french research teams (from academic and private institution) and conducted by Augustin Ernoult. Preliminary results will be presented at the French Congress of Acoustic in April 2022.
7.1.3 Pulsed-laser source characterization in laboratory seismic experiments
Participants: Julien Diaz, Chengyi Shen.
The present study aimed to characterize the properties of a laser-generated seismic source for laboratory-scale geophysical experiments. This consisted of generating seismic waves in aluminum blocks and a carbonate core via pulsed-laser impacts and measuring the wave-field displacement via laser vibrometry. The experimental data were quantitatively compared to both theoretical predictions and 2D/3D numerical simulations using a finite element method. Two well-known and distinct physical mechanisms of seismic wave generation via pulsed-laser were identified and characterized accordingly: a thermoelastic regime for which the incident laser power was relatively weak, and an ablation regime at higher incident powers. The radiation patterns of the pulsed-laser seismic source in both regimes were experimentally measured and compared with that of a typical ultrasonic transducer. This study showed that this point-like, contact-free, reproducible, simple-to-use laser-generated seismic source was an attractive alternative to piezoelectric sources for laboratory seismic experiments, especially those concerning small scale, sub-meter measurements.This work was published in Geomechanics and Geophysics for Geo-Energy and Geo-Resources 17, in collaboration with Clarisse Bordes, Daniel Brito, Federico Sanjuan (LFCR, UPPA), and Stéphane Garambois (ISterre).
7.1.4 Analytical solutions for elasto/poroelastic coupling
Participants: Julien Diaz.
Our software Gar6more computes the analytical solution of waves propagation problems in 2D homogeneous or bilayered media, based on the Cagniard-de Hoop method. In the bilayered case, we had implemented the following coupling: acoustic/acoustic, acoustic/elastic, acoustic poroelastic, elastic/elastic, poroelastic/poroelastic. In the framework of collaboration with Peter Moczo (Comenius University Bratislava and Slovak Academy of Sciences), David Gregor, Josef Kriztek, Miriam Kristekova (Comenius University Bratislava), Arnaud Mesgouez, Gaëlle Lefeuve-Mesgouez (Inrae, Avignon University) and Christina Morency (Laurence Livermore National Laboratory) and we have implemented the coupling between elastic and poroelastic media. The obtained results are presented in an article of Geophysical Journal Internation 16.7.1.5 Quantitative Analysis of Seismic Waves with Computational and Laboratory-Scale Experiments.
Participants: Florian Faucher.
We perform a quantitative analysis of the attenuation for seismic waves, with both numerical and physical experiments. We compare different rheologic models of attenuation and use body and surface waves propagation to infer their parameters. We first rely on numerical simulations, separating the body and surface waves and applying corrections of the geometrical spreading to focus on the attenuation behavior. This leads to a precise step-by-step strategy to retrieve the attenuation parameters from the wave field solutions. The computational study is supplemented with experimental acquisitions where we consider different samples. We design a dedicated setup using various Piezoelectric Transducers acting as seismic sources, and a moving Laser-Doppler Vibrometer as receivers for accurate non-contact time-domain measurements. Here, the main difficulty comes from the faces of the samples which cause wave conversions and reflections that appear strongly in the measurements.
This is the subject of Marine Deheuvels Ph.D. at UPPA, she is supervised by Daniel Brito (UPPA) and Florian Faucher. This work has been presented at the conference AGU-SEG, 25.
7.2 Mathematical modeling
7.2.1 Viscothermal phenomena in wind musical instruments: modeling and simulation
Participants: Juliette Chabassier, Alexis Thibault.
For the purpose of virtual prototyping, the high-precision calculation of the acoustic propagation in a conical musical instrument - such as the bassoon or the oboe - must include dissipative phenomena due to air viscosity and thermal diffusion. These boundary layer phenomena can be represented by complex coefficients in 1D models. However, the expressions commonly used for these coefficients come from calculations carried out in cylinders. The aim of this work is to understand the variation of these dissipative phenomena with the conicity of the pipe. This work has been done in collaboration with Thomas Hélie and Henri Boutin (STMS, UMR9912, CNRS-SU-IRCAM), was presented in 38, and a journal publication is upcoming.
In addition, we compared these results to simulations from models directly posed in three dimensions, based on various simplifying hypotheses. These comparisons provide a quantitative estimate of the errors made by the different models and reveals a hierarchy of the underlying assumptions. This work has been published in a research report 63.
Time domain simulation of these phenomena is non-trivial due to the memory effect they exhibit. A new model directly based on knowledge of the geometry of the instrument, accompanied by a second-order energy-preserving discretization scheme was published in 18
7.2.2 Modeling the influence of wall porosity and roughness on acoustic propagation in wind musical instruments
Participants: Juliette Chabassier, Alexis Thibault.
In wind instruments, the geometric irregularities at the surface of the inner wall, as well as its possible porous structure, have previously been shown to influence the acoustic propagation within the bore of the instrument. An investigative work has been started in order to write models of acoustic propagation in the instrument which take into account wall porosity and/or roughness. As the base equations are the same as in the study of viscothermal phenomena, some of the expertise and concepts deployed in that previous work can be applied there. The tools used stem from the theory of periodic homogenization and asymptotic analysis. The aim of this work is to allow simulations in time of instruments with porous and/or rough walls. Simulations of an instrument with a basic model of wall roughness have already been achieved.
This work has been done in collaboration with Thomas Hélie and Henri Boutin (STMS, UMR9912, CNRS-SU-IRCAM).
7.2.3 Simulation of the piano touch
Participants: Juliette Chabassier, Guillaume Castera.
In this PhD work, we develop physical models for the piano to understand the real influence of the pianist on the sound. Mechanical models [iMMC] will be paired with vibro-acoustical models [INRIA] to analyse the differences in sound depending on the pianist’s touch. We are currently working on convergence analysis of auxiliary variable based schemes to solve the non-linear string equation in the most efficient way. We are implementing the algorithms in python to analyse the influence of multiple parameters on the precision of the results. A three-weeks scientific visit in iMMC laboratory in Belgium allowed to pursue last year's work on friction modeling between the hammer and the string. Also first simulations were made with inria's MONTJOIE software and gave encouraging results. We directly used the force applied by the action on the hammer calculated by iMMC's Robotran software as an input.
This work has been done in collaboration with Paul Fisette and Sébastien Timmermans, université catholique de Louvain, Belgique. Preliminary results on the numerical scheme have been presented at ICOSAHOM 23.
7.2.4 Low-order Prandtl-Glauert-Lorentz based Absorbing Boundary Conditions for solving the convected Helmholtz equation with Discontinuous Galerkin methods
Participants: Hélène Barucq, Nathan Rouxelin, Sébastien Tordeux.
We have constructed Absorbing Boundary Conditions (ABC) for the convected Helmholtz equation. The construction is based upon the Prandtl-Glauert-Lorentz map which transforms the convected Helmholtz equation into the regular Helmholtz equation. The new ABCs are issued from classical Bayliss-Turkel conditions and are valid for carrier flows that vary inside the domain while becoming uniform at infinity. They lead to accurate numerical results for low and intermediate Mach numbers. It is worth noting that they are easy to implement in discontinuous finite element solvers. This work has been published in the preprint 47.7.2.5 Time domain analysis and localization of a non-local PML for dispersive wave equations
Participants: Julien Diaz.
In this work we design and analyze new perfectly matched layers (PML) for a dispersive waves equation : the Klein Gordon equation. We show that because of the dispersion, classical PMLs do not guarantee the convergence to zero of the error, which hampers the precision in long time simulation. We propose to consider a non-local PML for which we can obtain explicit uniform estimates for the reflected analytical solution in time domain, given by an integral representation formula. This uniform estimates ensure the convergence of the error to zero at fixed time t and guarantee the accuracy of the layer. For the implementation of the new PML, we propose a localization technique that we validate numerically.This is a joint work with Nacera Baara and Mounir Tlemcani (Oran University). It has been publised in JPC 9.
7.2.6 Physical based synthesis of heritage wind musical instruments
Participants: Juliette Chabassier, Augustin Ernoult, Tobias Van Baarsel.
During this second and last year of the project SYSIMPA 9.4.1, the work was aimed at finalising the study of the geometry of the wind instruments. First, uncertainties around the mouthpiece remained, due to the relative thickness of the metal walls of the main pipe that caused important biases in the measurement based on X-ray technology. This has been addressed by using a silicone moulding of the bore of the mouthpiece. This was done at the Cité de la Musique in Paris. The moulding offers a precise measurement of the inner radius which satisfyingly completes and validates the measurements done based on X-ray tomography.
The measurements based on X-ray tomography done in the first year had to be processed in order to be used in impedance / sound synthesis. The raw geometries yielded by the measurements need to be simplified in fewer simple elements for the sake of computational cost. This has been done using two optimisations: a first one based only on the geometry, so that the simplification is as close as possible to the original measurement. This step needs some human input as the measurements include either local aberrations due to X-ray artefacts, or are simply very noisy. The second optimisation is based on the input impedance of the air column. The input impedance of the simplified geometry is computed and compared to the input impedance measured experimentally on the original instrument at the Cité de la Musique. An optimisation algorithm is then used to slightly modify the geometry so that it minimises the difference between measured and computed input impedances. The result is a simplified geometry that accurately represents the original instrument, from the geometrical and the acoustic point of view.
Temporal simulations (i.e., sound synthesis) have been performed using such a geometry. The parameters for the excitator are tricky to find, and work still needs to be done in order to fully grasp the complexity of the phenomenon. However, a set of simple parameters has been found for which a sound can be synthesised. Based on the natural resonant frequencies of the instrument, the natural scale (for the first impedance peaks, i.e., the first notes of the harmonic series) has been synthesised.
The methodology around the geometry of the instrument has been done for each of the ten selected instruments from the Besson corpus. A simplified version is from now on available for each instrument, and can be used for impedance or sound simulation.
One instrument (labeled E0925 in the archives) has been selected for the making of a physical copy. Instrument-maker Jérôme Wiss was assigned to this task. The instrument should be finished in january 2022. Impedance measurements of this copy will be done at the Cité de la Musique for comparison with the original.
This work will be presented in the French Congress of Acoustics in April and an article is being written.
7.2.7 Outgoing modal solutions for Galbrun's equation in helioseismology.
Participants: Hélène Barucq, Florian Faucher, Ha Pham.
We construct modal outgoing Green's kernels for the simplified Galbrun's equation under spherical symmetry, in the context of helioseismology. The coefficients of the equation are C² functions representing the solar interior model S, complemented with an isothermal atmospheric model. We solve the equation in vectorial spherical harmonics basis to obtain modal equations for the different components of the unknown wave motions. These equations are then decoupled and written in Schrödinger form, whose coefficients are shown to be C² apart from at most two regular singular points, and to decay like a Coulomb potential at infinity. These properties allow us to construct an outgoing Green's kernel for each spherical mode. We also compute asymptotic expansions of coefficients up to order r-³ as r tends to infinity, and show numerically that their accuracy is improved by including the contribution from the gravity although this term is of order r-³.
This is a joint work with Laurent Gizon and Damien Fournier of the Max Plank Institute for Solar system research in Göttingen (MPS), supported by the INRIA associated team ANTS between Makutu and MPS. It is published in Journal of differential Equations, 13. Some of the results of barucq:hal-03406855v1 have been presented at SIAM Conference on Mathematical & Computational Issues in the Geosciences (GS21), June 21–24, 2021, Virtual Conference, see , see 22. It has also been presented at the ANTS Workshop on helioseismology, 27.
7.2.8 Non-perturbative computation of normal modes for rotating gas giant planets.
Participants: Florian Faucher.
The Cassini spacecraft detected waves in Saturn's rings caused by Lindland and vertical resonances between ring particles and normal modes excited in the planet's interior. The detection of these waves potentially provides us with a novel way to constrain Saturn's interior structure in the same way helioseismological measurements improved our understanding of the Sun. Perturbation theory along with internal structure modeling has been used to infer the properties of Saturn’s interior from the measurements of normal mode frequencies. However, due to the measurements’ high precision and Saturn’s rapid rotation, the perturbation theory-based approach does not allow one to fully exploit the normal modes dataset. we circumvent perturbative methods altogether and, instead, implement a non-perturbative approach for computing both the hydrostatic equilibrium structure of a planet and its acoustic normal mode spectrum. We use the Concentric Maclaurin Spheroids (CMS) method to compute the planet's interior structure in hydrostatic equilibrium that results from gravitational and centrifugal forces. We model gas giant interior using a polytropic equation of state (EOS) with a unity polytropic index. With this simplified EOS, pressure scales as density squared.
This is a joint work with Anton Ermakov (Space Sciences Lab, UC Berkeley), Burkhard Militzer (UC Berkeley) and Maarten V. de Hoop (Rice University). This work was presented at conference AGU fall meeting.
7.2.9 Modeling and numerical simulation of the propagation of electromagnetic waves in offshore cables: applications to the environmental impact on the marine ecosystem
Participants: Hélène Barucq, Marc Duruflé, Augustin Leclerc.
The development of low-carbon energies is one of the challenges of tomorrow and it opens the way to many research topics. In the context of this internship, we are interested in the modeling of the electromagnetic field generated by a cable connected to a wind turbine that would be located off the coast. Offshore wind turbines are of great interest because they are able to use the wind energy better than onshore wind turbines. Indeed, at sea, the wind encounters fewer obstacles, which makes it more regular and less turbulent. With the same power, an offshore wind turbine can therefore produce more energy than a land-based wind turbine. In this work, we focus on the modeling of the electromagnetic field generated by an electric cable connected to a wind turbine and immersed in the sea water. The objective is to develop a numerical simulation code to reproduce the electromagnetic field propagating in the cable in order to assess the impact of the cable on its environment. As a first step, we have considered two methods for solving Maxwell equations around a multiconductor cable in salt water, assuming the cable geometry is straight. The next step will consist in considering twisted cables as they are in realistic applications.This work is part of a PhD program which started in October 2021. The topic has been proposed by the SME Kraken Subsea and is now the heart of a collaboration between this SME, Makutu and INSA Rouen with Christian Gout and Antoine Thonnoir.
7.3 High-order numerical methods for time-dependent problems
7.3.1 Construction and convergence analysis of conservative second order local time discretisation for linear wave equations
Participants: Juliette Chabassier.
In this work we present and analyse a time discretisation strategy for linear wave equations t hat aims at using locally in space the most adapted time discretisation among a family of implicit or explicit centered second order schemes. The proposed family of schemes is adapted to domain decomposition methods such as the mortar element method. They correspond in that case to local implicit schemes and to local time stepping. We show that, if some regularity properties of the solution are satisfied and if the time step verifies a stability condition, then the family of proposed time discretisations provides, in a strong norm, second order space-time convergence. Finally, we provide 1D and 2D numerical illustrations that confirm the obtained theoretical results and we compare our approach on 1D test cases to other existing local time stepping strategies for wave equations.
This is a joint work with Sébastien Imperiale (M3DISIM Inria Saclay). It has been publised in M2AN 14.
7.3.2 Tent Pitcher algorithm for space-time integration of wave problems
Participants: Hélène Barucq, Julien Diaz, Vinduja Vasanthan.
In order to develop a method in time domain for wave problems that can combine sufficient flexibility to accommodate geophysical heterogeneities, rapidity of the algorithm, and precision of the solution, we consider Trefftz-DG methods. In Trefftz spaces, the basis functions are defined as elementwise solutions. The approximation space includes thus the Physics of the problem, which contributes to accuracy, a lower number of degrees of freedom and less numerical dispersion. Moreover, it is composed of Discontinuous Galerkin functions as the continuity at the interfaces of the elements cannot be imposed strongly. The resulting Trefftz-DG variational formulation is then applied on the boundaries of each cell of the mesh of the domain of interest with appropriate transmission conditions between the cells. However, the major drawback of this method is that it leads to an implicit scheme, which requires to solve a huge linear system. To overcome this difficulty, our Trefftz-DG formulation is implemented with the Tent-Pitching algorithm, which allows us to construct a causal mesh, hence leading to a locally-implicit scheme.
We have developed a Trefftz-DG framework for solving the acoustic wave equation using Tent-Pitching algorithms. During this past year, we worked along three lines of research : improving the meshing process, parallelizing the code and developing absorbing boundary conditions.
One important aspect of numerical modeling is the mesh, which should fit the domain as perfectly as possible, as to obtain the most accurate results. We extended the existing code to unstructured meshes, which led to a modified Tent-Pitching algorithm. In order to gain time during the execution of the code, parallelization is an essential tool. We propose a parallel version of our Trefftz-DG framework, which is carried out with the MPI library. The most interesting boundary conditions are the absorbing ones, allowing us to work in bounded domains with the same characteristics as an unbounded one, avoiding reflections at the interfaces. We developed a new Trefftz-DG method with Perfectly Matched Layers and non-polynomial type basis functions : Green’s functions.
This work has been done in the framework of DIP in collaboration with Henri Calandra and has been presented in several congresses, such as ECCOMAS 20 (jan. 2021), ICOSAHOM 39(jul. 2021) and MATHIAS DAYS 40 (oct. 2021).
7.3.3 Unstructured Isogeometric Analysis with Applications to Seismic Wave Propagation
Participants: Hélène Barucq, Julien Diaz, Stefano Frambati.
We explore the usefulness of spaces of unstructured spline functions in the resolution of hyperbolic problems discretized by explicit-time schemes, and especially the acoustic wave propagation problem with absorbing boundary conditions, and its associated inverse problem known as seismic inversion. We base our analysis on the known definition of simplex splines through polyhedral projections and Dirichlet averages, and we focus especially on the construction of polynomial-reproducing spaces of simplex splines. We introduce spline spaces associated to fine zonotopal tilings, which constitute a combinatorial extension of previous results on Delaunay configurations, and allow to construct spline spaces on point configurations including repeated and affinely dependent points. The resulting reduction in the regularity of the function space allows to define external boundary conditions, as well as subdivide the spline space into subdomains. Furthermore, the combinatorial properties of zonotopal tilings allow us to derive some useful algorithms for spline space construction in all space dimensions, generalizing previously known algorithms, as well as the evaluation of all the spline functions supported at a given point. We employ these spaces to define an unstructured version of known multi-patch Discontinuous Galerkin (DG) – isogeometric analysis (IGA) numerical schemes, showing that we can recover the usual Bernstein-Bézier DG scheme, as well as a fully unstructured IGA method, as special cases. We also show that the behavior of these spline spaces near the external and internal boundaries is very similar to the behavior of the standard DG bases, thus allowing to derive simple inverse inequalities and reuse the standard results of coercivity and a priori error analysis originally derived for the interior-penalty discontinuous Galerkin (IPGD) method. We illustrate the numerical properties of this discretization scheme with some numerical experiments.Finally, we explore some possible applications of unstructured spline functions to the seismic inversion problem, in the form of the full waveform inversion (FWI) technique. Specifically, we use the location of the spline knots as degrees of freedom for the inversion, using some known facts about the derivatives of these functions to dive the optimization process. Since the cost function of FWI is not generally differentiable with respect to the geometric degrees of freedom, we introduce this technique using subdifferentials, and we give a derivation of the adjoint state method for the computation of the gradient using a known convex duality theorem, valid for non-differentiable convex functions.This is the topic of the PhD of Stefano Frambati, defended in december 2021 41, in the framework of DIP. The construction of the spline spaces is presented in JCAM 11 This is a collaboration with Henri Calandra.
7.4 High-order numerical methods for time-harmonic problems
7.4.1 Trefftz methods for Maxwell equations
Participants: Margot Sirdey, Sébastien Tordeux.
The simulation of time-harmonic electromagnetic waves requires a matrix inversion whose cost, especially in three-dimensional cases, increases quickly with the size of the computational domain. This is a tangible issue regarding the memory consumption. Trefftz methods consist in using a discontinuous Galerkin method whose basis functions are specific to the considered physical problem and thus reduce numerical dispersion phenomena. We propose an iterative Trefftz solver based on a domain decomposition method which will reduce considerably the memory consumption. However, iterative Trefftz methods based on a plane wave approximation are ill-conditioned. To overcome this problem, we propose improvements of the Cessenat and Després preconditioner and a basis reduction. A matrix-free strategy allows to avoid the assembly of the matrix associated to the linear system and GMRES solver does not require the computation of the inverse anymore. This is a joint work with Sébastien Pernet (ONERA), which has been presented in several congresses such as SMAI (june 2021) 34 and ICOSAHOM (july 2021) 33.7.4.2 Discontinuous Galerkin Method based on Riemann fluxes for the time domain Maxwell System
Participants: Margot Sirdey, Sébastien Tordeux.
In the Inria Research report 48, we devise a discontinuous Galerkin method for the propagation of electromagnetic waves in a homogeneous medium. The numerical fluxes are deduced from the solution of a 1D electromagnetic problem. Numerical simulations illustrate the accuracy of the method. This is a joint work with Sébastien Pernet (ONERA) and Nadezhda Serdiuk (E2S Master student)7.4.3 Iterative Trefftz methods for anisotropic acoustic problems equations
Participants: Hélène Barucq, Ibrahima Djiba, Sébastien Tordeux.
During the master thesis of Ibrahima Djiba and the beginning of his PhD thesis, a numerical framework for the anisotropic wave equation thanks to a Trefftz method has been developped. We aim in solving a time harmonic problem without any matrix inversion. We resort to a Cessenat Després preconditioner and to a GMRES solver to accelerate the convergence of the algorithm wich allows to compute the solution of the considered problem with a low memory cost.7.4.4 A HDG framework for convected Helmholtz equation.
Participants: Hélène Barucq, Nathan Rouxelin, Sébastien Tordeux.
In this work, we introduce three variants of the HDG method based on two weak formulations of the convected Helmholtz equation. Two of them are standard HDG methods with the same interpolation degree for all the unknowns and the last uses a higher interpolation degree for the volumetric scalar unknown. For those three numerical methods, a detailed analysis including local and global well-posedness, as well as convergence estimates is carried out. We then provide implementation details and numerical experiments to illustrate our theoretical results. This work has been published in 46 and presented at ICOSAHOM 35 and ECCOMAS 36.7.4.5 Hybridizable Discontinuous Galerkin method for time-harmonic anisotropic poroelasticity in two dimensions.
Participants: Hélène Barucq, Julien Diaz, Ha Pham, Rose-Cloé Meyer.
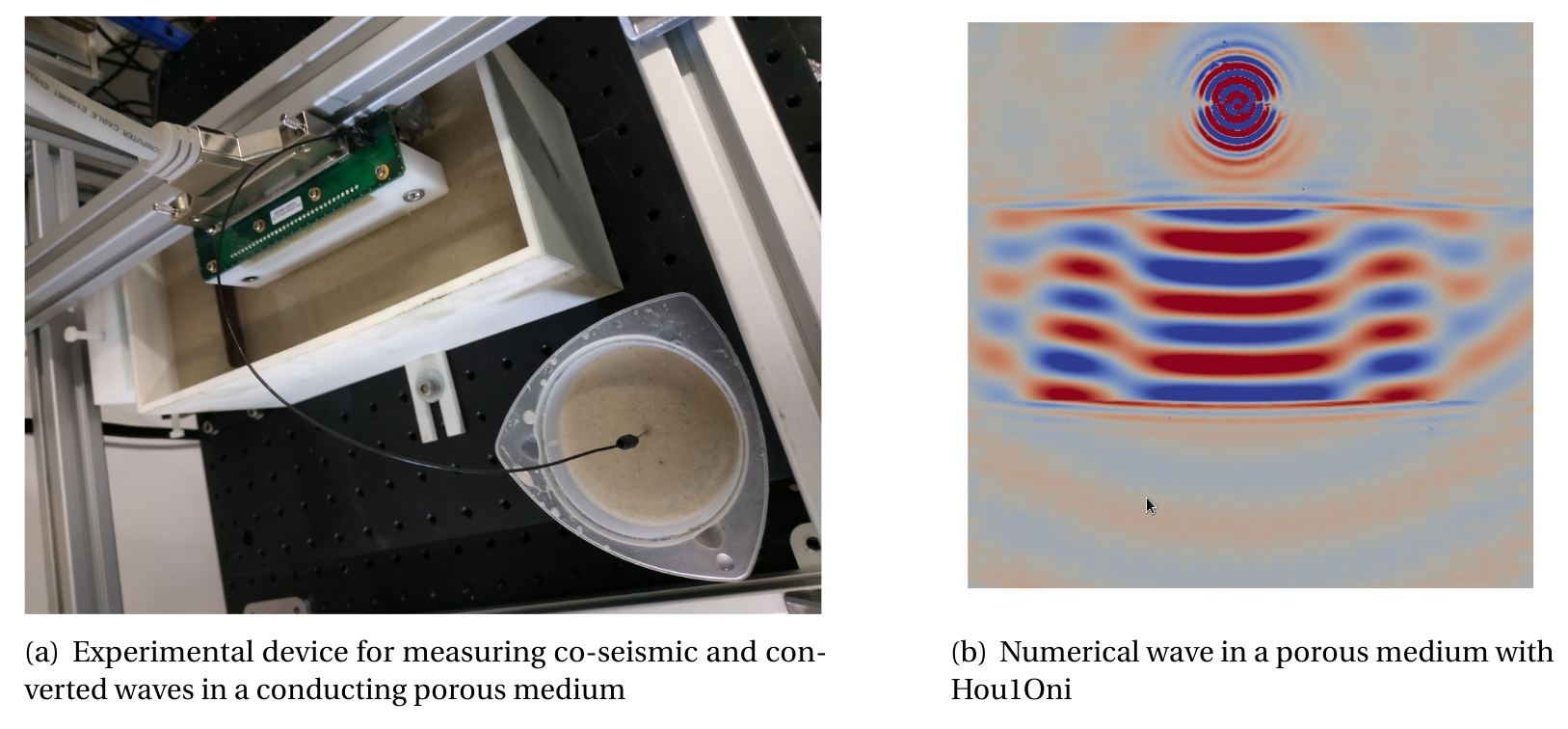
We consider the time-harmonic waves propagation in conducting poroelastic media. In poroelastic materials, whichare composed of an elastic solid frame and pores filled with fluid, wave propagation is described by Biot’s model. Ingeophysical media, due to the polarization of the fluid in the pores, one can observe the creation of elecromagneticwaves and even conversions between electromagnetic and seismic fields. They are the electrokinetic effects and aremodeled using Pride’s equations, a coupling between Maxwell’s and Biot’s equations. The electrokinetic couplinghas been observed in natural geophysical media both in laboratory and on the field. The converted waves are veryinteresting because they are heavily sensitive to the medium properties, and the seismoelectric conversions could forexample help to locate interfaces in the material that seismic waves cannot detect. The characterization of poroelasticor conducting poroelastic media is complex and involves many physical parameters, some of which depend non-linearlyon the frequencies. In addition, the seismic and electromagnetic speeds are significantly different, which is complicatedto handle for time domain simulations. Hence, we have chosen to solve the equations in the frequency domain andto use a Fourier transform to generate the seismograms in time domain. The main drawback to this is that we mustinvert one global linear system for each frequency, and this has a large computational cost because of the complexityof the equations and hence the high number of unknowns. In this work, we focus on the development and validation ofa Hybridizable Discontinuous Galerkin method for Pride’s model in the frequency regime. We validate the numericalmethod in two dimensions in circular geometry thanks to analytical solutions that we have constructed. Using theseanalytical solutions, we show in particular that the numerical method has an optimal order of convergence. In addition,to extend the method to infinite domains, we propose new radiation boundary condition for poroelastic equations andelectrokinetic equations. We have also implemented Perfectly Matched Layers and we have compared the performancesof the two methods. Finally, we show that the code we have developed is capable of modeling electrokinetic conversionsin the time domain. It is worth noting that we also provide details on the development of a HDG formulation for theporoelastic equations both in 2D and 3D.
This work is the topic of the PhD of Rose-Close Meyer, which has been funded by E2S-UPPA in the framework of the scientific challenge Chickpea. It has been defended in Septembre 2021 43. The HDG method for poroelastic material is presented in IJNME 12.
7.4.6 Local strategies for improving the conditioning of the plane-wave Ultra-Weak Variational Formulation
Participants: Hélène Barucq, Julien Diaz, Sébastien Tordeux.
Element-wise techniques based on SVD or QR Decomposition completely get rid of the usual ill-conditioning inherent to the plane-wave discretizations of the Ultra-Weak Variational Formulation (UWVF) for the Helmholtz equation. Associated preconditioning strategies lead to very low condition numbers of the corresponding linear system matrices, without any limitation on the number of plane waves per element. In addition, some of these procedures have the advantage of considerably reducing the size of the final system to be solved without altering the accuracy of the numerical solution.This is a joint work with Abderrahmane Bendali (Insa Toulouse). It has been published in JCP 10.
7.4.7 Efficient computation of modal Green's kernels for vectorial equations in helioseismology under spherical symmetry.
Participants: Hélène Barucq, Florian Faucher, Ha Pham.
We investigate the numerical computation of physical modal Green's kernels for the time-harmonic Galbrun's equation in helioseismology under spherical symmetry. These kernels are the coefficients of the 3D Green's kernels in the vector spherical harmonic expansion. In a previous work, we have characterized the physical kernels for the isothermal radial solar background model S-AtmoI and provide their well-posedness results. Here, we provide an algorithm to compute efficiently these kernels for all receiver and source positions in a region of interest and develop the technical ingredients for its implementation.
The kernels are built from the solution of a scalar wave equation for the radial displacement. The solution and its derivative which are both necessary to assemble the Green's kernel are obtained by solving a first-order system using the HDG method. This approach extends previous works considering a scalar wave equation and allows to model not only the pressure modes but also the surface and internal gravity waves. While being physically more interesting, this problem raises additional numerical difficulties. In particular, the solution of the Schrödinger equation for the radial displacement is singular without attenuation and it is thus preferable to solve the original equation. Moreover, for low frequencies and high-modes, the potential switches sign in the atmosphere which requires the position of the artificial boundary to be further away from the solar surface in order to capture the correct physical solution.
This is a joint work with Laurent Gizon and Damien Fournier of the Max Plank Institute for Solar system research in Göttingen (MPS), supported by the INRIA associated team ANTS between Makutu and MPS. A research report of 86 pages is available, 45.
7.4.8 Efficient computation of modal scalar Green's kernels with application to helioseismology.
Participants: Hélène Barucq, Florian Faucher, Ha Pham.
The computation of Green's kernels occupies an important place in terrestrial and extraterrestrial seismology which aim to reconstruct the interior from data on the surface. Currently, time-distance helioseismology relies on single-source computations which use Green's kernel with source s at fixed height. However, observed solar oscillations should be considered as an average over all depths weighted by transparency. This requires information of the ‘full’ Green's kernel, i.e., in the entire discretized region. Our algorithm solves for two regular solutions and the full kernel is assembled from these two simulations. It is thus independent of source position, in contrast to classical approaches which require different discretization as the source height varies. Additionally, the behavior of the kernel at the source position is described analytically and circumvents dealing with a singular source problem.
This is a joint work with Laurent Gizon and Damien Fournier of the Max Plank Institute for Solar system research in Göttingen (MPS), supported by the INRIA associated team ANTS between Makutu and MPS. It is the continuation of our work published in SIAM, 58, It has been presented at AGU Fall meeting, 26, the SIAM Conference on Mathematical & Computational Issues in the Geosciences, 22, and the ANTS Workshop on helioseismology, 28.
7.4.9 Recent work on sparse direct solvers to exploit numerical and structural properties of HDG discretizations.
Participants: Florian Faucher.
Efficient numerical simulation of wave propagation phenomena is needed in several applications such as seismic imaging, non-destructive testing, or helioseismology. We consider time-harmonic waves and the hybridizable discontinuous Galerkin discretization method, for which the efficiency of the wave propagator relies on the performance of finding the solution of systems of sparse linear equations. These systems have multiple sparse right-hand sides associated with several sources. This motivates the use of direct solvers which can efficiently reuse the LU factors to compute the solution of multiple right-hand sides at the cost however of a high memory footprint. Fortunately, matrices arising from the discretization of partial differential equations have been shown to have a low-rank property and the Block-Low Rank (BLR) format has been used to design fast direct solvers with reduced asymptotic complexity. In the context of 3D frequency-domain wave equations, the BLR factorization in 32-bit single precision arithmetic has been shown to provide accurate enough solutions. We further exploit lower precision formats (such as 24 and 16 bit arithmetics) in the representation of BLR blocks, while preserving a satisfactory accuracy. This allows us to reduce the memory footprint of the solver by further compressing both the LU factor matrices and the working space without affecting the precision of the solution. The performance are analyzed based upon hawen software, 71.
This is a joint work with the consortium MUMPS Technologies, in particular Patrick Amestoy (ENS Lyon), Jean-Yves L'Excellent (ENS Lyon), Théo Mary (Sorbonne University) and Chiara Puglisi. This work has been presented at ECCOMAS Conference and a preprint is being written. Some results regarding helioseismology have been presented at the ANTS Workshop on helioseismology, 29.
7.5 Reconstruction and design using full waveform inversion
7.5.1 Full waveform inversion for bore reconstruction of woodwind-like instruments
Participants: Juliette Chabassier, Augustin Ernoult.
The internal geometry of a wind instrument can be estimated from acoustic measurements. For woodwind instruments, this involves characterizing the inner shape (bore) but also the side holes (dimensions and location). In this study, the geometric parameters are recovered by a gradient-based optimization process, which minimizes the deviation between simulated and measured linear acoustic responses of the resonator for several fingerings through an observable function. The acoustic fields are computed by solving a linear system resulting from the 1D spectral finite elements spatial discretization of the wave propagation equations (including thermo-viscous effects, radiation and side holes). The “full waveform inversion” (FWI) technique exploits the fact that the gradient of the cost function can be computed by solving the same linear system as that of the direct problem but with a different source term. The gradient is computed with better accuracy and less additional cost than with finite-difference. The dependence of the cost function on the choice of the observed quantity, the frequency range and the fingerings used, is first analyzed. Then, the FWI is used to reconstruct, from measured impedances, an elementary instrument with 14 design variables. The results, obtained in about 1 minute on a laptop, are in excellent agreement with the direct geometric measurements.
This work has been done in collaboration with Samuel Rodriguez from I2M (University of Bordeaux, CNRS, Arts et Métier, Bordeaux INP) and the manufacturer Augustin Humeau from Humeau Factory. It has been published in 15.
7.5.2 Full Waveform Inversion on Seismic Data including Surface Waves.
Participants: Hélène Barucq, Julien Diaz, Florian Faucher, Chengyi Shen.
Makutu is collaborating with RealTimeSeismic (RTS) SME as part of the FEDER-Poctefa PIXIL project (Pyrenees Imaging eXperience: an InternationaL network) on the topic of Full Waveform Inversion (FWI), with a particular focus on the surface waves. The PIXIL project focuses on geophysical method development for geothermal surveys, where surface waves carry essential information of near- surfaces especially for shallow geothermal explorations. A good image of the near-surface can further help improve deep imaging. The collaboration RTS/Inria within the PIXIL project follows 3 main axes: data exchange/analyses, FWI strategy establishment and acquisition parameterization design. We aim at building a FWI tool suitable for surface waves and ultimately applying it onto real data acquired by RTS in a near-surface seismic exploration. The core of the numerical tool is a Fortran HPC code, named hawen 71 developed by Florian Faucher in time-harmonic domain featuring the Hybridizable Discontinuous Galerkin method. We conducted a 2D synthetic case study in order to establish Multi-level Strategies for FWI on seismic data including surface waves. A trade-off between robustness and high-resolution is achievable by elaborating suitable strategies such as combining seismic tomography and FWI featuring frequency groups, regularization and filtering. Meanwhile, Bash and Python programs are created to assist hawen for user-friendly concerns as well as data pre/post-processing, for instance, automatization of executions, data processing and visualization. We are currently making joint efforts to construct, test and validate a new cost-function in the Frequency-Wavenumber (FK) domain following the suggestions of literatures tackling surface waves 92, 85. Preliminary results confirm the major advantage of such a cost-function: the “attraction basin” is larger and smoother than in the Frequency-Space (FX) domain, which is a favorable condition for the convergence of the FWI result towards the targeted model. The FK domain is potentially the appropriate one in which the FWI featuring strong surface waves may work with both robustness and high-resolution.7.5.3 Time-Domain Full Waveform Inversion using advanced Discontinuous Galerkin methods
Participants: Hélène Barucq, Julien Diaz, Pierre Jacquet.
We developed tools for the reconstruction of subsurface media for seismic imaging and reservoir characterization in an industrial context. For that purpose, we used the Full Waveform Inversion (FWI) method. It is a reconstruction technique using data taken from seismic disturbances and whose behavior reflects the properties of the environment in which they propagate. In the framework of this thesis, we consider acoustic waves which are simulated thanks to Discontinuous Galerkin methods. These methods offer a very flexible discretization in space allowing to approach complex models and geometries. Discontinuous Galerkin methods are characterized by the use of fluxes in between each cell. Those fluxes contribute to have low communication costs which are highly recommended for High Performance Computing. Here, the wave equation is solved in time domain to overcome the memory limitations encountered in frequency domain for the reconstruction of large-scale 3D industrial media.To reconstruct quantitatively the physical model under study, we wrote the inverse problem as a minimization problem solved by adjoint state method. This method makes it possible to obtain the gradient of the cost function with respect to the physical parameters for the cost of two simulations; the direct problem and the backward problem also called adjoint problem.The adjoint state will be the solution of the discretized continuous adjoint problem ("Optimize Then Discretize"). This choice is justified by a 1D comparison with the strategy which consists in "Discretize then Optimize" completed by an algebraic study in superior dimension. The gradient thus calculated, is a key in the optimization procedure developed and integrated in the industrial environment provided by the industrial partner, TotalEnergies.The propagator is a keystone in solving the inverse problem. Indeed, it is repeated successively and represents the majority of the computation time of the optimization process. It is therefore important to control the discretization by the Discontinuous Galerkin method as well as possible. In particular, in this thesis, we have considered the idea of using different polynomial bases of approximation (Legendre or Bernstein-Bézier) as well as the choice of the parameterization, which can either be constant per element or variable thanks to the use of the Weight Adjusted Discontinuous Galerkin (WADG) method. This last strategy offers the opportunity to enlarge the mesh cells without losing information on the model and thus allows a more advanced use of the hp-adaptivity that we propose to fully exploit thanks to an adaptive mesh that is adjusted to the model meant to evolve with the iterations of the inverse problem.This is the topic of the PhD of Pierre Jacquet, defended in february 2021 42, in the framework of DIP. This is a collaboration with Henri Calandra.
7.5.4 Comparison of Fourier Reconstruction and Full Waveform Inversion for diffraction tomography.
Participants: Florian Faucher.
We study the mathematical imaging problem of diffraction tomography which is an inverse scattering technique used to find material properties of an object by illuminating it with probing waves and recording the scattered waves.Conventional DT relies on the Fourier diffraction theorem, which is applicable under the condition of weak scattering. However, if the object has high contrasts or is too large compared to the wavelength, it tends to produce multiple scattering, which complicates the reconstruction. We give a survey on diffraction tomography and compare the reconstruction of low and high contrast objects. We also implement and compare the reconstruction using the full waveform inversion method which, contrary to the Born and Rytov approximations, works with the total field and is more robust to multiple scattering.
This is a joint work with Clemens Kirisits (University of Vienna), Michael Quellmalz (TU Berlin), Otmar Scherzer (University of Vienna) and Eric Setterqvist (RICAM). A preprint is available online: 70.
7.5.5 Visco-acoustic ultrasound imaging allowing for attenuation model error.
Participants: Florian Faucher.
We perform ultrasound imaging in visco-acoustic media for the recovery of biological tissues and identification of embedded bodies. The attenuation of waves is encoded via different models in the propagation and we review the corresponding time-harmonic formulations to compare the resulting wave fields. For the reconstruction of the physical properties of the media, we use the full wave model for the propagation, and rely on a minimization algorithm to iteratively update the parameters. Firstly, we investigate the robustness of the algorithm with respect to model error, that is, when a different attenuation model is used between the data generation and the inversion. Secondly, to handle data-sets with multiple reflections generated by wall boundaries around the domain, we perform inversion using complex frequencies, and show that it offers a robust framework that alleviate the difficulties. To illustrate the performance of the algorithm, we carry out experiments with the imaging of a synthetic breast sample that contains an inclusion of sharp contrast in two and three dimensions, where the latter also serves to demonstrate the numerical feasibility in large-scale configuration.
This is a joint work with Otmar Scherzer (University of Vienna).
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
-
Depth Imaging Partnership (DIP3)
Period: 2019 May - 2021 December, Management: INRIA Bordeaux Sud-Ouest, Amount: 120000 euros/year.
-
Tent Pitcher algorithm for space-time integration of wave problems
Period: 2019 November - 2022 October, Management: INRIA Bordeaux Sud-Ouest, Amount: 165000 euros.
-
Numerical schemes assisted with Machine Learning for solving time-dependent seismic wave problems
Period: 2021 November - 2024 October, Management: INRIA Bordeaux Sud-Ouest, Amount: 90000 euros.
-
Isogeometric analysis of sharp boundaries in fullwaveform inversion
Period: 2019 January - 2021 December, Management: INRIA Bordeaux Sud-Ouest, Amount: 55000 euros.
-
Petrophysics in pre-salt carbonate rocks
Period: 2019 November - 2022 September, Management: INRIA Bordeaux Sud-Ouest, Amount: 110000 euros.
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Inria associate team not involved in an IIL or an international program
ANTS
-
Title:
Advanced Numerical meThods for helioSeismology
-
Duration:
2019 ->
-
Coordinator:
Laurent Gizon (gizon@mps.mpg.de)
-
Partners:
- Max Plank Institut
-
Inria contact:
Ha Howard Faucher
-
Summary:
Makutu is part of an Associate Team project, Advanced Numerical meThods for helioSeismology (ANTS), with the Max Planck Institute for Solar System Research (MPS), led by Laurent Gizon. The objective is to develop advanced software for accurate simulation of stellar oscillations and for the reconstruction of the Sun's interior. The novelty and challenge come from working with convected vector wave equations in the presence of complex flow and gravity, for a more accurate description of the physical phenomenon. The reference software is Hawen, based upon Hybridizable Discontinuous Galerkin (HDG) approximation and is complemented with the existing platform Montjoie which proposes classical finite element libraries. The scientific project benefits from the expertise of Makutu in seismic imaging, and the expert knowledge of the MPS group on Solar physics. The project also helps strengthen the on-going collaboration between Makutu and MPS, that started six years ago.
9.1.2 SEE4GEO project as part of European GEOTHERMICA initiative
SEE4GEO is for SeismoElectric Effects for GEOthermal resource assessment and monitoring. Information on the project is available here. The project is lead by Christina Morency, LLNL (Lawrence Livermore National Laboratory, US department of Energy). Makutu's is involved in the project as a joint team with UPPA (University of Pau and Pays de l'Adour).
9.2 International research visitors
9.2.1 Visits to international teams
Research stay abroad
Augustin Ernoult
-
Visited institution:
Erich Thienhaus Institute - Hochschule für Musik, Detmold
-
Country:
Germany
-
Dates:
Divided in two stays: 21/06/2021 to 21/07/2021 – 23/08/2021 to 17/10/2021
-
Context of the visit:
During the stay, two models of bassoon (French and German) have been compare in an acoustic point of view. This study encompass different set of measurements needing specific experimental set-ups and acoustic rooms. This included: sound recordings, impedance measurements, geometric measurements, measurements with artifical mouth, etc. All these data have been acquired, in collaboration with Timo Grothe within the ETI buildings, fully equiped for this kind of experimental campaign.
-
Mobility program/type of mobility:
Research stay funded by the DAAD (2.5k€) and the host institution (1k€)
9.3 European initiatives
9.3.1 FP7 & H2020 projects
MATHROCKS
-
Title:
Multiscale Inversion of Porous Rock Physics using High-Performance Simulators: Bridging the Gap between Mathematics and Geophysics
-
Duration:
April 2018 - March 2022
-
Coordinator:
Universidad Del Pais Vasco (EHU UPV)
-
Partners:
- BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
- BCAM - BASQUE CENTER FOR APPLIED MATHEMATICS (Spain)
- CURTIN UNIVERSITY OF TECHNOLOGY (Australia)
- PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE (Chile)
- REPSOL SA (Spain)
- UNIVERSIDAD CENTRAL DE VENEZUELA (Venezuela)
- UNIVERSIDAD DE BUENOS AIRES (Argentina)
- UNIVERSIDAD DEL PAIS VASCO/ EUSKAL HERRIKO UNIBERTSITATEA (Spain)
- UNIVERSIDAD NACIONAL DE COLOMBIA (Colombia)
- UNIVERSITAT POLITECNICA DE CATALUNYA (Spain)
-
Inria contact:
Hélène BARUCQ
-
Summary:
We will develop and exchange knowledge on applied mathematics, high-performance computing (HPC), and geophysics to better characterize the Earth´s subsurface. We aim to better understand porous rocks physics in the context of elasto-acoustic wave propagation phenomena. We will develop parallel high-continuity isogeometric analysis (IGA) simulators for geophysics. We will design and implement fast and robust parallel solvers for linear equations to model multi-physics electromagnetic and elasto-acoustic phenomena. We seek to develop a parallel joint inversion workflow for electromagnetic and seismic geophysical measurements. To verify and validate these tools and methods, we will apply the results to: characterise hydrocarbon reservoirs, determine optimal locations for geothermal energy production, analyze earthquake propagation, and jointly invert deep-azimuthal resistivity and elasto-acoustic borehole measurements. Our target computer architectures for the simulation and inversion software infrastructure consists of distributed-memory parallel machines that incorporate the latest Intel Xeon Phi processors. Thus, we will build a hybrid OpenMP and MPI software framework. We will widely disseminate our collaborative research results through publications, workshops, postgraduate courses to train new researchers, a dedicated webpage with regular updates, and visits to companies working in the area. Therefore, we will perform a significant role in technology transfer between the most advanced numerical methods and mathematics, the latest super-computer architectures, and the area of applied geophysics.
9.3.2 Other european programs/initiatives
PiXiL
-
Title:
Multiscale Inversion of Porous Rock Physics using High-Performance Simulators: Bridging the Gap between Mathematics and Geophysics
-
Duration:
September 2019 - April 2022
-
Coordinator:
BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
-
Partners:
- BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
- BCAM - BASQUE CENTER FOR APPLIED MATHEMATICS (Spain)
- UNIVERSIDAD DEL PAIS VASCO/ EUSKAL HERRIKO UNIBERTSITATEA (Spain)
- UNIVERSITAT de BARCELONA (Spain)
- REALTIMESEISMIC (RTS)
- PÔLE AVENIA
-
Inria contact:
Julien DIAZ
-
Summary:
Part of the FEDER Poctefa Program the PIXIL project is a transnational and multidisciplinary scientific and technological cooperation. Its main goal is to develop the most advanced tools to analyze the Earth's subsurface, with a special focus on fostering the uptake of geothermal energy in the region. The project will contribute to making the trans-Pyrenean area a technology hub in subsoil characterization within two years. Its success is expected to boost the wealth and creation of jobs related to the generation and management of underground natural resources in the area.
- See also:
9.4 National initiatives
9.4.1 SYSIMPA
-
Title:
Synthèse Sonore des Instruments de Musique du PAtrimoine
-
Durations
January 2020 – January 2022
-
Coordinator:
Inria
-
Partners:
- Cité de la Musique-Philharmonie de Paris (CM-P)
- Institut Technologique Européen des Métiers de la Musique (ITEMM) in le Mans
- Centre Culturel et de Restauration des Musées de France (C2RMF)
-
Summary:
This project aims at studying ancient music wind instruments (in this case, natural trumpets from around 1900) kept in the museum of CM-P using imaging technologies available at C2RMF and numerical methods developped at INRIA. The people involved in this project are : Tobias van Baarsel, Juliette Chabassier and Augustin Ernoult (INRIA) ; Romain Viala (ITEMM) ; Clotilde Boust and Elsa Lambert (C2RMF) ; Thierry Maniguet, Marguerite Jossic, Rodolphe Bailly, Cécile Cecconi and Sebastian Kirsch (CM-P).
-
Inria contact:
Tobias Van Baarsel
9.4.2 Depth Imaging Partnership
Magique-3D maintains active collaborations with Total. In the context of Depth Imaging, Magique-3D coordinates research activities dealing with the development of high-performance numerical methods for solving wave equations in complex media. This project has involved 2 other Inria Team-Projects (Hiepacs and Nachos) which have complementary skills in mathematics, computing and in geophysics. DIP is fully funded by Total by the way of an outline agreement with Inria .
The third phase of DIP began in 2019. Aurélien Citrain has been hired as engineer to work on the DIP platform. More than 10 PhD students have defended their PhD since the creation of DIP and most of them are now post-doctoral researchers or engineers in Europe. DIP is currently employing 3 PhD students.
9.5 Regional initiatives
9.5.1 Project supported by Conseil Régional d'Aquitaine
-
Title:
Revival.
-
Coordinator:
Juliette Chabassier
-
Other partners:
Univ Bordeaux, Univ Montreal (Canada), Univ Cath. Louvain (Belgium)
-
Summary:
The objective is to develop numerical tools for the virtual restoration of heritage instruments.
-
Financing:
This project is supported by the Conseil Régional d'Aquitaine, for a duration of 2 years and has funded the postdoctoral position of Tobias van Baarsel since Feb 2019.
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
Workshops:
- Tobias Van Baarsel organized a 2 days workshop with members of the SYSIMPA project 9.4.1.
- The ANTS Workshop on Helioseismology was organized online to present the latest results of the INRIA associated team ANTS between MAKUTU and the Max Plank Institute. It was held in March 2021.
Member of the organizing committees
- Hélène Barucq and Florian Faucher participated in the organization of the “Journées Calcul & Simulation en Nouvelle-Aquitaine”, held in Arcachon in December 2021.
10.1.2 Journal
Members of Makutu are regular reviewers for the following journals:
- Mathematics of Computation
- Numerical Methods in Engineering
- SIAM Journal on Scientific Computing
- ESAIM: Mathematical Modelling and Numerical Analysis
- Geophysical Journal International
- International Journal on Geomathematics
- Journal of Computational Physics
- International Journal for Numerical Methods in Engineering
- SIAM Journal on Scientific Computing
- SIAM Journal on Numerical Analysis
- SIAM journal on Applied Mathematics
- Inverse Problems
- Inverse Problems in Science & Engineering
- Journal of Acoustical Society of America
- Journal of Sound and Vibration
- Geophysics
- Journal of Inverse and Ill-Posed Problems
- Journal of Mathematical Imaging and Vision
10.1.3 Invited talks
Juliette Chabassier has been keynote speaker in the Journées d'Informatique Musicale 24.
10.1.4 Seminars
- Augustin Ernoult presented two seminars in the Erich Thienhaus Institute, Hochschule für Musik, Detmold, Germany, in the context of his research stay 9.2.1:
- "Modeling sound production in the recorder", 28/06/2021
- "Bassoon and Basson, an acoustical comparison", 11/10/2021
- Florian Faucher presented in the Mathematics & Statistics MACSI Seminar at the University of Limerick “Quantitative seismic imaging using recent sensing technology with Full Reciproity-gap Waveform Inversion”, in March 2021.
10.1.5 Leadership within the scientific community
- Augustin Ernoult is elected member of the "Groupe spécialisé d'acoustique musicale" (Gsam) of the french acoustical society.
- Hélène Barucq is member of the committee appointed by the Hcéres to carry out a national synthesis of the evaluations of French Mathematics
10.1.6 Scientific expertise
- Since 2017, Hélène Barucq is chairwoman of a committee which evaluates research projects in Mathematics, Computer Science, Electronics and Optics to be funded by the Regional Council New Aquitaine.
- Since 2018, Hélène Barucq is scientific officer for E2S project. She participates in the evaluation of each E2S call. She is also member of a committee having in charge the recruitment of non permanent researchers for E2S.
- Hélène Barucq acts as a scientific expert for the FWO (Research Foundation - Flanders.
- Hélène Barucq is member of the steering committee of CATIE.
10.1.7 Research administration
- Augustin Ernoult is member of the Center Commitee of Inria Bordeaux Sud-Ouest.
- Hélène Barucq is appointed member of the scientific board of the LMA2S (Laboratory of Mathematics Applied to Aeronautics and Space) created to federate the activities in Applied Mathematics which are carried out in seven departments of the ONERA.
- Julien Diaz is elected member of the Inria Technical Committee and of the Inria Administrative Board. He is appointed member of the Bureau du Comité des Projets (BCP) of Inria Bordeaux Sud-Ouest. Since 2018, he has been the head of the Mescal team of LMAP.
- Rose-Cloé Meyer is elected member of Laboratory Commitee of LMAP.
- Juliette Chabassier is member of the Research Position Commission of Inria Bordeaux Sud-Ouest.
10.2 Teaching - Supervision - Juries
- Licence : Rose-Cloé Meyer, Développements limités, suites et séries, 19.5h Eq. TD, L2, UPPA, France
- Master : Sébastien Tordeux, Outils Mathématiques pour la Mécanique, 49 eq. TD, Master1, UPPA, France
- Master : Margot Sirdey and Sébastien Tordeux, Introduction to wave phenomena, 48 eq. TD, Master, UPPA, France
- Licence : Sébastien Tordeux, Applied Mathematics, 18 eq. TD, L1, UPPA, France
- Master : Florian Faucher, Inversion/Optimization, UPPA, Pau, France, 5 eq. TD
10.2.1 Supervision
- PhD: Pierre Jacquet, Time domain Full Waveform Inversion involving hybrids numerical method to characterize elasto-acoustic media, February 25th, Hélène Barucq and Julien Diaz.
- PhD: Rose-Cloé Meyer, Modeling of conducting poro-elastic media using advanced numerical methods, Université de Pau et des Pays de l'Adour, September 30th, Hélène Barucq, Julien Diaz and Ha Howard Faucher.
- PhD: Nathan Rouxelin, Advanced numerical modeling of acoustic waves propagating below the surface of the Sun, Université de Pau et des Pays de l'Adour, December 10th, Hélène Barucq and Sébastien Tordeux.
- PhD: Stefano Frambati, Isogeometric analysis of sharp boundaries in full waveform inversion, December 13th, Hélène Barucq and Julien Diaz.
- PhD in progress: Victor Martins Gomez, Experimental characterization and modeling of seismo-electromagnetic waves, Université de Pau et des Pays de l'Adour, October 2018, Hélène Barucq and Daniel Brito (LFCR).
- PhD in progress : Margot Sirdey, Méthode de Trefftz pour l'électromagnétisme, October 2019, Sébastien Tordeux and Sébastien Pernet (Onera).
- PhD in progress : Vinduja Vasanthan, Tent Pitcher algorithm for space-time integration of wave problems, October 2019, Hélène Barucq and Julien Diaz.
- PhD in progress : Alexis Thibault, Modeling and simulation of wind musical instruments, October 2020, Juliette Chabassier and Thomas Hélie (IRCAM).
- PhD in progress : Guillaume Castera, Modeling and simulation of the piano touch, October 2020, Juliette Chabassier and Paul Fisette (Louvain Cath. Univ., Belgium).
- PhD in progress: Nicolas Victorion, Numerical schemes assisted with Machine Learning for solving time-dependent seismic wave problems, October 2021, Hélène Barucq, Florian Faucher and Emmanuel Franck (Inria Nancy Grand-Est, Tonus).
- PhD in progress: Arjeta Heta, Advanced numerical schemes to model seismoelectric effects and improve characterization of geological reservoirs, September 2021, Hélène Barucq and Julien Diaz.
- PhD in progress: Ibrahima Djiba, Trefftz domain decomposition method for wave propagation in geophysics, October 2021, Hélène Barucq et Sébastien Tordeux.
- PhD in progress: Marine Deheuvels, from quantitative analysis of wave amplitudes to full waveform inversion, October 2020, Daniel Brito (UPPA) et Florian Faucher
10.2.2 Juries
- Hélène Barucq: Hajer Methenni, Mathematical and numerical modeling for the simulation of ultrasonic integrated health monitoring of laminated composite plates, March 26th 2021, Reviewer
- Hélène Barucq: Paul Stocker (Vienna University, Austria), Space-time finite elment methods, July 1rst 2021, Reviewer
- Hélène Barucq: Adèle Veilleux (ISAE, Université Fédérale Toulouse Midi-Pyrénées), Extension of the Spectral Difference method to simplex cells and hybrid grids, March 24th 2021, Committee chair
- Hélène Barucq: Milad Farshad (Mines ParisTech, PSL, Université Paris), Multi-parameter seismic linear waveform imaging, December 9th 2021
- Hélène Barucq and Sébastien Tordeux: Ronan Cranny (ISAE, Université Fédérale Toulouse Midi-Pyrénées), Study of a hybrid finite volume - finite difference method and of a skewed thin wire model for electromagnetic compatibility applications, December 17th 2021, Examiner
- Hélène Barucq: Ibtissem Zaafrani (Université de Lorraine), Dynamics and stabilization of a cold magnetic plasma, December 19th 2021, Reviewer
- Julien Diaz : Alexandre Goupy (Université de Paris Saclay), Une approche spectrale de la métamodélisation multi-échelle appliquée à la propagation acoustique, March 26th 2021, Reviewer
- Juliette Chabassier : Pierre Carré (IRCAM) : Méthodes numériques d’inspiration géométrique pour la synthèse sonore par modèle physique; application à un modèle de corde géométriquement exact, Dec 21st, 2021, Examiner
- Juliette Chabassier : Nathan Rouxelin (Inria), Méthodes numériques mixtes condensées pour l’étude de la propagation des ondes acoustiques en écoulement. Applications en héliosismologie, Dec 10th2021, Examiner
- Juliette Chabassier : Hajer Methenni, Mathematical and numerical modeling for the simulation of ultrasonic integrated health monitoring of laminated composite plates, March 26th 2021, Examiner
- Florian Faucher : Nathan Rouxelin (Inria), Méthodes numériques mixtes condensées pour l’étude de la propagation des ondes acoustiques en écoulement. Applications en héliosismologie, Dec 10th2021, Examiner
10.3 Popularization
Juliette Chabassier participated in a round table during the popularization congress Science & You 30.
10.3.1 Articles and contents
10.3.2 Interventions
- Tobias Van Baarsel participated to the Musicora exhibition in Paris, on the 19th-21th of Novemebr 2021. He gave a public talk to present the project SYSIMPA 9.4.1 and the numerical restoration of an historical trumpet.
10.4 Creation of media or tools for science outreach
Juliette Chabassier co-created with the Ensemble Les Précieuses the show Louis 14.0 that presents how ancient instruments can be restored via numerical techniques, and played in real time in a musical and theatral show.
11 Scientific production
11.1 Major publications
- 1 articleLocal strategies for improving the conditioning of the plane-wave Ultra-Weak Variational Formulation.Journal of Computational Physics441September 2021, 110449
- 2 articlePolynomial-reproducing spline spaces from fine zonotopal tilings.Journal of Computational and Applied Mathematics402March 2022, 113812
- 3 articleImplementation of Hybridizable Discontinuous Galerkin method for time-harmonic anisotropic poroelasticity in two dimensions..International Journal for Numerical Methods in Engineering2021
- 4 articleOutgoing modal solutions for Galbrun's equation in helioseismology.Journal of Differential Equations286June 2021, 494-530
- 5 articleConstruction and convergence analysis of conservative second order local time discretisation for linear wave equations.ESAIM: Mathematical Modelling and Numerical Analysis554July 2021, 1507-1543
- 6 articleFull waveform inversion for bore reconstruction of woodwind-like instruments.Acta AcusticaNovember 2021
- 7 articleEfficient hybrid method for the modal analysis of optical microcavities and nanoresonators.Journal of the Optical Society of America. A Optics, Image Science, and Vision388July 2021, 1224
- 8 articleDissipative time-domain one-dimensional model for viscothermal acoustic propagation in wind instruments..Journal of the Acoustical Society of America1502August 2021, 1165-1175
11.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
11.3 Other
Scientific popularization
11.4 Cited publications
- 50 bookAsteroseismology.Springer Science & Business Media2010
- 51 articleProbing the interior physics of stars through asteroseismology.arXiv preprint arXiv:1912.123002019
- 52 articleInverse problem for the Helmholtz equation with Cauchy data: reconstruction with conditional well-posedness driven iterative regularization.ESAIM: Mathematical Modelling and Numerical Analysis533May 2019, 1005-1030
- 53 articleThe mechanism producing initial transients on the clarinet.The Journal of the Acoustical Society of America14262017, 3376-3386
- 54 articleQuasistatic nonlinear characteristics of double-reed instruments.The Journal of the Acoustical Society of America12112007, 536-546
- 55 articleAbout the stability of the inverse problem in 1-D wave equations—Application to the interpretation of seismic profiles.Applied Mathematics and Optimization511979, 1--47
- 56 articleSpace-time Trefftz-DG approximation for elasto-acoustics.Applicable Analysis00August 2018, 1 - 16
- 57 articleStability analysis of heterogeneous Helmholtz problems and finite element solution based on propagation media approximation.Mathematics of Computation863072017, 2129 - 2157
- 58 articleEfficient and Accurate Algorithm for the Full Modal Green's Kernel of the Scalar Wave Equation in Helioseismology.SIAM Journal on Applied Mathematics806December 2020, 2657-2683
- 59 articleGlobal seismology of the Sun.Living Reviews in Solar Physics1312016, 2
- 60 articleDirect Simulation of Reed Wind Instruments.Computer Music Journal3342009, 43-55
- 61 articleHybridizable discontinuous Galerkin method for the two-dimensional frequency-domain elastic wave equations.Geophysical Journal International2131April 2018, 637--659
- 62 articleInterpretation of helioseismic travel times.Space Science Reviews1961-42015, 201--219
- 63 techreportViscothermal models for wind musical instruments.RR-9356Inria Bordeaux Sud-OuestAugust 2020
- 64 inproceedingsIdentification of functional parameters in partial differential equations.Joint Automatic Control Conference121974, 155--156
- 65 articleHelioseismology.Reviews of Modern Physics7442002, 1073
- 66 articleImproved precision in measurements of acoustic impedance spectra using resonance-free calibration loads and controlled error distribution.The Journal of the Acoustical Society of America12132007, 1471-1481
- 67 articleTransfer matrix of a truncated cone with viscothermal losses: application of the WKB method.Acta Acustica42May 2020
- 68 articleWoodwind instrument design optimization based on impedance characteristics with geometric constraints.Journal of the Acoustical Society of America1485November 2020, 2864-2877
- 69 phdthesisContributions to Seismic Full Waveform Inversion for Time Harmonic Wave Equations: Stability Estimates, Convergence Analysis, Numerical Experiments involving Large Scale Optimization Algorithms.Université de Pau et des Pays de l'AdourNovember 2017
- 70 unpublishedDiffraction Tomography, Fourier Reconstruction, and Full Waveform Inversion.October 2021, 31 pages, 21 figures
- 71 articlehawen: time-harmonic wave modeling and inversion using hybridizable discontinuous Galerkin discretization.Journal of Open Source Software657January 2021, 2699
- 72 articleSensitivity kernels for time-distance helioseismology-Efficient computation for spherically symmetric solar models.Astronomy & Astrophysics6162018, A156
- 73 articleAcoustical impedance measurements by the two‐microphone‐three‐calibration (TMTC) method.The Journal of the Acoustical Society of America8861990, 2533-2545
- 74 articleComputational helioseismology in the frequency domain: acoustic waves in axisymmetric solar models with flows.Astronomy and Astrophysics - A&A600April 2017, A35
- 75 articleLocal helioseismology.Living Reviews in Solar Physics212005, 6
- 76 articleLocal helioseismology: three-dimensional imaging of the solar interior.Annual Review of Astronomy and Astrophysics482010, 289--338
- 77 articleSignal and noise in helioseismic holography.Astronomy & Astrophysics6202018, A136
- 78 articleReal-time synthesis of clarinet-like instruments using digital impedance models.The Journal of the Acoustical Society of America11812005, 483-494
- 79 articleThe dispersion of surface waves on multilayered media.Bulletin of the seismological Society of America4311953, 17--34
- 80 articleGiant star seismology.The Astronomy and Astrophysics Review2512017, 1
- 81 inproceedingsSeismic imaging of supercritical geothermal reservoir using full-waveform inversion method.Proceedings2019
- 82 bookSeismic wave propagation in stratified media.ANU Press2009
- 83 article3-D seismic exploration across the deep geothermal research platform GroßSchönebeck north of Berlin/Germany.Geothermal Energy712019, 1--18
- 84 inproceedingsThe seismic inverse problem as a sequence of before stack migrations.Conference on inverse scattering: theory and applicationSiam Philadelphia, PA1983, 206--220
- 85 phdthesisInversion of surface waves in an oil and gas exploration context.Université Grenoble Alpes (ComUE)2016
- 86 articleA review of the adjoint-state method for computing the gradient of a functional with geophysical applications.Geophysical Journal International16722006, 495--503
- 87 articleGauss--Newton and full Newton methods in frequency--space seismic waveform inversion.Geophysical Journal International13321998, 341--362
- 88 articleTwo-dimensional velocity models from wide-angle seismic data by wavefield inversion.Geophysical Journal International12421996, 323--340
- 89 articleINVERSE THEORY APPLIED TO MULTI-SOURCE CROSS-HOLE TOMOGRAPHY. PART 1: ACOUSTIC WAVE-EQUATION METHOD 1.Geophysical prospecting3831990, 287--310
- 90 articleSeismic attenuation due to wave-induced flow.J. Geophys. Res.1092004, 681-693
- 91 articleWebster's Horn Equation Revisited.SIAM Journal on Applied Mathematics6562005, 1981-2004
- 92 phdthesisTwo-dimensional near-surface seismic imaging with surface waves: alternative methodology for waveform inversion.Ecole Nationale Supérieure des Mines de Paris2013
- 93 articleProperty modelling of a potential CO2 storage site using seismic inversion.EGUGA2013, EGU2013--10470
- 94 bookSurface wave methods: acquisition, processing and inversion.2003
- 95 bookInverse problem theory and methods for model parameter estimation.89siam2005
- 96 bookInverse problem theory: methods for data fitting and model parameter estimation.Amsterdam, NetherlandsElsevier Science Publishers1987
- 97 articleTransmission of elastic waves through a stratified solid medium.Journal of applied Physics2121950, 89--93
- 98 articleDemonstrating storage of CO2 in geological reservoirs: The Sleipner and SACS projects.Energy299-102004, 1361--1369
- 99 articleA comparison of a one-dimensional finite element method and the transfer matrix method for the computation of wind music instrument impedance.Acta Acustica united with Acustica52019, 838
- 100 articleSound production in recorderlike instruments. II. A simulation model.The Journal of the Acoustical Society of America10151997, 2925-2939
- 101 articleInfluence of fluid displacement patterns on seismic velocity during supercritical CO2 injection: Simulation study for evaluation of the relationship between seismic velocity and CO2 saturation.International Journal of Greenhouse Gas Control462016, 197--204
- 102 phdthesisModeling experiments in helioseismic holography.Niedersächsische Staats-und Universitätsbibliothek Göttingen2019

