Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.4. Model reduction
- A6.5.1. Solid mechanics
- A6.5.2. Fluid mechanics
- A9.2. Machine learning
Other Research Topics and Application Domains
- B2.2.1. Cardiovascular and respiratory diseases
- B4.2. Nuclear Energy Production
- B4.3.2. Hydro-energy
- B4.3.3. Wind energy
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Michel Bergmann [Inria, Researcher, HDR]
- Tommaso Taddei [Inria, Researcher]
Faculty Members
- Angelo Iollo [Team leader, Univ de Bordeaux, Professor, HDR]
- Afaf Bouharguane [Univ de Bordeaux, Associate Professor]
Post-Doctoral Fellows
- Antoine Fondaneche [Inria, from Oct 2021]
- Nishant Kumar [Inria, from Oct 2021]
- Gwladys Ravon [Inria]
- Sebastien Riffaud [Inria, from Apr 2021 until Oct 2021]
- Lei Zhang [Inria, until Sep 2021]
PhD Students
- Eki Agouzal [Inria, CIFRE, from Mar 2021]
- Beatrice Battisti [Ecole Polytechnique de Turin]
- Michele Giuliano Carlino [Inria]
- Antoine Fondaneche [Univ de Bordeaux, until Aug 2021]
- Caroline Anna Lise Andrea Le Guern [Inria, from Oct 2021 until Nov 2021]
- Karl Maroun [Univ de Poitiers, from Nov 2021]
- Thomas Philibert [Ecole Polytechnique de Turin]
- Michele Romanelli [ONERA, from Oct 2021]
- Ludovica Saccaro [Inria]
- Giulia Sambataro [ANDRA]
- Alexis Tardieu [Univ de Bordeaux, from Oct 2021]
Interns and Apprentices
- Pascal Engelibert [Univ de Bordeaux, from Jun 2021 until Jul 2021]
Administrative Assistant
- Anne-Laure Gautier [Inria]
Visiting Scientists
- Andrea Christine Thomann [ University of Insubria in Como (Italy), from Sep 2021 until Oct 2021]
- Elena Travaglia [Ecole Polytechnique de Turin, Oct 2021]
External Collaborator
- Majdi Azaiez [Institut National Polytechnique de Bordeaux, HDR]
2 Overall objectives
2.1 Multi-physics numerical modeling
2.1.1 Reduced-order models: convergence between PDE models and data
Unprecedented opportunities exist to directly use already collected computational or experimental data to improve and build predictive models that can be used online for the simulation of parametric problems, robust design, and control in science and engineering. In this regard, our goal is to combine mechanistic causal models based on partial differential equations (PDEs) with large data sets to reduce the marginal cost of predictions.
Reduced-order models (ROMs) are our main tool for this purpose. ROMs are parametric mathematical models derived from the full set of PDEs using previously computed solutions. In many applications, the solution space turns out to be low-dimensional, so one can trade a minimal loss of accuracy for speed and scalability. ROMs counteract the curse of dimensionality by significantly reducing computational complexity.
Overall, ROMs have reached a certain level of maturity during the last decade, allowing their implementation in large-scale industrial codes, mainly in structural mechanics. Nevertheless, some hard points stand. Parametric problems governed by strong advection fields or sensibly compact-support solutions such as moving shocks suffer from a limited possibility of dimensional reduction and, at the same time, insufficient generalization of the model (out-of-sample solutions). The main reason for this is that the solution space is usually approximated by an affine or linear representation, which is intrinsically broad band for such problems.
We have worked on the development of model order reduction (MOR) techniques for nonlinear, advection-dominated problems, with emphasis on projection-based Galerkin and Petrov-Galerkin ROMs. First, we worked on the development of effective sampling strategies to reduce training costs. Second, we developed nonlinear, registration-based approximation techniques, to overcome limitations of linear approximation methods (e.g., proper orthogonal decomposition, POD) to deal with strong advection fields. Third, we developed hybrid formulations that combine reduced-order and full-order models to deal with complex flow features and/or complex parameterizations.
2.1.2 Schemes for Hierarchical meshes, multi-physics and asymptotic limits
The schemes we have developed aim at simulating complex multiphysics phenomena through appropriate PDE modeling, automatic implicit geometry representation (level sets), hierarchical Cartesian schemes (quad-octrees), parallel simulations, and accurate treatment of boundaries. Discretization schemes on hierarchical meshes allow multiscale solution of PDEs on non-body-fitted meshes with a drastic reduction in computational setup overhead. The key idea is to use an octree mesh to approximate the solution fields, while the geometry is captured by level set functions. The boundary conditions are determined by appropriate interpolation methods to achieve sufficient accuracy. This approach eliminates the need for boundary conforming meshes, which require time-consuming and error-prone mesh generation procedures, and opens the door to easy parallel simulation of very complex geometries.
One of the limitations of this approach is that a mesh with a fixed aspect ratio is not optimal for very anisotropic fields such as boundary layers. For such cases, we explored the idea of using a body-fitted grid near the immersed obstacles and a hierarchical mesh in the background. Essentially, we use the techniques we have developed to impose boundary conditions on non-body-matched meshes further from the boundary, where the solution is smoother and more isotropic. Our current investigations build on discontinuous Galerkin (DG) methods / ADER approaches to combine efficient interpolation strategies at the grid interfaces and compact reconstruction of the data at the grid level.
Part of our activity has been dedicated to improve schemes for all Mach number flows in both fluid dynamics and continuum mechanics. Phenomena of interest involve fluid flows and elastic materials whose deformations are investigated within a monolithic Eulerian framework. With this approach any material (gas, liquid or solid) can be described with the same system of conservation equations and a suitable general formulation of the constitutive law.
These schemes are accurate in computing steady state solutions as well as in approximating material wave propagation in various Mach regimes and different materials. We are presently studying methods to overcome the need to solve for auxiliary relaxation variables while preserving the properties of the linearly implicit schemes. To achieve this, we split the stiff relaxation source terms from the fluxes and then reformulate the homogeneous part in an elliptic form.
3 Research program
Coherently with our investigation approach, we will start from applications to identify key methodological problems, study those problems and go back to actual code implementation.
3.1 Numerical models
We aim to further develop automated model-order reduction (MOR) procedures for large-scale systems in computational mechanics — here, automated refers to the ability to complete the analysis with minimal user intervention. First, we wish to combine nonlinear MOR with mesh adaptation to simultaneously learn rapid and reliable ROMs and effective high-fidelity discretizations over a range of parameters. Second, we wish to develop component-based MOR procedures to build inter-operable components for steady and unsteady nonlinear PDEs: towards this end, we should develop efficient localized training procedures to build local ROMs for each archetype component, and also domain decomposition techniques to glue together the local models for prediction. We also wish to develop and analyze hybrid approaches that combine and merge first-principle models with data-fit models, and also full-order and reduced-order models for prediction of global engineering quantities of interest.
These objectives, hence, do not substantially differ in the long term from the previously but some of the methods that we develop can be complemented by available tools form machine learning, like solution clustering, optimal sampling, classification of the solutions... In this respect, a leap forward in industrial applications that we will pursue is without doubts the possibility of capitalizing on previous experience drawn from already acquired simulations to build non-intrusive models combining non-linear interpolations and non-linear regression. New perspectives in this direction are offered by the Chair Onera-Nouvelle Aquitaine. This Chair (Angelo Iollo and Denis Sipp of Onera are the PIs) was pre-funded in late 2021 and is endowed with 6 PhD grants and 2 post docs. This framework partly funded by Onera, the french aerospace lab, and the region Nouvelle Aquitaine will be dedicated to several aspects of reduced modeling and data driven models involving research and industrial partners. One PhD thesis funded by the Chair has already started end 2021 dedicated to data driven wall-law models for turbulent simulations (Michele Romanelli). The goal is to apply deep learning approaches to approximate wall laws for airfoils. In this direction, with the PhD of Thomas Philibert funded by Politecnico di Torino in co-direction with our team, we will be investigating data-driven models that intrinsically respect physical constraints for turbulence modeling. Two additional PhD thesis funded by the Onera-Nouvelle Aquitain Chair are foreseen in 2022 dedicated to distributed non-linear interpolations and surrogate models (response surface, clustering, active subspaces).
As for approximation schemes for PDEs, with respect to the previous evaluation, emphasis will be put on the representation of the solution in each computational cell by adopting a DG / ADER approach to improve accuracy at the level jumps. This approach will be complemented with a Chimera grid at the boundaries in order to improve accuracy by a body fitted mesh avoiding grid generation complexity for a general, possibly varying, geometrical topology. The thesis of Alexis Tardieu started in October 2021 and funded by the university of Bordeaux will study this approach. Still in this direction we will continue to study asymptotic scheme for multimaterials, towards a unified approach for compressible and incompressible materials.
In parallel, we will continue our exploration of schemes that contour the problem of accuracy and time stepping in the asymptotic regimes such as low and high mach numbers for multi-material flows, the Graal being an asymptotic preserving scheme that is able to capture phenomena at the time scale of the fast waves and of the material waves with the same accuracy, exclusively choosing the appropriate time-scale.
3.2 Applications
For energy applications, we will continue our investigations on wave energy converters and windturbines. Relative to wave energy converters, we are developing multifidelty models coupling the incompressible Navier-Stoke equations (NSE) around the floater with a Proper Orthogonal (POD) Reduced Order Model elsewhere. In April 2022, a two year post doc, funded by Inria and the Region Nouvelle Aquitaine, will continue in that direction replacing the POD model with an asymptotic one like shallow water equation or Boussinesq model. A similar approach (NSE-POD coupling) is also considering for wind-turbines. In the two year post doc of Nishant Kumar, founded by the Inria-IfpEN program and started in October 2021, we implement a multi-fidelity approach within the SOWFA framework. In the PhD of Caroline Le Guern, funded by the Inria-IfpEN program and started in December 2021, we are studying the fluid-structure interactions of a new generation of large windturbines (250 meter rotor) using the Deeplines software co-developed by IfpEN. The collaboration with EDF is likely to be continued in the direction of multi-fidelity models (HFM-ROM) in the Telemac Mascaret code.
Within the ARIA project, in collaboration with Nurea and the bio-mechanics lab of the Politecnico di Torino, we will investigate the idea of data augmentation starting from a given aneurysm database. We will construct statistically relevant synthetic aneurysms that can provide both heterogeneity and closeness to reality to test new bio-markers for aneurysm rupture. The thesis of Ludovica Saccaro funded by Inria is dedicated to this subject.
We are proposing a DFG-CNRS project (with Wolfgang Schröder, RWTH Aachen University) related the Finite Size Objects Interacting in Turbulent Flows, and more precisely on the development of particle-interaction models for spheroidal particles in turbulent free jets. We are also participating in proposing a European Project around Green Aviation/Airport with focus on reduced order models, gappy data and surrogate models.
We will also increase our interactions with biological and physicists partners. In the ANR DRAGON, we will build a digital twin of a snake swimming based on data obtained by biologists.
The sofware development will be continued. We will pursue the development of the NEOS library: NEOS will be distributed in open source LGPL-3.0. The HIWIND software will be rewritten based on NEOS library.
4 Application domains
4.1 Energy conversion
We apply the methods developed in our team to the domain of wind engineering and sea-wave converters. In Figure 1, we show results of a numerical model for a sea-wave energy converter. We here rely on a monolithic model to describe the interaction between the rigid floater, air and water; material properties such as densities, viscosities and rigidity vary across the domain. The appropriate boundary conditions are imposed at interfaces that arbitrarily cross the grid using adapted schemes built thanks to geometrical information computed via level set functions 37. The background method for fluid-structure interface is the volume penalization method 28 where the level set functions is used to improve the degree of accuracy of the method 4 and also to follow the object. The underlined mathematical model is unsteady, and three dimensional; numerical simulations based on a grid with degrees of freedom are executed in parallel using 512 CPUs.

See-wave converter


In the context of the Aerogust (Aeroelastic gust modelling) European project, together with Valorem, we investigated the behavior of wind turbine blades under gust loading. The aim of the project was to optimize the design of wind turbine blades to maximize the power extracted. A meteorological mast (Figure 2(a)) has been installed in March 2017 in Brittany to measure wind on-site: data provided by the mast have been exploited to initialize the mathematical model. Due to the large cost of the full-order mathematical model, we relied on a simplified model 35 to optimize the global twist. Then, we validated the optimal configuration using the full-order Cartesian model based on the NaSCar solver. Figure 2(b) shows the flow around the optimized optimized wind turbine rotor.
4.2 Schemes for turbulent flow simulations using Octrees
We have initially developed and tested a 3D first-order Octree code for unsteady incompressible Navier-Stokes equations for full windmill simulations with an LES model and wall laws. We have validated this code on Occigen for complex flows at increasing Reynolds numbers. This step implied identifying stable and feasible schemes compatible with the parallel linear Octree structure. The validation has been conducted with respect to the results of a fully Cartesian code (NaSCAR) that we run on Turing (with significantly more degrees of freedom) and with respect to experimental results.
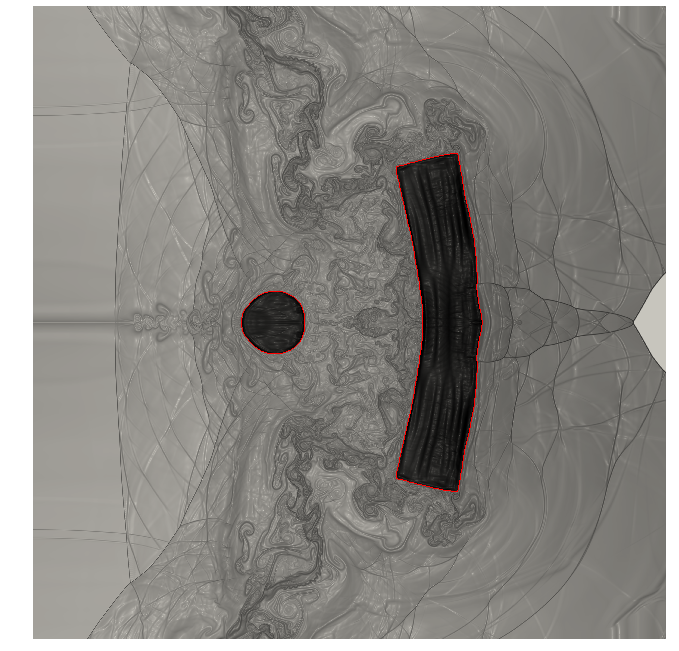
Subsequently, we have developed a second-order Octree scheme that has been validated on Occigen for a sphere at a moderate Reynolds number (), see Table 1. Then, for a cylinder at () (Figures 3(a) and 3(b)), close to real applications, we have preliminary validation results for the second-order scheme with respect to experimental drag coefficient (Table 2). Additional resources will be asked on Occigen to complete the study.
| Mesh | number of cells | (1st-order scheme) | (2nd-order scheme) | |
| 1 | N.A. | |||
| 2 | ||||
| 3 | ||||
| 4 |
| Case | |
| Octree, 1st-order scheme | |
| Octree, 2nd-order scheme | |
| Cartesian | |
| Experimental estimate 32 |

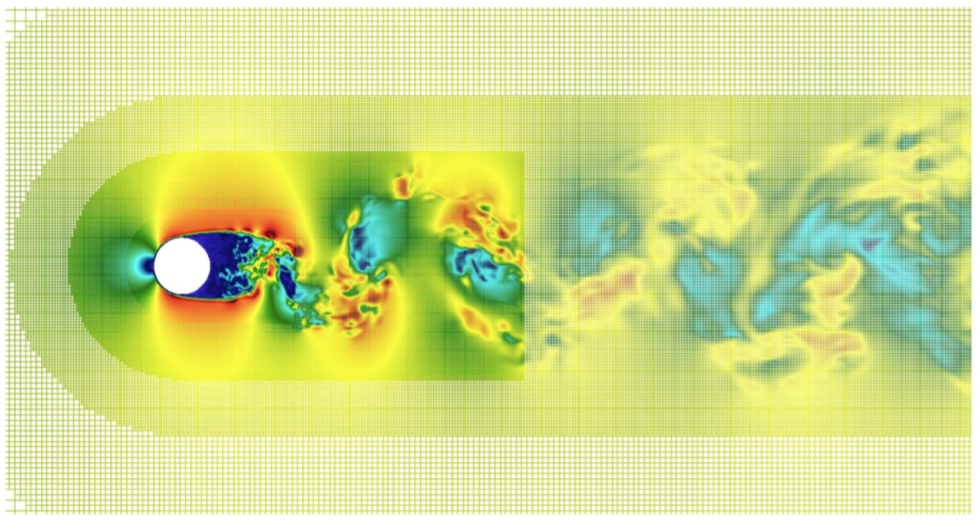
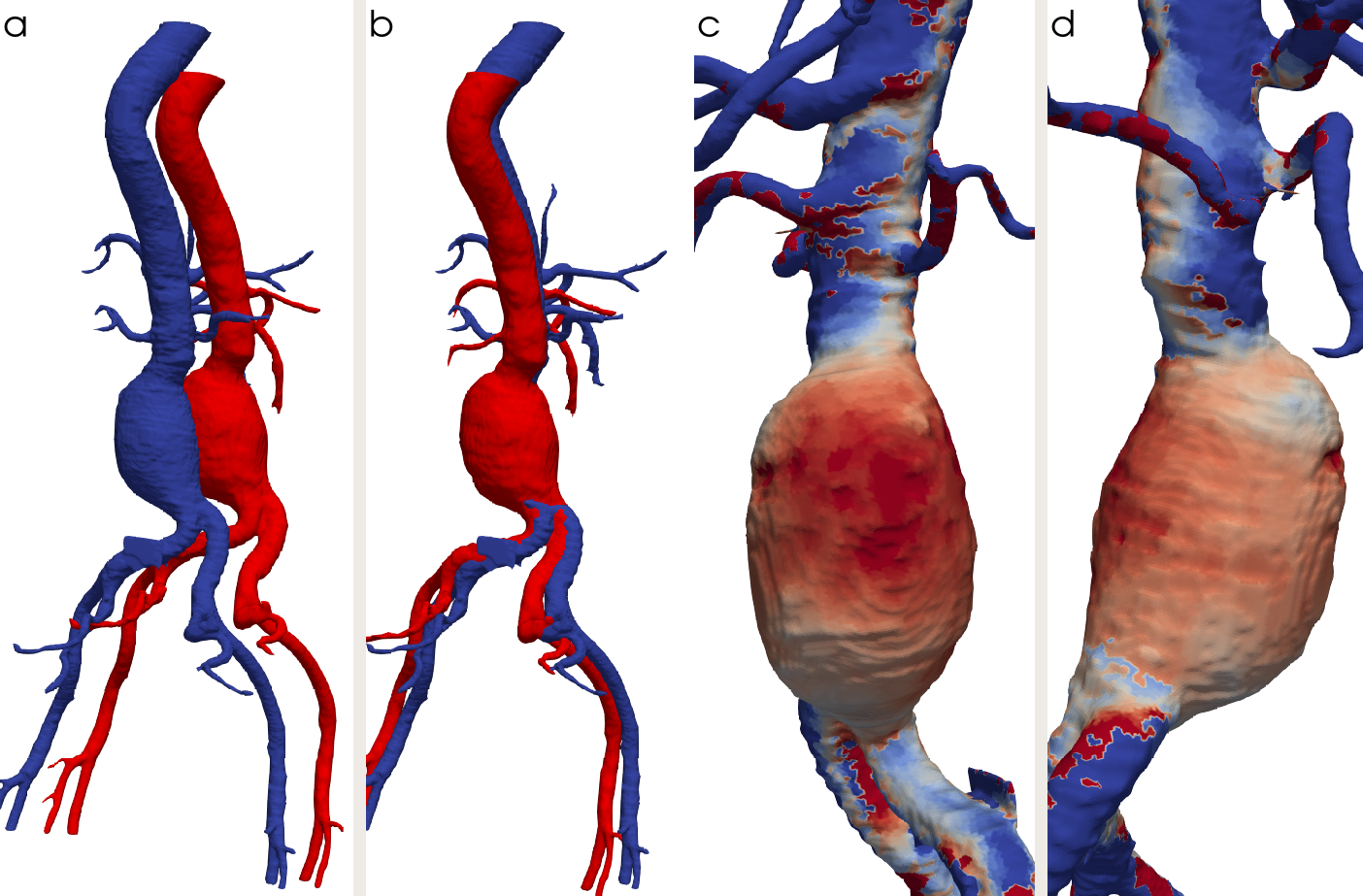
4.3 Vascular flows
A new research direction pursued by the team is the mathematical modelling of vascular blood flows in arteries. Together with the start-up Nurea and the surgeon Eric Ducasse, we aim at developing reliable and automatic procedures for aneurysm segmentation and for the prediction of aneurysm rupture risk. Our approach exploits two sources of information: (i) numerical simulations of blood flows in complex geometries, based on an octree discretization, and (ii) computed tomography angiography (CTA) data. Figure 4 shows the force distribution on the walls of the abdominal aorta in presence of an aneurysm; results are obtained using a parallelized hierarchical Cartesian scheme based on octrees.
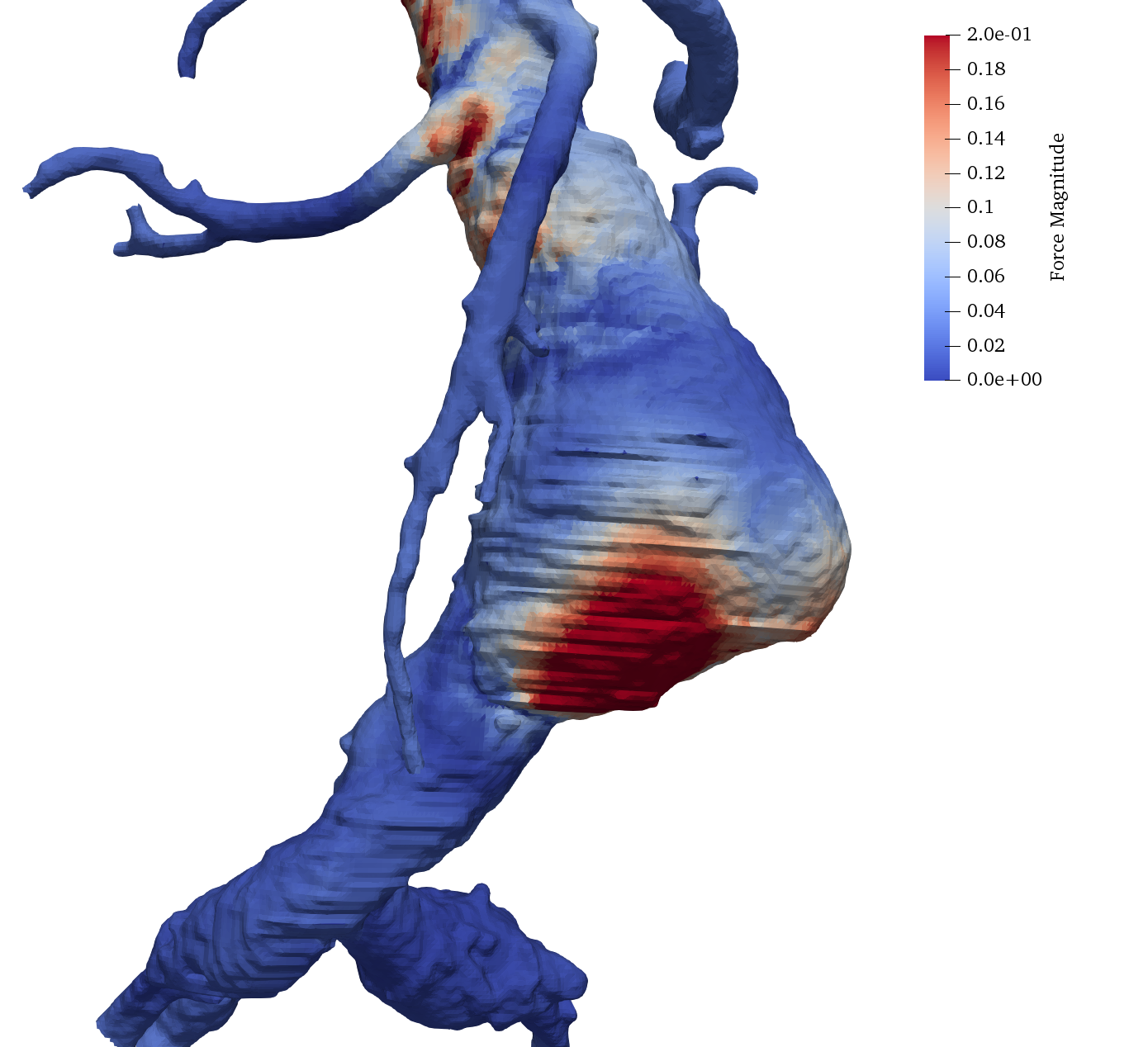
Aneurysm simulation
4.4 Fluid-structure interactions using Eulerian non-linear elasticity models
Mathematical and numerical modeling of continuum systems undergoing extreme regimes is challenging due to the presence of large deformations and displacements of the solid part, and due to the strongly non-linear behavior of the fluid part. At the same time, proper experiments of impact phenomena are particularly dangerous and require expensive facilities, which make them largely impractical. For this reason, there is a growing interest in the development of predictive models for impact phenomena.
In MEMPHIS, we rely on a fully Eulerian approach based on conservation laws, where the different materials are characterized by their specific constitutive laws, to address these tasks. This approach was introduced in 34 and subsequently pursued and extended in 36, 33, 29, 31 and 9. In Figure 5, we show the results of the numerical simulation of the impact of a copper projectile immersed in air over a copper shield. Results are obtained using a fully parallel monolithic Cartesian method, based on a fixed Cartesian grid. Simulations are performed on a cluster of 512 processors, and benefits from the isomorphism between grid partitioning and processor topology.

In figure 6, we show the results of a three dimensional simulation of a cardiac pump (LVAD, left ventricule assisted device).
Cardiac pump simulation
Other examples are given in the sections dedicated to the new results.
5 Social and environmental responsibility
One main focus of the team is the renewable energy. We develop mathematical models and numerical methods to study problems related to renewable energies.
5.1 Impact of research results
We are studying two types of green energy extractors.
The first one is around wave energy converters (WECs). For this application, we are working with the PoliTO (Torino, Italy) to model the ISWEC, and we are also starting to work with a Bordeaux-based start-up for another device for extracting the energy from the waves via an Inria-Tech project and a Nouvelle Aquitaine Regional Project submitted by Memphis in collaboration with the CARDAMOM team.
The second one is around wind energy, and in particular wind turbines. In the past, we have supervised two PhD CIFRE thesis with VALOREM-Valeol, and are currently working with them in a European RISE ARIA project led by Memphis. We are also starting to work with IFPEN around the aeroelastic modeling of large wind turbines and the study and optimization of turbines farms in the framework of the joint laboratory Inria-IFPEN with a thesis funded by IFPEN and a post-doc funded by Inria (which will start in October 2021).
In conjunction with these activities we investigate with ANDRA, the national agency for storage of nuclear waste, reduced models allowing efficient and accurate simulations for deep geological storage planning. This activity is concretized with the PhD thesis of Giulia Sambataro.
6 Highlights of the year
Optimal transport on quadtree mesh
The idea of the optimal mass transportation is to find an optimal mapping which realizes the transfer of a density to another one. This modeling tool finds its application in ROMs, as discussed above, and in fluid-structure interactions problems as dicussed in the applications. In essence, it provides a rational approach to non-linearly interpolate distributed data. Our research aim at the numerical development of algorithms to solve the L2 Monge-Kantorovich problems. In particular, in 30 two computational algorithms based on extension of the Newton method have been proposed to solve the optimal mass transfer problem for compactly supported densities. These schemes have been shown to be computationally efficient for data that are relatively close in the sense of the Wasserstein distance, but they seem to be less robust when the data are far away because they also require a continuation approach. Thus, we first fixed this problem by modifying the previous schemes and then we used the numerical tools developed within Memphis (NEOS) to solve the problem on quadtree meshes. The combination of these two developments allows the numerical implementation of extremely fast schemes for solving the L2 Monge-Kantorovich problem. A publication is in preparation.
7 New results
7.1 Fluid-Fluid-Structure interactions
The following results are obtained with the software NaSCar based on our previous works 4, 5, 6, 10. These numerical simulations have been carried out on the cluster CURTA from the mesocentre MCIA, using 384 CPUs over 24 hours. Periodic boundary conditions are imposed on the horizontal boundaries. A special treatment is perfomed on the triple line, defined as being the line separeting the three phases, i.e. warter, air and the structure. A model derived form the Cox's one is used. An example of the snake swimming on the water surface is shown in Figure 7. The generation of the gravity waves are in good agreements with experiments and nature observations.

Snake swimming
7.2 Component-based model order reduction for radioactive waste management
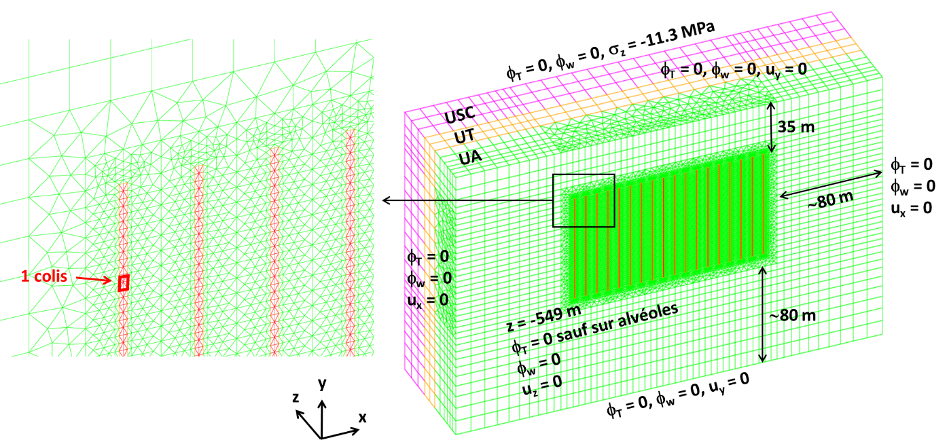
At the end of their cycle, radioactive materials are placed in arrays of cylindrical boreholes (dubbed alveoli) deep underground; due to the large temperatures of the radioactive waste, the thermal flux generated by the alveoli drives a complex time-dependent phenomenon which involves the thermal, hydraulic and mechanical (THM) response of the medium. The role of simulations is to predict the long-term system response and ultimately assess the impact of the repository site to the surrounding areas: Figure 8(a) shows a typical system configuration considered for numerical investigations. Due to the complex nature of the equations (a system of five coupled nonlinear time-dependent three-dimensional equations) and due to the uncertainty in several parameters of the model and on boundary conditions, MOR techniques are important to reduce the computational burden associated with thorough parametric studies.
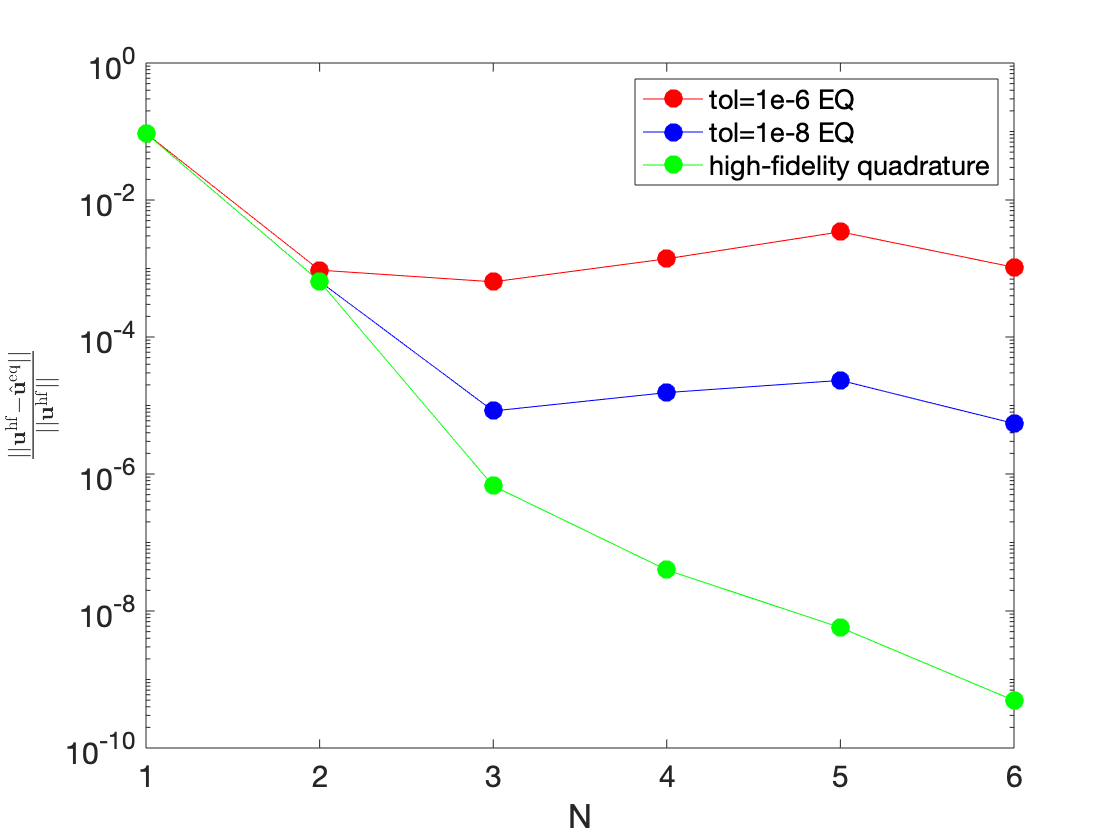
The PhD project of Giulia Sambataro aims to devise a rapid and reliable component-based MOR technique for THM systems, for radioactive waste management applications. Domain decomposition methods are required to deal with varying numbers of alveoli, and also to reduce the training costs of the ROM by avoiding full-scale offline simulations. During the first year of her PhD, Giulia has worked on a two-dimensional hydro-mechanical (HM) model problem and has studied the performance of projection-based hyper-reduced MOR strategies. Figure 8(b) shows the convergence of the relative solution error with respect to the size of the ROM and highlights the impact of hyper-reduction, which reduces the "integration domain" to improve efficiency.
7.3 Registration methods for advection-dominated PDEs
A major issue of state-of-the-art MOR techniques based on linear approximation spaces is the inability to deal with parameter-dependent sharp gradients, which characterize the solutions to advection-dominated problems. To address this issue, we propose a registration technique to align local features in a fixed reference domain. In computer vision and pattern recognition, registration refers to the process of finding a transformation that aligns two datasets; here, registration refers to the process of finding a parametric spatio-temporal transformation that improves the linear compressibility of the solution manifold.
A registration procedure has been proposed in 38, 16 and then further developed in 40, 39. In particular, in 40, we considered the application to one-dimensional applications in hydraulics; in an ongoing collaboration with EDF, we aim to extend the approach to two-dimensional steady and unsteady problems. Figure 9 shows results for a Saint-Venant problem (flow past a bump): Figures 9(a) and 9(b) show the free surface for two different parameters and two time instants, while Figure 9(c) shows the behavior of the out-of-sample projection error associated with a snapshot-based POD space with and without registration. We observe that registration is key to improve performance of linear compression strategies such as POD.
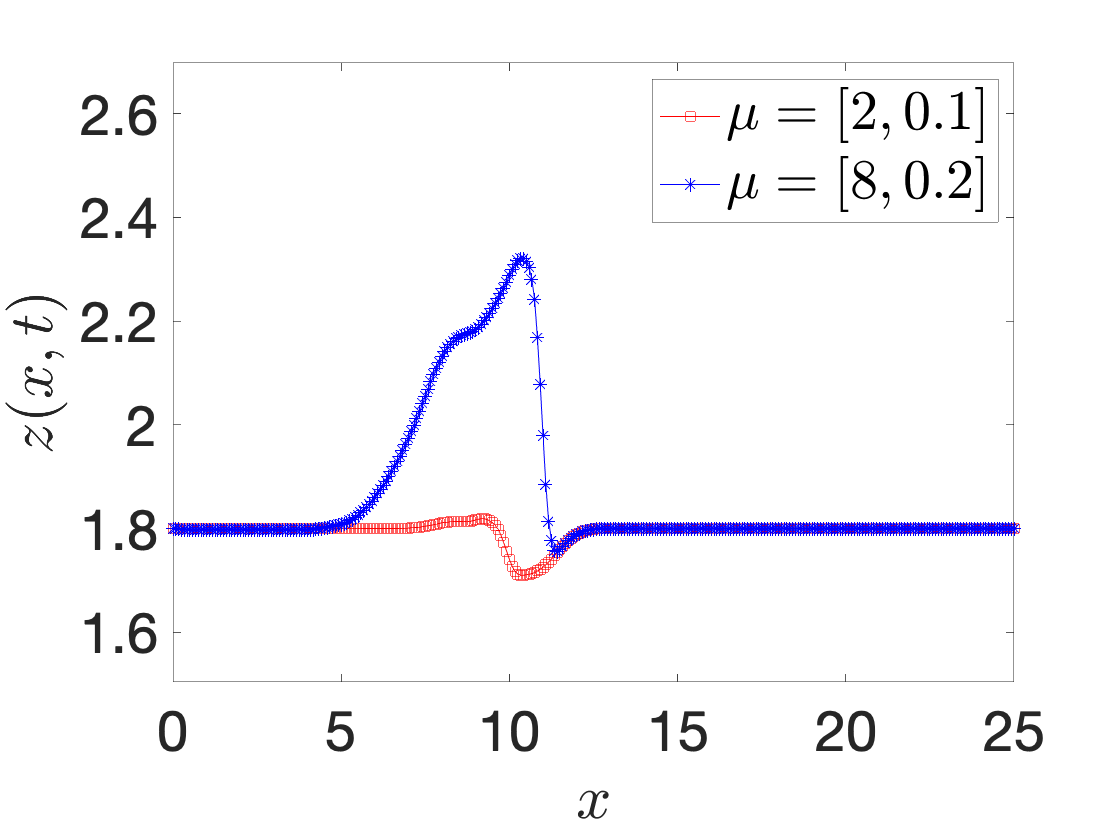
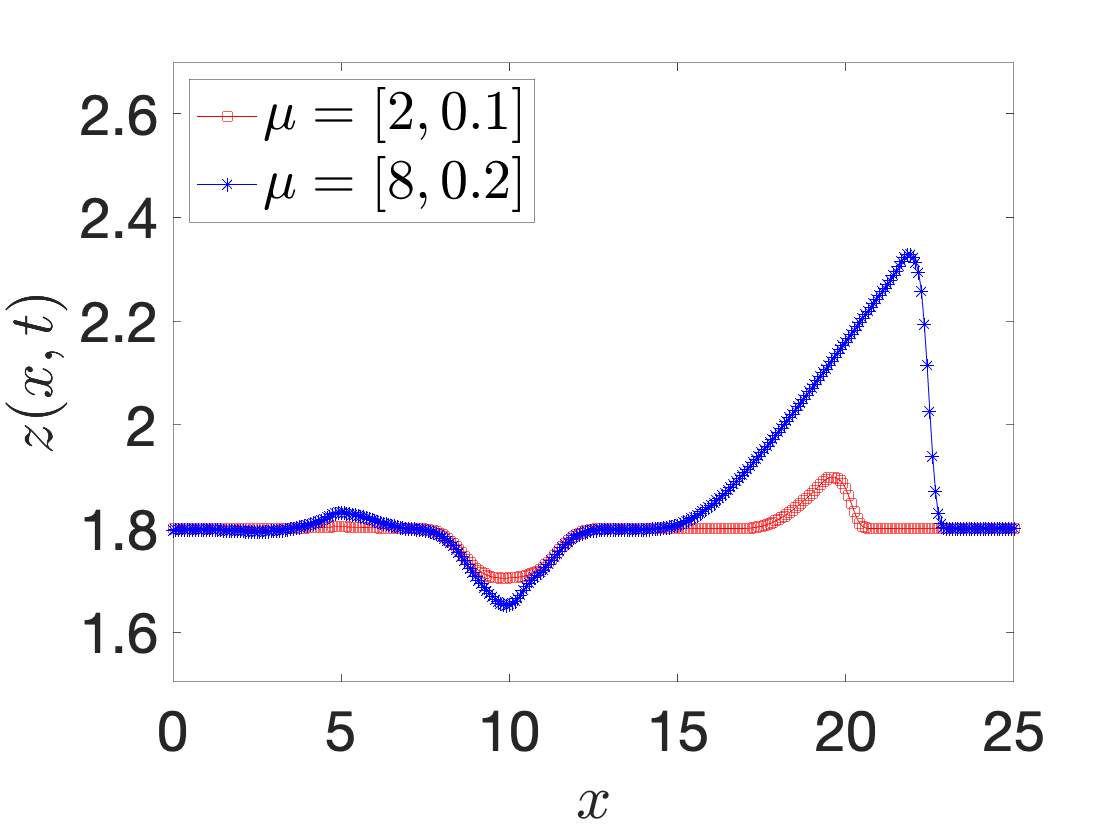
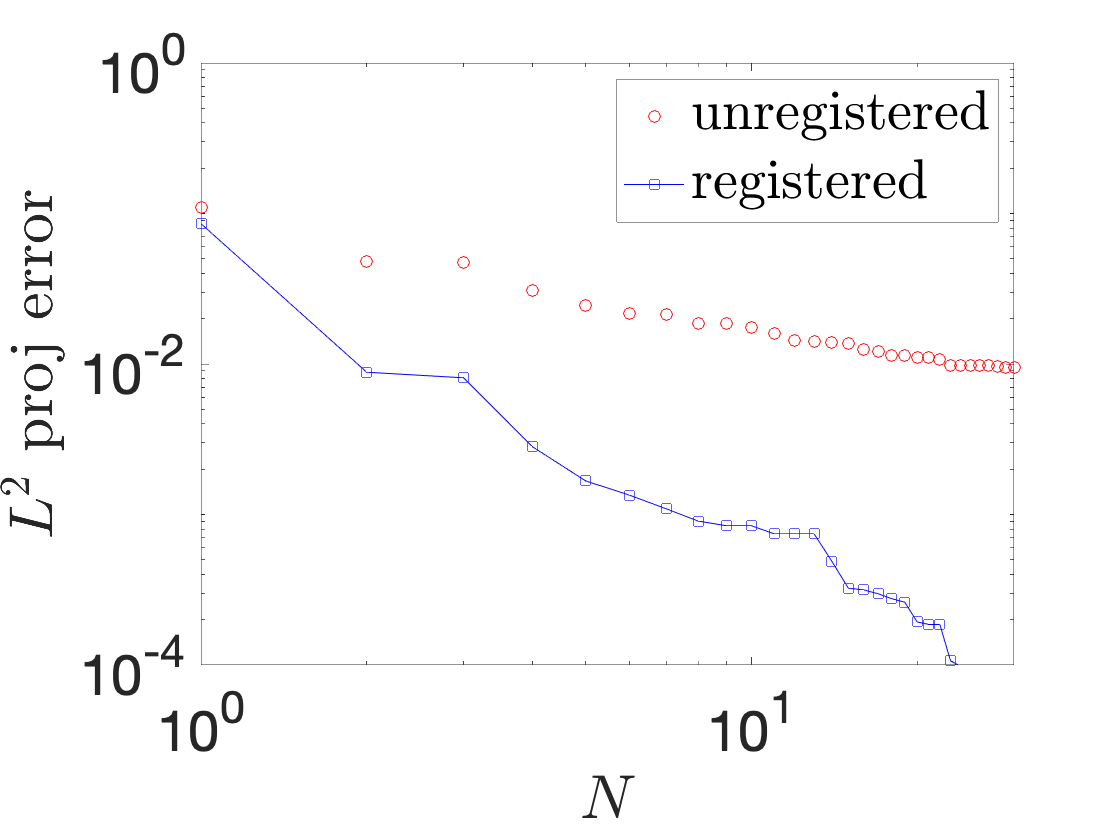
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
space-time registration for shallow water equations. (a)-(b) free surface for two different parameters and two different time instants. (c) out-of-sample projection error with and without registration.: In , Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain Ω\Omega and the states U0,U1:Ω→ℝU_0,U_1:\Omega \rightarrow \mathbb {R}, we aim to determine an interpolation U^:[0,1]×Ω→ℝ\widehat{U}:[0,1] \times \Omega \rightarrow \mathbb {R} such that U^(0,·)=U0\widehat{U}(0,\cdot ) = U_0 and U^(1,·)=U1\widehat{U}(1,\cdot ) = U_1. The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define U^\widehat{U}. The mapping built at step (ii) might not satisfy the bijectivity constraint in Ω\Omega : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
In 25, Iollo and Taddei proposed a general (i.e., independent of the underlying PDE) nonlinear interpolation technique based on optimal transportation of Gaussian models of coherent structures of the flow. Given the domain and the states , we aim to determine an interpolation such that and . The key features of the approach are (i) a scalar testing function that selects relevant features of the flow; (ii) an explicit mapping procedure that exploits explicit formulas valid for Gaussian distributions; (iii) a nonlinear interpolation dubbed “convex displacement interpolation” to define . The mapping built at step (ii) might not satisfy the bijectivity constraint in : to address this issue, a nonlinear projection procedure over a space of admissible maps based on registration is proposed.
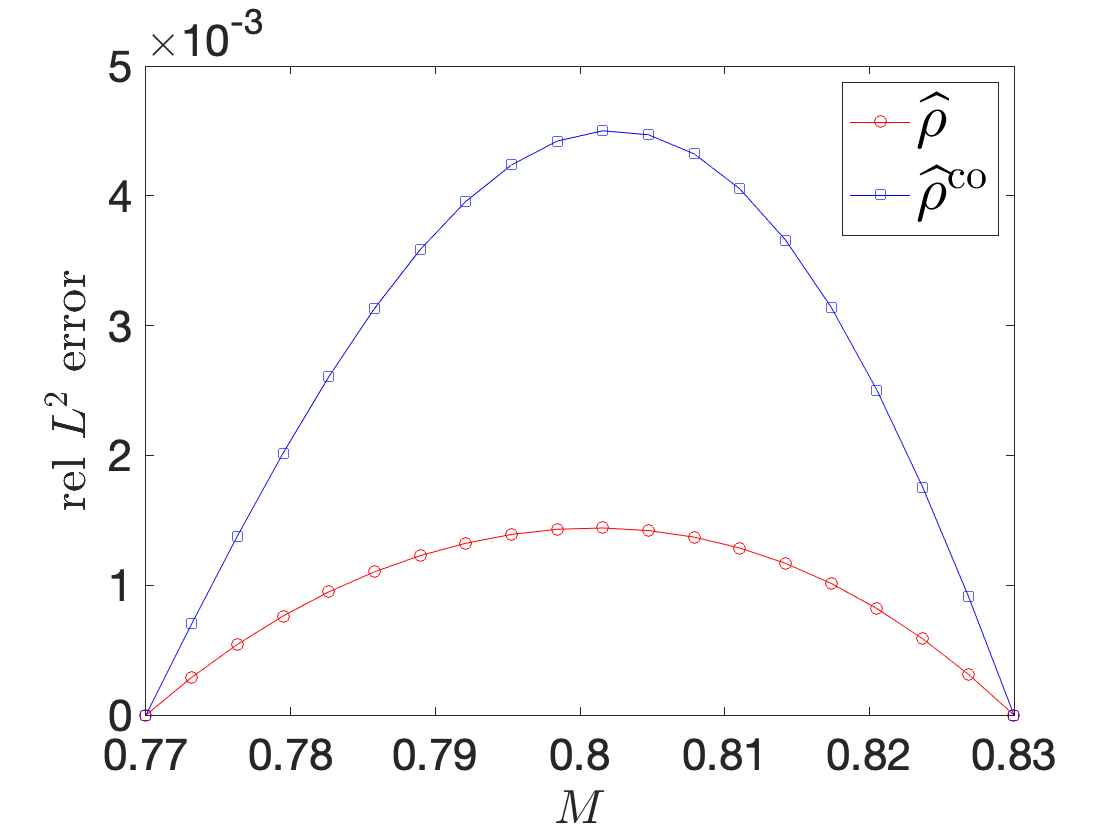
Figure 10 illustrates performance of our procedure for a compressible inviscid flow past a NACA0012 profile at angle of attack 4o for varying free-stream Mach number between and . Figures 10(a) and 10(b) show the fluid density for and , while Figure 10(c) shows an interpolation for an intermediate Mach number: we observe that the nonlinear interpolation smoothly deforms the shock attached to the airfoil. Figure 10(d) compares performance of the nonlinear interpolation with the linear convex interpolation : we observe that the proposed nonlinear interpolation is significantly more accurate than linear interpolation, for the same amount of high-fidelity information.
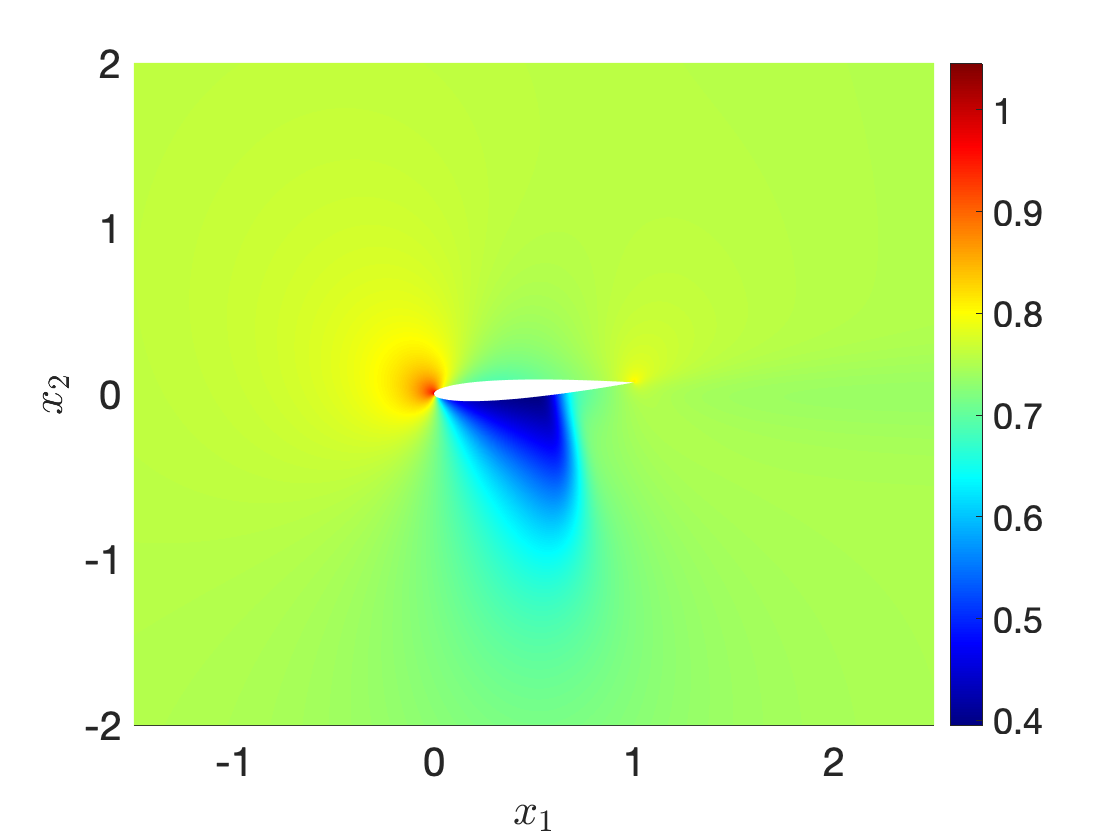

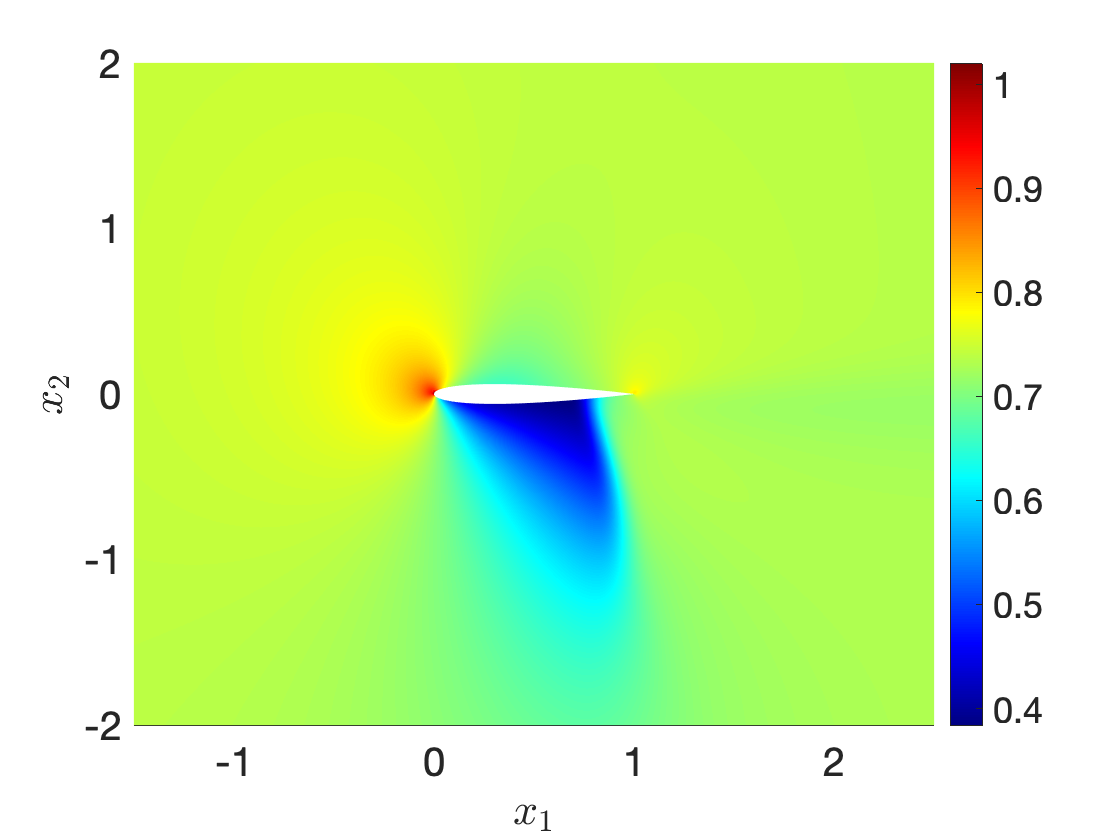
Ma=0.77Ma=0.77
Ma=0.83Ma=0.83
Ma=0.8Ma=0.8 (int)
7.4 Numerical modeling of a real zebrafish swimming: an effort test
Zebrafish is used by biologists as an animal model to study the effects of neurotoxicants and drugs on locomotion and develop pharmacological treatments. Very few fish swimming simulations have been derived from real body deformations to investigate the complex and stereotyped escape response of zebrafish and support animal experimentation. An experiment-driven numerical approach has been developed to model the body deformations from experimental imaging and perform three-dimensional (3D) numerical simulations to compute the actual energetic performances. To this end, a novel 3D zebrafish shape described by Lagrangian markers, was reconstructed based on 1,600 transverse slices and deformed according to experimental data (see figure 11). As a first application, three escape locomotion were recorded and simulated across six high-viscosity fluids in the range of mPa.s to 15 mPa.s. In addition to kinematic data such as traveled distance, velocity, and bending amplitude, the expended energy and cost of transport were computed based on the power output. Eventually, fictitious simulations were performed by combining body deformations and fluid viscosity, especially for challenging the experimental escape motions. Such simulations have revealed energetic expenditure could be emphasized by increasing fluid viscosity. Therefore, those preliminary results provided new insights for the implementation of an effort test, involving zebrafish experiments, viscous fluids, and energetic performances from numerical simulations. The main goal of effort tests designed by biologists is to highlight zebrafish swimming performances altered by genetics or chemical compounds, by computing the power output expended in higher-viscosity fluids.
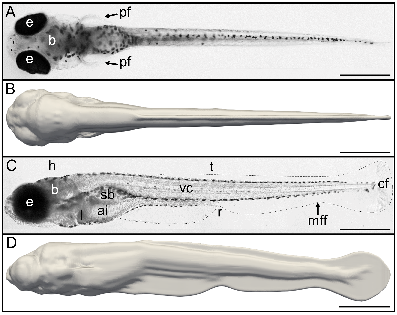
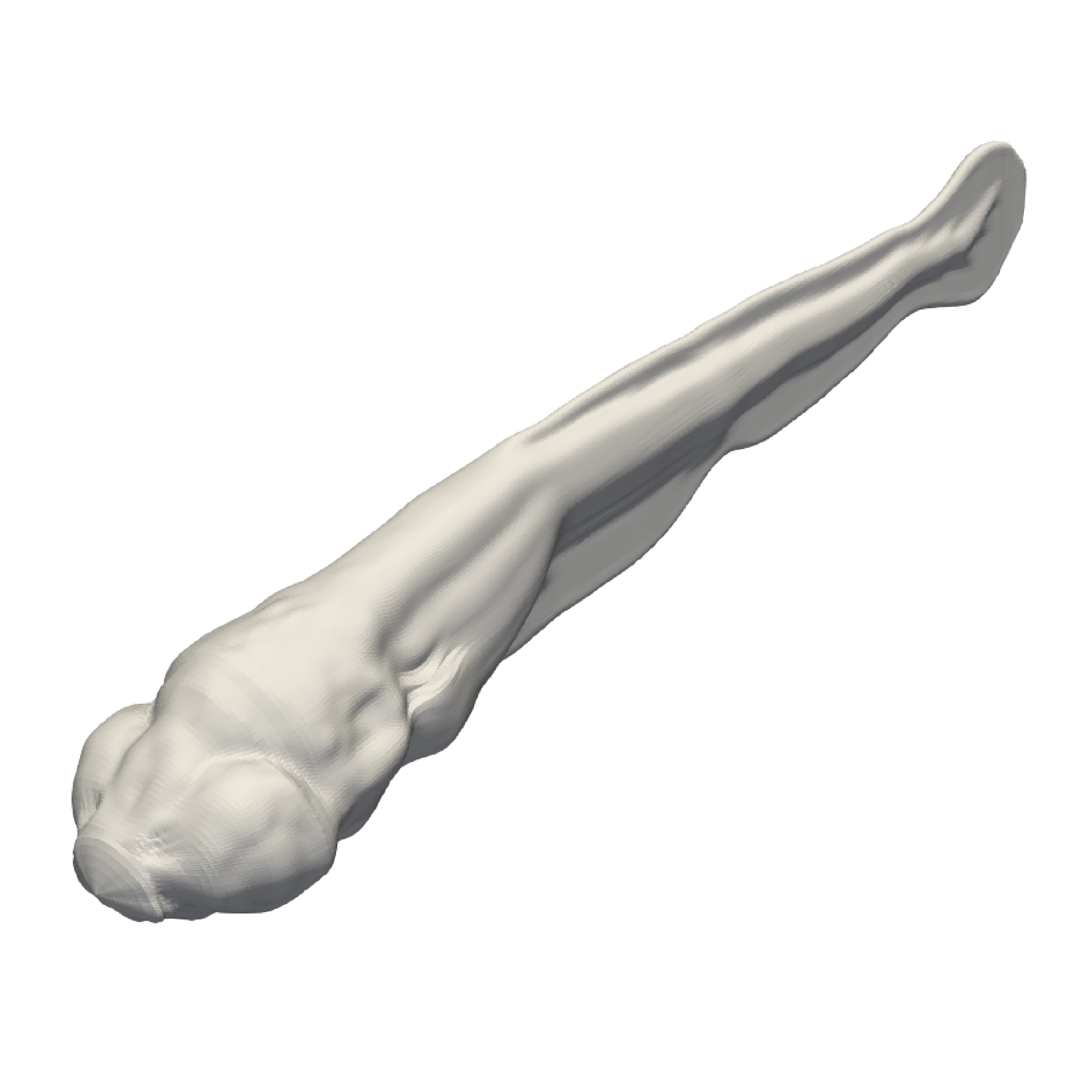
Top and side views
3D reconstruction
7.5 Fluid-structure interactions on AMR enabled quadree grids
A versatile fully Eulerian method has been developed for the simulation of fluid-structure interaction problems in two dimensions, involving stiff hyper-elastic materials 19. The unified single continuum model is solved in a monolithic way using a quadtree-based Finite Volume scheme, built on very compact discretizations. In the context of fictitious domain methods, the geometry of a structure is captured through a level-set formalism, which enables to define a diffuse fluid-structure interface.
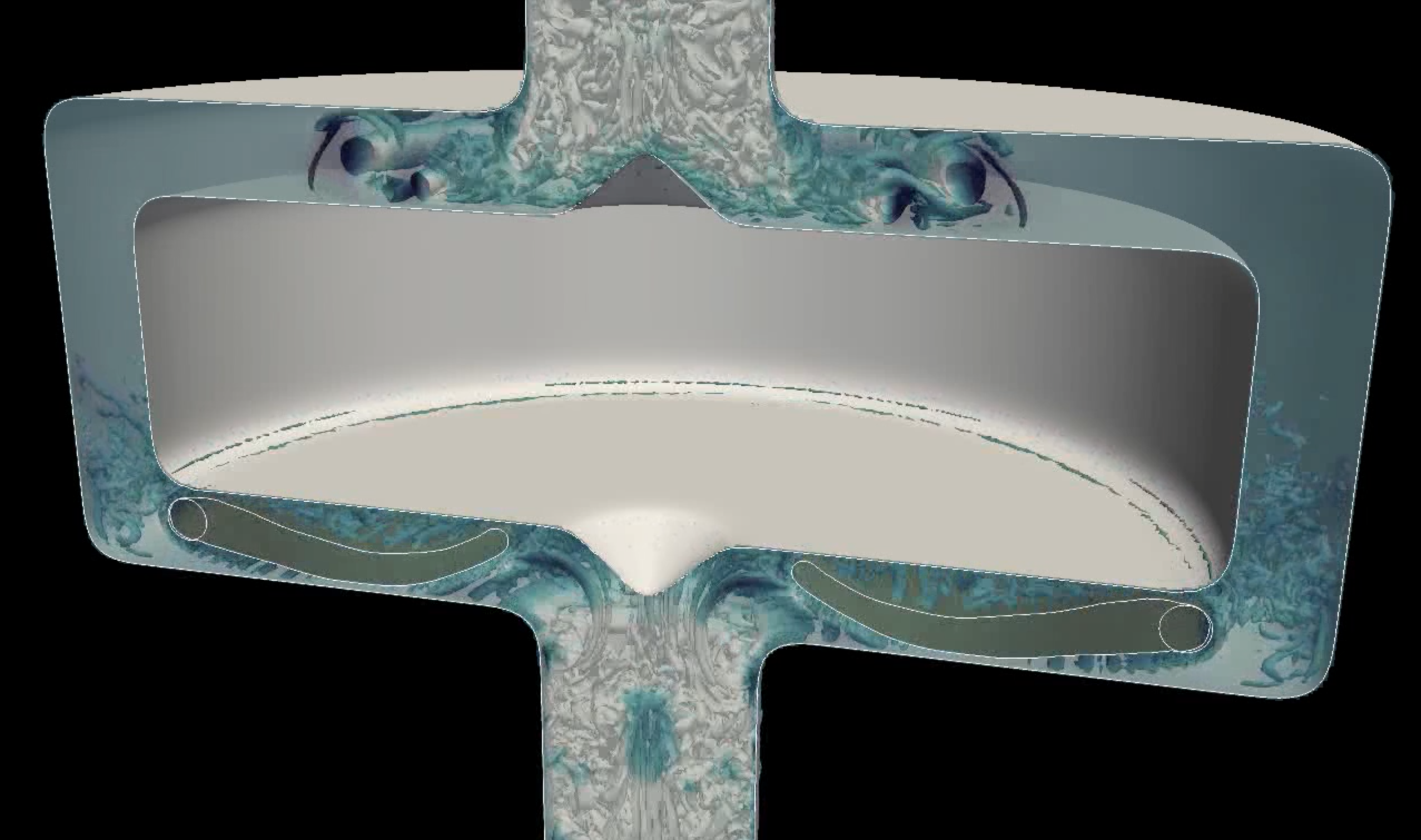
The numerical method has been validated with respect to the literature and the benefits obtained in terms of computational costs through the use of dynamic adaptive meshes has been highlighted. The low impact of coarsening on the structure deformation has been emphasized and the results suggest that the numerical method offers a valuable compromise between accuracy and feasibility of the simulation. As depicted in Figure 12, the simulation of a two-dimensional axi-symmetric flow in a cardiac assist device (LVAD geometry) has finally been proposed as a biomedical application. One paper is submitted.
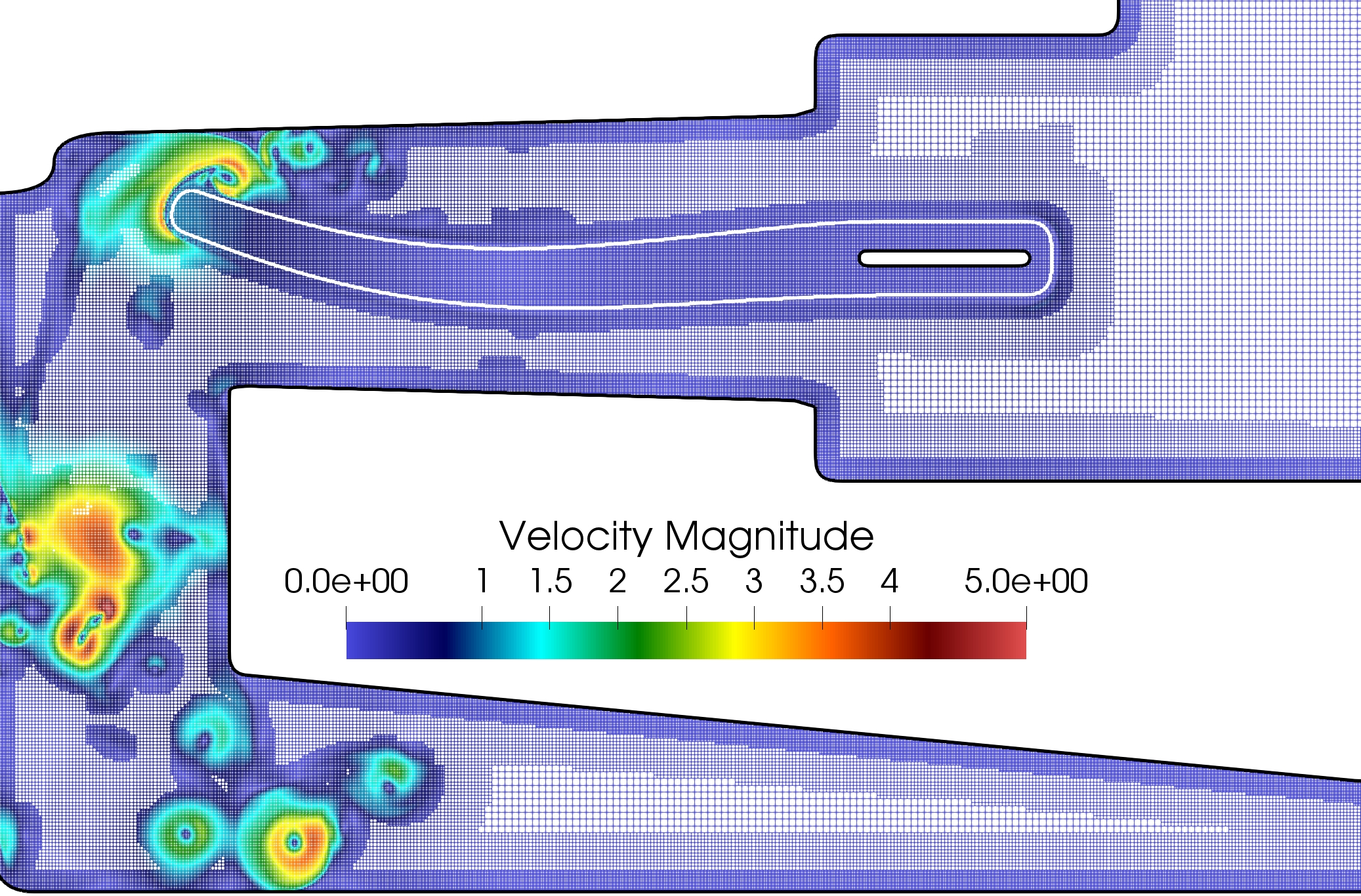
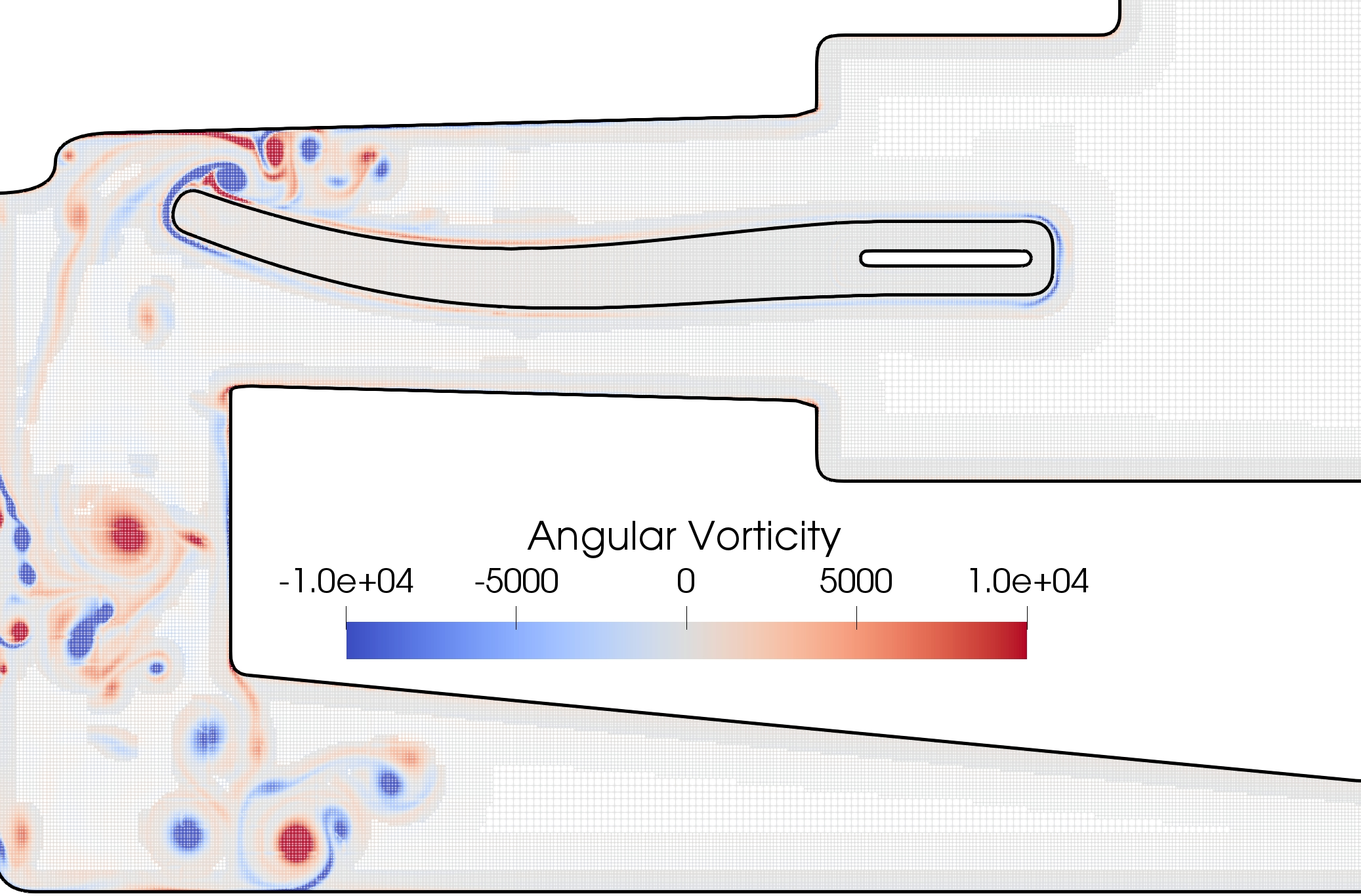
7.6 An ADER approach for the incompressible Navier-Stokes model on Overset Grids
One of the difficulties in the simulation of a fluid flow problem is the representation of the computational domain with a unique block mesh. As a matter of fact, not only the geometry could be particularly complex in itself, but it could change during the simulation and this necessary involves an in itinere geometrical adaptation of the mesh, with consequent high computational costs. One of the ways to overcome this problem is to use multiple overlapping mesh blocks that together define a Chimera or overset grid. Once the different mesh blocks are generated, they are properly composed by the creation of holes and, consequently, an overlapping zone between two overlapping blocks is defined. The overlapping zone is necessary for the the communication and data transfer from one mesh to another through an appropriate definition of local stencils of cells, both within and at the border of the individual blocks. In our simulations, the Chimera grid is composed of a background and a foreground mesh (see Figure 13). In particular, the foreground mesh can move and deform. The Navier-Stokes equations for incompressible fluids are solved through a projection method (Chorin-Temam) using second order schemes 20, 21. Solution at two different time instances of an advection-diffusion PDE over an evolving nontrivial domain discretized through an overset grid are preesnted in Figure 13.
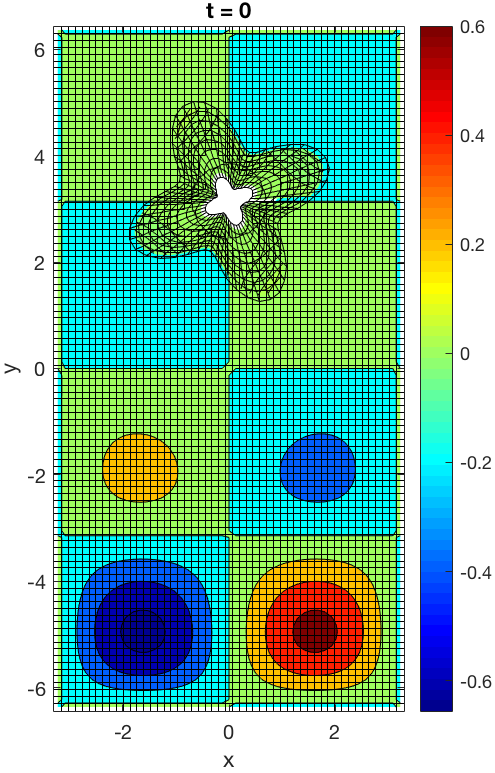
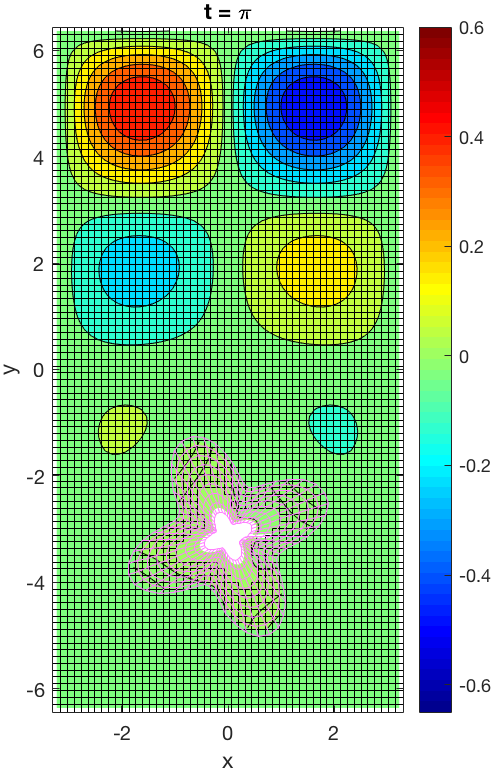
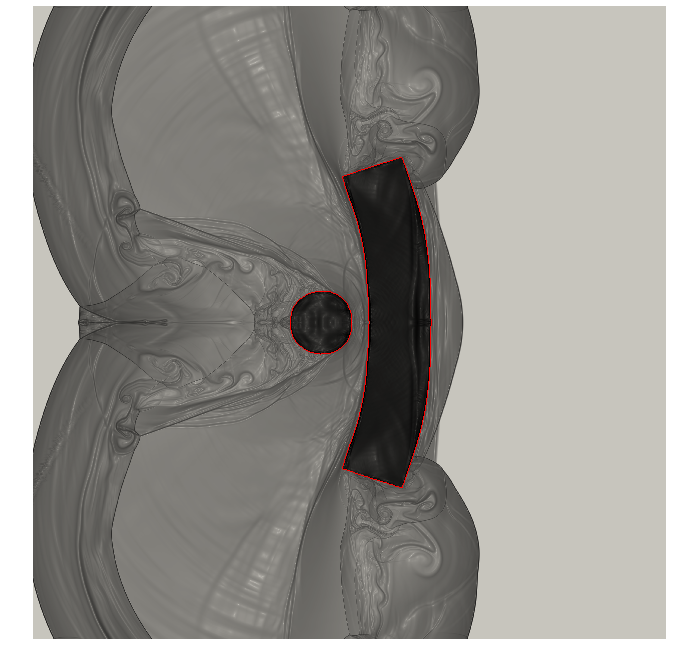
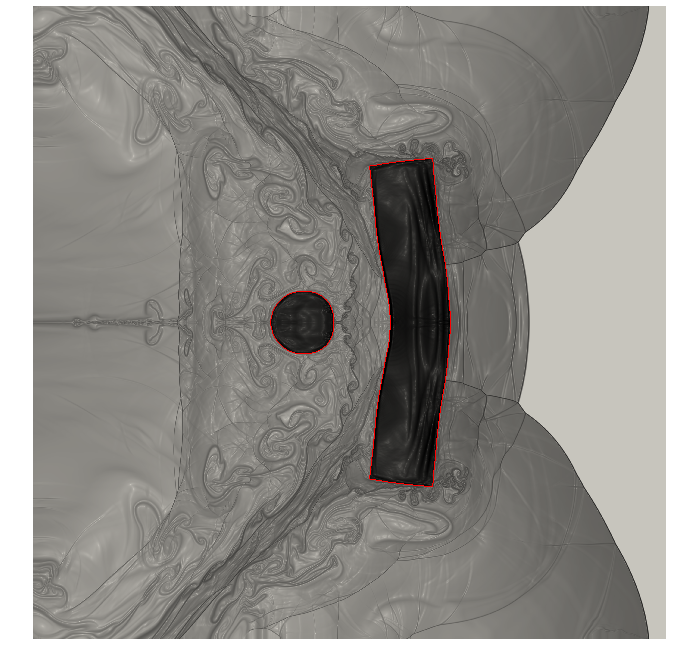
7.7 Projection-based reduced-order models for unsteady compressible flows
An analysis of calibration for reduced-order models (ROMs) is done in 17. The Galerkin and least-squares Petrov-Galerkin (LSPG) methods are tested on compressible flows involving a disparity of temporal scales. A novel calibration strategy is proposed for the LSPG method and two test cases are analyzed. The first consists of a subsonic airfoil flow where boundary layer instabilities are responsible for trailing-edge noise generation and the second comprises a supersonic airfoil flow with a transient period where a detached shock wave propagates upstream at the same time that shock-vortex interaction occurs at the trailing edge. Results show that calibration produces stable and long-time accurate Galerkin and LSPG ROMs for both cases investigated. The impact of hyper-reduction is tested on LSPG models via an accelerated greedy missing point estimation (MPE) algorithm. The location for hyper-reduction points is depicted in Figure 14. For the first case investigated, LSPG solutions obtained with hyper-reduction show good comparison with those obtained by the full order model. However, for the supersonic case the transient features of the flow need to be properly captured by the sampled points of the accelerated greedy MPE method. Otherwise, the dynamics of the moving shock wave are not fully recovered. The impact of different time-marching schemes is also assessed and, differently than reported in literature, Galerkin models are shown to be more accurate than those computed by LSPG when the non-conservative form of the Navier-Stokes equations is solved. For the supersonic case, the Galerkin and LSPG models (without hyper-reduction) capture the overall dynamics of the detached and oblique shock waves along the airfoil. However, when shock-vortex interaction occurs at the trailing-edge, the Galerkin ROM is able to capture the high-frequency fluctuations from vortex shedding while the LSPG presents a more dissipative solution, not being able to recover the flow dynamics.

Hyper-reduction
7.8 Aortic aneurysms: automatic segmentation and registration
We developed a new artificial neural network to automatically segment aortic aneurysm. The main idea with this approach was to consider each pixel of the image individually and to see if a model could learn how to categorize it as lumen only from its own intensity and the intensity of its 26 neighbors. We tested different types of input (values, means, variances...) and architecture: a sequential model was retained. For the input, each sample is a vector of 27 intensity values. Only pixels whose intensity is between 100 and 700 are kept for training and prediction.
The second axis of development concerned registration. When a patient have several scans taken at different times, the segmentations are not in the same frame so any comparison would be complicated. The objective was to bring the second segmentation in the frame of the first one. We tested different points-based approaches: register the centerline of the segmentation or the geometry; consider only the lumen or the entire aneurysm. The best results were obtained with the surface of the aneurysm and the iterative closest point algorithm. Once the registration is performed (Figure 15) we can visualize how the aneurysm has evolved.
Aneurysm geometries
8 Bilateral contracts and grants with industry
8.1 Bilateral Contracts with Industry
EDF ROM HYDRAU dates: 15/08/2020 au 15/12/2021
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Associate Teams in the framework of an Inria International Lab or in the framework of an Inria International Program
MARE
-
Title:
Multiscale Accurate Reduced-order model Enablers
-
Duration:
2019 -> 2022
-
Coordinator:
Angelo Iollo
-
Partners:
VNU University of Engineering and Technology, Stanford (United States)
-
Inria contact:
Angelo Iollo
-
Summary:
Reduced-order models (ROMs) are simplified mathematical models derived from the full set of partial differential equations governing the physics of the phenomenon of interest. We focus on ROMs that are data-driven as they are based on relevant solution data previously obtained. In particular we will focus on multiscale adaptive models where the large scales are governed by a PDE and the small scales are described by data driven models. To do that we will leverage on tools from data geometry, numerical PDEs and machine learning.
9.1.2 Inria International Partners
Declared Inria International Partners Politecnico di Torino (Giovanni Bracco, Francesco Larocca), with two co-tutelle PhDs: Beatrice BATTISTI (Sujet : Multi-fidelity Multi-scale numerical modelling og wave energy converters farms)
Thomas PHILIBERT (Sujet : Data-driven models for aerospace propulsion)
Informal International Partners La Sapienza Universita' di Roma (Gabriella Puppo, Dipartimento di Matematica) Università di Pisa (UNIPI) (Simone Camarri, Department of Civil and Industrial Engineering)
9.2 International research visitors
9.2.1 Visits of international scientists
- Andrea Christine Thomann University of Insubria in Como (Italy), from Sep 2021 until Oct 2021.
- Elena Travaglia Ecole Polytechnique de Turin, Oct 2021.
9.2.2 Visits to international teams
Michel Bergmann: OPTIMAD, Turin (ARIA) : 16/11/2021-20/11/2021.
9.3 European initiatives
9.3.1 FP7 & H2020 projects
ARIA
-
Title:
Accurate Roms for Industrial Applications
-
Duration:
2019 - 2023
-
Partners:
- STANFORD: Aeronautics & Astronautics Department (United States)
- ESTECO SpA: Department of Research and Development (Italy)
- Politecnico di Milano: Laboratory for Modeling and Scientific Computing (MOX) (Italy)
- Politecnico di Torino: Department of Science and Mathematics (Italy)
- Scuola Internazionale Superiore di Studi Avanzati di Trieste: Mathematics Area/mathLab (Italy)
- Universidad de Sevilla: Instituto de Matemáticas de la Universidad de Sevilla (IMUS) (Spain)
- University of South Carolina: Department of Mathematics (United States)
- VALOREM SAS: R & D Department (France)
- Virginia Tech - Department of Mathematics (United States)
- Virtualmechanics, S.L. (Spain)
- Optimad: R& D Department (Italy)
- Volkswagen AG: Group Research, Vehicle Technology (Germany)
-
Inria contact:
contact@rise-aria.eu
-
Summary:
The project Accurate Roms for Industrial Applications aims at developing an array of mathematical methods for constructing predictive reduced-order models (ROMs) with guaranteed accuracy, robustness, reliability and efficiency for applications involving complex physical phenomena. New approaches to this challenge are proposed here with a focus on the Euler and Navier–Stokes equations of fluid flow, two of the most challenging continuum models with an extraordinary rich range of industrial applications. The mathematical modeling and solution of the Euler and Navier-Stokes equations is sometimes cited as the greatest challenge in continuum modeling of physical phenomena. This topic is selected as our principal focus because of its intrinsic importance, but also because the mathematical methods developed in addressing this very challenging task may well have an impact on other fields of knowledge. We plan to tackle these challenging objectives in this staff exchange program by combining the unique expertise of our extended research team whose members have made significant progress in ROM research during the past decade. This academic expertise is cross-fertilized by the exchange with knowledge intensive SMEs ans start up and well established industrial partners that will benefit from the scientific and technological results of the team and will challenge the solutions found with applications in real world problems.
9.3.2 Collaborations with Major European Organizations
EDF ROM HYDRAU : dates: 15/08/2020 au 15/12/2021.
9.4 National initiatives
- ANR (national agency for research funding) DRAGON2. Partners : CNRS/Université de Poitiers/Inria. 27 k€+ 1 PhD. The goal is study the aquatic swimming a several snakes using biomimetism and bioinspiration. In this project, we have experimental data for snake swimming, and we are building a numerical twin to compute integral quantities like the efficiency. Reinforcement learning is also considered to optimize the snake swimming.
9.5 Regional initiatives
- Contrat Région Nouvelle Aquitaine MODEM " MODélisation multi-échelles et multi-fidélités pour l'extraction d'Energies Marines". 48k€. Description: the goal of this project is to develop a multi-fidelity approach for the modeling and the optimization of Wave Energey Converters (WECs). We compute the fluid structure interaction problem in a close neighbourhood of the WEC using accurate but expensive non linear Navier-Stokes equations. The far field is computed using using a simpler linear or weakly non linear reduced order model, like the shallow water or Boussinesq models.
10 Dissemination
10.1 Promoting scientific activities
Angelo Iollo: 2019-. Nominated at the council of "Département de Sciences du Numérique et Ingénierie" of the University of Bordeaux.
10.1.1 Scientific events: organisation
Tommaso TADDEI has co-organized CEMRACS 2021 on data assimilation and model reduction in high-dimensional problems.
Michel Bergmann & Tommaso Taddei. Organisation of the minisymposium at the SIAM CSE conference, 2021 (with K. Smetana).
Reviewer - Reviewing Activities
The members of the team were reviewers for: Journal of Computational Physics, International Journal of CFD, Journal of Non-linear Analysis B, ASME Journal of Computational and Nonlinear Dynamics, Journal of Fluid Mechanics, Acta Mechanica, AIAA Journal, International Journal Numerical Methods in Fluids, Computers & Fluids, Journal of Engineering Mathematics, European Journal of Mechanics / B Fluids, Journal Europeen de Systemes Automatises, Applied Mathematics and Computation. Nuclear Science and Engineering, Computer Methods in Applied Mechanics and Engineering, Journal of Theoretical Biology, Computational Optimization and Applications, Applied science, Meccanica, SIAM journal on scientific computing, SIAM journal on uncertainty quantification, Advances in Computational Mathematics.
10.1.2 Journal
Michel Bergmann is Topic Editor in FLUIDS.
Michel Bergmann is Guest Editor in Scientific Computing in Fluids, FLUIDS (2021)
Michel Bergmann is Guest Editor in Data-Driven Modeling and Optimization in Fluid Dynamics: From Physics-Based to Machine Learning Approaches, Frontiers in Physics (2021-2022)
10.1.3 Invited talks
Angelo Iollo is invited in international conferences or workshops:
- November 8-9, 2021. Année de la mécanique. Séminaire à IHP: Mathématiques et Mécanique. Parameterized flows: examples of convergence between data and computational science. .
- June, 17th, 2021. Euromech Conference on Machine learning methods for prediction and control of turbulent flows. “Parameterized flows: examples of convergence between data and computational science”.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
Two members of the team are Professor (Angelo Iollo) or Assistant Professor (Afaf Bouharguane) at Université de Bordeaux and have teaching duties, which consist in courses and practical exercises in numerical analysis and scientific computing. Michel Bergmann (CR) also teaches around 64 hours per year (practical exercises in programming for scientific computing). Tommaso Taddei (CR) also teaches around 50 hours per year (practical exercises in numerical analysis and scientific computing).
10.2.2 Supervision
- 2018-2021. Antoine Fondanèche. Bourse Université de Bordeaux. Interaction fluide-structure dans les endoprothèses et autres dispositifs vasculaires actifs. Advisors: Michel Bergmann, Angelo Iollo.
- 2021-2024. Eki AGOUZAL Cifre. (Industrial thesis), EDF. Estimation de l'état mécanique d'enceintes de confinement par assimilation de données provenant de la maquette Vercors. Advisors: Michel Bergmann, Tommaso Taddei.
- 2020-2023. Beatrice BATTISTI, Politecnico di Torino. Multi-fidelity multi-scale numerical modelling of wave energy converters farms. Advisors: Michel Bergmann, Giovanni Bracco.
- 2018-2021. Michele Giuliano CARLINO, Inria. Fluid-structure Interactions models on Chimera grids. Advisors: Michel Bergmann, Angelo Iollo.
- Caroline LE GUERN, Ifpen. Modelisation de l'aero-elasticité en grandes transformations par un couplage partitioné: application aux grandes eoliennes. Advisor: Michel Bergmann.
- 2021-2024. Karl MAROUN, Université de Poitiers (ANR Dragon2). Biomimetism and bioinspiration of a snakes's anguilliform swimming: numerical twin and machine learning. Advisors: Michel Bergmann, Philippe Traoré.
- 2020-2023. Thomas PHILIBERT, Politecnico di Torino. Convergence between models and data for the simulation of turbulent flows in aeronautical propulsion. Advisors: Angelo Iollo, Francesco Larocca.
- 2021-2024. Michele ROMANELLI, Chaire ONERA. Lois de Paroi à Apprentissage Profond pour Simulations Aérodynamiques. Advisors: Héloïse Beaugendre, Michel Bergmann.
- 2020-2023. Ludovica SACCARO, Inria. Identification of mechanical biomarkers for assessing the risk of rupture of abdominal aortic aneurysms. Advisor: Angelo Iollo.
- 2021-2024. Alexis TARDIEU, Université de Bordeaux. Approches Galerkin Discontinues spatio-temporelles sur des mailles hiérarchiques pour les équations de Navier-Stokes incompressibles. Advisors: Angelo Iollo, Afaf Bouharguane.
- 2019-2022. Giulia SAMBATARO, Andra. Component-based reduction strategies for THM equations. Advisors: Angelo Iollo, Tommaso Taddei.
10.2.3 Juries
Michel Bergmann: membre of the Phd jury of Luca Berti « méthodes numériques et optimisation pour la micro-natation», Université de Strasbourg, 13 décembre 2021.
Angelo Iollo:
Rapporteur de la thèse de Matteo Zancanaro, SISSA département de mathématiques, «Model order reduction for compressible turbulent flows: hybrid approaches in physics and geometry parametrization», september 24th, 2021. Trieste.
Rapporteur de la thèse en mécanique de Nan Deng, “Deep mean-field modelling for successive bifurcations exemplified for the fluidic pinball”, 27 septembre 2021. ENSTA Paris.
Président du jury de thèse mention mathématiques de Stefano Pezzano, « Méthode de Galerkin Discontinue Isogéométrique avec domaines dépendants du temps », 13 septembre 2021, Inria Sophia Antipolis, Université de Nice.
10.3 Popularization
In September 2021, Tommaso TADDEI has presented his research at the event Unithé ou Café at Inria Bordeaux.
11 Scientific production
11.1 Major publications
- 1 articleAn all-speed relaxation scheme for gases and compressible materials.Journal of Computational Physics3512017, 1-24
- 2 articleFluid--solid Floquet stability analysis of self-propelled heaving foils.Journal of Fluid Mechanics9102021, A28
- 3 articleEnablers for robust POD models.Journal of Computational Physics22822009, 516--538
- 4 articleAn accurate cartesian method for incompressible flows with moving boundaries.Communications in Computational Physics1552014, 1266--1290
- 5 articleBioinspired swimming simulations.Journal of Computational Physics3232016, 310 - 321
- 6 articleModeling and simulation of fish-like swimming.Journal of Computational Physics23022011, 329 - 348
- 7 articleAccurate Asymptotic Preserving Boundary Conditions for Kinetic Equations on Cartesian Grids.Journal of Scientific Computing2015, 34
- 8 articleNumerical solution of the Monge--Kantorovich problem by density lift-up continuation.ESAIM: Mathematical Modelling and Numerical Analysis4961577November 2015
- 9 articleA Cartesian Scheme for Compressible Multimaterial Models in 3D.Journal of Computational Physics3132016, 121-143
- 10 articleEnablers for high-order level set methods in fluid mechanics.International Journal for Numerical Methods in Fluids79December 2015, 654-675
11.2 Publications of the year
International journals
Doctoral dissertations and habilitation theses
Reports & preprints
11.3 Cited publications
- 28 articleA penalization method to take into account obstacles in a incompressible flow.Numerische Mathematik8141999, 497-520
- 29 articleExact and approximate solutions of Riemann problems in non-linear elasticity.Journal of Computational Physics228182009, 7046-7068
- 30 articleNumerical solution of the Monge-Kantorovich problem by density lift-up continuation.ESAIM: M2AN4962015, 1577-1592
- 31 articleA Cartesian scheme for compressible multimaterial models in 3D.Journal of Computational Physics3132016, 121-143URL: http://www.sciencedirect.com/science/article/pii/S0021999116000966
- 32 articleAn experimental study of entrainment and transport in the turbulent near wake of a circular cylinder.Journal of fluid mechanics1361983, 321--374
- 33 articleModelling wave dynamics of compressible elastic materials.Journal of Computational Physics22752008, 2941-2969
- 34 bookElements of continuum mechanics.Nauka Moscow1978
- 35 phdthesisConstruction d'une chaîne d'outils numériques pour la conception aérodynamique de pales d'éoliennes.Université de Bordeaux2014
- 36 articleA Conservative Three-Dimensional Eulerian Method for Coupled Solid-Fluid Shock Capturing.Journal of Computational Physics18312002, 26-82
- 37 bookLevel Set Methods and Fast Marching Methods.Cambridge University Press, Cambridge, UK1999
- 38 articleA registration method for model order reduction: data compression and geometry reduction.SIAM Journal on Scientific Computing4222020, A997--A1027
- 39 articleRegistration-based model reduction in complex two-dimensional geometries.submitted to Journal of Scientific Computing2021
- 40 articleSpace-time registration-based model reduction of parameterized one-dimensional hyperbolic PDEs.ESAIM: Mathematical Modelling and Numerical Analysis (accepted)2020

