Keywords
Computer Science and Digital Science
- A5.5.1. Geometrical modeling
- A5.5.2. Rendering
- A6.2.8. Computational geometry and meshes
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
Other Research Topics and Application Domains
- B3.3.1. Earth and subsoil
- B5.1. Factory of the future
- B5.7. 3D printing
- B9.2.2. Cinema, Television
- B9.2.3. Video games
1 Team members, visitors, external collaborators
Research Scientists
- Laurent Alonso [Inria, Researcher]
- Etienne Corman [CNRS, Researcher]
- Nicolas Ray [Inria, Researcher]
Faculty Members
- Dmitry Sokolov [Team leader, Univ de Lorraine, Associate Professor, HDR]
- Dobrina Boltcheva [Univ de Lorraine, Associate Professor]
Post-Doctoral Fellow
- David Lopez [Inria, from Nov 2021]
PhD Students
- Justine Basselin [Rhino Terrain, CIFRE]
- Guillaume Coiffier [Univ de Lorraine]
- Yoann Coudert-Osmont [Univ de Lorraine, from Sep 2021]
- David Desobry [Inria]
- David Lopez [NC, from Apr 2021 until Oct 2021]
- Francois Protais [Inria]
Technical Staff
- David Lopez [Univ de Lorraine, Engineer, until Apr 2021]
Interns and Apprentices
- Edmond Covanov [CNRS, from May 2021 until Jul 2021]
- Anna Sushko [Inria, from Jun 2021 until Aug 2021]
Administrative Assistants
- Celine Cordier [Inria]
- Virginie Priester [CNRS, until Mar 2021]
Visiting Scientist
- Yoann Coudert-Osmont [École Normale Supérieure de Lyon, from Apr 2021 until Aug 2021]
External Collaborators
- Herve Barthelemy [Rhino Terrain]
- Jeanne Pellerin [TOTAL-Pau, from Feb 2021]
2 Overall objectives
PIXEL is a research team stemming from team ALICE founded in 2004 by Bruno Lévy. The main scientific goal of ALICE was to develop new algorithms for computer graphics, with a special focus on geometry processing. From 2004 to 2006, we developed new methods for automatic texture mapping (LSCM, ABF++, PGP), that became the de-facto standards. Then we realized that these algorithms could be used to create an abstraction of shapes, that could be used for geometry processing and modeling purposes, which we developed from 2007 to 2013 within the GOODSHAPE StG ERC project. We transformed the research prototype stemming from this project into an industrial geometry processing software, with the VORPALINE PoC ERC project, and commercialized it (TotalEnergies, Dassault Systems, + GeonX and ANSYS currently under discussion). From 2013 to 2018, we developed more contacts and cooperations with the “scientific computing” and “meshing” research communities.
After a part of the team “spun off” around Sylvain Lefebvre and his ERC project SHAPEFORGE to become the MFX team (on additive manufacturing and computer graphics), we progressively moved the center of gravity of the rest of the team from computer graphics towards scientific computing and computational physics, in terms of cooperations, publications and industrial transfer.
We realized that geometry plays a central role in numerical simulation, and that “cross-pollinization” with methods from our field (graphics) will lead to original algorithms. In particular, computer graphics routinely uses irregular and dynamic data structures, more seldom encountered in scientific computing. Conversely, scientific computing routinely uses mathematical tools that are not well spread and not well understood in computer graphics. Our goal is to establish a stronger connection between both domains, and exploit the fundamental aspects of both scientific cultures to develop new algorithms for computational physics.
2.1 Scientific grounds
Mesh generation is a notoriously difficult task. A quick search on the NSF grant web page with “mesh generation AND finite element” keywords returns more than 30 currently active grants for a total of $8 million. NASA indicates mesh generation as one of the major challenges for 2030 43, and estimates that it costs 80% of time and effort in numerical simulation. This is due to the need for constructing supports that match both the geometry and the physics of the system to be modeled. In our team we pay a particular attention to scientific computing, because we believe it has a world changing impact.
It is very unsatisfactory that meshing, i.e. just “preparing the data” for the simulation, eats up the major part of the time and effort. Our goal is to make the situation evolve, by studying the influence of shapes and discretizations, and inventing new algorithms to automatically generate meshes that can be directly used in scientific computing. This goal is a result of our progressive shift from pure graphics (“Geometry and Lighting”) to real world problems (“Shape Fidelity”).
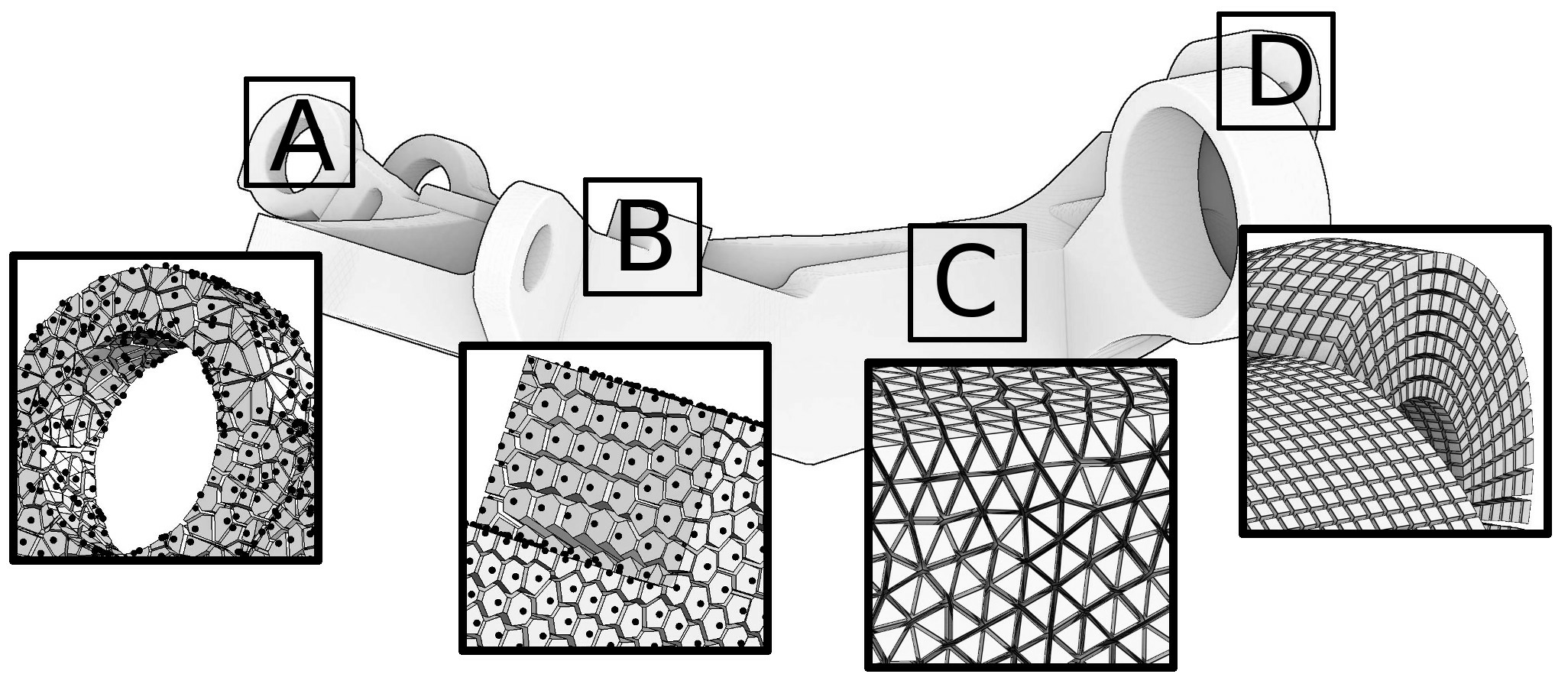
Meshing is so central in geometric modeling because it provides a way to represent functions on the objects studied (texture coordinates, temperature, pressure, speed, etc.). There are numerous ways to represent functions, but if we suppose that the functions are piecewise smooth, the most versatile way is to discretize the domain of interest. Ways to discretize a domain range from point clouds to hexahedral meshes; let us list a few of them sorted by the amount of structure each representation has to offer (refer to Figure 1).
-
At one end of the spectrum there are point clouds: they exhibit no structure at all (white noise point samples) or very little (blue noise point samples). Recent explosive development of acquisition techniques (e.g. scanning or photogrammetry) provides an easy way to build 3D models of real-world objects that range from figurines and cultural heritage objects to geological outcrops and entire city scans. These technologies produce massive, unstructured data (billions of 3D points per scene) that can be directly used for visualization purposes, but this data is not suitable for high-level geometry processing algorithms and numerical simulations that usually expect meshes. Therefore, at the very beginning of the acquisition-modeling-simulation-analysis pipeline, powerful scan-to-mesh algorithms are required.
During the last decade, many solutions have already been proposed 39, 22, 34, 33, 25, but the problem of building a good mesh from scattered 3D points is far from being solved. Beside the fact that the data is unusually large, the existing algorithms are challenged also by the extreme variation of data quality. Raw point clouds have many defects, they are often corrupted with noise, redundant, incomplete (due to occlusions): they all are uncertain.
-
Triangulated surfaces are ubiquitous, they are the most widely used representation for 3D objects. Some applications like 3D printing do not impose heavy requirements on the surface: typically it has to be watertight, but triangles can have an arbitrary shape. Other applications like texturing require very regular meshes, because they suffer from elongated triangles with large angles.
While being a common solution for many problems, triangle mesh generation is still an active topic of research. The diversity of representations (meshes, NURBS, ...) and file formats often results in a “Babel” problem when one has to exchange data. The only common representation is often the mesh used for visualization, that has in most cases many defects, such as overlaps, gaps or skinny triangles. Re-injecting this solution into the modeling-analysis loop is non-trivial, since again this representation is not well adapted to analysis.
-
Tetrahedral meshes are the volumic equivalent of triangle meshes, they are very common in the scientific computing community. Tetrahedral meshing is now a mature technology. It is remarkable that still today all the existing software used in the industry is built on top of a handful of kernels, all written by a small number of individuals 27, 41, 47, 29, 40, 42, 28, 51.
Meshing requires a long-term, focused, dedicated research effort, that combines deep theoretical studies with advanced software development. We have the ambition to bring this kind of maturity to a different type of mesh (structured, with hexahedra), which is highly desirable for some simulations, and for which, unlike tetrahedra, no satisfying automatic solution exists. In the light of recent contributions, we believe that the domain is ready to overcome the principal difficulties.
-
Finally, at the most structured end of the spectrum there are hexahedral meshes composed of deformed cubes (hexahedra). They are preferred for certain physics simulations (deformation mechanics, fluid dynamics ...) because they can significantly improve both speed and accuracy. This is because (1) they contain a smaller number of elements (5-6 tetrahedra for a single hexahedron), (2) the associated tri-linear function basis has cubic terms that can better capture higher order variations, (3) they avoid the locking phenomena encountered with tetrahedra 20, (4) hexahedral meshes exploit inherent tensor product structure and (5) hexahedral meshes are superior in direction dominated physical simulations (boundary layer, shock waves, etc). Being extremely regular, hexahedral meshes are often claimed to be The Holy Grail for many finite element methods 21, outperforming tetrahedral meshes both in terms of computational speed and accuracy.
Despite 30 years of research efforts and important advances, mainly by the Lawrence Livermore National Labs in the U.S. 46, 45, hexahedral meshing still requires considerable manual intervention in most cases (days, weeks and even months for the most complicated domains). Some automatic methods exist 32, 49, that constrain the boundary into a regular grid, but they are not fully satisfactory either, since the grid is not aligned with the boundary. The advancing front method 19 does not have this problem, but generates irregular elements on the medial axis, where the fronts collide. Thus, there is no fully automatic algorithm that results in satisfactory boundary alignment.
3 Research program
3.1 Point clouds
Currently, transforming the raw point cloud into a triangular mesh is a long pipeline involving disparate geometry processing algorithms:
- Point pre-processing: colorization, filtering to remove unwanted background, first noise reduction along acquisition viewpoint;
- Registration: cloud-to-cloud alignment, filtering of remaining noise, registration refinement;
- Mesh generation: triangular mesh from the complete point cloud, re-meshing, smoothing.
The output of this pipeline is a locally structured model which is used in downstream mesh analysis methods such as feature extraction, segmentation in meaningful parts or building Computer-Aided Design (CAD) models.
It is well known that point cloud data contains measurement errors due to factors related to the external environment and to the measurement system itself 44, 38, 23. These errors propagate through all processing steps: pre-processing, registration and mesh generation. Even worse, the heterogeneous nature of different processing steps makes it extremely difficult to know how these errors propagate through the pipeline. To give an example, for cloud-to-cloud alignment it is necessary to estimate normals. However, the normals are forgotten in the point cloud produced by the registration stage. Later on, when triangulating the cloud, the normals are re-estimated on the modified data, thus introducing uncontrollable errors.
We plan to develop new reconstruction, meshing and re-meshing algorithms, with a specific focus on the accuracy and resistance to all defects present in the input raw data. We think that pervasive treatment of uncertainty is the missing ingredient to achieve this goal. We plan to rethink the pipeline with the position uncertainty maintained during the whole process. Input points can be considered either as error ellipsoids 48 or as probability measures 31. In a nutshell, our idea is to start by computing an error ellipsoid 50, 35 for each point of the raw data, and then to cumulate the errors (approximations) committed at each step of the processing pipeline while building the mesh. In this way, the final users will be able to take the uncertainty knowledge into account and rely on this confidence measure for further analysis and simulations. Quantifying uncertainty for reconstruction algorithms, and propagating them from input data to high-level geometry processing algorithms has never been considered before, possibly due to the very different methodologies of the approaches involved. At the very beginning we will re-implement the entire pipeline, and then attack the weak links through all three reconstruction stages.
3.2 Parameterizations
One of the favorite tools we use in our team are parameterizations, and we have major contributions to the field: we have solved a fundamental problem formulated more than 60 years ago 2. Parameterizations provide a very powerful way to reveal structures on objects. The most omnipresent application of parameterizations is texture mapping: texture maps provide a way to represent in 2D (on the map) information related to a surface. Once the surface is equipped with a map, we can do much more than a mere coloring of the surface: we can approximate geodesics, edit the mesh directly in 2D or transfer information from one mesh to another.
Parameterizations constitute a family of methods that involve optimizing an objective function, subject to a set of constraints (equality, inequality, being integer, etc.). Computing the exact solution to such problems is beyond any hope, therefore approximations are the only resort. This raises a number of problems, such as the minimization of highly nonlinear functions and the definition of direction fields topology, without forgetting the robustness of the software that puts all this into practice.
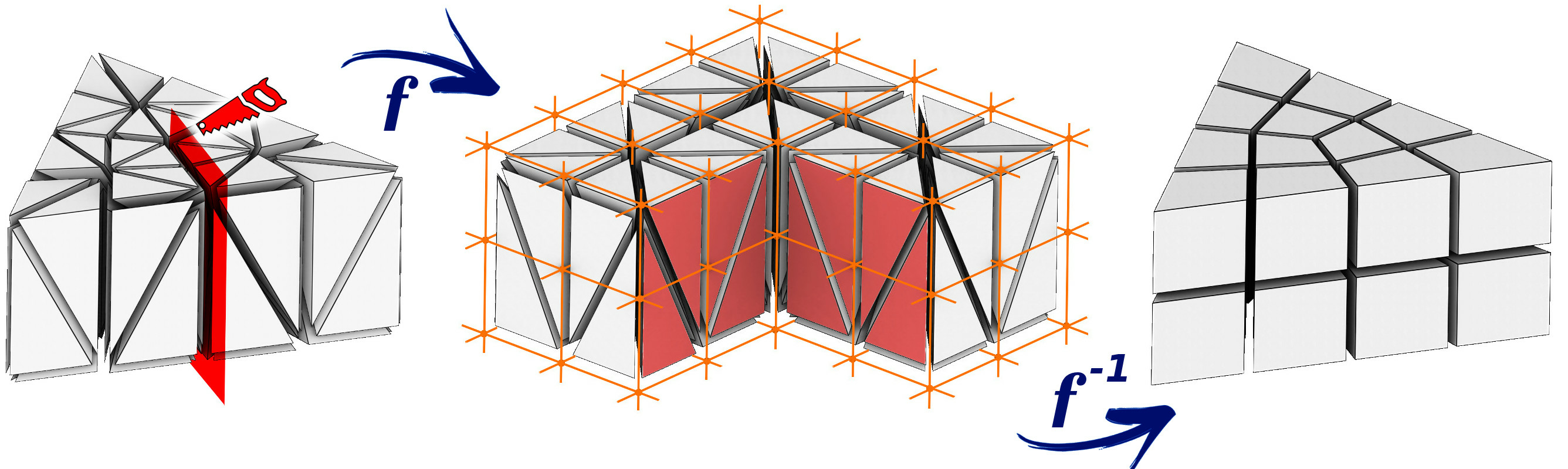
We are particularly interested in a specific instance of parameterization: hexahedral meshing. The idea 6, 4 is to build a transformation from the domain to a parametric space, where the deformed domain can be meshed by a regular grid. The inverse transformation applied to this grid produces the hexahedral mesh of the domain, aligned with the boundary of the object. The strength of this approach is that the transformation may admit some discontinuities. Let us show an example: we start from a tetrahedral mesh (Figure 2, left) and we want deform it in a way that its boundary is aligned with the integer grid. To allow for a singular edge in the output (the valency 3 edge, Figure 2, right), the input mesh is cut open along the highlighted faces and the central edge is mapped onto an integer grid line (Figure 2, middle). The regular integer grid then induces the hexahedral mesh with the desired topology.
Current global parameterizations allow grids to be positioned inside geometrically simple objects whose internal structure (the singularity graph) can be relatively basic. We wish to be able to handle more configurations by improving three aspects of current methods:
- Local grid orientation is usually prescribed by minimizing the curvature of a 3D steering field. Unfortunately, this heuristic does not always provide singularity curves that can be integrated by the parameterization. We plan to explore how to embed integrability constraints in the generation of the direction fields. To address the problem, we already identified necessary validity criteria, for example, the permutation of axes along elementary cycles that go around a singularity must preserve one of the axes (the one tangent to the singularity). The first step to enforce this (necessary) condition will be to split the frame field generation into two parts: first we will define a locally stable vector field, followed by the definition of the other two axes by a 2.5D directional field (2D advected by the stable vector field).
- The grid combinatorial information is characterized by a set of integer coefficients whose values are currently determined through numerical optimization of a geometric criterion: the shape of the hexahedra must be as close as possible to the steering direction field. Thus, the number of layers of hexahedra between two surfaces is determined solely by the size of the hexahedra that one wishes to generate. In this setting degenerate configurations arise easily, and we want to avoid them. In practice, mixed integer solvers often choose to allocate a negative or zero number of layers of hexahedra between two constrained sheets (boundaries of the object, internal constraints or singularities). We will study how to inject strict positivity constraints into these cases, which is a very complex problem because of the subtle interplay between different degrees of freedom of the system. Our first results for quad-meshing of surfaces give promising leads, notably thanks to motorcycle graphs 24, a notion we wish to extend to volumes.
- Optimization for the geometric criterion makes it possible to control the average size of the hexahedra, but it does not ensure the bijectivity (even locally) of the resulting parameterizations. Considering other criteria, as we did in 2D 30, would probably improve the robustness of the process. Our idea is to keep the geometry criterion to find the global topology, but try other criteria to improve the geometry.
3.3 Hexahedral-dominant meshing
All global parameterization approaches are decomposed into three steps: frame field generation, field integration to get a global parameterization, and final mesh extraction. Getting a full hexahedral mesh from a global parameterization means that it has positive Jacobian everywhere except on the frame field singularity graph. To our knowledge, there is no solution to ensure this property, but some efforts are done to limit the proportion of failure cases. An alternative is to produce hexahedral dominant meshes. Our position is in between those two points of view:
- We want to produce full hexahedral meshes;
- We consider as pragmatic to keep hexahedral dominant meshes as a fallback solution.
The global parameterization approach yields impressive results on some geometric objects, which is encouraging, but not yet sufficient for numerical analysis. Note that while we attack the remeshing with our parameterizations toolset, the wish to improve the tool itself (as described above) is orthogonal to the effort we put into making the results usable by the industry. To go further, our idea (as opposed to 36, 26) is that the global parameterization should not handle all the remeshing, but merely act as a guide to fill a large proportion of the domain with a simple structure; it must cooperate with other remeshing bricks, especially if we want to take final application constraints into account.
For each application we will take as an input domains, sets of constraints and, eventually, fields (e.g. the magnetic field in a tokamak). Having established the criteria of mesh quality (per application!) we will incorporate this input into the mesh generation process, and then validate the mesh by a numerical simulation software.
4 Application domains
4.1 Geometric Tools for Simulating Physics with a Computer
Numerical simulation is the main targeted application domain for the geometry processing tools that we develop. Our mesh generation tools will be tested and evaluated within the context of our cooperation with Hutchinson, experts in vibration control, fluid management and sealing system technologies. We think that the hex-dominant meshes that we generate have geometrical properties that make them suitable for some finite element analyses, especially for simulations with large deformations.
We also have a tight collaboration with a geophysical modeling specialists via RING consortium. In particular, we produce hexahedral-dominant meshes for geomechanical simulations of gas and oil reservoirs. From a scientific point of view, this use case introduces new types of constraints (alignments with faults and horizons), and allows certain types of nonconformities that we did not consider until now.
Our cooperation with RhinoTerrain pursues the same goal: reconstruction of buildings from point cloud scans allows to perform 3D analysis and studies on insolation, floods and wave propagation, wind and noise simulations necessary for urban planification.
5 Highlights of the year
Participants: Dmitry Sokolov, Nicolas Ray, François Protais, David Lopez, Étienne Corman, David Desobry, Yoann Coudert-Osmont.
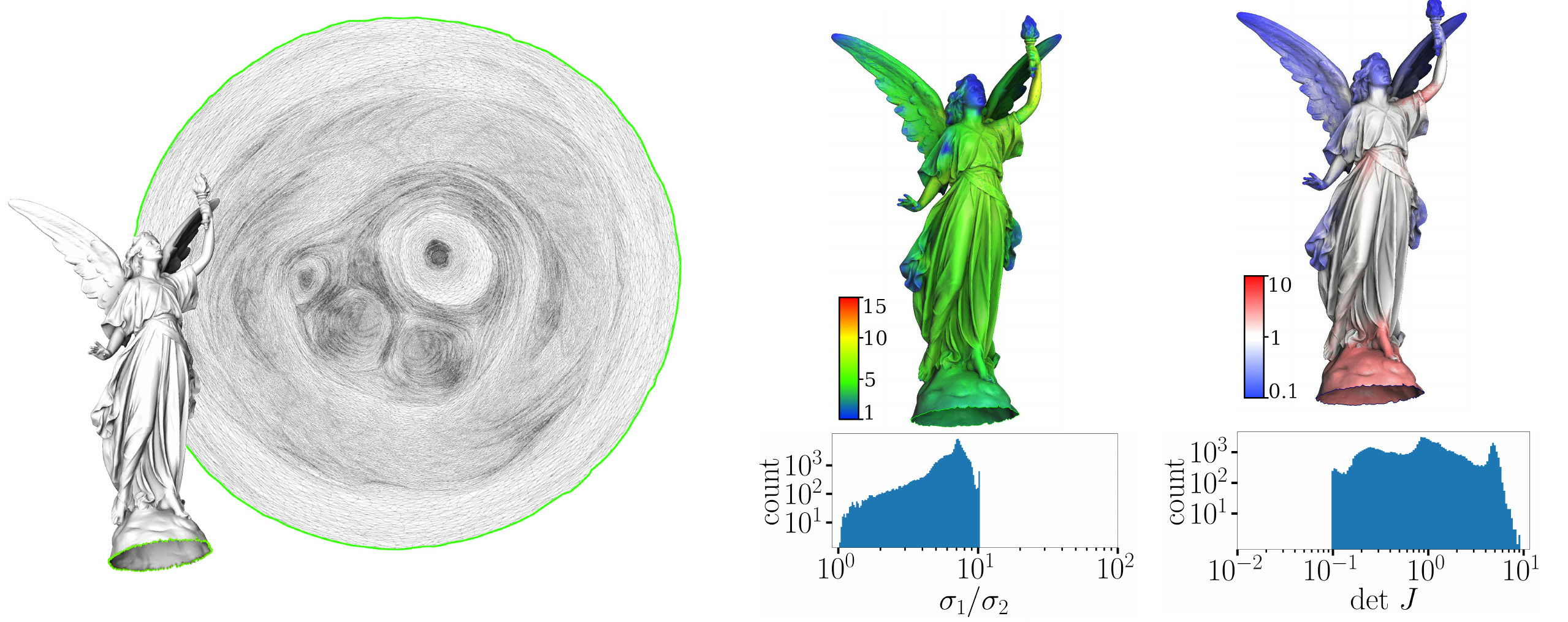
Mapping a triangulated surface to 2D plane (or a tetrahedral mesh to 3D space) is the most fundamental problem in geometry processing. The critical property of a good map is a (local) invertibility, and it is not an easy one to obtain. With our russian colleagues Vladimir Garanzha, Igor Kaporin and Liudmila Kudryavtseva from Dorodnicyn Computing Centre of Russian Academy of Sciences, we proposed a mapping method 12, 13 inspired by the mesh untangling problem. In computational physics, untangling plays an important role in mesh generation: it takes a mesh as an input, and moves the vertices to get rid of foldovers. In fact, mesh untangling can be considered as a special case of mapping, where the geometry of the object is to be defined in the map space and the geometric domain is not explicit, supposing that each element is regular. This approach allows us to produce locally invertible maps, which is the major challenge of mapping. In practice, our method succeeds in very difficult settings, and with less distortion than the previous work, both in 2D and 3D.
While the general concepts used in our algorithm (deformation of hyperelastic material and penalization of folds) are known since the 80s, a transition to a working algorithm is not trivial. We are the first to actually bring theoretical guarantees for the mesh untangling problem.
Our method is very robust and is already integrated into GMSH.
5.1 Awards
- David Lopez has received the best presentation award during GTMG2021
- Our paper 10 has received the 2nd best paper award for SPM2021
6 New results
Participants: Dmitry Sokolov, Nicolas Ray, Étienne Corman, Laurent Alonso, François Protais, David Lopez, Justine Basselin, Guillaume Coiffier, David Desobry, Yoann Coudert-Osmont.
6.1 Restricted Power Diagrams on the GPU
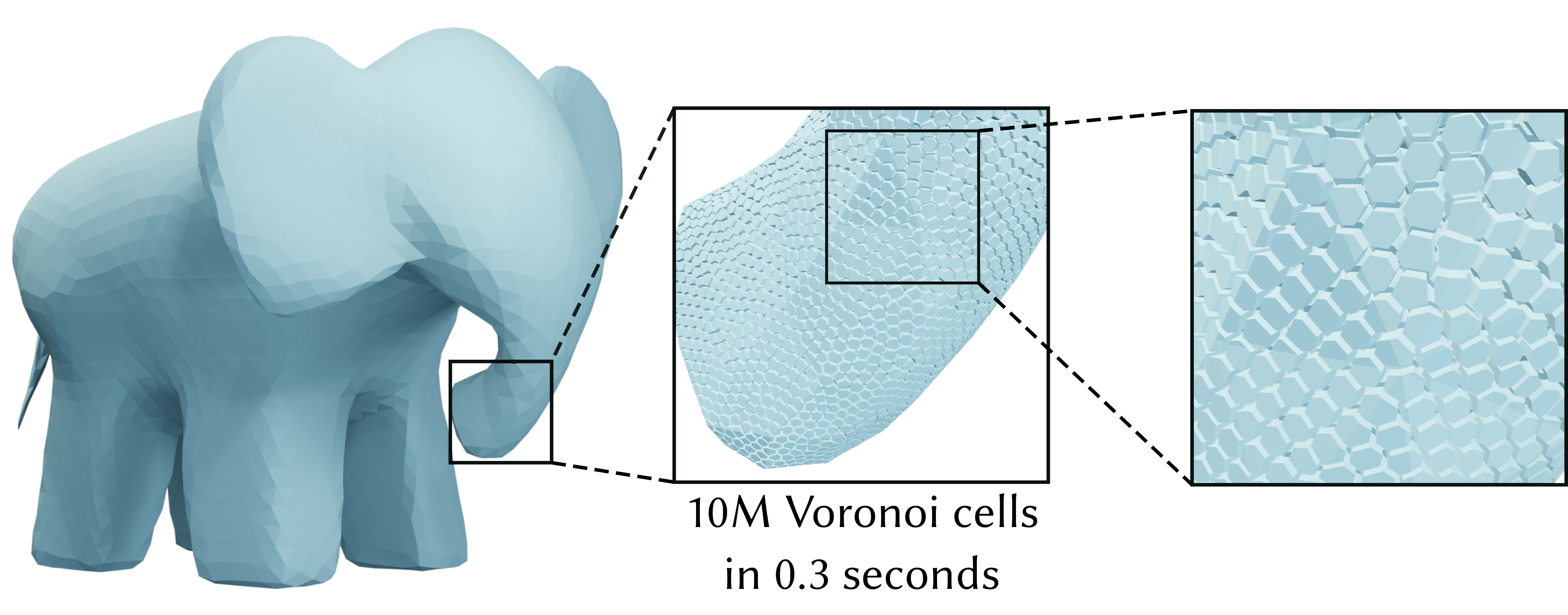
We continue to improve performance of meshing algorithms. Few years ago we have proposed a GPU version of Voronoi diagrams computation 3, this year we have proposed a method 8 to simultaneously decompose a 3D object into power diagram cells and to integrate given functions in each of the obtained simple regions. We offer a novel, highly parallel algorithm that lends itself to an efficient GPU implementation. It is optimized for algorithms that need to compute many decompositions, for instance, centroidal Voronoi tesselation algorithms and incompressible fluid dynamics simulations.
We propose an efficient solution that directly evaluates the integrals over every cell without computing the power diagram explicitly and without intersecting it with a tetrahedralization of the domain, Fig. 4 provides an illustration. Most computations are performed on the fly, without storing the power diagram. We manipulate a triangulation of the boundary of the domain (instead of tetrahedralizing the domain) to speed up the process. Moreover, the cells are treated independently one from another, making it possible to trivially scale up on a parallel architecture.
Despite recent Voronoi diagram generation methods optimized for the GPU, computing integrals over restricted power diagrams still poses significant challenges; the restriction to a complex simulation domain is difficult and likely to be slow. It is not trivial to determine when a cell of a power diagram is completely computed, and the resulting integrals (e.g. the weighted Laplacian operator matrix) do not fit into fast (shared) GPU memory. We address all these issues and boost the performance of the state-of-the-art algorithms by a factor 2 to 3 for (unrestricted) Voronoi diagrams and a speed-up with respect to CPU implementations for restricted power diagrams. An essential ingredient to achieve this is our new scheduling strategy that allows us to treat each Voronoi/power diagram cell with optimal settings and to benefit from the fast memory.
6.2 Roof fitting

This work is done as part of our contract between our team and RhinoTerrain. Automatic extraction of building roofs from remote sensing data is important for many applications including 3D city modeling, urban planning, disaster management, and simulations. In this project, we propose an automatic workflow for roof reconstruction by polygonal models from airbourne LIDAR data (Figure 5). This year we have published one paper on this subject 9. The main idea is to extend the VSDM algorithm (Voronoï Squared Distance Minimization) developed by the team 37 to the case of fitting parametric template models to point clouds. Using a high quality mesh as geometric template to fit a point cloud is a common practice to generate animation of faces or even full bodies from a depth camera. We are interested here to match the human-made objects whose acceptable deformations are not as rigid as possible, but rather described by a parametric template. The motivation is to be able to retrieve CAD objects or buildings in a point cloud. While it has a very broad applicability range, we are particularly interested in fitting roof templates to airborne LIDAR point clouds. Most previous works detect characteristic features (planes, ridges, contours) to combine them into a roof. We instead formulate it as a global fitting problem, and propose an efficient way to solve it. The originality of our approach is to fit a mesh with geometric constraints (a roof template) to the point cloud by a fast and robust numerical optimization. More precisely, we simultaneously consider the distance from the model to the point cloud, and the distance from the point cloud to the model, with a biweight estimator to integrate outliers rejection directly in our numerical optimization framework. With our formulation, we do not need to alternate between matching and fitting steps. The objective function being smooth everywhere, it can be minimized by quasi-Newtonian methods like the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm. The advantage of our method is that the feature matching, roof trimming, point cloud segmentation, and integrity roof constraints are all supported in a unique numerical optimization problem that can be solved very efficiently.
6.3 Frame fields and parameterization
As we have mentioned in § 3.2, all global parameterization approaches contain two main steps:
- Frame field generation: this step defines the orientation of the grid at each point of the domain.
- Field integration: this step computes the position and the size of the grid cells aligned with the input orientation field.
We have new results for both of them.
Frame field generation
The generation of frame fields is a key component of recent quad meshing algorithms based on global parameterization, as it defines the orientation of the final facets. State-of-the-art methods are able to generate smooth frame fields subject to some hard constraints (direction and topology) or smooth constraints (matching the curvature direction). When dealing with CAD models, the field must be aligned with feature edges. Unfortunately, the smoothest frame field that respects this constraint have a topology that is considered as degenerate for producing quad meshes. More precisely, most CAD models contains at least one sharp corner i.e. a conflicting feature edge configuration, that would produce unmeshable cartographic pole in the frame field. Our approach 10, 11 is to trade some smoothness against preventing generation of such singularities: we change the objective function to increase the cost of producing these singularities. We also relax the frame field orthogonality constraint that induces too much distortion on CAD objects.
Parameterization
One of the types of hexahedral grids that is the most commonly used for the subsurface is 3D structured grids. It is computational efficient, honoring the geometry of the faults and horizons of the geological model and the standard format of most of the current standard flow simulators. To build the grid, it requires that the faults to be distinguishable in two principal directions U and V. When it is not the case, the current technologies require that the fault network be either simplified structure-wise or approximated geometry-wise by a stair-step representation, both at the expense of honoring the complexity and precision of the input geological model.
With our colleagues from the start-up Tessael we propose a new method 14 of building structured hexahedral grids without compromising the complexity of the structural model. Unlike current methods that generate the gridding based on a 3D parameterization UVW in which the U and V coordinates are constrained by separate families of surfaces respectively, our method does not have the limitation of classifying faults in U and V families. Our method uses a pair of parameterizations for the UV coordinates that can have local frame transformations (rotation+translation). Thus offering additional degrees of freedom during the gridding process to honor the geometry of faults on a larger family of complex geological models. To validate the results, we present the results of simulations on our grids using standard flow and geomechanical simulation software.
6.4 Auxiliary stabilization systems for legged robots

Demands on leg degrees of freedom and control precision for bipedal robotics are steadily increasing, especially for the tasks involving walking on a rough terrain. We present an alternative, as well as a working proof-of-concept. We propose to give robots an additional “support point” without touching the rest of the mechanical system. We have created an electromechanical auxiliary stabilization system able to compensate for external disturbances and control errors with aid of control moment gyroscopes.
This year we have published two papers15, 7 on the subject in flagship venues (Automatica and ICRA2021). Meet gyrubot: a 5-link almost planar bipedal robot with a torso complemented by a nonanthropomorphic stabilization system, capable of blindly walking through uneven areas (refer to Fig. 6). Despite being almost planar, the robot does not need any support in the frontal plane! We provide the experimental evidence of the ability of gyrubot to navigate across non-flat terrains.
Gyrubot is a biped with 2 DoF legs stabilized by two orthogonal scissored-pair control moment gyroscopes. To challenge the stabilization system, the legs' controller is completely ignorant of the inertial measurement unit (IMU) readings. Moreover, the robot is built around low-end ($2.5k) servo drives. Despite that, our prototype successfully walks blindfolded even through (slightly) rough terrains. To conclude the above, gyrubot is a bold little step away from the mainstream developments in legged robotics.
7 Bilateral contracts and grants with industry
Participants: Dmitry Sokolov, Nicolas Ray, Justine Basselin, François Protais, David Desobry.
7.1 Bilateral contracts with industry
-
Company: CEA
Duration: 01/10/2019 – 30/09/2022
Participants: Dmitry Sokolov, Nicolas Ray and François Protais
Amount: 45k euros
Abstract: This project revolves around generation of Polycubes guided by orientation fields. The first goal of the project is to define a new Polycube method that deforms an object along a previously generated 3D orientation field. Such a solution would overcome two major defects of Polycube methods, namely : (1) The possible absence of aligned mesh layers along the smooth edges; (2) The poor treatment of sharp edges (which is very common on mechanical parts in CAD).
-
Company: RhinoTerrain
Duration: 01/12/2019 – 30/03/2024
Participants: Dmitry Sokolov, Nicolas Ray and Justine Basselin
Amount: 50k euros
Abstract: In this project, we are interested in the reconstruction phase in the context of LIDAR point clouds of city districts. These data are acquired via an airplane and contain every object present in the city: cars, trees, building roofs, roads and ground features, etc. Applications of these data, ranging from city visualization for tourism to flood and wind simulation, require the reconstruction of buildings as geometrical objects. As LIDAR point cloud are acquired from the sky, buildings are only represented by their roofs. Hence, determining the polygonal surfaces of roofs enables the reconstruction of the whole city by extrusion.
-
Company: TotalEnergies
Duration: 01/10/2020 – 30/03/2024
Participants: Dmitry Sokolov, Nicolas Ray and David Desobry
Amount: confidential
Abstract: The goal of this project is to improve the accuracy of rubber behavior simulations for certain parts produced by TotalEnergies, notably gaskets. To do this, both parties need to develop meshing methods adapted to simulations of large deformation in non-linear mechanics. The Pixel team has a great expertise in hex-dominant meshing, TotalEnergies has a strong background in numerical simulations within an industrial context. This collaborative project aims to take advantage of both expertises.
8 Partnerships and cooperations
8.1 International initiatives
Participant: François Protais.
8.1.1 Visits to international teams
Research stays abroad
François Protais has spent 1 month at the University of Cagliari, working on mapping problems with Marco Livesu.
9 Dissemination
Participants: Dmitry Sokolov, Nicolas Ray, Étienne Corman, Dobrina Boltcheva, Guillaume Coiffier, François Protais, David Desobry.
9.1 Promoting scientific activities
Member of the conference program committees
Members of the team were IPC members for SPM and ISVC.
Reviewer
Members of the team were reviewers for Eurographics, SIGGRAPH, SIGGRAPH Asia, ISVC, Pacific Graphics, and SPM.
9.1.1 Journal
Members of the team were reviewers for Computer Aided Design (Elsevier), Computer Aided Geometric Design (Elsevier), Transactions on Visualization and Computer Graphics (IEEE), Transactions on Graphics (ACM), and Computers & Graphics (Elsevier).
9.1.2 Invited talks
Dmitry Sokolov gave invited talks at Massachusetts Institute of Technology, University of Burgundy and Aix-Marseille University as well as an invited talk at Mmg Day 2021.
9.1.3 Research administration
Dmitry Sokolov is responsible for the Industrial Club of GdR IG-RV (Groupement de recherche Informatique Géométrique et Graphique, Réalité Virtuelle et Visualisation)
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
- Licence : Dobrina Boltcheva, Computer Graphics, 30h, 3A, IUT Saint-Dié-des-Vosges
- Licence : Dobrina Boltcheva, Advanced Object Oriented Programming & UML, 60h, 2A, IUT SaintDié-des-Vosges
- Licence : Dobrina Boltcheva, Advanced algorithmics, 50h, 2A, IUT Saint-Dié-des-Vosges
- Licence : Dobrina Boltcheva, Image Processing, 30h, 2A, IUT Saint-Dié-des-Vosges
- Licence : Dobrina Boltcheva, UML Modeling, 20h, 1A, IUT Saint-Dié-des-Vosges
- Master : François Protais, Analyse et Conception de Logiciels, 11h, M1, University of Lorraine
- Master : François Protais, Représentations des Données Visuelles, 8, M1, University of Lorraine
- Master : François Protais, Fonctionnement d'un moteur du rendu 3D, 12h, M1, University of Lorraine
- License : Guillaume Coiffier, Automata and Langage theory, 16h, L2, University of Lorraine
- License : Guillaume Coiffier, Programming, 16h + 16h, L1, University of Lorraine
- License : Guillaume Coiffier, Optimization, 16h, L3, University of Lorraine
- Licence : Dmitry Sokolov, Programming, 48h, 2A, University of Lorraine
- Licence : Dmitry Sokolov, Logic, 30h, 3A, University of Lorraine
- Licence : Dmitry Sokolov, Algorithmics, 25h, 3A, University of Lorraine
- Licence : Dmitry Sokolov, Computer Graphics, 16h, M1, University of Lorraine
- Master : Dmitry Sokolov, Logic, 22h, M1, University of Lorraine
- Master : Dmitry Sokolov, Computer Graphics, 30h, M1, University of Lorraine
- Master : Dmitry Sokolov, 3D data visualization, 15h, M1, University of Lorraine
- Master : Dmitry Sokolov, 3D printing, 12h, M2, University of Lorraine
- Master : Dmitry Sokolov, Numerical modeling, 12h, M2, University of Lorraine
9.2.2 Supervision
Dmitry Sokolov took the responsibility of the 3d year of computer science licence at the University of Lorraine.
9.2.3 Juries
- Dmitry Sokolov participated in the PhD jury of Dat Vo Quoc (ITMO, Saint Petersburg, Russia) as a reviewer.
- Nicolas Ray participated in the PhD jury of Jovana Jezdimirović (Louvain Catholic University, Belgium) as a reviewer.
- Dobrina Boltcheva participated in the PhD jury of Aureliane Gailliegue (Sorbonne University, Paris) as an examinator.
9.3 Popularization
9.3.1 Education
Dmitry Sokolov, Nicolas Ray and Étienne Corman gave a long course at SIGGRAPH 2021 entitled “Least squares for programmers”. This course presents how least squares methods can solve numerous problems encountered in mesh manipulation. Unlike classical tools for mesh manipulation via combinatorial optimization, with this approach, instead of describing each step of the program flow, we define properties of our goal, and let a numerical solver to discover it. In the world of numerical optimization, least squares are particularly simple to implement because they do not require advanced mathematical knowledge. In addition, existing solvers are so efficient... that a vast number of other methods rely on solving sequences of least squares problems. This simplicity of implementation, combined with the efficiency of the solvers, makes this approach the ideal candidate to introduce some numerical optimization in design, rendering, etc. This course presents least squares by illustrating it on simple cases; for this great tool to be fully harnessed, one must above all know how to recognize the situations in which it will be effective. A four-hours course obviously cannot replace years of experience, but we have listed a set of simple use cases representative of the variety of configurations in which least squares have solved problems in computer graphics. For a deeper understanding of this method, we will clarify its positioning with respect to other scientific fields: what is the relation to the probability theory? In which case is it equivalent to a FEM formulation? Is there any connection to neural networks?
10 Scientific production
10.1 Major publications
- 1 articleRestricted Power Diagrams on the GPU.Computer Graphics Forum402June 2021
- 2 articleFoldover-free maps in 50 lines of code.ACM Transactions on GraphicsVolume 40issue 4July 2021, Article No.102, pp 1–16
- 3 articleMeshless Voronoi on the GPU.ACM Trans. Graph.376December 2018, 265:1--265:12URL: http://doi.acm.org/10.1145/3272127.3275092
- 4 articlePractical 3D Frame Field Generation.ACM Trans. Graph.356November 2016, 233:1--233:9URL: http://doi.acm.org/10.1145/2980179.2982408
- 5 articleRobust Polylines Tracing for N-Symmetry Direction Field on Triangulated Surfaces.ACM Trans. Graph.333June 2014, 30:1--30:11URL: http://doi.acm.org/10.1145/2602145
- 6 articleHexahedral-Dominant Meshing.ACM Transactions on Graphics3552016, 1 - 23
10.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
10.3 Other
Educational activities
10.4 Cited publications
- 19 articleA frontal approach to hex-dominant mesh generation.Adv. Model. and Simul. in Eng. Sciences112014, 8:1--8:30URL: https://doi.org/10.1186/2213-7467-1-8
- 20 inproceedingsA Comparison of All-Hexahedral and All-Tetrahedral Finite Element Meshes for Elastic and Elasto-Plastic Analysis.International Meshing Roundtable conf. proc.1995
- 21 inproceedingsMeeting the Challenge for Automated Conformal Hexahedral Meshing.9th International Meshing Roundtable2000, 11--20
- 22 miscCloud Compare.http://www.danielgm.net/cc/release/
- 23 articleMeasurement uncertainty on the circular features in coordinate measurement system based on the error ellipse and Monte Carlo methods.Measurement Science and Technology27122016, 125016URL: http://stacks.iop.org/0957-0233/27/i=12/a=125016
- 24 inproceedingsMotorcycle Graphs: Canonical Quad Mesh Partitioning.Proceedings of the Symposium on Geometry ProcessingSGP '08Aire-la-Ville, Switzerland, SwitzerlandCopenhagen, DenmarkEurographics Association2008, 1477--1486URL: http://dl.acm.org/citation.cfm?id=1731309.1731334
- 25 miscGRAPHITE.http://alice.loria.fr/software/graphite/doc/html/
- 26 articleRobust Hex-Dominant Mesh Generation using Field-Guided Polyhedral Agglomeration.ACM Transactions on Graphics (Proceedings of SIGGRAPH)364July 2017
- 27 articleFully Automatic Mesh Generator for 3D Domains of Any Shape.IMPACT Comput. Sci. Eng.23December 1990, 187--218URL: http://dx.doi.org/10.1016/0899-8248(90)90012-Y
- 28 articleGmsh: a three-dimensional finite element mesh generator.International Journal for Numerical Methods in Engineering79112009, 1309-1331
- 29 inproceedingsReliable Isotropic Tetrahedral Mesh Generation Based on an Advancing Front Method.International Meshing Roundtable conf. proc.2004
- 30 inproceedingsLeast squares conformal maps for automatic texture atlas generation.ACM transactions on graphics (TOG)21ACM2002, 362--371
- 31 articleNotions of Optimal Transport theory and how to implement them on a computer.Computer and Graphics2018
- 32 inproceedingsA New Approach to Octree-Based Hexahedral Meshing.International Meshing Roundtable conf. proc.2001
- 33 miscMeshMixer.http://www.meshmixer.com/
- 34 miscMeshlab.http://www.meshlab.net/
- 35 inproceedingsUncertainty Propagation for Terrestrial Mobile Laser Scanner.SPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences2016
- 36 articleCubeCover - Parameterization of 3D Volumes.Computer Graphics Forum3052011, 1397-1406URL: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-8659.2011.02014.x
- 37 articleFitting polynomial surfaces to triangular meshes with Voronoi squared distance minimization.Engineering with Computers3032014, 289--300
- 38 miscSpatial Uncertainty Model for Visual Features Using a Kinect Sensor.2012
- 39 miscPoint Cloud Library.http://www.pointclouds.org/downloads/
- 40 articleNETGEN An advancing front 2D/3D-mesh generator based on abstract rules.Computing and visualization in science111997
- 41 articleAutomatic three-dimensional mesh generation by the finite octree technique.International Journal for Numerical Methods in Engineering3241991
- 42 articleTetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator.ACM Trans. on Mathematical Software4122015
- 43 techreportCFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences.NASA/CR-2014-218178, NF1676L-183322014
- 44 articleScanning geometry: Influencing factor on the quality of terrestrial laser scanning points.ISPRS Journal of Photogrammetry and Remote Sensing6642011, 389 - 399URL: http://www.sciencedirect.com/science/article/pii/S0924271611000098
- 45 inproceedingsUnconstrained Paving & Plastering: A New Idea for All Hexahedral Mesh Generation.International Meshing Roundtable conf. proc.2005
- 46 articleThe whisker weaving algorithm.International Journal of Numerical Methods in Engineering1996
- 47 articleEfficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints.International Journal for Numerical Methods in Engineering37121994, 2005--2039URL: http://dx.doi.org/10.1002/nme.1620371203
- 48 inproceedingsRobust and Practical Depth Map Fusion for Time-of-Flight Cameras.Image AnalysisChamSpringer International Publishing2017, 122--134
- 49 inproceedingsAdaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data.International Meshing Roundtable conf. proc.2004
- 50 articlePoint cloud uncertainty analysis for laser radar measurement system based on error ellipsoid model.Optics and Lasers in Engineering792016, 78 - 84URL: http://www.sciencedirect.com/science/article/pii/S0143816615002675
-
51
misc
, Computational Geometry Algorithms Library.http://www.cgal.org

