Keywords
Computer Science and Digital Science
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.7. High performance computing
- A6.5.2. Fluid mechanics
Other Research Topics and Application Domains
- B4.2.2. Fusion
1 Team members, visitors, external collaborators
Research Scientists
- Emmanuel Franck [Inria, Researcher]
- Victor Michel-Dansac [Inria, Starting Faculty Position]
Faculty Members
- Philippe Helluy [Team leader, Univ de Strasbourg, Professor, HDR]
- Clémentine Courtès [Univ de Strasbourg, Associate Professor]
- Michaël Gutnic [Univ de Strasbourg, Associate Professor]
- Laurent Navoret [Univ de Strasbourg, Associate Professor]
- Yannick Privat [Univ de Strasbourg, Professor, HDR]
Post-Doctoral Fellow
- Ali Aboudou Elarif [Inria]
PhD Students
- Mickael Bestard [Univ de Strasbourg]
- Léo Bois [Inria]
- Clément Flint [Univ de Strasbourg]
- Romane Helie [Univ de Strasbourg]
- Guillaume Mestdagh [Univ de Strasbourg]
- Tom Sprunck [Inria, from Nov 2021]
- Guillaume Steimer [Inria, from Oct 2021]
Technical Staff
- Matthieu Boileau [CNRS, Engineer]
- Pierre Gerhard [Univ de Strasbourg, Engineer]
- Laura Mendoza [Inria, Engineer, until May 2021]
Interns and Apprentices
- Khaoula Chahdi [Inria, from Apr 2021 until Aug 2021]
- Guillaume Steimer [Inria, from Feb 2021 until Aug 2021]
Administrative Assistant
- Ouiza Herbi [Inria]
2 Overall objectives
TONUS started in January 2014. It is a team of the Inria Nancy-Grand Est center. It is located in the mathematics institute (IRMA) of the University of Strasbourg.
The International Thermonuclear Experimental Reactor (ITER) is a large-scale scientific experiment that aims to demonstrate that it is possible to produce energy from fusion, by confining a very hot hydrogen plasma inside a toroidal chamber, called tokamak. In addition to physics and technology research, tokamak design also requires mathematical modelling and numerical simulations on supercomputers.
The objective of the TONUS project is to deal with such mathematical and computing issues. We are mainly interested in kinetic, gyrokinetic and fluid simulations of tokamak plasmas. In the TONUS project-team we are working on the development of new numerical methods devoted to such simulations. We investigate several classical plasma models, study new reduced models and new numerical schemes adapted to these models. We implement our methods in two software projects: Selalib and SCHNAPS adapted to recent computer architectures.
We have strong relations with the CEA-IRFM team and participate in the development of their gyrokinetic simulation software GYSELA. We are involved in two Inria Project Labs, respectively devoted to tokamak mathematical modelling and high performance computing. The numerical tools developed from plasma physics can also be applied in other contexts. For instance, we collaborate with a small company in Strasbourg specialized in numerical software for applied electromagnetism. We also study kinetic acoustic models with the CEREMA and multiphase flows with EDF.
Finally, our topics of interest are at the interaction between mathematics, computer science, High Performance Computing, physics and practical applications.
3 Research program
3.1 Kinetic models for plasmas
The fundamental model for plasma physics is the coupled Vlasov-Maxwell kinetic model: the Vlasov equation describes the distribution function of particles (ions and electrons), while the Maxwell equations describe the electromagnetic field. In some applications, it may be necessary to take relativistic particles into account, which leads to consider the relativistic Vlasov equation, even if in general, tokamak plasmas are supposed to be non-relativistic. The distribution function of particles depends on seven variables (three for space, three for the velocity and one for time), which yields a huge amount of computation. To these equations we must add several types of source terms and boundary conditions for representing the walls of the tokamak, the applied electromagnetic field that confines the plasma, fuel injection, collision effects, etc.
Tokamak plasmas possess particular features, which require developing specialized theoretical and numerical tools.
Because the magnetic field is strong, the particle trajectories have a very fast rotation around the magnetic field lines. A full resolution would require a prohibitive amount of computation. It is necessary to develop reduced models for large magnetic fields in order to obtain tractable calculations. The resulting model is called a gyrokinetic model. It allows us to reduce the dimensionality of the problem. Such models are implemented in GYSELA and Selalib.
On the boundary of the plasma, the collisions can no more be neglected. Fluid models, such as MagnetoHydroDynamics (MHD) become again relevant. For the good operation of the tokamak, it is necessary to control MHD instabilities that arise at the plasma boundary. Computing these instabilities requires special implicit numerical discretizations with excellent long time behavior.
In addition to theoretical modelling tools, it is necessary to develop numerical schemes adapted to kinetic, gyrokinetic and fluid models. Three kinds of methods are studied in TONUS: Particle-In-Cell (PIC) methods, semi-Lagrangian and fully Eulerian approaches.
3.2 Gyrokinetic models: theory and approximation
In most phenomena where oscillations are present, we can establish a three-model hierarchy: the model parameterized by the oscillation period, the limit model and the two-scale model, possibly with its corrector. In a context where one wishes to simulate such a phenomenon where the oscillation period is small and the oscillation amplitude is not small, it is important to have numerical methods based on an approximation of the two-scale model. If the oscillation period varies significantly over the domain of simulation, it is important to have numerical methods that approximate properly and effectively the model parameterized by the oscillation period and the two-scale model. Implementing two-scale numerical methods (for instance by Frénod et al. 26) is based on a numerical approximation of the Two-Scale model. These are called of order 0. A Two-Scale Numerical Method is called of order 1 if it incorporates information from the corrector and from the equation of which this corrector is a solution. If the oscillation period varies between very small values and values of order 1, it is necessary to have new types of numerical schemes (Two-Scale Asymptotic Preserving Schemes of order 1 or TSAPS) that preserve the asymptotics between the model parameterized by the oscillation period and the Two-Scale model with its corrector. A first work in this direction has been initiated by Crouseilles et al. 25.
3.3 Semi-Lagrangian schemes
The Strasbourg team has a long and recognized experience in numerical methods for Vlasov-type equations. We are specialized in both particle and phase space solvers for the Vlasov equation: Particle-in-Cell (PIC) methods and semi-Lagrangian methods. We also have a long-standing collaboration with CEA Cadarache for the development of the GYSELA software for gyrokinetic tokamak plasmas.
The Vlasov and the gyrokinetic models are partial differential equations that express the transport of the distribution function in the phase space. In the original Vlasov case, the phase space is the six-dimension position-velocity space. For the gyrokinetic model, the phase space is five-dimensional because we consider only the parallel velocity in the direction of the magnetic field and the gyrokinetic angular velocity instead of three velocity components.
A few years ago, Eric Sonnendrücker and his collaborators introduced a new family of methods for solving transport equations in the phase space. This family of methods are the semi-Lagrangian methods. The principle of these methods is to solve the equation on a grid of the phase space. The grid points are transported with the flow of the transport equation for a time step and interpolated back periodically onto the initial grid. The method is then a mix of particle Lagrangian methods and Eulerian methods. The characteristics can be solved forward or backward in time leading to the Forward Semi-Lagrangian (FSL) or Backward Semi-Lagrangian (BSL) schemes. Conservative schemes based on this idea can be developed and are called Conservative Semi-Lagrangian (CSL).
GYSELA is a 5D full gyrokinetic code based on a classical backward semi-Lagrangian scheme (BSL) 30 for the simulation of core turbulence that has been developed at CEA Cadarache in collaboration with our team 27.
More recently, we have started to apply the semi-Lagrangian methods to more general kinetic equations. Indeed, most of the conservation laws of physics can be represented by a kinetic model with a small set of velocities. Compressible fluids or MHD equations have such representations. Semi-Lagrangian methods then become a very appealing and efficient approach for solving these equations.
3.4 PIC methods
Historically PIC methods have been very popular for solving the Vlasov equations. They allow solving the equations in the phase space at a relatively low cost. The main disadvantage of this approach is that, due to its random aspect, it produces an important numerical noise that has to be controlled in some way, for instance by regularizations of the particles, or by divergence correction techniques in the Maxwell solver. We have a long-standing experience in PIC methods and we started implementing them in Selalib. An important aspect is to adapt the method to new multicore computers. See the work by Crestetto and Helluy 24.
3.5 Fluid and reduced kinetic models for plasmas
As already said, kinetic plasmas computer simulations are very intensive, because of the gyrokinetic turbulence. In some situations, it is possible to make assumptions on the shape of the distribution function that simplify the model. We obtain in this way a family of fluid or reduced models.
Assuming that the distribution function has a Maxwellian shape, for instance, we obtain the MagnetoHydroDynamic (MHD) model. It is physically valid only in some parts of the tokamak (at the edges for instance). The fluid model is generally obtained from the hypothesis that the collisions between particles are strong.
But the reduction is not necessarily a consequence of collisional effects. Indeed, even without collisions, the plasma may still relax to an equilibrium state over sufficiently long time scales (Landau damping effect).
In the fluid or reduced-kinetic regions, the approximation of the distribution function could require fewer data while still achieving a good representation, even in the collisionless regime.
Therefore, a fluid or a reduced model is a model where the explicit dependency on the velocity variable is removed. In a more mathematical way, we consider that in some regions of the plasma, it is possible to exhibit a (preferably small) set of parameters that allows us to describe the main properties of the plasma with a generalized "Maxwellian” . Then
In this case it is sufficient to solve for . Generally, the vector is the solution of a first order hyperbolic system.
Another way to reduce the model is to try to find an abstract kinetic representation with an as small as possible set of kinetic velocities. The kinetic approach has then only a mathematical meaning. It allows solving very efficiently many equations of physics.
3.6 Numerical schemes
As previously indicated, an efficient method for solving the reduced models is the Discontinuous Galerkin (DG) approach. It is possible to make it of arbitrary order. It requires limiters when it is applied to nonlinear PDEs occurring for instance in fluid mechanics. But the reduced models that we intend to write are essentially linear. The nonlinearity is concentrated in a few coupling source terms.
In addition, this method, when written in a special set of variables, called the entropy variables, has nice properties concerning the entropy dissipation of the model. It opens the door to constructing numerical schemes with good conservation properties and no entropy dissipation, as already used for other systems of PDEs 31, 23, 29, 28.
3.7 Matrix-free implicit schemes
In tokamaks, the reduced model generally involves many time scales. Among these time scales, many of them, associated to the fastest waves, are not relevant. In order to filter them out, it is necessary to adopt implicit solvers in time. When the reduced model is based on a kinetic interpretation, it is possible to construct implicit schemes that do not impose solving costly linear systems. In addition the resulting solver is stable even at a very high CFL (Courant–Friedrichs–Lewy) number.
3.8 Electromagnetic solvers
Precise resolution of the electromagnetic fields is essential for proper plasma simulation. Thus it is important to use efficient solvers for the Maxwell systems and its asymptotics: Poisson equation and magnetostatics.
The proper coupling of the electromagnetic solver with the Vlasov solver is also crucial for ensuring conservation properties and stability of the simulation.
Finally, plasma physics implies very different time scales. It is thus very important to develop implicit Maxwell solvers and Asymptotic Preserving (AP) schemes in order to obtain good behavior on long time scales.
3.9 Coupling
The coupling of the Maxwell equations to the Vlasov solver requires some precautions. The most important one is to control the charge conservation errors, which are related to the divergence conditions on the electric and magnetic fields. We will generally use divergence correction tools for hyperbolic systems presented for instance in 22 (and the references therein).
3.10 Implicit solvers
As already pointed out, in a tokamak, the plasma presents several different space and time scales. It is not possible in practice to solve the initial Vlasov-Maxwell model. It is first necessary to establish asymptotic models by letting some parameters (such as the Larmor frequency or the speed of light) tend to infinity. This is the case for the electromagnetic solver and this requires implementing implicit time solvers in order to efficiently capture the stationary state, the solution of the magnetic induction equation or the Poisson equation.
4 Application domains
4.1 Controlled fusion and ITER
The search for alternative energy sources is a major issue for the future. Among others, controlled thermonuclear fusion in a hot hydrogen plasma is a promising possibility. The principle is to confine the plasma in a toroidal chamber, called a tokamak, and to attain the necessary temperatures to sustain nuclear fusion reactions.The International Thermonuclear Experimental Reactor (ITER) is a tokamak being constructed in Cadarache, France. This was the result of a joint decision by an international consortium including the European Union, Canada, USA, Japan, Russia, South Korea, India and China. ITER is a huge project. As of today, the budget is estimated at 20 billion euros. The first plasma shot is planned for 2025 and the first deuterium-tritium operation for 2027. Many technical and conceptual difficulties have to be overcome before the actual exploitation of fusion energy. Consequently, much research has been carried out around magnetically confined fusion. Among these studies, it is important to carry out computer simulations of the burning plasma. Thus, mathematicians and computer scientists are also needed in the design of ITER. The reliability and the precision of numerical simulations allow a better understanding of the physical phenomena and thus would lead to better designs. TONUS's main involvement is in such research. The required temperatures to attain fusion are very high, of the order of a hundred million degrees. Thus it is imperative to prevent the plasma from touching the tokamak inner walls. This confinement is obtained thanks to intense magnetic fields. The magnetic field is created by poloidal coils, which generate the toroidal component of the field. The toroidal plasma current also induces a poloidal component of the magnetic field that twists the magnetic field lines. The twisting is very important for the stability of the plasma. The idea goes back to research by Tamm and Sakharov, two Russian physicists, in the 50's. Other devices are essential for the proper operation of the tokamak: a divertor for collecting the escaping particles, microwave heating for reaching higher temperatures, a fuel injector for sustaining the fusion reactions, toroidal coils for controlling instabilities, etc.
4.2 Other applications
The software and numerical methods that we develop can also be applied to other fields of physics or of engineering.
- For instance, we have a collaboration with the company AxesSim in Strasbourg for the development of efficient Discontinuous Galerkin (DG) solvers on hybrid computers (CPU/GPU). The applications are electro-magnetic simulations for the conception of antennas, electronic devices or aircraft electromagnetic compatibility.
- The acoustic conception of large rooms requires huge numerical simulations. It is not always possible to solve the full wave equation and many reduced acoustic models have been developed. A popular model consists in considering "acoustic" particles moving at the speed of sound. The resulting Partial Differential Equation (PDE) is very similar to the Vlasov equation. The same modelling is used in radiation theory. We have started to work on the reduction of the acoustic particles model and realized that our reduction approach perfectly applies to this situation. A PhD with CEREMA (Centre d’études et d’expertise sur les risques, l’environnement, la mobilité et l’aménagement) has started in October 2015 (PhD of Pierre Gerhard). The objective was to investigate the model reduction and to implement the resulting acoustic model in our DG solver.
- In September 2017, we started a collaboration with EDF Chatou (PhD of Lucie Quibel) on the modelling of multiphase fluids with complex equations of state. The goal is to simulate the high temperature liquid-vapor flow occurring in a nuclear plant. Among others, we will apply our recent kinetic method for designing efficient implicit schemes for this kind of flows.
5 Highlights of the year
5.1 Awards
- Y. Privat is a junior member of the “Institut Universitaire de France” (IUF), from 10/2021 until 09/2026.
6 New software and platforms
6.1 New software
6.1.1 KOUGLOFV
-
Name:
Kinetic schemes On Unstructured Grids for Large Optimized Finite Volume simulations
-
Keywords:
Discontinuous Galerkin, Parallel numerical solvers
-
Functional Description:
This code, written with the RUST language, solves Mawell's equations on a generic tetrahedral mesh, for applications in electromagnetism. The underlying numerical method is stable without a restrictive CFL condition on the time step, and the quasi-explicit resolution ensures a low computational cost. Thanks to these properties, the code is able to handle multi-scale aspects in the mesh. In addition, the code is enhanced with shared-memory parallelization.
-
Contact:
Victor Michel-Dansac
7 New results
7.1 Convolutional Neural Networks for PDEs
Participants: Léo Bois [IRMA, Strasbourg], Emmanuel Franck [IRMA, Strasbourg], Laurent Navoret [IRMA, Strasbourg], Vincent Vigon [IRMA, Strasbourg].
In this work, which was the object of L. Bois's M2 internship, we have considered the Vlasov-Poisson equation for plasma physics. To reduce the CPU cost, it is usual to consider a model on the first moments in the velocity space (Euler equations). To obtain the final model it is important to add a closure (writing the last moment using the others). The classical closures are obtained by asymptotic analysis and are valid only on some regimes. In this work 3 we have proposed a closure based on a convolutional neural network call V-net and reference simulations obtained with a kinetic code. We have obtained a closure accuracy uniformly compared to the regime.
7.2 Numerical methods for fluids and plasma dynamics
7.2.1 Parallel lattice-boltzmann transport solver in complex geometry
Participants: Bérenger Bramas [Inria CAMUS], Matthieu Boileau, Emmanuel Franck, Romane Hélie, Philippe Helluy, Laurent Navoret.
In the preprint 17, we have developed a two-level parallelization to simulate plasma flow in toroidal tokamak configurations. The toroidal domain is meshed into regular planes in the toroidal direction, each of these poloidal planes being meshed by unstructured quadrangles.
- on each poloidal plane, a domain decomposition allows a task-based parallelization using an in-house library that minimizes the task management cost,
- each poloidal plane is managed by the process of a distributed memory parallelization (MPI) with processes.
During the computation, the whole solution is regularly collected and exported as a time series of three-dimensional data, to be exploited by visualization software. Thanks to this approach, we were able to reproduce the theoretical instability of the so-called diocotron case in a 3D configuration with an efficient parallelization. The results are depicted in figure 1.
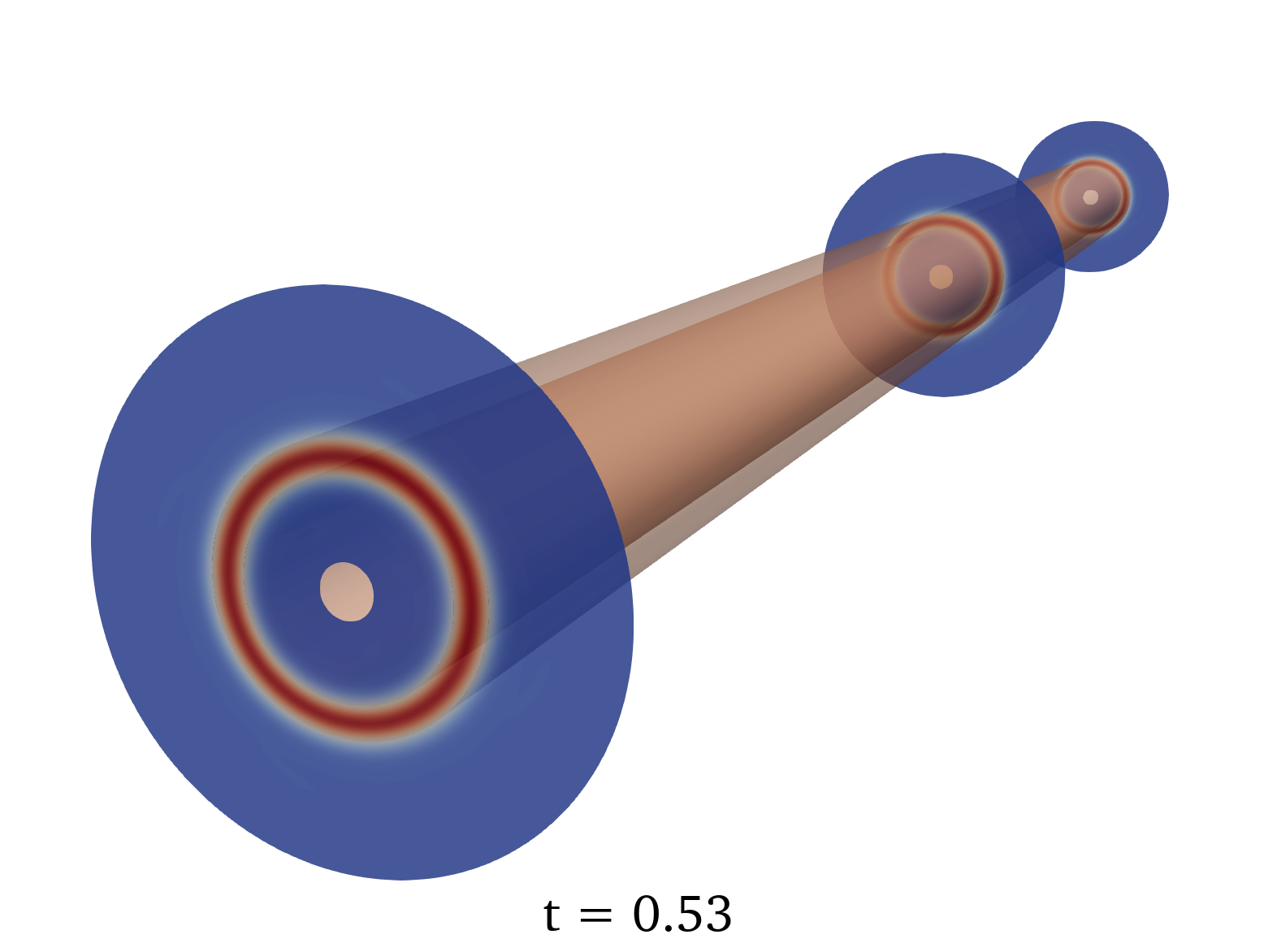
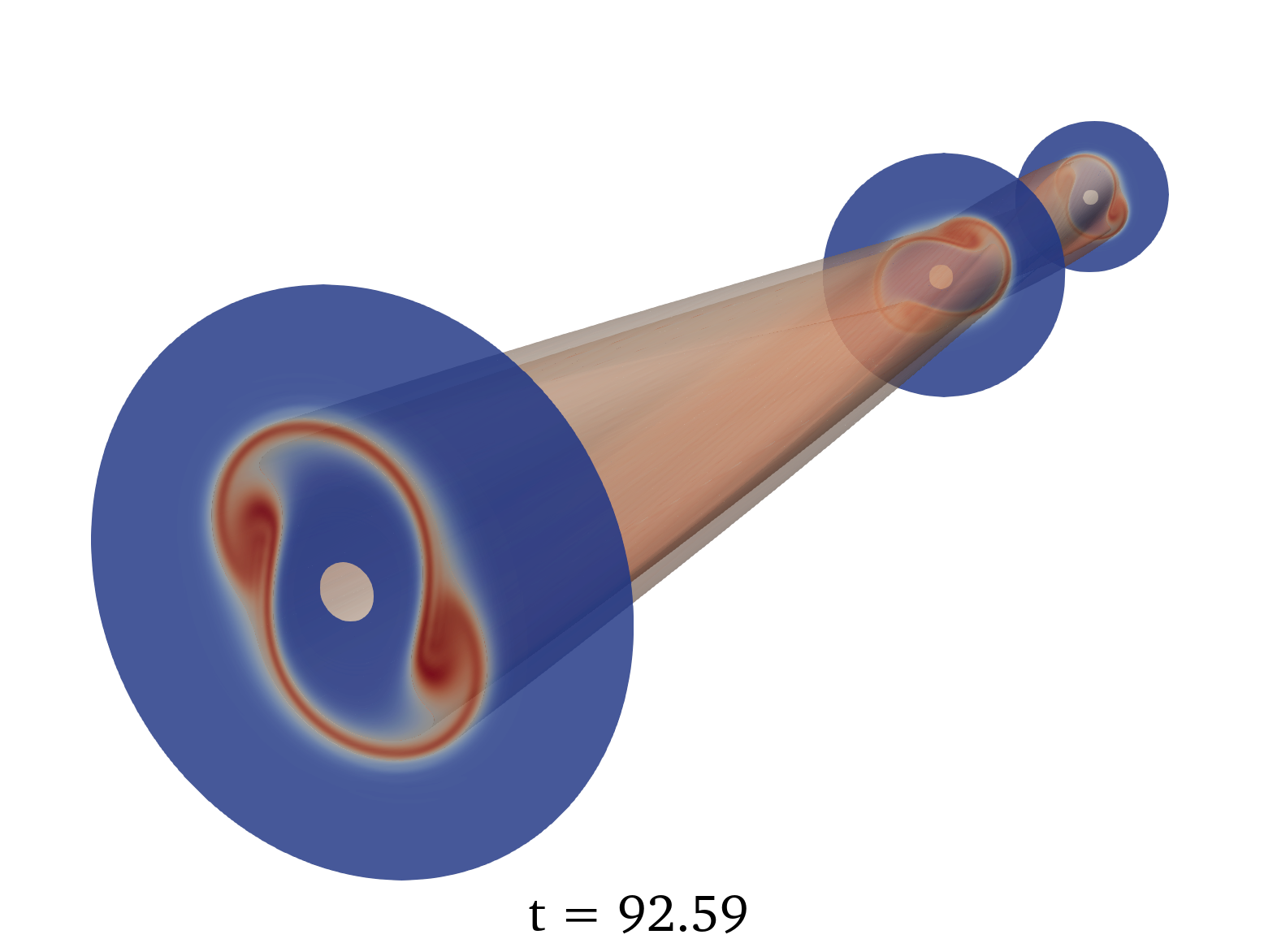
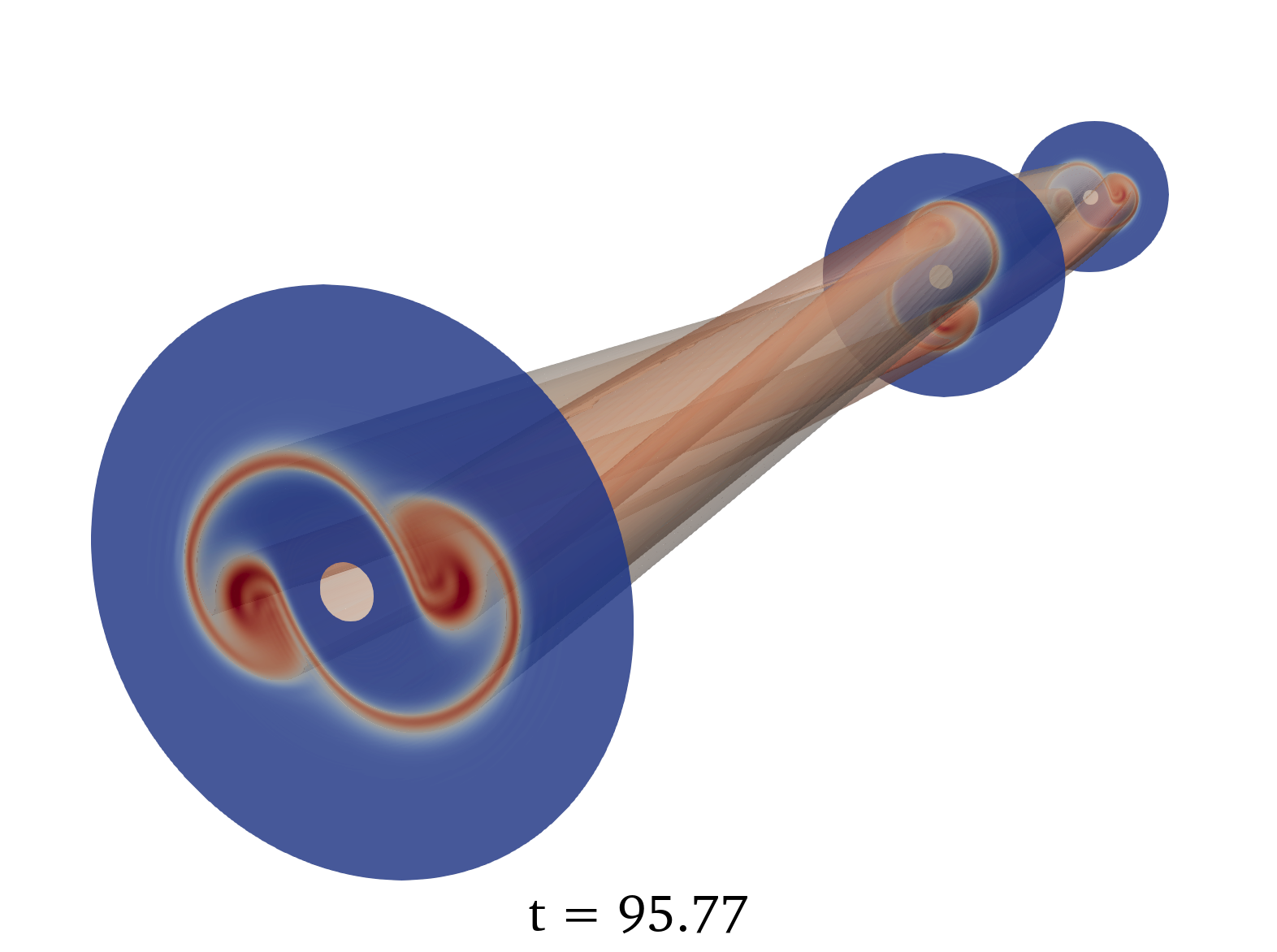
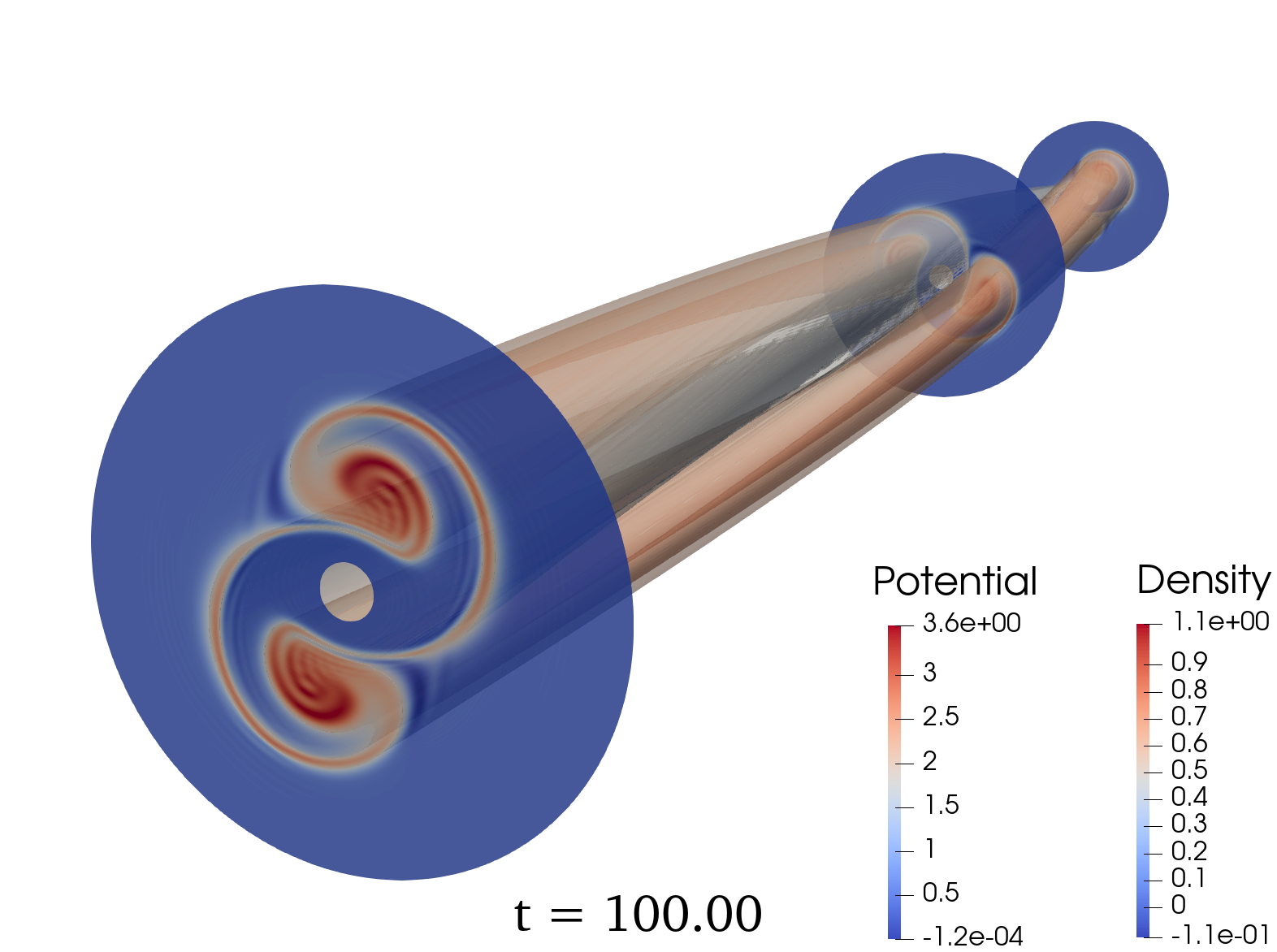
7.2.2 A robust and efficient solver based on kinetic schemes for Magnetohydrodynamics (MHD) equations
Participants: Hubert Baty [Observatoire Astronomique de Strasbourg], Florence Drui [CEA, Saclay], Emmanuel Franck [Univ. Würzburg, Germany], Philippe Helluy [Univ. Würzburg, Germany], Christian Klingenberg [Univ. Würzburg, Germany], Lukas Thanhäuser [Univ. Würzburg, Germany].
The recent preprint 15 is devoted to the simulation of magnetohydrodynamic (MHD) flows with complex structures. This kind of flow presents instabilities that generate shock waves. We proposed a robust and accurate Lattice Boltzmann scheme valid in any physical regime compared to the classical LBM approach. We detailed how to adjust the numerical viscosity in order to obtain stable and accurate results in smooth or discontinuous parts of the flow and reduced divergence errors. The scheme is implemented on GPU using PyOpenCL and allows to use very fine grids. The method is validated on complex resistive instabilities.
7.2.3 CFL-less and parallel Discontinuous Galerkin solver
Participants: Philippe Helluy, Pierre Gerhard, Victor Michel-Dansac.
The Discontinuous Galerkin method is a general method for solving conservation laws. In 18, we describe a parallel and quasi-explicit Discontinuous Galerkin (DG) kinetic scheme for solving systems of balance laws. The solver is unconditionally stable (i.e., the CFL number can be arbitrary) and has the complexity of an explicit scheme. It can be applied to any hyperbolic system of balance laws. In this work, we assessed the performance of the scheme in the particular case of the three-dimensional wave equation and of Maxwell's equations. We measured the benefit of the unconditional stability by performing experiments with very large CFL numbers. In addition, the parallel possibilities of the method were investigated.
A version of this solver (presented in section 6.1.1) has been implemented in the RUST language. It is a very reliable language that allows us to avoid most of the common memory bugs at compile time. It also provides nice tools for automatic and robust shared-memory parallelization. This parallelization was tested in the code, and good efficiency results were obtained. Ongoing work concerns the addition of distributed-memory parallelization (via MPI) to the code. Once this aspect has been handled, large-scale simulations will be performed in collaboration with the AxesSim company, in the context of the grant detailed in section 8.1.
7.2.4 Generic high-order well-balanced numerical schemes
Participants: Christophe Berthon [Nantes University], Solène Bulteau [Maison de la Simulation, Saclay], Françoise Foucher [École Centrale de Nantes], Meissa M'Baye [Nantes University], Victor Michel-Dansac.
Following the publication of 11, where a linear high-order well-balanced scheme was built in the specific case of the shallow water equations, we pursued this line of inquiry in 16, this time considering a general framework, suited to almost any equation describing the motion of a fluid or a plasma.
This new preprint deals with a well-known issue of high-order well-balanced schemes. Indeed, such high-order schemes are based on a polynomial reconstruction, must preserve the steady states under consideration in order to get the required well-balancedness property. A priori, to capture such a steady state, one needs to solve some strongly nonlinear equations. Here, a very easy, linear correction is designed under the generic framework of a system of hyperbolic balance laws, which describe most of the fluid or plasma systems. This correction can be applied to any scheme of order greater than or equal to 2, such as a MUSCL-type scheme, and ensures that this scheme exactly preserves the steady solutions. The main discrepancy with usual techniques lies in never having to invert the nonlinear function governing the steady solutions.
7.2.5 Optimal design of stellarators
Participants: Yannick Privat [Inria CAGE], Rémi Robin [Inria CAGE], Mario Sigalotti [Inria CAGE].
In a recent pre-publication 21, we have been interested, with M. Sigalotti and R. Robin, in the optimal design of stellarators, devices for the production of controlled nuclear fusion reactions, alternative to tokamaks. The confinement of the plasma is entirely achieved by a helical magnetic field created by the complex arrangement of coils powered by high currents around a toric domain. These coils describe a surface called “coil winding surface” (CWS). We have modeled the design of the CWS as a shape optimization problem, so that the cost function reflects both the optimal plasma properties, through a least squares functional, and also manufacturability, through geometric terms involving the lateral surface and curvature of the CWS.
7.3 Other applications
While the main focus of the numerical tools we develop is plasma physics, these tools can also be used for other applications. We list below two of these applications.
7.3.1 Optimal control for population dynamics
Participants: Luís Almeida [CNRS, LJLL, Inria MAMBA, Paris], Jesús Bellver Arnau [LJLL, Inria MAMBA, Paris], Michel Duprez [Inria MIMESIS, Strasbourg], Romane Hélie [IECL, Nancy], Antoine Henrot [IECL, Nancy], Idriss Mazari [CEREMADE, Paris], Grégoire Nadin [CNRS, LJLL, Paris], Yannick Privat [Paris 13 University], Nicolas Vauchelet [Paris 13 University].
In collaboration with M. Duprez and N. Vauchelet, we pursued a series of works dedicated to the analysis and simulation of solutions of an optimal control problem motivated by population dynamics issues. In order to control the spread of mosquito-borne arboviruses, the sterile insect technique (SIT) consists in releasing mosquitoes infected with a bacterium called Wolbachia into the environment, which considerably reduces the transmission of the virus to humans. The goal is to effectively release the mosquitoes spatially so that the population of infected mosquitoes overwhelms the population of uninfected mosquitoes. Assuming very high mosquito fecundity rates, an asymptotic model on the proportion of infected mosquitoes is introduced, leading to an optimal control problem to determine the best spatial strategy to adopt. We tackled this problem in 7, more specifically studying the optimality of the natural candidates, introducing an adapted optimization algorithm and performing first numerical simulations to illustrate the relevance of the optimal control strategy. We are currently pursuing this work by trying to take into account more realistic models.
In addition, references 8, 10, 14, 20 are dedicated to the study of some qualitative properties of optimal control problems involving diffusion reaction systems used to describe the spatio-temporal dynamics of mosquito vectors of diseases such as dengue. These works, although fundamental and not dedicated to any particular application, have notably led to efficient optimization algorithms for the solution of the above mentioned applied problems.
7.3.2 Spontaneous rotations in epithelia as an interplay between cell polarity and RhoA activity at boundaries
Participants: Simon Lo Vecchio [IGBMC, Strasbourg], Olivier Pertz [Cellular Dynamics lab, Berne], Marcela Szopos [MAP5, Paris], Laurent Navoret [IGBMC, Strasbourg], Daniel Riveline [IGBMC, Strasbourg].
Directed flows of cells in vivo are essential in morphogenesis. They shape living matter in phenomena involving cell mechanics and regulations of the acto-myosin cytoskeleton. However the onset of coherent motion during collective cell migration is still poorly understood. In 19 we show that coherence is set by spontaneous alignments of cell polarity by designing cellular rings of controlled dimensions. A tug-of-war between opposite polarities dictates the onset of coherence, as assessed by tracking live cellular shapes and motions in various experimental conditions. In addition, we identify an internally driven constraint by cellular acto-myosin cables at boundaries as essential to ensure coherence and active force is generated as evaluated by the high RhoA activity. Its contribution is required to trigger coherence as shown by our numerical simulations based on a novel Vicsek-type model including free active boundaries. Altogether, spontaneous coherent motion results from basic interplay between cell orientations and active cables at boundaries.
7.3.3 Other applications in (shape) optimization
Participants: Alexandre Delyon [IECL, Nancy & IRMA, Strasbourg], Alexis Courtais [IECL, Nancy], Antoine Henrot [IECL, Nancy], Abderrazak Latifi [ENSIC, LRGP, Nancy], François Lesage [ENSIC, LRGP, Nancy], Cyril Pelaingre [CIRTES, Saint-Dié-des-Vosges], Yannick Privat.
In the framework of Alexis Courtais' thesis that Y. Privat co-supervised, we were interested in the optimal design of fixed bed reactors, chemical reactors that are widely used in industry, in Process Engineering. This application allowed the development of a shape optimization algorithm for coupled systems (here, fluid mechanics and parabolic equation) including geometrical constraints related to the manufacturing of the reactor. In order to make it manufacturable, a minimum thickness constraint has been included in the numerical approach implemented. We believe that this approach is general enough to be reproduced in many other applications. This work led to several preprints and publications 4, 5, 12, 13.
In addition, reference 6 concerns a fundamental work on the determination of universal geometrical inequalities between the area, the diameter and the inradius of a convex body. The objective was to answer a question asked by a colleague from the Museum of Natural History in Paris, about the origin of the surprising shapes of crustacean eggs observed in nature.
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
We are involved in a common project with the company AxesSim in Strasbourg. The objective is to help to the development of a commercial software for the numerical simulation of electromagnetic phenomena. The applications are directed towards antenna design and electromagnetic compatibility. This project was partly supported by DGA through "RAPID" funds. A software engineer position (P. Gerhard) has started in 2021 on this subject. The objective is to implement a matrix-free CFL-less Discontinuous Galerkin (DG) scheme for solving Maxwell equations. In this way it is possible to get rid of the very small time steps imposed by small cells in automatically generated meshes. Preliminary results were very promising: stability and second order accuracy is observed for simulations with CFL numbers greater than 10. This project is supported by the Labex IRMIA++ (engineer position of P. Gerhard) and the French 2021 "Plan de relance": it allows to host an AxesSim engineer in the Tonus team for one year for working on the joint DG solver.
9 Partnerships and cooperations
9.1 International research visitors
9.1.1 Visits of international scientists
Other international visits to the team
Andrea Thomann
-
Status:
post-doc
-
Institution of origin:
JGU Mainz
-
Country:
Germany
-
Dates:
03-05/11/2021
-
Context of the visit:
Collaboration with V. Michel-Dansac
-
Mobility program/type of mobility:
research stay
9.1.2 Visits to international teams
Research stays abroad
Emmanuel Franck
-
Visited institution:
JGU Mainz
-
Country:
Germany
-
Dates:
24-26/11/2021
-
Context of the visit:
Collaboration with A. Thomann
-
Mobility program/type of mobility:
research stay
Victor Michel-Dansac
-
Visited institution:
JGU Mainz
-
Country:
Germany
-
Dates:
23-26/11/2021
-
Context of the visit:
Collaboration with A. Thomann
-
Mobility program/type of mobility:
research stay
9.2 National initiatives
9.2.1 National projects
-
Étude de stratégies multi-échelles pour la simulation en compatibilité électromagnétique:
- Acronym: ANR M2CEM
- Duration: 01/2021 – 12/2023
- Coordinator: X. Ferrières, ONERA Toulouse
- Partners: Tonus, IRMA, AxesSim, ONERA
- Participants: Ph. Helluy, V. Michel-Dansac, P. Gerhard
- Abstract: The objective of this project is to improve the numerical solvers of the partners for electromagnetic compatibility simulations. These tools are applied for the design of antennae or connected objects. Several aspects will be explored: code coupling, adaptative time stepping, CFL-less schemes, locally implicit schemes, innovative time integrators and mesh management.
-
MOdeling and SImulation of COmplex Ferromagnetic systems:
- Acronym: ANR MOSICOF
- Duration: 10/2021 – 10/2025
- Coordinator: S. Labbé, Sorbonne Université
- Partners: Sorbonne université, Université de Pau et des Pays de l'Adour, Université de Strasbourg
- Participants: C. Courtès, Y. Privat
- Abstract: During the last decade, promising applications of ferromagnetic materials have emerged in the domains of nanoelectronics (spintronic) and data storage: complex ferromagnetic systems are increasingly used for digital data recording and logic devices. They reduce the energy storage cost while improving the performance of the devices. The goal of this proposal is to bring together mathematicians and physicists around the understanding of the properties of ferromagnetism. One of the main objectives is to highlight and treat new multi-physics models, allowing for optimization and control of the magnetizations, and to simulate the phenomena in a more efficient and less expensive way. We wish to develop approaches leading to mathematically justified and physically relevant solutions for the analysis and optimization of these materials, and which could ultimately lead to implementation on devices.
-
Machine Learning for Kinetic equations
- Acronym: ANR MILK
- Duration: 01/2022 – 12/2024
- Coordinator: E. Franck, Inria Nancy - Grand Est & E. Sonnendrücker, Technische Universität München (TUM)
- Partners: Inria Nancy - Grand Est & TUM
- Participants: C. Courtès, E. Franck, L. Navoret
- Abstract: Kinetic models are accurate descriptions of interacting particle systems in physics. However, their numerical resolution is often too demanding, as they are defined in the large-dimensional position/velocity phase space and involve multi-scale dynamics. For this reason, reduced models have been developed that represent optimal trade-offs between numerical cost and modeling completeness. In general, this reduction is carried out in two ways. The first is based on asymptotic models that filter out fast dynamics and are obtained when a small parameter tends towards zero (collision/oscillation limit). The second, called reduced order modeling, consists in finding a smaller representation of the problem able to describe the dynamics (POD). The main objective of this project is to design new reduced order models that are more efficient than classical ones, based on machine learning techniques applied to kinetic data. Ensuring the stability of the models obtained will be a key point studied
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
- 27-28 September 2021: member of the organizing committees of the centenial of the International mathematical Union (IMU) in Strasbourg (Ph. Helluy)
- 21-23 June 2021: organizer of the third IRMA-EDF workshop on multiphase flows in Strasbourg (Ph. Helluy)
Member of the organizing committees
- 05/2021 – now: Member of the scientific board of the 2021 SMAI congress (Y. Privat)
Seminar organization
- 09/2021 – now: Organization of the PDE Seminar at Strasbourg University (C. Courtès and V. Michel-Dansac)
- 01/2021 – now: Organization of the Machine Learning working group at Strasbourg University (E. Franck)
10.1.2 Journal
Member of the editorial boards
- 07/2021 – now (Y. Privat): Member of the editorial board of the journal Numerical Algebra, Control & Optimization
- 07/2021 – now (Y. Privat): Member of the editorial board of the journal Advances in Continuous and Discrete Models
- 05/2020 – now (Y. Privat): Member of the editorial board of the Journal of Optimization, Theory and Applications
- 11/2019 – now (Y. Privat): Member of the editorial board of the AIMS Applied Mathematics books series
- 04/2018 – now (Y. Privat): Member of the editorial board of the journal Evolution Equations and Control Theory
Reviewer - reviewing activities
- Applied Mathematics and Computation (V. Michel-Dansac)
- Bulletin of the Iranian Mathematical Society (V. Michel-Dansac)
- Communications in Mathematical Sciences (L. Navoret)
- Communications in Nonlinear Science and Numerical Simulation (C. Courtès)
- Computers and Fluids (Ph. Helluy)
- ESAIM: Mathematical Modelling and Numerical Analysis (V. Michel-Dansac)
- European Journal of Mechanics - B/Fluids (Ph. Helluy)
- Journal of Applied and Computational Mathematics (V. Michel-Dansac)
- Journal of Computational Physics (Ph. Helluy)
- Proceedings of the Combustion Institute (M. Boileau)
- SMAI-JCM (Ph. Helluy)
10.1.3 Invited talks
- 12/2021: “Modélisation TIS”, La Réunion (Y. Privat)
- 11/2021: Workshop SystemX: Simulation and machine learning hybrid modeling, Paris (E. Franck)
- 11/2021: Scientific Computing and Modeling Seminar, Bordeaux (Ph. Helluy)
- 10/2021: Numerical Analysis and PDE seminar, Lille (Ph. Helluy)
- 10/2021: Journées 2021 du GDR EMILI, Palaiseau (L. Navoret)
- 07/2021: ICNAAM 21, 19th International Conference of Numerical Analysis and Applied Mathematics (Y. Privat)
- 07/2021: Scientific computing and Modeling meeting, Amiens (Y. Privat)
- 06/2021: SMAI 2021, La Grande-Motte (Ph. Helluy)
- 06/2021: NumKin21, Marseille (L. Navoret)
- 06/2021: Third Workshop on Compressible Multiphase Flows, Strasbourg (L. Navoret)
- 05/2021: University of Orsay, online working group “Schémas de Boltzmann sur réseau” (Ph. Helluy)
- 05/2021: Journée Calcul Scientifique et Modélisation, univ. Amiens (Y. Privat)
- 03/2021: Groupe de travail EDP-CS & LMI, Rouen (Y. Privat)
- 01/2021: Seminar of the “PDE and Numerical Analysis” team, Nice, online (C. Courtès)
- 01/2021: CEA Gamni, Paris, online (E. Franck)
- 01/2021: WCCN 2021, Paris, online (E. Franck)
10.1.4 Research administration
- Manager of the “GDR Calcul” (M. Boileau)
- Member of the CdT Inria Nancy (M. Boileau)
- Head of the mathematics department (IRMA) in Strasbourg university (M. Gutnic)
- Comex Inria Nancy-Grand-Est (Ph. Helluy)
- Elected member of the “Commission de la Recherche” of the University of Strasbourg (Ph. Helluy)
- Head of the CNRS Lab IRMA “Institut de Recherche Mathématique Avancée”, UMR 7501 (Ph. Helluy)
- 04/2021 – now: nominated member of the Inria Nancy - Grand Est “comité de centre” (C. Courtès)
- 11/2019 – now: Member of CNU Section 26 (Y. Privat)
- 04/2019 – now: Member of the IRMA expert committee (Y. Privat)
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- Licence 1, “Mathematics for biology”, 12h lectures + 23h exercise sessions, Strasbourg University, France (M. Gutnic)
- Licence 1, “Mathematics for health studies”, 36h, Strasbourg University, France (M. Gutnic)
- Licence 2, “Multivariable functions”, 56h exercise sessions, Strasbourg University, France (C. Courtès)
- Licence 2, “Applied numerical analysis”, 18h, Strasbourg University, France (C. Courtès)
- Licence 2, “Object-Oriented Programming in Python”, 16h lectures (E. Franck, V. Michel-Dansac) + 16h computer labs (V. Michel-Dansac), Strasbourg University, France
- Licence 2, “Scientific computing”, 20h lectures + 17h computer labs, Strasbourg University, France (M. Gutnic)
- “Probability and Statistics”, 30h, CNAM, France (M. Gutnic)
- Licence 3, “Numerical analysis techniques 1”, 15h lectures + 19h computer labs, Strasbourg University, France (C. Courtès)
- Licence 3, “Scientific computing”, 65h lectures + exercise sessions, Strasbourg University, France (C. Courtès)
- Licence 3, “Nonlinear Optimization”, 36h lectures + 18h exercise sessions, Strasbourg University, France (C. Courtès)
- Licence 3, “Advanced C++”, 20h lectures (E. Franck) + 34h computer labs (E. Franck, L. Navoret), Strasbourg University, France
- Licence 3, “Numerical analysis techniques 2”, 34h, Strasbourg University, France (Ph. Helluy)
- Licence 3, “Introduction to C++”, 34h, Strasbourg University, France (V. Michel-Dansac)
- Master 1, “Parallel Computing”, 20h, Strasbourg University, France (M. Boileau)
- Master 1, “Machine Learning”, 4h lectures + 4h computer labs, Strasbourg University, France (E. Franck)
- Master 1 Pure Mathematics, “Scientific computing”, 13h lectures (Ph. Helluy) + 14h computer labs (Ph. Helluy & V. Michel-Dansac), Strasbourg University, France
- Master 1 Applied Mathematics, “Scientific computing”, 35h, Strasbourg University, France (L. Navoret)
- Master 1, “Optimization”, 70h, Strasbourg University, France (Y. Privat)
- Master 2 Cell Physics, “Basics in mathematics”, 24h, Strasbourg University, France (L. Navoret)
- Master 2 Agrégation, “Scientific computing”, 28h, Strasbourg University, France (Ph. Helluy)
- Master 2 Agrégation, “Analysis”, 7.5h, Strasbourg University, France (L. Navoret)
- Master 2 Agrégation, “Scientific computing”, 66h, Strasbourg University, France (L. Navoret)
- Master 2 Agrégation, “Text study”, 30h, Strasbourg University, France (Y. Privat)
- Master 2, “Data Sciences”, 20h, Strasbourg University, France (M. Boileau)
- Master 2, “Numerical methods for hyperbolic PDEs”, 35h, Strasbourg University, France (Ph. Helluy)
- Master 2, “Theory and numerics for incompressible fluids”, 10h, Sorbonne University, France (Y. Privat)
- Master 2, “Optimal control”, 70h, Strasbourg University, France (Y. Privat)
- Training Course, “Basics for scientific python”, 33h, Urfist (Unité Régionale de Formation à l'Information Scientifique et Technique), France (M. Boileau)
10.2.2 Supervision
- L3 thesis: L. Palazzolo, “Etude du soliton des équations de Korteweg de Vries et de Schrödinger non-linéaire”, 04/2021 – 07/2021. C. Courtès.
- L3 thesis: V. Boulay-Colonna, “Introduction au contrôle en dimension finie”, 03/2021 – 07/2021. Y. Privat.
- M1 internship: K. Lutz, “Optimal control for epidemiologic reduced models with heterogeneity population”, 05/2021 – 07/2021. C. Courtès, E. Franck, L. Navoret and Y. Privat.
- M1 internship: C. Mengel, “Graph Neural Networks for discontinuity treatment in numerical analysis”, 05/2021 – 06/2021. E. Franck, L. Navoret and V. Vigon.
- M2 thesis: R. Sublet, “Problèmes de classification et méthode des machines à vecteurs de support”, since 12/2021. C. Courtès.
- M2 project: C. Holler, “Problèmes de classification et méthode des machines à vecteurs de support”, since 10/2021. J. Aghili, E. Franck and V. Michel-Dansac.
- M2 thesis: S. Moatti, “Contrôle et stabilisation d'EDO”, 03/2021 – 07/2021. Y. Privat.
- M2 internship: K. Chahdi, “Acoustic super-resolution”, 04/2021 – 08/2021. A. Deleforge and E. Franck.
- M2 internship: G. Steimer, “Reduced model based on machine learning for the Vlasov Poisson equations”, 02/2021 – 08/2021. E. Franck, L. Navoret and V. Vigon.
- PhD in progress: J. B. Arnau, “Stratégie de contrôle d'une population de moustiques pour la lutte contre les arbovirus.” Beginning: September 2019. Y. Privat and L. Almeida.
- PhD in progress: G. Mestdagh, “Suivi de tumeur en temps réel par des méthodes d'optimisation”, Strasbourg university. Beginning: September 2019. Y. Privat and S. Cotin.
- PhD in progress: R. Hélie, “Relaxation methods for kinetic models in plasma physics.”. Beginning: October 2019. M. Boileau, E. Franck,
Ph. Helluy and L. Navoret. - PhD in progress: M. Bestard, “Optimal control for numerical simulation in physics plasma.”. Beginning: September 2020. E. Franck, L. Navoret and Y. Privat.
- PhD in progress: L. Bois, “Machine learning for numericals methods. Application in plasma physics.”. Beginning: September 2020.
Ph. Helluy, E. Franck, L. Navoret and V. Vigon. - PhD in progress: C. Flint, “Efficient data compression for high-performance PDE solvers.”. Beginning: October 2020.
Ph. Helluy and S. Genaud. - PhD in progress: T. Sprunck, “Can one hear the shape of a room?”. Beginning: September 2021. A. Deleforge and Y. Privat.
- PhD in progress: N. Victorion, “Numerical methods assisted by deep learning for wave problems”. Beginning: September 2021. H. Barucq (Inria MAKUTU) and E. Franck.
- PhD in progress: G. Steimer, “Model reduction using deep learning for plasma physics”. Beginning: October 2021. R. Côte, E. Franck and L. Navoret.
- Postdoc: G. Ferrière, “Stabilité et contrôle optimal de modèles ferromagnétiques”, since 09/2021. R. Côte, C. Courtès and Y. Privat.
10.2.3 Juries
- 12/2021: reviewer in the PhD jury of R. Cranny, ONERA, Université de Toulouse (Ph. Helluy)
- 11/2021: reviewer in the PhD jury of V. Pagès, Sorbonne Université (Ph. Helluy)
- 11/2021: member of the PhD jury of G. Lance, Sorbonne Université (Y. Privat)
- 11/2021: reviewer in the PhD jury of L. Lu, Sorbonne Université (Y. Privat)
- 06/2021: reviewer in the Habilitation jury of V. Perrier, Inria & Université de Pau (Ph. Helluy)
- 05/2021: member of the PhD jury of C. Paulin, University of Paris Saclay (Ph. Helluy)
- 04/2021: reviewer in the PhD jury of E. H. L. Sokhna, University of Montpellier (Y. Privat)
- 02/2021: member of the PhD jury of F. Noël, University of Nice (Y. Privat)
- 02/2021: member of the PhD jury of F. Oumri, University of Reims (Y. Privat)
- 01/2021: member of the PhD jury of J.-B. Clément, University of Toulon (Ph. Helluy)
10.2.4 Teaching administration
- since 2021: Member of the “conseil de perfectionnement de la licence pluri-sciences” (C. Courtès)
- 07/2021 – now: Head of the “Licence concours administratifs” (C. Courtès)
- 12/2021 – now: Elected member of Strasbourg University's “commission des mathématiciens” (C. Courtès)
- Director of studies of the Interdisciplinary Thematic Institute, IRMIA++, Université de Strasbourg (L. Navoret)
10.3 Popularization
10.3.1 Education
- 02/2021: Talk and interview during the “Ose à la recherche” campaign, organized by Le Vaisseau and CNRS (M. Boileau)
- 03/2021: Intervention at the Sébastien Brant middle school in Eschau, during the “math week” (M. Boileau)
11 Scientific production
11.1 Major publications
- 1 articleA neural network closure for the Euler-Poisson system based on kinetic simulations.Kinetic and Related Models 2021
- 2 articleVectorial kinetic relaxation model with central velocity. Application to implicit relaxations schemes.Communications in Computational Physics274April 2020
11.2 Publications of the year
International journals
Conferences without proceedings
Scientific book chapters
Reports & preprints
11.3 Cited publications
- 22 inproceedingsA local time-stepping Discontinuous Galerkin algorithm for the MHD system.Modélisation et Simulation de Fluides Complexes - CEMRACS 2008Marseille, FranceJuly 2009
- 23 articleOn the role of involutions in the discontinous Galerkin discretization of Maxwell and magnetohydrodynamic systems.IMA Vol. Math. Appl.1422006, 69–88
- 24 inproceedingsResolution of the Vlasov-Maxwell system by PIC Discontinuous Galerkin method on GPU with OpenCL.CEMRACS'1138FranceEDP Sciences2011, 257--274
- 25 articleTwo-Scale Macro-Micro decomposition of the Vlasov equation with a strong magnetic field.Mathematical Models and Methods in Applied Sciences23082013, 1527--1559
- 26 article Long time simulation of a beam in a periodic focusing channel via a two-scale PIC-method.Mathematical Models and Methods in Applied Sciences192ACM 82D10 35B27 76X052009, 175-197URL: http://hal.archives-ouvertes.fr/hal-00180700/en/
- 27 articleA drift-kinetic Semi-Lagrangian 4D Vlasov code for ion turbulence simulation.J. of Comput. Phys. 2172006, 395
- 28 articleConvex Duality and Entropy-Based Moment Closures: Characterizing Degenerate Densities.SIAM J. Control Optim.472008, 1977–2015
- 29 articleEntropy-based moment closures for kinetic equations. Transport Theory Statist. Phys.264-51997, 591–606
- 30 articleThe semi-Lagrangian method for the numerical resolution of the Vlasov equation.J. Comput. Phys.14921999, 201--220
- 31 incollectionEntropy conservative finite element schemes.Numerical methods for Compressible Flows, Finite Difference Element and Volume TechniquesProc. Winter Annual Meeting, Amer. Soc. Mech. Eng, AMD- Vol. 781986, 149

