Keywords
Computer Science and Digital Science
- A2.5. Software engineering
- A3.3.2. Data mining
- A3.4.1. Supervised learning
- A3.4.2. Unsupervised learning
- A6.1.4. Multiscale modeling
- A6.2.4. Statistical methods
- A6.2.8. Computational geometry and meshes
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
- A8.7. Graph theory
- A9.2. Machine learning
Other Research Topics and Application Domains
- B1.1.1. Structural biology
- B1.1.5. Immunology
- B1.1.7. Bioinformatics
1 Team members, visitors, external collaborators
Research Scientists
- Frédéric Cazals [Team leader, INRIA, Senior Researcher, HDR]
- Dorian Mazauric [INRIA, Researcher, HDR]
- Edoardo Sarti [INRIA, Researcher]
Post-Doctoral Fellow
- Vladimir Krajnak [INRIA, until Nov 2022]
PhD Student
- Timothee O'Donnell [INRIA, until Mar 2022]
Interns and Apprentices
- Viraj Agash [Indian Institute of Technology Delhi, from Jun 2022 until Jul 2022]
- Antoine Agre [INSA Hauts-de-France, from Sep 2022]
- Rahul Gupta [Indian Institute of Technology Delhi, from Jun 2022 until Jul 2022]
- Jules Herrmann [Université Paris, from Jun 2022 until Aug 2022]
- Mael Riviere [INRIA, from Oct 2022]
- Théo Roncalli [Université Paris-Saclay, from Mar 2022 until Sep 2022]
Administrative Assistant
- Florence Barbara [INRIA]
External Collaborators
- Charles Robert [CNRS, HDR]
- David Wales [Cambridge University ]
2 Overall objectives
Biomolecules and their function(s).
Computational Structural Biology (CSB) is the scientific domain concerned with the development of algorithms and software to understand and predict the structure and function of biological macromolecules. This research field is inherently multi-disciplinary. On the experimental side, biology and medicine provide the objects studied, while biophysics and bioinformatics supply experimental data, which are of two main kinds. On the one hand, genome sequencing projects give supply protein sequences, and ~200 millions of sequences have been archived in UniProtKB/TrEMBL – which collects the protein sequences yielded by genome sequencing projects. On the other hand, structure determination experiments (notably X-ray crystallography, nuclear magnetic resonance, and cryo-electron microscopy) give access to geometric models of molecules – atomic coordinates. Alas, only ~150,000 structures have been solved and deposited in the Protein Data Bank (PDB), a number to be compared against the sequences found in UniProtKB/TrEMBL. With one structure for ~1000 sequences, we hardly know anything about biological functions at the atomic/structural level. Complementing experiments, physical chemistry/chemical physics supply the required models (energies, thermodynamics, etc). More specifically, let us recall that proteins with atoms has Cartesian coordinates, and fixing these (up to rigid motions) defines a conformation. As conveyed by the iconic lock-and-key metaphor for interacting molecules, Biology is based on the interactions stable conformations make with each other. Turning these intuitive notions into quantitative ones requires delving into statistical physics, as macroscopic properties are average properties computed over ensembles of conformations. Developing effective algorithms to perform accurate simulations is especially challenging for two main reasons. The first one is the high dimension of conformational spaces – see above, typically several tens of thousands, and the non linearity of the energy functionals used. The second one is the multiscale nature of the phenomena studied: with biologically relevant time scales beyond the millisecond, and atomic vibrations periods of the order of femto-seconds, simulating such phenomena typically requires conformations/frames, a (brute) tour de force rarely achieved 45.
Computational Structural Biology: three main challenges.
The first challenge, sequence-to-structure prediction, aims to infer the possible structure(s) of a protein from its amino acid sequence. While recent progress has been made recently using in particular deep learning techniques 44, the models obtained so far are static and coarse-grained.
The second one is protein function prediction. Given a protein with known structure, i.e., 3D coordinates, the goal is to predict the partners of this protein, in terms of stability and specificity. This understanding is fundamental to biology and medicine, as illustrated by the example of the SARS-CoV-2 virus responsible of the Covid19 pandemic. To infect a host, the virus first fuses its envelope with the membrane of a target cell, and then injects its genetic material into that cell. Fusion is achieved by a so-called class I fusion protein, also found in other viruses (influenza, SARS-CoV-1, HIV, etc). The fusion process is a highly dynamic process involving large amplitude conformational changes of the molecules. It is poorly understood, which hinders our ability to design therapeutics to block it.
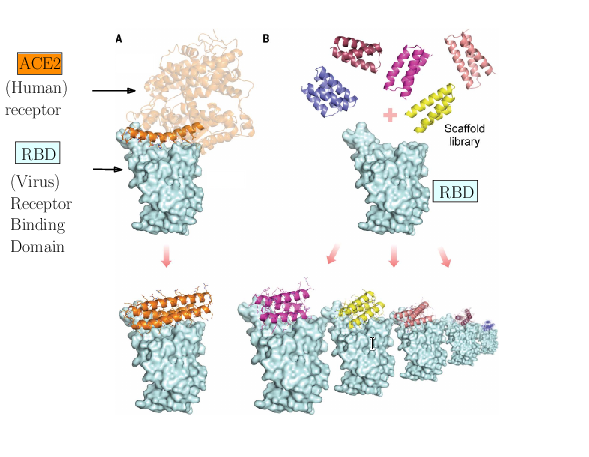
The spike of SARS-CoV-2 is responsible for the infection. Molecules can be engineered to compete with the receptor of the spike, and block infection.
Finally, the third one, large assembly reconstruction, aims at solving (coarse-grain) structures of molecular machines involving tens or even hundreds of subunits. This research vein was promoted about 15 years back by the work on the nuclear pore complex 32. It is often referred to as reconstruction by data integration, as it necessitates to combine coarse-grain models (notably from cryo-electron microscopy (cryo-EM) and native mass spectrometry) with atomic models of subunits obtained from X ray crystallography. Fitting the latter into the former requires exploring the conformation space of subunits, whence the importance of protein dynamics.
As an illustration of these three challenges, consider the problem of designing proteins blocking the entry of SARS-CoV-2 into our cells (Fig. 1). The first challenge is illustrated by the problem of predicting the structure of a blocker protein from its sequence of amino-acids – a tractable problem here since the mini proteins used only comprise of the order of 50 amino-acids (Fig. 1(A), 35). The second challenge is illustrated by the calculation of the binding modes and the binding affinity of the designed proteins for the RBD of SARS-CoV-2 (Fig. 1(B)). Finally, the last challenge is illustrated by the problem of solving structures of the virus with a cell, to understand how many spikes are involved in the fusion mechanism leading to infection. In 35, the promising designs suggested by modeling have been assessed by an array of wet lab experiments (affinity measurements, circular dichroism for thermal stability assessment, structure resolution by cryo-EM). The hyperstable minibinders identified provide starting points for SARS-CoV-2 therapeutics 35. We note in passing that this is truly remarkable work, yet, the designed proteins stem from a template (the bottom helix from ACE2), and are rather small.
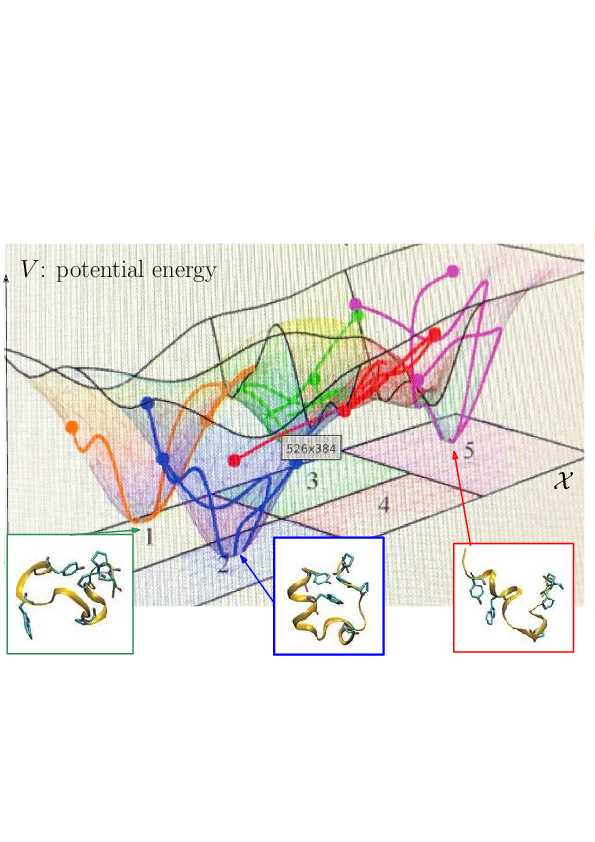
Prosaically, the energy landscape of a molecular system is the set of valleys and passes connecting them, corresponding to stable states and transitions between them.
Protein dynamics: core CS - maths challenges.
To present challenges in structural modeling, let us recall the following ingredients (Fig. 2). First, a molecular model with atoms is parameterized over a conformational space of dimension in Cartesian coordinates, or in internal coordinate–upon removing rigid motions, also called degree of freedom (d.o.f.). Second, recall that the potential energy landscape (PEL) is the mapping from to providing a potential energy for each conformation 46, 43. Example potential energies (PE) are CHARMM, AMBER, MARTINI, etc. Such PE belong to the realm of molecular mechanics, and implement atomic or coarse-grain models. They may embark a solvent model, either explicit or implicit. Their definition requires a significant number of parameters (up to ), fitted to reproduce physico-chemical properties of (bio-)molecules 47.
These PE are usually considered good enough to study non covalent interactions – our focus, even tough they do not cover the modification of chemical bonds. In any case, we take such a function for granted 1.
The PEL codes all structural, thermodynamic, and kinetic properties, which can be obtained by averaging properties of conformations over so-called thermodynamic ensembles. The structure of a macromolecular system requires the characterization of active conformations and important intermediates in functional pathways involving significant basins. In assigning occupation probabilities to these conformations by integrating Boltzmann's distribution, one treats thermodynamics. Finally, transitions between the states, modeled, say, by a master equation (a continuous-time Markov process), correspond to kinetics. Classical simulation methods based on molecular dynamics (MD) and Monte Carlo sampling (MC) are developed in the lineage of the seminal work by the 2013 recipients of the Nobel prize in chemistry (Karplus, Levitt, Warshel), which was awarded “for the development of multiscale models for complex chemical systems”. However, except for highly specialized cases where massive calculations have been used 45, neither MD nor MC give access to the aforementioned time scales. In fact, the main limitation of such methods is that they treat structural, thermodynamic and kinetic aspects at once 39. The absence of specific insights on these three complementary pieces of the puzzle makes it impossible to optimize simulation methods, and results in general in the inability to obtain converged simulations on biologically relevant time-scales.
The hardness of structural modeling owes to three intertwined reasons.
First, PELs of biomolecules usually exhibit a number of critical points exponential in the dimension 33; fortunately, they enjoy a multi-scale structure 36. Intuitively, the significant local minima/basins are those which are deep or isolated/wide, two notions which are mathematically qualified by the concepts of persistence and prominence. Mathematically, problems are plagued with the curse of dimensionality and measure concentration phenomena. Second, biomolecular processes are inherently multi-scale, with motions spanning 15 and 4 orders of magnitude in time and amplitude respectively 31. Developing methods able to exploit this multi-scale structure has remained elusive. Third, macroscopic properties of biomolecules, i.e., observables, are average properties computed over ensembles of conformations, which calls for a multi-scale statistical treatment both of thermodynamics and kinetics.
Validating models.
A natural and critical question naturally concerns the validation of models proposed in structural bioinformatics. For all three types of questions of interest (structures, thermodynamics, kinetics), there exist experiments to which the models must be confronted – when the experiments can be conducted.
For structures, the models proposed can readily be compared against experimental results stemming from X ray crystallography, NMR, or cryo electron microscopy. For thermodynamics, which we illustrate here with binding affinities, predictions can be compared against measurements provided by calorimetry or surface plasmon resonance. Lastly, kinetic predictions can also be assessed by various experiments such as binding affinity measurements (for the prediction of and ), or fluorescence based methods (for kinetics of folding).
3 Research program
Our research program ambition to develop a comprehensive set of novel concepts and algorithms to study protein dynamics, based on the modular framework of PEL.
3.1 Modeling the dynamics of proteins
Keywords: Molecular conformations, conformational exploration, energy landscapes, thermodynamics, kinetics.
As noticed while discussing Protein dynamics: core CS - maths challenges, the integrated nature of simulation methods such as MD or MC is such that these methods do not in general give access to biologically relevant time scales. The framework of energy landscapes 46, 43 (Fig. 2) is much more modular, yet, large biomolecular systems remain out of reach.
To make a definitive step towards solving the prediction of protein dynamics, we will serialize the discovery and the exploitation of a PEL 4, 13, 3. Ideas and concepts from computational geometry/geometric motion planning, machine learning, probabilistic algorithms, and numerical probability will be used to develop two classes of probabilistic algorithms. The first deals with algorithms to discover/sketch PELs, i.e., enumerate all significant (persistent or prominent) local minima and their connections across saddles, a difficult task since the number of all local minima/critical points is generally exponential in the dimension. To this end, we will develop a hierarchical data structure coding PELs as well as multi-scale proposals to explore molecular conformations. (NB: in Monte Carlo methods, a proposal generates a new conformation from an existing one.) The second focuses on methods to exploit/sample PELs, i.e., compute so-called densities of states, from which all thermodynamic quantities are given by standard relations 3442. This is a hard problem akin to high-dimensional numerical integration. To solve this problem, we will develop a learning based strategy for the Wang-Landau algorithm 41–an adaptive Monte Carlo Markov Chain (MCMC) algorithm, as well as a generalization of multi-phase Monte Carlo methods for convex/polytope volume calculations 40, 38, for non convex strata of PELs.
3.2 Algorithmic foundations: geometry, optimization, machine learning
Keywords: Geometry, optimization, machine learning, randomized algorithms, sampling, optimization.
As discussed in the previous Section, the study of PEL and protein dynamics raises difficult algorithmic / mathematical questions. As an illustration, one may consider our recent work on the comparison of high dimensional distribution 6, statistical tests / two-sample tests 7, 10, the comparison of clustering 8, the complexity study of graph inference problems for low-resolution reconstruction of assemblies 9, the analysis of partition (or clustering) stability in large networks, the complexity of the representation of simplicial complexes 2. Making progress on such questions is fundamental to advance the state-of-the art on protein dynamics.
We will continue to work on such questions, motivated by CSB / theoretical biophysics, both in the continuous (geometric) and discrete settings. The developments will be based on a combination of ideas and concepts from computational geometry, machine learning (notably on non linear dimensionality reduction, the reconstruction of cell complexes, and sampling methods), graph algorithms, probabilistic algorithms, optimization, numerical probability, and also biophysics.
3.3 Software: the Structural Bioinformatics Library
Keywords: Scientific software, generic programming, molecular modeling.
While our main ambition is to advance the algorithmic foundations of molecular simulation, a major challenge will be to ensure that the theoretical and algorithmic developments will change the fate of applications, as illustrated by our case studies. To foster such a symbiotic relationship between theory, algorithms and simulation, we will pursue high quality software development and integration within the SBL, and will also take the appropriate measures for the software to be widely adopted.
Software in structural bioinformatics.
Software development for structural bioinformatics is especially challenging, combining advanced geometric, numerical and combinatorial algorithms, with complex biophysical models for PEL and related thermodynamic/kinetic properties. Specific features of the proteins studied must also be accommodated. About 50 years after the development of force fields and simulation methods (see the 2013 Nobel prize in chemistry), the software implementing such methods has a profound impact on molecular science at large. One can indeed cite packages such as CHARMM, AMBER, gromacs, gmin, MODELLER, Rosetta, VMD, PyMol, .... On the other hand, these packages are goal oriented, each tackling a (small set of) specific goal(s). In fact, no real modular software design and integration has taken place. As a result, despite the high quality software packages available, inter-operability between algorithmic building blocks has remained very limited.
The SBL.
Predicting the dynamics of large molecular systems requires the integration of advanced algorithmic building blocks / complex software components. To achieve a sufficient level of integration, we undertook the development of the Structural Bioinformatics Library (SBL, SB) 5, a generic C++/python cross-platform library providing software to solve complex problems in structural bioinformatics. For end-users, the SBL provides ready to use, state-of-the-art applications to model macro-molecules and their complexes at various resolutions, and also to store results in perennial and easy to use data formats (SBL Applications). For developers, the SBL provides a broad C++/python toolbox with modular design (SBL Doc). This hybrid status targeting both end-users and developers stems from an advanced software design involving four software components, namely applications, core algorithms, biophysical models, and modules (SBL Modules). This modular design makes it possible to optimize robustness and the performance of individual components, which can then be assembled within a goal oriented application.
3.4 Applications: modeling interfaces, contacts, and interactions
Keywords: Protein interactions, protein complexes, structure/thermodynamics/kinetics prediction.
Our methods will be validated on various systems for which flexibility operates at various scales. Example such systems are antibody-antigen complexes, (viral) polymerases, (membrane) transporters.
Even very complex biomolecular systems are deterministic in prescribed conditions (temperature, pH, etc), demonstrating that despite their high dimensionality, all d.o.f. are not at play at the same time. This insight suggests three classes of systems of particular interest. The first class consists of systems defined from (essentially) rigid blocks whose relative positions change thanks to conformational changes of linkers; a Newton cradle provides an interesting way to envision such as system. We have recently worked on one such system, a membrane proteins involve in antibiotic resistance (AcrB, see 14). The second class consists of cases where relative positions of subdomains do not significantly change, yet, their intrinsic dynamics are significantly altered. A classical illustration is provided by antibodies, whose binding affinity owes to dynamics localized in six specific loops 11, 12. The third class, consisting of composite cases, will greatly benefit from insights on the first two classes. As an example, we may consider the spikes of the SARS-CoV-2 virus, whose function (performing infection) involves both large amplitude conformational changes and subtle dynamics of the so-called receptor binding domain. We have started to investigate this system, in collaboration with B. Delmas (INRAe) 15.
In ABS, we will investigate systems in these three tiers, in collaboration with expert collaborators, to hopefully open new perspectives in biology and medicine. Along the way, we will also collaborate on selected questions at the interface between CSB and systems biology, as it is now clear that the structural level and the systems level (pathways of interacting molecules) can benefit from one another.
4 Application domains
The main application domain is Computational Structural Biology, as underlined in the Research Program.
5 Social and environmental responsibility
5.1 Footprint of research activities
A tenet of ABS is to carefully analyse the performances of the algorithms designed–either formally or experimentally, so as to avoid massive calculations. Therefore, the footprint of our research activities has remained limited.
5.2 Impact of research results
The scientific agenda of ABS is geared towards a fine understanding of complex phenomena at the atomic/molecular level. While the current focus is rather fundamental, as explained in Research program, an overarching goal for the current period (i.e. 12 years) is to make significant contributions to important problems in biology and medicine.
6 Highlights of the year
In Decembre 2022, Côme Le Breton has joined ABS as engineer in charge of the Structural Bioinformatics Library. This is a critical addition which will help the project-team streamline the distribution of the library, help new users, evolve the code basis (C++, python), and integrate new packages.
A main achievement has been the completion of the PhD thesis of Timothee O'Donnell, entitled A kinematic view of protein loop flexibility, with applications to conformational exploration 29. As detailed in the Results section, the thesis indeed proposes novel sampling algorithms to explore the conformational space of flexible proteins. These non supervised approaches are in sharp contrast with a number of ongoing works based on deep learning techniques exploiting static databases of protein structures. See also 37.
Finally, TerraNumerica@Sophia has been inaugurated on June 11th, 2022. Terra Numerica is an ambitious scientific popularisation project and its main goal is to develop a "Dedicated Digital space" in the south of France, (in the spirit of the "Cité des Sciences" or "Palais de la découverte" in Paris).
7 New software and platforms
7.1 New software
7.1.1 SBL
-
Name:
Structural Bioinformatics Library
-
Keywords:
Structural Biology, Biophysics, Software architecture
-
Functional Description:
The SBL is a generic C++/python cross-platform software library targeting complex problems in structural bioinformatics. Its tenet is based on a modular design offering a rich and versatile framework allowing the development of novel applications requiring well specified complex operations, without compromising robustness and performances.
More specifically, the SBL involves four software components (1-4 thereafter). For end-users, the SBL provides ready to use, state-of-the-art (1) applications to handle molecular models defined by unions of balls, to deal with molecular flexibility, to model macro-molecular assemblies. These applications can also be combined to tackle integrated analysis problems. For developers, the SBL provides a broad C++ toolbox with modular design, involving core (2) algorithms, (3) biophysical models, and (4) modules, the latter being especially suited to develop novel applications. The SBL comes with a thorough documentation consisting of user and reference manuals, and a bugzilla platform to handle community feedback.
-
Release Contributions:
In 2022, three major actions were undertaken, to reach a broader community of users. The first one, albeit hardly visible, was to revamp the software architecture underlying the SBL web site and server (https://sbl.inria.fr). The second one concerns the conda based installation procedure, which now makes it possible to install the SBL on all major Linux platforms and also Mac-OS. The third one yielded interactive demos for selected application packages, available from the Applications page, see https://sbl.inria.fr/applications/. These demos make applications easy to test, without any installing the whole library. They are also meant to draw attention on more specialized interfaces, such as those provided for VMD and pymol.
- URL:
- Publication:
-
Contact:
Frédéric Cazals
8 New results
Participants: F. Cazals, D. Mazauric, E. Sarti.
8.1 Modeling the dynamics of proteins
Keywords: Protein flexibility, protein conformations, collective coordinates, conformational sampling, loop closure, kinematics, dimensionality reduction.
8.1.1 Enhanced conformational exploration of protein loops using a global parameterization of the backbone geometry
Participants: F. Cazals, T. O'Donnell.
Flexible loops are paramount to protein functions, with action modes ranging from localized dynamics contributing to the free energy of the system, to large amplitude conformational changes accounting for the repositioning whole secondary structure elements or protein domains. However, generating diverse and low energy loops remains a difficult problem.
This work 24 introduces a novel paradigm to sample loop conformations, in the spirit of the Hit-and-Run (HAR) Markov chain Monte Carlo technique. The algorithm uses a decomposition of the loop into tripeptides, and a novel characterization of necessary conditions for Tripeptide Loop Closure to admit solutions. Denoting the number of tripeptides, the algorithm works in an angular space of dimension . In this space, the hyper-surfaces associated with the aforementioned necessary conditions are used to run a HAR-like sampling technique. On classical loop cases up to 15 amino acids, our parameter free method compares favorably to previous work, generating more diverse conformational ensembles. We also report experiments on a 30 amino acids long loop, a size not processed in any previous work.
8.2 Algorithmic foundations
Keywords: Computational geometry, computational topology, optimization, graph theory, data analysis, statistical physics.
8.2.1 Geometric constraints within tripeptides and the existence of tripeptide reconstructions
Participants: F. Cazals, T. O'Donnell.
In collaboration with V. Agashe, IIT Delhi.
Designing movesets providing high quality protein conformations remains a hard problem, especially when it comes to deform a long protein backbone segment, and a key building block to do so is the so-called tripeptide loop closure (TLC) 21. Consider a tripeptide whose first and last bonds ( and ) are fixed, and so are all internal coordinates except the six dihedral angles associated to the three carbons. Under these conditions, the TLC algorithm provides all possible values for these six dihedral angles–there exists at most 16 solutions. TLC moves atoms up to in one step and retains low energy conformations, whence its pivotal role to design move sets sampling protein loop conformations.
In this work 23, we relax the previous constraints, allowing the last bond () to freely move in 3D space–or equivalently in a 5D configuration space. We exhibit necessary geometric constraints in this 5D space for TLC to admit solutions. Our analysis provides key insights on the geometry of solutions for TLC. Most importantly, when using TLC to sample loop conformations based on consecutive tripeptides along a protein backbone, we obtain an exponential gain in the volume of the -dimensional configuration space to be explored.
8.2.2 Efficient computation of the volume of a polytope in high-dimensions using Piecewise Deterministic Markov Processes
Participant: F. Cazals.
In collaboration with A. Chevallier and P. Fearnhead (Lancaster Univ., UK).
Computing the volume of a polytope in high dimensions is computationally challenging but has wide applications 18. Current state-of-the-art algorithms to compute such volumes rely on efficient sampling of a Gaussian distribution restricted to the polytope, using, e.g., Hamiltonian Monte Carlo. In this work 27, we present a new sampling strategy that uses a Piecewise Deterministic Markov Process. Like Hamiltonian Monte Carlo, this new method involves simulating trajectories of a non-reversible process and inherits similar good mixing properties. However, importantly, the process can be simulated more easily due to its piecewise linear trajectories — and this leads to a reduction of the computational cost by a factor of the dimension of the space. Our experiments indicate that our method is numerically robust and is one order of magnitude faster (or better) than existing methods using Hamiltonian Monte Carlo. On a single core processor, we report computational time of a few minutes up to dimension 500.
8.2.3 Overlaying a hypergraph with a graph with bounded maximum degree, with application for low-resoluton reconstructions of molecular assemblies
Participants: F. Cazals, D. Mazauric.
In collaboration with F. Havet, T. V. H. Nguyen laboratoire I3S (CNRS, Université Côte d'Azur).
In 19, we analyze a generalization of the minimum connectivity inference problem (MCI) that models the computation of low-resolution structures of macro-molecular assemblies, based on data obtained by native mass spectrometry. The generalization studied in this work, allows us to consider more refined constraints for the characterization of low resolution models of large assemblies, such as degree constraints (e.g., a protein has a limited number of other proteins in contact).
More precisely, let and be respectively a graph and a hypergraph defined on a same set of vertices, and let be a graph. We say that -overlays a hyperedge of if the subgraph of induced by contains as a spanning subgraph, and that -overlays if it -overlays every hyperedge of . For a fixed graph and a fixed integer , the problem --Overlay consists in deciding whether there exists a graph with maximum degree at most that -overlays a given hypergraph . In 22, we prove that for any graph which is neither complete nor anticomplete, there exists an integer such that --Overlay is NP-complete for all .
8.2.4 Conflict coloring problems: complexity and application to high resolution biological assembly modeling
Participants: F. Cazals, D. Mazauric.
In collaboration with F. Havet, T. V. H. Nguyen laboratoire I3S (CNRS, Université Côte d'Azur).
Given a graph , a color set for each vertex , a bipartite graph between color sets and for every edge , Conflict Coloring consists in deciding whether exists a conflict coloring, that is a coloring in which is not an edge of the bipartite graph. Conflict Coloring is motivated by computational structural biology problems, high resolution determination of molecular assemblies. The graph represents the subunits and the interaction between them, the colors are the given conformations, and the edges of the bipartite graphs are the incompatible conformations of two subunits.
In 30, we first establish the complexity dichotomies (polynomial vs NP-complete) for Conflict Coloring and its variants. We provide some experiments in which we build instances of Conflict Coloring associated to Voronoi diagram in the plane, and we then analyse the existences of a solution related to parameters used in our experimental setup.
8.3 Applications in structural bioinformatics and beyond
Keywords: Docking, scoring, interfaces, protein complexes, phylogeny, evolution.
8.3.1 Gene prioritization based on random walks with restarts and absorbing states, to define gene sets regulating drug pharmacodynamics from single-cell analyses
Participant: F. Cazals, D. Mazauric, A. Sales de Queiroz, G. Sales Santa Cruz.
In collaboration with Alain Jean-Marie (Inria Neo) and Jérémie Roux (Inserm and CNRS and UCA).
Prioritizing genes for their role in drug sensitivity, is an important step in understanding drugs mechanisms of action and discovering new molecular targets for co-treatment. In this work 25, we formalize this problem by considering two sets of genes and respectively composing the predictive gene signature of sensitivity to a drug and the genes involved in its mechanism of action, as well as a protein interaction network (PPIN) containing the products of and as nodes. We introduce Genetrank, a method to prioritize the genes in for their likelihood to regulate the genes in .
Genetrank uses asymmetric random walks with restarts, absorbing states, and a suitable renormalization scheme. Using novel so-called saturation indices, we show that the conjunction of absorbing states and renormalization yields an exploration of the PPIN which is much more progressive than that afforded by random walks with restarts only. Using MINT as underlying network, we apply Genetrank to a predictive gene signature of cancer cells sensitivity to tumor-necrosis-factor-related apoptosis-inducing ligand (TRAIL), performed in single-cells. Our ranking provides biological insights on drug sensitivity and a gene set considerably enriched in genes regulating TRAIL pharmacodynamics when compared to the most significant differentially expressed genes obtained from a statistical analysis framework alone. We also introduce gene expression radars, a visualization tool to assess all pairwise interactions at a glance.
Genetrank is made available in the Structural Bioinformatics Library (Genetrank). It should prove useful for mining gene sets in conjunction with a signaling pathway, whenever other approaches yield relatively large sets of genes.
8.3.2 Structural biochemistry-guided sequence alignment server
Participant: E. Sarti.
In collaboration with Lucy Forrest, Emily Yaklich (NIH), René Staritzbichler, Nikola Ristic and Peter W Hildebrand (IMPB Leipzig).
Among the peculiar characteristics shared by membrane proteins, evolutionary divergence of their sequences and low compositional complexity of their hydrophobic regions are important obstacles often preventing their correct alignment with traditional algorithms. The AlignMe method and the corresponding AlignMe webserver have been improving throughout the last decade by integrating ever more information sources on top of a generalized version of the classical Needleman-Wunsch algorithm. Yet, user-guided information (e.g., coming from individual and point-wise experimental setups) were still excluded from the AlignMe input types.
In this work 26 we release a new version of the AlignMe webserver that allows the user to bias the resulting sequence alignment with an arbitrary number of forced couplings called anchors, yet still retaining the global optimization given by the extended Needleman-Wunsch algorithm.
Other technical advancements include the possibility of submitting job batches and the visualization of the alignment characteristics on any user-provided structure.
8.3.3 Functional annotation and structure-function association of FBA paralogs
Participant: E. Sarti.
In collaboration with Théo Le Moigne, Stéphane Lemaire, Julien Henri, Alessandra Carbone (LCQB Sorbonne Université), Antonin Nourisson (Institut Pasteur) and Mirko Zaffagnini (University of Bologna)
Chloroplast fructose-1,6-bisphosphate aldolase (FBA) is an enzyme taking part in the Calvin-Benson cycle, responsible for fixing carbon dioxide into organic triosephosphates. In the unicellular green alga Chlamydomonas reinhardtii (Cr), FBA has four paralogs: the chloroplast FBA and other three cytoplasmic enzymes that are not connected with photosynthesis and whose functions have been extensively studied. This work 20 describes the newly obtained crystal structure of plastidial FBA from C. reinhardtii.
The functional annotation of this molecule has been confirmed using ProfileView, a novel algorithm for protein function prediction based on hidden Markov models able to discriminate functional patterns without needing input multiple sequence alignments. For the first time, we applied ProfileView for discriminating the function of paralgous sequences, which are much more similar in sequence identity than the average similarity between any two protein sequences chosen at random from a same family.
ProfileView has also been able to highlight structural feature that are key differences between FBA paralogs. This has paved the way for a more generic study of paralog functional annotation with ProfileView.
8.3.4 A webserver for the study of convolutional signals on protein structures
Participant: E. Sarti.
In collaboration with Francesca Nadalin, Francesco Oteri and Alessandra Carbone (LCQB Sorbonne Université)
Residue coevolution signals provide most of the information for even the most advanced, AI-based approaches to protein structure prediction. This work 22 presents iBISAnalyzer, a new freely available web server that implements iBIS2, an iterative version of the Blocks in Sequence (BIS) algorithm for finding groups of coevolving residues.
For the first time the user can visualize, compare and inspect clusters of coevolving residues by mapping them onto sequences, alignments or structures of choice, greatly simplifying downstream analysis steps. A rich and interactive graphic interface facilitates the biological interpretation of the results.
9 Partnerships and cooperations
Participants: F. Cazals, D. Mazauric, E. Sarti.
9.1 International research visitors
9.1.1 Visits of international scientists
Inria International Chair
- David Wales, Cambridge University, is endowed chair within 3IA 3IA Côte d'Azur / ABS.
9.1.2 Visits to international teams
Edoardo Sarti
-
Visited institution:
Universidad Complutense de Madrid
-
Country:
Spain
-
Dates:
June, November
-
Context of the visit:
Collaboration on a research project
-
Mobility program/type of mobility:
research stay, seminar
10 Dissemination
Participant: F. Cazals, D. Mazauric, E. Sarti.
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
Frédéric Cazals was involved in the organization of:
- Winter School Algorithms in Structural Bioinformatics: Intrinsic Disorder in Protein, from Non-Folding to Fuzzy Recognition to Phase Separation, CNRS center of Cargese, November 21st – 25th. Web: AlgoSB.
- GDR BIM/GT MASIM: Machine learning and sampling in structural bioinformatics. Co-organization of a four day long meeting Machine Learning and Sampling, Sorbonne Univ., Dec 5-8, 2022. Web: ML & Sampling.
Member of the conference program committees
Frédéric Cazals participated to the following program committees:
- Symposium on Solid and Physical Modeling
- Intelligent Systems for Molecular Biology (ISMB) / European Conference on Computational Biology (ECCB)
- Journées Ouvertes en Biologie, Informatique et Mathématiques (JOBIM)
10.1.2 Invited talks
Frédéric Cazals gave the following invited talks/lectures:
- New perspectives on protein flexibility, GDR BIM/GT Masim workshop on Sampling, Paris, December 2022.
- On Monte Carlo Markov Chain algorithms for structural and thermodynamic studies on proteins, Structural Bioinformatics seminar, Institut Pasteur Paris, November 2022.
- Theoretical biophysics beyond Alphafold: new perspectives on protein flexibility, NICE_SEQ SEMINAR SERIES, Nice, September 2022.
- A kinematic view of protein loop flexibility, with applications to conformational exploration, Les Houches-TSRC Protein Dynamics Workshop, Aussois, May 2022.
- Sampling molecular conformations: a kinetic approach in high-dimensional angular spaces, DataShape workshop, Porquerolles, May 2022.
- About two geometric problems arising in computational structural biology; cours, Journées Nationales de Calcul Formel, CIRM, Marseille, Mars 2022.
10.1.3 Leadership within the scientific community
Frédéric Cazals
- 2010-...: Member of the steering committee of the GDR Bioinformatique Moléculaire, for the Structure and macro-molecular interactions theme.
- 2017-...: Co-chair, with Yann Ponty, of the working group / groupe de travail (GT MASIM - Méthodes Algorithmiques pour les Structures et Interactions Macromoléculaires), within the GDR de BIoinfor- matique Moléculaire (GDR BIM, GDR BIM).
10.1.4 Research administration
Frédéric Cazals
- 2018-July 2022: Member of the bureau du comité des équipes projets.
- 2020-...: Member of the bureau of the EUR Life, Université Côte d’Azur.
Dorian Mazauric
- 2019-...: Member of the comité Plateformes.
Edoardo Sarti
- 2020-...: Member of the Commission de Développement Technologique at Inria Université Côte d’Azur
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- 2014–...: Master Data Sciences Program (M2), Department of Applied Mathematics, Ecole Centrale-Supélec; Foundations of Geometric Methods in Data Analysis; F. Cazals and M. Carrière, Inria Sophia / (ABS, DataShape). Web: FGMDA.
- 2021–...: Master Data Sciences & Artificial Intelligence (M1), Université Côte d’Azur; Introduction to machine learning (course practicals); E. Sarti.
- 2021–...: Master Data Sciences & Artificial Intelligence (M2), Université Côte d’Azur; Geometric and topological methods in machine learning; F. Cazals, J-D. Boissonnat and M. Carrière, Inria Sophia / (ABS, DataShape, DataShape); Web: GTML.
- 2021–...: Master Cancérologie et Recherche Translationnelle (M2), Université Côte d’Azur; Binding affinity maturation and protein interaction network analysis: two examples of bioinformatics applications in medicine; F. Cazals.
- 2020–...: Master Sciences du Vivant (M2), parcours Biologie, Informatique, Mathématiques, Université Côte d’Azur; Introduction to statistical physics of biomolecules; F. Cazals.
- 2022–...: Master : Algorithmique et Complexité, 42h Cours et TD, niveau M1, Polytech Nice Sophia, Université Côte d'Azur, filière Sciences Informatiques, France; D. Mazauric.
- 2022–...: Bachelor Sciences de la Vie (L2), Université Côte d'Azur; Introduction à la programmation, E. Sarti
- 2021–...: Bachelor Informatique (L1), Université Côte d'Azur; Introduction aux Systemes Unix (practicals), E. Sarti
- Dizaine de formations (pour les enseignantes et enseignants, personnels de médiathèque, d'associations, etc.)
10.2.2 Supervision
PhD thesis:
- Defended PhD thesis, June 2022: Timothée O'Donnel, A kinematic view of protein loop flexibility, with applications to conformational exploration. Co-advised with B. Delmas, INRAe.
10.2.3 Juries
Frédéric Cazals participated to the following committees:
- Clement Lagisquet, Université Savoie Mont-Blanc. December 2022. Committee member for the PhD thesis Discrete geometry and combinatorial aspects of biomolecular fibers and condensates. Advisor: L. Vuillon.
- Vincent Mallet, Université Paris Cité. November 2022. Rapporteur for the PhD thesis Geometric Deep Learning for Structural Bioinformatics. Advisors: Michael Nilges and Jean-Philippe Vert.
- Aria Gheeraert, Université Savoie Mont-Blanc. July 2022. Rapporteur for the PhD thesis Une approche multidisciplinaire de l'étude de la dynamique des protéines et de la transmission de signaux. Advisors: Laurent Vuillon and Ivan Rivalta.
10.3 Popularization
10.3.1 Internal or external Inria responsibilities
Dorian Mazauric
- 2019-...: Head of Commission Mastic (Médiation et Animation des MAthématiques, des Sciences et Techniques Informatiques et des Communications), Centre Inria d'Université Côte d'Azur.
- 2019-...: Coordinator of Terra Numerica – vers une Cité du Numérique, an ambitious scientific popularisation project. Its main goal is to create a "Dedicated Digital space" in the south of France, (in the spirit of the "Cité des Sciences" or "Palais de la découverte" in Paris). To do so, Terra Numerica is developing and structuring popularisation activities, supports which are spread in different antennas throughout the territory (e.g. Espace Terra Numerica - Valbonne Sophia Antipolis, MIA, in schools, exhibition extensions...). This large-scale project involves (brings together) all the actors of research, education, industry, associations and collectivities... It is actually composed of more than one hundred people.
- 2018-...: Member of the Conseil d'Administration de l'association les Petits Débrouillards.
- 2017-...: Member of projet de médiation Galéjade : Graphes et ALgorithmes : Ensemble de Jeux À Destination des Ecoliers... (mais pas que).
10.3.2 Articles and contents
Frédéric Cazals authored the following article L’intelligence artificielle au défi du design de protéines : des prouesses et limites d’AlphaFold.
Dorian Mazauric
- Participation to the development of Terra Numerica Resources.
- Participation to the development of popularization videos games Terra Numerica videos games.
10.3.3 Interventions
Nous détaillons ci-dessous les interventions de Dorian Mazauric. Voir l'intégralité des interventions.
Fête de la Science 2022:
- Village des Sciences de Villeneuve-Loubet
- Village des sciences de la vallée de la Vésubie avec Les Apprentis Pas Sages
- Village des Sciences de Mouans-Sartoux
- Festival des sciences de Nice d’Université Côte d’Azur
- Interventions au collège de Roquebillière
- Conférences à la médiathèque Camus d'Antibes Village des Sciences et de l’Innovation de la CASA à Antibes Juan-les-Pins
Cordées de la réussite (coordonné par Université Côte d'Azur): projet avec le collège Henri Nans d'Aups (Var)
Programme Chiche: dizaine de sessions.Chiche!
In Schools: quinzaine d'interventions en primaire, collèges, lycées.
At TerraNumerica@Sophia: animation pour une trentaine de classes en 2022.
Internships: 30 stagiaires de troisième accueillis à TerraNumerica@Sophia.
11 Scientific production
11.1 Major publications
- 1 articleDistributed Link Scheduling in Wireless Networks.Discrete Mathematics, Algorithms and Applications1252020, 1-38
- 2 articleOn the complexity of the representation of simplicial complexes by trees.Theoretical Computer Science617February 2016, 17
- 3 articleEnergy landscapes and persistent minima.The Journal of Chemical Physics14452016, 4URL: https://www.repository.cam.ac.uk/handle/1810/253412
- 4 articleConformational Ensembles and Sampled Energy Landscapes: Analysis and Comparison.J. of Computational Chemistry36162015, 1213--1231URL: https://hal.science/hal-01076317
- 5 articleThe Structural Bioinformatics Library: modeling in biomolecular science and beyond.Bioinformatics338April 2017
- 6 inproceedingsBeyond Two-sample-tests: Localizing Data Discrepancies in High-dimensional Spaces.IEEE/ACM International Conference on Data Science and Advanced AnalyticsIEEE/ACM International Conference on Data Science and Advanced AnalyticsIEEE/ACM International Conference on Data Science and Advanced AnalyticsParis, FranceMarch 2015, 29
- 7 inproceedingsLow-Complexity Nonparametric Bayesian Online Prediction with Universal Guarantees.NeurIPS 2019 - Thirty-third Conference on Neural Information Processing SystemsVancouver, CanadaDecember 2019
- 8 articleComparing Two Clusterings Using Matchings between Clusters of Clusters.ACM Journal of Experimental Algorithmics241December 2019, 1-41
- 9 articleComplexity dichotomies for the Minimum F -Overlay problem.Journal of Discrete Algorithms52-53September 2018, 133-142
- 10 articleA Sequential Non-Parametric Multivariate Two-Sample Test.IEEE Transactions on Information Theory645May 2018, 3361-3370
- 11 reportHigh Resolution Crystal Structures Leverage Protein Binding Affinity Predictions.RR-8733InriaMarch 2015
- 12 articleNovel Structural Parameters of Ig–Ag Complexes Yield a Quantitative Description of Interaction Specificity and Binding Affinity.Frontiers in Immunology8February 2017, 34
- 13 articleHybridizing rapidly growing random trees and basin hopping yields an improved exploration of energy landscapes.J. Comp. Chem.3782016, 739--752URL: https://hal.inria.fr/hal-01191028
- 14 articleStudying dynamics without explicit dynamics: A structure‐based study of the export mechanism by AcrB.Proteins - Structure, Function and BioinformaticsSeptember 2020
11.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
Reports & preprints
11.3 Cited publications
- 31 articleMolecular dynamics: survey of methods for simulating the activity of proteins.Chemical reviews10652006, 1589--1615
- 32 articleThe molecular architecture of the nuclear pore complex.Nature45071702007, 695--701
- 33 articleDynamics on statistical samples of potential energy surfaces.The Journal of chemical physics11151999, 2060--2070
- 34 bookThermodynamics and an Introduction to Thermostatistics.Wiley1985
- 35 articleDe novo design of picomolar SARS-CoV-2 miniprotein inhibitors.Science37065152020, 426--431
- 36 articleEnergy landscapes and persistent minima.The Journal of Chemical Physics14452016, 4URL: https://www.repository.cam.ac.uk/handle/1810/253412
- 37 articleOpinion: Protein folds vs. protein folding: Differing questions, different challenges.PNAS12012023, 1--4
- 38 articleA practical volume algorithm.Mathematical Programming Computation822016, 133--160
- 39 bookUnderstanding molecular simulation.Academic Press2002
-
40
articleRandom walks and an
) volume algorithm for convex bodies.Random Structures & Algorithms1111997, 1--50 - 41 bookA guide to Monte Carlo simulations in statistical physics.Cambridge university press2014
- 42 bookFree energy computations: A mathematical perspective.World Scientific2010
- 43 articlePrediction, determination and validation of phase diagrams via the global study of energy landscapes.Int. J. of Materials Research10022009, 135
- 44 articleImproved protein structure prediction using potentials from deep learning.Nature2020, 1--5
- 45 articleAtomic-level characterization of the structural dynamics of proteins..Science33060022010, 341--346URL: http://dx.doi.org/10.1126/science.1187409
- 46 bookEnergy Landscapes.Cambridge University Press2003
- 47 articleBuilding force fields: an automatic, systematic, and reproducible approach.The journal of physical chemistry letters5112014, 1885--1891

