Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.7. High performance computing
Other Research Topics and Application Domains
- B4. Energy
- B4.3.4. Solar Energy
- B5.3. Nanotechnology
- B5.5. Materials
- B8. Smart Cities and Territories
- B8.2. Connected city
1 Team members, visitors, external collaborators
Research Scientists
- Stéphane Lanteri [Team leader, INRIA, Senior Researcher, HDR]
- Theophile Chaumont-Frelet [INRIA, Researcher]
- Mahmoud Elsawy [INRIA, Researcher]
- Frédéric Valentin [LNCC, Petropolis, Brazil, Advanced Research Position]
Faculty Members
- Yves D Angelo [Université Côte d'Azur, Professor, HDR]
- Stéphane Descombes [Université Côte d'Azur, Professor, HDR]
- Claire Scheid [Université Côte d'Azur, Associate Professor, HDR]
Post-Doctoral Fellows
- Josselin Defrance [INRIA, until Aug 2022]
- Nicolas Lebbe [INRIA, until Jan 2022]
PhD Students
- Jérémy Grebot [STMicroelectronics, CIFRE]
- Enzo Isnard [Thales R&T, CIFRE, from Oct 2022]
- Zakaria Kassali [INRIA]
- Thibault Laufroy [Université Côte d'Azur]
- Cedric Legrand [INRIA]
- Martin Lepers [STMicroelectronics, from Apr 2022, CIFRE]
- Massimiliano Montone [INRIA]
Technical Staff
- Alexis Gobé [INRIA, Engineer, Member of SED]
- Guillaume Leroy [INRIA, Engineer]
Interns and Apprentices
- Amine Bennini [INRIA, from Mar 2022 until Aug 2022]
- Arthur Clini De Souza [INRIA, from Oct 2022 until Nov 2022]
- Enzo Isnard [INRIA, until Sep 2022]
- Maha Ouali [INRIA, from Jun 2022 until Aug 2022]
- Alan Youssef [INRIA, from Nov 2022]
Administrative Assistant
- Montserrat Argente [INRIA]
2 Overall objectives
Nanostructuring of materials has paved the way for manipulating and enhancing wave-matter interactions, thereby opening the door for the full control of these interactions at the nanoscale. In particular, the interaction of light waves (or more general optical waves) with matter is a subject of rapidly increasing scientific importance and technological relevance. Indeed, the corresponding science, referred to as nanophotonics56, aims at using nanoscale light-matter interactions to achieve an unprecedented level of control on light. Nanophotonics encompasses a wide variety of topics, including metamaterials, plasmonics, high resolution imaging, quantum nanophotonics and functional photonic materials. Previously viewed as a largely academic field, nanophotonics is now entering the mainstream, and will play a major role in the development of exciting new products, ranging from high efficiency solar cells, to personalized health monitoring devices able to detect the chemical composition of molecules at ultralow concentrations. Plasmonics 61 is a field closely related to nanophotonics. Metallic nanostructures whose optical scattering is dominated by the response of the conduction electrons are considered as plasmonic media. If the metallic structure presents an interface with a positive permittivity dielectric, collective oscillations of surface electrons create waves (called surface plasmons) that are guided along the interface, with the unique characteristic of subwavelength-scale confinement. Nanofabricated systems that exploit these plasmon waves offer fascinating opportunities for crafting and controlling the propagation of light in matter. In particular, it can be used to channel light efficiently into nanometer-scale volumes. As light is squeezed down into nanoscale volumes, field enhancement effects occur resulting in new optical phenomena that can be exploited to challenge existing technological limits and deliver superior photonic devices. The resulting enhanced sensitivity of light to external parameters (for example, an applied electric field or the dielectric constant of an adsorbed molecular layer) shows also great promise for applications in sensing and switching.
In ATLANTIS, our research activities aim at studying and impacting some scientific and technological challenges raised by physical problems involving optical waves in interaction with nanostructured matter. A crucial component in the implementation of this scientific endeavor lies in a close networking with physicists who bring the experimental counterpart of the proposed research. Driven by a number of nanophotonics-related physical drivers, our overall objectives are to design and develop innovative numerical methodologies for the simulation of nanoscale light-matter interactions and to demonstrate their capabilities by studying challenging applications in close collaboration with our physicist partners. On the methodological side, the Discontinous Galerkin (DG) family of methods is a cornerstone of our contributions. In particular, we study various variants of DG methods that can deal with complex material models and coupled PDE systems that are relevant to the study of nanoscale light-matter interactions. Moreover, mathematical modeling is a central activity of the team, in particular for shaping initial and boundary value problems in view of devising accurate, efficient and robust numerical methods in the presence of multiple space and time scales or/and geometrical singularities. Additional methodological topics that are considered in close collaboration with colleagues from other Inria teams or external applied mathematics research groups are model order reduction, inverse design. Novel methodological contributions on these topics in the context of the physical problems studied in ATLANTIS are eventually implemented in the DIOGENeS software suite, which is a unique software plaform dedicated to computationl nanophotonics.
3 Research program
3.1 Driving physical fields
Our research activities eventually materialize as innovative computational techniques for studying concrete questions and applications that are tightly linked to specific physical fields (driving physical fields) related to nanophotonics and plasmonics. In most cases, these scientific topics and applications are addressed in clos collaboration with physicists.
Quantum plasmonics. The physical phenomena involved in the deep confinement of light when interacting with matter opens a major route for novel nanoscale devices design. Indeed, the recent progress of fabrication at the nanoscale makes it possible to conceive metallic structures with increasingly large size mismatch, in which microscale devices can be characterized by sub-nanometer features 49. These advances have also allowed to achieve spatial separation between metallic elements of only few nanometers 47. At such sizes quantum effects become non-negligible, producing huge variations in the macroscopic optical response. Following this evolution, the quantum plasmonics field has emerged, and with it the possibility of building quantum-controled devices, such as single photon sources, transistors and ultra-compact circuitry at the nanoscale. In ATLANTIS, we study novel numerical modeling methods for solving some semi-classical models of quantum plasmonic effects such as in the context of the PhD work of Nikolkai Schmitt 70-14.
Planar optics. Nanostructuring of matter can be tailored to shape, control wavefront and achieve unusual device operations. Recent years have seen tremendous advances in the fabrication and understanding of two-dimensional (2D) materials, giving rise to the field of planar optics. In particular, the concept of quasi-2D metasurfaces has started to develop into an exciting research area, where nanostructured surfaces are designed for novel functionalities 57- 48- 52. Metasurfaces are planar metamaterials with subwavelength thickness, consisting of single-layer or few-layer stacks of nanostructures. They can be readily fabricated using lithography and nanoprinting methods, and the ultrathin thickness in the wave propagation direction can greatly suppress the undesirable losses. Metasurfaces enable a spatially varying optical response (e.g. scattering amplitude, phase, and polarization). They mold optical wavefronts into shapes that can be designed at will, and facilitate the integration of functional materials to accomplish active control and greatly enhanced nonlinear response. Our first contributions on this topic have been obtained in the context of the ANR OPERA project (completed in September 2022) are are concerned with numerical modeling methods for the inverge design of metasurfaces 7-5 and metalenses 6.
Thermoplasmonics. Plasmonic resonances can be exploited for many applications 61. In particular, the strong local field enhancement associated with the plasmonic resonances of a metallic nanostructure, together with the absorption properties of the metal, induce a photo-thermal energy conversion. Thus, in the vicinity of the nanostructure, the temperature increases. These effects, viewed as ohmic losses, have been for a long time considered as a severe drawback for the realization of efficient devices. However, the possibility to control this temperature rise with the illumination wavelength or polarization has gathered strong interest in the nano-optics community, establishing the basis of thermoplasmonics 45. By increasing temperature in their surroundings, metal nanostructures can be used as integrated heat nanosources. Decisive advances are foreseen in nanomedicine with applications in photothermal cancer therapy, nano-surgery, drug delivery, photothermal imaging, protein tracking, photoacoustic imaging, but also in nano-chemistry, optofluidics, solar and thermal energy harvesting (thermophotovoltaics).
Optoelectronics and nanoelectronics. Semiconductors also play a major role in leveraging nanoscale light-matter interactions. Emission or absorption of light by a semiconductor is at the heart of optoelectronics, which is concerned with devices that source, detect or control light. Photodiodes, solar cells, light emitting diodes (LEDs), optical fibers and semiconductor lasers are some typical examples of optoelectronic devices. The attractive properties of these devices is based on their efficiency in converting light into electrical signals (or vice versa). Using a structuration with low dimensional materials and carrier-photons interaction, optoelectronics aims at improving the quality of these systems. A closeby field is nanoelectronics 62, i.e., the physical field that, while incorporating manufacturing constraints, tries to describe and understand the influence of the nanostructuration of electronic devices on their electronic properties. This area has quickly evolved with the increasing fabrication capabilities. One striking motivating example is the drastic increase of the number of transistors (of a few nanometer size) per chip on integrated circuits. At the achieved nanostructuration scales, inter-atomic forces, tunneling or quantum mechanical properties have a non-negligible impact. A full understanding of these effects is mandatory for exploiting them in the design of electronic components, thereby improving their characteristics.
3.2 Research agenda
The processes that underly the above-described physical fields raise a number of modeling challenges that motivate our research agenda:
- They exhibit multiple space and time scales;
- They are highly sensitive to exquisite geometrical features of nanostructures and matter nanostructuring;
- They impose dealing with unconventional material models;
- They may require to leave the comfortable setting of linear differential models;
- Some of them are inherently multiphysics processes.
3.2.1 Core research topics
Our research activities are organized around core theoretical and methodological topics to address the above-listed modeling challenges.
High order DG methods. Designing numerical schemes that are high order accurate on general meshes, i.e., unstructured or hybrid structured/unstructured meshes, ia a major objective of our core research activities in ATLANTIS. We focus on the family of Discontinuous Galerkin (DG) methods that has been extensively developed for wave propagation problems during the last 15 years. We investigate several variants, namely nodal DGTD for time-domain problems, and HDG (Hybridized DG) for frequency-domain problems, with the general goal of devising, analyzing and developing extensions of these methods in order to deal with the above-mentioned physical drivers: nonlinear features, in particular in relation with generation of higher order harmonics in electromagnetic wave interaction with nonlinear materials, and nonlinear models of electronic response in metallic and semiconductor materials; multiphysic couplings such as for instance when considering PDE models relevant to thermoplasmonics, optoelectronics and nanoelectronics. There are to date very few works promoting DG-type methods for these situations. Our methodological contributions of these methods eventually materialize in the DIOGENeS software suite.
Multiscale modeling. The physical models that we consider may feature three different space scales. First, the size of the computational domain is fixed by the nanostructure under consideration and the required observables. Second, the solution wavelength depends on the operating frequency and on the light velocity in the constitutive materials. Finally, the finest scale involved corresponds to the nanostructuring length. These three space scales can differ by orders of magnitude, leading to unaffordable computational costs, if the discretization scheme must resolve the nanostructure details. We thus aim at designing multiscale numerical schemes, that can embed fine scale information into a coarser mesh. Such methodologies lead to embarrassingly parallel two-level algorithms, that are especially suited for HPC environments and produce accurate numerical approximations. These multiscale schemes are designed in the framework of MHM (Multiscale Hybrid-Mixed) formulations that we study in the context of a long-term collaboration with the research group of Frédéric Valentin at LNCC, Petropolis, Brazil. In the MHM framework, the inherent upscaling procedure that is at the heart of the approach, allows to incorporate more physics in the numerical schemes themselves, as the upscaling principle is used to construct physical basis functions that resolve the fine scales. At the second level, one defines a set of boundary value problems, whose solutions call for adapted versions of classical finite element or DG methods, and yield the upscaled basis functions.
Time integration for multiscale problems. Multiscale physical problems with complex geometries or heterogeneous media are extremely challenging for conventional numerical simulations. Adaptive mesh refinement is an attractive technique for treating such problems and will be developed in our research activities in ATLANTIS. Local mesh refinement imposes a severe stability condition on explicit time integration since the allowed maximal time step size is constrained by the smallest element in the mesh. We consider different ways to overcome this stability condition, especially by using implicit-explicit (IMEX) methods where a time implicit scheme is used only for the refined part of the mesh, and a time explicit scheme is used for the other part.
Reduced-order and surrogate modeling. Reduced-order modeling aims at reducing the computational requirements of costly high-fidelity solution methods while maintaining an acceptable level of accuracy. One of the most studied methods for establishing the reduced-order model is POD, also known as Karhunen-Loéve decomposition, principal component analysis, or singular value decomposition, which uses the solutions of high fidelity numerical simulations or experiments at certain time instants, typically called snapshots, to compute a set of POD basis vectors spanning a low-dimensional space. POD is very popular in the computational fluid dynamics field. However, the development of POD for time-domain electromagnetics has been more scarce. We study POD-based reduced-order modeling strategies in the context of a long-term collaboration with the research group of Liang Li at the School of Mathematical Sciences of the University of Electronic Science and Technology of China in Chengdu 11-9-10. Alternatively, several works in the recent years have promoted highly efficient surrogate modeling approaches based on Deep Neural Networks (DNNs) but most of these approaches rely on the availability of large data set of solutions for training. We initiated in 2022 a new research direction on a particular family of DNNs referred as Physics-Informed Neural Networks (PINNs) 68 that we plan to investigate for PDE models relevant nanophotonics with the goal of designing non-intrusive surrogate modeling approaches that require a minimal amount of data.
Error estimation and adaptivity. While standard theory ensures the convergence of the discrete approximation to the correct solution, it does not permit to quantitatively estimate the discretization error in actual applications. As a result, the selection of the discretization parameters is often carried out by the practitioners themselves, based on their experience and hence manual approaches to guarantee a sufficient accuracy level. We aim at providing reliable measurements of the discretization error and devising a more systematic and rigorous procedure to select and adapt discretization parameters — in particular the mesh size and the discretization order — through the use of a posteriori estimators. On the one hand, we propose to design a posteriori error estimators for the wave-matter interaction problems we consider in ATLANTIS, able to provide a fully reliable error estimation. On the other hand, such estimators can be employed to drive hp-adaptive algorithms, where the mesh and discretization order are iteratively improved to fit the complicated structure of the solution.
Dealing with complex materials. Physically relevant simulations deal with increasing levels of complexity in the geometrical and/or physical characteristics of nanostructures, as well as their interaction with light. Standard simulation methods may fail to reproduce the underlying physical phenomena, therefore motivating the search for more sophisticated light-matter interaction numerical modeling strategies. A first direction consists in refining classical linear dispersion models and we put a special focus on deriving a complete hierarchy of models, that will encompass standard linear models to more complex and nonlinear ones (such as Kerr-type materials, nonlinear quantuum hydrodynamic theory models, etc.). One possible approach relies on an accurate description of the Hamiltonian dynamics with intricate kinetic and exchange correlation energies, for different modeling purposes. A second direction is motivated by the study of 2D materials. A major concern is centered around the choice of the modeling approach between a full costly 3D modeling and the use of equivalent boundary conditions, that could in all generality be nonlinear. Assessing these two directions requires efficient dedicated numerical algorithms that are able to tackle several types of nonlinearities and scales.
Dealing with coupled models. Several of our target physical fields are multiphysics in essence and require going beyond the sole description of the electromagnetic response. In thermoplasmonics, the various phenomena (heat transfer through light concentration, bubbles formation and dynamics) call for different kinds of governing PDEs (Maxwell, conduction, fluid dynamics). Since, in addition, these phenomena can occur in significatively different space and time scales, drawing a quite complete picture of the underlying physics is a challenging task, both in terms of modeling and numerical treatment. In the nanoelectronics field, an accurate description of the electronic properties involves including quantum effects. A coupling between Maxwell’s and Schrödinger equations (again at significantly different time and space scales) is a possible relevant scenario. In the optoelectronics field, the accurate prediction of semiconductors optical properties is a major concern. A possible strategy may require to solve both the electromagnetic and the drift-diffusion equations. In all these aforementioned examples, difficulties mainly arise both from the differences in physical nature as well as in the time/space scales at which each physical phenomenon occurs. Accurately modeling/solving their coupled interactions remains a formidable challenge.
High performance computing (HPC). HPC is transversal to almost all the other research topics considered in the team, and is concerned with both numerical algorithm design and software development. We work toward taking advantage of fine grain massively parallel processing offered by GPUs in modern exascale architectures, by revisiting the algorithmic structure of the computationally intensive numerical kernels of the high order DG-based solvers that we develop in the framework of the DIOGENeS software suite.
3.2.2 Complementary topics
Beside the above-discussed core reserach topics, we have also identified additional topics that are important or compulsory in view of maximizing the impact in nanophotonics or nanophononics of our core activities and methodological contributions.
Numerical optimization. Inverse design has emerged rather recently in nanophotonics, and is currently the subject of intense research as witnessed by several reviews 63. Artificial Intelligence (AI) techniques are also increasingly investigated within this context 72. In ATLANTIS, we will extend the modeling capabilities of the DIOGENeS software suite by using statistical learning techniques for the inverse design of nanophotonic devices. When it is linked to the simulation of a realistic 3D problem making use of one of the high order DG and HDG solvers we develop, the evaluation of a figure of merit is a costly process. Since a sufficiently large input data set of candidate designs, as required by using Deep Learning (DL), is generally not available, global optimization strategies relying on Gaussian Process (GP) models are considered in the first place. This activity will be conducted in close collaboration with researchers of the ACUMES project-team. In particular, we investigate GP-based inverse design strategies that were initially developed for optimization studies in relation with fluid flow problems 53- 54 and fluid-structure interaction problems 69.
Uncertainty analysis and quantification. The automatic inverse design of nanophotonic devices enables scientists and engineers to explore a wide design space and to maximize a device performance. However, due to the large uncertainty in the nanofabrication process, one may not be able to obtain a deterministic value of the objective, and the objective may vary dramatically with respect to a small variation in uncertain parameters. Therefore, one has to take into account the uncertainty in simulations and adopt a robust design model 58. We study this topic in close collaboration with researchers of the ACUMES project-team one on hand, and researchers at TU Braunschweig in Germany.
Numerical linear algebra. Sparse linear systems routinely appear when discretizing frequency-domain wave-matter interaction PDE problems. In the past, we have considered direct methods, as well as domain decomposition preconditioning coupled with iterative algorithms to solve such linear systems 12. In the future, we would like to further enhance the efficiency of our solvers by considering state-of-the-art linear algebra techniques such as block Krylov subspace methods 44, or low-rank compression techniques 67. We will also focus on multi-incidence problems in periodic structures, that are relevant to metagrating or metasurface design. Indeed, such problems lead to the resolution of several sparse linear systems that slightly differ from one another and could benefit from dedicated solution algorithms. We will collaborate with researchers of the CONCACE (Inria center at Université de Bordeaux) industrial project-team to develop efficient and scalable solution strategies for such questions.
4 Application domains
Nanoscale wave-matter interactions find many applications of industrial and societal relevance. The applications discussed in this section are those that we address in the first place in the short- to medium-term. Our general goal is to impact scientific discovery and technological development in these application topics by leveraging our methodological contributions for the numerical modeling of nanoscale wave-matter interactions, and working in close collaboration with external partners either from the academic or the industrial world. Each of these applications is linked to one or more of the driving physical fields described in section 3.1 except nanoelectronics that we consider as a more prospective, hence long-term application.
4.1 Nanostructures for sunlight harvesting
Photovoltaics (PV) converts photon energy from the sun into electric energy. One of the major challenges of the PV sector is to achieve high conversion efficiencies at low cost. Indeed, the ultimate success of PV cell technology requires substantial progress in both cost reduction and efficiency improvement. An actively studied approach to simultaneously achieve both objectives is to exploit light trapping schemes. Light trapping enables solar cells absorption using an active material layer much thinner than the material intrinsic absorption length. This then reduces the amount of materials used in PV cells, cuts cell cost, facilitates mass production of these cells that are based on less abundant material and moreover can improve cell efficiency (due to better collection of photo- generated charge carriers). Enhancing the light absorption in ultrathin film silicon solar cells is thus of paramount importance for improving efficiency and reducing costs. Our activities in relation with this application field aim at precisely studying light absorption in nanostructured solar cell structures with the help of an adapted numerical procedure. We consider both the characterization of light trapping for a given texturing of material layers, and the goal-oriented inverse design of the nanostructuring.
4.2 Metasurfaces for light shaping
Metasurfaces produce abrupt changes over the scale of the free-space wavelength in the phase, amplitude and/or polarization of a light beam. Metasurfaces are generally created by assembling arrays of miniature, anisotropic light scatterers (i.e. resonators such as optical antennas). The spacing between antennas and their dimensions are much smaller than the wavelength. As a result the metasurfaces, on account of Huygens principle, are able to mould optical wavefronts into arbitrary shapes with subwavelength resolution by introducing spatial variations in the optical response of the light scatterers. Designing metasurfaces for realistic applications such as metalenses 71 is a challenging inverse problem. In this context, the ultimate goal of our activities is to develop numerical methodologies for the inverse design of large-area metasurfaces 66.
4.3 THz wave generation
Recent research on the interaction of short optical pulses with semiconductors has stimulated the development of low power terahertz (THz) radiation transmitters. The THz spectral range of electromagnetic waves (0.1 to 10 THz) is of great interest. In particular, it includes the excitation frequencies of semiconductors and dielectrics, as well as rotational and vibrational resonances of complex molecules. As a result, THz waves have many applications in areas ranging from the detection of dangerous or illicit substances and biological sensing to diagnosis and diseases treatment in medicine. The most common mecanism of THz generation is based on the use of THz photoconductive antennas (PCA), consisting of two electrodes spaced by a given gap and placed onto a semiconductor surface. The excitation of the gap by a femtosecond optical pulse induces a sharp increase of the concentration of charge carriers for a short period of time, and a THz pulse is generated. Computer simulation plays a central role in understanding and mastering these phenomena in order to improve the design of PCA devices. The numerical modeling of a general 3D PCA configuration is a challenging task. Indeed, it requires the simultaneous solution of charge transport in the semiconductor substrate and the electromagnetic wave radiation from the antenna 65- 73. The recently-introduced concept of hybrid photoconductive antennas leveraging plasmonic effects is even more challenging 60. So far, existing simulation approaches are based on the FDTD method, and are only able to deal with classical PCAs. In relation with the design of photonic devices for THz waves generation and manioulation, we intend to a multiscale numerical modeling strategy for solving the system of Maxwell equations coupled to various models of charge carrier dynamics in semiconductors.
4.4 Plasmonic nanostructures for nanoscale sensing
The propagation of light in a slit between metals is known to give rise to guided modes. When the slit is of nanometric size, plasmonic effects must be taken into account, since most of the mode propagates inside the metal. Indeed, light experiences an important slowing-down in the slit, the resulting mode being called gap plasmon. Hence, a metallic structure presenting a nanometric slit can act as a light trap, i.e. light will accumulate in a reduced space and lead to very intense, localized fields. Nanocubes are extensively studied in this context and have been shown to support such gap plasmon modes. At visible frequencies, the lossy behavior of metals will cause the progressive absorption of the trapped electromagnetic field, turning the metallic nanocubes into efficient absorbers. The frequencies at which this absorption occurs can be tuned by adjusting the dimensions of the nanocube and the spacer. Such metallic nanocubes can be used for a broad range of applications including plasmonic sensing, surface enhanced Raman scattering (SERS), metamaterials, catalysis, and bionanotechnology. We aim at devising a numerical methodology for characterizing the impact of geometrical parameters such as the dimensions of the cube, the rounding of nanocube corners or the size of the slit separating the cube and the substrate, on the overall performance of these absorbers. In practice, this leads us to address two main modeling issues. First, as the size of the slit is decreased, spatial dispersion effects 51 have to be taken into account when dealing with plasmonic structures. For this purpose, we consider a fluid model in the form of a nonlocal hydrodynamic Drude model 50, which materializes as a system of PDEs coupled to Maxwell's equations 14-13. The second issue is concerned with the assessment of geometrical uncertainties and their role in the development of spatial dispersion effects.
4.5 Plasmonic nanostructures for photothermal effects
The field of thermoplasmonics has developed an extensive toolbox to produce, control and monitor heat at the nanometer scale. Nanoparticles are promising nano-sensing and nano-manipulating tools, and recent studies yielded remarkable advances in design, synthesis, and implementation of luminescent nanoparticles. Some applications deal with bio-imaging and bio-sensing, like e.g. luminescent nanothermometers, nanoparticles capable of providing contactless thermal reading through their light emission properties 59. Also, bio-functionalized gold nanorods are promising candidates for light-induced hyperthermia 64, to cause local and selective damage in malignant tissue. At the same time, laser pulse interaction with plasmonic nanostructures can also be exploited for cell nanosurgery 46, including plasmonic enhanced cell transfection, molecular surgery and drug delivery. In parallel to all these bio-oriented applications, plasmonic nanoparticles can also be thought of as prototypic systems for understanding fundamental aspects of nanoscale material as well as light-matter interaction. Specific numerical modeling tools are essential to provide a good insight in this understanding.
5 Social and environmental responsibility
5.1 Impact of research results
The parts of our research activities that are addressing the design of nanostructures for sunlight harvesting on one hand, and of nanostructures for photothermal effects on the other hand, target applications concerned with production of renewable energy and biomedical engineering (ranging from light controlled drug-release to the ongoing battle against Covid-19).
6 Highlights of the year
This year, thanks to the innovative computational and inverse design methods that we develop in the team, we have investigated for the first time a novel active metasurface design that relies on the position of topological singularities, namely zeros and poles of the reflection coefficient, to address full phase modulation of light reflected off the metasurface with almost unity efficiency (see section 8.6 for more details).
7 New software and platforms
7.1 New software
7.1.1 DIOGENeS
-
Name:
DIscOntinuous GalErkin Nanoscale Solvers
-
Keywords:
High-Performance Computing, Computational electromagnetics, Discontinuous Galerkin, Computational nanophotonics
-
Functional Description:
The DIOGENeS software suite provides several tools and solvers for the numerical resolution of light-matter interactions at nanometer scales. A choice can be made between time-domain (DGTD solver) and frequency-domain (HDGFD solver) depending on the problem. The available sources, material laws and observables are very well suited to nano-optics and nano-plasmonics (interaction with metals). A parallel implementation allows to consider large problems on dedicated cluster-like architectures.
- URL:
-
Authors:
Stéphane Lanteri, Nikolai Schmitt, Alexis Gobe, Jonathan Viquerat, Guillaume Leroy
-
Contact:
Stéphane Lanteri
8 New results
8.1 High order methods for coupled problems
In this section, we present ongoing studies aiming at designing, analyzing and developing novel high order methods for solving electromagnetic wave propagation problems in general on one hand, and for differential systems modeling nanoscale light-matter interactions with complex media on the other hand. We focus on the family of Discontinuous Galerkin (DG) methods. In the time-domain setting, the starting point of these works is the DGTD (Discontinuous Galerkin Time-Domain) method introduced in 8. In the frequency-domain setting, the HDGFD (Hybridized Discontinuous Galerkin Frequency-Domain) method 1 is considered as the basis of our works.
8.1.1 Time-domain numerical modeling of gain media
Participants: Stéphane Descombes, Stéphane Lanteri, Cédric Legrand, Gian Luca Lippi [INPHYNI laboratory, Sophia Antipolis].
In laser physics, gain or amplification is a process where the medium transfers part of its energy to an incident electromagnetic radiation, resulting in an increase in optical power. This is the basic principle of all lasers. Quantitatively, gain is a measure of the ability of a laser medium to increase optical power. Modeling optical gain requires to study the interaction of the atomic structure of the medium with the incident electromagnetic wave. Indeed, electrons and their interactions with electromagnetic fields are important in our understanding of chemistry and physics. In the classical view, the energy of an electron orbiting an atomic nucleus is larger for orbits further from the nucleus of an atom. However, quantum mechanical effects force electrons to take on discrete positions in orbitals. Thus, electrons are found in specific energy levels of an atom. In a semiclassical setting, such transitions between atomic energy levels are generally described by the so-called rate equations. These rate equations model the behavior of a gain material, and they need to be solved self-consistently with the system of Maxwell equations. So far, the resulting coupled system of Maxwell-rate equations has mostly been considered in a time-domain setting using the FDTD method for which several extensions have been proposed. In the context of the PhD of Cédric Legrand, we study an alternative numerical modeling approach based on a high order DGTD method. This year, we have proposed a first variant that extends the DGTD method introduced in 55. This novel DGTD method has been formulated and analyzed in the three-dimensional case. A fully discrete stability analysis has been conducted and a computer implementation has been finalized. Numerical validations are underway before proceeding to a concrete application in the field of random lasing in collaboration with Gian Luca Lippi at INPHYNI laboratory.
8.1.2 Time-domain numerical modeling of semiconductor devices
Participants: Eric Guichard [Silvaco Inc., Santa Clars, CA, USA], Stéphane Lanteri, Massimiliano Montone, Claire Scheid.
In the field of semiconductor physics modeling, charge carrier transport is the starring phenomenon that needs to be predicted in order to build a mathematical model, based on higher-level quantities (e.g. electric current and voltage), that can be practically used for device simulation. Charge carrier transport is generally described by a drift-diffusion model. This yields a system of coupled partial differential equations which can be solved at two levels: (1) quasistatic approximation: the external force applied to the crystal is electrostatic, and drift-diffusion equations are coupled to a Poisson equation for the electrostatic potential. The goal is to determine the spatial distribution of carrier concentrations and the electric field (deduced from the potential); (2) fullwave model: the crystal is subject to an applied electromagnetic field, and Maxwell equations are coupled with transport equations for carrier dynamics. The goal is to determine the space-time evolution of carrier concentrations and the electromagnetic field. The quasistatic approximation is rigorous when the steady state of the semiconductor has to be calculated. For example, this could be a preliminary step to the fullwave simulation of a device that is biased prior to responding to a (time-varying) electromagnetic excitation. The fullwave model is particularly relevant to electro-optics, i.e. when light-matter interaction is investigated. Indeed, such study is essential to understanding and accurately modeling the operation of photonic devices for light generation, modulation, absorption. In the context of the PhD of Massimiliano Montone we have a designed a DGTD method for solving the coupled system of Maxwell equations and drift-diffusion equations in the fullwave setting. The method has been formulated in the general three-dimensional case, and a computer implementation has been realized in a two-dimensional setting.
8.1.3 Controllability method for Maxwell's equations
Participants: Théophile Chaumont-Frelet, Marcus Gröte [University of Basel, Switzerland], Stéphane Lanteri, Jet Tang [University of Basel, Switzerland].
The limiting amplitude principle predicts the asymptotic harmonic regime of a structure that is monochromatically illuminated. This makes a frequency-domain approach relevant, viewed as a long time asymptotic of a monochromatic time-domain simulation setting. Besides, it means that a time-domain solver may be used to solve frequency-domain problems, avoiding an explicit linear system solve. In this context, we investigate a modeling approach that allows to build bridges between the frequency- and time-domain approaches. This works heavily relies on the possibility of having reliable, accurate and high order discretization strategies for approximating time-domain problems. In collaboration with Marcus J. Grote and Jet Tang, University of Basel, Switzerland, we consider the use of time-domain solvers to efficiently solve frequency-domain problems in non dispersive materials. Specifically, we consider an approach called conjugate gradient controlability method that we study theoretically in 3D and numerically in 2D and 3D 18. We have shown that the proposed method converges toward the time-harmonic solution, and numerical examples suggest that the method is robust in the high-frequency regime and/or in the presence of trapped waves in complex geometries.
8.1.4 Efficient approximation of high-frequency Helmholtz problems
Participants: Théophile Chaumont-Frelet, Victorita Dolean [LJAD, Université Côte d'Azur], Maxime Ingremeau [LJAD, Université Côte d'Azur], Florentin Proust.
Helmholtz problems describe the periodic solutions of the wave equation (possibly in a heterogeneous medium, in a bounded medium, with boundary conditions,...). In general, there is no explicit solution to such an equation, and an approximate solution of the equation must be computed numerically. All the existing methods (finite elements, finite differences...) have in common that they are more and more expensive when the frequency of the waves increases. In 32, we study new finite-dimensional spaces specifically designed to approximate the solutions to high-frequency Helmholtz problems with smooth variable coefficients. These discretization spaces are spanned by Gaussian coherent states, that have the key property to be localised in phase space. We carefully select the Gaussian coherent states spanning the approximation space by exploiting the (known) micro-localisation properties of the solution. This work in conducted in the context of the POPEG Exploratory Research Action and the topic is also at the heart of the PhD thesis of Florentin Proust. In the beginning of this thesis, such a method has been implemented for a simple one-dimensional problem.
8.2 Data-driven reduced-order modeling
In short, reduced order modeling (ROM) allows to construct simplifications of high fidelity, complex models. The resulting lower fidelity (also referred as surrogate) models capture the salient features of the source models so that one can quickly study a system's dominant effects using minimal computational resources. In collaboration with researchers at the University of Electronic Science and Technology of China (UESTC) and the Southwestern University of Finance (SUFEC) and Economics, which are both located in Chengdu, we study ROM for time-domain electromagnetics and nanophotonics. More precisely, we have considered the applicability of the proper orthogonal decomposition (POD) technique for the system of time-domain Maxwell equations, possibly coupled to a Drude dispersion model, which is employed to describe the interaction of light with nanometer scale metallic structures. Our first contributions are described in 9-11 where we have proposed POD approach for building a reduced subspace with a significantly smaller dimension given a set of space-time snapshots that are extracted from simulations with a high order DGTD method. Then, a POD-based ROM is established by projecting (Galerkin projection) the global semi-discrete DG scheme onto the low-dimensional space spanned by the POD basis functions.
8.2.1 Non-intrusive ROM for parameterized electromagnetic problems
Participants: Stéphane Lanteri, Kun Li [SUFEC, Chengdu, China], Liang Li [UESTC, Chengdu, China], Ying Zhao [UESTC, Chengdu, China].
In 10, we have introduced a non-intrusive variant of the POD-based ROM initially introduced in 9-11, in the context of parameterized time-domain electromagnetic scattering problems. The considered parameters are the electric permittivity and the temporal variable. The snapshot vectors are produced by a high order DGTD method formulated on an unstructured simplicial mesh. Because the second dimension of the snapshots matrix is large, a two-step or nested POD method is employed to extract time- and parameter-independent POD basis functions. By using the singular value decomposition (SVD) method, the principal components of the projection coefficient matrices (also referred to as the reduced coefficient matrices) of full-order solutions onto the reduced-basis (RB) subspace are extracted. A cubic spline interpolation-based (CSI) approach is proposed to approximate the dominating time- and parameter-modes of the reduced coefficient matrices without resorting to Galerkin projection. The generation of snapshot vectors, the construction of POD basis functions and the approximation of reduced coefficient matrices based on the CSI method are completed during the offline stage. The RB solutions for new time and parameter values can be rapidly recovered via outputs from the interpolation models in the online stage. In particular, the offline and online stages of the proposed POD-CSI method are completely decoupled, which ensures the computational validity of the method. Moreover, a surrogate error model is constructed as an efficient error estimator for the POD-CSI method.
More recently, in 23, we have designed an improved version of the POD-CSI method 10. During the offline stage, the training parameters are chosen by using a Smolyak sparse grid method with a fixed approximation level L over a target parameterized space. For each selected parameter, the snapshot vectors are first produced by a high order DGTD method. In order to minimize the overall computational cost in the offline stage and to improve the accuracy of the NIMOR method, a radial basis function (RBF) interpolation method is then used to construct more snapshot vectors at the sparse grid with approximation level L+1, which includes the sparse grids from approximation level L. Moreover, a Gaussian process regression (GPR) method is proposed to approximate the dominating time- and parameter-modes of the reduced coefficient matrices. During the online stage, the reduced-order solutions for new time and parameter values can be rapidly recovered via outputs from the regression models without using the DGTD method.
Finally, in 22, we study the simulation of the interaction of light with 3D metallic nanostructures using an adapted version of the method initially introduced in 9-11.
8.2.2 Combining POD and CAE for time-domain electromagnetics
Participants: Stéphane Lanteri, Xiao-Feng He [UESTC, Chengdu, China], Kun Li [SUFEC, Chengdu, China], Liang Li [UESTC, Chengdu, China].
Linear reduction methods such as POD hardly capture the complex dynamics of highly nonlinear systems, therefore nonlinear manifold learning methods such as kernel principal component analysis (PCA) and Hessian feature maps have recieved much attention in the recent years. Assuming that data points lie in a low dimensional manifold embedded in an higher dimensional Euclidean space, manifold learning aims to identify the intrinsic dimensionality equal to the number of parameters that describe the system, and thus obtain low dimensional representations of the data points. Although kernel PCA and Hessian feature maps are effective in providing low dimensional representations for high dimensional data points, their main drawback is that they do not provide an analytical formula to decode the compressed data back to their high dimensional representation in the original space. An autoencoder (AE) overcomes this disadvantage by learning how to compress (encode) a high dimensional data to a low dimensional code and then reconstruct (decode) the code to a representation as close to the original input as possible. The encoder and decoder parts of an autoencoder are trained simultaneously but can be used separately, which provides an opportunity to build a mapping between the input time/parameter and encoded representation. Directly applying large-scale simulation data (snapshots) to a fully-connected autoencoder is not only computationally prohibitive, but also ignores the opportunity to exploit the structure of features in high dimensional. As an extension of ordinary AEs, convolutional autoencoders (CAEs) are characterized by shared parameters and local connectivity which help to reduce the memory as well as computational costs. This study is concerned with a non-intrusive ROM that combines matrix decomposition and deep neural networks for parameterized electromagnetic scattering problems 37. A database collecting snapshots of high-fidelity solutions is built by solving the parameterized time-domain Maxwell equations with a high order DGTD method. To perform a prior dimensionality reduction, a set of RB functions are extracted from the database via a two-step POD method. Projection coefficients of RB functions are further compressed through a convolutional autoencoder (CAE) network. SVD is then used to extract the principal components of the reduced-order matrices generated by CAE, and a CSI approach is employed for approximating the dominating time- and parameter-modes of the reduced-order matrices. The generation of the RB and the training of the CAE and CSI are accomplished in the offline stage, thus the RB solution for given time/parameter values can be quickly recovered via outputs of the interpolation model and decoder network.
8.2.3 Calculation of optical quasi-normal modes with contour integral methods
Participants: Théophile Chaumont-Frelet, Josselin Defrance, Stéphane Lanteri.
Recently, semi-analytical methods became quite popular to solve Maxwell’s equations. These methods are based on the derivation of optical resonances also called quasi-normal modes (QNM). Locating optical resonant frequencies within the complex plane provides precious information. Indeed, the real and imaginary parts of complex resonant frequencies provide the excitation frequency and the quality factor of each quasinormal mode. In addition, the symmetries and hotspots occuring in the field distribution associated to each resonance indicates how each resonance can be excited and where the density of electromagnetic energy will be the highiest. Such information is already enough to draw useful conclusions, i.e., identify where sharp features will occur in the transmission and reflection spectra, which resonance will contribute the most to the scattering process or which part of a nanostructure will be subject to high absorption and nonlinear phenomena. Thus, quasi-normal modes give access to the value of many observable at any frequencies whithout the necessity to solve Maxwell’s equations more than the few times that are necessary to derive the needed optical resonances. Additionnally, the knowledge of the resonant frequencies and fields of a structure is enought to predict the optical characteristics of other structures presenting structural changes with respect to the originally known system. This approach is known as the resonant state expansion, which offer powerfull tools particularily in the scope of optimisation algorithms. Another and not the least advantage of this approach is that it can be implemented on top of many frequency domain solvers such as Fourier modal methods, finite element methods (FEM) solvers or discontinuous Garlekin methods (DG). Efficient algorithms to derive swiftly and accurately quasi-normal modes is more and more needed. In this context, we have conductive a comparative study in the 2D case about the efficiency of two contour integral methods to derive optical resonances, known as the FEAST and Beyn methods. This is a fisrt step toward the development of a scalable QNM solver for 3D problems in the framework of the DIOGENeS software suite.
8.2.4 Multi-fidelity modeling and optimization
Participants: Mickaël Binois [ACUMES project-team], Régis Duvigneau [ACUMES project-team], Stéphane Lanteri, Henry Moss [SecondMind, Cambridge, UK], Victor Picheny [SecondMind, Cambridge, UK].
To reduce the computational cost related to the use of high-fidelity simulations when evaluating the cost function, we investigate the construction of multi-fidelity auto-regressive Gaussian Process models, that can rely on different physical models (e.g. inviscid or viscous flows) or numerical accuracy (e.g. coarse or fine meshes). The objective is to construct a model that is accurate regarding the high-fidelity evaluations, but mostly based on low-fidelity simulations. Of particular interest is the definition of an efficient acquisition function, that selects both the next design point to evaluate and the corresponding fidelity level to use. This work is achieved in collaboration with SecondMind company and was the topic of Maha Ouali's internship.
8.3 Multiscale modeling
In this section, we present ongoing studies aiming at designing, analyzing and developing novel numerical methods for dealing with multiscale problems. The corresponding works are concerned with the multiscale schemes that are designed in the framework of MHM (Multiscale Hybrid-Mixed) formulations. They are conducted in the context of a long-term collaboration with the research group of Frédéric Valentin at LNCC, Petropolis, Brazil.
8.3.1 Unfitted meshes with the Multiscale Hybrid-Mixed Method
Participants: Théophile Chaumont-Frelet, Diego Paredes [Universidad de Concepción, Chile], Frédéric Valentin [LNCC, Petropolis, Brazil].
The flux variable determines the approximation quality of numerical methods based on hybridization. We prove that the approximation of flux variables in discontinuous polynomial spaces from the L2 orthogonal projection is superconvergent in meshes that are not aligned with jump coefficient interfaces. The results only assume the local regularity of exact solutions on physical partitions. Based on the proposed flow approximation, we demonstrate that MHM method is superconvergent on non-aligned grids, supporting the numerical results presented in seminal MHM works. Such results are sufficiently generic to be used to prove the superconvergence of the MHM method when applied to other operators. This work is described in the preprint 33.
8.3.2 Multiscale convergence analysis for Helmholtz problems
Participants: Théophile Chaumont-Frelet, Zakaria Kassali, Stéphane Lanteri, Frédéric Valentin [LNCC, Petropolis, Brazil].
The robustness of MHM discretizations of Helmholtz problems with respect to the frequency parameter have been previously addressed in the literature. Here, we analyze the stability and accuracy of the MHM method in highly heterogeneous periodic multiscale media with a (small) period and (possibly) large frequency . In particular, we derive error estimates that are uniform in the limit where and explicit in the frequency parameter . These results can be found in the PhD thesis of Zakaria Kassali.
8.4 Dealing with complex models
8.4.1 Toward thermoplasmonics
Participants: Yves D'Angelo, Stéphane Lanteri, Thibault Laufroy, Claire Scheid.
Although losses in metal are viewed as a serious drawback in many plasmonics experiments, ther- moplasmonics is the field of physics that tries to take advantage of the latter. Indeed, the strong field enhancement obtained in nanometallic structures lead to a localized temperature increase in its vicin- ity, leading to interesting photothermal effects. Therefore, metallic nanoparticles may be used as heat sources that can be easily integrated in various environments. This is especially appealing in the field of nanomedecine and can for example be used for diagnosis purposes or nanosurgery to cite but just a few. Due to the various scales and phenomena that come into play, accurate numerical modeling is challenging. Laser illumination first excites a plasmon oscillation (reaction of the electrons of the metal) that relaxes to a thermal equilibrium and in turn excites the metal lattice (phonons). The latter is then responsible for heating the surroundings. A relevant modeling approach thus consists in describing the electron-phonon coupling through the evolution of their respective temperature. Maxwell’s equations are then coupled to a set of coupled nonlinear hyperbolic equations for the temperatures of respectively electrons, phonons and environment. The nonlinearities and the different time scales at which each thermalization occurs make the numerical approximation of these equations quite challenging. In the context of the PhD of Thibault Laufroy, which has started in October 2020, we propose to develop a suitable numerical framework for studying thermoplasmonics. As a first step, we have reviewed the models used in thermoplasmonics that are most often based on strong or weak (nonlinear) couplings of Maxwell’s equations with nonlinear equations modeling heat transfer (hyperbolic or parabolic). We also layed the foundations of the numerical approximation framework and provided a first stability study.
8.4.2 Numerical modeling of conformal metasurfaces with GSTCs
Participants: Patrice Genevet [CRHEA, Sophia Antipolis], Sandeep Golla [CRHEA, Sophia Antipolis], Stéphane Lanteri, Nicolas Lebbe.
For centuries, optical design consisted in developing thin films and various coating to address light reflection, transmission and/or diffusion at interfaces. Developments in nanophotonics have strongly improved our ability to control light scattering processes with optically resonant nanostructures. Artificial optical materials, also dubbed metamaterials and metasurfaces, presenting unexpected light propagation effects have been realized, leading to cloacking, negative refraction, subwavelength focusing, generalized refraction and vectorial electromagnetic field control. These metamaterials and metasurfaces are realized by assembling subwavelength photonic structures. The study of the device’s optical response is generally complex and requires lengthy numerical simulations that describe in detail the effect of light interaction with a large number of nanophotonic building blocks. To avoid modeling thousands and billions of small geometrical features, homogenisation methods that approximate the complexity of an inhomogeneous material filed with nanoscale inclusions by its effective medium response, i.e., homogeneous artificial material, have been proposed. For the case of metasurfaces, consisting of a surfacic two-dimensional arrangement of nanostructures, equivalent transition conditions linking the values of the macroscopic field quantities on both sides of a thin homogenized layer have been derived. In fact, such transition conditions are well known in electromagnetics but also in acoustics and are commonly used to simplify physical interpretation or ease numerical simulations. Metasurfaces have thus been modeled using advanced effective transition conditions, called Generalized Sheet Transition Conditions (GSTCs). These transition conditions conceal in a tensorial form the equivalent response occurring on reflecting and transmitting fields at complex interfaces. Efforts to reproduce above-mentioned intriguing effects using GSTC formulation, including anomalous refraction, cloaking and vectorial electromagnetic field control have been realized recently But so far, most works dealing with GSTCs only considered layers manufactured on planar surfaces. In this work, we address theoretically the problem of electromagnetic field transition conditions at conformal interfaces to achieve surface topography-dependent transmitted and reflected fields. Our analysis, supported by 2D and 3D finite element simulations, provides a solid theoretical framework to design metasurfaces for cloaking, wearable optics and next generation of freeform imaging systems 21.
8.5 Deep Learning methods
We initiated in 2022 a prospective research direction on alternative numerical modeling methods based on Neural Networks (NN). We investigate both data-driven and model-driven approaches for dealing with the system of Maxwell equations possibly coupled with various material models of interest to nanophotonics. One first question that we want to address is wether DL methods can yield highly efficient surrogate models of 3D time-domain electromagnetic wave propagation problems. Beside, we are also interested in devising DL-based methods for dealing with problems which are more difficult to handle with traditional numerical methods such as electromagnetic wave interaction with space-time adaptive materials or nonlinear media.
8.5.1 Dynamic metasurface control using Deep Reinforcement Learning
Participants: Stéphane Lanteri, Liang Li [UESTC, Chengdu, China], Jonathan Viquerat [CEMEF, Mines ParisTech, Sophia Antipolis], Ying Zhao [UESTC, Chengdu, China].
Dynamic metasurface is an emerging concept for achieving a flexible control of electromagnetic waves. Generalized sheet transition conditions (GSTCs) can be used to model the relationship between the electromagnetic response and surface susceptibility parameters characterizing a metasurface. However, when it comes to the inverse problem of designing and controlling a metasurface in a space–time varying context based on GSTCs, the dynamic synthesis of the susceptibility parameters is a difficult and non-intuitive task. In this study, we transform the inverse problem of solving dynamic susceptibility parameters into a sequence of control problems. Based on FDTD numerical simulations, a Deep Reinforcement Learning (DRL) framework using a proximal policy optimization (PPO) algorithm and a fully connected neural network is designed to control the susceptibility parameters intelligently and efficiently, promoting the further expansion of the application range of metasurface and thus helping realize more flexible and effective control of electromagnetic waves. This work has been published in 24 where we provide numerical results in a 1D setting to show the applicability, correctness and effectiveness of the proposed approach.
8.5.2 Physics-based Deep Learning for time-domain electromagnetics
Participants: Amine Bennini, Antonio Tadeu Gomes [LNCC, Petropolis, Brazil], Stéphane Lanteri, Frédéric Valentin [LNCC, Petropolis, Brazil].
Numerical simulations of electromagnetic wave propagation problems primarily rely on spatially and temporally discretization of the system of time-domain Maxwell equations using finite difference or finite element type methods. For complex and realistic three-dimensional situations, such a process can be computationally prohibitive, especially in view of many-query analyses (e.g., optimization design and uncertainty quantification). Therefore, developing cost-effective surrogate models is of great practical significance. Among the different possible approaches for building a surrogate model of a given PDE system in a non-intrusive way (i.e., with minimal modifications to an existing discretization-based simulation methodology), approaches based on neural networks and Deep Learning (DL) has recently shown new promises due to their capability of handling nonlinear or/and high dimensional problems. In the present study, we propose to focus on the particular case of Physics-Informed Neural Networks (PINNs) introduced in 68. PINNs are neural networks trained to solve supervised learning tasks while respecting any given1q laws of physics described by a general (possibly nonlinear) PDE system. They seamlessly integrate the information from both the measurements and partial differential equations (PDEs) by embedding the PDEs into the loss function of a neural network using automatic differentiation. In 2022, we have initiated a study dedicated to the applicability of PINNs for building efficient surrogate models of the system Maxwell equations in 2D. Our first results have been presented in the workshop entitled "HPC and Data Sciences meet Scientific Computing" that was organized in the context of the CARLA 2022 conference.
8.5.3 Interplay of Physics-Informed Neural Networks and multiscale numerical methods
Participants: Antonio Tadeu Gomes [LNCC, Petropolis, Brazil], Stéphane Lanteri, Larissa Miguez Da Silva [LNCC, Petropolis, Brazil], Frédéric Valentin [LNCC, Petropolis, Brazil].
Hybrid-Mixed (MHM) algorithms to improve accuracy and make MHM methods more cost-effective. For that, we adopted numerical analysis tools based on hybridization techniques as usual, and in a more innovative way investigating the interaction between multiscale methods and the new field of Scientific Artificial Intelligence (SciIA). Specifically, we investigate alternatives to the current computational cost of the MHM method method, notably associated with the calculation of multiscale basis functions. In fact, it can become particularly prohibitive in time-dependent or nonlinear 3D problems. We foresee the strategies to resolve such a drawback by proposing a hybrid strategy to adapt the MHM methodology to incorporate scientific physics-driven machine learning techniques (PINNs-Physical-Informed Neural Network, for example). We believe that such a methodology will be at the forefront of the next wave of data-driven scientific discoveries in the physical and engineering sciences.
8.5.4 Data-driven Deep Learning for the optimal design of nanophotonic devices
Participants: Arthur Clini De Souza, Mahmoud Elsawy, Hugo Figueroa [LEMAC, University of Campinas, Brazil], Badre Kerzabi [Solnil, Marseille], Stéphane Lanteri.
We have initiated this year a study to develop accurate and efficient DL-based surrogate models for the numerical characterization of light-matter interactions with nanostructured materials, more particularly for metasurfaces. Metasurfaces are an evolution of artificially structured materials on a smaller scale than the wavelength, known as metamaterials. The latter derive their optical properties not only from the intrinsic properties of the base materials, but above all from the precise geometry, size, orientation and arrangement of their structural elements. In this way, materials with unexpected and sometimes specific optical properties can be designed, exceeding the limits of what can be achieved with existing materials. In this preliminary study during the internship of Arthur Clini De Souza, we consider convolutional autoencoder and variational convolutional autoencoder NNs and compare their relative performance for the inverse design of a single nanoresonator, which is a base meta-atom for a Huygens metasurface. This study is conducted in collaboration with Hugo Enrique Hernandez Figueroa who is the head of the Laboratory of Applied and Computational Electromagnetics (LEMAC), which is part of the School of Electrical and Computer Engineering (FEEC) at the University of Campinas (UNICAMP).
8.6 Discovering novel nanoscale structures
At the creation of the team in February 2020, our collaborations with physicists from the nanophotonics domain aimed at leveraging our developed numerical modeling methodologies in order to study specific topics in relation with concrete applications (see Section 8.8 for more details). An evolution that started in 2022 was our will to adapt and exploit these numerical methodologies to discover nanostructure organizations exhibiting behaviors and performances opening the road to new application perspectives.
8.6.1 Universal active metasurfaces for ultimate wavefront molding
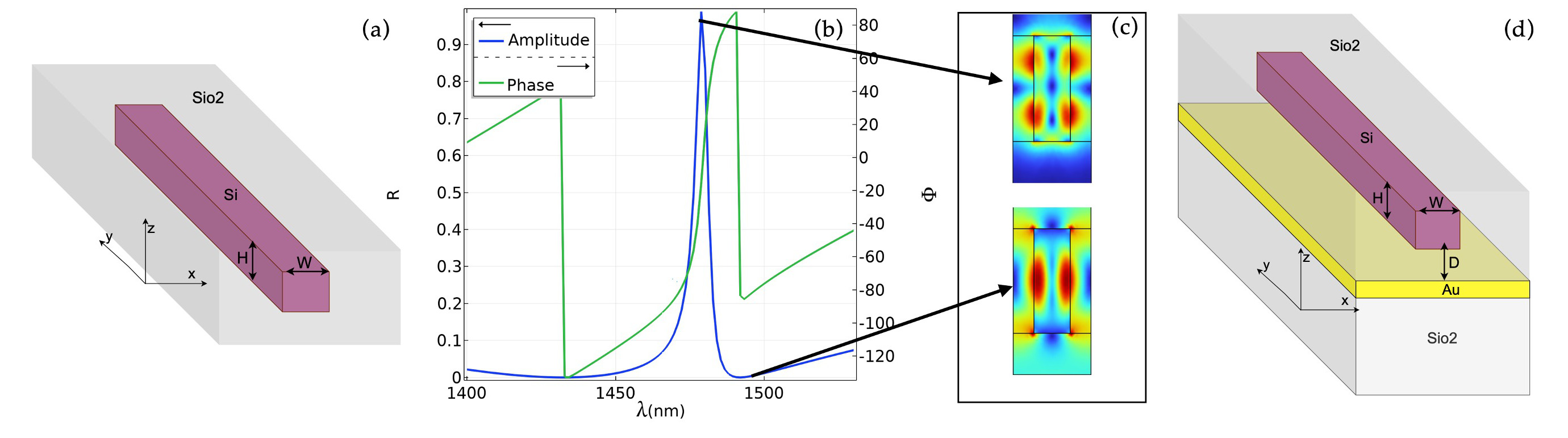
Participants: Rémi Colom [CRHEA, Sophia Antipolis], Jean-Yves Duboz [CRHEA, Sophia Antipolis], Mahmoud Elsawy, Patrice Genevet [CRHEA, Sophia Antipolis], Khosro Zangeneh Kamali [TMOS, The Australian National University, Canberra, Australia], Christina Kyrou [CRHEA, Sophia Antipolis], Elena Mikheeva [CRHEA, Sophia Antipolis], Stéphane Lanteri, Dragomir Neshev [TMOS, The Australian National University, Canberra, Australia].
Optical metasurfaces are becoming ubiquitous optical components to mold the amplitude, phase, and polarization of light. So far, most of these devices are passive in essence, that is, they cannot be arbitrarily reconfigured or optimized according to the user's interest and/or change in the surrounding environment. In this work, we propose an innovative design strategy relying on the position of topological singularities, namely zeros and poles of the reflection coefficient, to address full phase modulation of light reflected off an active metasurface with almost unity efficiency. The active metasurface unit cells, consisting of asymmetric Gires-Tournois resonators filled with either silicon or hetero-structured materials to leverage on the thermo-optical or electro-optical effects, respectively. In both cases, a full phase modulation associated with reflection amplitude is observed even when dealing with extremely low refractive index change, on the order of . Improving the deflection efficiencies for each deflection angle and accounting for the near-field coupling between strongly resonant pixels is performed by calculating the refractive index modulation profile in the extended unit cell using an advanced optimization methodology relying on statistical learning. Consequently, active beam steering designs for active thermo-optical effect with ultimate performance exceeding have been optimized. Furthermore, active wavefront splitting using electro-optics materials was optimized to reach ultimate modulation performances with nearly efficiency. The realization of highly efficient active beam-forming operating at high frequencies would open important applications in imaging microscopy, high-resolution image projection, optical communication, and 3D light detection and ranging (LiDAR).
|
8.7 Software developments in DIOGENeS
Participants: Alexis Gobé, Guillaume Leroy, Stéphane Lanteri.
In order to maximize the impact of our research activities described in section 3, a modern software platform is necessary. For that purpose, the team develops the DIOGENeS (DIscOntinuous GalErkin Nanoscale Solvers) software suite, which is dedicated to the numerical modeling of nanoscale wave-matter interactions in the 3D case. The initial (and current) version of this software concentrates on light-matter interactions with nanometer scale structures, for applications to nanophotonics and nanoplasmonics. DIOGENeS is a unique numerical framework leveraging the capabilities of discontinuous Galerkin methods for the simulation of multiscale problems relevant to nanophotonics and nanoplasmonics. DIOGENeS is a major asset in our strategy to demonstrate that the methodological contributions that we produce can be successfully applied to problems addressed by physicists and engineers trying to exploit specific features of nanoscale wave-matter interactions for scientific and technological applications.
This suite is organized around the following components:
- A core library containing all the basic building blocks for the construction of high order discontinuous Galerkin methods formulated on tetrahedral, orthogonal hexahedral and hybrid tetrahedral-hexahedral meshes;
- Fullwave solvers implementing high order discontinuous Galerkin methods for the discretization of time domain (DGTD - Discontinuous Galerkin Time-Domain) and in frequency domain (HDGFD - Hybridized Discontinuous Galerkin Frequency-Domain) coupled to a generalized model models of physical dispersion in metallic or semiconductor materials;
- A library of geometric modeling modules for the definition of simulation configurations involving nanostructures or nanostructured materials. This library exploits the Python API of the GMSH solver;
- A bridge component between fullwave solvers, geometric modeling modules and numerical optimization algorithms for the inverse design of nanostructures. This component integrates shape parameterization modules, but also scripts defining optimization workflows driving the use of statisticale learning-based global optimization algorithms from the Triese toolbox, which is built on TensorFlow and is dedicated to Bayesian optimization;
- A library of core modules for allowing users to define their own physical observables, e.g., total transmittance, volumic absorptance, scattering parameters, etc., form results of fullwave simulations.
The core library and the fullwave solvers are based on an object-oriented architecture implemented in Fortran 2008. The DGTD and HDGFD solvers are adapted to high performance computing platforms. Two levels of parallelization are currently exploited: a coarse-grained parallelization in distributed memory (between SMP computation nodes) combining a partitioning of the computation mesh and a parallel programming based on the message exchange model using the MPI standard.
This year several novel features have been developed that are concerned with the GFactory and Observer components (see Fog. 2).
|
8.8 Applications
8.8.1 Advanced modeling of nanostructured CMOS imagers based on DG methods
Participants: Jérémy Grebot, Stéphane Lanteri, Denis Rideau [STMicroelectronics, Crolles].
The exploitation of nanostructuring to improve the performance of CMOS imagers based on microlens grids is a very promising avenue. In this perspective, numerical modeling is a key component to accurately characterize the absorption properties of these complex imaging structures, which are intrinsically multiscale (from the micrometer scale of the lenses to the nanometric characteristics of the nanostructured material layers). The FDTD (Finite Difference Time-Domain) method is the solution adopted in the first instance for the simulation of the interaction of light with this type of structure. However, because FDTD is based on a Cartesian mesh, this method shows limitations when it comes to accurately account for complex geometric features such as the curvature of microlenses or the texturing of material layer surfaces. In this context of the PhD of Jérémy Grebot, our main objectives are (1) to leverage locally refined meshes with a high order DGTD method for modeling the propagation of light in a nanostructured CMOS imager and, (2) to study and optimize the impact of nanostructuring for improving light absorption. In particular, for what concern the second objective, an inverse design methodology combining a high order DGTD method with a statistical learning-based global optimization algorithm is developed for studying various nanostructuring patterns of the surface of the absorbing semiconductor material such as one- and two-dimensional gratings.
8.8.2 Nanoimprint color filter metasurface for imaging devices
Participants: David Grosso [Institut Matériaux Microélectronique Nanosciences de Provence (IM2NP) Aix-Marseille Université and Solnil], Marco Abbarchi [Institut Matériaux Microélectronique Nanosciences de Provence (IM2NP) Aix-Marseille Université and Solnil], Badre Kerzabi [Solnil], Mahmoud Elsawy, Alexis Gobé, Stéphane Lanteri.
Due to the rapid growth of metasurface applications, several manufacturing techniques have been developed in the past few years. Among them, NanoImprint Lithography (NIL) has been considered as a promising fabrication possibility for metasurface. NIL can achieve features below 100 nm without the need for complex and expensive optics and light sources needed to achieve similar resolutions in advanced photolithography. Yet, despite the advantages of this fabrication procedure, it has some limitations related to the dimensions of the single nanoresonators. In other words, the fabrication constraints related to the aspect ratio (ratio between height and width) is important. Typically, a maximum aspect ratio of 2 can be considered in such a technique. In this work, together with our collaborators from IM2NP, Aix-Marseille Université and the Solnil startup who are specialists in nanoimprint technology, we aim at optimizing a low cost colour filtering metasurface for imaging applications taking into account all the fabrication constraints. The main goal of this study is to deploy our optimization methodology to maximize the efficiency of such metasurface configuration. Various shapes with different physical mechanisms have been investigated It is worth mentioning that in this study various shapes have been optimized and studied numerically, yet, as a starting point for the fabrication, the cylindrical pillars will be considered as a first illustration for the nanoimprint fabrication.
8.8.3 Optimization of light trapping in nanostructured solar cells
Participants: Stéphane Collin [Sunlit team, C2N-CNRS, Paris-Saclay], Alexis Gobé, Stéphane Lanteri.
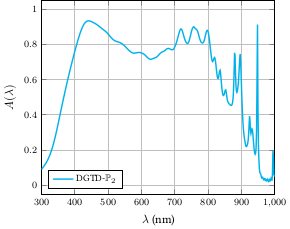
There is significant recent interest in designing ultrathin crystalline silicon solar cells with active layer thickness of a few micrometers. Efficient light absorption in such thin films requires both broadband antireflection coatings and effective light trapping techniques, which often have different design considerations. In collaboration with physicists from the Sunlit team at C2N-CNRS, We exploit statistical learning methods for the inverse design of material nanostructuring with the goal of optimizing light trapping properties of ultraphin solar cells. This objective is challenging because the underlying electromagnetic wave problems exhibit multiple resonances, while the geometrical settings are non-trivial. Such multi-resonant solar cell structures are attractive for maximizing light absorption for the full solar light spectrum as illustrated in Fig. 3. We exploit statistical learning methods for the inverse design of material nanostructuring with the goal of optimizing light trapping properties of ultraphin solar cells. This study is conducted in collaboration with the Sunlit headed by Stéphane Collin at the Center for Nanoscience and Nanotechnology (C2N, CNRS).

|
|
8.8.4 Plasmonic sensing with nanocubes
Participants: Antoine Moreau [Institut Pascal, Clermont-Ferrand], Stéphane Lanteri, Guillaume Leroy, Claire Scheid.
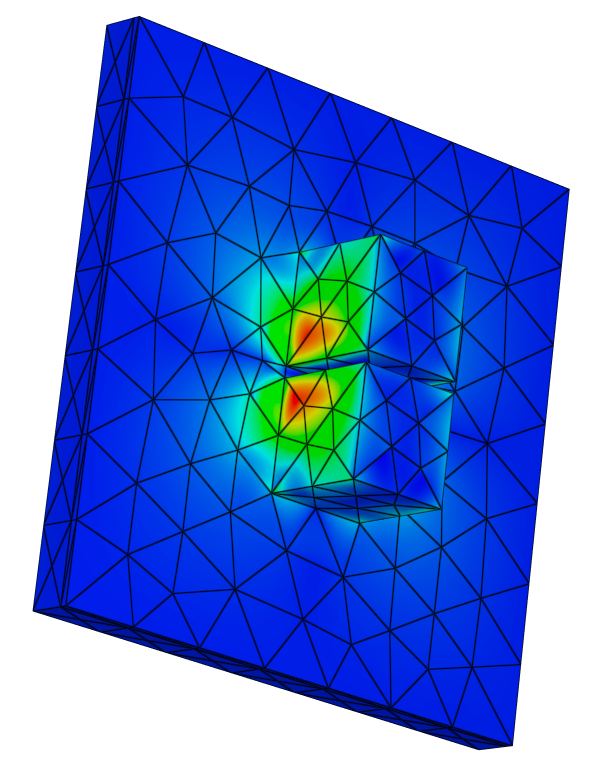
The propagation of light in a slit between metals is known to give rise to guided modes. When the slit is of nanometric size, plasmonic effects must be taken into account, since most of the mode propagates inside the metal. Indeed, light experiences an important slowing-down in the slit, the resulting mode being called gap-plasmon. Hence, a metallic structure presenting a nanometric slit can act as a light trap, i.e. light will accumulate in a reduced space and lead to very intense, localized fields. We study the generation of gap plasmons by various configurations of silver nanocubes separated from a gold substrate by a dielectric layer, thus forming a narrow slit under the cube. When excited from above, this configuration is able to support gap-plasmon modes which, once trapped, will keep bouncing back and forth inside the cavity. We exploit statistical learning methods for the goal-oriented inverse design of cube size, dielectric and gold layer thickness, as well as gap size between cubes in a dimer configuration. This study is conducted in collaboration with Antoine Moreau at Institut Pascal (CNRS).
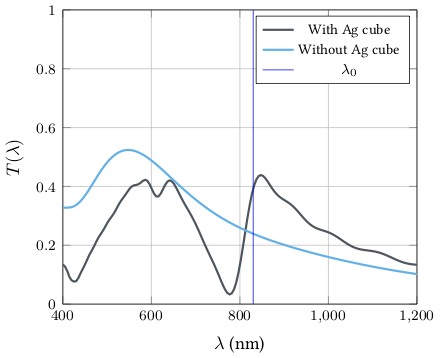
|
8.8.5 Multiple scattering in random media
Participants: Stéphane Descombes, Stéphane Lanteri, Guillaume Leroy, Cédric Legrand, Gian Luca Lippi [INPHYNI laboratory, Sophia Antipolis].
Fluorescence signals emitted by probes, used to characterize the expression of biological markers in tissues or cells, can be very hard to detect due to a small amount of molecules of interest (proteins, nucleic sequences), to specific genes expressed at the cellular level, or to the limited number of cells expressing these markers in an organ or a tissue. Access to information coming from weaker emitters can only come from strengthening the signal, since electronic post-amplification raises the noise floor as well. While costly and molecule-specific biochemical processes are being developed for this purpose, a new mechanism based on the simultaneous action of stimulated emission and multiple scattering, induced by nanoparticles suspended in the sample, has been recently demonstrated to effectively amplify weak fluorescence signals. A precise assessment of the signal fluorescence amplification that can be achieved by such a scattering medium requires a electromagnetic wave propagation modeling approach capable of accurately and efficiently coping with multiple space and time scales, as well as with non-trivial geometrical features (shape and topological organization of scatterers in the medium). In the context of a collaboration with physicists from the Institut de Physique de Nice INPHYNI (Gian Luca Lippi from the complex photonic systems and materials group), we initiated this year a study on the simultaneous action of stimulated emission and multiple scattering by randomly distributed nanospheres in a bulk medium. From the numerical modeling point of view, or short term goal is to develop a time-domain numerical methodology for the simulation of random lasing in a gain medium.

|
8.8.6 Nonlinear wavefront shaping with optical metasurfaces
Participants: Giuseppe Leo [MPQ, Université Paris Cité, France],, Jean-Michel Gerard [PHELIQS, CEA and Université Grenoble Alpes, France], Mahmoud Elsawy, Stéphane Lanteri.
In recent years, the control of subwavelength light-matter interactions has enabled the observation of new linear optical phenomena, further establishing a new class of ultra-thin devices for real-world applications. To extend metasurface functionality and implement nonlinear manipulations, the scientific community has considered optical metasurfaces for harmonic emission field control. However, the performance of nonlinear metasurfaces is still modest. Flat optics have also shown their potential in the nonlinear optics with wavefront shaping in far-harmonic fields. There is currently a related effort by the nonlinear nanophotonics community to seek higher conversion efficiencies across narrow resonances of the quasi-bound states of the continuum (qBIC) associated with strong near-field coupling and nonlocal resonance modes. However, the overall performance is relatively weak as most of the current studies ignore the strong near-field coupling between neighboring cells. In the context of a collaboration that has started in 2022 with the groups of Giuseppe Leo at the MPQ laboratory (Matériaux et Phénomènes Quantiques, CNRS UMR 7162, Université Paris Cité) and Jean-Michel Gerard at the PHELIQS laboratory (PHotonique, ELectronique et Ingénierie QuantiqueS, UMR-E of CEA and Université Grenoble Alpes), we exploit the specific advantages of thin resonators that behave like phased-array antennas, unlike photonic crystals with strong localized energies, to develop highly efficient nonlinear metasurfaces for nonlinear wavefront shaping. Within this strategy, we improve the performance of nonlinear wavefront shaping by inverse design optimization of both meta-atoms and meta-molecules. In addition, we consider long-term design options for nonlinear metasurfaces based on perfect nonlocal responses and long-range near-field coupling, and rigorous computational methods to address nonlinearities in terms of nonlocal configurations. Our preliminary results show the ability to improve the second harmonic generation signal by almost a factor of seven. Fabrication and characterization of the structure is currently underway, and the results will be published in a prominent journal.
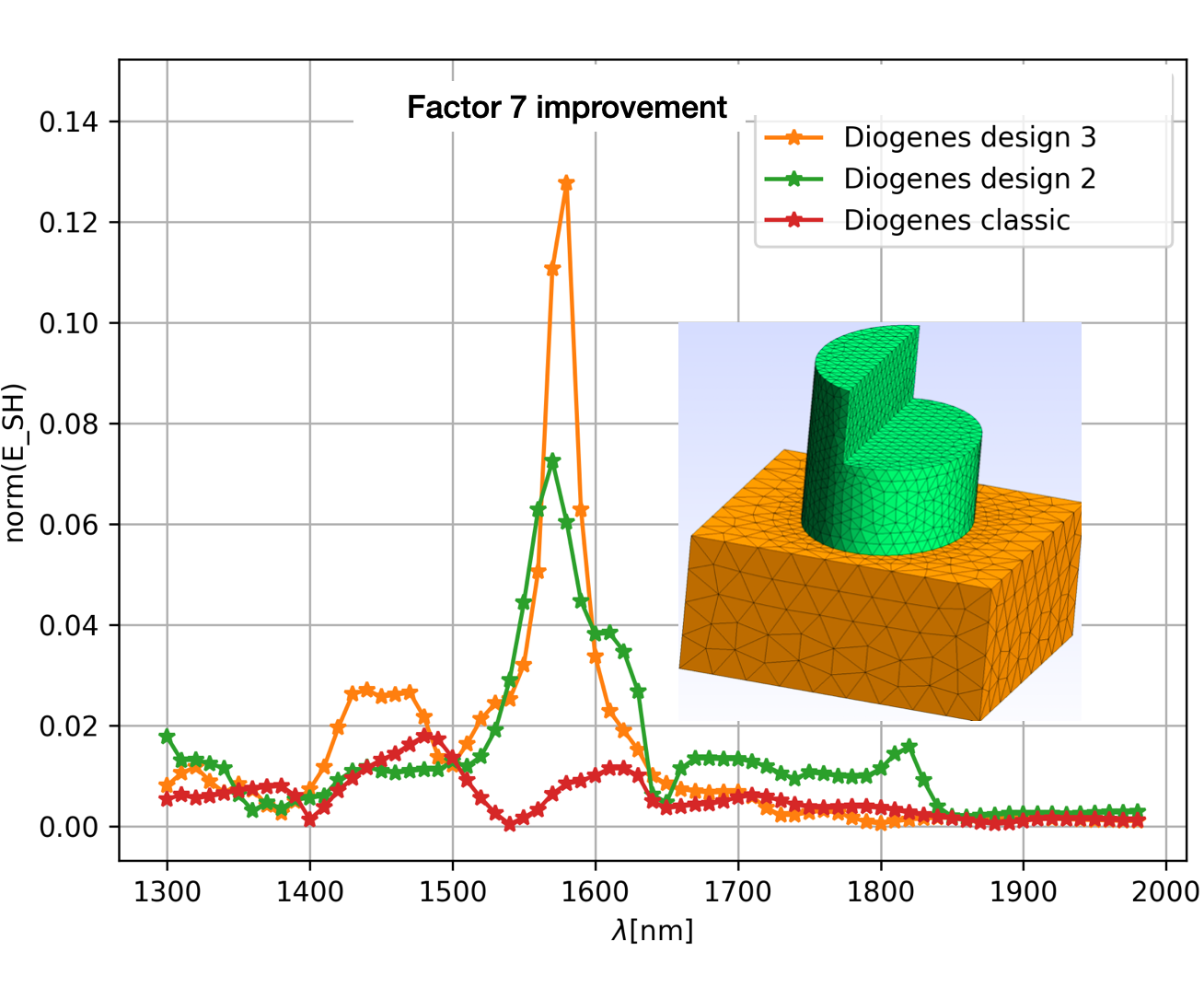
|
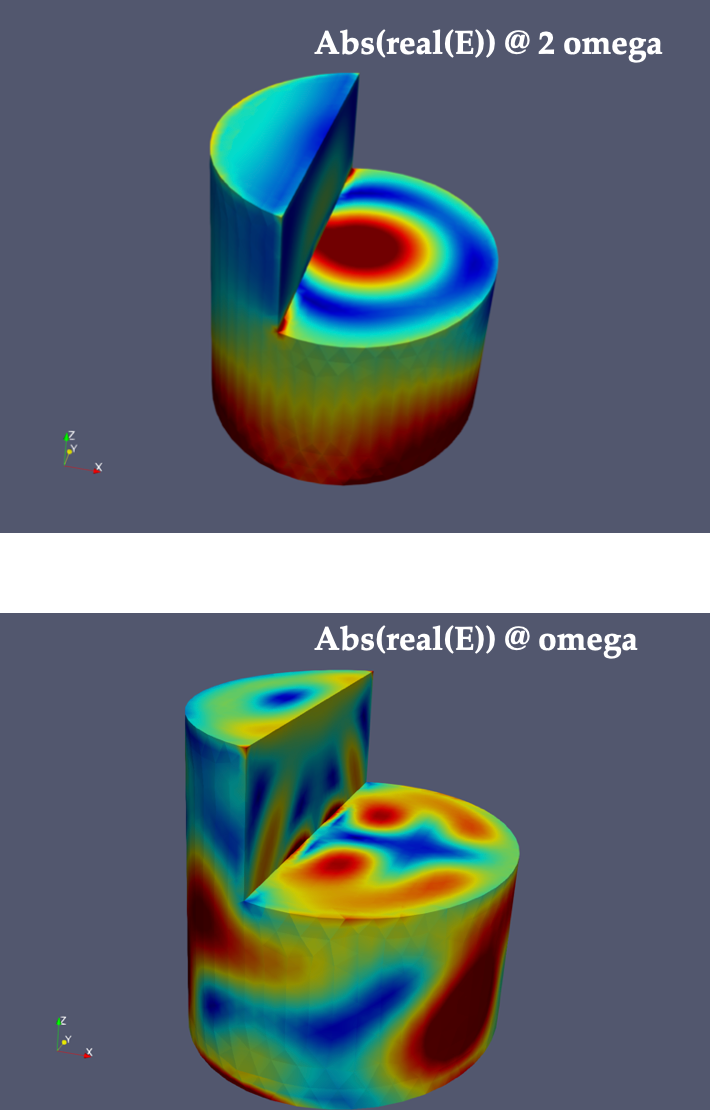
|
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
Nom: SEASIDE - numerical Study of mEtasurfAceS by Inverse DEsign
Participants: Mahmoud Elsawy, Alexis Gobé, Guillaume Leroy, Stéphane Lanteri.
- Duration: Sep 2022 - Aug 2023
- Local coordinator: Stéphane Lanteri
- Participants: Abbarchi, David Grosso and Badre Kerzabi [Solnil, Marseille]
- Solnil is a startup company launched in 2020. Its activities are concerned with the design, development, operation and provision of products, hardware, software services, automatons or complex machines, implementing innovative technologies resulting from research on processes for the nano-fabrication of sol-gel materials and in particular, the direct nano-printing of such materials for various applications in the fields of optics and optoelectronics. Solnil carries out research and development operations, as well as scientific and technical studies. The company's ambition is to exploit and industrialize a low-cost nano-fabrication process for optical applications. This process is an evolution of an existing technology, referred as nanoimprinting, which can be described as a molding process at sub-micrometer resolutions. The industrial applications of nanoimprinting are numerous today numerous: 3D measurements for recognition, DNA sequencing augmented reality glasses, anti-reflection films, LED sources etc. In the present project, which a first step toward a longer term partnership, we resort to numerical modeling for the optimal design of metasurface-based multispectral sensors.
Nom: DGTD solvers for semiconductor device modeling
Participants: Mahmoud Elsawy, Massimiliano Montone, Claire Scheid.
- Duration: Nov 2019-Jan 2023
- Local coordinator: Stéphane Lanteri
- Participants: Eric Guichard [Silvaco Inc., Santa Clara, USA], Massimiliano Montone, Claire Scheid, Slim Chourou [Silvaco Inc., Santa Clara, USA], Mark Townsend [Silvaco Inc., Santa Clara, USA]
- This contract with the TCAD division of Silvaco Inc. is closely linked to the PhD project of Massimiliano Montone and is concerned with the numerical modeling of semiconductor-based photonic devices using high order DGTD methods. More precisely, the main methodological objective of the PhD project is to design, analyze and develop DG-based approaches for solving the system of time-domain Maxwell equations coupled to the unsteady drift-diffusion equations in 3D. On the application side, in close collaboration with Silvaco Inc., microLEDs and CMOS image sensors will constitute the driving technologies for the application of the methodological developments achieved in the PhD work; moreover, Nanostructured solar cells and photoconductive antennas (including hybrid photoconductive antennas leveraging plasmonic effects) will serve as more prospective applications that will possibly be considered in collaboration with physicists from academic groups, which are partners of the ATLANTIS project-team.
9.2 Grants with industry
Nom: DGTD solvers for modeling light absorption in CMOS imagers
Participants: Alexis Gobé, Jérémy Grebot, Guillaume Leroy, Stéphane Lanteri.
- Duration: Jan 2019-Jun 2023
- Local coordinator: Stéphane Lanteri
- Participants: Marios Barlas [STMicroelectronics, Crolles], Alexis Gobé, Valentin Goblot [STMicroelectronics, Crolles], Jérémy Grebot, Denis Rideau [STMicroelectronics, Crolles], Guillaume Leroy, Claire Scheid
- This grant is part of the Nano 2022 IPCEI (Important Projects of Common European Interest) program, which involves several european industrial groups and companies in the microelectronics field. The team is involved in a subproject conducted in close collaboration with STMicrolectronics (CMOS Imagers division of the Technology for Optical Sensors department) in Crolles. The exploitation of nanostructuring to improve the performance of CMOS imagers based on microlens grids is a very promising path. In this perspective, numerical modeling is a key component to accurately characterize the absorption properties of these complex imager structures that are intrinsically multiscale (from the micrometer scale of lenses to the nanometric characteristics of nanostructured layers of materials). The FDTD method (for Finite Difference Time-Domain) is the solution adopted in the first instance for the numerical simulation of the interaction of light with this type of structure. However, because it is based on a Cartesian mesh (mostly uniform structured mesh), this method has limitations when it comes to accurately account for complex geometrical features such as microlens curvature or texturing of material layer surfaces. In this context, the main objective of our study is to take advantage of the possibilities offered by the DGTD method with realistic geometric models of complex imager structures based on locally refined tetrahedral meshes.
10 Partnerships and cooperations
10.1 International initiatives
10.1.1 STIC/MATH/CLIMAT AmSud projects
EOLIS
-
Title:
Efficient Off-Line numerical Strategies for multi-query problems
-
Program:
MATH-AmSud
-
Duration:
Jan 2021 - Dec 2022
-
Local supervisor:
Theophile Chaumont-Frelet
-
Partners:
- LNCC, Brazil
- Universidad de Concepción, Chile (UdeC), Chile
- Universidad Católica de la Santísima Concepción (USCS), Chile
- Inria, Fance
-
Inria contact:
Theophile Chaumont-Frelet
-
Summary:
This project is concerned with the design, anlysis and implementation of novel preprocessing and postprocessing strategies for solving multi-query partial differential equation problems with finite element methods. By multi-query, we mean applications, such as inverse problems, optimal design or uncertainty quantification, that require a set of solution to the related PDE problems with different parameters. Instead of focusing on one particular PDE solve, we strive to reduce the computational cost for the whole set of PDE problems and focus on three main strategies: -adaptivity, multiscale modelling, and preconditioning. The design of nanostructures for light manipulation and the quantification of uncertainties associated with media fields on fluid flows will be the main benchmarks we consider.
10.2 International research visitors
10.2.1 Visits of international scientists
Inria International Chair
- Frédéric Valentin from LNCC, Petropolis, Brasil, is holding an Inria International Chair from January 2018 until May 2023. He is currently visiting the team (since October 2021 and until February 2023).
10.3 European initiatives
10.3.1 H2020 projects
EPEEC (European joint effort toward a highly productive programming environment for heterogeneous exascale computing)
Participants: Alexis Gobé, Stéphane Lanteri.
- Type: H2020
- Link
- Duration: Oct 2018 - Mar 2022
- Coordinator: Barcelona Supercomputing Center
- Partner: Barcelona Supercomputing Center (Spain)
- Coordinator: CEA
- Partners:
- Fraunhofer–Gesellschaft (Germany)
- CINECA (Italy)
- IMEC (Blegium)
- INESC ID (Portugal)
- Appentra Solutions (Spain)
- Eta Scale (Sweden)
- Uppsala University (Sweden)
- Inria (France)
- Cerfacs (France)
- Inria contact: Stéphane Lanteri
- EPEEC’s main goal is to develop and deploy a production-ready parallel programming environment that turns upcoming overwhelmingly-heterogeneous exascale supercomputers into manageable platforms for domain application developers. The consortium will significantly advance and integrate existing state-of-the-art components based on European technology (programming models, runtime systems, and tools) with key features enabling 3 overarching objectives: high coding productivity, high performance, and energy awareness. An automatic generator of compiler directives will provide outstanding coding productivity from the very beginning of the application developing/porting process. Developers will be able to leverage either shared memory or distributed-shared memory programming flavours, and code in their preferred language: C, Fortran, or C++. EPEEC will ensure the composability and interoperability of its programming models and runtimes, which will incorporate specific features to handle data-intensive and extreme-data applications. Enhanced leading-edge performance tools will offer integral profiling, performance prediction, and visualisation of traces. Five applications representative of different relevant scientific domains will serve as part of a strong inter-disciplinary co-design approach and as technology demonstrators. EPEEC exploits results from past FET projects that led to the cutting-edge software components it builds upon, and pursues influencing the most relevant parallel programming standardisation bodies.
RISC2 (A network for supporting the coordination of High-Performance Computing research between Europe and Latin America)
Participants: Luc Giraud [HIEPACS project-team, Inria Bordeaux - Sud-Ouest], Stéphane Lanteri, Patrick Valduriez [ZENITH project-team].
- Type: H2020 (Coordinated Support Action)
- Link.
- Duration: Jan 2021 - Jun 2023
- Coordinator: Barcelona Supercomputing Center
- Partners:
- Forschungzentrum Julich GMBH (Germany)
- Inria (France)
- Bull SAS (France)
- INESC TEC (Portugal)
- Universidade de Coimbra (Portugal)
- CIEMAT (Spain)
- CINECA (Italy)
- Universidad de Buenos Aires (Argentina)
- Universidad Industrial de Santander (Columbia)
- Universidad de le Republica (Uruguay)
- Laboratorio Nacional de Computacao Cientifica (Brazil)
- Centro de Investigacion y de Estudios Avanzados del Instituto Politecnico Nacional (Mexico)
- Universidad de Chile (Chile)
- Fundacao Coordenacao de Projetos Pesquisas e Estudos Tecnologicos COPPETEC (Brazil)
- Fundacion Centro de Alta Tecnologia (Costa Rica)
- Inria contact: Stéphane Lanteri
- Recent advances in AI and the Internet of things allow high performance computing (HPC) to surpass its limited use in science and defence and extend its benefits to industry, healthcare and the economy. Since all regions intensely invest in HPC, coordination and capacity sharing are needed. The EU-funded RISC2 project connects eight important European HPC actors with the main HPC actors from Argentina, Brazil, Chile, Colombia, Costa Rica, Mexico and Uruguay to enhance cooperation between their research and industrial communities on HPC application and infrastructure development. The project will deliver a cooperation roadmap addressing policymakers and the scientific and industrial communities to identify central application areas, HPC infrastructure and policy needs.
10.4 National initiatives
10.4.1 ANR project
OPERA (Adpative planar optics)
Participants: Emmanuel Agullo [HIEPACS project-team, Inria Bordeaux - Sud-Ouest], Régis Duvigneau [ACUMES project-team], Mahmoud Elsawy, Patrice Genevet [CRHEA laboratory, Sophia Antipolis], Luc Giraud [HIEPACS project-team, Inria Bordeaux - Sud-Ouest], Stéphane Lanteri.
- Type: ANR ASTRID Maturation
- See also: www-sop.inria.fr/nachos/opera
- Duration: Apr 2019 to Sep 2022
- Coordinator: Inria
- Partner: CRHEA laboratory in Sophia Antipolis and NAPA Technologies in Archamps
- Inria contact: Stéphane Lanteri
- Abstract: In the OPERA project, we are investigating and optimizing the properties of planar photonic devices based on metasurfaces using numerical modelling. The scientific and technical activities that constitute the project work programme are organized around 4 main workpackages. The numerical characterization of the optical properties of planar devices based on metasurfaces, as well as their optimization are at the heart of the activities and objectives of two horizontal (transversal) workpackages. These numerical methodologies will be integrated into the DIOGENeS software framework that will eventually integrates (1) discontinuous Galerkin-type methods that have been tested over the past 10 years for the discretization of Maxwell equations in time and frequency regimes, mainly for applications in the microwave band, (2) parallel resolution algorithms for sparse linear systems based on the latest developments in numerical linear algebra, (3) modern optimization techniques based on learning and metamodeling methods and (4) software components adapted to modern high performance computing architectures. Two vertical workpackages complete this program. One of them aims to demonstrate the contributions of methodological developments and numerical tools resulting from transversal workpackages through their application to diffusion/radiation control by passive planar devices. The other, more prospective, concerns the study of basic building blocks for the realization of adaptive planar devices.
11 Dissemination
11.0.2 Scientific events: organisation
General chair, scientific chair
- Théophile Chaumont-Frelet has chaired the Journés Singulières 2022, November 2-4, 2022, Université Côte d'Azur
Member of the organizing committees
- Claire Scheid has been member of Scientific Commitee of the Waves2022, the 15th Conference on Mathematical and Numerical Aspects of Wave Propagation, July 25-29 2022, Palaiseau, France
- Mahmoud Elsawy and Stéphane Lanteri have been involved in the organizing committee of the AI4Waves workshop AI4Waves, October 10-12, 2022, Inria Research Center at Université Côte d’Azur
- Stéphane Lanteri has been involved in the organizing committee of the 2nd Colloquium on Physics and Applications of Metasurfaces, July 18-22, 2022, Firenze, Italy
- Stéphane Lanteri and Frédéric Valentin have been involved in the organizing committee of the workshop on HPC and Data Sciences meet Scientific Computing during the 2022 Latin America High Performance Computing Conference CARLA 2022, Porto Alegre, Brazil, from September 26-30, 2022.
- Théophile Chaumont-Frelet has been involved in the organizing committee of Journés Ondes JCJC Ondes 2022, November 28-30, 2022, Inria Research Center at Université Côte d'Azur
- Théophile Chaumont-Frelet has co-organized with Markus Melenk (TU Wien, Austria) the minisymposium entitled "Discretization methods for indefinite wave propagation problems" at CRC 1173 - Understanding Wave Phenomena, February 14-18, 2022, Karlsruhe Institute of Technology, Germany
- Théophile Chaumont-Frelet has been involved in the organizing committee of the minisymposium "Robust and scalable numerical methods for wave propagation in heterogeneous media: design, analysis and application" at ECCOMAS 2022, June 5-9, 2022, Oslo, Norway
11.0.3 Journal
Reviewer - reviewing activities
- Stéphane Lanteri: Journal of Computational Physics, SMAI Journal of Computational Mathematics
- Théophile Chaumont-Frelet: IMA Journal of Numerical Analysis, SIAM Journal on Numerical Analysis, Mathematics of Computation
- Claire Scheid: IMA Journal of Numerical Analysis
11.0.4 Invited talks
- "Universal active metasurface modulation with ultimate performance in reflection", Mahmoud Elsawy, 2nd Colloquium on Physics and Applications of Metasurfaces, July 18-22, 2022, Firenze, Italy
- "Advanced numerical modeling methods for the characterization and optimization of metasurfaces", Stéphane Lanteri, AT-AP-RASC 2022, 3rd URSI Atlantic and Asia Pacific Radio Science Meeting, Gran Canaria, Spain
- "A posteriori error estimation via flux equilibration for magnetostatic problems", Théophile Chaumont-Frelet, CEA-EDF-Inria summer school on "Certification of errors in numerical simulations", EDF Lab, Paris-Saclay, June 27–July 1st, 2022
- "Scattering by finely-layered obstacles: frequency-explicit stability and homogenization", Théophile Chaumont-Frelet, CRC 1173 - Understanding Wave Phenomena, February 14-18, 2022, Karlsruhe Institute of Technology, Germany
- "Efficient a posteriori estimates for the wave equation", Théophile Chaumont-Frelet, European Finite Element Fair 2022, June 3-4, Aalto University, Espoo, Finland
- "A multiscale hybrid-mixed method for Helmholtz problems in periodic structures", Théophile Chaumont-Frelet, ECCOMAS 2022, June 5-9, 2022, Oslo, Norway
- "Efficient approximation of high-frequency Helmholtz solutions by Gaussian coherent states", Théophile Chaumont-Frelet, Computational Methods in Applied Mathematics (CMAM 2022), TU Wien, August 29- September 2, 2022
11.0.5 Leadership within the scientific community
Research administration
- Yves D'Angelo: head of the J.A. Dieudonné Mathematics Laboratory
- Stéphane Descombes: director of the “Maison de la Modélisation, de la Simulation et des Interactions” (MSI) at Université Côte d'Azur
- Stéphane Lanteri: member of the Project-team Committee's Bureau of the Inria research center at Université Côte d'Azur
- Stéphane Lanteri: Deputy Head of Science of Inria Research Center at Université Côte d'Azur (since September 2022)
- Stéphane Lanteri: member of Evaluation Committee of Inria (since September 2022)
- Stéphane Lanteri: member of the Scientific Committee of the Wavecomplexity initiative at Université Côte d'Azur
- Stéphane Lanteri: member of the “Comité de Chercheurs Calculant au CINES”
11.1 Teaching - Supervision - Juries
11.1.1 Teaching
- Claire Scheid, EDP et Différences finies, Practical works, Master 1 MPA, 18h, Université Côte d'Azur
- Claire Scheid, Optimisation et éléments finis. Lecture, practical works, M1 MPA and IM, 72h eq.TD, Université Côte d'Azur
- Claire Scheid, Option modélisation. Lectures and practical works, M2 Agrégation, 45h eq.TD, Université Côte d'Azur
- Claire Scheid, Approximation Numérique des fonctions, intégrales et équations différentielles. Lecture, L3, 56h, Université Côte d'Azur
- Yves D'Angelo, Modélisation Simulation Numérique, Master 1 IM/MPA, 50 h, Université Côte d'Azur
- Yves D'Angelo, Modélisation de la Turbulence dans l'Industrie, Master 1 MPA and IM, 16 h, Université Côte d'Azur
- Stéphane Descombes, Introduction to partial differential equations Master 1 MPA and IM, 30 h, Université Côte d'Azur
- Stéphane Descombes, Principal component analysis and supervised analysis, Master 2 SIRIS, Université Côte d'Azur
- Stéphane Descombes, Mathematics practical works, L1 SocioEco, 18 h, Université Côte d'Azur
- Engineering: Stéphane Lanteri, High performance scientific computing, 24 h, MAM5, Polytech Nice Sophia - Université Côte d'Azur
11.1.2 Supervision
- PhD in progress: Jérémy Grebot, Advanced modeling of nanostructured CMOS imagers, Stéphane Lanteri and Claire Scheid
- PhD in progress: Enzo Isnard, Modeling and optimization of freeform optical metasurfaces integrated to an imaging system, Mahmoud Elsawy and Stéphane Lanteri
- PhD in progress: Zakaria Kassali, Multiscale finite element simulations applied to the design of photovoltaic cells, Théophile Chaumont-Frelet and Stéphane Lanteri
- PhD in progress: Cédric Legrand, High order finite element type solvers for modeling gain media, Stéphane Descombes and Stéphane Lanteri
- PhD in progress: Thibault Laufroy, High order finite element type solvers for thermoplamonics, Yves d'Angelo and Claire Scheid
- PhD in progress: Martin Leppers, Microlenses based on metasurfaces for image sensor pixels, Patrice Genevet (CRHEA, Sophia Antipolis) and Stéphane Lanteri
- PhD in progress: Massimiliano Montone, High order finite element type solvers for the coupled Maxwell-semiconductor equations in the time-domain, Stéphane Lanteri and Claire Scheid
- PhD in progress: Florentin Proust, Novel finite element methods for dealing with high frequency wave propagation problems, Maxime Ingremeau (Université Côte d'Azur, LJAD) and Théophile Chaumont-Frelet
11.1.3 Juries
- Stéphane Lanteri was a reviewer and a member of the PhD defense committee of Philippe Marchner, Université de Lorraine et Université de Liège, June 16, 2022
- Stéphane Lanteri was a reviewer and a member of the PhD defense committee of Pauline Bennet, Université Clermont Auvergne, November 8, 2022
- Stéphane Lanteri was a member of the PhD defense committee of Yanfei Xiang, Université de Bordeaux, December 8, 2022
- Stéphane Lanteri was a reviewer and a member of the PhD defense committee of Margot Sirdey, Université de Pau et des Pays de l'Adour, December 19, 2022
- Claire Scheid was a member of the PhD committee of Akram Beni Hamad, ENSTA, Institut Polytechnique de Paris, September 30, 2022
- Claire Scheid was a reviewer of the PhD and a member of the PhD committee of Anthony Nahas, Lille University, France, October 11, 2022
12 Scientific production
12.1 Major publications
- 1 articleHigh order HDG method and domain decomposition solvers for frequency‐domain electromagnetics.International Journal of Numerical Modelling: Electronic Networks, Devices and FieldsOctober 2019
- 2 unpublishedOn the derivation of guaranteed and p-robust a posteriori error estimates for the Helmholtz equation.August 2020, working paper or preprint
- 3 articleLocally implicit discontinuous Galerkin time domain method for electromagnetic wave propagation in dispersive media applied to numerical dosimetry in biological tissues.SIAM Journal on Scientific Computing3852016, A2611-A2633
- 4 articleTemporal convergence analysis of a locally implicit discontinuous galerkin time domain method for electromagnetic wave propagation in dispersive media.Journal of Computational and Applied Mathematics316May 2017, 122--132
- 5 articleOptimization of metasurfaces under geometrical uncertainty using statistical learning.Optics Express29192021, 29887
- 6 articleMultiobjective statistical learning optimization of RGB metalens.ACS photonics88July 2021, 2498–2508
- 7 articleGlobal optimization of metasurface designs using statistical learning methods.Scientific Reports91November 2019
- 8 articleAnalysis of a Generalized Dispersive Model Coupled to a DGTD Method with Application to Nanophotonics.SIAM Journal on Scientific Computing393January 2017, A831 - A859
- 9 articleA reduced-order discontinuous Galerkin method based on a Krylov subspace technique in nanophotonics.Applied Mathematics and Computation358October 2019, 128-145
- 10 articleNon-intrusive reduced-order modeling of parameterized electromagnetic scattering problems using cubic spline interpolation.Journal of Scientific Computing872May 2021
- 11 articlePOD-based model order reduction with an adaptive snapshot selection for a discontinuous Galerkin approximation of the time-domain Maxwell's equations.Journal of Computational Physics396November 2019, 106-128
- 12 articleA hybridizable discontinuous Galerkin method combined to a Schwarz algorithm for the solution of 3d time-harmonic Maxwell's equations.Journal of Computational Physics256January 2014, 563-581
- 13 articleA DGTD method for the numerical modeling of the interaction of light with nanometer scale metallic structures taking into account non-local dispersion effects.Journal of Computational Physics316July 2016
- 14 articleSimulation of three-dimensional nanoscale light interaction with spatially dispersive metals using a high order curvilinear DGTD method.Journal of Computational Physics373November 2018, 210-229
12.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Reports & preprints
Other scientific publications
12.3 Cited publications
- 44 articleBlock GMRES method with ineact breackdowns and deflated restarting.SIAM J. Matrix Anal. Appl.3542014, 1625--1261
- 45 bookThermoplasmonics.Cambridge University Press2017
- 46 articlePlasmonics for pulsed-laser cell nanosurgery: fundamentals and applications.J. Photochem. Photobiol. C: Photochem. Rev.172013, 26--49
- 47 articleAtomic layer lithography of wafer-scale nanogap arrays for extreme confinement of electromagnetic waves.Nature Comm.42013, 2361
- 48 articleA review of metasurfaces: physics and applications.Rep. Progr. Phys.7972016, 076401
- 49 articleProbing the ultimate limits of plasmonic enhancement.Science33760982012, 1072--1074
- 50 articleHydrodynamic model for plasmonics: a macroscopic approach to a microscopic problem.Chemphyschem1462013, 1109--1116
- 51 articleInfluence of spatial dispersion in metals on the optical response of deeply subwavelength slit arrays.Phys. Rev. B9342016, 045413
- 52 articleGradient metasurfaces: a review of fundamentals and applications.Rep. Progr. Phys.8122018, 026401
- 53 articleKriging-based optimization applied to flow control.Int. J. Num. Fluids692012, 1701--1714
- 54 articleComparison of turbulence closures for optimized active control.Comput. Fluids1242016, 67--77
- 55 articleConvergence and stability of a discontinuous Galerkin time-domain method for the 3D heterogeneous Maxwell equations on unstructured meshes.ESAIM: Math. Model. Num. Anal.3962005, 1149--1176
- 56 bookIntroduction to nanophotonics.Cambridge University Press2010
- 57 articleHolographic optical metasurfaces: a review of current progress.Rep. Progr. Phys.7822015, 024401
- 58 articleUncertainty quantification guided robust design for nanoparticles morphology.Comp. Meth. Appl. Mech. Engrg.893362018, 578--593
- 59 articleLuminescence nanothermometry.Nanoscale4152012, 4301-4326
- 60 articleEnhancement of terahertz photoconductive antenna operation by optical nanoantennas.Laser Phot. Rev.1112017, 1600199
- 61 bookPlasmonics - Fundamentals and applications.Springer2007
- 62 bookIntroduction to nanoelectronics.Cambridge University Press2012
- 63 articleInverse design in nanophotonics.Nat. Phot.122018, 659--670
- 64 articleOptimum morphology of gold nanorods for light-induced hyperthermia.Nanoscale1052018, 2632--2638
- 65 articleTime-domain numerical modeling of THz photoconductive antennas.IEEE Trans. Terah. Sci. Technol.442014, 490--500
- 66 articleInverse design of large-area metasurfaces.Opt. Expr.26262018, 33732--33747
- 67 articleSparse supernodal solver using block low-rank compression: design performance and analysis.J. Comp. Sci.272018, 255--270
- 68 articlePhysics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations.J. Comput. Phys.3782019, 686--707
- 69 articleEfficient optimization procedure in non-linear fluid-structure interaction problem: application to mainsail trimming in upwind conditions.J. Fluids and Struct.692017, 209--231
- 70 phdthesisHigh order simulation and calibration strategies for spatial dispersion models in nanophotonics.University of Nice-Sophia Antipolis2018
- 71 articleLarge area metalenses: design, characterization, and mass manufacturing.Opt. Expr.262018, 1573--1585
- 72 articleIntelligent nanophotonics: merging photonics and artificial intelligence at the nanoscale.Nanophot.832019, Open AccessURL: https://doi.org/10.1515/nanoph-2018-0183
- 73 articleContribution assessment of antenna structure and in-gap photocurrent in terahertz radiation of photoconductive antenna.J. Appl. Phys.1242018, 053107

