Keywords
Computer Science and Digital Science
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.5. Numerical Linear Algebra
- A6.2.6. Optimization
- A6.3.1. Inverse problems
- A6.3.4. Model reduction
- A6.4.3. Observability and Controlability
- A6.4.4. Stability and Stabilization
- A6.4.5. Control of distributed parameter systems
- A6.5.4. Waves
- A8.2. Optimization
- A8.3. Geometry, Topology
- A8.4. Computer Algebra
Other Research Topics and Application Domains
- B1.2.3. Computational neurosciences
- B2.6.1. Brain imaging
- B3.1. Sustainable development
- B3.3. Geosciences
- B4.5. Energy consumption
1 Team members, visitors, external collaborators
Research Scientists
- Juliette Leblond [Team leader, INRIA, Senior Researcher, HDR]
- Laurent Baratchart [INRIA, Emeritus, from Sep 2022, HDR]
- Laurent Baratchart [INRIA, Senior Researcher, until Aug 2022, HDR]
- Sylvain Chevillard [INRIA, Researcher]
- Martine Olivi [INRIA, Researcher, HDR]
- Dmitry Ponomarev [INRIA, ISFP, from Oct 2022]
Post-Doctoral Fellow
- Cristóbal Villalobos Guillén [INRIA]
PhD Students
- Paul Asensio [INRIA]
- Masimba Nemaire [UNIV BORDEAUX]
- Anass Yousfi [UNIV COTE D'AZUR, from Oct 2022]
Interns and Apprentices
- Anass Yousfi [INRIA, until Sep 2022]
Administrative Assistant
- Florence Barbara [INRIA, part time in the team]
External Collaborators
- Vanna Lisa Coli [UNIV COTE D'AZUR]
- Adam Simon Cooman [IMEC, Leuven, Belgium]
- Jean-Paul Marmorat [ENSMP, CMA, Sophia Antipolis]
- Fabien Seyfert [HighFSolutions, Nice]
2 Overall objectives
The team develops constructive, function-theoretic approaches to inverse problems arising in modeling and design, in particular for electro-magnetic systems as well as in the analysis of certain classes of signals.
Data typically consist of measurements or desired behaviors. The general thread is to approximate them by families of solutions to the equations governing the underlying system. This leads us to consider various interpolation and approximation problems in classes of rational and meromorphic functions, harmonic gradients, or solutions to more general elliptic partial differential equations (PDE), in connection with inverse potential problems. A recurring difficulty is to control the singularities of the approximants.
The mathematical tools pertain to complex and harmonic analysis, approximation theory, potential theory, system theory, differential topology, optimization and computer algebra. Targeted applications mostly concern non-destructive control from field measurements in medical engineering (source recovery in magneto/electro encephalography), paleomagnetism (determining the magnetization of rock samples), and since recently, obstacle identification (finding electrical characteristics of an object), for which an endeavor of the team is to develop algorithms resulting in dedicated software.
3 Research program
3.1 Introduction
Within the extensive field of inverse problems, much of the research by Factas deals with reconstructing solutions of classical elliptic PDEs from their boundary behavior. Perhaps the simplest example lies with harmonic identification of a stable linear dynamical system: the transfer-function can be evaluated at any point of the imaginary axis from the response to a periodic input at frequency . Since is holomorphic in the right half-plane, it satisfies there the Cauchy-Riemann equation , and recovering amounts to solve a Dirichlet problem which can be done in principle using, e.g., the Cauchy formula.
Practice is not nearly as simple, for is only measured pointwise in the pass-band of the system which makes the problem ill-posed 84. Moreover, the transfer function is usually sought in specific form, displaying the necessary physical parameters for control and design. For instance if is rational of degree , then where the are its poles and is a Dirac unit mass at . Thus, to find the domain of holomorphy (i.e., to locate the ) amounts to solve a (degenerate) free-boundary inverse problem, this time on the left half-plane. To address such questions, the team has developed a two-step approach as follows.
-
Step 1: To determine a complete model, that is, one which is defined at every frequency, in a sufficiently versatile function class (e.g., Hardy spaces). This ill-posed issue requires regularization, for instance constraints on the behavior at non-measured frequencies.
-
Step 2: To compute a reduced order model. This typically consists of rational approximation of the complete model obtained in step 1, or phase-shift thereof to account for delays. We emphasize that deriving a complete model in step 1 is crucial to achieve stability of the reduced model in step 2.
Step 1 relates to extremal problems and analytic operator theory, see Section 3.3.1. Step 2 involves optimization, and some Schur analysis to parametrize transfer matrices of given Mc-Millan degree when dealing with systems having several inputs and outputs, see Section 3.3.2. It also makes contact with the topology of rational functions, in particular to count critical points and to derive bounds, see Section 3.3.2. Step 2 raises further issues in approximation theory regarding the rate of convergence and the extent to which singularities of the approximant (i.e., its poles) tend to singularities of the approximated function; this is where logarithmic potential theory becomes instrumental, see Section 3.3.3.
Applying a realization procedure to the result of step 2 yields an identification procedure from incomplete frequency data which was first demonstrated in 92 to tune resonant microwave filters. Harmonic identification of nonlinear systems around a stable equilibrium can also be envisaged by combining the previous steps with exact linearization techniques from 42.
The previous example of harmonic identification quickly suggests a generalization of itself. Indeed, on identifying with , holomorphic functions become conjugate-gradients of harmonic functions, so that harmonic identification is, after all, a special case of a classical issue: to recover a harmonic function on a domain from partial knowledge of the Dirichlet-Neumann data; when the portion of boundary where data are not available is itself unknown, we meet a free boundary problem. This framework for 2-D non-destructive control was first advocated in 74 and subsequently received considerable attention. It makes clear how to state similar problems in higher dimensions and for more general operators than the Laplacian, provided solutions are essentially determined by the trace of their gradient on part of the boundary which is the case for elliptic equations 1 40, 95. Such questions are particular instances of the so-called inverse potential problem, where a measure has to be recovered from the knowledge of the gradient of its potential (i.e., the field) on part of a hypersurface (a curve in 2-D) encompassing the support of . For Laplace's operator, potentials are logarithmic in 2-D and Newtonian in higher dimensions. For elliptic operators with non constant coefficients, the potential depends on the form of fundamental solutions and is less manageable because it is no longer of convolution type. Nevertheless it is a useful concept bringing perspective on how problems could be raised and solved, using tools from harmonic analysis.
Inverse potential problems are severely indeterminate because infinitely many measures within an open set of produce the same field outside this set; this phenomenon is called balayage 83. In the two steps approach previously described, we implicitly removed this indeterminacy by requiring in step 1 that the measure be supported on the boundary (because we seek a function holomorphic throughout the right half-space), and by requiring in step 2 that the measure be discrete in the left half-plane (in fact: a finite sum of point masses ). The discreteness assumption also prevails in 3-D inverse source problems, see Section 4.2. Conditions that ensure uniqueness of the solution to the inverse potential problem are part of the so-called regularizing assumptions which are needed in each case to derive efficient algorithms.
To recap, the gist of our approach is to approximate boundary data by (boundary traces of) fields arising from potentials of measures with specific support. This differs from standard approaches to inverse problems, where descent algorithms are applied to integration schemes of the direct problem; in such methods, it is the equation which gets approximated (in fact: discretized).
Along these lines, Factas advocates the use of steps 1 and 2 above, along with some singularity analysis, to approach issues of nondestructive control in 2-D and 3-D 1, 51, 55. The team is currently engaged in the generalization to inverse source problems for the Laplace equation in 3-D, to be described further in Section 3.2.1. There, holomorphic functions are replaced by harmonic gradients; applications are to inverse source problems in neurosciences (in particular in EEG/MEG) and inverse problems in geosciences.
The approximation-theoretic tools developed by Factas to handle issues mentioned so far are outlined in Section 3.3. In Section 3.2 to come, we describe in more detail which problems are considered and which applications are targeted.
We also began to investigate inverse scattering problems of plane waves by obstacles (playing here the role of a source term), with partners at LEAT. Such problems are again governed by Maxwell's equations and, in the time-harmonic regime, these reduce to Helmholtz equations depending on the frequency of the plane wave. Such issues have applications to detection and identification of metal objects, and this is part of LEAT research program, but at this early stage our study has remained academic (see Section 7.4).
3.2 Range of inverse problems
3.2.1 Elliptic partial differential equations (PDE)
Participants: Paul Asensio, Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Masimba Nemaire, Dmitry Ponomarev, Cristóbal Villalobos Guillén, Anass Yousfi.
By standard properties of conjugate differentials, reconstructing Dirichlet-Neumann boundary conditions for a function harmonic in a plane domain, when these conditions are already known on a subset of the boundary, is equivalent to recover a holomorphic function in the domain from its boundary values on . This is the problem raised on the half-plane in step 1 of Section 3.1. It makes good sense in holomorphic Hardy spaces where functions are entirely determined by their values on boundary subsets of positive linear measure, which is the framework for Problem more precisely described in Section 3.3.1.Let , a sub-arc of , , and ; find a function such that and is of minimal norm in under this constraint.
Such issues naturally arise in nondestructive testing of 2-D (or 3-D cylindrical) materials from partial electrical measurements on the boundary. For instance, the ratio between the tangential and the normal currents (the so-called Robin coefficient) tells one about corrosion of the material. Thus, solving Problem where is chosen to be the response of some uncorroded piece with identical shape yields non destructive testing of a potentially corroded piece of material, part of which is inaccessible to measurements. This was an initial application of holomorphic extremal problems to non-destructive control 67, 69.
Studying Hardy spaces of conjugate Beltrami equations is another interesting topic. For Sobolev-smooth coefficients of exponent greater than 2, they were investigated in 5, 43. The case of the critical exponent 2 is treated in 39, which apparently provides the first example of well-posed Dirichlet problem in the non-strictly elliptic case: the conductivity may be unbounded or zero on sets of zero capacity and, accordingly, solutions need not be locally bounded. More importantly perhaps, the exponent 2 is also the key to a corresponding theory on very general (still rectifiable) domains in the plane, as coefficients of pseudo-holomorphic functions obtained by conformal transformation onto a disk are merely of -class in general, even if the initial problem deals with coefficients of -class for some . Such generalizations are now under study within the team, in collaboration with E. Pozzi (Saint Louis Univ., Missouri, USA) and E. Russ (Univ. J. Fourier, Grenoble), and fairly deep connections between the regularity of the conformal parametrization of the domain and the range of exponents for which the Dirichlet problem is solvable in were brought to light.
Generalized Hardy classes as above are used in 40 where we address the uniqueness issue in the classical Robin inverse problem on a Lipschitz domain of , , with uniformly bounded Robin coefficient, Neumann data and conductivity of Sobolev class , . We show that uniqueness of the Robin coefficient on a subset of the boundary, given Cauchy data on the complementary part, does hold in dimension , thanks to a unique continuation result, but needs not hold in higher dimension. In higher dimension, this raises an open issue on harmonic gradients, namely whether the positivity of the Robin coefficient is compatible with identical vanishing of the boundary gradient on a subset of positive measure.
The 3-D version of step 1 in Section 3.1 is another subject investigated by Factas: to recover a harmonic function (up to an additive constant) in a ball or a half-space from partial knowledge of its gradient. This prototypical inverse problem (i.e., inverse to the Cauchy problem for the Laplace equation) often recurs in electromagnetism. At present, Factas is involved with solving instances of this inverse problem arising in two fields, namely medical imaging, e.g., for electroencephalography (EEG) or magneto-encephalography (MEG), and paleomagnetism (recovery of rocks magnetization) 1, 47, see Section 7.1. The question is considerably more difficult than its 2-D counterpart, due mainly to the lack of multiplicative structure for harmonic gradients. Still, substantial progress has been made over the last years using methods of harmonic analysis and operator theory.
The team is further concerned with 3-D generalizations and applications to non-destructive control of step 2 in Section 3.1. A typical problem is here to localize inhomogeneities or defaults such as cracks, sources or occlusions in a planar or 3-dimensional object, knowing thermal, electrical, or magnetic measurements on the boundary. These defaults can be expressed as a lack of harmonicity of the solution to the associated Dirichlet-Neumann problem, thereby posing an inverse potential problem in order to recover them. In 2-D, finding an optimal discretization of the potential in Sobolev norm amounts to solve a best rational approximation problem, and the question arises as to how the location of the singularities of the approximant (i.e., its poles) reflects the location of the singularities of the potential (i.e., the defaults we seek). This is a fairly deep issue in approximation theory, to which the project Apics (predecessor of Factas2) contributed convergence results for certain classes of fields (expressed as Cauchy integrals over extremal contours for the logarithmic potential 7, 48, 66). Initial schemes to locate cracks or sources via rational approximation on planar domains were obtained this way 51, 55, 67. It is remarkable that finite inverse source problems in 3-D balls, or more general algebraic surfaces, can be approached using these 2-D techniques upon slicing the domain into planar sections 9, 52. More precisely, each section cuts out a planar domain, the boundary of which carries data which can be proved to match an algebraic function. The singularities of this algebraic function are not located at the 3-D sources, but are related to them: the section contains a source if and only if some function of the singularities in that section meets a relative extremum. Using bisection it is thus possible to determine an extremal place along all sections parallel to a given plane direction, up to some threshold which has to be chosen small enough that one does not miss a source. This way, we reduce the original source problem in 3-D to a sequence of inverse poles and branch-points problems in 2-D. This bottom line generates a steady research activity within Factas, and again applications are sought to medical imaging and geosciences, see Sections 4.2, 4.3 and 7.1.
Conjectures may be raised on the behavior of optimal potential discretization in 3-D, but answering them is an ambitious program still in its infancy.
3.2.2 Systems, transfer and scattering
Participants: Laurent Baratchart, Sylvain Chevillard, Adam Cooman, Martine Olivi, Fabien Seyfert.
Through contacts with CNES (French space agency), members of the team became involved in identification and tuning of microwave electromagnetic filters used in space telecommunications. The initial problem was to recover, from band-limited frequency measurements, physical parameters of the device under examination. The latter consists of interconnected dual-mode resonant cavities with negligible loss, hence its scattering matrix is modeled by a unitary-valued matrix function on the frequency line, say the imaginary axis to fix ideas. In the bandwidth around the resonant frequency, a modal approximation of the Helmholtz equation in the cavities shows that this matrix is approximately rational, of Mc-Millan degree twice the number of cavities.
This is where system theory comes into play, through the so-called realization process mapping a rational transfer function in the frequency domain to a state-space representation of the underlying system of linear differential equations in the time domain. Specifically, realizing the scattering matrix allows one to construct a virtual electrical network, equivalent to the filter, the parameters of which mediate in between the frequency response and the geometric characteristics of the cavities (i.e., the tuning parameters).
Hardy spaces provide a framework to transform this ill-posed issue into a series of regularized analytic and meromorphic approximation problems. More precisely, the procedure sketched in Section 3.1 goes as follows:
- infer from the pointwise boundary data in the bandwidth a stable transfer function (i.e., one which is holomorphic in the right half-plane), that may be infinite dimensional (numerically: of high degree). This is done by solving a problem analogous to in Section 3.2.1, while taking into account prior knowledge on the decay of the response outside the bandwidth, see 12 for details.
- A stable rational approximation of appropriate degree to the model obtained in the previous step is performed. For this, a descent method on the compact manifold of inner matrices of given size and degree is used, based on an original parametrization of stable transfer functions developed within the team 35, 12.
- Realizations of this rational approximant are computed. To be useful, they must satisfy certain constraints imposed by the geometry of the device. These constraints typically come from the coupling topology of the equivalent electrical network used to model the filter. This network is composed of resonators, coupled according to some specific graph. This realization step can be recast, under appropriate compatibility conditions 68, as solving a zero-dimensional multivariate polynomial system. To tackle this problem in practice, we use Gröbner basis techniques and continuation methods which team up in the Dedale-HF software (see Section 3.4.2).
Factas also investigates issues pertaining to design rather than identification. Given the topology of the filter, a basic problem in this connection is to find the optimal response subject to specifications that bear on rejection, transmission and group delay of the scattering parameters. Generalizing the classical approach based on Chebyshev polynomials for single band filters, we recast the problem of multi-band response synthesis as a generalization of the classical Zolotarev min-max problem for rational functions 34, 86. Thanks to quasi-convexity, the latter can be solved efficiently using iterative methods relying on linear programming. These were implemented in the software easy-FF. Currently, the team is engaged in the synthesis of more complex microwave devices like multiplexers and routers, which connect several filters through wave guides. Schur analysis plays an important role here, because scattering matrices of passive systems are of Schur type (i.e., contractive in the stability region). The theory originates with the work of I. Schur 91, who devised a recursive test to check for contractivity of a holomorphic function in the disk. The so-called Schur parameters of a function may be viewed as Taylor coefficients for the hyperbolic metric of the disk, and the fact that Schur functions are contractions for that metric lies at the root of Schur's test. Generalizations thereof turn out to be efficient to parametrize solutions to contractive interpolation problems 37. Dwelling on this, Factas contributed differential parametrizations (atlases of charts) of lossless matrix functions 35, 87, 78 which are fundamental to our rational approximation software RARL2 (see Section 3.4.5). Schur analysis is also instrumental to approach de-embedding issues, and provides one with considerable insight into the so-called matching problem. The latter consists in maximizing the power a multiport can pass to a given load, and for reasons of efficiency it is all-pervasive in microwave and electric network design, e.g., of antennas, multiplexers, wifi cards and more. It can be viewed as a rational approximation problem in the hyperbolic metric. Factas made significant contributions to this subject 6, in particular within the framework of the (defense funded) ANR Cocoram.
In recent years, our attention was driven by CNES and UPV (Bilbao) to questions about stability of high-frequency amplifiers. Contrary to previously discussed devices, these are active components. The response of an amplifier can be linearized around a set of primary current and voltages, and then admittances of the corresponding electrical network can be computed at various frequencies, using the so-called harmonic balance method. The initial goal is to check for stability of the linearized model, so as to ascertain existence of a well-defined working state. The network is composed of lumped electrical elements namely inductors, capacitors, negative and positive resistors, transmission lines, and controlled current sources. Our research so far has focused on describing the algebraic structure of admittance functions, so as to set up a function-theoretic framework where the two-steps approach outlined in Section 3.1 can be put to work. The main discovery is that the unstable part of each partial transfer function is rational and can be computed by analytic projection, see 10. We now start investigating the linearized harmonic transfer-function around a periodic cycle, to check for stability under non necessarily small inputs.
3.3 Approximation
Participants: Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Martine Olivi, Masimba Nemaire, Dmitry Ponomarev, Cristóbal Villalobos Guillén.
3.3.1 Best analytic approximation
In dimension 2, the prototypical problem to be solved in step 1 of Section 3.1 may be described as: given a domain , to recover a holomorphic function from its values on a subset of the boundary of . For the discussion it is convenient to normalize , which can be done by conformal mapping. So, in the simply connected case, we fix to be the unit disk with boundary unit circle . We denote by the Hardy space of exponent , which is the closure of polynomials in -norm if and the space of bounded holomorphic functions in if . Functions in have well-defined boundary values in , which makes it possible to speak of (traces of) analytic functions on the boundary.
To find an analytic function in matching some measured values approximately on a sub-arc of , we formulate the constrained best approximation problem as in Section 3.2.1.
There, is a reference behavior capturing a priori assumptions on the behavior of the model off , while is some admissible deviation thereof. The value of reflects the type of stability which is sought and how much one wants to smooth out the data. The choice of classes is suited to handle pointwise measurements.
To fix terminology, we refer to as a bounded extremal problem. As shown in 11, 50, 53, 61, the solution to this convex infinite-dimensional optimization problem can be obtained when upon iterating with respect to a Lagrange parameter the solution to spectral equations for appropriate Hankel and Toeplitz operators. These spectral equations involve the solution to the special case of , which is a standard extremal problem 76:
() Let and ; find a function such that is of minimal norm in .
In the case , partial results are known but computational issues remain open.
Various modifications of can be tailored to meet specific needs. For instance when dealing with lossless transfer functions, one may want to express the constraint on in a pointwise manner: a.e. on , see 54. In this form, the problem comes close to (but still is different from) frequency optimization used in control 79, 90. One can also impose bounds on the real or imaginary part of on , which is useful when considering Dirichlet-Neumann problems.
In view of our current research on stability of active devices via analyticity of the harmonic transfer function, on inverse magnetization issues, and on inverse scattering via identification of the frequency response, bounded extremal problems for analytic functions are receiving renewed interest by the team. In such issues, a function on an interval of the real line (or an arc of the circle) must be approximated by the trace of a function holomorphic in the half-plane (or the disk), that meets suitable size constraints.
The analog of Problem on an annulus, being now the outer boundary, can be seen as a means to regularize a classical inverse problem occurring in nondestructive control, namely to recover a harmonic function on the inner boundary from Dirichlet-Neumann data on the outer boundary (see Sections 3.2.1, 4.2, 7.1.2). It may serve as a tool to approach Bernoulli type problems, where we are given data on the outer boundary and we seek the inner boundary, knowing it is a level curve of the solution. In this case, the Lagrange parameter indicates how to deform the inner contour in order to improve data fitting. Similar topics are discussed in Section 3.2.1 for more general equations than the Laplacian, namely isotropic conductivity equations of the form where is no longer constant (i.e., varies in the space). Then, the Hardy spaces in Problem are those of a so-called conjugate Beltrami equation: 80, with , which are studied for in 5, 39, 43 and 70. Expansions of solutions needed to constructively handle such issues in the specific case of linear fractional conductivities have been expounded in 73.
Though originally considered in dimension 2, Problem carries over naturally to higher dimensions where analytic functions get replaced by gradients of harmonic functions. Namely, given some open set and some -valued vector field on an open subset of the boundary of , we seek a harmonic function in whose gradient is close to on .
When is a ball or a half-space, a substitute for holomorphic Hardy spaces is provided by the Stein-Weiss Hardy spaces of harmonic gradients 93. Conformal maps are no longer available when , so that can no longer be normalized. More general geometries than spheres and half-spaces have not been much studied so far.
On the ball, the analog of Problem is
Let and the unit ball. Fix an open subset of the unit sphere . Let further and be -valued vector fields. Given , find a harmonic gradient such that and is of minimal norm in under this constraint.
When , Problem was solved in 1 as well as its analog on a shell, when the tangent component of is a gradient (when is Lipschitz the general case follows easily from this). The solution extends the work in 50 to the 3-D case, using a generalization of Toeplitz operators. The case of the shell was motivated by applications to the processing of EEG data. An important ingredient is a refinement of the Hodge decomposition, that we call the Hardy-Hodge decomposition, allowing us to express a -valued vector field in , , as the sum of a vector field in , a vector field in , and a tangential divergence free vector field on ; the space of such divergence-free fields is denoted by . If or , must be replaced by the real Hardy space or the space of functions with bounded mean oscillation. More generally this decomposition, which is valid on any sufficiently smooth surface (see Section 7.1), seems to play a fundamental role in inverse potential problems. In fact, it was first introduced formally on the plane to describe silent magnetizations supported in (i.e., those generating no field in the upper half space) 47.
Just like solving problem appeals to the solution of problem , our ability to solve problem will depend on the possibility to tackle the special case where :
Let and be a -valued vector field. Find a harmonic gradient such that is minimum.
Problem is simple when by virtue of the Hardy-Hodge decomposition together with orthogonality of and , which is the reason why we were able to solve in this case. Other values of cannot be treated as easily and are still under investigation, especially the case which is of particular interest and presents itself as a 3-D analog to the Nehari problem 88.
Companion to problem is problem below.
Let and be a -valued vector field. Find and such that is minimum.
Note that and are identical in 2-D, since no non-constant tangential divergence-free vector field exists on . It is no longer so in higher dimension, where both and arise in connection with inverse potential problems in divergence form, like source recovery in electro/magneto encephalography and paleomagnetism, see Sections 3.2.1 and 4.2.
3.3.2 Best meromorphic and rational approximation
The techniques set forth in this section are used to solve step 2 in Section 3.2 and they are instrumental to approach inverse boundary value problems for the Poisson equation , where is some (unknown) measure.
Scalar meromorphic and rational approximation
We put for the set of rational functions with at most poles in . By definition, meromorphic functions in are (traces of) functions in .
A natural generalization of problem is:
() Let , an integer, and ; find a function such that is of minimal norm in .
Only for and continuous is it known how to solve in semi-closed form. The unique solution is given by AAK theory (named after Adamjan, Arov and Krein), which connects the spectral decomposition of Hankel operators with best approximation 88.
The case where is of special importance for it reduces to rational approximation. Indeed, if we write the Hardy decomposition where and , then where is a best approximant to from in . Moreover, has no pole outside , hence it is a stable rational approximant to . However, in contrast to the case where , this best approximant may not be unique.
The Miaou project (predecessor of Apics) already designed a dedicated steepest-descent algorithm for the case whose convergence to a local minimum is guaranteed; the algorithm has evolved over years and still now, it seems to be the only procedure meeting this property. This gradient algorithm proceeds recursively with respect to on a compactification of the parameter space 41. Although it has proved to be effective in all applications carried out so far, it is still unknown whether the absolute minimum can always be obtained by choosing initial conditions corresponding to critical points of lower degree (as can be done with the RARL2 software, Section 3.4.5).
In order to establish global convergence results, the team has undertaken a deeper study of the number and nature of critical points (local minima, saddle points, ...), in which tools from differential topology and operator theory team up with classical interpolation theory 57, 60. Based on this work, uniqueness or asymptotic uniqueness of the approximant was proved for certain classes of functions like transfer functions of relaxation systems (i.e., Markov functions) 62 and more generally Cauchy integrals over hyperbolic geodesic arcs 63. These are the only results of this kind. Research on this topic remained dormant for a while by reasons of opportunity, but revisiting the work 38 in higher dimension is a worthy and timely endeavor today. Meanwhile, an analog to AAK theory was carried out for in 61. Although not as effective computationally, it was recently used to derive lower bounds 3. When , problem is still quite open.
A common feature to the above-mentioned problems is that critical point equations yield non-Hermitian orthogonality relations for the denominator of the approximant. This stresses connections with interpolation, which is a standard way to build approximants, and in many respects best or near-best rational approximation may be regarded as a clever manner to pick interpolation points. This was exploited in 64, 65, and is used in an essential manner to assess the behavior of poles of best approximants to functions with branched singularities, which is of particular interest for inverse source problems (cf. Sections 3.4.3 and 7.1).
In higher dimensions, the analog of Problem is best approximation of a vector field by gradients of discrete potentials generated by point masses. This basic issue is by no means fully understood, and it is an exciting field of research. It is connected with certain generalizations of Toeplitz or Hankel operators, and with constructive approaches to so-called weak factorizations for real Hardy functions 72.
Besides, certain constrained rational approximation problems, of special interest in identification and design of passive systems, arise when putting additional requirements on the approximant, for instance that it should be smaller than 1 in modulus (i.e., a Schur function). In particular, Schur interpolation lately received renewed attention from the team, in connection with matching problems. There, interpolation data are subject to a well-known compatibility condition (positive definiteness of the so-called Pick matrix), and the main difficulty is to put interpolation points on the boundary of while controlling both the degree and the extremal points (peak points for the modulus) of the interpolant. Results obtained by the team in this direction generalize a variant of contractive interpolation with degree constraint as studied in 77. We mention that contractive interpolation with nodes approaching the boundary has been a subsidiary research topic by the team in the past, which plays an interesting role in the spectral representation of certain non-stationary stochastic processes 46, 49.
Matrix-valued rational approximation
Matrix-valued approximation is necessary to handle systems with several inputs and outputs but it generates additional difficulties as compared to scalar-valued approximation, both theoretically and algorithmically. In the matrix case, the McMillan degree (i.e., the degree of a minimal realization in the System-Theoretic sense) generalizes the usual notion of degree for rational functions. For instance when poles are simple, the McMillan degree is the sum of the ranks of the residues.
The basic problem that we consider now goes as follows: let and an integer; find a rational matrix of size without poles in the unit disk and of McMillan degree at most which is nearest possible to in . Here the norm of a matrix is the square root of the sum of the squares of the norms of its entries.
The scalar approximation algorithm derived in 41 and mentioned in Section 3.3.2 generalizes to the matrix-valued situation 75. The first difficulty here is to parametrize inner matrices (i.e., matrix-valued functions analytic in the unit disk and unitary on the unit circle) of given McMillan degree . Indeed, inner matrices play the role of denominators in fractional representations of transfer matrices (using the so-called Douglas-Shapiro-Shields factorization). The set of inner matrices of given degree is a smooth manifold that allows one to use differential tools as in the scalar case. In practice, one has to produce an atlas of charts (local parametrizations) and to handle changes of charts in the course of the algorithm. Such parametrization can be obtained using interpolation theory and Schur-type algorithms, the parameters of which are vectors or matrices (35, 78, 87). Some of these parametrizations are also interesting to compute realizations and achieve filter synthesis (78, 87). The rational approximation software “RARL2” developed by the team is described in Section 3.4.5.
Difficulties relative to multiple local minima of course arise in the matrix-valued case as well, and deriving criteria that guarantee uniqueness is even more difficult than in the scalar case. The case of rational functions of degree or small perturbations thereof (the consistency problem) was solved in 56. Matrix-valued Markov functions are the only known example beyond this one 58.
Let us stress that RARL2 seems the only algorithm handling rational approximation in the matrix case that demonstrably converges to a local minimum while meeting stability constraints on the approximant. It is still a working pin of many developments by Factas on frequency optimization and design.
3.3.3 Behavior of poles of meromorphic approximants
Participants: Paul Asensio, Laurent Baratchart.
We refer here to the behavior of poles of best meromorphic approximants, in the -sense on a closed curve, to functions defined as Cauchy integrals of complex measures whose support lies inside the curve. Normalizing the contour to be the unit circle , we are back to Problem in Section 3.3.2; invariance of the latter under conformal mapping was established in 55. Research so far has focused on functions whose singular set inside the contour is polar, meaning that the function can be continued analytically (possibly in a multiple-valued manner) except over a set of logarithmic capacity zero.
Generally speaking in approximation theory, assessing the behavior of poles of rational approximants is essential to obtain error rates as the degree goes large, and to tackle constructive issues like uniqueness. However, as explained in Section 3.2.1, the original twist by Apics, now Factas, is to consider this issue also as a means to extract information on singularities of the solution to a Dirichlet-Neumann problem. The general theme is thus: how do the singularities of the approximant reflect those of the approximated function? This approach to inverse problem for the 2-D Laplacian turns out to be attractive when singularities are zero- or one-dimensional (see Section 4.2). It can be used as a computationally cheap initial condition for more precise but much heavier numerical optimizations which often do not even converge unless properly initialized. As regards crack detection or source recovery, this approach boils down to analyzing the behavior of best meromorphic approximants of given pole cardinality to a function with branch points, which is the prototype of a polar singular set. For piecewise analytic cracks, or in the case of sources, we were able to prove (7, 55, 48), that the poles of the approximants accumulate, when the degree goes large, to some extremal cut of minimum weighted logarithmic capacity connecting the singular points of the crack, or the sources 51. Moreover, the asymptotic density of the poles turns out to be the Green equilibrium distribution on this cut in , therefore it charges the singular points if one is able to approximate in sufficiently high degree (this is where the method could fail, because high-order approximation requires rather precise data).
The case of two-dimensional singularities is still an outstanding open problem.
It is remarkable that inverse source problems inside a sphere or an ellipsoid in 3-D can be approached with such 2-D techniques, as applied to planar sections, see Section 7.1. The technique is implemented in the software FindSources3D, see Section 3.4.3.
Another, extremely classical technique to approximate –more accurately: extrapolate– a function given pointwise values is to compute a rational interpolant of minimal degree to match the values. This method, know as Padé (or multipoint Padé) approximation has been intensively studied for decades 36 but fails to produce pointwise convergence, even if the data are analytic. The best it can give in general is convergence in capacity, at least to functions whose singular set has capacity zero, and this does not prevent spurious poles of the approximant from wandering about the domain of analyticity of the approximated function 85. This phenomenon is standard in numerical practice, and gives rise in physics and engineering circles to a distinction between “mathematical” and “physical” poles; note that this distinction ignores the possibility that the function has other singularities than poles (for example branch-points or essential singularities). A modification of the multipoint Padé technique, where the degree is kept much smaller than the number of data and only approximate interpolation is performed in the least-square sense, has become especially popular over the last decade under the name vector fitting; this is in trend with the soaring development of computational methods in the frequency domain. Although their behavior looks similar to the one of multipoint Padé approximants from a numerical viewpoint, there seems to be no convergence result available for such approximate interpolants so far. Motivated by the behavior of numerical schemes developed at LEAT to recover resonance frequencies of conductors under electromagnetic inverse scattering (see section 4.5), we started investigating the behavior of such least-square rational approximants to functions with polar singular set, see section 7.4.
3.4 Software tools of the team
In addition to the above-mentioned research activities, Factas develops and maintains a number of long-term software tools that either implement and illustrate effectiveness of the algorithms theoretically developed by the team or serve as tools to help further research by team members. We present briefly the most important of them.
3.4.1 pisa
-
Name:
pisa
-
Keywords:
Electrical circuit, Stability
-
Functional Description:
To minimise prototyping costs, the design of analog circuits is performed using computer-aided design tools which simulate the circuit's response as accurately as possible.
Some commonly used simulation tools do not impose stability, which can result in costly errors when the prototype turns out to be unstable. A thorough stability analysis is therefore a very important step in circuit design. This is where pisa is used.
pisa is a Matlab toolbox that allows designers of analog electronic circuits to determine the stability of their circuits in the simulator. It analyses the impedance presented by a circuit to determine the circuit's stability. When an instability is detected, pisa can estimate location of the unstable poles to help designers fix their stability issue.
-
Release Contributions:
First version
- URL:
- Publications:
-
Authors:
Adam Cooman, David Martinez Martinez, Fabien Seyfert, Martine Olivi
-
Contact:
Fabien Seyfert
3.4.2 DEDALE-HF
-
Keyword:
Microwave filter
-
Scientific Description:
Dedale-HF consists in two parts: a database of coupling topologies as well as a dedicated predictor-corrector code. Roughly speaking each reference file of the database contains, for a given coupling topology, the complete solution to the C.M. problem associated to particular filtering characteristics. The latter is then used as a starting point for a predictor-corrector integration method that computes the solution to the C.M. corresponding to the user-specified filter characteristics. The reference files are computed off-line using Gröbner basis techniques or numerical techniques based on the exploration of a monodromy group. The use of such continuation techniques, combined with an efficient implementation of the integrator, drastically reduces the computational time.
Dedale-HF has been licensed to, and is currently used by TAS-Espana.
-
Functional Description:
Dedale-HF is a software dedicated to solve exhaustively the coupling matrix synthesis problem in reasonable time for the filtering community. Given a coupling topology, the coupling matrix synthesis problem (C.M. problem for short) consists in finding all possible electromagnetic coupling values between resonators that yield a realization of given filter characteristics. Solving the latter problem is crucial during the design step of a filter in order to derive its physical dimensions as well as during the tuning process where coupling values need to be extracted from frequency measurements.
- URL:
-
Contact:
Fabien Seyfert
-
Participant:
Fabien Seyfert
3.4.3 FindSources3D
-
Keywords:
Health, Neuroimaging, Visualization, Compilers, Medical, Image, Processing
-
Scientific Description:
Though synthetic data could be static, actual signal recordings are dynamical. The time dependency is either neglected and the data processed instant by instant, or separated from the space behavior using a singular value decomposition (SVD). This preliminary step allows to estimate the number of independent activities (uncorrelated sources) and to select the corresponding quantity of principal static components. After a first data transmission (“cortical mapping”) step of the static data, using the harmonicity property of the potential in the outermost layers (solving BEP problems on spherical harmonics bases), FS3D makes use of best rational approximation on families of 2-D planar cross-sections and of the software RARL2 in order to locate singularities and to determine the expected quantity of sources. From those planar singularities, the 3-D sources are finally estimated, together with their moment, in a last clustering step. Through this process, FS3D is able to recover time correlated sources, which is an important advantage. When simultaneously available, EEG and MEG data can now be processed together, and this also improves the recovery performance. In case of dynamical data, a recent additional step is to find the linear combination of the preliminary selected static components (change of basis) that produces source estimates which minimize the error w.r.t. data, an original criterion, which allows to improve the recovery quality.
-
Functional Description:
FindSources3D (FS3D) is a software program written in Matlab dedicated to the resolution of inverse source problems in brain imaging, electroencephalography (EEG) and magnetoencephalography (MEG). From data consisting in pointwise measurements of the electrical potential taken by electrodes on the scalp (EEG), or of a component of the magnetic field taken on a helmet (MEG), FS3D estimates pointwise dipolar current sources within the brain in a spherical layered model. Each layer (brain, skull, scalp) is assumed to have a constant conductivity.
- URL:
-
Contact:
Juliette Leblond
-
Participants:
Jean-Paul Marmorat, Juliette Leblond, Maureen Clerc, Nicolas Schnitzler, Théodore Papadopoulo
3.4.4 PRESTO-HF
-
Keywords:
CAO, Telecommunications, Microwave filter
-
Scientific Description:
For the matrix-valued rational approximation step, Presto-HF relies on RARL2. Constrained realizations are computed using the Dedale-HF software. As a toolbox, Presto-HF has a modular structure, which allows one for example to include some building blocks in an already existing software.
The delay compensation algorithm is based on the following assumption: far off the pass-band, one can reasonably expect a good approximation of the rational components of S11 and S22 by the first few terms of their Taylor expansion at infinity, a small degree polynomial in 1/s. Using this idea, a sequence of quadratic convex optimization problems are solved, in order to obtain appropriate compensations. In order to check the previous assumption, one has to measure the filter on a larger band, typically three times the pass band.
This toolbox has been licensed to (and is currently used by) Thales Alenia Space in Toulouse and Madrid, Thales airborne systems and Flextronics (two licenses). Xlim (University of Limoges) is a heavy user of Presto-HF among the academic filtering community and some free license agreements have been granted to the microwave department of the University of Erlangen (Germany) and the Royal Military College (Kingston, Canada).
-
Functional Description:
Presto-HF is a toolbox dedicated to low-pass parameter identification for microwave filters. In order to allow the industrial transfer of our methods, a Matlab-based toolbox has been developed, dedicated to the problem of identification of low-pass microwave filter parameters. It allows one to run the following algorithmic steps, either individually or in a single stroke:
- Determination of delay components caused by the access devices (automatic reference plane adjustment),
- Automatic determination of an analytic completion, bounded in modulus for each channel,
- Rational approximation of fixed McMillan degree,
- Determination of a constrained realization.
- URL:
-
Contact:
Fabien Seyfert
-
Participants:
Fabien Seyfert, Jean-Paul Marmorat, Martine Olivi
3.4.5 RARL2
-
Name:
Réalisation interne et Approximation Rationnelle L2
-
Keyword:
Approximation
-
Scientific Description:
The method is a steepest-descent algorithm. A parametrization of MIMO systems is used, which ensures that the stability constraint on the approximant is met. The implementation, in Matlab, is based on state-space representations.
RARL2 performs the rational approximation step in the software tools PRESTO-HF and FindSources3D. It is distributed under a particular license, allowing unlimited usage for academic research purposes. It was released to the universities of Delft and Maastricht (the Netherlands), Cork (Ireland), Brussels (Belgium), Macao (China) and BITS-Pilani Hyderabad Campus (India).
-
Functional Description:
RARL2 is a software for rational approximation. It computes a stable rational L2-approximation of specified order to a given L2-stable (L2 on the unit circle, analytic in the complement of the unit disk) matrix-valued function. This can be the transfer function of a multivariable discrete-time stable system. RARL2 takes as input either:
- its internal realization,
- its first N Fourier coefficients,
- discretized (uniformly distributed) values on the circle. In this case, a least-square criterion is used instead of the L2 norm.
It thus performs model reduction in the first or the second case, and leans on frequency data identification in the third. For band-limited frequency data, it could be necessary to infer the behavior of the system outside the bandwidth before performing rational approximation.
An appropriate Möbius transformation allows to use the software for continuous-time systems as well.
- URL:
-
Contact:
Martine Olivi
-
Participants:
Jean-Paul Marmorat, Martine Olivi
3.4.6 Sollya
-
Keywords:
Computer algebra system (CAS), Supremum norm, Proof synthesis, Code generator, Remez algorithm, Curve plotting, Numerical algorithm
-
Functional Description:
Sollya is an interactive tool where the developers of mathematical floating-point libraries (libm) can experiment before actually developing code. The environment is safe with respect to floating-point errors, i.e., the user precisely knows when rounding errors or approximation errors happen, and rigorous bounds are always provided for these errors.
Among other features, it offers a fast Remez algorithm for computing polynomial approximations of real functions and also an algorithm for finding good polynomial approximants with floating-point coefficients to any real function. As well, it provides algorithms for the certification of numerical codes, such as Taylor Models, interval arithmetic or certified supremum norms.
It is available as a free software under the CeCILL-C license.
- URL:
-
Contact:
Sylvain Chevillard
-
Participants:
Christoph Lauter, Jérôme Benoit, Marc Mezzarobba, Mioara Joldes, Nicolas Jourdan, Sylvain Chevillard
-
Partners:
CNRS, UPMC, ENS Lyon, LIP6, UCBL Lyon 1, Loria
4 Application domains
4.1 Introduction
Application domains are naturally linked to the problems described in Sections 3.2.1 and 3.2.2, under a common umbrella of function-theoretic techniques as described in Section 3.3.
4.2 Inverse source problems in EEG
Participants: Paul Asensio, Laurent Baratchart, Juliette Leblond, Jean-Paul Marmorat, Masimba Nemaire.
Solving over-determined Cauchy problems for the Laplace equation on a spherical layer (in 3-D) in order to extrapolate incomplete data (see Section 3.2.1) is a necessary ingredient of the team's approach to inverse source problems, in particular for applications to EEG, see 9. Indeed, the latter involves propagating the initial conditions through several layers of different conductivities, from the boundary shell down to the center of the domain where the singularities (i.e., the sources) lie. Once propagated to the innermost sphere, it turns out that traces of the boundary data on 2-D cross sections coincide with analytic functions with branched singularities in the slicing plane 7, 52. The singularities are related to the actual location of the sources, namely their moduli reach in turn a maximum when the plane contains one of the sources. Hence we are back to the 2-D framework of Section 3.3.3, and recovering these singularities can be performed via best rational approximation. The goal is to produce a fast and sufficiently accurate initial guess on the number and location of the sources in order to run heavier descent algorithms on the direct problem, which are more precise but computationally costly and often fail to converge if not properly initialized. Our belief is that such a localization process can add a geometric, valuable piece of information to the standard temporal analysis of EEG signal records.
Numerical experiments obtained with our software FindSources3D give very good results on simulated data and we are now engaged in the process of handling real experimental data, simultaneously recorded by EEG and MEG devices, in collaboration with our partners at INS, hospital la Timone, Marseille (see Section 7.1.2).
Furthermore, another approach is being studied for EEG, that consists in regularizing the inverse source problem by a total variation constraint on the source term (a measure), added to the quadratic data approximation criterion. It is similar to the path that is taken for inverse magnetization problems (see Sections 4.3 and 7.1.1), and it presently focuses on surface-distributed models.
4.3 Inverse magnetization problems
Participants: Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Masimba Nemaire, Dmitry Ponomarev, Cristóbal Villalobos Guillén, Anass Yousfi.
Generally speaking, inverse potential problems, similar to the one appearing in Section 4.2, occur naturally in connection with systems governed by Maxwell's equation in the quasi-static approximation regime. In particular, they arise in magnetic reconstruction issues. A specific application is to geophysics, which led us to form the Inria Associate Team Impinge (Inverse Magnetization Problems IN GEosciences) together with MIT and Vanderbilt University that reached the end of its term in 2018.To set up the context, recall that the Earth's geomagnetic field is generated by convection of the liquid metallic core (geodynamo) and that rocks become magnetized by the ambient field as they are formed or after subsequent alteration. Their remanent magnetization provides records of past variations of the geodynamo, which is used to study important processes in Earth sciences like motion of tectonic plates and geomagnetic reversals. Rocks from Mars, the Moon, and asteroids also contain remanent magnetization which indicates the past presence of core dynamos. Magnetization in meteorites may even record fields produced by the young sun and the protoplanetary disk which may have played a key role in solar system formation.
For a long time, paleomagnetic techniques were only capable of analyzing bulk samples and compute their net magnetic moment. The development of SQUID microscopes has recently extended the spatial resolution to sub-millimeter scales, raising new physical and algorithmic challenges. The associate team Impinge aimed at tackling them, experimenting with the SQUID microscope set up in the Paleomagnetism Laboratory of the department of Earth, Atmospheric and Planetary Sciences at MIT. Typically, pieces of rock are sanded down to a thin slab, and the magnetization has to be recovered from the field measured on a planar region at small distance from the slab.
Mathematically speaking, both inverse source problems for EEG from Section 4.2 and inverse magnetization problems described presently amount to recover the (3-D valued) quantity (primary current density in case of the brain or magnetization in case of a thin slab of rock) from measurements of the potential:
outside the volume of the object. Depending on the geometry of models, the magnetization distribution may lie in a volume or spread out on a surface. This results in quite different identifiability properties, see 47 and Section 7.1.1, but the two situations share a substantial mathematical common core.
Another timely instance of inverse magnetization problems lies with geomagnetism. Satellites orbiting around the Earth measure the magnetic field at many points, and nowadays it is a challenge to extract global information from those measurements. In collaboration with C. Gerhards (Geomathematics and Geoinformatics Group, Technische Universität Bergakademie Freiberg, Germany), we started to work on the problem of separating the magnetic field due to the magnetization of the globe's crust from the magnetic field due to convection in the liquid metallic core. The techniques involved are variants, in a spherical context, from those developed within the Impinge associate team for paleomagnetism, see Section 7.1.1.
4.4 Structure and stability of active devices
Participants: Laurent Baratchart, Sylvain Chevillard, Jean-Paul Marmorat, Martine Olivi, Fabien Seyfert.
Through contacts with CNES (Toulouse) and UPV (Bilbao), the team got involved in the design of amplifiers which, unlike filters, are active devices. A prominent issue here is stability. A twenty years back, it was not possible to simulate unstable responses, and only after building a device could one detect instability. The advent of so-called harmonic balance techniques, which compute steady state responses of linear elements in the frequency domain and look for a periodic state in the time domain of a network connecting these linear elements via static non-linearities made it possible to compute the harmonic response of a (possibly nonlinear and unstable) device 94. This has had tremendous impact on design, and there is a growing demand for software analyzers. The team is also becoming active in this area.
In this connection, there are two types of stability involved. The first is stability of a fixed point around which the linearized transfer function accounts for small signal amplification. The second is stability of a limit cycle which is reached when the input signal is no longer small and truly nonlinear amplification is attained (e.g., because of saturation). Initial applications by the team have been concerned with the first type of stability, and emphasis was put on defining and extracting the “unstable part” of the response, see Section 7.2. Since then, the stability check for limit cycles has made important theoretical advances. Specifically, the exponential stability of the high frequency limit of a circuit was established last year in 4, implying that there are at most finitely many unstable poles and no other unstable singularity for the monodromy operator around the cycle. Furthermore, the links between the monodromy operator and the (operator-valued) harmonic transfer function of the linearized system along the trajectory were brought to light in 27. Numerical algorithms are now under investigation, while important pending issues involve: (i) whether poles of the harmonic transfer function must be poles of each entry thereof, at least generically and (ii) describing the stable spectrum of the harmonic transfer function of the linearized system, in particular understand its continuous and essential part.
4.5 Identification of resonating frequencies of compact metallic objects in electromagnetic inverse scattering
Participants: Paul Asensio, Laurent Baratchart, Juliette Leblond, Martine Olivi, Dmitry Ponomarev, Fabien Seyfert.
One of the best training grounds for function-theoretic applications by the team is the identification and design of physical systems whose performance is assessed frequency-wise. This is the case of electromagnetic resonant systems which are of common use in telecommunications.
In space telecommunications (satellite transmissions), constraints specific to on-board technology lead to the use of filters with resonant cavities in the microwave range. These filters serve multiplexing purposes (before or after amplification), and consist of a sequence of cylindrical hollow bodies, magnetically coupled by irises (orthogonal double slits). The electromagnetic wave that traverses the cavities satisfies the Maxwell equations, forcing the tangent electrical field along the body of the cavity to be zero. A deeper study of the Helmholtz equation states that an essentially discrete set of wave vectors is selected.
Study of resonances also led us to another inverse problem. There, the singularity expansion method featuring the above-mentioned discrete set of wave vectors is instrumental to the object detection. In this respect, we started an academic collaboration with LEAT (Univ. Côte d'Azur, France, J.-Y. Dauvignac, N. Fortino, Y. Zaki) on the topic of inverse scattering using frequency dependent measurements. As opposed to classical electromagnetic imaging where several spatially located sensors are used to identify the shape of an object by means of scattering data at a single frequency, a discrimination process between different metallic objects is here being sought for by means of a single, or a reduced number of sensors that operate on a whole frequency band. For short the spatial multiplicity and complexity of antenna sensors is here traded against a simpler architecture performing a frequency sweep.
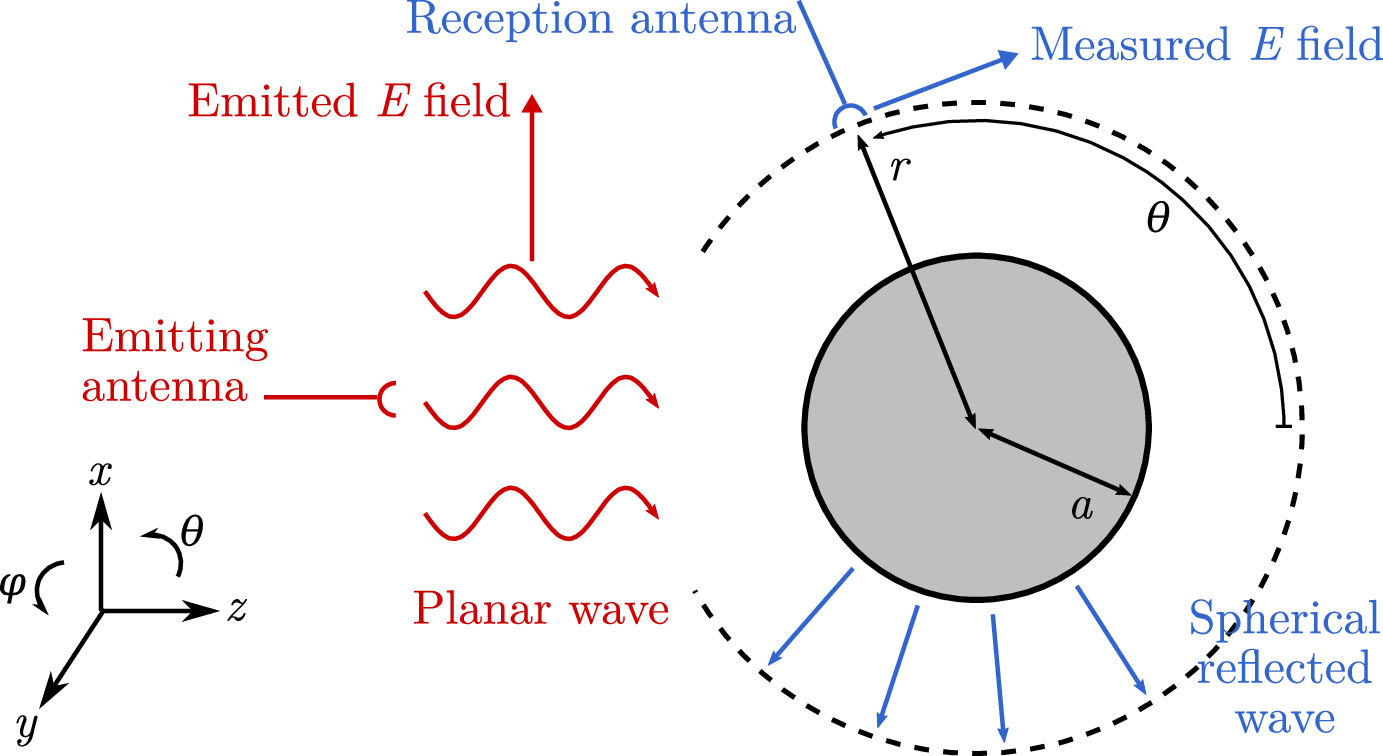
A schematic view of the problem: an antenna (horizontal and on the left) emits a planar wave (propagating horizontally, towards the right and shown in red) with an emitted electric field EE perpendicular to it (represented by a vertical arrow on the figure). On the right, a sphere of radius aa reflects the wave. The reflected wave is radial to the sphere, directed towards its exterior, and is shown in blue. A reception antenna points towards the center of the sphere, and is located at a distance rr of the center of the sphere, while making an angle θ\theta with respect to the horizontal. It measures the reflected electric field, which is perpendicular to it.
The setting is shown on Figure 1. The total field is the sum of the incident field (here a plane wave) and scattered field , that is at every point in space we have . A harmonic time dependency (, where is the imaginary unit: ) is supposed for the incident wave, so that by linearity of Maxwell equations and after a transient state, the following holds:
The subscripts and stand here for «observation point» and «emission point»: the scattered field at the observation point is therefore related to the emitted planar wave field at the emission point via the transfer function . The emission point is here supposed fixed, so the dependency in is omitted in . Under regularity conditions on the scatterer's boundary the function can be shown to admit an analytic continuation into the complex left half plane for the variable, away from a discrete set (with a possible accumulation point a infinity) where it admits poles. Thus, is a meromorphic function in the variable . Its poles are called the resonating frequencies of the scattering object. Recovering these resonating frequencies from frequency scattering measurement, that is measurements of at particular is the primary objective of this project.
In order to gain some insight we started a full study of the particular case when the scatterer is a spherical PEC (Perfectly Electric Conductor). In this case Maxwell equations can be solved «explicitly» by means of expansions in series of vectorial spherical harmonics. We showed in particular that in this case admits following simple structure:
where is a meromorphic functions with poles at zeros of the spherical Hankel functions and their derivatives and is independent of the frequency. Identification procedures, surprisingly close to the ones we developed in connection with amplifier stability analysis, are currently being studied to gain information about the resonating frequencies by means of a rational approximation of the function once it has been de-embedded. A preliminary study resulted in a common publication with the LEAT team 96.
In order to perform the rational approximation of the function , its behavior outside the range of measured frequencies, specifically at high frequencies, is being studied for the particular case when the scatterer is a spherical PEC (Perfectly Electric Conductor). In this case, can be written as:
where and are respectively the optic and creeping wave parts. Their high-frequency behaviors are given by:
where the coefficients , , and are identified when the observation point and the emission point coincide. The above asymptotics of is called the Luneberg-Kline expansion; its first terms were analytically computed (solving eikonal and transport equations).
Numerical simulations showed that even though the creeping wave part is negligible in front of the optic part at high frequencies, it needs to be taken into account around the band of measured frequencies for the rational approximation.
Furthermore, the physical interpretation of these two terms leads to consider that the creeping wave part should carry more information about the scatterer and we want to investigate the conjecture that the poles of are those of hence that is analytic.
We plan in the future to investigate a generalization of this form for other PEC scatterers.
4.6 Imaging and modeling ancient materials
Participants: Vanna Lisa Coli, Juliette Leblond.
This is a recent activity of the team, linked to image classification in archaeology in the framework of the projects ToMaT and Arch-AI-Story, see Section 9.4; it is pursued in collaboration with L. Blanc-Féraud (project-team Morpheme, I3S-CNRS/Inria Sophia/iBV), D. Binder (CEPAM-CNRS, Nice), in particular.
The pottery style is classically used as the main cultural marker within Neolithic studies. Archaeological analyses focus on pottery technology, and particularly on the first stages of pottery manufacturing processes. These stages are the most demonstrative for identifying the technical traditions, as they are considered as crucial in apprenticeship processes. Until now, the identification of pottery manufacturing methods was based on macro-traces analysis, i.e., surface topography, breaks and discontinuities indicating the type of elements (coils, slabs, ...) and the way they were put together for building the pots. Overcoming the limitations inherent to the macroscopic pottery examination requires a complete access to the internal structure of the pots. Micro-computed tomography (CT) has recently been used for exploring ancient materials micro-structure. This non-invasive method provides quantitative data for a big set of proxies and is perfectly adapted to the analysis of cultural heritage materials.
The main challenge of our current analyses aims to overcome the lack of existing protocols to apply in order to quantify observations. In order to characterize the manufacturing sequences, the mapping of the paste variability (distribution and composition of temper) and the discontinuities linked to different classes of pores, fabrics and/or organic inclusions appears promising. The totality of the acquired images composes a set of 2-D and 3-D surface and volume data at different resolutions and with specific physical characteristics related to each acquisition modality (multimodal and multi-scale data). Specific shape recognition methods need to be developed by application of robust imaging techniques and 3-D-shapes recognition algorithms.
We devised a method to isolate pores from the 3-D data volumes in binary 3-D images, to which we apply a process named Hough transform (derived from Radon transform). This method, of which the generalization from 2-D to 3-D is quite recent, allows us to evaluate the presence of parallel lines going through the pores. The quantity of such lines and their parallelism furnish good indicators of the “coiling” manufacturing, that they allow to distinguish from the other “spiral patchwork” technique, in particular, 24.
5 Social and environmental responsibility
- M. Olivi is a member of the CLDD (Commission Locale de Développement Durable) and in charge of coordination. She is a member of the GDS EcoInfo (CNRS) and of Labos1point5.
- M. Olivi was a member of the delegation Université Côte d'Azur at COP 27 (Charm el Cheick). She wrote an advocacy “Digital science to contribute to the ecological transition” for the Academic Advocacy Collection published by the University.
- M. Olivi participated in “Journées EcoInfo” (October 10-12, Orsay).
- S. Chevillard and M. Olivi participated to a one-day “Atelier SEnS” (stands for “Science, Environment and Society”; it is a reflexion group aiming at brainstorming together on the impact of science and the way we are doing it on the environment and society) animated by E. Tannier.
5.1 Footprint of research activities
Participants: Sylvain Chevillard, Martine Olivi.
We pursued in 2022 the work initiated in 2021 regarding the carbon footprint of the research center: last year, we used the GES1p5 methodology to evaluate this footprint for year 2019, but we did not have the time to analyze the results in detail. In 2022, we performed a thorough analysis of the part of that footprint due to the travels of agents for missions. The lessons that we learn from this analysis are manifold:- Almost all missions (85% of them) are made by plane. Considering the much lower footprint of the train with respect to the plane, the carbon footprint of missions is, at first order, only due to the use of the plane.
- Missions can be roughly separated in two categories: a minority of missions that emit each a huge amount of , and a huge number of missions that have individually a small impact, but overall an important impact. Namely, the 10% of missions that emit the most represents half of the footprint of the missions (that is, about 260 tons of ), while most of the other half is caused by missions that all emit individually only a few hundreds of kilograms of . This means that there is no easy target: significantly reducing the carbon footprint of missions cannot only be based on replacing the plane by the train for short distance missions, and neither only be based on reducing the number of long distance missions.
- For about a third of all missions, the final destination was Paris and the travel made by plane. They represent 20% of the total footprint. Of course, the localization of Sophia Antipolis with respect to Paris explains that the plane is preferred over the train: Nice-Paris is an hour by plane, compared to six hours by train. Replacing plane by train for such missions appears feasible, but would require important change of habits (it would become impossible to do the journey to Paris and back on the same day).
- The data used to compute the footprint of missions, and provided by Oreli, contain a significant number of errors (especially when train/plane tickets have been reserved first, but modified afterwards). This does not really affect the footprint overall for a year like 2019, but it prevented us to reproduce these computations for year 2020: there, due to the Covid crisis and the huge number of cancellations and reports of missions, the data by Oreli would be way too unreliable.
We wrote a detailed blog post describing our analysis (in French).
6 Highlights of the year
We want to highlight the following serious issues experienced by the team and colleagues in 2022.
- Difficulties and shameful situations arising from Eksae's early deployment, affecting our administrative colleagues and delaying payment of suppliers and experts (for more than one year), but also affecting our own work. To quote just a few: late reimbursements (in particular, for PhD students' missions), reduced period to order material, and frequent worrisome and inopportune messages regarding electronic accounts.
- Untimely organized and advertised national events like, e.g., “Journées scientifiques de l'Inria (JSI)” or the last 2022 CRTH hiring process, and delayed treatment of emeritus applications.
- Fuzzy and contradictory statements by the management of Inria regarding the work by the Evaluation Board; this causes distrust both in the management and in the hiring and promoting process.
- Altogether, public addresses by the institute give the impression that research is now only an auxiliary activity thereof.
7 New results
7.1 Inverse problems for Poisson-Laplace equations
Participants: Paul Asensio, Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Jean-Paul Marmorat, Masimba Nemaire, Dmitry Ponomarev, Cristóbal Villalobos Guillén, Anass Yousfi.
7.1.1 Inverse magnetization issues for planar and volumetric samples
The goal is to invert magnetizations carried by a rock sample from measurements of the magnetic field nearby. A typical application is when the sample is shaped into thin slabs, with measurements taken by a superconducting quantum interference device (SQUID). Figure 2 sketches the corresponding experimental set up, brought up to our knowledge by collaborators from the Earth and Planetary Sciences Laboratory at MIT.
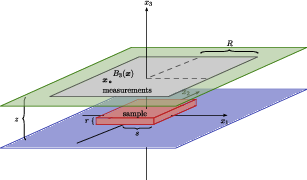
Schematic view of the experimental setup : the horizontal plane on which the rock sample lies (the sample being a parallelepiped with height rr and a square basis of half-size ss). Its basis is at height 0, and the center of the square basis is at the origin of the system of coordinates). Above, the measurements are performed on a parallel plane at height zz. Here, for instance, it is a square, whose half-size is RR and which is horizontally centered.
This year, we resumed computations – initiated a few years ago – to derive explicit formulas for the adjoint operator applied to a polynomial function , in the case when the measurements are performed on a rectangle. It turns out that the integrals involved in its expression admit closed forms, which involve recurrences based on the coefficients of . The best way to implement these recurrences in order to explicitly evaluate is not yet completely clear, though. This constitutes the starting point of A. Yousfi's PhD. Such explicit computations are expected to be useful for efficiently evaluating the solution of the bounded extremal problem set up in 2, and are also useful to compute asymptotic estimates for the net magnetization moment, when the measurement are taken on a rectangle.
In the same vein, when the measurement area is a disk, the issue of asymptotic estimates has undergone new developments. In particular, for this setting, asymptotic estimates of the net moment of a volumetric sample previously obtained in 89 up to the second order have now been mathematically proven. Additionally, and what is more practically important, a new set of higher order (fourth and fifth order) estimates has been rigorously derived. From the derivation strategy, it has also become clear that estimates for each net moment component could be performed at an arbitrarily high order once a certain asymptoticness criterion on the size of the measurement area is satisfied. The higher order estimates rely on finer analytic properties of the magnetic field and are thus more sensitive to noise, a fact that has been also confirmed numerically in 33.
The work on moment estimates has become a starting point for new efforts in 2 directions: noise filtering and field prolongation. One way to attempt both issues at once is to use the so-called spectral extrapolation. Such an approach consists in finding a suitable choice of basis functions which are adapted to problem structure and geometry, but at the same time are naturally defined outside of the original region. Using an eigenbasis of the suitable integral operator related to the forward problem, we could construct a field extrapolant which extends the available measurements in a physically meaningful way (in particular, respecting the smoothness property and the behavior at infinity). Restricting the number of terms in the expansion over this basis also provides a regularization strategy achieving a desired degree of the field denoising. The preliminary results have been tested on synthetic data and partially on a set of experimental measurements coming from quantum diamond microscope (QDM). Multiple aspects of this work are yet to be understood on both theoretical and practical levels.
As far as the extrapolation of the magnetic field is concerned, another piece of work began in the team in order to explore advantages of incorporating additional measurements. Namely, the set-up of limited-area planar measurements available at 2 different heights (corresponding to 2 lift-offs from the magnetization sample) is an experimental possibility. Can such additional measurements drastically improve the results of the approaches that use only one-height data? Here, there are several ways to address the issue using the framework of constrained optimization. While it is fairly easy to formulate bounded extremal problems yielding equations for field extensions, numerical solution of such problems is computationally non-trivial as it involves many repetitive integrations over unbounded domains. However, a recent observation based on the analyticity properties of the field allows reduction to the auxiliary problem whose solution would only involve integration over bounded regions. Similarly to the extrapolation and noise-filtering procedure described above, the appropriate spectral functions are expected to be useful for further reduction of the computational effort. Numerical experiments verifying the approach (together with the whole benefit of dealing with measurements at 2 heights) are still yet to be conducted.
In another connection, as a joint research effort with E. A. Lima and B. P. Weiss (EAPS dept. MIT, USA), C. S. Borlina (EAPS dept. Johns Hopkins Univ. USA) and D. Hardin (Vandebilt Univ. USA), the following question was investigated: is it possible to estimate the moment of an unknown magnetization by the one of a magnetization producing a field close enough to the observations? In other words, is full-inversion a demonstrably good (though admittedly costly) method to estimate the moment? We were able this year to show that the answer is essentially no. More precisely, the field-to-moment map (that exists because silent magnetizations have zero moment) is discontinuous, even when magnetizations are endowed with fairly weak topology (for instance the weak-star topology for distributions of fixed order and given support) and even if magnetization models are restricted to a very small class (for example multipoles). In fact, the quality of approximation of the observed field by the field of a magnetization of the selected model class does compete with the norm of the operator mapping the moment to the field for that model class in order to determine if full inversion is efficient or not to estimate the moment in the case at hand. This opens up new and interesting ground for investigation, still in progress. An article reporting our findings so far is under writing.
7.1.2 Inverse problems in medical imaging
In 3-D, functional or clinically active regions in the cortex are often modeled by pointwise sources that have to be localized from measurements, taken by electrodes on the scalp, of an electrical potential satisfying a Laplace equation (EEG, electroencephalography). In the works 7, 52 on the behavior of poles in best rational approximants of fixed degree to functions with branch points, it was shown how to proceed via best rational approximation on a sequence of 2-D disks cut along the inner sphere, for the case where there are finitely many sources (see Section 4.2).
In this connection, a dedicated software FindSources3D (FS3D, see Section 3.4.3) has been developed, in collaboration with the Inria team Athena (now Cronos) and the CMA - Mines ParisTech. Its Matlab version now incorporates the treatment of MEG data, the aim being to handle simultaneous EEG–MEG recordings available from our partners at INS, hospital la Timone, Marseille. Indeed, it is now possible to use simultaneously EEG and MEG measurement devices, in order to measure both the electrical potential and a component of the magnetic field (its normal component on the MEG helmet, that can be assumed to be spherical). Solving the inverse source problem from joint EEG and MEG data actually improves accuracy of the source estimation. Note that FS3D takes as inputs actual EEG and MEG measurements, like time signals, and performs a suitable singular value decomposition in order to separate independent sources.
It appears that, in the rational approximation step, multiple poles possess a nice behavior with respect to branched singularities. This is due to the very physical assumptions on the model from dipolar current sources: for EEG data that correspond to measurements of the electrical potential, one should consider triple poles; this will also be the case for MEG – magneto-encephalography – data. However, for (magnetic) field data produced by magnetic dipolar sources within rocks, one should consider poles of order five. Though numerically observed in 9, there is no mathematical justification so far why multiple poles generate such strong accumulation of the poles of the approximants. This intriguing property, however, is definitely helping source recovery and will be the topic of further study. It is used in order to automatically estimate the “most plausible” number of sources (numerically: up to 3, at the moment).
FS3D is now used by some of our collaborators. Together with M. Darbas (LAGA, Univ. Sorbonne Paris Nord) and P.-H. Tournier (labo. JLL, Sorbonne Univ), we recently began to handle the EEG inverse problem with a variable conductivity in the intermediate skull layer, in order to model hard / spongy bones, especially for neonates. Coupled with FS3D, the related transmission step is performed using a mixed variational regularization and finite elements (FreeFem++) on tetrahedral meshes, and furnishes very promising results 30.
We also studied the uniqueness of a critical point of the quadratic criterion in the electroencephalography problem for a single dipole situation (PhD of P. Asensio). This issue is essential for the use of descent algorithms. This leads to the study of the following criterion:
where and (actual dipole position) are in a smooth open set included in and , (actual dipole moment) belong to . In the half-space case where , we have proven that there is a unique critical point; i.e., a unique location and moment pair where the gradient of vanishes, which is but (the absolute minimum). We currently try to obtain an analogous result on the ball, which is considerably more difficult because no translation invariance holds anymore. For the spherical case where is the ball of center 0 and radius 1, we only obtained partial results so far, and managed to prove the uniqueness of the critical point in the specific case where is located at the center of . We also studied the uniqueness of the critical point of the quadratic criterion in the charge localization problem for a single charge situation. This leads to the study of the following criterion:
where and (actual charge position) are in a smooth open set included in and , (actual charge quantity) belong to . In both cases (the half-space case and the spherical one), we have proven that there is a unique critical point, 26.
We started considering a different class of models, not necessarily dipolar, and related estimation algorithms. Such models may be supported on the surface of the cortex or in the volume of the encephalon. We represent sources by vector-valued measures, and in order to favor sparsity in this infinite-dimensional setting we use a TV (i.e. total variation) regularization term as in Section 7.1.1. The approach follows that of 8 and is implemented through two different algorithms, whose convergence properties are currently being studied. Tests on synthetic data from a few dipolar sources provide results of different qualities that need to be better understood. In particular, a weight is being added in the TV term in order to better identify deep sources. This is the topic of the PhD researches of P. Asensio and M. Nemaire. Ultimately, the results will be compared to those of FS3D and other available software tools.
Three nested ovoids illustrating the three layers of the head (denoted Ωi\Omega _i with i=0,1,2i=0,1,2, 0 being the index of the inner layer). The conductivity of the ii-th layer is denoted with σi\sigma _i and its boundary is denoted with Γi\Gamma _i. Two red straight lines illustrate how deep electrodes take measurements in the inner layer. Little segments perpendicular to each electrode illustrate the different sensors that lie along the electrode. A blue closed curve, denoted SS, in the inner layer illustrates the surface where the sources lie, and little arrows show that their orientation is normal to the curve.
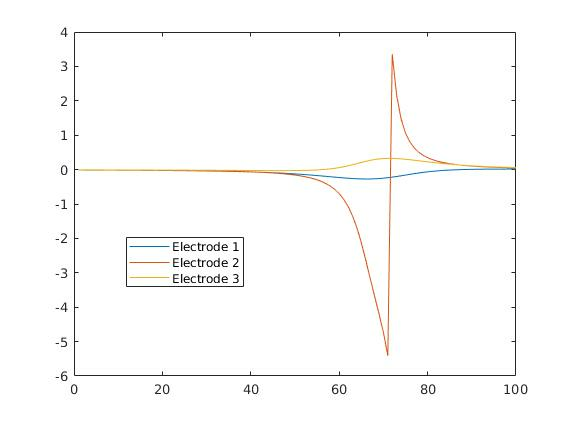
Progresses were made on the inverse problem of “Stereo” EEG (SEEG), where the potential is measured by deep electrodes and sensors within the brain as in the scheme of Figure 3. Assuming that the current source term is a -valued vector field (or a measure, or a dipolar distribution) supported on a surface and normally oriented to , makes it possible to describe the potential generated by as a double layer potential:
The associated forward and inverse problems were solved for both an infinite medium conductor and a more realistic single model of the brain (as first step towards nested domains for the head). Concerning the latter, it is preliminary assumed that , whence consists in patches on the cortex surface.
The numerical implementation was done by approximating the density of the double layer potential with linear shape functions on triangulations of the involved surface . For the discretized version, is then approximated on every triangle by a piecewise linear function, and the associated moment is taken to be located at the center of the triangle, perpendicular to the triangle. Note that explicit expressions of the double layer potential are also available at points located on (that supports ).
The inverse problem for SEEG is ill-posed and a Tychonov regularization is used in order to solve the problem: find a distribution defined on the prescribed surface such that is minimized, where is the given data in , is the “forward model” (measurements of the double layer potential), is an appropriate regularization term that results in having some desired properties (being bounded in norm or or on ), and a (Lagrange) parameter. Because is only furnished at sensor positions, the term in the above criterion becomes an term. Figures 4 and 5 show the obtained results.
We now consider within the brain, at the gray / white matters interface and we handle outer layers and for the skull and the scalp, as illustrated in Figure 3. Such configurations involve a data transmission / “cortical mapping” step relating the potential and normal current values at the boundaries , that the present double layer formulation allows us to solve with the source localization issue. It only requires to solve the transmission problem for the surface electrical potentials hence this reduces the complexity of the problem. Numerically, this is a feasible implementation of the problem because the expressions for double layer potentials do not suffer from numerical singularities, hence this suffices to give reasonable solutions.
We are now able to handle MEG, EEG, SEEG modalities, simultaneously or not. The simultaneous handling of the different modalities is made the more straightforward by coupling the source localization problem and the inverse transmission problem.
The data transmission needs to be considered in the source localization problem so that the problem remains faithful to the data (electric or magnetic) when realistic head geometries are used in the computations. This also allows one to exploit properties of the problem that bring more regularity to the solutions. These considerations warrant that the transmission problem be solved simultaneously with the source localization problem, but in this connection the vector spaces used to model the sources and electrical properties need to be handled with care. The mathematical formulation allows for the source to be a distribution whereas the electric potential is always a function. This leads to the consideration that the optimal methods to recover the source and electric potential may not be the same. We proposed an alternating minimization procedure to solve the problem. We managed to show that this procedure converges to the desired solution and converges to the Tychonov functional linearly.
For more general source terms (vector valued measures, vector-fields), an alternating minimization procedure between refining the cortical mapping and the source localization is being studied and implemented. It takes advantage of the fact that both the source and the surface potentials are assumed to be elements of Banach spaces that have certain smoothness properties which enable the convergence to a solution as soon as the problem is convex. This alleviates problems that may be encountered when the regularizing term is non-smooth. This opens up the possibility to consider sources that may exhibit properties usually associated with distributions rather than functions 23.
7.2 Stability assessment of microwave circuits
Participants: Laurent Baratchart, Sylvain Chevillard, Fabien Seyfert, Adam Cooman.
This year we pursued the study, initiated in 27 in collaboration with J.-B. Pomet from the McTao team (Inria Sophia Antipolis), of the harmonic transfer function (HTF) of a linear difference delay control system having finitely many (possibly non-commensurable) delays and periodic coefficients (having the same period). That is, an input-output system of the form:
where are positive delays and real matrices depending periodically on time , while is the -valued input and the -valued output (complex coefficients can of course be handled in the same way). The HTF, that generalizes the usual transfer function of linear constant systems, is an analytic function of the Laplace-Fourier variable which is valued in the space of operators a Hilbert space of periodic functions (the period being that of the system). We were able to construct a simple nonlinear circuit whose linearization around a periodic trajectory has a spectrum containing a whole circle; we currently investigate whether the singularities of the Fourier coefficients of the HTF (that are themselves analytic functions) also contain that circle. Indeed, just like a series of functions may diverge even though the summands are smooth, it is a priori possible that the HTF has a singularity at a point whereas its Fourier coefficients do not. Note that these coefficients are all one can estimate by harmonic balance techniques, and therefore the above question is of great practical relevance.
7.3 Hardy-Hodge decomposition with applications to silent sources
Participants: Laurent Baratchart, Juliette Leblond, Masimba Nemaire, Cristóbal Villalobos Guillén.
In a joint work with T. Qian and P. Dang from the university of Macao 59, we proved that on a compact hypersurface embedded in , a -valued vector field of class decomposes as the sum of a harmonic gradient from inside , a harmonic gradient from outside , and a tangent divergence-free field, provided that , where and depend on the Lipschitz constant of the surface. We also showed that the decomposition is valid for when is -smooth (i.e. is locally the graph of Lipschitz function with derivatives in ). By projection onto the tangent space, this gives us a Helmholtz-Hodge decomposition for vector fields on a compact Lipschitz hypersurface, which is apparently new since existing results deal with smooth surfaces. In fact, the Helmholtz-Hodge decomposition holds on Lipschitz surfaces (not just hypersurfaces), In 44, we had also showed that -magnetizations (i.e. -valued vector fields) on a compact connected Lipschitz surface embedded in that are silent outside (i.e. that produce no magnetic field in the unbounded component of the complement of the surface) form the orthogonal space to harmonic gradients inside the surface. This result teams up with the Hardy-Hodge decomposition to produce a description of silent magnetizations distributions of -class on a surface as solutions to a certain spectral equation for the double layer potential (for restricted range of when the surface is only Lipschitz). This last piece of research was a collaboration with C. Gerhards and A. Kegeles from TU Freiberg.
In a similar vein, a version of the Hardy-Hodge decomposition has been developed this year for the Helmholtz equation, in collaboration with H. Haddar from the team IDEFIX (Inria Saclay). This work was presented in part at the 2022 Waves conference 22. Our motivation to study such issues stems from a linearized model for an acoustic scattering problem with anisotropic layer, in the limit as the thickness of the layer goes to 0. From the mathematical point of view, the problem generalizes the one of recovering magnetizations mentioned above. Here, we work with sources belonging to , where is a bounded Lipschitz domain in . The generalization comes from taking the Helmholtz equation instead of the Poisson equation, that is:
where and is the restriction of 2-dimensional Hausdorff measure to . Since the inverse problem of recovering is non uniquely solvable with kernel of infinite dimension, the decomposition of the space of sources to come is useful for it allows one to discuss constraints that restore uniqueness. Below, we take to be the exterior unit normal to , and denote the normal component of while is its tangential component. We define three spaces as follows:
Like in the Poisson case, it can be shown that if and only . However, unlike the Poisson equation case, there is a nontrivial (but still finite-dimensional) space whose nontrivial elements produce a field that cannot be decomposed as the sum of fields which are zero except on one component of . The dimension of this space depends on the wave number of the Helmholtz equation and is at most the number of connected components of (it is in fact, the dimension of the vector space generated by piecewise constant and continuous normal functions on which are non-silent). Then, it holds that . Using this decomposition it is clear that the problem of recovering sources when measurements are merely taken in the unbounded component of the complement of the sample (this is the only accessible component) is solvable only up to an element of , so that any approach to solve this inverse problem should take this into consideration.
It should be noted that reference 22, instead of working in , focuses on those such that and (the 1-form that is the flat of , i.e., for -a.e. and tangent to at , ) has coefficients in . This class of magnetizations admits an analogous decomposition that is easier to prove, but it is more difficult to grasp. For this reason, and the fact that working with functions has better applications, we are currently focusing on .
We also pursued this year our work on a direct characterization of silent , () vector-fields; that is, vector fields representing magnetizations whose field is zero almost everywhere off . Specifically, we showed that a vector field carried by a finitely connected bounded open set , with boundary of zero measure, is silent outside if and only if, in its Helmholtz decomposition as the sum of a gradient and a divergence-free field on , both summands vanish a.e. outside of . Moreover, under the mild conditions on that its boundary be of zero Lebesgue measure and that if two connected components of meet then the intersection is “thick in the capacitory sense”, a magnetization is silent if and only if where lies in the Sobolev space and belongs to the closure of smooth functions with gradient compactly supported in , while the extension by zero of ,, is divergence-free on . When , without any additional smoothness assumption, this is enough to conclude that lies in the closure of smooth, silent vector field compactly supported in . When , this raises the issue as to when divergence free vector fields carried by lie in the closure of smooth divergence free fields compactly supported in .
When is Lipschitz, such regularity issues are easily unwound, entailing that silent vector-fields (i.e. vector fields representing magnetizations that produce the zero magnetic field outside ) are of the form with (the familiar space of Sobolev functions with locally constant trace, with possibly different constant on different connected components of the boundary) and divergence-free with zero normal component on the boundary 28. It should be noticed that this holds for , even though the Helmholtz decomposition in may not hold for every -field (in general, for Lipschitz open sets, it only holds for in a neighborhood of ). The previous characterization makes it possible to describe the norm-minimizing equivalent vector-field to a given vector-field . Here, two vector-fields are equivalent if their magnetic potentials outside differ by a constant (possibly different constants in different connected components of the complement), or equivalently if the vector-fields differ by a silent source. To this effect, we exploited the fact that the norm-minimizing equivalent source can be written as with a harmonic function in with orthogonal to all silent magnetizations in . This yields in passing a nonlinear Hodge-like decomposition, valid for all on Lipschitz open sets, containing an extra -divergence-free term. Moreover, maximizes among all harmonic gradients orthogonal to silent sources in with -norm 1. In practice, when is Lipschitz, one may further use that can be expressed as a single layer potential, say with maximizing the duality pairing on (here is the Newton potential of the distributional divergence of ) under appropriate constraints. Thus, a Galerkin-type method can be used to approach the problem numerically, using a frame of the space of distributions that can be constructed as in 82. Alternatively, in the case where and is a simply connected domain, a minimization procedure that alternates between approximating by a silent gradient and a silent divergence-free vector-field can be used. This alternating minimization procedure makes connection with a non-linear stationary Maxwell system and a -Laplace boundary value problem, both of which can be solved via Galerkin methods with the use of finite elements methods. Of course, with sparsity properties in mind, it would be very interesting to derive counterparts of these results in the case , on smooth domains at least. Note that the present definition of a silent magnetization is different, when the boundary of is not connected, from the one defined in 45.
7.4 Identification of resonating frequencies of compact metallic objects in electromagnetic inverse scattering
Participants: Paul Asensio, Laurent Baratchart, Juliette Leblond, Martine Olivi, Fabien Seyfert, Dmitry Ponomarev.
Some fundamental aspects of the temporal behavior of the solution of the time-domain wave equation (in spatial dimensions 1, 2 and 3) have been studied in recent works 13, 14 in connection with designing an efficient time-domain solver for the Helmholtz equation in high-frequency regime and with smooth coefficients 25. In physical 3D settings, the rate of the stabilization of the solution is linked to the location and the strength of the resonances (poles of meromorphic continuation of the resolvent operator). Since the information on the resonances is useful for the inverse problems (object identification), some of the already developed numerical methods could be employed for their efficient computation. Those methods would often rely on the complex-scaling (PML) approach to the open-domain problems 81 and have yet to be compared with the present rational-approximation viewpoint adopted by the team.
Another connection between time-domain methods for elliptic PDE problems and inverse problems is the so-called controllability approach which has recently received a renewed interest 71. In such an approach, one seeks to accelerate temporal convergence to the stationary solution of the time-domain wave equation with a periodic source term by minimizing the difference of the initial solution and the solution after one time-period. Once properly set up, this would yield the solution to the original Helmholtz equation without large computational costs of simulating the time-domain problem for long times. Potential extension of such methods could be a possibility for future joint work with Atlantis team.
Related to our collaboration with LEAT, the rational approximation of the transfer function defined in Section 4.5 is performed with a least-squares version of Padé approximant: given by:
where , and are integers such that and is a collection of points at which is analytic. Here, is the set of polynomials of degree less than and is the set of monic polynomials of degree . We seek an extension of the Nuttall-Pommerenke theorem for this approximation scheme; i.e., that the capacity of the set where the pointwise error is bigger than some goes to zero as , and go to infinity, while meeting some constraints to be made precise (expressing typically that remains much larger than ). Such a theorem would be very interesting, as it would further imply that certain poles of can indeed be retrieved using this method 21.
7.5 Other elliptic PDE problems: from direct to inverse problems
Participants: Juliette Leblond, Dmitry Ponomarev.
Some direct problems have been considered from an analytical viewpoint that could shed light on their inverse counterparts.
Simplest wave processes, such as scattering problem for the Schrödinger equation (instrumental in the inverse scattering method), have been investigated constructively due to a recently observed connection with a first-order ODE involving the complex-conjugation non-linearity 16. D-bar problems are not new to the team and since this ODE can be viewed as a one-dimensional version of the d-bar equation 5, it is a first step in exploring the advantages it could bring to analysis and constructive solution of some classes of the the d-bar problem.
The papers 15, 32 deal with the extension of classical model of contact problem with sliding punch in presence of material wear. The semi-explicit form of the obtained results and the generality of the model call for looking into relevant inverse problems. These could include, for example, determining an optimal initial shape of the punch profile that would minimize the worn volume.
In a joint work (to be published in 2023) with E. Pozzi (Saint Louis Univ., Missouri, USA), we present an operator theoretical approach of some inverse problems. It gives an overview of the solution to linear forward and inverse problems for a class of elliptic PDE in two-dimensional domains, in the framework of Banach spaces and operators. We focused on the conductivity equation, with smooth enough conductivity (see Section 3.2.1), and with Dirichlet or Neumann or mixed boundary conditions. For domains with Dini-smooth boundary, the approach is based on the properties of generalized Hardy spaces.
7.6 Spectra of Toeplitz operators
Participants: Juliette Leblond, Masimba Nemaire.
When solving fixed point problems using iterative methods, the rate of convergence is determined by the spectral radius of the operator and how quickly the iterative methods settle to the convergence rates is determined by the growth of the resolvent of the operator. It is therefore of interest to study the spectra of operators, here we studied the spectra of Toeplitz operators, together with S. Kupin (IMB, Univ. Bordeaux) and L. Golinskii (B. Verkin Institute for Low Temperature Physics and Engineering, Kharkiv, Ukraine).
Let be the unit disk in the complex plane, and let . We showed that the essential spectrum of a Toeplitz operator with symbol is equal to the essential spectrum of a Toeplitz-Bergman operator with symbol that is the harmonic extension of to 31.
7.7 Tools for numerically guaranteed computations
Participants: Sylvain Chevillard.
The overall and long-term goal is to enhance the quality of numerical computations. The software tool Sollya (see Section 3.4.6), developed together with C. Lauter (University of Texas at El Paso, UTEP) intends to provide an interactive environment for performing numerically rigorous computations. It comes as a standalone tool and also as a C library that allows one to benefit from all the features of the tool in C programs.
In February 2022, we released version 8.0. This release keeps up to date with recent changes in the API of the libfplll library which is a dependency of Sollya. It implements general improvements of the tool (better complexity of some algorithms, better consistency in the results by different commands, etc.) and add two new commands (namely interpolate and bezout to compute respectively interpolation polynomials and extended gcd).
8 Bilateral contracts and grants with industry
8.1 Bilateral Contracts with Industry
Contract Inria-Inoveos
Participants: Laurent Baratchart, Sylvain Chevillard, Martine Olivi, Fabien Seyfert.
We had a contract with the SMB company Inoveos in order to build a prototypical robot dedicated to the automatic tuning of microwave devices. In addition to Inria, this project included the university of Limoges Xlim and the engineering center Cisteme.9 Partnerships and cooperations
9.1 International research visitors
9.1.1 Visits of international scientists
Other international visits to the team
Maxim Yattselev
-
Status:
Researcher
-
Institution of origin:
Indiana University-Purdue University Indianapolis
-
Country:
Indiana, USA
-
Dates:
July 6-19, 2023
-
Context of the visit:
This is a long term research effort to describe the behavior of poles and zeros of asymptotically optimal meromorphic approximant to functions with singular set of capacity zero.
-
Mobility program/type of mobility:
Research stay
9.2 European initiatives
9.2.1 Other european programs/initiatives
Participants: Paul Asensio, Laurent Baratchart, Masimba Nemaire, Martine Olivi, Cristóbal Villalobos Guillén.
Factas is part of the European Research Network on System Identification (ERNSI) since 1992. System identification deals with the derivation, estimation and validation of mathematical models of dynamical phenomena from experimental data.
9.3 National initiatives
Participants: Paul Asensio, Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Masimba Nemaire, Martine Olivi, Cristóbal Villalobos Guillén, Anass Yousfi.
ANR REPKA
ANR-18-CE40-0035, “REProducing Kernels in Analysis and beyond” (2019–2023).
Led by Aix-Marseille Univ. (IMM), involving Factas team, together with Bordeaux (IMB), Paris-Est, Toulouse Universities.
The project consists of several interrelated tasks dealing with topical problems in modern complex analysis, operator theory and their important applications to other fields of mathematics including approximation theory, probability, and control theory. The project is centered around the notion of the so-called reproducing kernel of a Hilbert space of holomorphic functions. Reproducing kernels are very powerful objects playing an important role in numerous domains such as determinantal point processes, signal theory, Sturm-Liouville and Schrödinger equations.
This project supports the PhD of M. Nemaire within Factas, co-advised by IMB partners.
GDR AFHP
GDR “Analyse Fonctionnelle, Harmonique et Probabilités”.
Led by Gustave Eiffel Univ. (LAMA), involving Factas team, together with several universities.
The GDR is concerned with five main axes: linear dynamics, Banach spaces and their operators, holomorphic dynamics, harmonic analysis, analysis and probability, and with the interactions between them.
9.4 Regional initiatives
Participants: Juliette Leblond, Vanna Lisa Coli.
Arch-AI-Story
The collaborative project Arch-AI-Story funded by the Idex started last year brings together researchers in archaeology and history, physical, and mathematical sciences, with, in particular, the purpose of modeling and detecting low level signals in 3-D images of ancient potteries, see Section 4.6. It involves scientists from CEPAM-CNRS-UCA (project coordinator: Isabelle Théry), Nice, the team Morpheme, UCA-CNRS-I3S-Inria, together with other institutions, and supports the research of Vanna Lisa Coli.
10 Dissemination
Participants: Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Martine Olivi.
10.1 Promoting scientific activities
10.1.1 Scientific events: selection
Member of the conference program committees
- L. Baratchart was sitting on the program committee of IPMS 2022.
10.1.2 Journal
Member of the editorial boards
- L. Baratchart is a member of the editorial boards of CMFT and CAOT.
Reviewer - reviewing activities
- S. Chevillard was a reviewer for Computational Methods and Function Theory.
- J. Leblond was a reviewer for Asymptotic Analysis.
10.1.3 Invited talks
- L. Baratchart was an invited speaker at the conference “Operators, Functions, Systems: Classical and Modern” (12.06-18.06.2022, Bedlewo, Poland).
10.1.4 Research administration
- J. Leblond is a member of the “Conseil Scientifique” and of the “Commission Administrative Paritaire” of Inria, and of the “équipe transformation” of the Research Center.
- M. Olivi is a member of the CLDD (Commission Locale de Développement Durable) and in charge of coordination.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- S. Chevillard gives “Colles” (oral examination preparing undergraduate students for the competitive examination to enter French Engineering Schools) at Centre International de Valbonne (CIV) (2 hours per week). In 2022, he also gave a course on Carbon Footprints at Polytech Sophia Antipolis, as a participant of the course Environmental Issues addressed to all students of Polytech, whatever their pathway (level L3; the course on Carbon Footprints was 2 hours long and represented a fifth of the whole course; it was repeated 3 times, due to the year group being divided into three sub-groups).
10.2.2 Supervision
- PhD in progress: P. Asensio, Inverse source estimation problems in EEG and MEG, since November 2019, advisers: L. Baratchart, J. Leblond.
- PhD in progress: M. Nemaire, Inverse potential problems with application to quasi-static electromagnetics, since October 2019, advisers: L. Baratchart, J. Leblond, S. Kupin (IMB, Univ. Bordeaux).
- PhD in progress: A. Yousfi, Methods to estimate the net magnetic moment of rocks, since October 2022 (Pre-PhD from October 2021 to September 2022), advisers: S. Chevillard, J. Leblond.
- Post-doc.: C. Villalobos-Guillén, Inverse source problems for magnetization , primary current and inverse scattering, since December 2021; adviser: L. Baratchart.
10.2.3 Juries
- L. Baratchart was leading the examining committee for the defense of the PhD thesis of T. Metzlaff.
10.3 Popularization
10.3.1 Internal or external Inria responsibilities
- M. Olivi is a member of the Committee MASTIC (Commission d'Animation et de Médiation Scientifique) and of Terra Numerica.
10.3.2 Articles and contents
- S. Chevillard and M. Olivi wrote an article with D. Saucez (DIANA) for the platform Pixees (Ressources pour les sciences du numérique): Peut-on dire que la croissance des émissions de CO2 est exponentielle ?
10.3.3 Education
- Stage MathC2+: M. Olivi prepared a workshop “Mathématique et Environnement” with D. Saucez (DIANA) and C. Djuikem (BIOCORE)
- M. Olivi co-supervised a master intern at Terra Numerica: B. Pellegrinetti.
10.3.4 Interventions
- C@fé-in: Sobriété numérique ou numérique frugal ? M. Olivi
- “Fête des Maths” at INSPE Liegeard: J. Leblond and M. Olivi
- “Village des Sciences et de l'Innovation” Antibes Juan-les-Pins: presentation of the MOOC “Impacts Environnementaux du Numérique” and the epoc “Le Smartphone et la Planète”, M. Olivi with A. Schneider and A. Lagarrigue.
- Intervention at “Lycée Simone Veil” (2 hours, classe de seconde): M. Olivi with B. Pellegrinetti (master intern Terra Numerica).
- S. Chevillard gave (three times) a general audience conference “Que peut-on faire contre le réchauffement climatique ?” as a member of the Science pour tous association whose goal is to popularize science in the Département des Alpes-Maritimes.
- L. Baratchart was a speaker at the analysis seminar of CMI (Université de Provence).
- P. Asensio, L. Baratchart, M. Nemaire, C. Villalobos-Guillén gave talks at IMPS 2022 (Malta).
- L. Baratchart gave a talk at the SMAI-SIGMA conference C&S 2022 (Arcachon, France).
- P. Asensio, M. Nemaire, C. Villalobos-Guillén gave talks at Waves 2022 (Palaiseau, France).
- C. Villalobos-Guillén gave a talk at SIAM Conference on Imaging Science (online).
11 Scientific production
11.1 Major publications
- 1 articleBounded extremal and Cauchy-Laplace problems on the sphere and shell.J. Fourier Anal. Appl.162Published online Nov. 20092010, 177--203URL: http://dx.doi.org/10.1007/s00041-009-9110-0
- 2 articleMagnetic moment estimation and bounded extremal problems.Inverse Problems and Imaging 131February 2019, 29
-
3
articleMinimax principle and lower bounds in
-rational approximation.Journal of Approximation Theory2062015, 17--47 - 4 articleSufficient Stability Conditions for Time-varying Networks of Telegrapher's Equations or Difference Delay Equations.SIAM Journal on Mathematical Analysis532021, 1831–1856
- 5 articleHardy spaces of the conjugate Beltrami equation.Journal of Functional Analysis25922010, 384-427URL: http://dx.doi.org/10.1016/j.jfa.2010.04.004
- 6 articleBoundary Nevanlinna-Pick interpolation with prescribed peak points. Application to impedance matching.SIAM Journal on Mathematical Analysis2017
- 7 articleWeighted Extremal Domains and Best Rational Approximation.Advances in Mathematics2292012, 357-407URL: http://hal.inria.fr/hal-00665834
- 8 articleInverse Potential Problems for Divergence of Measures with Total Variation Regularization.Foundations of Computational Mathematics202020, 1273-1307
- 9 articleSource localization using rational approximation on plane sections.Inverse Problems285May 2012, Article number 055018 - 24 pages
- 10 articleModel-Free Closed-Loop Stability Analysis: A Linear Functional Approach.IEEE Transactions on Microwave Theory and Techniqueshttps://arxiv.org/abs/1610.032352017
- 11 inbookOn some extremal problems for analytic functions with constraints on real or imaginary parts.Advances in Complex Analysis and Operator Theory: Festschrift in Honor of Daniel Alpay's 60th BirthdayBirkhauser2017, 219-236
- 12 articleIdentification of microwave filters by analytic and rational H2 approximation.Automatica492January 2013, 317-325
11.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Scientific book chapters
Reports & preprints
11.3 Cited publications
- 34 bookElements of the Theory of Elliptic Functions.AMS1990
- 35 articleOn the Differential Structure of Matrix-Valued Rational Inner Functions.Operator Theory~: Advances and Applications731994, 30--66
- 36 bookPadé approximants.Cambridge University Press2010
- 37 bookInterpolation of rational matrix functions.Birkhäuser1990
-
38
articleA remark on uniqueness of best rational approximants of degree 1 in
of the circle. Elec. Trans.on Numerical Anal.252006, 54--66 - 39 articlePseudo-holomorphic functions at the critical exponent.Journal of the European Mathematical Society1892016
- 40 articleUniqueness results for inverse Robin problems with bounded coefficient.Journal of Functional Analysis2016
-
41
articleIdentification and rational
approximation: a gradient algorithm.Automatica271991, 413--418 - 42 articleA Grobman-Hartman theorem for control systems.J. Dyn. Differential Eqs.192007, 75-107
- 43 articleDirichlet/Neumann problems and Hardy classes for the planar conductivity equation.Complex Variables and Elliptic Equations2014, 41
- 44 articleDecomposition of L2-vector fields on Lipschitz surfaces: characterization via null-spaces of the scalar potential.SIAM Journal on Mathematical Analysis5342021, 4096 - 4117
- 45 articleUnique reconstruction of simple magnetizations from their magnetic potential.Inverse Problems3710September 2021, 105006
- 46 inproceedingsOrthogonal rational functions and nonstationary stochastic processes: a Szegő theory.Proc. 19th Symposium on Mathematical Theory of Networks and SystemsBudapest2010
- 47 articleCharacterizing kernels of operators related to thin-plate magnetizations via generalizations of Hodge decompositions.Inverse Problems2912013, URL: https://hal.inria.fr/hal-00919261
- 48 articleZero distributions via orthogonality.Annales de l'Institut Fourier5552005, 1455--1499
- 49 articleMultipoint Schur algorithm and orthogonal rational functions: convergence properties, I.Journal d'Analyse1122011, 207-255URL: https://arxiv.org/abs/0812.2050v3
-
50
articleHardy approximation to
functions on subsets of the circle with .Constructive Approximation141998, 41--56 - 51 articleHow can meromorphic approximation help to solve some 2D inverse problems for the Laplacian?Inverse Problems1511999, 79--90URL: https://dx.doi.org/10.1088/0266-5611/15/1/012
- 52 articleSources identification in 3D balls using meromorphic approximation in 2D disks.Electronic Transactions on Numerical Analysis (ETNA)252006, 41--53
-
53
articleHardy approximation to
functions on subsets of the circle.Constructive Approximation121996, 423--435 - 54 articleConstrained extremal problems in H2 and Carleman's formulas.Matematicheskii Sbornik20972018, 36
- 55 article2D inverse problems for the Laplacian: a meromorphic approximation approach.Journal de Math. Pures et Appliquées862008, 1-41
-
56
articleCritical points and error rank in best
matrix rational approximation of fixed McMillan degree.Constructive Approximation141998, 273--300 -
57
articleIndex of critical points in
-approximation.System and Control Letters101988, 167--174 -
58
inproceedingsOn the
Rational Approximation of Markov Matrix-Valued Functions.Proc. 17th Symposium on Mathematical Theory of Networks and Systems (MTNS)Kyoto, Japon2006, 180--182 - 59 unpublishedHardy-Hodge decomposition of vector fields on compact Lipschitz hypersurfaces., in preparation
-
60
articleA criterion for uniqueness of a critical point in
rational approximation.Journal d'Analyse701996, 225--266 -
61
articleAn
analog to AAK theory for .Journal of Functional Analysis19112002, 52--122 -
62
articleAsymptotic uniqueness of best rational approximants of given degree to Markov functions in
of the circle.Constr. Approx.1712001, 103--138 -
63
incollectionAsymptotic uniqueness of best rational approximants to complex Cauchy transforms in
of the circle.Recent trends in orthogonal polynomials and approximation theory507Contemp. Math.Providence, RIAmer. Math. Soc.2010, 87--111 - 64 articleConvergent Interpolation to Cauchy Integrals over Analytic Arcs with Jacobi-Type Weights.International Mathematics Research Notices2010222010, 4211--4275URL: https://hal.inria.fr/hal-00508314
- 65 articleConvergent interpolation to Cauchy integrals over analytic arcs.Found. Comp. Math.962009, 675--715
- 66 articleMeromorphic approximants for complex Cauchy transforms with polar singularities.Mat. Sbornik20092009, 3-40
- 67 articleSources recovery from boundary data: a model related to electroencephalography.Mathematical and Computer Modelling4911--122009, 2213--2223URL: https://dx.doi.org/10.1016/j.mcm.2008.07.016
- 68 articleExhaustive approach to the coupling matrix synthesis problem and application to the design of high degree asymmetric filters.International Journal of RF and Microwave Computer-Aided Engineering1712007, 4--12URL: https://hal.inria.fr/hal-00663777
- 69 articleLogarithmic stability estimates for a Robin coefficient in 2D Laplace inverse problems.Inverse Problems2012004, 49--57URL: https://dx.doi.org/10.1088/0266-5611/20/1/003
- 70 phdthesisAnalyse complexe et problèmes de Dirichlet dans le plan : équation de Weinstein et autres conductivités non bornées.Mathématiques et Informatique de Marseille2013
- 71 articleA controllability method for Maxwell's equations.arXiv preprint arXiv:2106.028582021
- 72 articleFactorization theorems for Hardy spaces in several variables.Ann. Math.1031976, 611--635
- 73 phdthesisApproximation des des classes de fonctions analytiques généralisées et résolution de problèmes inverses pour les tokamaks.Univ. Nice Sophia Antipolis2011, URL: https://tel.archives-ouvertes.fr/tel-00643239/
- 74 articleDetermining cracks by boundary measurements.Indiana Univ. Math. J.3831989, 527--556
-
75
articleMatrix rational
-approximation: a gradient algorithm based on Schur analysis.SIAM J. on Control & Optim.361998, 2103--2127 - 76 bookBounded analytic functions.Academic Press1981
- 77 articleA topological approach to Nevanlinna-Pick interpolation.SIAM J. Math. Anal.1851987, 1248--1260
- 78 articleBalanced realizations of discrete-time stable all-pass systems and the tangential Schur algorithm.Linear Algebra and its Applications4182006, 793-820URL: https://dx.doi.org/10.1016/j.laa.2006.09.029
- 79 articleFrequency domain analysis and analytic selections.Indiana Univ. Math. J.3911990, 157--184
- 80 bookGeometric function theory and non-linear analysis.Oxford Univ. Press2001
- 81 articleThe computation of resonances in open systems using a perfectly matched layer.Mathematics of Computation782672009, 1375--1398
- 82 articleOn the construction of frames for spaces of distributions.Journal of Functional Analysis2572009, 2159--2187
- 83 bookFoundations of modern potential theory.Springer-Verlag1972
- 84 bookSome Improperly Posed Problems of Mathematical Physics.Springer1967
- 85 inbookTopics in Classical and Modern Analysis. Applied and Numerical Harmonic Analysis.M.M. AbellE.E. IacobA.A. StokolosS.S. TaylorS.S. TikhonovJ.J. ZhuBirkhäuser2019, The Spurious Side of Diagonal Multipoint Padé Approximants
- 86 articleCertified Computation of Optimal Multiband Filtering Functions.IEEE Transactions on Microwave Theory and Techniques5612008, 105-112URL: https://dx.doi.org/10.1109/TMTT.2007.912234
- 87 articleNudelman Interpolation, Parametrization of Lossless Functions and balanced realizations.Automatica432007, 1329--1338URL: https://dx.doi.org/10.1016/j.automatica.2007.01.020
- 88 bookHankel Operators and their Applications.Springer2003
- 89 phdthesisSome inverse problems with partial data.INRIA Sophia Antipolis - MéditerranéeJune 2016
- 90 articleConstrained Hardy space approximation.J. Approx. Theory82010, 1466--1483
- 91 articleÜber Potenzreihen die im innern des einheitskreises beschränkt sind.J. Reine Angew. Math.1471917, 205--232
- 92 inproceedingsExtraction of coupling parameters for microwave filters: determinati on of a stable rational model from scattering data.2003 IEEE MTT-S International Microwave Symposium Digest1Philadelphie, États-UnisIEEE2003, 25--28URL: https://hal.inria.fr/hal-00663504
- 93 bookHarmonic Analysis.Princeton University Press1993
- 94 bookStability analysis of nonlinear microwave circuits.Artech House2003
-
95
inproceedingsCounterexamples with harmonic gradients in
.Essays on Fourier analysis in honor of Elias M. Stein42Math. Ser.Princeton Univ. Press1995, 321--384 - 96 inproceedingsComparison of SEM Methods for Poles Estimation from Scattered Field by Canonical Objects.Renaissance meets advancing technologyFlorence, ItalySeptember 2020, 6URL: https://hal.science/hal-02941637

