Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.4. Multiscale modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.3. Probabilistic methods
- A6.3. Computation-data interaction
- A6.3.4. Model reduction
Other Research Topics and Application Domains
- B1. Life sciences
- B1.2. Neuroscience and cognitive science
- B1.2.1. Understanding and simulation of the brain and the nervous system
- B1.2.2. Cognitive science
1 Team members, visitors, external collaborators
Research Scientists
- Mathieu Desroches [Team leader, INRIA, Researcher, HDR]
- Fabien Campillo [INRIA, Senior Researcher, HDR]
- Anton Chizhov [INRIA, Advanced Research Position, from Jun 2022, HDR]
- Pascal Chossat [CNRS, Emeritus, HDR]
- Olivier Faugeras [INRIA, Emeritus, HDR]
- Maciej Krupa [UNIV COTE D'AZUR, Senior Researcher, HDR]
Post-Doctoral Fellows
- Mattia Sensi [INRIA]
- Marius Emar Yamakou [UNIV ERLANGEN, from Oct 2022]
Interns and Apprentices
- Ufuk Cem Birbiri [UNIV COTE D'AZUR, from May 2022 until Sep 2022]
Administrative Assistant
- Marie-Cecile Lafont [INRIA]
Visiting Scientist
- Jordi Penalva Vadell [UNIV BALEARIC ISLANDS, from Oct 2022, Y304]
External Collaborators
- Serafim Rodrigues [Team leader, BCAM, from Apr 2022 until Apr 2022, HDR]
- Frederic Lavigne [UNIV COTE D'AZUR, from Sep 2022, Y509, HDR]
2 Overall objectives
MathNeuro focuses on the applications of multi-scale dynamics to neuroscience. This involves the modelling and analysis of systems with multiple time scales and space scales, as well as stochastic effects. We look both at single-cell models, microcircuits and large networks. In terms of neuroscience, we are mainly interested in questions related to synaptic plasticity and neuronal excitability, in particular in the context of pathological states such as epileptic seizures and neurodegenerative diseases such as Alzheimer.
Our work is quite mathematical but we make heavy use of computers for numerical experiments and simulations. We have close ties with several top groups in biological neuroscience. We are pursuing the idea that the "unreasonable effectiveness of mathematics" can be brought, as it has been in physics, to bear on neuroscience.
Modeling such assemblies of neurons and simulating their behavior involves putting together a mixture of the most recent results in neurophysiology with such advanced mathematical methods as dynamical systems theory, bifurcation theory, probability theory, stochastic calculus, theoretical physics and statistics, as well as the use of simulation tools.
We conduct research in the following main areas:
- Neural networks dynamics
- Mean-field and stochastic approaches
- Neural fields
- Slow-fast dynamics in neuronal models
- Modeling neuronal excitability
- Synaptic plasticity
- Memory processes
- Visual neuroscience
3 Research program
3.1 Neural networks dynamics
The study of neural networks is certainly motivated by the long term goal to understand how brain is working. But, beyond the comprehension of brain or even of simpler neural systems in less evolved animals, there is also the desire to exhibit general mechanisms or principles at work in the nervous system. One possible strategy is to propose mathematical models of neural activity, at different space and time scales, depending on the type of phenomena under consideration. However, beyond the mere proposal of new models, which can rapidly result in a plethora, there is also a need to understand some fundamental keys ruling the behaviour of neural networks, and, from this, to extract new ideas that can be tested in real experiments. Therefore, there is a need to make a thorough analysis of these models. An efficient approach, developed in our team, consists of analysing neural networks as dynamical systems. This allows to address several issues. A first, natural issue is to ask about the (generic) dynamics exhibited by the system when control parameters vary. This naturally leads to analyse the bifurcations 59 60 occurring in the network and which phenomenological parameters control these bifurcations. Another issue concerns the interplay between the neuron dynamics and the synaptic network structure.
3.2 Mean-field and stochastic approaches
Modeling neural activity at scales integrating the effect of thousands of neurons is of central importance for several reasons. First, most imaging techniques are not able to measure individual neuron activity (microscopic scale), but are instead measuring mesoscopic effects resulting from the activity of several hundreds to several hundreds of thousands of neurons. Second, anatomical data recorded in the cortex reveal the existence of structures, such as the cortical columns, with a diameter of about 50
Our group is developing mathematical methods allowing to produce dynamic mean-field equations from the physiological characteristics of neural structure (neurons type, synapse type and anatomical connectivity between neurons populations). These methods use tools from advanced probability theory such as the theory of Large Deviations 48 and the study of interacting diffusions 3.
3.3 Neural fields
Neural fields are a phenomenological way of describing the activity of population of neurons by delayed integro-differential equations. This continuous approximation turns out to be very useful to model large brain areas such as those involved in visual perception. The mathematical properties of these equations and their solutions are still imperfectly known, in particular in the presence of delays, different time scales and noise.
Our group is developing mathematical and numerical methods for analysing these equations. These methods are based upon techniques from mathematical functional analysis, bifurcation theory 18, 62, equivariant bifurcation analysis, delay equations, and stochastic partial differential equations. We have been able to characterize the solutions of these neural fields equations and their bifurcations, apply and expand the theory to account for such perceptual phenomena as edge, texture 42, and motion perception. We have also developed a theory of the delayed neural fields equations, in particular in the case of constant delays and propagation delays that must be taken into account when attempting to model large size cortical areas 61. This theory is based on center manifold and normal forms ideas 17.
3.4 Slow-fast dynamics in neuronal models
Neuronal rhythms typically display many different timescales, therefore it is important to incorporate this slow-fast aspect in models. We are interested in this modeling paradigm where slow-fast point models, using Ordinary Differential Equations (ODEs), are investigated in terms of their bifurcation structure and the patterns of oscillatory solutions that they can produce. To insight into the dynamics of such systems, we use a mix of theoretical techniques — such as geometric desingularisation and centre manifold reduction 52 — and numerical methods such as pseudo-arclength continuation 46. We are interested in families of complex oscillations generated by both mathematical and biophysical models of neurons. In particular, so-called mixed-mode oscillations (MMOs)12, 44, 51, which represent an alternation between subthreshold and spiking behaviour, and bursting oscillations45, 50, also corresponding to experimentally observed behaviour 43; see Figure 1. We are working on extending these results to spatio-temporal neural models 2.
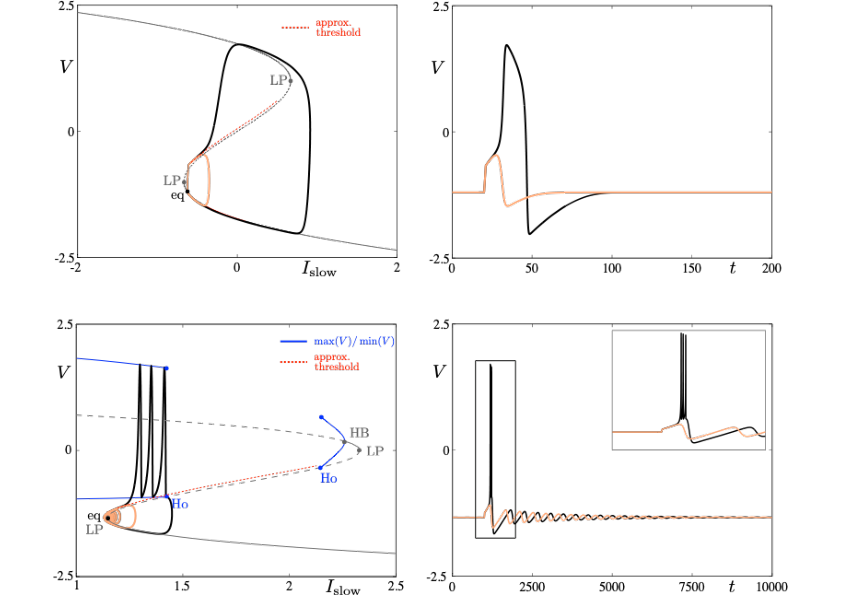
Excitability threshold as slow manifolds in a simple spiking model, namely the FitzHugh-Nagumo model, (top panels) and in a simple bursting model, namely the Hindmarsh-Rose model (bottom panels).
3.5 Modeling neuronal excitability
Excitability refers to the all-or-none property of neurons 47, 49. That is, the ability to respond nonlinearly to an input with a dramatic change of response from “none” — no response except a small perturbation that returns to equilibrium — to “all” — large response with the generation of an action potential or spike before the neuron returns to equilibrium. The return to equilibrium may also be an oscillatory motion of small amplitude; in this case, one speaks of resonator neurons as opposed to integrator neurons. The combination of a spike followed by subthreshold oscillations is then often referred to as mixed-mode oscillations (MMOs) 44. Slow-fast ODE models of dimension at least three are well capable of reproducing such complex neural oscillations. Part of our research expertise is to analyse the possible transitions between different complex oscillatory patterns of this sort upon input change and, in mathematical terms, this corresponds to understanding the bifurcation structure of the model. In particular, we also study possible combinations of different scenarios of complex oscillations and their relevance to revisit unexplained experimental data, e.g. in the context of bursting oscillations 45. In all case, the role of noise 40 is important and we take it into consideration, either as a modulator of the underlying deterministic dynamics or as a trigger of potential threshold crossings. Furthermore, the shape of time series of this sort with a given oscillatory pattern can be analysed within the mathematical framework of dynamic bifurcations; see the section on slow-fast dynamics in Neuronal Models. The main example of abnormal neuronal excitability is hyperexcitability and it is important to understand the biological factors which lead to such excess of excitability and to identify (both in detailed biophysical models and reduced phenomenological ones) the mathematical structures leading to these anomalies. Hyperexcitability is one important trigger for pathological brain states related to various diseases such as chronic migraine 56, epilepsy 58 or even Alzheimer's Disease 53. A central central axis of research within our group is to revisit models of such pathological scenarios, in relation with a combination of advanced mathematical tools and in partnership with biological labs.
3.6 Synaptic Plasticity
Neural networks show amazing abilities to evolve and adapt, and to store and process information. These capabilities are mainly conditioned by plasticity mechanisms, and especially synaptic plasticity, inducing a mutual coupling between network structure and neuron dynamics. Synaptic plasticity occurs at many levels of organization and time scales in the nervous system 39. It is of course involved in memory and learning mechanisms, but it also alters excitability of brain areas and regulates behavioral states (e.g., transition between sleep and wakeful activity). Therefore, understanding the effects of synaptic plasticity on neurons dynamics is a crucial challenge.
Our group is developing mathematical and numerical methods to analyse this mutual interaction. On the one hand, we have shown that plasticity mechanisms 10, 16, Hebbian-like or STDP, have strong effects on neuron dynamics complexity, such as dynamics complexity reduction, and spike statistics.
3.7 Memory processes
The processes by which memories are formed and stored in the brain are multiple and not yet fully understood. What is hypothesised so far is that memory formation is related to the activation of certain groups of neurons in the brain. Then, one important mechanism to store various memories is to associate certain groups of memory items with one another, which then corresponds to the joint activation of certain neurons within different subgroup of a given population. In this framework, plasticity is key to encode the storage of chains of memory items. Yet, there is no general mathematical framework to model the mechanism(s) behind these associative memory processes. We are aiming at developing such a framework using our expertise in multi-scale modelling, by combining the concepts of heteroclinic dynamics, slow-fast dynamics and stochastic dynamics.
The general objective that we wish to pursue in this project is to investigate non-equilibrium phenomena pertinent to storage and retrieval of sequences of learned items. In previous work by team members 9, 1, 14, it was shown that with a suitable formulation, heteroclinic dynamics combined with slow-fast analysis in neural field systems can play an organizing role in such processes, making the model accessible to a thorough mathematical analysis. Multiple choice in cognitive processes require a certain flexibility in the neural network, which has recently been investigated in the submitted paper 28.
Our goal is to contribute to identify general processes under which cognitive functions can be organized in the brain.
4 Application domains
The project underlying MathNeuro revolves around pillars of neuronal behaviour –excitability, plasticity, memory– in link with the initiation and propagation of pathological brain states in diseases such as cortical spreading depression (in link with certain forms of migraine with aura), epileptic seizures and Alzheimer’s Disease. Our work on memory processes can also potentially be applied to studying mental disorders such as schizophrenia or obsessive disorder troubles.
5 Highlights of the year
The team decided to invest significantly in software development in collaboration with the SED (Service d’Expérimentation et de Développement) of Sophia Antipolis and the team led by Serafim Rodrigues at BCAM in Bilbao, see Section 6.
6 New software and platforms
Until now the team has only developed small ad-hoc simulation tools associated with articles. This year we have decided to implement a systematic and ambitious development strategy and to move to tested, reliable, documented and disseminable tools.
6.1 Interface and toolkit
Participants: Mathieu Desroches, Fabien Campillo, Serafim Rodrigues [BCAM Bilbao and external collaborator of MathNeuro], Anton Chizhov, Guillaume Girier.
In collaboration with Joanna Danielewicz, Research Technician (biologist) in MCEN at BCAM, Bilbao.
MathNeuro wishes to call upon the support and competence of the SED of Sophia Antipolis Méditerrannée to develop a collaborative project around an electrophysiology laboratory currently set up in Bilbao, which has already benefited from the support of Inria Sophia Antipolis Méditerrannée.
The goal of this project is to develop a software environment that will play an important role within MathNeuro and will be the focus of our collaboration with the MCEN lab (BCAM Bilbao) directed by Serafim Rodrigues.
The MCEN experimental neurophysiological dynamic-clamp device 57, 41 to interact with: an artificial neuron, an in vitro neuron, an in vivo neuron, to which we also want to add numerical simulations (neuron in silico). Beyond the activity of a single neuron, this device can also monitor the activity of a single ion channel or the activity of several neurons. This device is not only a measuring device, it also allows to inject a current into the neuron and thus to control the nerve cell 55.
6.2 Some simulation demonstration tools
Participant: Fabien Campillo.
Fabien Campillo has recently updated and made available four demonstration programs: three simulation of individual based models (IBM forest, IBM cellulose, IBM clonal) as well as a set of particle filtering demonstration software (SMC demos); see the gitlab repositories and the dedicated web page.
These tools are not recent, they are written in Matlab and we wish to update them in Python. The IBM models are Markov models now very developed and analyzed in life sciences. SMC Demos has met with some success and has participated in the diffusion of particle filtering tools.
7 New results
7.1 Neural networks as dynamical systems
7.1.1 Bump attractors and waves in networks of leaky integrate-and-fire neurons
Participant: Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro], Joshua Davis [University of Nottingham, UK], Kyle Wedgwood [University of Exeter, UK].
This work was partially carried out during an invitation of Daniele Avitabile within the MathNeuro team.
Bump attractors are wandering localised patterns observed in in vivo experiments of spatially-extended neurobiological networks. They are important for the brain's navigational system and specific memory tasks. A bump attractor is characterised by a core in which neurons fire frequently, while those away from the core do not fire. We uncover a relationship between bump attractors and travelling waves in a classical network of excitable, leaky integrate-and-fire neurons. This relationship bears strong similarities to the one between complex spatiotemporal patterns and waves at the onset of pipe turbulence. Waves in the spiking network are determined by a firing set, that is, the collection of times at which neurons reach a threshold and fire as the wave propagates. We define and study analytical properties of the voltage mapping, an operator transforming a solution's firing set into its spatiotemporal profile. This operator allows us to construct localised travelling waves with an arbitrary number of spikes at the core, and to study their linear stability. A homogeneous "laminar" state exists in the network, and it is linearly stable for all values of the principal control parameter. Sufficiently wide disturbances to the homogeneous state elicit the bump attractor. We show that one can construct waves with a seemingly arbitrary number of spikes at the core; the higher the number of spikes, the slower the wave, and the more its profile resembles a stationary bump. As in the fluid-dynamical analogy, such waves coexist with the homogeneous state, are unstable, and the solution branches to which they belong are disconnected from the laminar state; we provide evidence that the dynamics of the bump attractor displays echoes of the unstable waves, which form its building blocks.
This work has been accepted for publication in SIAM Review and is available as 19.
7.2 Mean field theory and stochastic processes
7.2.1 Network torus canards and their mean-field limits
Participants: Emre Baspinar [Institut des Neurosciences Paris-Saclay, MathNeuro], Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro], Mathieu Desroches.
This work was partially achieved during a stay of Daniele Avitabile in MathNeuro.
We show that during the transition from and to elliptic burstings both classical and mixed-type torus canards appear in a Wilson-Cowan type neuronal network model, as well as in its corresponding mean-field framework. We show numerically the overlap between the network and mean-field dynamics. We comment on that mixed-type torus canards result from the nonsymmetric fast subsystem. This nonsymmetricity provides the dynamics linked to an associated canonical form presented in 38, and it occurs mainly due to the three-timescale nature of the Wilson-Cowan type models.
This work is available as 34.
7.2.2 Cross-scale excitability in networks of quadratic integrate-and-fire neurons
Participants: Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro], Mathieu Desroches, G. Bard Ermentrout [University of Pittsburgh, USA].
This work was partially carried out during an invitation of Daniele Avitabile within the MathNeuro team.
From the action potentials of neurons and cardiac cells to the amplification of calcium signals in oocytes, excitability is a hallmark of many biological signalling processes. In recent years, excitability in single cells has been related to multiple-timescale dynamics through canards, special solutions which determine the effective thresholds of the all-or-none responses. However, the emergence of excitability in large populations remains an open problem. We show that the mechanism of excitability in large networks and mean-field descriptions of coupled quadratic integrate-and-fire (QIF) cells mirrors that of the individual components. We initially exploit the Ott-Antonsen ansatz to derive low-dimensional dynamics for the coupled network and use it to describe the structure of canards via slow periodic forcing. We demonstrate that the thresholds for onset and offset of population firing can be found in the same way as those of the single cell. We combine theoretical analysis and numerical computations to develop a novel and comprehensive framework for excitability in large populations, applicable not only to models amenable to Ott-Antonsen reduction, but also to networks without a closed-form mean-field limit, in particular sparse networks.
This work has been published in PLoS Computational Biology and is available as 20.
7.2.3 Bursting in a next generation neural mass model with synaptic dynamics: a slow-fast approach
Participants: Halgurd Taher, Mathieu Desroches, Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro].
This work was partially achieved during a stay of Daniele Avitabile in MathNeuro.
We report a detailed analysis on the emergence of bursting in a recently developed neural mass model that takes short-term synaptic plasticity into account. The one being used here is particularly important, as it represents an exact meanfield limit of synaptically coupled quadratic integrate & fire neurons, a canonical model for type I excitability. In absence of synaptic dynamics, a periodic external current with a slow frequency
This work was published in Nonlinear Dynamics and is available as 32.
7.3 Neural fields theory
7.3.1 Projection methods for Neural Field equations
Participants: Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro].
This work was partially carried out during an invitation of the author within the MathNeuro team.
We propose a numerical analysis framework for the study of the numerical approximation of nonlinear integro-differential equations for the evolution of neuronal activity. Neural fields are often simulated heuristically and, in spite of their popularity in mathematical neuroscience, their numerical analysis is not yet fully established. We introduce generic projection methods for neural fields, and derive a priori error bounds for these schemes. We extend an existing framework for stationary integral equations to the time-dependent case, which is relevant for neuroscience applications. We find that the convergence rate of a projection scheme for a neural field is determined to a great extent by the convergence rate of the projection operator. This abstract analysis, which unifies the treatment of collocation and Galerkin schemes, is carried out in operator form, without resorting to quadrature rules for the integral term, which are introduced only at a later stage, and whose choice is enslaved by the choice of the projector.
This work has been accepted for publication in SIAM Journal on Numerical Analysis and is available as 21.
7.4 Slow-fast dynamics in Neuroscience
7.4.1 Classification of bursting patterns: A tale of two ducks
Participants: Mathieu Desroches, John Rinzel [Courant Institute of Mathematical Sciences and Center for Neural Science, New York University, New York, USA], Serafim Rodrigues [BCAM, Bilbao, and external collaborator of MathNeuro].
This work has been partially done during a stay of Serafim Rodrigues in MathNeuro.
Bursting is one of the fundamental rhythms that excitable cells can generate either in response to incoming stimuli or intrinsically. It has been a topic of intense research in computational biology for several decades. The classification of bursting oscillations in excitable systems has been the subject of active research since the early 1980s and is still ongoing. As a by-product, it establishes analytical and numerical foundations for studying complex temporal behaviors in multiple timescale models of cellular activity. In this review, we first present the seminal works of Rinzel and Izhikevich in classifying bursting patterns of excitable systems. We recall a complementary mathematical classification approach by Bertram and colleagues, and then by Golubitsky and colleagues, which, together with the Rinzel-Izhikevich proposals, provide the state-of-the-art foundations to these classifications. Beyond classical approaches, we review a recent bursting example that falls outside the previous classification systems. Generalizing this example leads us to propose an extended classification, which requires the analysis of both fast and slow subsystems of an underlying slow-fast model and allows the dissection of a larger class of bursters. Namely, we provide a general framework for bursting systems with both subthreshold and superthreshold oscillations. A new class of bursters with at least 2 slow variables is then added, which we denote folded-node bursters , to convey the idea that the bursts are initiated or annihilated via a folded-node singularity. Key to this mechanism are so-called canard or duck orbits, organizing the underpinning excitability structure. We describe the 2 main families of folded-node bursters, depending upon the phase (active/spiking or silent/nonspiking) of the bursting cycle during which folded-node dynamics occurs. We classify both families and give examples of minimal systems displaying these novel bursting patterns. Finally, we provide a biophysical example by reinterpreting a generic conductance-based episodic burster as a folded-node burster, showing that the associated framework can explain its subthreshold oscillations over a larger parameter region than the fast subsystem approach.
This work has been published in PLoS Computational Biology and is available as 23.
7.4.2 Multiple-timescale dynamics, mixed mode oscillations and mixed affective states in a model of Bipolar Disorder
Participants: Efstathios Pavlidis [Neuromod Institute, UCA and Inria MathNeuro], Fabien Campillo, Albert Goldbeter [Free University Brussels, Belgium], Mathieu Desroches.
Mixed affective states in bipolar disorder (BD) is a common psychiatric condition that occurs when symptoms of the two opposite poles coexist during an episode of mania or depression. A four-dimensional model by A. Goldbeter [27, 28] rests upon the notion that manic and depressive symptoms are produced by two competing and auto-inhibited neural networks. Some of the rich dynamics that this model can produce, include complex rhythms formed by both small-amplitude (subthreshold) and large-amplitude (suprathreshold) oscillations and could correspond to mixed bipolar states. These rhythms are commonly referred to as mixed mode oscillations (MMOs) and they have already been studied in many different contexts [7, 50]. In order to accurately explain these dynamics one has to apply a mathematical apparatus that makes full use of the timescale separation between variables. Here we apply the framework of multiple-timescale dynamics to the model of BD in order to understand the mathematical mechanisms underpinning the observed dynamics of changing mood. We show that the observed complex oscillations can be understood as MMOs due to a so-called folded-node singularity. Moreover, we explore the bifurcation structure of the system and we provide possible biological interpretations of our findings. Finally, we show the robustness of the MMOs regime to stochastic noise and we propose a minimal three- dimensional model which, with the addition of noise, exhibits similar yet purely noise-driven dynamics. The broader significance of this work is to introduce mathematical tools that could be used to analyse and potentially control future, more biologically grounded models of BD.
This work was published in Cognitive Neurodynamics and is available as 29.
7.4.3 Slow passage through a Hopf-like bifurcation in piecewise linear systems: Application to elliptic bursting
Participant: Jordi Penalva Vadell [University of the Balearic Islands, Spain], Mathieu Desroches, Antonio E. Teruel [University of the Balearic Islands, Spain], Catalina Vich [University of the Balearic Islands, Spain].
The phenomenon of slow passage through a Hopf bifurcation is ubiquitous in multiple-timescale dynamical systems, where a slowly varying quantity replacing a static parameter induces the solutions of the resulting slow–fast system to feel the effect of the Hopf bifurcation with a delay. This phenomenon is well understood in the context of smooth slow–fast dynamical systems; in the present work, we study it for the first time in piecewise linear (PWL) slow–fast systems. This special class of systems is indeed known to reproduce all features of their smooth counterpart while being more amenable to quantitative analysis and offering some level of simplification, in particular, through the existence of canonical (linear) slow manifolds. We provide conditions for a PWL slow–fast system to exhibit a slow passage through a Hopf-like bifurcation, in link with possible connections between canonical attracting and repelling slow manifolds. In doing so, we fully describe the so-called way-in/way-out function. Finally, we investigate this slow passage effect in the Doi–Kumagai model, a neuronal PWL model exhibiting elliptic bursting oscillations.
7.4.4 A Generalization of Lanchester's Model of Warfare
Participant: Nicolò Cangiotti [Polytechnic University of Milan, Italy], Marco Capolli [Polish Academy of Sciences, Poland], Mattia Sensi.
The classical Lanchester's model is shortly reviewed and analysed, with particular attention to the critical issues that intrinsically arise from the mathematical formalization of the problem. We then generalize a particular version of such a model describing the dynamics of warfare when three or more armies are involved in the conflict. Several numerical simulations are provided.
This work has been submitted for publication and is available as 35.
7.4.5 Entry-exit functions in fast-slow systems with intersecting eigenvalues
Participant: Panagiotis Kaklamanos [Maxwell Institute for Mathematical Sciences, University of Edinburgh, UK], Christian Kuehn [TU Munich, Germany], Nikola Popović [Maxwell Institute for Mathematical Sciences, University of Edinburgh, UK], Mattia Sensi.
We study delayed loss of stability in a class of fast-slow systems with two fast variables and one slow one, where the linearization of the fast vector field along a one-dimensional critical manifold has two real eigenvalues which intersect before the accumulated contraction and expansion are balanced along any individual eigendirection. That interplay between eigenvalues and eigendirections renders the use of known entry-exit relations unsuitable for calculating the point at which trajectories exit neighborhoods of the given manifold. We illustrate the various qualitative scenarios that are possible in the class of systems considered here, and we propose novel formulae for the entry-exit functions that underlie the phenomenon of delayed loss of stability therein.
This work has been submitted for publication and is available as 36.
7.5 Mathematical modelling of neuronal excitability
7.5.1 A phenomenological model for interfacial water near hydrophilic polymers
Participants: Ashley Earls [BCAM, Bilbao, Spain], Maria-Carme Calderer [University of Minnesota, USA], Mathieu Desroches, Arghir Zarnescu [BCAM, Bilbao, Spain], Serafim Rodrigues [BCAM, Bilbao, and external collaborator of MathNeuro].
This work was partially done during a stay of Serafim Rodrigues in MathNeuro.
We propose a minimalist phenomenological model for the 'interfacial water' phenomenon that occurs near hydrophilic polymeric surfaces. We achieve this by combining a Ginzburg–Landau approach with Maxwell's equations which leads us to a well-posed model providing a macroscopic interpretation of experimental observations. From the derived governing equations, we estimate the unknown parameters using experimental measurements from the literature. The resulting profiles of the polarization and electric potential show exponential decay near the surface, in qualitative agreement with experiments. Furthermore, the model's quantitative prediction of the electric potential at the hydrophilic surface is in excellent agreement with experiments. The proposed model is a first step towards a more complete parsimonious macroscopic model that will, for example, help to elucidate the effects of interfacial water on cells (e.g. neuronal excitability, the effects of infrared neural stimulation or the effects of drugs mediated by interfacial water.
This work was published in Journal of Physics: Condensed Matter and is available as 24.
7.6 Mathematical modelling of memory processes
7.6.1 Dynamic branching in a neural network model for probabilistic prediction of sequences
Participant: Elif Köksal Ersöz [LTSI, Inserm, Rennes], Pascal Chossat, Martin Krupa [LJAD, UCA and Inria MathNeuro], Frédéric Lavigne [BCL, UCA].
An important function of the brain is to predict which stimulus is likely to occur based on the perceived cues. The present research studied the branching behavior of a computational network model of populations of excitatory and inhibitory neurons, both analytically and through simulations. Results show how synaptic efficacy, retroactive inhibition and short-term synaptic depression determine the dynamics of selection between different branches predicting sequences of stimuli of different probabilities. Further results show that changes in the probability of the different predictions depend on variations of neuronal gain. Such variations allow the network to optimize the probability of its predictions to changing probabilities of the sequences without changing synaptic efficacy.
This work was published in Journal of Computational Neuroscience and is available as 28.
7.7 Modelling the visual system
7.7.1 Spatial and color hallucinations in a mathematical model of primary visual cortex
Participant: Olivier Faugeras.
In collaboration with Anna Song (Imperial College London, The Francis Crick Institute) and Romain Veltz (on secondment to Inria).
We study a simplified model of the representation of colors in the primate primary cortical visual area V1. The model is described by an initial value problem related to a Hammerstein equation. The solutions to this problem represent the variation of the activity of populations of neurons in V1 as a function of space and color. The two space variables describe the spatial extent of the cortex while the two color variables describe the hue and the saturation represented at every location in the cortex. We prove the well-posedness of the initial value problem. We focus on its stationary and periodic in space solutions. We show that the model equation is equivariant with respect to the direct product G of the group of the Euclidean transformations of the planar lattice determined by the spatial periodicity and the group of color transformations, isomorphic to O(2), and study the equivariant bifurcations of its stationary solutions when some parameters in the model vary. Their variations may be caused by the consumption of drugs and the bifurcated solutions may represent visual hallucinations in space and color. Some of the bifurcated solutions can be determined by applying the Equivariant Branching Lemma (EBL) by determining the axial subgroups of G. These define bifurcated solutions which are invariant under the action of the corresponding axial subgroup. We compute analytically these solutions and illustrate them as color images. Using advanced methods of numerical bifurcation analysis we then explore the persistence and stability of these solutions when varying some parameters in the model. We conjecture that we can rely on the EBL to predict the existence of patterns that survive in large parameter domains but not to predict their stability. On our way we discover the existence of spatially localized stable patterns through the phenomenon of "snaking".
This work has been published in Compte Rendus Mathématique and is available as 25.
7.7.2 Geometry of spiking patterns in early visual cortex: a topological data analytic approach
Participants: Andrea Guidolin [BCAM, Bilbao, and KTH, Sweden], Mathieu Desroches, Jonathan Victor [Feil Family Brain and Mind Research Institute, Weill Cornell Medical College, New York, USA], Keith Purpura [Feil Family Brain and Mind Research Institute, Weill Cornell Medical College, New York, USA], Serafim Rodrigues [BCAM Bilbao and external collaborator of MathNeuro].
This work was partially achieved during a stay of Serafim Rodrigues in MathNeuro.
In the brain, spiking patterns live in a high-dimensional space of neurons and time. Thus, determining the intrinsic structure of this space presents a theoretical and experimental challenge. To address it, we introduce a new framework for applying topological data analysis (TDA) to spike train data and use it to determine the geometry of spiking patterns in the visual cortex. Key to our approach is a parametrized family of distances based on the timing of spikes that quantifies the dissimilarity between neuronal responses. We applied TDA to visually driven single-unit and multiple single-unit spiking activity in macaque V1 and V2. TDA across timescales reveals a common geometry for spiking patterns in V1 and V2 which, among simple models, is most similar to that of a low-dimensional space endowed with Euclidean or hyperbolic geometry with modest curvature. Remarkably, the inferred geometry depends on timescale and is clearest for the timescales that are important for encoding contrast, orientation and spatial correlations.
This work was published in Journal of the Royal Society Interface and is available as 27.
7.8 Studies on ageing
7.8.1 Interaction Mechanism Between the HSV-1 Glycoprotein B and the Antimicrobial Peptide Amyloid-beta
Participants: Mathieu Desroches, Serafim Rodrigues [BCAM Bilbao and external collaborator of MathNeuro].
This work was notably done in collaboration with Tamás Fülöp (Centre de recherche sur le vieillissement, CSSS-UIGS, Université de Sherbrooke). This work was partially done during a stay of Serafim Rodrigues in MathNeuro.
Unravelling the mystery of Alzheimer’s disease (AD) requires urgent resolution given the worldwide increase of the aging population. There is a growing concern that the current leading AD hypothesis, the amyloid cascade hypothesis, does not stand up to validation with respect to emerging new data. Indeed, several paradoxes are being discussed in the literature, for instance, both the deposition of the amyloid-β peptide (Aβ) and the intracellular neurofibrillary tangles could occur within the brain without any cognitive pathology. Thus, these paradoxes suggest that something more fundamental is at play in the onset of the disease and other key and related pathomechanisms must be investigated. The present study follows our previous investigations on the infectious hypothesis, which posits that some pathogens are linked to late onset AD. Our studies also build upon the finding that Aβ is a powerful antimicrobial agent, produced by neurons in response to viral infection, capable of inhibiting pathogens as observed in in vitro experiments. Herein, we ask what are the molecular mechanisms in play when Aβ neutralizes infectious pathogens? Methods: To answer this question, we probed at nanoscale lengths with FRET (Förster Resonance Energy Transfer), the interaction between Aβ peptides and glycoprotein B (responsible of virus-cell binding) within the HSV-1 virion Results: The experiments show an energy transfer between Aβ peptides and glycoprotein B when membrane is intact. No energy transfer occurs after membrane disruption or treatment with blocking antibody. Conclusion: We concluded that Aβ insert into viral membrane, close to glycoprotein B, and participate in virus neutralization.
This work have been published in Journal of Alzheimer's Disease Reports and is available as 22.
7.8.2 Immunosenescence and Altered Vaccine Efficiency in Older Subjects: A Myth Difficult to Change
Participants: Mathieu Desroches, Serafim Rodrigues [BCAM, Bilbao, and external collaborator of MathNeuro].
Notably with Tamás Fulop (Centre de recherche sur le vieillissement - CSSS-UIGS, Université de Sherbrooke). This work was partially achieved during a stay of Serafim Rodrigues in MathNeuro.
Organismal ageing is associated with many physiological changes, including differences in the immune system of most animals. These differences are often considered to be a key cause of age-associated diseases as well as decreased vaccine responses in humans. The most often cited vaccine failure is seasonal influenza, but, while it is usually the case that the efficiency of this vaccine is lower in older than younger adults, this is not always true, and the reasons for the differential responses are manifold. Undoubtedly, changes in the innate and adaptive immune response with ageing are associated with failure to respond to the influenza vaccine, but the cause is unclear. Moreover, recent advances in vaccine formulations and adjuvants, as well as in our understanding of immune changes with ageing, have contributed to the development of vaccines, such as those against herpes zoster and SARS-CoV-2, that can protect against serious disease in older adults just as well as in younger people. In the present article, we discuss the reasons why it is a myth that vaccines inevitably protect less well in older individuals, and that vaccines represent one of the most powerful means to protect the health and ensure the quality of life of older adults.
7.9 Numerics
7.9.1 The one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering
Participant: Samuel Nyobe [University of Yaoundé, Cameroon], Fabien Campillo, Serge Moto [University of Yaoundé, Cameroon], Vivien Rossi [Cirad and University of Yaoundé, Cameroon].
We have considerably revised and improved a preprint from last year. This work consists in improving the prediction step in the particle filter. This step is still delicate since if the particles explore areas of the state space that will not match the next observation via the likelihood function, the filter will lose the state track and the filter will be inoperative. We have improved this prediction step by using a simple technique, which may be close to a smoothing technique, that uses the next observation.
This work has been submitted for publication and is available as 54.
7.10 Some studies in epidemiology
Participant: Mattia Sensi.
These works of Mattia Sensi, that are outside the themes of MathNeuro, were started before his stay at Inria were completed this year, and were done in collaboration in first with Stefania Ottaviano (Dipartimento di Matematica, Padova), second with Sara Sottile (University of Trento), and in the other hand in collaboration with Sara Sottile and Ozan Kahramanoğulları (University of Trento), and third with Massimo A. Achterberg (TU Delft).
In a first paper 37 we consider the global stability of multi-group SAIRS epidemic models with vaccination. The role of asymptomatic and symptomatic infectious individuals is explicitly considered in the transmission pattern of the disease among the groups in which the population is divided. We provide a global stability analysis for the model.
In a second paper 31, we study how network properties and epidemic parameters influence stochastic SIR dynamics on scale-free random networks. With the premise that social interactions are described by power-law distributions, we study a SIR stochastic dynamic on a static scale-free random network generated via configuration model. We verify our model with respect to deterministic considerations and provide a theoretical result on the probability of the extinction of the disease. We explore the variability in disease spread by stochastic simulations.
In a third paper 33, we study a minimal model for adaptive SIS epidemics. The interplay between disease spreading and personal risk perception is of key importance for modelling the spread of infectious diseases. We propose a planar system of ordinary differential equations (ODEs) to describe the co-evolution of a spreading phenomenon and the average link density in the personal contact network. Contrary to standard epidemic models, we assume that the contact network changes based on the current prevalence of the disease in the population. We assume that personal risk perception is described using two functional responses: one for link-breaking and one for link-creation.
8 Partnerships and cooperations
8.1 International initiatives
8.1.1 Inria associate team not involved in an IIL or an international program
Participants: Mathieu Desroches, Fabien Campillo.
NeuroTransSF
-
Title:
NeuroTransmitter cycle: A Slow-Fast modeling approach
-
Duration:
2019 -> 2022
-
Coordinator:
Serafim Rodrigues (srodrigues@bcamath.org)
-
Partner:
Basque Center for Applied Mathematics (BCAM) (Espagne)
-
Inria contact:
Mathieu Desroches
-
Summary:
This associated team project proposes to deepen the links between two young research groups, on strong Neuroscience thematics. This project aims to start from a joint work in which we could successfully model synaptic transmission delays for both excitatory and inhibitory synapses, matching experimental data, and to supplant it in two distinct directions. On the one hand, by modeling the endocytosis so as to obtain a complete mathematical formulation of the presynaptic neurotransmitter cycle, which will then be integrated within diverse neuron models (in particular interneurons) hence allowing a refined analysis of their excitability and short-term plasticity properties. On the other hand, by modeling the postsynaptic neurotransmitter cycle in link with long-term plasticity and memory. We will incorporate these new models of synapse in different types of neuronal networks and we will then study their excitability, plasticity and synchronisation properties in comparison with classical models. This project will benefit from strong experimental collaborations (UCL, Alicante) and it is coupled to the study of brain pathologies linked with synaptic dysfunctions, in particular certain early signs of Alzheimer's Disease. Our initiative also contains a training aspect with two PhD student involved as well as a series of mini-courses which we will propose to the partner institute on this research topic; we will also organise a "wrap-up" workshop in Sophia at the end of it. Finally, the project is embedded within a strategic tightening of our links with Spain with the objective of pushing towards the creation of a Southern-Europe network for Mathematical, Computational and Experimental Neuroscience, which will serve as a stepping stone in order to extend our influence beyond Europe.
8.2 International research visitors
8.2.1 Visits of international scientists
Other international visits to the team
Marius Yamakou
-
Status
(post-Doc)
-
Institution of origin:
Friedrich-Alexander-Universität, Erlangen-Nürnberg
-
Country:
Germany
-
Dates:
1-8 March 2022
-
Context of the visit:
Establish a collaboration in the context of the study of synchronisation in neuronal networks
-
Mobility program/type of mobility:
research stay
Serafim Rodrigues
-
Status
(research Professor)
-
Institution of origin:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
2-19 May 2022
-
Context of the visit:
Collaboration with M. Desroches in the context of the associated team NeuroTransSF
-
Mobility program/type of mobility:
research stay
Marius Yamakou
-
Status
post-Doc
-
Institution of origin:
Friedrich-Alexander-Universität, Erlangen-Nürnberg
-
Country:
Germany
-
Dates:
1-31 October 2022
-
Context of the visit:
Complete the study started during the first visit and write a joint article
-
Mobility program/type of mobility:
research stay
Jordi Penalva Vadell
-
Status
(PhD)
-
Institution of origin:
University of the Balearic Islands, Palma
-
Country:
Spain
-
Dates:
1 October - 31 December 2022
-
Context of the visit:
Collaboration with M. Desroches in the context of piecewise-linear neuronal dynamical systems
-
Mobility program/type of mobility:
research stay
8.2.2 Visits to international teams
Research stays abroad
Mathieu Desroches
-
Visited institution:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
19-28 March 2022
-
Context of the visit:
Collaboration with S. Rodrigues in the context of the associated team NeuroTransSF
-
Mobility program/type of mobility:
research stay
Mathieu Desroches
-
Visited institution:
Instituto Superior Politecnico, Lisbon
-
Country:
Portugal
-
Dates:
20-29 July 2022
-
Context of the visit:
Establish collaboration with J. Morgado on modelling neurogenesis
-
Mobility program/type of mobility:
research stay
Mathieu Desroches
-
Visited institution:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
1-30 September 2022
-
Context of the visit:
Collaboration with S. Rodrigues in the context of neuromorphic computing
-
Mobility program/type of mobility:
research stay
Mathieu Desroches
-
Visited institution:
Vrije Universiteit Amsterdam
-
Country:
Netherlands
-
Dates:
1-8 December 2022
-
Context of the visit:
Collaboration with D. Avitabile in the context of spatiotemporal models of neural activity
-
Mobility program/type of mobility:
research stay
8.2.3 H2020 projects
HBP SGA3
HBP SGA3 project on cordis.europa.eu
-
Title:
Human Brain Project Specific Grant Agreement 3
-
Duration:
From April 1, 2020 to September 30, 2023
-
Inria contact:
Bertrand Thirion
- Coordinator:
-
Summary:
The last of four multi-year work plans will take the HBP to the end of its original incarnation as an EU Future and Emerging Technology Flagship. The plan is that the end of the Flagship will see the start of a new, enduring European scientific research infrastructure, EBRAINS, hopefully on the European Strategy Forum on Research Infrastructures (ESFRI) roadmap. The SGA3 work plan builds on the strong scientific foundations laid in the preceding phases, makes structural adaptations to profit from lessons learned along the way (e.g. transforming the previous Subprojects and Co-Design Projects into fewer, stronger, well-integrated Work Packages) and introduces new participants, with additional capabilities.
The SGA3 work plan is built around improved integration and a sharpening of focus, to ensure a strong HBP legacy at the end of this last SGA. In previous phases, the HBP laid the foundation for empowering empirical and theoretical neuroscience to approaching the different spatial and temporal scales using state-of-the-art neuroinformatics, simulation, neuromorphic computing, neurorobotics, as well as high-performance analytics and computing. While these disciplines have been evolving for some years, we now see a convergence in this field and a dramatic speeding-up of progress. Data is driving a scientific revolution that relies heavily on computing to analyse data and to provide the results to the research community. Only with strong computer support, is it possible to translate information into knowledge, into a deeper understanding of brain organisation and diseases, and into technological innovation. In this respect, the underlying Fenix HPC and data e-infrastructure, co-designed with the HBP, will be key.
9 Dissemination
9.1 Promoting scientific activities
Member of the organizing committees
- Olivier Faugeras was co-organiser of the Workshop on Mathematical modeling and statistical analysis in Neuroscience, 31 January - 4 February 2022, Henri Poincaré Institute, Paris.
9.1.1 Journal
Member of the editorial boards
- Mathieu Desroches is associate editor of the journal Frontiers in Physiology (impact factor 4.8).
- Olivier Faugeras is founder and editor-in-chief of the journal Mathematical Neuroscience and Applications, under the diamond model (no charges for authors and readers) supported by Episciences.
Reviewer - reviewing activities
- Fabien Campillo acted as a reviewer for the Journal of Mathematical Biology.
- Mathieu Desroches acted as a reviewer for the journals SIAM Journal on Applied Dynamical Systems (SIADS), Journal of Mathematical Biology, PLoS Computational Biology, Biological Cybernetics, Journal de Mathématiques Pures et Appliquées, Journal of Nonlinear Science, Nonlinear Dynamics, Physica D, Applied Mathematics Modelling, Journal of the European Mathematical Society, Nonlinearity, Automatica.
9.1.2 Invited talks
- Pascal Chossat gave a talk entitled “A neural network model for production and dynamic branching of sequences of learned items” at the French Regional Conference on Complex Systems - FRCCS 2022, 21 June 2022, Paris.
- Pascal Chossat and Frédéric Lavigne (BCL, UCA) gave a joint talk entitled “Dynamic branching of sequences for probabilistic prediction: A neural network model and behavioral experiment” at the Neuromod Institute annual meeting, 1 June 2022, Antibes.
- Mathieu Desroches and Afia B. Ali (University College London, UK) gave a joint online talk entitled “Understanding Synaptic Mechanisms: Why a Multi-disciplinary Approach is Important?” at the Workshop on Mathematical modeling and statistical analysis in Neuroscience, 3 February 2022, Henri Poincaré Institute, Paris.
- Mathieu Desroches gave a talk entitled “Cross-scale excitability in networks of synaptically-coupled quadratic integrate-and-fire neurons” at the 40th congress of the francophone society for theoretical biology (SFBT), 28 June 2022, Poitiers.
- Mathieu Desroches gave an online talk entitled “Classification of Bursting Patterns: A Tale of Two Ducks” in the Mini-Symposium on Multiscale Oscillations in Biological Systems, at the SIAM Life Science conference, 14 July 2022, Pittsburgh, USA.
- Mathieu Desroches gave a webinar talk entitled “Classification of Bursting Patterns: A Tale of Two Ducks” at the Mathematical Biology Seminar of the Mathematics Dept, University of Iowa, 12 September 2022, Iowa City, USA.
- Mattia Sensi gave a seminar talk entitled “Entry-exit functions: beyond eigenvalue separation” at the Edinburgh Dynamical Systems Study Group, 11 March 2022, University of Edinburgh, UK.
- Mattia Sensi gave a talk entitled “A Geometric Singular Perturbation approach to epidemic compartmental models” at the 100 UMI 800 UniPD conference, 24 May 2022, University of Padova, Italy.
- Mattia Sensi gave a talk entitled “Delayed loss of stability in multiple time scale models of natural phenomena” in the Mini-Symposium on Slow-Fast Systems and Phenomena, at the ENOC 2022 Conference, 19 July 2022, Lyon.
- Mattia Sensi gave a talk entitled “A generalization of the full SNARE-SM model”, in the minisymposium on “Recent advances in mathematical modelling in neuroscience”, at the ECMTB 2022 Conference, 23 September 2022, Heidelberg, Germany.
- Mattia Sensi gave a seminar talk entitled “A Geometric Singular Perturbation approach to epidemic compartmental models” at the Dynamics Seminar, Maths Dept, VU Amsterdam, Netherlands, 21 November 2022.
- Mattia Sensi gave a seminar talk entitled “Entry-exit functions in fast-slow systems with intersecting eigenvalues” at the Floris Takens Seminar, University of Groningen, Netherlands, 23 November 2022.
- Mattia Sensi gave a seminar talk entitled “Delayed loss of stability in multiple time scale models of natural phenomena” at the Mathematics Seminar, University of Trento, Italy, 7 December 2022.
9.2 Leadership within the scientific community
- Fabien Campillo is a founding member of the African scholarly Society on Digital Sciences (ASDS).
- Mathieu Desroches was on the Scientific Committee of the Complex Systems Academy of the UCA JEDI Idex.
9.2.1 Scientific expertise
- Mathieu Desroches has been reviewing grant proposals for the Complex Systems Academy of the UCA JEDI Idex.
9.3 Research administration
- Mathieu Desroches is supervising the PhD seminar at the Inria centre at Université Côte d'Azur.
- Fabien Campillo is member of the “health and safety committee” (CSHCT) at INRIA Sophia–Antipolis.
9.4 Teaching - Supervision - Juries
9.4.1 Teaching
-
Master:
Mathieu Desroches, Modèles Mathématiques et Computationnels en Neuroscience (Lectures, example classes and computer labs), 18 hours (Feb. 2022), M1 (BIM), Sorbonne Université, Paris, France.
-
Master:
Mathieu Desroches, Dynamical Systems in the context of neuron models, (Lectures, example classes and computer labs), 9 hours (Jan. 2022) and 9 hours (Nov.-Dec. 2022), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
-
Masters and Engineer schools:
With the project to write a book, Fabien Campillo propose a set of applications of particle filtering in tracking developed in the context of lectures given during many years in Masters and Engineer schools. See the associated web page and git repository.
9.4.2 Supervision
-
PhD:
Guillaume Girier, Basque Center for Applied Mathematics (BCAM, Bilbao, Spain) is doing a PhD on “A mathematical, computational and experimental study of neuronal excitability”, co-supervised by S. Rodrigues (BCAM) and M. Desroches.
-
PhD:
Jordi Penalva Vadell, University of the Balearic Islands (UIB, Palma, Spain) is doing a PhD on “Neuronal piecewise linear models reproducing bursting dynamics”, co-supervised by A. E. Teruel (UIB), C. Vich (UIB) and M. Desroches.
-
PhD:
Samuel Nyobe, University of Yaoundé, is doing a PhD on Particle Filtering, co-supervised with Vivien Rossi (CIRAD – UMMISCO, University Yaoundé).
-
Master 2 internship:
Efstathios Pavlidis (Université Côte d'Azur - UCA, Nice), “Multiple-timescale dynamics and mixed states in a model of Bipolar Disorder”, supervised by Mathieu Desroches, September 2021 - February 2022. An article was published, see 29.
-
Master 2 internship:
Alihan Kayabas (Sorbonne Université, Paris), “Slow-fast dissection of a theta-gamma neural oscillator: single neuron and networks”, co-supervised by Mathieu Desroches and Boris Gutkin (ENS, Paris), March - June 2022.
-
Master 1 internship:
Lyna Bouikni (UCA, Nice),“Latching dynamics in biologically inspired neural networks”, co-supervised by Pascal Chossat and Frédéric Lavigne (BCL, UCA), March - May 2022.
-
Master 1 internship:
Ufuk Cem Birbiri (UCA, Nice), “Topological data analysis of human brain data”, supervised by M. Desroches, June - September 2022.
9.4.3 Juries
- Fabien Campillo was member of the jury and reviewer of the PhD of Gaëtan Vignoud entitled “Synaptic plasticity in stochastic neuronal networks”, supervised by Philipe Robert (Inria Paris Research Centre), 8 April 2022.
- Mathieu Desroches was member of the jury of the PhD of Evgenia Kartsaki entitled “How specific classes of retinal cells contribute to vision: a computational model”, supervised by Bruno Cessac (Inria at UCA, France) and Evelyne Sernagor (University of Newcastle, UK), 17 March 2022.
- Mathieu Desroches was member of the jury and president of the jury of the PhD of Côme Le Breton entitled “Usability of phase synchrony neuromarkers in neurofeedback protocols for epileptic seizures reduction”, supervised by Theodore Papadopoulo and Maureen Clerc (Inria at UCA, France), 18 October 2022.
10 Scientific production
10.1 Major publications
- 1 articleLatching dynamics in neural networks with synaptic depression.PLoS ONE128August 2017, e0183710
- 2 articleSpatiotemporal canards in neural field equations.Physical Review E 954April 2017, 042205
- 3 articleMean-field description and propagation of chaos in networks of Hodgkin-Huxley neurons.The Journal of Mathematical Neuroscience21We derive the mean-field equations arising as the limit of a network of interacting spiking neurons, as the number of neurons goes to infinity. The neurons belong to a fixed number of populations and are represented either by the Hodgkin-Huxley model or by one of its simplified version, the FitzHugh-Nagumo model. The synapses between neurons are either electrical or chemical. The network is assumed to be fully connected. The maximum conductances vary randomly. Under the condition that all neurons~ initial conditions are drawn independently from the same law that depends only on the population they belong to, we prove that a propagation of chaos phenomenon takes place, namely that in the mean-field limit, any finite number of neurons become independent and, within each population, have the same probability distribution. This probability distribution is a solution of a set of implicit equations, either nonlinear stochastic differential equations resembling the McKean-Vlasov equations or non-local partial differential equations resembling the McKean-Vlasov-Fokker-Planck equations. We prove the wellposedness of the McKean-Vlasov equations, i.e. the existence and uniqueness of a solution. We also show the results of some numerical experiments that indicate that the mean-field equations are a good representation of the mean activity of a finite size network, even for modest sizes. These experiments also indicate that the McKean-Vlasov-Fokker-Planck equations may be a good way to understand the mean-field dynamics through, e.g. a bifurcation analysis.2012, URL: http://www.mathematical-neuroscience.com/content/2/1/10
- 4 articleA sub-Riemannian model of the visual cortex with frequency and phase.The Journal of Mathematical Neuroscience101December 2020
- 5 articleLinks between deterministic and stochastic approaches for invasion in growth-fragmentation-death models.Journal of mathematical biology736-72016, 1781--1821URL: https://hal.science/hal-01205467
- 6 articleWeak convergence of a mass-structured individual-based model.Applied Mathematics & Optimization7212015, 37--73URL: https://hal.inria.fr/hal-01090727
- 7 articleAnalysis and approximation of a stochastic growth model with extinction.Methodology and Computing in Applied Probability1822016, 499--515URL: https://hal.science/hal-01817824
- 8 articleEffect of population size in a predator--prey model.Ecological Modelling2462012, 1--10URL: https://hal.inria.fr/hal-00723793
- 9 articleHeteroclinic cycles in Hopfield networks.Journal of Nonlinear ScienceJanuary 2016
- 10 articleShort-term synaptic plasticity in the deterministic Tsodyks-Markram model leads to unpredictable network dynamics.Proceedings of the National Academy of Sciences of the United States of America 110412013, 16610-16615
- 11 articleModeling cortical spreading depression induced by the hyperactivity of interneurons.Journal of Computational NeuroscienceOctober 2019
- 12 articleCanards, folded nodes and mixed-mode oscillations in piecewise-linear slow-fast systems.SIAM Review584accepted for publication in SIAM Review on 13 August 2015November 2016, 653-691
- 13 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106
- 14 articleNeuronal mechanisms for sequential activation of memory items: Dynamics and reliability.PLoS ONE1542020, 1-28
- 15 unpublishedCanard-induced complex oscillations in an excitatory network.November 2018, working paper or preprint
- 16 articleTime-coded neurotransmitter release at excitatory and inhibitory synapses.Proceedings of the National Academy of Sciences of the United States of America 1138February 2016, E1108-E1115
- 17 articleA Center Manifold Result for Delayed Neural Fields Equations.SIAM Journal on Mathematical Analysis4532013, 1527-1562
- 18 articleA center manifold result for delayed neural fields equations.SIAM Journal on Applied Mathematics (under revision)RR-8020July 2012
10.2 Publications of the year
International journals
- 19 articleBump attractors and waves in networks of leaky integrate-and-fire neurons.SIAM ReviewDecember 2022
- 20 articleCross-scale excitability in networks of quadratic integrate-and-fire neurons.PLoS Computational Biology1810October 2022, e1010569
- 21 articleProjection methods for Neural Field equations.SIAM Journal on Numerical AnalysisDecember 2022
- 22 articleInteraction Mechanism Between the HSV-1 Glycoprotein B and the Antimicrobial Peptide Amyloid-β.Journal of Alzheimer's Disease Reports61September 2022, 599-606
- 23 articleClassification of bursting patterns: A tale of two ducks.PLoS Computational Biology182February 2022, e1009752
- 24 articleA phenomenological model for interfacial water near hydrophilic polymers.Journal of Physics: Condensed Matter3435June 2022, 355102
- 25 articleSpatial and color hallucinations in a mathematical model of primary visual cortex.Comptes Rendus. Mathématique3602022, 59-87
- 26 articleImmunosenescence and Altered Vaccine Efficiency in Older Subjects: A Myth Difficult to Change.Vaccines104April 2022, 607
- 27 articleGeometry of spiking patterns in early visual cortex: a topological data analytic approach.Journal of the Royal Society Interface19196November 2022
- 28 articleDynamic branching in a neural network model for probabilistic prediction of sequences.Journal of Computational NeuroscienceAugust 2022
- 29 articleMultiple-timescale dynamics, mixed mode oscillations and mixed affective states in a model of Bipolar Disorder.Cognitive Neurodynamics2022
- 30 articleSlow passage through a Hopf-like bifurcation in piecewise linear systems: Application to elliptic bursting.Chaos: An Interdisciplinary Journal of Nonlinear Science3212December 2022, 123109
- 31 articleHow network properties and epidemic parameters influence stochastic SIR dynamics on scale-free random networks.Journal of SimulationAugust 2022, 1-14
- 32 articleBursting in a next generation neural mass model with synaptic dynamics: a slow-fast approach.Nonlinear DynamicsApril 2022
Reports & preprints
- 33 miscA minimal model for adaptive SIS epidemics.November 2022
- 34 miscNetwork torus canards and their mean-field limits.February 2022
- 35 miscA Generalization of Lanchester's Model of Warfare.November 2022
- 36 miscEntry-exit functions in fast-slow systems with intersecting eigenvalues.November 2022
- 37 miscGlobal stability of multi-group SAIRS epidemic models.November 2022
10.3 Cited publications
- 38 articleCanonical models for torus canards in elliptic bursters.Chaos: An Interdisciplinary Journal of Nonlinear Science3162021, 063129
- 39 articleTheory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex.The Journal of Neuroscience211982, 32--48
- 40 articleThe non linear dynamics of retinal waves.Physica D: Nonlinear Phenomena4392022, 133436
- 41 articleFiring clamp: a novel method for single-trial estimation of excitatory and inhibitory synaptic neuronal conductances.Frontiers in cellular neuroscience82014, 86
- 42 articleHyperbolic planforms in relation to visual edges and textures perception.PLoS Computational Biology5122009, e1000625
- 43 articleA role for fast rhythmic bursting neurons in cortical gamma oscillations in vitro.Proceedings of the National Academy of Sciences of the United States of America101182004, 7152--7157
- 44 articleMixed-Mode Oscillations with Multiple Time Scales.SIAM Review542May 2012, 211-288
- 45 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106
- 46 articleThe geometry of slow manifolds near a folded node.SIAM Journal on Applied Dynamical Systems742008, 1131--1162
- 47 bookMathematical foundations of neuroscience.35Springer2010
- 48 articleA large deviation principle and an expression of the rate function for a discrete stationary gaussian process.Entropy16122014, 6722--6738
- 49 bookDynamical systems in neuroscience.MIT press2007
- 50 articleNeural excitability, spiking and bursting.International Journal of Bifurcation and Chaos10062000, 1171--1266
- 51 articleMixed-mode oscillations in a three time-scale model for the dopaminergic neuron.Chaos: An Interdisciplinary Journal of Nonlinear Science1812008, 015106
- 52 articleRelaxation oscillation and canard explosion.Journal of Differential Equations17422001, 312--368
- 53 articleAmyloid precursor protein: from synaptic plasticity to Alzheimer's disease.Annals of the New York Academy of Sciences104812005, 149--165
- 54 articleThe one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering.HAL hal-034649872023, URL: https://hal.inria.fr/hal-03464987
- 55 articleDynamic clamp constructed phase diagram for the Hodgkin and Huxley model of excitability.Proceedings of the National Academy of Sciences11772020, 3575--3582
- 56 articlePathophysiology of migraine.Annual review of physiology752013, 365--391
- 57 articleDynamic clamp: computer-generated conductances in real neurons.Journal of neurophysiology6931993, 992--995
- 58 articleDynamical diseases of brain systems: different routes to epileptic seizures.IEEE transactions on biomedical engineering5052003, 540--548
- 59 articleA Markovian event-based framework for stochastic spiking neural networks.Journal of Computational Neuroscience30April 2011
- 60 articleNeural Mass Activity, Bifurcations, and Epilepsy.Neural Computation2312December 2011, 3232--3286
- 61 articleA Center Manifold Result for Delayed Neural Fields Equations.SIAM Journal on Mathematical Analysis4532013, 1527-562
- 62 articleLocal/Global Analysis of the Stationary Solutions of Some Neural Field Equations.SIAM Journal on Applied Dynamical Systems93August 2010, 954--998URL: http://arxiv.org/abs/0910.2247

