Keywords
Computer Science and Digital Science
- A3.1.1. Modeling, representation
- A3.4.1. Supervised learning
- A3.4.2. Unsupervised learning
- A3.4.4. Optimization and learning
- A3.4.5. Bayesian methods
- A3.4.6. Neural networks
- A3.4.8. Deep learning
- A6.2.4. Statistical methods
- A6.2.6. Optimization
- A9.2. Machine learning
- A9.3. Signal analysis
- A9.7. AI algorithmics
Other Research Topics and Application Domains
- B1.2. Neuroscience and cognitive science
- B1.2.1. Understanding and simulation of the brain and the nervous system
- B1.2.2. Cognitive science
- B1.2.3. Computational neurosciences
- B2.6.1. Brain imaging
1 Team members, visitors, external collaborators
Research Scientists
- Philippe Ciuciu [Team leader, CEA, Senior Researcher, HDR]
- Alexandre Gramfort [INRIA, Senior Researcher, HDR]
- Thomas Moreau [INRIA, Researcher]
- Bertrand Thirion [INRIA, Senior Researcher, HDR]
- Demian Wassermann [INRIA, Researcher, until Sep 2022]
- Demian Wassermann [INRIA, Senior Researcher, from Oct 2022, HDR]
Post-Doctoral Fellows
- Antoine Collas [INRIA, from Oct 2022]
- Richard Hoechenberger [INRIA, until Aug 2022]
- Hugo Richard [INRIA, until Mar 2022]
- Cedric Rommel [INRIA]
- David Sabbagh [INRIA, from Feb 2022]
- David Sabbagh [INSERM, until Jan 2022]
- Sheng H Wang [University of Helsinki, from Aug 2022, In delegation to CEA/NeuroSpin]
PhD Students
- Cedric Allain [INRIA]
- Serge Brosset [CEA, from Oct 2022]
- Charlotte Caucheteux [FACEBOOK]
- Ahmad Chamma [INRIA]
- Thomas Chapalain [ENS PARIS-SACLAY]
- L'Emir Omar Chehab [INRIA]
- Pierre-Antoine Comby [ENS PARIS SACLAY, CEA/NeuroSpin]
- Mathieu Dagreou [INRIA]
- Guillaume Daval-Frerot [CEA, until Nov 2022]
- Merlin Dumeur [UNIV PARIS SACLAY, PhD in cotutelle with Aalto University]
- Chaithya Giliyar Radhkrishna [CEA]
- Theo Gnassounou [ENS PARIS-SACLAY, from Oct 2022]
- Ambroise Heurtebise [INRIA, from Oct 2022]
- Hubert Jacob Banville [INTERAXON, until Jan 2022]
- Julia Linhart [UNIV PARIS-SACLAY]
- Benoit Malezieux [INRIA]
- Elsa Manquat [AP/HP, from Feb 2022]
- Apolline Mellot [INRIA]
- Raphael Meudec [INRIA]
- Florent Michel [UNIV PARIS SACLAY, from Apr 2022 until Sep 2022]
- Tuan Binh Nguyen [INRIA, until Feb 2022]
- Alexandre Pasquiou [INRIA]
- Zaccharie Ramzi [CEA, until Feb 2022]
- Louis Rouillard-Odera [INRIA]
- Alexis Thual [CEA]
- Gaston Zanitti [INRIA]
Technical Staff
- Majd Abdallah [INRIA, Engineer]
- Himanshu Aggarwal [INRIA, Engineer]
- Guillaume Favelier [INRIA, Engineer, until Apr 2022]
- Yasmin Mzayek [INRIA, Engineer, from Apr 2022]
- Agnes Perez-Millan [Univ. Pompeo Fabra (Barcelona, Spain), from Oct 2022, Visitor]
- Ana Ponce Martinez [INRIA, Engineer, from May 2022]
- Kumari Pooja [CEA, Engineer]
Interns and Apprentices
- Gabriela Gomez Jimenez [INRIA, from Nov 2022]
- Alexandre Le Bris [INRIA, from Sep 2022]
- Florent Michel [UNIV PARIS SACLAY, from Nov 2022]
- Joseph Paillard [INRIA, from Feb 2022 until Jul 2022]
Administrative Assistant
- Corinne Petitot [INRIA]
External Collaborators
- Zaineb Amor [CEA, PhD student at NeuroSpin, primarily assigned with BAOBAB.]
- Pierre Bellec [CRIUGM, from Oct 2022]
- Julie Boyle [CRIUGM, from Oct 2022]
- Jérôme-Alexis Chevalier [EMERTON DATA]
- Samuel Davenport [UNIV CALIFORNIE, until Feb 2022]
- Elizabeth Dupre [UNIV STANFORD, from Jun 2022 until Jun 2022]
- Ana Grilo Pinho [Western University, Canada, from Feb 2022 until Jul 2022]
- Yann Harel [CRIUGM, from Oct 2022]
- Karim Jerbi [UNIV MONTREAL, from Oct 2022]
- Gunnar Konig [IBE-LMU, from Sep 2022]
- Matthieu Kowalski [UNIV PARIS SACLAY]
- Tuan Binh Nguyen [IMT, from Mar 2022]
- François Paugam [CRIUGM, from Oct 2022]
- Hao-Ting Wang [CRIUGM, from Sep 2022]
2 Overall objectives
The Mind team, which finds its origin in the Parietal team, is uniquely equipped to impact the fields of statistical machine learning and artificial intelligence (AI) in service to the understanding of brain structure and function, in both healthy and pathological conditions.
AI with recent progress in statistical machine learning (ML) is currently aiming to revolutionize how experimental science is conducted by using data as the driver of new theoretical insights and scientific hypotheses. Supervised learning and predictive models are then used to assess predictability. We thus face challenging questions like Can cognitive operations be predicted from neural signals? or Can the use of anesthesia be a causal predictor of later cognitive decline or impairment?
To study brain structure and function, cognitive and clinical neuroscientists have access to various neuroimaging techniques. The Mind team specifically relies on non-invasive modalities, notably on one hand, magnetic resonance imaging (MRI) at ultra-high magnetic field to reach high spatial resolution and, on the other hand, electroencephalography (EEG) and magnetoencephalography (MEG), which allow the recording of electric and magnetic activity of neural populations, to follow brain activity in real time. Extracting new neuroscientific knowledge from such neuroimaging data however raises a number of methodological challenges, in particular in inverse problems, statistics and computer science. The Mindproject aims to develop the theory and software technology to study the brain from both cognitive to clinical endpoints using cutting-edge MRI (functional MRI, diffusion weighted MRI) and MEG/EEG data. To uncover the most valuable information from such data, we need to solve a large panoply of inverse problems using a hybrid approach in which machine or deep learning is used in combination with physics-informed constraints.
Once functional imaging data is collected the challenge of statistical analysis becomes apparent. Beyond the standard questions (Where, when and how can statistically significant neural activity be identified?), Mind is particularly interested in addressing driving effect or the cause of such activity in a given cortical region. Answering these basic questions with computer programs requires the development of methodologies built on the latest research on causality, knowledge bases and high-dimensional statistics.
The field of neuroscience is now embracing more open science standards and community efforts to address the referenced to as “replication crisis” as well as the growing complexity of the data analysis pipelines in neuroimaging. The Mindteam is ideally positioned to address these issues from both angles by providing reliable statistical inference schemes as well as open source software that are compliant with international standards.
The impact of Mindwill be driven by the data analysis challenges in neuroscience but also by the fundamental discoveries in neuroscience that presently inspire the development of novel AI algorithms. The Parietal team has proved in the past that this scientific positioning leads to impactful research. Hence, the newly created Mind team formed by computer scientists and statisticians with a deep understanding of the field of neuroscience, from data acquisition to clinical needs, offers a unique opportunity to expand and explore more fully uncharted territories.
3 Research program
The scientific project of Mind is organized around four core developments (machine learning for inverse problems, heterogeneous data & knowledge bases, statistics and causal inference in high dimension, and machine Learning on spatio-temporal signals).
3.1 Machine learning for inverse problems
Participants:
P. Ciuciu, A. Gramfort, T. Moreau, D. Wassermann
Inverse problems are ubiquitous in observational science. This necessitates the reconstruction of a signal/image of interest, or more generally a vector of parameters, from remote observations that are possibly noisy and scarce. The link between the parameters of interest and the observations is physics, and is commonly well understood. Yet, the recovery of parameters is challenging as the problem is often ill-posed due to the ill-conditioning of the forward model. Machine learning is now more frequently used to address such problems, using likelihood-free inference (LFI) to inverse nonlinear systems, or prior learning using bi-level optimization and reinforcement learning to guide the way to collect observations.
3.1.1 From linear inverse problems to simulation based inference
| Expected breakthrough: Boosts in MR image quality and reconstruction speed and in spatio-temporal resolution of M/EEG source imaging |
| Findings: Development of data-driven regularizing functions for inverse problems, as well as deep invertible and cost-effective network architectures amenable to solve nonlinear inverse problems on neuroscience data. |
Solving an inverse problem consists in estimating the unobserved parameters at the origin of some measurements. Typical examples are image denoising or image deconvolution, where, given noisy or low resolution data, the objective is to obtain an underlying high-quality image. Inverse problems are pervasive in experimental sciences such as physics, biology or neuroscience. The common problem across these fields is that the measurements are noisy and generally incomplete.
Mathematically speaking, these inverse problem can be formulated as estimating from . Here, is an additive noise and is a (generally non-injective) mapping to a lower-dimensional space. For example, in magneto- and electroenchephalography (M/EEG), is a real linear mapping and is considered white and Gaussian, while in magnetic resonance imaging (MRI), is a complex linear mapping and is circular complex white Gaussian. Despite the linearity of and , estimating is a challenging task when the measurements are incomplete, i.e., and the problem is ill-posed. This is often the case due to physical limitations on the measurement device (M/EEG) or the acquisition time (MRI). Moreover, the linear Fourier operator only reflects an ideal acquisition process and part of the acquisition artifacts (e.g. B0 inhomogeneity) can be compensated by considering nonlinear models at the cost of estimating additional parameters along with the MR image.
To tackle these inverse problems, using adequate regularization will promote the right structure for the data to be recovered. Over the last decade the members of Mind have proposed state-of-the-art models and efficient algorithms based on sparsity assumptions 74, 123, 96, 79, 124, 108, 107, 94, 99, 95. MNE is the reference software developed by the team that implements these methods for MEG/EEG data while pysap-mri proposes solvers for MR image reconstruction.
The field is now progressing with novel approaches based on deep learning by either learning the regularization from data in the context of MRI reconstruction 146, 145, or by considering nonlinear models grounded in the physics underlying the data. The team has started to explore this direction using so-called Likelihood-Free Inference (LFI) techniques built on deep invertible networks 147, 106. A particular application has been on diffusion MRI (dMRI), where we have linked the dMRI signal with physiological tissue models of grey matter tissue 106. Still in MRI but in susceptibility weighted imaging, another approach 88 has consisted in directly estimating the B0 field map from non-Cartesian k-space data to correct for off-resonance effects in non-Fourier operators . The Mind project will continue along this direction studying nonlinear simulators of imaging data as building blocks. A key aspect of the work proposed is to exploit knowledge on the physics of the data generation mechanisms.
3.1.2 Bi-level optimization
| Expected breakthrough: Efficient algorithms to select hyper-parameters and priors for source localisation in MEG and image reconstruction in MRI/fMRI. |
| Findings: Bi-level optimization solvers exploiting gradients to scale with the large number of samples and hyper-parameters. |
In recent years, bi-level optimization – minimizing over a parameter which is itself the solution of another optimization problem – has raised great interest in the machine learning community. Indeed, many methods in ML reduce to this bi-level framework, typically the problem of hyper-parameter optimization.
In most practical cases, hyper-parameter selection is done using cross-validation (CV), which basically consists in splitting the whole dataset in training and validation sets. The parameters of the method are computed by minimizing a loss function on the training set, and the hyper-parameters are then set by minimizing the loss function on the validation set. This approach is a bi-level optimization problem.
Other instances of such problems can be found in dictionary learning, robust training of neural networks or the use of implicit layers in deep learning. In all these applications, the model or the latent variables are learned by minimizing some loss while the parameters or the dictionary are updated by minimizing a second optimization problem depending on the outcome of the first problem. While theoretical results were produced in the early 70's 87, there are still many challenges related to bi-level optimization that need to be addressed to produce methods that are both theoretically well grounded and computationally efficient. Recently, the members of Mind have published several works related to the subject 57, 58, 69, 81. We intend to pursue this effort in the following directions.
Stochastic bi-level solvers.
Bi-level solvers require the use of the whole training set before doing an update on an outer-level problem: In this sense, they are full-batch methods 69. We propose to study stochastic methods for this task, where some improvement on the optimization can be achieved using only a few samples from the training data. Stochastic algorithms are notoriously faster than full-batch methods for large datasets, but are also generally harder to analyse from a theoretical standpoint. In addition to being fast, the proposed algorithm should come with some statistical guarantees. These solvers can have many applications, from stochastic prior learning for inverse problem to hyper-parameters tuning in general machine learning.
Neural Dictionary Learning.
Bi-level optimization framework offers a canvas to advance the state of the art in dictionary and prior learning. Indeed, dictionary learning has long been seen as a bi-level optimization problem 122. Practical algorithms are mainly based on alternate minimization and rarely account for the sub-optimality of each sub-problem. With advances in bi-level optimization and algorithm unrolling 57, we aim at providing efficient and theoretically justified dictionary learning algorithms, that will be able to leverage the technologies of differentiable programming 55, 141.
Deep Equilibrium Models.
The use of Deep learning, and in particular unrolled algorithms 102, has introduced a quantum leap in the resolution of inverse problems compared to variational approaches, specifically in terms of computing efficiency and image/signal recovery performance. However, these networks are very demanding in memory for the training, which currently limits their potential. Different methods exist to alleviate this problem both on the modeling (gradient check-pointing, reversible networks) and the implementation side (model parallelism, mixed precision), but come at the expense of larger computational cost. However, a promising research avenue, illustrated by 100, is the use of Deep Equilibrium Models. These models are defined implicitly and amount to unrolling an infinite number of iterations, thereby using much less memory. These implicit layers constitute another instance of bi-level optimization problem and we plan to work on these directions in the near future as a means to address DL image reconstruction in realistic 3D and 4D multi-coil MRI setting, both for structural and functional imaging.
3.1.3 Reinforcement learning for active k-space sampling
| Expected breakthrough: New hardware compliant under-sampling patterns in MRI k-space that accelerate anatomical and functional scans while optimizing MR image quality. |
| Findings: Develop novel principles of active sampling in the reinforcement learning framework which optimizes a sampling policy tightly linked to the reconstructed image quality. |
Current under-sampling schemes in MRI allow for shorter scan acquisition times, however at the cost of artifacts in various regions of the reconstructed MR image. These artifacts arise due to uncertainties in some heavily under-sampled regions of the acquired Fourier space (i.e. also called k-space). Modern reconstruction algorithms, with the use of strong priors, either hand-crafted or learned, tend to reduce these uncertainties and behave as if the acquisition is fixed.
To go beyond the state of the art, we argue that there is a need to jointly learn an algorithm that designs the optimal under-sampling pattern in k-space as well as the reconstruction network.
As it can be summarized to learning a sequential decision algorithm, we will rely on reinforcement learning (RL) to build up optimal k-space sampling patterns while enforcing physical constraints on the MRI sequence, as originally proposed in 77, 72, 115.
The k-space acquisition can be modeled by a sampling policy and the rewards for the joint network are based on reconstructed image quality. Under this paradigm, after every fixed scan time, an instantaneous reconstruction can be obtained and the Fourier space uncertainty maps analysed in depth. Based on this, the scan can continue by actively sampling the k-space and enforcing denser samples in regions where uncertainty is larger. In this way, the learned k-space trajectories may become more patient and organ specific. Further, the trajectory can run and lead to instantaneous best results of reconstruction under a given variable scan time budget. These aspects define one of the core directions we will investigate to produce the next generation of state-of-the-art MR data sampling and image reconstruction algorithms. Recent contributions 159, 142 only approach the problem in the Cartesian framework and hence perform 1D variable density sampling along the phase encoding dimension. Given our expertise on non-Cartesian sampling in developing SPARKLING for both for 2D and 3D MR imaging 115, 116, 75, we plan to extend this framework to non-Cartesian acquisition setups while still remaining compatible with hardware constraints on the gradient system. The access to various MRI scanners at CEA/NeuroSpin is necessary and an added advantage to the success of the Mind team.
3.2 Heterogeneous Data & Knowledge Bases
Participants:
B. Thirion, D. Wassermann
Inferring the relationship between the physiological bases of the human brain and its cognitive functions requires articulating different datasets in terms of their semantics and representation. Examples of these are spatio-temporal brain images, tabular datasets, structured knowledge represented as ontologies, and probabilistic datasets. Developing a formalism that can integrate all these modalities requires constructing a framework able to represent and efficiently perform computations on high-dimensional datasets as well as to combine hybrid data representations in deterministic and probabilistic settings. We will take on two main angles to achieve this task: on one hand, the automated inference of cross-dataset features, or coordinated representations and on the other hand, the use of probabilistic logic for knowledge representation and inference. The probabilistic knowledge representation part is now well advanced with the Neurolang project. It is yet a long-term endeavor. The learning of coordinated representations is less advanced.
3.2.1 Learning coordinated representations
| Expected breakthrough: Process semantic information together with image data to bridge large-scale resources and knowledge bases |
| Findings: Set up a learning model that leverages heterogeneous data: Images, annotations, texts, and coordinate tables. |
Inference is the pathway that leads from data to knowledge. One crucial aspect is that in the context of neuroscience, data comes in different forms: Full texts, images and tables. Annotations may be full texts or simply tags associated with observed images. One challenge is thus to develop automated techniques that learn coordinated representations across such heterogeneous data sources.
This learning endeavor rests on several key machine learning techniques: Compression, embeddings, and multi-layer networks. Compression (sketching) consists in building a reduced representation of some input that leads from large sparse and complex representation to low-dimension ones, while minimizing some distortion criterion. Embedding techniques also create representations, but possibly bias them to enhance some aspects of the data. It thus incorporates prior information on data distribution or the relevance of features. Finally, multi-layer networks create intermediate representation of data that are suitable to achieve a prediction goal. Such representations are rich enough in particular in multi-task settings, where the outputs of the network are multi-dimensional. Following 64, we call such latent data models coordinated representations.
Deep learning is well suited to the goal of learning intermediate representations. As an example, we plan to develop a framework that coalesces in one deep learning formulation, the task of estimating brain structures, cognitive concepts, and their relationships.
Brain structures and cognitive concepts will appear as intermediate representations responsible for linking brain activity to observed behavior. However deep learning cannot be considered as a standard means to understand coordinated representations, due to the limited data available, their poor signal-to-noise ratio (SNR) and their heterogeneity. Deep learning needs instead to be adapted by injecting our expertise on statistical structure of the data (see e.g. 104, 126). Since the challenge is to train such models on limited and noisy data, we will extend our recent work 62 that has developed regularization schemes for deep-learning models: it relies on structured stochastic regularizations (a.k.a. structured dropout). Such approaches are efficient, powerful and can be used in wide settings. We will enhance them with more generic, cross-layer, grouping schemes. Additionally, we will develop two strategies: i) aggregation of predictors for variance reduction and stability of the model 104 and ii) data augmentation – i.e. learning to augment, based on unlabeled data – to improve the fit with limited data. For this we will consider plausible generative mechanisms.
3.2.2 Probabilistic Knowledge Representation
| Expected breakthrough: A domain-specific language (DSL) capable of articulating heterogeneous probabilistic data sources in neuroimaging is a way to relate physiology to cognition. |
| Findings: Self-optimizing probabilistic solvers for discrete and continuous hierarchical models able to scale for neuroimaging problems. |
Neuroscientific data used to infer the relationships between physiology of the human brain and its cognitive function goes well beyond text, image, and tables. Knowledge graphs representing human knowledge, and the ability to encode reasoning strategies in neuroscience are also key to effectively bridge current data-centric approaches and decades-old domain knowledge. A main challenge in performing inferences combining demographic data-centric approaches, imaging measurements, and domain knowledge, is to be able to infer new knowledge soundly and efficiently taking into account the noisy nature of demographic and imaging measurements, and the common open-world assumption of ontologies and knowledge graphs. Such probabilistic hybrid logic approaches are known to be, in general, intractable in the deterministic 60 as well as in the probabilistic case 156. Nonetheless, there is an opportunity to be seized in identifying tractable segments of probabilistic hybrid logic representations able to solve open neuroscientific questions.
A noticeable opportunity to incorporate all statistical evidence gathered from noisy data into a usable knowledge base is to formalize the inferred relationships into probabilistic symbolic representations 105. These representations are much better suited to simultaneously handle data across topologies and logic systems, implementing inferential algorithms avoiding the brittleness of deterministic logic as well as causal probabilistic reasoning.
A typical application of such heterogeneous data processing is meta-analytic applications which combine neuroimaging data with results found in the scientific literature. Current tools to perform this task are NeuroSynth or Neuroquery (developed by the team). However, knowledge inferred by such tools is tremendously limited by the expressive power of the language used to query the data. Current meta-analytic tools are able to express queries relating test makers, article annotations, and their relationship with reported brain activations, support propositional logic only. Propositional logic requires the user to explicitly express every desired term with their characteristics and their relationships. Our goal is to extend the inference capabilities of such applications by leveraging current advances in probabilistic logic languages and embedding them in the Neurolang language. Neurolang enables the encoding of complex knowledge in terms of more expressive queries. Neurolang queries first-order logic segment, FO, with a tractable probabilistic extension allowing for high-dimensional and large dataset computations. Such segment of first order logic enables formalising questions such as “what brain areas are most likely reported active in a study specifically when terms related to consciousness are mentioned in such study”, hence being able to infer, amongst other tasks, specificity and causality 157 of diverse neuroscience phenomena. To disseminate our results allowing complex expressive searches of massively aggregated diverse data, we will leverage Neurolang. The latter produces a domain-specific language (DSL) for human neuroscience research, while being able to combine imaging data, anatomical descriptions and ontologies. Three main characteristics of the DSL are key to fulfilling this goal: First, it represents neuroimaging-derived information and spatial relationships in a syntax close to natural language used by neuroscientists 158. Second, through a back-end belonging to the Datalog family, it allows querying ontologies with the same expressive power as current standards SPARQL and OWL 66. Finally, we will extend Neurolang to a probabilistic language able to express graphical models allowing the implementation of a wide variety of causal inference and machine learning algorithms 63 in high-dimensional settings which are specific to neuroimaging research. In sum, by leveraging recent advances in deductive database systems 66 and this novel DSL 158 we will provide a more flexible tool to express and infer knowledge on brain structure-function relationships.
3.3 Statistics and causal inference in high dimension
Participants:
A. Gramfort, T. Moreau, B. Thirion, D. Wassermann
Statistics is the natural pathway from data to knowledge. Using statistics on brain imaging data involves dealing with high-dimensional data that can induce intensive computation and low statistical power. Besides, statistical models on large-scale data also need to take potential confounding effects and heterogeneity into account. To address these questions the Mind team will employ causal modeling and post-selection inference. Conditional and post-hoc inference are rather short-term perspectives, while the potential of causal inference stands as a longer-term endeavor.
3.3.1 Conditional inference in high dimension
| Expected breakthrough: Obtain statistical guarantees on the parameters of very-high dimensional generalized linear or non-parametric models. |
| Findings: Develop computationally efficient procedures that allow inference for such models, by leveraging structural priors on the solutions. |
Conditional inference consists of assessing the importance of a certain feature in a predictive model, while taking into account the information carried by alternative features. One motivation for using this inference scheme is that brain regions that sustain behavior and cognition are strongly interacting. Taking these interactions into account is critical to avoid confusing correlation with causation in brain/behavior analysis.
Technical difficulties come when the set of explanatory features becomes extremely large as frequently met in neuroimaging: Conditioning on many variables (or equivalently, high dimensional variables) is computationally costly and statistically inefficient. The main solutions to date are based either on linear model debiasing 110, as well as simulation-based approaches (knockoff inference 73 or conditional randomization tests 119). Importantly the latter involves simulating data with statistical characteristics described explicitly (in a parametric family) or implicitly (by samples). There remain two gaps to bridge for these methods: i) The computational gap, as the algorithmic complexity of these approaches is typically cubic in the number of samples, unless more efficient generative mechanisms are available; ii) the power gap, related to the limited number of available samples. The best solution thus far consists of associating these inference procedures with dimension reduction procedures 133. The next step is adaptation to more general settings: Conditional inference has been formulated in the linear framework, where it boils down to controlling that the corresponding coefficient is non-zero, hence it has to be generalized to nonlinear models: Non-parametric models like random forests, then possibly deep networks.
3.3.2 Post-selection inference on image data
| Expected breakthrough: Statistical control of false discovery proportion (FDP) for data under arbitrary correlation structure. |
| Findings: A computationally efficient non-parametric statistical test procedure, and a benchmark against alternative techniques. |
Large-scale statistical testing is pervasive in many scientific fields, where high-dimensional datasets are collected and compared with an outcome of interest. In such high-dimensional contexts, false discovery rate (FDR) control 68 is attractive because it yields reasonable power, while providing an explicit and interpretable control on false positives. Yet the FDR rate is the expectation of the FDP. Controlling the FDR does not mean that the FDP is controlled, a distinction that is most often ignored by practitioners. For the sake of scientific reproducibility, there is a need for methods controlling the FDP.
Such an approach has been developed in the context of neuroimaging, namely the all-resolution inference framework 148 based on classical multiple correction error control bounds. Yet, the empirical behavior of this method remains to be assessed. Moreover, it has been clearly established that the procedure is over-conservative in some settings 70. Indeed, it relies on the Simes statistical bound, that is not adaptive to the specific type of dependence for a particular data set. To bypass these limitations, 70 have proposed a randomization-based procedure known as -calibration, which yields tighter mathematical bounds that are adapted to the dependency observed in the dataset at hand. It rests on a non-parametric (permutation-based) estimation of the null distribution, leading to tight and valid inference under general assumptions.
In this research axis, we propose to fix some of the open issues with the approach described in 70, namely the choice of a template family to calibrate the error distribution in the permutation procedure. We hope to propose a practical choice for this family to avoid putting the burden of choice on practitioners.
We will characterize by simulations and theoretical arguments the behavior of these error control procedures and develop efficient computational methods for the use of these tools in brain imaging analysis.
3.3.3 Causal inference for population analysis
| Expected breakthrough: Provide a reference methodology for causal and mediation analysis in high-dimensional settings. |
| Findings: Benchmark state-of-the-art techniques and further adapt them to the high-dimensional setting. |
Modern health datasets present population characteristics with many variables and in multiple modalities. They can ground prediction and understanding of individual outcomes, using machine learning techniques. Still, heterogeneous variables have complex relationships, making it hard to tease apart each factor in an outcome of interest. Potential outcome theory 150 provides a valuable framework to evaluate the impact of treatment (interventions). Treatment effects can be heterogeneous. In particular, interactions between background and treatment variables have to be considered.
The statistical behavior (consistency and efficiency) under non-parametric models is actively investigated 61, 135. However, their behavior in high-dimensional settings, when both the number of features and the number of samples are large, is still poorly understood. Our objective is thus to extend the theory and algorithms of causal inference to noisy high-dimensional settings, where the noise level implies that effects sizes are proportionally small, and classic methods often become inefficient and potentially inaccurate due to overfitting. More specifically, we plan to explore the following directions.
Mediation analysis and conditional independence
Mediation analysis considers the question of whether a variable mediates all the effect of another variable onto a target variable , a.k.a. outcome. It turns out that full-mediation analysis amounts to testing whether ( is independent from given ), which is handled by a conditional independence test. When the dimensions of these variables ( in particular, but also and to some extent ) grow, the underlying statistical inference procedures typically lose power, or even possibly error control. We propose to leverage our experience on such high-dimensional inference problems 82, 134 to set up computationally efficient and accurate solutions to this problem.
Latent variable models and confounders
The most important aspect of inferring causal effects from observational data is the handling of confounders, i.e., factors that affect both an intervention and its outcome. For instance, age has a clear impact on brain characteristics as well as on behavior, potentially biasing brain/behavior statistical associations. A carefully designed observational study attempts to measure all important confounders. When one does not have direct access to all confounders, there may exist noisy and uncertain measurements of proxies for confounders. A possible solution to this problem relies on generative modeling, such as Variational Autencoders (VAE) and Generative Adversarial Networks (GANs), to sample the unknown latent space summarizing the confounders on datasets with incomplete information; the seminal work of 121 is promising, but still requires improvements to become usable in realistic settings.
The quest of model selection and validation
In the classical potential outcome theory 150, causal effects are determined by both factual and counterfactual outcomes, ground-truth effects can never be measured in an observational study. In the absence of such measures, how can we evaluate the performance of causal inference methods? Addressing this question is an important step for practical problems, in which one has to determine if an effect can safely be considered non-zero, or heterogeneous through a population. We propose to revisit the promising work of 59 analysing in detail the shortcomings of the procedure (regarding both bias and variance), especially when the model becomes high-dimensional.
3.4 Machine Learning on spatio-temporal signals
Participants:
P. Ciuciu, A. Gramfort, T. Moreau, D. Wassermann, B.Thirion
The brain is a dynamic system. A core task in neuroscience is to extract the temporal structures in the recorded signals as a means to linking them to cognitive processes or to specific neurological conditions. This calls for machine learning methods that are designed to handle multivariate signals, possibly mapped to some spatial coordinate system (e.g. like in fMRI).
3.4.1 Injecting structural priors with Physics-informed data augmentation
| Expected breakthrough: Obtain models with more predictive power when trained on small datasets. |
| Findings: Efficient data-augmentation strategy tailored to brain signals. |
Data augmentation consists of virtually increasing dataset size during learning by applying random, yet plausible, transformations to the input data. In computer vision, this means altering data by applying symmetries, rotations, geometric deformations etc. While such strategies are reasonable for natural or medical images 140, it is still unclear how neural or BOLD signals can be augmented in order to improve prediction performance and robustness.
Some purely data driven strategies have been proposed to augment EEG data using spectral transforms 120 or advanced strategies such as channel, time or frequency masking or phase randomizations 114, 117. Although dozens of transformations have been considered in the literature to augment EEG signals, it is now apparent that different augmentation strategies should be applied to the data as a function of the prediction task to be handled. For example when considering sleep stage classification or BCI applications, the spatial sampling of electrodes and the duration of signals varies considerably, with the consequence being that different augmentation parameters and even transformations need to be employed.
In this line of work we will develop algorithms that can quickly identify the relevant augmentation techniques, building for example on 85, 119. The aim is to provide a system that can automatically learn invariance within a class and across subjects in order to maximize the prediction performance on unseen data. The methodology developed will be relevant beyond neuroscience as long as a family of physics-informed transformations is available for prediction tasks at hand.
3.4.2 Learning structural priors with self-supervised learning
| Expected breakthrough: Unveiling the latent structure of brain signals from large datasets without human supervision as well as improving the prediction performance when learning from limited data. |
| Findings: Self-supervised algorithms for multivariate brain signals. |
Self-supervised learning (SSL) is a recently developed area of research that provides a compelling approach for exploiting large unlabeled datasets. With SSL, the structure of the data is used to turn an unsupervised learning problem into a supervised one, called a “pretext task”, such as solving Jigsaw puzzles from images 137 or learning how to color gray-scaled images. The representation learned on the pretext task can then be reused for unsupervised data exploration or on a supervised downstream task, with the potential to greatly reduce the number of labeled examples required to train a good predictive model.
In fields like computer vision 137, 128 and time series processing 138, SSL has shown great promise in terms of prediction performance but also in ease of use. Indeed, SSL simplifies model selection and evaluation as it relies on prediction scores and cross-validation, contrarily to unsupervised learning methods like ICA 56.
Recently the team has applied SSL to two large cohorts of clinical EEG data 65 revealing insights on the data without any human supervision. However many challenges remain. For example in Mind, we aim to explore novel SSL strategies applicable to electrophysiology as well as to haemodynamic signals measured with fMRI. As such, our goal is to expand the recent multivariate method we have introduced in the field for the blind deconvolution of BOLD signals in both task-related and resting-state experiments 80.
While rather small networks have been employed so far on EEG data 76, 149 due to limited sets of annotations, the use of SSL tasks opens the possibility to work with much larger labeled datasets, and therefore many more overparametrized models. We aim to explore these directions, hoping to reach a state where pre-trained models could be available for EEG or MEG signals as is presently the case for images or for natural language processing (NLP) tasks.
3.4.3 Revealing spatio-temporal structures with convolutional sparse coding and driven point processes
| Expected breakthrough: A novel way to study and quantify temporal dependencies between neural processes, going beyond connectomes based on spectral analysis. |
| Findings: Temporal pattern finding algorithms that scale to massive MEG/EEG datasets with parallel processing and point-process inference algorithms. |
The convolutional sparse linear model is one established unsupervised learning framework designed for signals. Using algorithms known as convolutional sparse coding (CSC), this framework allows for the learning of shift-invariant patterns to sparsely reconstruct a time series. These patterns, also called atoms, correspond to recurrent structures present in the data. While some of our recent advances have improved the computational tractability of these methods 130, 129 and adapted them to neurophysiological data 109, 93, 80, there are still many shortcomings that make them unpractical for applications beyond denoising.
Model validation
The main challenge for the evaluation of unsupervised convolutional models comes from current theoretical limitations: What can we guarantee statistically concerning the recovered atoms? Due to their non-convexity, existing algorithms can only guarantee convergence to local minima, which might be sub-optimal. In this setting, it is challenging to quantify if the model parameters are well estimated and if they are actually representative of the signals. In Mind, we aim to develop statistical quantification of the uncertainty associated with such models and in this regard, provide objective selection criteria for the model and its parameters. This topic of research will benefit from our other developments on bi-level optimization (cf. ssub:bilevel) and on FDR control (cf. ssub:postselection) as well as the expertise of the team members on dictionary learning 130, 127, 129.
Capturing temporal dependencies with point processes
Another shortcoming of these models is that they do not capture temporal dependencies between the occurrences of the different atoms. However, neural activity at level of the whole brain is highly distributed. Different brain regions form networks that are characterized by the presence of statistical dependencies in their activity 139. An interesting question to formulate is how one can model and learn these time dependencies between brain areas from the MEG or EEG recordings using an unsupervised event-based approach such as CSC. One of the approaches considered is based on point processes (PP; 71, 103). PP are classical tools to study event trains (e.g. sequence of spikes) and to model their dependency structure. We aim here to develop PP-based inference algorithms as a means to capture network effects in different brain areas, but also to quantify how experimental stimuli are affecting the temporal statistics of temporal patterns 139. To model this latter scenario, we will develop the so-called driven PP. In a second stage, we aim to design fully unsupervised methods to capture the connections between different brain areas leveraging the full temporal resolution of non-invasive electrophysiological signals.
4 Application domains
The four research axes we presented earlier have been thought of in tight interaction with four main applications (large-scale predictive modeling, mapping cognition & brain networks, modeling clinical endpoints, from brain images and bio-signals to quantitative biology and physics).
4.1 Population modeling, large-scale predictive modeling
4.1.1 Unveiling Cognition Through Population Modeling
Linking the human brain's structure and function with cognitive abilities has been a research epicenter for the past 40 years. The sophistication of brain mapping machinery such as MRI, EEG and MEG, has produced a treasure trove of data. Nonetheless, the effect size of the phenomena leading to understanding cognition is often drowned out by noise and inter-individual variability. A main goal of Mind is to simultaneously harness the power of large-scale general purpose datasets, such as the Human Connectome Project (HCP) and the Adolescent Brain Cognitive Development Study (ABCD), as well as small scale high precision ones, such as the Individual Brain Charting (IBC) dataset 144, to understand the link between the human brain's architecture and function, and cognition. Parietal's expertise has already been demonstrated in this field. Examples of this include using diffusion MRI (dMRI) to link the brain's macrostructure with language comprehension 78, tissue microstructure with cognitive control 125, functional gradients on the cortical surface 91 to functional territory segregation 143.
Mind project will continue this task by seizing our core methodological developments, described in the previous section, and our global collaborative network of cognitive scientists.
4.1.2 Imaging for health in the general population
Individual differences in brain function and cognition have historically been investigated by studies carried out by individual laboratories having access mainly to small sample sizes. The growing availability of public large-scale data of epidemiological dimensions curated by dedicated consortia (e.g. UK Biobank) has enabled studying the relationship between cognition and the brain with unparalleled granularity and statistical power. These resources now allow researchers to relate brain signals/images to rich descriptions of the participants including behavioral and clinical assessments in addition to social and lifestyle factors. Machine learning has proven essential when modeling biomedical outcomes from the large-scale and high-dimensional data brought by consortia and biobanks. It is used to to build predictive models of heterogenous biomedial outcomes (cognitive, social, clinical) based on different neuroscientific modalities. Taken together, this facilitates the study of lifestyle and health-related behavior in the general population, potentially revealing risk factors leading to biomarker discovery.
Mind will greatly contribute to this effort by focusing on population modeling as a tool for enhancing the analysis of clinical data and mental health.
4.1.3 Proxy measures of brain health
Clinical datasets tend to be small as sharing of data is not incentivized or institutional and economic resources are missing. As a consequence, the capacity of machine learning to learn functions that relate complex-to-grasp biomedical outcomes to heterogeneous data cannot be fully exploited. This has stimulated growing interest in proxy measures of neurological conditions derived from the general population, such as individual biological aging. One counter-intuitive aspect of the methodology is that measures of biological aging (e.g. via brain imaging) can be obtained by focusing on the age of a person, which is known in advance and is, in itself not interesting as a target. However, by predicting the age, machine-learning can capture the relevant information about aging. Based on a population of brain images, it extracts the best guess for the age of a person, indirectly positioning that person within the population. Individual-specific prediction errors therefore reflect deviations from what is statistically expected 155. The brain of a person can look similar to brains commonly seen in older (or younger) people. The resulting brain-predicted age reflects physical and cognitive impairment in adults 154, 83, 92 and reveals neurodegenerative processes 118, 101, which could be overlooked without using machine learning.
Mind will extend this line of research in two directions: 1) Assessment of brain age using EEG and non-brain data such as health-records and 2) proxy measures of mental health beyond aging.
4.1.4 Studying brain age using electrophysiology
MRI is not yet available in all clinical situations and certain aspects of brain function are better understood using electrophysiological modalities (M/EEG). Until recently, it was unclear if brain age can be meaningfully estimated from M/EEG. In a recent study 97, we demonstrated, using the Cam-CAN cohort (), that combining MRI and MEG enhanced detection of cognitive dysfunction. The proposed approach not only achieved integration of brain signals from distinct modalities but explicitly handled the absence of MEG or MRI recordings, adapting ideas from 111. This is key for clinical translation where one cannot afford excluding cases because one modality is missing. In the clinical setting, EEG is predominantly used (and not MEG). Clinical recordings are far noisier than lab EEG and gold-standard source modeling with MRI is rarely done outside the lab. Supported by theoretical analysis and simulations, we found through empirical benchmarks 152 that Riemannian embeddings 1) capture individual head geometry 2) bring robustness to extreme noise and, 3) enable good age prediction from clinical 20-channel EEG (n=1300) with performance close to 306-channel lab MEG.
Mind will extend this line of research by translating EEG-based brain age measures into the hospital setting and probe these in different patient populations in which ageing-related differences in brain structure and function are part of the clinical picture, e.g., neurodevelopmental disorders, postoperative cognitive decline and dementia (cf. MIND:subsec:MCE).
4.1.5 Proxy measures of mental health beyond brain aging
Quantitative measures of mental health remain challenging despite substantial research efforts 112. Mental health, can only be probed indirectly through psychological constructs, e.g. intelligence or anxiety gauged by valid and statistically relevant questionnaires or structured examinations by a specialist. In practice, full neuropsychological evaluation is not an automated process but relies on expert judgment to confront multiple responses and interpret them in the context of a larger environmental context including the cultural background of the participant. Inspired by brain age, we set out to build empirical measures of mental health 86 by predicting traditional and broadly used psychological constructs such as fluid intelligence or neuroticism in the UK Biobank. Our results have shown that all proxies captured the target constructs and were more useful than the original measures for characterizing real-world health behavior (sleep, exercise, tobacco, alcohol consumption). In the long run, we anticipate that using proxies could complement psychometric assessments by corroborating data and potentially providing more accurate data faster and more efficiently for clinical populations.
Mind will expand this line of research by systematically searching for proxy measures of physical and mental health derived from large clinical population using electronic health records or transcripts from clinical interviews. We will propose a systematic causal analysis (treatment effect size and mediation) to provide a clearer understanding of the relationships between the many variables that characterize mental health. We will study more in detail the impact of general health markers on brain status, as this may well fit much of the unexplained variance on brain health.
4.2 Mapping cognition & brain networks
4.2.1 Problem statement
Cognitive science and psychiatry aim at describing mental operations: cognition, emotion, perception and their dysfunction. As an investigation device, they use functional brain imaging, that provides a unique window to bridge these mental concepts to the brain, neural firing and wiring. Yet aggregating results from experiments probing brain activity into a consistent description faces the roadblock that cognitive concepts and brain pathologies are ill-defined. Separation between them is often blurry. In addition, these concepts (a.k.a. psychological constructs) may not correspond to actual brain structures or systems. To tackle this challenge, we propose to leverage rapidly increasing data sources: text and brain locations described in neuroscientific publications, brain images and their annotations taken from public data repositories, and several reference datasets.
4.2.2 What machine learning can do for neuroscience
Recent works in computer vision 89 or natural language processing 84, 90 have tackled predictions on a large number of classes, getting closer to open-ended knowledge. These approaches, that rely on uncovering some form of relational structure across these classes, in effect capture the semantics of the domain 84, including the similarity structure of the relevant classes and the ambiguities across classes or the multiple aspects of a class. Broadly speaking, these contributions converge to the concept of representation learning 67, i.e. estimating latent factors that reformulate a learning problem into a new set of input features or output classes that are more natural for the data and help further analysis. These new tools enable extraction of knowledge, for instance ontology induction, with statistical learning 136. They are at the root of heterogeneous data integration, such as multi-modal machine learning 64. The machine learning challenges that we aim to tackle are three-fold:
- Existing multi-modal machine learning techniques have been developed for relatively abundant data, with overall high SNR: text, natural images, videos, sound. These data are most often non-ambiguous, while brain data typically are, due to the low SNR per image and, more crucially, poor annotation quality. We propose to tackle this by adapting machine learning solutions to this low-SNR regime: introduction of priors, aggressive dimension reduction, aggregation approaches and data augmentation to reduce overfitting.
- Leveraging implicit supervisory signals: While data sources contain lots of implicit information that could be used as targets in supervised learning, there is most often no obvious way to extract it. We propose to tackle this by using additional, ill- or not-annotated data, relying on self-supervision methods.
- Model interpretability: Our goal is to provide clear assertions on the relationships between brain structures and cognition: the inference should always lead to an updated knowledge base, i.e. updated relationships between concepts pertaining to neuroscience on one hand, psychology on the other hand. Specifically, one should be able to reason about the information extracted within Mind. For this, we will develop dedicated statistical, causal and formal (ontology-based) data analysis schemes.
Associating knowledge engineering with statistical learning to boost cognitive neuroimaging, requires tackling the challenge of multimodal machine learning under noisy conditions with limited data. Doing so, it will capture links between behavior and brain activity, and enable aggregating the information carried by neuroimaging data to redefine and link concepts in psychology and psychiatry.
4.2.3 Perspective taken: combine distributional semantics with brain images
In natural language processing (NLP), distributional semantics capture meanings of words using similarities in the way they appear in their environment. We want to adapt these ideas to learn data-driven organizations of psychological concepts. Importantly, applying these techniques solely to the psychology literature merely captures the current status quo of the field. Including brain images is necessary to bring new information.
To link observed cognition to brain activity, two typical statistical learning problems arise: encoding, that seeks to describe brain activity from behavior; and decoding, that seeks the converse, predicting behavior from brain activity 113. In addition, statistical modeling of each aspect of the data on its own generates knowledge, typically spatial decompositions from resting-state data, and topic modeling on descriptions of behavior. The research strategy followed in this proposal is to combine the different statistical learning problems in a unified framework to extract core structures from the aggregation of neuroimaging data: on one side brain structures, and on the other side semantic relationships and concepts in psychological sciences.
Mind will in particular publish automated functional meta-analyses to give a systematic assessment of the publicly available data and question the limitations of the current conceptual framework of systems neuroscience as well as of these resources.
4.3 Modeling clinical endpoints
When sufficient data is available, machine learning can be employed to directly model various clinical endpoints (such as diagnosis, drug response, and neuropsychological scores) from brain signals without the need for proxy measures. This approach has the potential to significantly and meaningfully simplify statistical modeling in clinical research. Machine learning facilitates combining heterogeneous input data (different modalities) and does not need high confidence in underlying generative models linking the data to the clinical endpoint. As a consequence, the same class of models can be applied regardless of the endpoint. Its focus is on bounding the approximation error of the endpoint instead of correct parameter estimates. As such, it provides generalizing models that are more robust. Our team has pushed this type of research program through several important collaborations with our European clinical partners using EEG and MRI.
4.3.1 EEG-based modeling of clinical endpoints
Neurological and psychiatric disorders can show complex neurological patterns. Diagnosis is often performed clinically (based on cerebral signs and behavioral symptoms), leading to important variability across doctors. In clinical neuroscience, predicting diagnosis from brain signals is therefore a common application. In the clinical context, EEG is an economically viable option that can be applied in a wide array of circumstances. In collaboration with the Salpêtrière Hospital and the Paris Brain Institute (ICM) we have developed and validated an approach for an EEG-based modeling of diagnosis for severely brain injured patients suffering from consciousness disorders (DoC) 98. Expert-defined features from consciousness studies were rigorously combined using random forest classification. Sensitivity analysis and benchmarks showed robustness across EEG-configurations (channels, time points), protocols (resting state vs evoked responses), label noise and differences between recording sites. When changes in the signal are more subtle than they are in DoC patients (average power turned out to be one of the strongest stand-alone features) more general approaches are needed.
Our future activities will focus on extending this line of research to other clinical populations and other endpoints. We have started a collaboration with the Institut Pasteur (GHFC team, T Bourgeron, R Delorme) and the University of Montreal (PPSP team, G Dumas), to characterize differences between normally developing children and children diagnosed with autism spectrum disorders. A wide array of EEG tasks will be used and endpoints (i.e. developmental timepoints) will go beyond the usually accurate diagnosis, focusing on symptom severity and social developmental scores. With the anesthesiology department at the Lariboisière hospital (A Mebazaa, E Gayat, F Vallée) and the cognitive neurology unit (C Paquet) we aim at developing EEG-based models of cognitive decline and dysfunction in two different settings. Postoperative cognitive decline is an important complication after general anesthesia and its antecedents must be better understood. As this might be an indicator for a latent neurodegenerative condition, we plan to use our EEG-based models of both Alzheimer's Disease and Lewy body dementia in which disease progression is an important change over time.
This widening scope calls for a more general methodology as compared to our previous work on DoC. For example, in these conditions involving neurodegenerative problems, we have observed that both subtle and condition-specific spatial patterns matter more than strong and global amplitude changes. To approach these challenges we will draw on our latest M/EEG-methods that were recently developed for population-level modeling of brain health and brain aging 97. We found that frequency band-specific spatial patterns of M/EEG power spectra conveyed important information of cognitive function (memory and cognitive performance) that were not explained by MRI or fMRI. This was implemented by predicting from a filter-bank of frequency-band-specific source power and source connectivity features. Core challenges to enable clinical translation include lower SNR and absence of individual anatomical MRI scans needed for gold-standard source modeling. Through theoretical analysis, simulations and benchmarks we found 152, 151 that, in M/EEG sensor space, covariance matrices in combination with spatial filtering techniques and Riemannian embeddings provide good workarounds for absent anatomical MRI scans. This covariance-based approach allows to capture fine-grained spatial information related to power and connectivity without performing biophysics-based source localization. Moreover, Riemannian embeddings make predictive modeling from M/EEG covariance matrices more robust to noise, whereas their interpretability is more challenging than that of spatial filters, indicating a direction for further research. Another challenge is given by the limited numbers of labeled samples for supervised learning and EEG-devices with small channel numbers, such as monitoring or user-grade EEG with 2-4 electrodes for which random loss of electrodes can be frequent. In this context, we expect important enhancements from self-supervised learning approaches 65 and deep learning methods for data-augmentation for which we have obtained the first results on non-clinical data. In these settings, the previous elements from classical approaches such as Riemannian geometry or spatial filtering can be readily implemented alongside more involved computations and transformations.
4.3.2 MRI-based modeling of clinical endpoints
Image based biomarkers can be objectively measured and are a sign of normal or abnormal processes, of a condition or disease. Incorporating new potential imaging biomarkers requires several steps, often in parallel and complementary to each other, to be undertaken for translation into clinical practice. These can be divided into the following phases after identification: Development and evaluation, validation, implementation, qualification, and utilization. Our team aims to cross two main translational gaps, that is, the translation from patients first and then to practice. Our aim through our current and active projects is to ensure that potential biomarkers, like the clear delineation of subterritories of the subthalamic nucleus (STN) in pharmaco-resistant Parkinson's disease (PD) patients (i.e.candidates for implantation of a deep brain stimulator) are `fit for purpose' and associated with the clinical endpoint of interest with the overarching goal being to demonstrated efficacy and health impact. This process is key to the translation into clinical practice and widespread utilization.
Through the ANR VLFMRI grant we aim to derive new MR imaging-based biomarkers related to prematurity and abnormal neurodevelopment of hospitalized neonates at low magnetic field (20 mTesla). In this setup, the objective is to perform an almost continuous monitoring to detect early signs of adverse events including ischemic stroke or encephalopathy (collaboration with Prof. V. Biran, APHP Robert Debré Hospital). An additional collaboration is already underway with the AP-HP Henri Mondor Hospital (neuroradiologist Dr B. Bapst, doing part of her PhD at NeuroSpin), to achieve high-resolution susceptibility weighted imaging (600 µisotropic) in a scan time of 2m30s for an accurate delineation of the STN in PD patients prior to surgical planning. A database of 123 patients has already been collected using both the standard SWI imaging protocol and ours based on the SPARKLING technology. This annotated database will be key to compare the diagnosis power of our solution with that of the current care, analyse to what extent a higher image resolution is instrumental in providing a more accurate clinical diagnostic, and finally make our protocol more widely accepted in the clinical practice.
Our key contribution in these projects is to translate to the clinical realm both the SPARKLING technology on the acquisition side 116, 75 as well as our PySAP software 99 for MR image reconstruction. In this regard, the recently accepted CEA postdoc funding should help us move the technology to clinical 7T MR Systems (Magnetom Terra Siemens-Healthineers) in the University hospital of Poitiers through a nascent collaboration with Prof. Rémy Guillevin. Their interest is to use the high-resolution SPARKLING SWI protocol at 7T to better delineate the anomalies along the central vein for the diagnostic of multiple sclerosis as the number of anomalies predicts the grade/severity of this inflammatory pathology. On a longer perspective, we aim to generalize the use of our recently DL networks for MR image reconstruction 146, 145 to multiple acquisition setups and other downstream tasks (e.g. motion correction and correction of off-resonance artifacts related to inhomogeneities).
4.4 From brain images and bio-signals to quantitative biology and physics
Thanks to the developments in MIND:subsec:MLIP and MIND:subsec:MLSTP we aim to approximate more accurately the biophysical models underlying MRI and electrophysiological signals. By estimating quantities grounded in the physics of the data (time, spatial localization, tissue properties) we ambition to offer more actionable outputs for cognitive, clinical and pharmacological applications.
Technologies like 4D SPARKLING should in the future allow us to carry out both fast high resolution multi-parametric quantitative imaging (e.g. T1, T2 and proton density mapping) and laminar (i.e. layer-based) functional imaging in BOLD-fMRI. First, in the mqMRI and fMRI setting, the fourth dimension is respectively the weighting contrast and time axis. mqMRI imaging enables a precise quantification of biomarkers such as iron stores in the pathological brain. Measuring these parameters intra-cortically in Parkinsonian patients defines one of the key challenges in the coming years, especially at 7 Tesla, to earlier stratify the PD patients and the evolution of their disease. Second, a particular attention will be paid to the impact of the developments performed in MIND:subsec:MLIP on the statistical sensitivity of brain activity detection, which eventually defines the final validation metric of the data acquisition/image reconstruction pipeline. For this purpose, robust experimental activation protocols such as retinotopic mapping will be used for validation on the 7T scanner and eventually on the 11.7T Iseult MR system. The finest target resolution is 500 isotropic in 3D.
Novel development on bi-level optimization for hyper-parameter selection from ssub:bilevel will bring state-of-the-art inverse methods to end users currently facing the difficulty of performing model selection on empirical data efficiently. This will lead to more accurate quantitative assessments, in sub-millimeters and milliseconds, of where neural activity occurs.
The line of work on inverse problems should also impact how non-invasive neuroimaging and electrophysiology, based on MRI, EEG and MEG, is considered by more traditional neurophysiologists working with animal data. By considering biophysical models of the data and aiming to estimate their parameters from empirical recordings our hope is to present estimates of physical quantities (tissue properties, neural interactions strengths, etc.). The line of work based on stochastic simulation based inference (SBI) can revolutionize the way MEG, EEG and MRI data are apprehended. For this line of work we will explore the inversion of the models as offered by major software such as The Virtal Brain (TVB) 153 or the Human Neocortical Neurosolver (HNN) 132. A student from the group of Prof. S. Jones at the origin of the HNN software visited the team in 2022.
5 New software and platforms
5.1 New software
5.1.1 MNE
-
Name:
MNE-Python
-
Keywords:
Neurosciences, EEG, MEG, Signal processing, Machine learning
-
Functional Description:
Open-source Python software for exploring, visualizing, and analyzing human neurophysiological data: MEG, EEG, sEEG, ECoG, and more.
-
Release Contributions:
https://mne.tools/stable/whats_new.html
- URL:
-
Contact:
Alexandre Gramfort
-
Partners:
HARVARD Medical School, New York University, University of Washington, CEA, Aalto university, Telecom Paris, Boston University, UC Berkeley, Macquarie University, University of Oregon, Aarhus University
5.1.2 NeuroLang
-
Name:
NeuroLang
-
Keywords:
Neurosciences, Probabilistic Programming, Logic programming
-
Functional Description:
NeuroLang is a probabilistic logic programming system specialised in the analysis of neuroimaging data, but not exclusively determined by it.
-
Release Contributions:
https://neurolang.github.io/
- URL:
-
Contact:
Demian Wassermann
5.1.3 Nilearn
-
Name:
NeuroImaging with scikit learn
-
Keywords:
Health, Neuroimaging, Medical imaging
-
Functional Description:
NiLearn is the neuroimaging library that adapts the concepts and tools of scikit-learn to neuroimaging problems. As a pure Python library, it depends on scikit-learn and nibabel, the main Python library for neuroimaging I/O. It is an open-source project, available under BSD license. The two key components of NiLearn are i) the analysis of functional connectivity (spatial decompositions and covariance learning) and ii) the most common tools for multivariate pattern analysis. A great deal of efforts has been put on the efficiency of the procedures both in terms of memory cost and computation time.
-
Release Contributions:
HIGHLIGHTS - Updated docs with a new theme using furo. - permuted_ols and non_parametric_inference now support TFCE statistic. - permuted_ols and non_parametric_inference now support cluster-level Family-wise error correction. - save_glm_to_bids has been added, which writes model outputs to disk according to BIDS convention.
NEW - save_glm_to_bids has been added, which writes model outputs to disk according to BIDS convention. - permuted_ols and non_parametric_inference now support TFCE statistic. - permuted_ols and non_parametric_inference now support cluster-level Family-wise error correction. - Updated docs with a new theme using furo.
See all details in https://nilearn.github.io/stable/changes/whats_new.html
- URL:
-
Contact:
Bertrand Thirion
-
Participants:
Alexandre Abraham, Alexandre Gramfort, Bertrand Thirion, Elvis Dohmatob, Fabian Pedregosa Izquierdo, Gael Varoquaux, Loic Esteve, Michael Eickenberg, Virgile Fritsch
5.1.4 Benchopt
-
Keywords:
Mathematical Optimization, Benchmarking, Reproducibility
-
Functional Description:
BenchOpt is a package to simplify, make more transparent and more reproducible the comparisons of optimization algorithms. It is written in Python but it is available with many programming languages. So far it has been tested with Python, R, Julia and compiled binaries written in C/C++ available via a terminal command. If it can be installed via conda, it should just work!
BenchOpt is used through a simple command line and ultimately running and replicating an optimization benchmark should be as easy a cloning a repo and launching the computation with a single command line. For now, BenchOpt features benchmarks for around 10 convex optimization problems and we are working on expanding this to feature more complex optimization problems. We are also developing a website to display the benchmark results easily.
-
Release Contributions:
https://github.com/benchopt/benchopt/releases/tag/1.3.0
-
Contact:
Thomas Moreau
5.1.5 Scikit-learn
-
Keywords:
Clustering, Classification, Regression, Machine learning
-
Scientific Description:
Scikit-learn is a Python module integrating classic machine learning algorithms in the tightly-knit scientific Python world. It aims to provide simple and efficient solutions to learning problems, accessible to everybody and reusable in various contexts: machine-learning as a versatile tool for science and engineering.
-
Functional Description:
Scikit-learn can be used as a middleware for prediction tasks. For example, many web startups adapt Scikitlearn to predict buying behavior of users, provide product recommendations, detect trends or abusive behavior (fraud, spam). Scikit-learn is used to extract the structure of complex data (text, images) and classify such data with techniques relevant to the state of the art.
Easy to use, efficient and accessible to non datascience experts, Scikit-learn is an increasingly popular machine learning library in Python. In a data exploration step, the user can enter a few lines on an interactive (but non-graphical) interface and immediately sees the results of his request. Scikitlearn is a prediction engine . Scikit-learn is developed in open source, and available under the BSD license.
- URL:
- Publications:
-
Contact:
Olivier Grisel
-
Participants:
Alexandre Gramfort, Bertrand Thirion, Gael Varoquaux, Loic Esteve, Olivier Grisel, Guillaume Lemaitre, Jeremie Du Boisberranger, Julien Jerphanion
-
Partners:
Boston Consulting Group - BCG, Microsoft, Axa, BNP Parisbas Cardif, Fujitsu, Dataiku, Assistance Publique - Hôpitaux de Paris, Nvidia
5.1.6 joblib
-
Keywords:
Parallel computing, Cache
-
Functional Description:
Facilitate parallel computing and caching in Python.
- URL:
-
Contact:
Gael Varoquaux
6 New results
6.1 Accelerated acquisition in MRI
Participants: Chaithya Giliyar Radhakrishna, Guillaume Daval-Frérot, ZAineb Amor, Philippe Ciuciu.
Main External Collaborators: Alexandre Vignaud [CEA/NeuroSpin], Pierre Weiss [CNRS, IMT (UMR 5219), Toulouse], Aurélien Massire [Siemens-Healthineers, France].
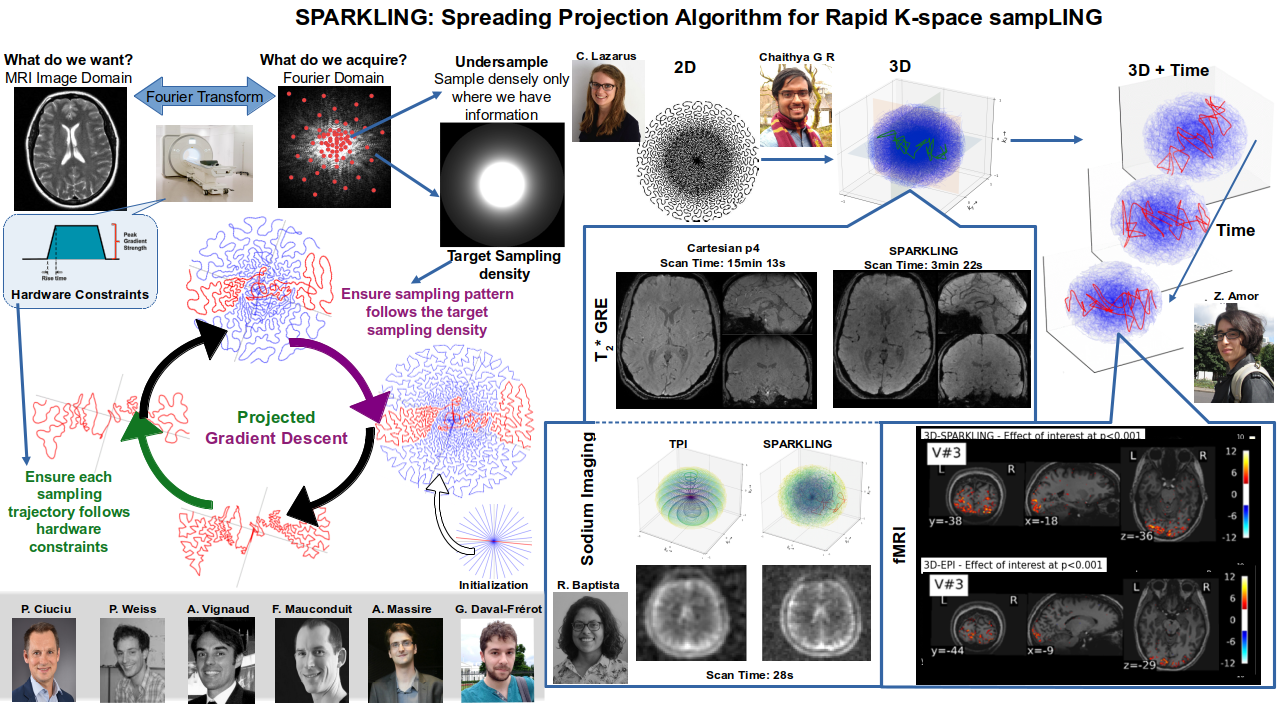
MRI is a widely used neuroimaging technique used to probe brain tissues, their structure and provide diagnostic insights on the functional organization as well as the layout of brain vessels. However, MRI relies on an inherently slow imaging process. Reducing acquisition time has been a major challenge in high-resolution MRI and has been successfully addressed by Compressed Sensing (CS) theory. However, most of the Fourier encoding schemes under-sample existing k-space trajectories which unfortunately will never adequately encode all the information necessary. Recently, the Mind team has addressed this crucial issue by proposing the Spreading Projection Algorithm for Rapid K-space sampLING (SPARKLING) for 2D/3D non-Cartesian T2* and susceptibility weighted imaging (SWI) at 3 and 7Tesla (T) 115, 116, 4. These advancements have interesting applications in cognitive and clinical neuroscience as we already have adapted this approach to address high-resolution functional and metabolic (Sodium 23Na) MR imaging at 7T – a very challenging feat 38, 40. Fig. 1 illustrates the SPARKLING application to anatomical, functional and metabolic imaging. Additionally, we have shown that this SPARKLING under-sampling strategy can be used to internally estimate the static B0 field inhomogeneities a necessary component to avoid the need for additional scans prior to correcting off-resonance artifacts due to these inhomogeneities. This finding has been published in 16 and a patent application has been filed in the US (US Patent App. 63/124,911). Ongoing extensions such as Minimized Off Resonance SPARKLING or MORE-SPARKLING tend to avoid such long-lasting processing by introducing a more temporally coherent sampling pattern in the k-space and then correcting these off-resonance effects already during data acquisition 42.
6.2 Deep learning for MR image reconstruction and artifact correction
Participants: Zaccharie Ramzi, Guillaume Daval-Frérot, Chaithya Giliyar Radhakrishna, Philippe Ciuciu.
Main External Collaborators: Jean-Luc Starck [CEA/DAp/CosmoStat], Mariappan Nadar [Siemens-Healthineers, USA], Boris Mailhé [Siemens-Healthineers, USA].
Although CS is used extensively, this approach suffers from a very slow image reconstruction process, which is detrimental to both patients and rapid diagnosis. To counteract this delay and improve image quality, as explained in Sec. 3.1 deep learning is used. In 2020 we secured the second spot in the 2020 brain fastMRI challenge (1.5 and 3T data) 131 with the XPDNet (Primal Dual Network where X plays the role of a magic card) deep learning architecture. Additionally, we assessed XPDNet's transfer learning capacity on 7T NeuroSpin T2 images. However this DL reconstruction process was limited to Cartesian encoding, thus incompatible with our SPARKLING related technological push. In 2022, we went therefore further by proposing the NCPD-Net deep learning architecture for non-Cartesian imaging. NCPD-Net stands for Non-Cartesian Primal Dual Network and is able to handle both 2D and 3D non-Cartesian k-space data such as those collected with the full 3D SPARKLING encoding scheme 6. This progress allowed us to make a significant leap in image quality when implementing high resolution imaging while maintaining a high acceleration rate (e.g. 8-fold scan time reduction). Fig. 2 shows how NC-PDNet outperforms its competitors through an ablation study in 2D spiral and radial imaging and some preliminary results in 3D anatomical -weighted imaging.
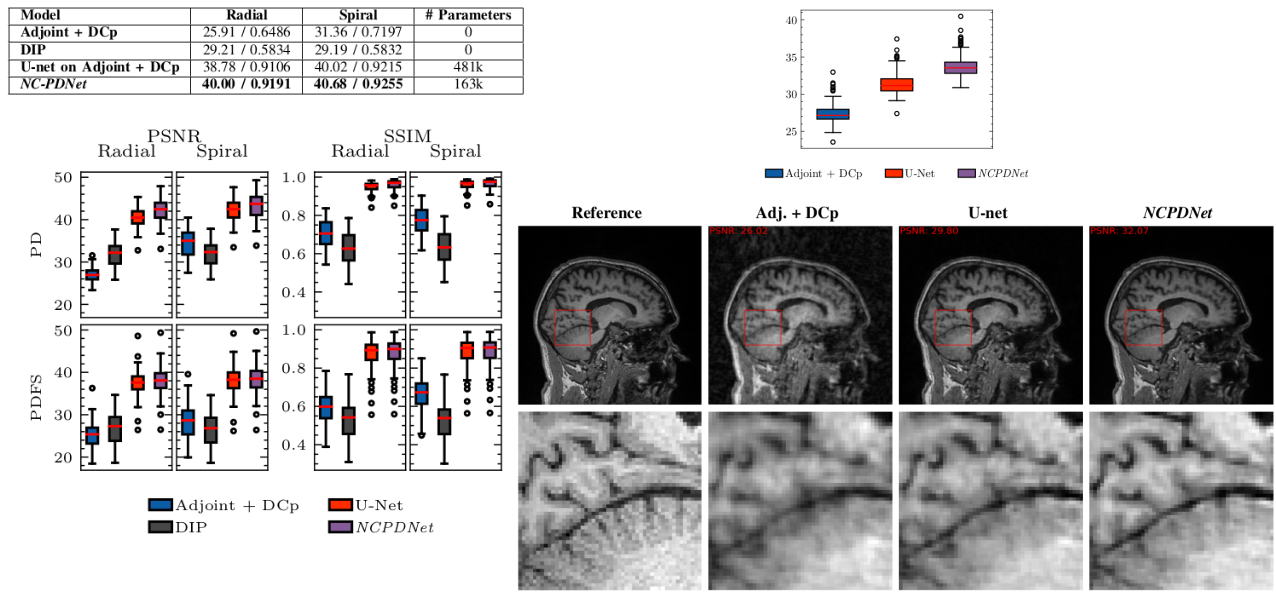
Non-Cartesian Primal Dual network for MR image reconstruction. Top Left: Table comparing the different 2D reconstruction models with respect the image quality metrics (PSNR and SSIM scores:) from 4-fold undersampled k-space data. The density compensated (DCp) adjoint is the extension of the zero-filled inverse Fourier transform to non-Cartesian data where we account for variable density sampling. DIP stands for the Deep Image Prior model. U-net is a standard convolutional neural network (CNN) combined here with the DCp mechanism. bottom left: Box plot results showing that the best PSNR (in dB) SSIM scores are achieved by the 2D NC-PDNet architecture for both Proton Density (top row) weighted images and Fat Saturated PD images (bottom row) in both spiral and radial imaging. Top right: Box plot associated with the 3D imaging results, confirming the superiority of NC-PDNet over the same competitors. Bottom right: Sagittal view of an anatomical T1T_1-weighted image reconstructed using the different methods. Zoom-in associated with the red frame localized in the cerebellum to demonstrate the gain in accuracy using NC-PDNet.
Once the NC-PDNet architecture has been validated for 3D MR image reconstruction, it has then been combined with physics-driven model to speed up the correction of off-resonance effects induced by the inhomogeneities of the static magnetic field 50. Fig. 3[left column] shows the signal void in the frontal region of the brain when not applying any correction. The CS correction yields a limited improvement when constraining its processing time to a little portion (actually 1/70) of the brute force correction shown in the top right column (Reference). Next, we show that the best correction of off-resonance artifacts is achieved by combining the NC-PDNet architecture (Network, 4th column in Fig. 3) with non Fourier encoding model in a 70-fold faster process compared to the reference correction (left column). In contrast, using a standard NC-PDNet architecture that is not physically informed by the degradation process causing these off-resonance artifacts leads to oversmoothed correction (cf. middle column in Fig. 3). Overall, this work has demonstrated how investigating into the combination of physics-informed deep learning architectures was instrumental in obtaining high image quality in clinically viable processing time.
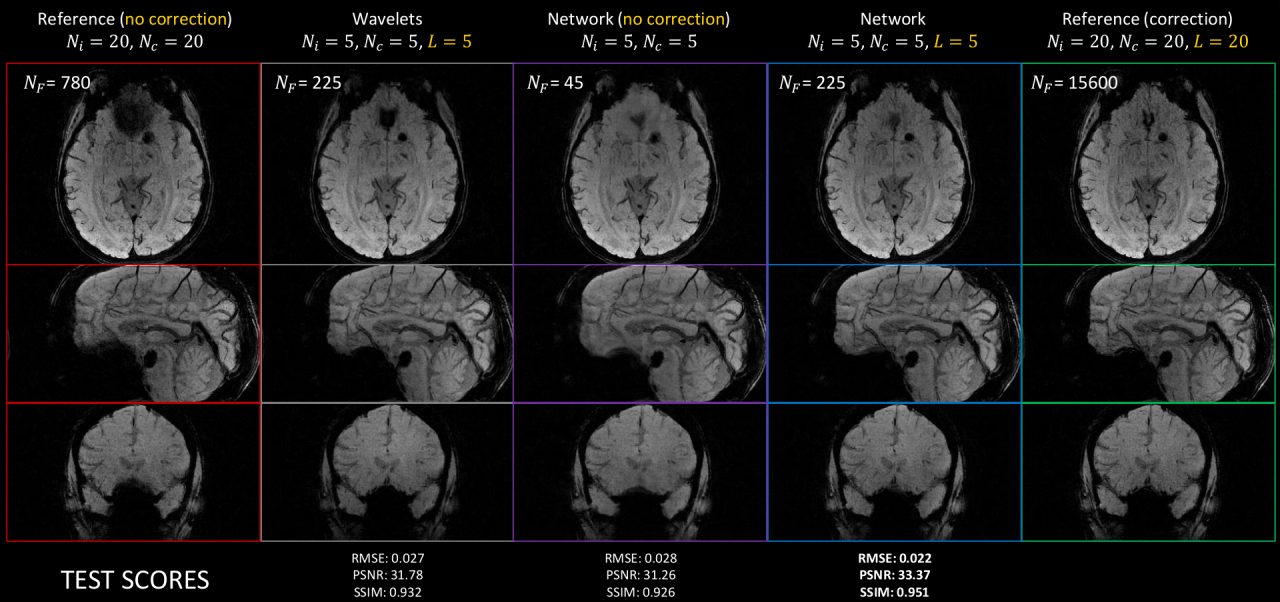
Deep learning physics-informed correction of off-resonance artifacts during MR image reconstruction using the NC-PDnet architecture. Illustration on a single SWI volume (high resolution: 600 μ\mu m). Left (red): Compressed Sensing (CS) reconstruction with no artifact correction, computed in 25min. Center left: CS reconstruction using a reduced non-Fourier forward model to correct for B0B_0 inhomgoneities in approximately 10min. Middle (purple): Network or NC-PDnet based reconstruction without physics based knowledge to correct forB0B_0 inhomgoneities (approx. 1min of computation). Center right (blue): NC-PDnet based reconstruction without physics based knowledge to correct forB0B_0 inhomgoneities (7min of computation). Right (green): Classical CS reconstruction and off-resonance artifact correction based on an extended non-Fourier model, which costs 8 hours of computation. The best result is that in the blue frame.
6.3 Neuroimaging Meta-analyses with NeuroLang: Harnessing the Power of Probabilistic Logic Languages
Participants: Demian Wassermann, Majd Abdallah, Gaston Zanitti.
Main External Collaborators: Vinod Menon [Stanford University, USA], Maria Vanina Martinez [Univ. de Buenos Aires, Argentina].
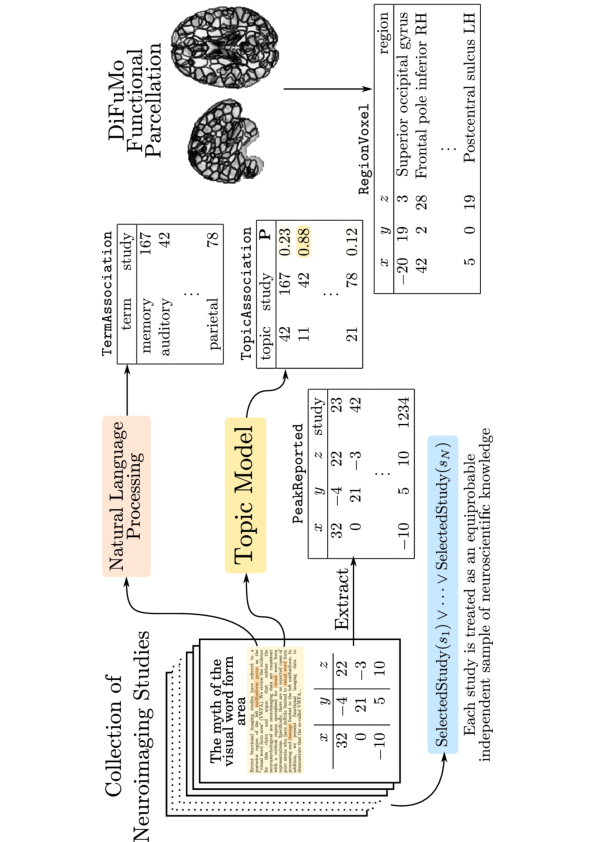
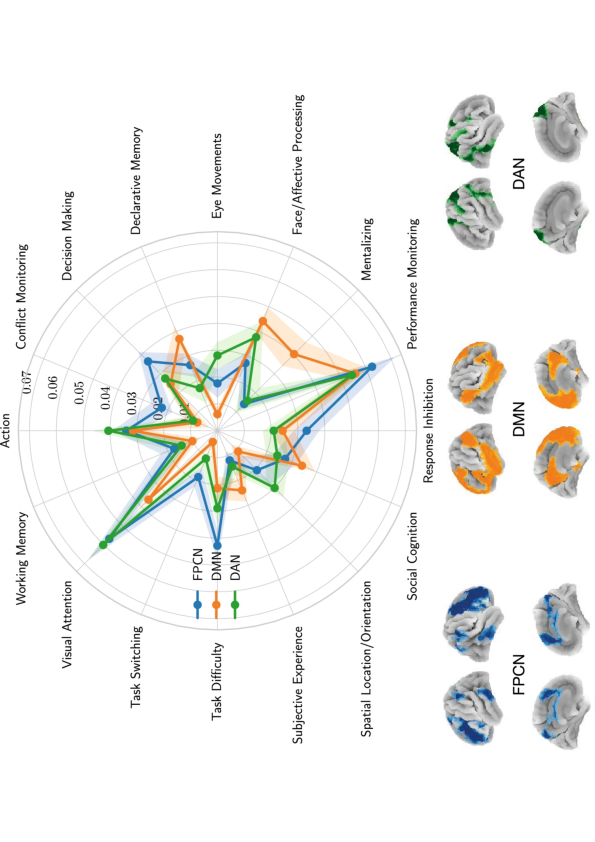
Inferring reliable brain-behavior associations requires synthesizing evidence from thousands of functional neuroimaging studies through meta-analysis. However, existing meta-analysis tools are limited to investigating simple neuroscience concepts and expressing a restricted range of questions. Here, we expand the scope of neuroimaging meta-analysis by designing NeuroLang: a domain-specific language to express and test hypotheses using probabilistic first-order logic programming. This new result is a developement of our main objective on Probabilistic Knowledge Representation, described in Subsec. 3.2.2. By leveraging formalisms found at the crossroads of artificial intelligence and knowledge representation, NeuroLang provides the expressivity to address a larger repertoire of hypotheses in a meta-analysis, while seamlessly modeling the uncertainty inherent to neuroimaging data. We demonstrate the language’s capabilities in conducting comprehensive neuroimaging meta-analysis through use-case examples that address questions of structure-function associations. The schematic and results of this work can be seen in Fig. 4.
Specifically, we have produced three main advancements. First, we have formally defined and implemented a scalable query answering system which covers the functional requirements to address neuroimaging meta-analyses: NeuroLang. This system is described Zanitti et al. 29. Subsequently, we showed the capabilities of this language by performing a variety of neuroimaging meta-analyses which confirm and challenge current knowledge on the relationship between different regions and networks of the brain, and cognitive tasks 8. Finally, we have used NeuroLang to shed light onto the organization of the lateral prefrontal cortex 9, and, within the context of our project LargeSmallBrainNets (see 8.1.1) on the learning process for children with mathematical disabilities 13.
6.4 Efficient Bilevel optimization solvers
Participants: Mathieu Dagréou, Zaccharie Ramzi, Philippe Ciuciu, Thomas Moreau.
Main External Collaborators: Pierre Ablin [CNRS/Apple], Samuel Vaiter [CNRS].
In recent years, bi-level optimization – solving an optimization problem that depends on the results of another optimization problem – has raised much interest in the machine learning community and, particularly, for hyper-parameter tuning, meta-learning or dictionary learning. This problem is made particularly hard by the fact that computing the gradient of the problem can be computationally expensive, as it requires to solve the inner problem as well as some large linear system. In the recent years, several solvers have been proposed to mitigate such cost, in particular by proposing ways to efficiently approximate the gradient. This year, we proposed two approaches that advanced the state-of-the-art solvers for such problems. First, we proposed a solver that is able to share inverse hessian estimate for the resolution of both the inner problem and the linear system, efficiently leveraging the structure of the problem to reduce the computations. This result was presented in Ramzi et al. 36. Then we proposed a stochastic solver for bi-level problems with variance reduction (e.g. see SABA in Fig. 5), and showed that such algorithm had the same convergence rate as its single level counter part. This algorithm was presented in Dagréou et al. 3 and it received an Oral (AR < 5%). These results are prerequisites to scale the resolution of bi-level optimization problems to larger applications such as the one in neurosciences.

6.5 Benchopt: Reproducible, efficient and collaborative optimization benchmarks
Participants: Thomas Moreau, Mathieu Dagréou, Zaccharie Ramzi, Benoit Malézieux, En Lai, Alexandre Gramfort.
Main External Collaborators: Mathurin Massias [Inria, Dante], Joseph Salmon [Univ. Montpellier].
Numerical validation is at the core of machine learning research as it allows researchers in this field to assess the actual impact of new methods, and to confirm the agreement between theory and practice. Yet, the rapid development of the field poses several challenges: researchers are confronted with a profusion of methods to compare, limited transparency and consensus on best practices, as well as tedious re-implementation work. As a result, validation is often very partial, which can lead to wrong conclusions that slow down the progress of research. We proposed Benchopt, a collaborative framework to automate, reproduce and publish optimization benchmarks in machine learning across programming languages and hardware architectures (see Fig. 6). Benchopt simplifies benchmarking for the community by providing an off-the-shelf tool for running, sharing and extending experiments. To demonstrate its broad usability, we showcased benchmarks on many standard learning tasks including -regularized logistic regression, Lasso, and ResNet18 training for image classification. These benchmarks highlight key practical findings that give a more nuanced view of the state-of-the-art for these problems, showing that for practical evaluation, the devil is in the details. This library and the associated benchmarks were presented in Moreau et al. 5.
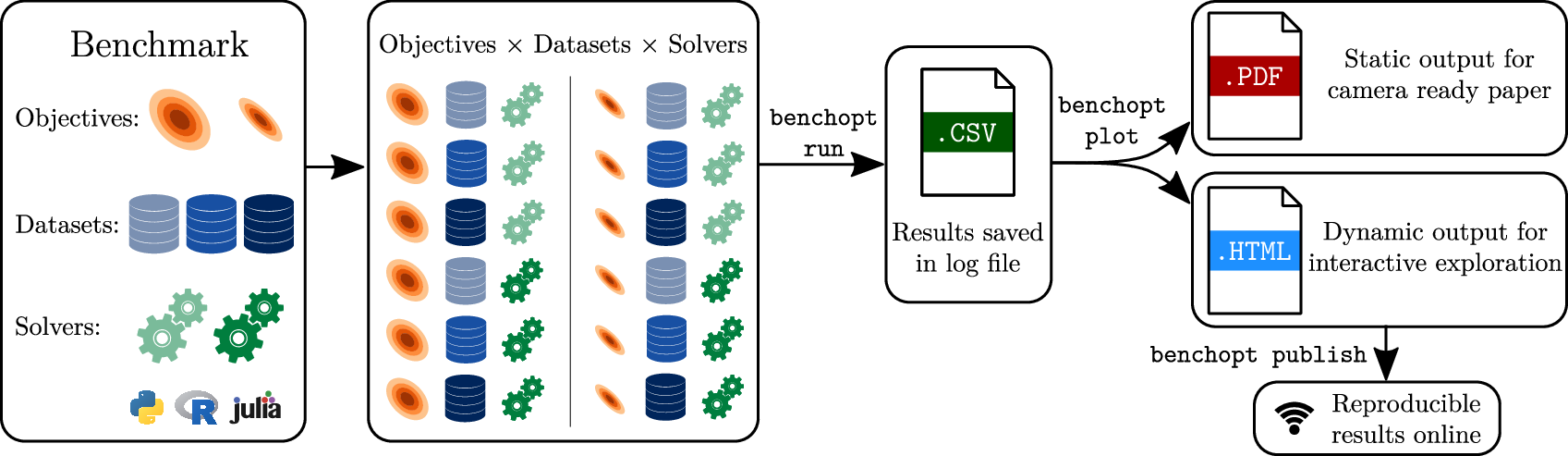
6.6 Comprehensive decoding mental processes from Web repositories of functional brain images
Participants: Bertrand Thirion, Raphael Meudec.
Main External Collaborators: Romuald Menuet [Owkin], Jérome Dockès [Univ. Mc Gill], Gael Varoquaux [Inria, Soda].
Associating brain systems with mental processes requires statistical analysis of brain activity across many cognitive processes. These analyses typically face a difficult compromise between scope—from domain-specific to system-level analysis—and accuracy. Using all the functional Magnetic Resonance Imaging (fMRI) statistical maps of the largest data repository available, we trained machine-learning models that decode the cognitive concepts probed in unseen studies. For this, we leveraged two comprehensive resources: NeuroVault — an open repository of fMRI statistical maps with unconstrained annotations — and Cognitive Atlas — an ontology of cognition. We labeled NeuroVault images with Cognitive Atlas concepts occurring in their associated metadata. We trained neural networks to predict these cognitive labels on tens of thousands of brain images. Overcoming the heterogeneity, imbalance and noise in the training data, we successfully decoded more than 50 classes of mental processes on a large test set. This success demonstrates that image-based meta-analyses can be undertaken at scale and with minimal manual data curation. It enables broad reverse inferences, that is, concluding on mental processes given the observed brain activity.
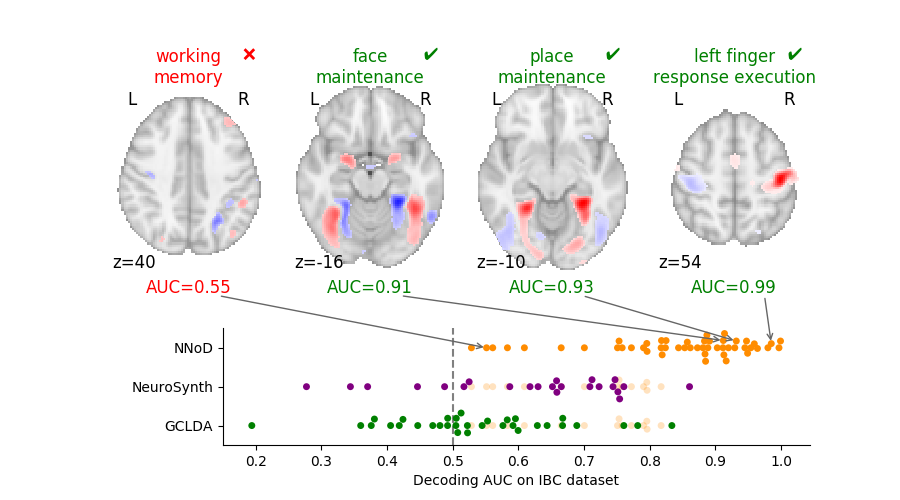
6.7 Notip: Non-parametric True Discovery Proportion control for brain imaging
Cluster-level inference procedures are widely used for brain mapping. These methods compare the size of clusters obtained by thresholding brain maps to an upper bound under the global null hypothesis, computed using Random Field Theory or permutations. However, the guarantees obtained by this type of inference-i.e. at least one voxel is truly activated in the cluster-are not informative with regards to the strength of the signal therein. There is thus a need for methods to assess the amount of signal within clusters; yet such methods have to take into account that clusters are defined based on the data, which creates circularity in the inference scheme. This has motivated the use of post hoc estimates that allow statistically valid estimation of the proportion of activated voxels in clusters. In the context of fMRI data, the All-Resolutions Inference framework introduced in 148 provides post hoc estimates of the proportion of activated voxels. However, this method relies on parametric threshold families, which results in conservative inference. In this paper, we leverage randomization methods to adapt to data characteristics and obtain tighter false discovery control. We obtain Notip: a powerful, non-parametric method that yields statistically valid estimation of the proportion of activated voxels in data-derived clusters. Numerical experiments demonstrate substantial power gains compared with state-of-the-art methods on 36 fMRI datasets. The conditions under which the proposed method brings benefits are also discussed.
Participants: Bertrand Thirion, Alexandre Blain.
Main External Collaborators: Pierre Neuvial [IMT, Univ. Toulouse].
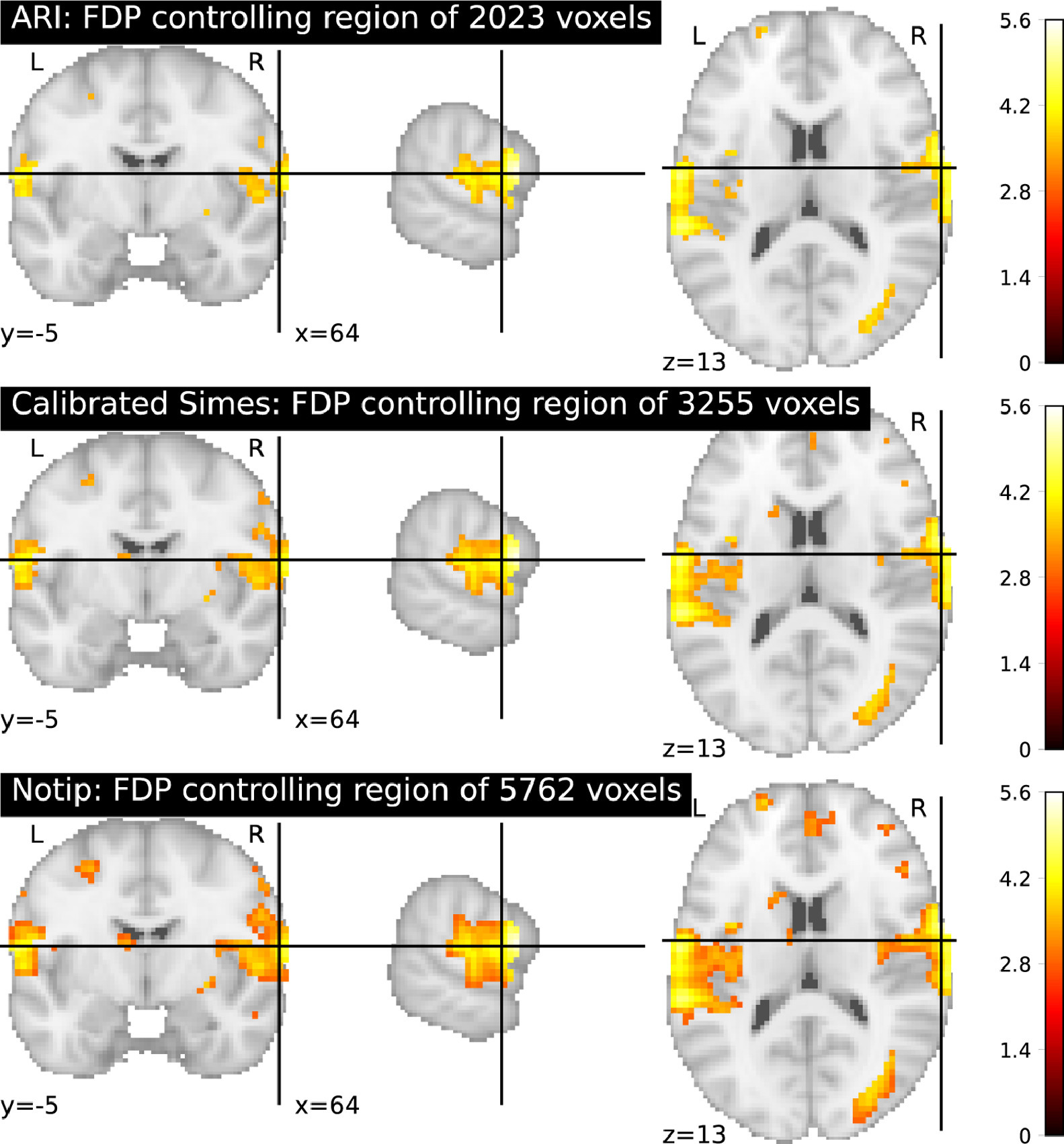
6.8 Data augmentation for machine learning on EEG
The use of deep learning for electroencephalography (EEG) classification tasks has been rapidly growing in the last years, yet its application has been limited by the relatively small size of EEG datasets. Data augmentation, which consists in artificially increasing the size of the dataset during training, can be employed to alleviate this problem. While a few augmentation transformations for EEG data have been proposed in the literature, their positive impact on performance is often evaluated on a single dataset and compared to one or two competing augmentation methods. In two works published in 2022 we have made progress towards there usage for EEG research. First in 28, we have evaluated 13 data augmentation approaches through a unified and exhaustive analysis in two applicative contexts (Sleep medicine and BCI systems). We have demonstrated that employing the adequate data augmentations can bring up to 45% accuracy improvements in low data regimes compared to the same model trained without any augmentation. Our experiments also show that there is no single best augmentation strategy, as the good augmentations differ on each task and dataset. This brings us towards our second major contribution in this topic. In 37, 45, we proposed two innovative approaches to automatically learn augmentation policies from data. The AugNet method published at NeurIPS 2022 is illustrated in 9. In this model the parameters of the augmentation policy are learnt end-to-end with a supervised task and back-propagation, and doing so reveal the invariance present in the data.
Participants: Alexandre Gramfort, Thomas Moreau, Cedric Rommel.
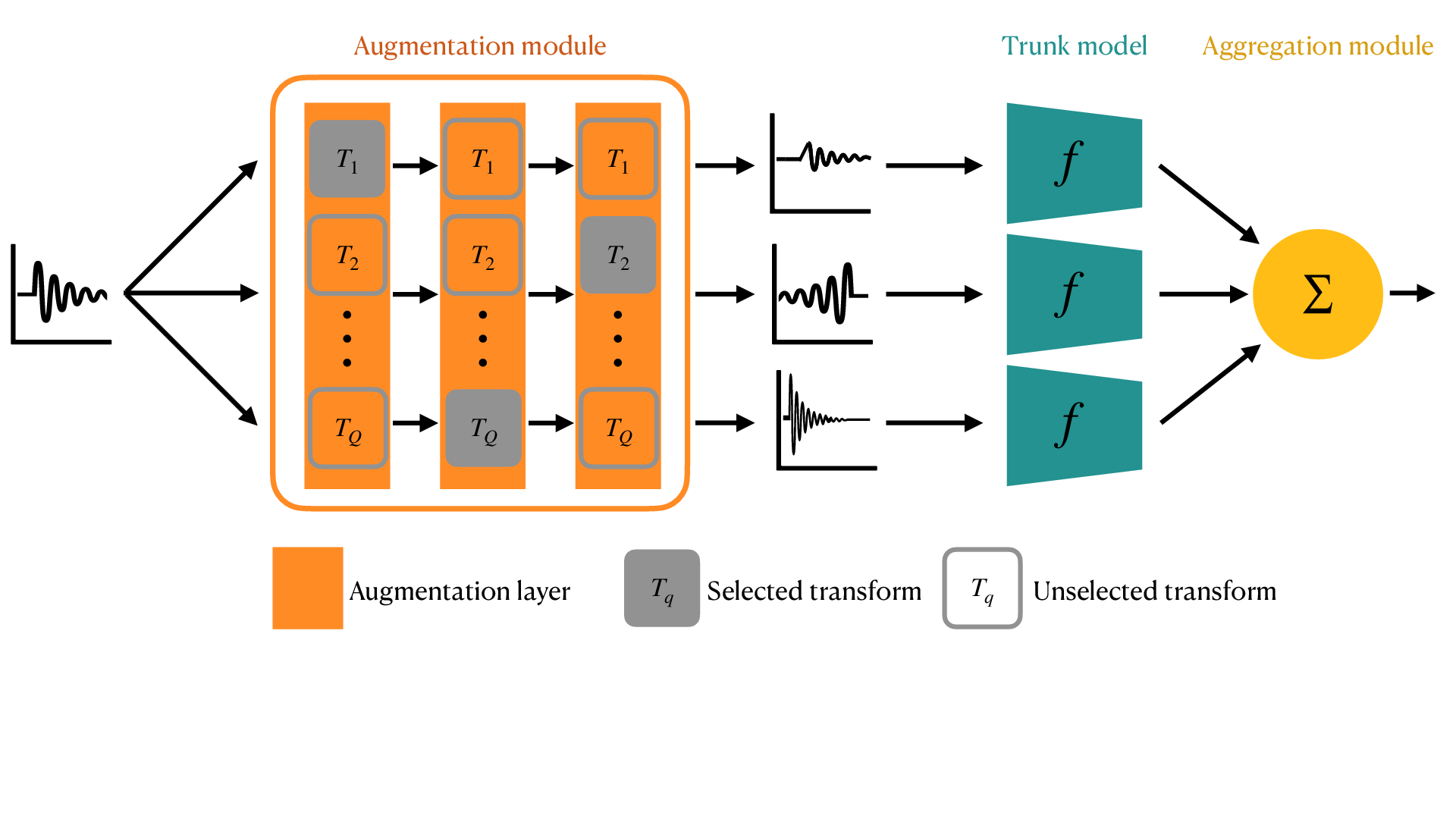
6.9 Language processing in deep neural networks and the human brain
Deep language algorithms, like GPT-2, have demonstrated remarkable abilities to process text, and now constitute the backbone of automatic translation, summarization and dialogue. However, whether and how these models operate in a way that is similar to the human brain remains controversial. In 12, we showed that the representations of GPT-2 not only map onto the brain responses to spoken stories, but they also predict the extent to which subjects understand the corresponding narratives. To this end, we analyzed 101 subjects recorded with functional Magnetic Resonance Imaging while listening to 70 min of short stories. We then fit a linear mapping model to predict brain activity from GPT-2’s activations. Doing so, we showed that this mapping reliably correlates with subjects’ comprehension scores as assessed for each story. Overall, this study illustrated in 10 shows how deep language models help clarify the brain computations underlying language comprehension.
While this latter work offers interesting insights in how the brain processes language, it does not address the question of how it learns it. Indeed, while several deep neural networks have been shown to generate activations similar to those of the brain in response to the same input, these algorithms remain largely implausible: they require (1) extraordinarily large amounts of data, (2) unobtainable supervised labels, (3) textual rather than raw sensory input, and / or (4) implausibly large memory (e.g. thousands of contextual words). Focusing on the issue of speech processing, in 32 we tested if self-supervised algorithms trained on the raw waveform constitute a promising candidate. Specifically, we compared a recent self-supervised architecture, Wav2Vec 2.0, to the brain activity of 412 English, French, and Mandarin individuals recorded with functional Magnetic Resonance Imaging (fMRI), while they listened to 1h of audio books. With this work, we showed that this algorithm learns brain-like representations with as little as 600 hours of unlabelled speech – a quantity comparable to what infants can be exposed to during language acquisition. Second, its functional hierarchy aligns with the cortical hierarchy of speech processing. Third, different training regimes reveal a functional specialization akin to the cortex: Wav2Vec 2.0 learns sound-generic, speech-specific and language-specific representations similar to those of the prefrontal and temporal cortices. These elements, resulting from the largest neuroimaging benchmark to date, show how self-supervised learning can account for a rich organization of speech processing in the brain.
Participants: Alexandre Gramfort, Charlotte Caucheteux.
Main External Collaborators: Jean-Rémi King [CNRS/Meta AI], Christope Pallier [CNRS/CEA Neurospin].
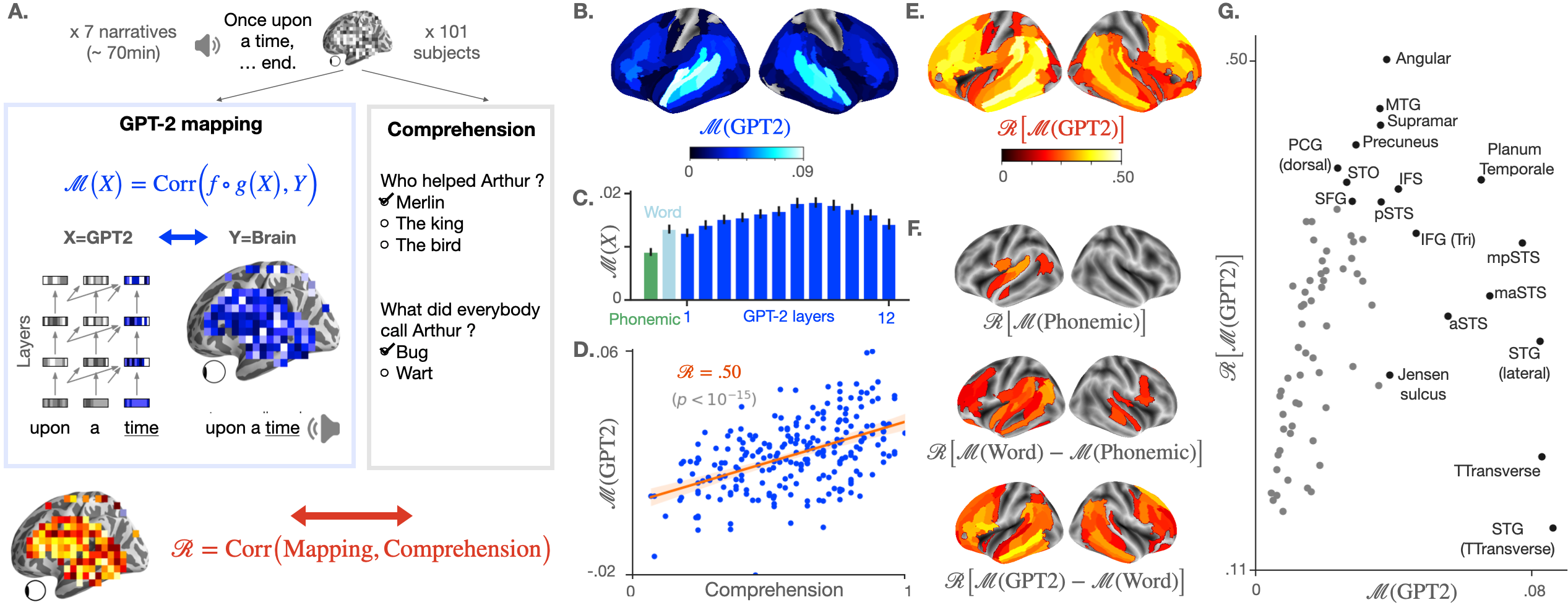
Deep language algorithms predict semantic comprehension from brain activity.A. 101 subjects listen to narratives (70 min of unique audio stimulus in total) while their brain signal is recorded using functional MRI. At the end of each story, a questionnaire is submitted to each subject to assess their understanding, and the answers are summarized into a comprehension score specific to each (narrative, subject) pair (grey box). In parallel (blue box on the left), we measure the mapping between the subject's brain activations and the activations of GPT2, a deep network trained to predict a word given its past context, both elicited by the same narrative. To this end, a linear spatio-temporal model is fitted to predict the brain activity of each voxel, given GPT2 activations as input. The degree of mapping, called "brain score" is defined for each voxel as the Pearson correlation between predicted and actual brain activity on held-out data. B. Brain scores (fMRI predictability) of the activations of the eighth layer of GPT2. Only significant regions are displayed. C. Brain scores, averaged across fMRI voxels, for different activation spaces: phonological features (word rate, phoneme rate, phonemes, tone and stress, in green), the non-contextualized word embedding of GPT2 ("Word", light blue) and the activations of the contextualized layers of GPT2 (from layer one to layer twelve, in blue). D. Comprehension and GPT2 brain scores, averaged across voxels, for each (subject, narrative) pair. In red, Pearson's correlation between the two (denoted ℛ\mathcal {R}), the corresponding regression line and the 95% confidence interval of the regression coefficient. E. Correlations (ℛ\mathcal {R}) between comprehension and brain scores over regions of interest. Only significant correlations are displayed (threshold: .05). F. Correlation scores (ℛ\mathcal {R}) between comprehension and the subjects' brain mapping with phonological features (ℳ( Phonemic \mathcal {M}(\mathrm {Phonemic}) (i), the share of the word-embedding mapping that is not accounted by phonological features ℳ( Word )-ℳ( Phonemic )\mathcal {M}(\mathrm {Word}) - \mathcal {M}(\mathrm {Phonemic}) (ii) and the share of the GPT2 eighth layer's mapping not accounted by the word-embedding ℳ( GPT 2)-ℳ( Word )\mathcal {M}(\mathrm {GPT2}) - \mathcal {M}(\mathrm {Word}) (iii). G. Relationship between the average GPT2-to-brain mapping (eighth layer) per region of interest (similar to B.), and the corresponding correlation with comprehension (ℛ\mathcal {R}, similar to D.). Only regions of the left hemisphere, significant in both B. and E. are displayed.
7 Bilateral contracts and grants with industry
Participants: Philippe Ciuciu, Guillaume Daval-Frérot, Alexandre Gramfort, Charlotte Caucheteux, Thomas Moreau.
7.1 Bilateral contracts with industry
7.1.1 Siemens Healthineers & AI lab (Princeton, USA)
Since Fall 2019, Philippe Ciuciu has actively collaborated with the Siemens-Healthineers AI lab, led by Mariappan Nadar in the context of the joint supervision of Guillaume Daval-Frérot's CIFRE PhD thesis dedicated to Deep learning for off-resonance artifact correction in MR image reconstruction in the specific application of susceptibility weighted imaging at 3 Tesla. On top of the PhD funding, this contract has generated 45k€ for Mind and was managed by CEA/NeuroSpin. G. Daval-Frérot's PhD defense was held on December, 16 2022. As this first collaboration was successful, we engaged strategic discussions with the Siemens-Healthineers headquarters (Erlangen, Germany) during Spring 2022 to pursue this partnership and eventually set up a new one in 2023 with again a CIFRE PhD thesis starting this Spring. The PhD candidate, M. Ahmed Boughdiri, has been recently selected. The focus of this PhD thesis will be self-supervised 3D MR image reconstruction still in the deep learning setting.
7.1.2 Facebook AI Research (FAIR)
There is currently a CIFRE PhD between FAIR and Mind (Alexandre Gramfort) to investigate the differences between deep learning models and the brain, especially considering NLP machine learning models. As the collaboration is led by Alexandre Gramfort in the team, it is therefore financially managed by Inria.
7.1.3 Saint Gobain Research (SGR)
There is currently a consulting contract between SGR and Mind (Thomas Moreau) to provide an expertise in machine learning to process temporal data, numerical optimization and scientific computing. The expertise is provided one half-day per month, in SGR offices, and it consists in scientific discussion sessions on the ML projects leaded by SGR data scientists.
8 Partnerships and cooperations
Participants: Demian Wassermann, Bertrand Thirion, Philippe Ciuciu, Alexandre Gramfort.
8.1 International initiatives
8.1.1 Associate Teams in the framework of an Inria International Lab or in the framework of an Inria International Program
LargeSmallBrainNets
-
Title:
Characterizing Large and Small-scale Brain Networks in Typical Populations Using Novel Computational Methods for dMRI and fMRI-based Connectivity and Microstructure
-
Duration:
2019 ->
-
Coordinator:
Vinod Menon (menon@stanford.edu)
-
Partners:
- Stanford University Stanford (États-Unis)
-
Inria contact:
Demian Wassermann
-
Summary:
In the past two decades, brain imaging of neurotypical individuals and clinical populations has primarily focused on localization of function and structures in the brain, revealing activation in specific brain regions during performance of cognitive tasks through modalities such as functional MRI. In parallel, technologies to identify white matter structures have been developed using diffusion MRI. Lately, interest has shifted towards developing a deeper understanding of the brain's macroscopic and microscopic architectures and their influence on cognitive and affective information processing. Using for this resting state fMRI and diffusion MRI to build the functional and structural networks of the human brain.
The human brain is a complex patchwork of interconnected regions, and graph-theoretical approaches have become increasingly useful for understanding how functionally connected systems engender, and constrain, cognitive functions. The functional nodes of the human brain, i.e. cortical regions, and their structural inter-connectivity, collectively the brain’s macrostructure or "connectome", are, however, poorly understood. Quantifying in vivo how these nodes’ microstructure, specifically cellular composition or cytoarchitecture, influences the cognitive tasks in which these are involved is fundamental problem in understanding the connectome. Furthermore, the coupling between within and across-subject contributions to the connectome and cognitive differences hampers the identification and understanding of the link between brain structure and function, and human cognition.
Critically, there is a dearth of computational methods for reliably identifying functional nodes of the brain, their micro and macrostructure in vivo, and separating the population and subject-specific effects. Devising and validating methods for investigating the human connectome has therefore taken added significance.
The first major goal of this project is to develop and validate appropriate sophisticated computational and mathematical tools relate the brain’s macrostructure with its function. Specifically, we will focus on being able to separate population and subject-specific contributions within these models using state-of-the-art human brain imaging techniques and open-source data from the Human Connectome Project (HCP) and the Adolescent Brain Cognitive Development study (ABCD). To this end, we will first develop and validate novel computational tools for (1) formulating and fitting large scale random effect models on graphs derived from functional and structural connectivity and (2) implement techniques enabling us to impose different regularization schemes based on sparsity and multicollinearity of the model parameters.
The second major goal of this project is characterizing the cytoarchitecture of the nodes, i.e. cortical regions, at the microscopic level and their relationship with the brain’s hemodynamical function and cognition. For this, we will (1) identify cortical areas with specific cytoarchitecture in the human cortex and use them to develop diffusion MRI-based models, (2) validate these models with numerical simulations of the dMRI signal and animal models, and (3) establish the relationship between cytoarchitecture and hemodynamical function measured from fMRI and cognition. For this we will leverage multi-shell high-angular diffusion MRI from public databases such as HCP and ABCD.
Finally, we will use to use our newly developed computational tools to characterize normal structural and functional brain networks in neurotypical adults. Due to the complementarity of the cognitive science and imaging techniques expertise the synergy between the two laboratories of this associate team will allow us to reveal in unprecedented detail the structural and functional connectivity of the human brain and its relation to cognition.
8.1.2 Inria associate team not involved in an IIL or an international program
NeuroMind
-
Title:
Precision mapping of the Brain by Neuromod & Mind
-
Duration:
2022 ->
-
Coordinator:
Pierre Bellec (pierre.bellec@criugm.qc.ca)
-
Partners:
- Université de Montréal Montréal (Canada)
-
Inria contact:
Bertrand Thirion
-
Summary:
Among the main advances of the last decade, the development of powerful AI systems for vision, language processing, as well as reinforcement learning, have led to sophisticated cognitive systems that can be compared to the human brain, and sometimes surpass human performance. Brain/AI system comparison is a great opportunity for AI and for neuroscience. One of the most urgent tasks for cognitive neuroscience is thus to put together datasets that probe the brain system and are comprehensive enough to allow a reliable comparison of brain activity to the representations generated by AI systems. To address this endeavor, Parietal and NeuroMod have launched ambitious data acquisitions initiative (individual Brain CHarting and Courtois Neuromod), that consist in collecting huge amounts of brain data in few participants. These unprecedented data collection efforts bring novel challenges for data analysis: handling TB-scale data, automation, and better integration of analysis pipeline. Software such as Nilearn and MNE increasingly face the challenge of scaling up to larger datasets. Addressing this challenge in the context of IBC and Courtois Neuromod is thus a unique opportunity.
8.2 International research visitors
8.2.1 Visits of international scientists
Other international visits to the team
Nicholas Tolley
-
Status
PhD
-
Institution of origin:
Brown University
-
Country:
USA
-
Dates:
January 2022 - July 2022
-
Context of the visit:
6 months visit
-
Mobility program/type of mobility:
Internship funded by a Chateaubriand fellowship
8.3 European initiatives
8.3.1 Horizon Europe
EBRAIN HEALTH
-
Title:
EBRAIN-HEALTH
-
Duration:
2023 -> 2026
-
Coordinator:
Petra Ritter (Charité, Berlin)
-
Partners:
- CHARITE - UNIVERSITAETSMEDIZIN BERLIN
- EBRAINS
- FORSCHUNGSZENTRUM JULICH GMBH
- STICHTING RADBOUD UNIVERSITEIT
- UNIVERSIDAD POMPEU FABRA
- OSLO UNIVERSITETSSYKEHUS HF
- TP21 GMBH
- FRAUNHOFER GESELLSCHAFT ZUR FORDERUNG DER ANGEWANDTEN FORSCHUNG EV
- INDOC RESEARCH EUROPE GGMBH
- UNIVERSITAT WIEN
- UNIVERSIDAD COMPLUTENSE DE MADRID
- EODYNE SYSTEMS SL
- ATHINA-EREVNITIKO KENTRO KAINOTOMIAS STIS TECHNOLOGIES TIS PLIROFORIAS, TON EPIKOINONION KAI TIS GNOSIS
- UNIVERSITETET I OSLO
- STICHTING VUMC
- UNIVERSITA DEGLI STUDI DI ROMA LA SAPIENZA
- ALZHEIMER EUROPE
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE
-
Inria contact:
Bertrand Thirion
-
Summary:
The project aims to develop a decentralized, data protection-compliant research platform capable of simulating some of the brain’s complex neurobiological phenomena. As part of the project, researchers will collate an array of different types of information, including data from PET and MRI scans, EEG tests, behavioral studies and lifestyle surveys, as well as clinical data from thousands of patients and healthy controls. These will be combined with biological information from knowledge databases and made available for research purposes. The resultant digital ‘brain twins’ will enable large numbers of researchers to conduct innovative research within a powerful digital infrastructure.
Thanks to its transparent analytical pipelines, the new research infrastructure will also help to promote reproducible research.
Furthermore, complex, personalized brain simulations which take into account large quantities of data may be able to provide a better understanding of the mechanisms underlying brain function and disorders. Virtual brain modeling may also improve diagnostics and disease prediction, in addition to enabling the optimization of treatment plans. The project consortium comprises 20 partners and operates in cooperation with EBRAINS AISBL, the coordinating entity of the EU-funded flagship ‘Human Brain Project’.
8.4 National initiatives
ANR DARLING
-
Title:
DARLING: Distributed adaptation and learning over graph signals
-
Duration:
2020 ->
-
Coordinator:
Cédric Richard (cedric.richard@unice.fr),Professor 3IA Senior Chair in UCA
-
Partners:
- Université Côte d'Azur Nice, France
- CNRS, École Normale Supérieure, Lyon, France
- Gipsa-lab, UMR 5216, CNRS, UGA, Grenoble, France
- CentraleSupélec, University of Paris-Saclay, Gif-sur-yvette, France
-
Inria contact:
Philippe Ciuciu
-
Summary:
The DARLING project will aim to propose new adaptive learning methods, distributed and collaborative on large dynamic graphs in order to extract structured information of the data flows generated and/or transiting at the nodes of these graphs. In order to obtain performance guarantees, these methods will be systematically accompanied by an in-depth study of random matrix theory. This powerful tool, never exploited so far in this context although perfectly suited for inference on random graphs, will thereby provide even avenues for improvement. Finally, in addition to their evaluation on public data sets, the methods will be compared with each other using two advanced imaging techniques in which two of the partners are involved: radio astronomy with the giant SKA instrument (Obs. Côte d'Azur) and MEG brain imaging (Inria MIND at NeuroSpin, CEA Saclay). Sheng Wang as a postdoc in MIND and Merlin Dumeur as a MIND PhD student in co-tutelle with Matias Palva from Aalto University, Finland are actually involved in the processing of MEG and S/EEG time series on graphs, notably to analyze scale-free (i.e. critical and bistability) phenomena across these graphs and extract potentially new biomarkers for characterizing the pathophysiology of epileptogenic zone (EZ) in drug resistant epilepsy.
ANR VLFMRI
-
Title:
VLFMRI: Very low field MRI for babies
-
Duration:
2021 ->
-
Coordinator:
Claude Fermon (CEA Saclay, DRF/IRAMIS/SPECT)
-
Partners:
- CEA/SHFJ/BIOMAPS, Orsay, France
- CEA/NeuroSpin, Gif-sur-Yvette, France
- APHP Robert Debré hospital, Paris, France
- APHP Bicêtre hospital, Kremlin-Bicêtre, France
-
Inria contact:
Philippe Ciuciu
-
Summary:
VLFMRI aims at developing a very low-field Magnetic Resonance Imaging (MRI) system as an alternative to conventional high-field MRI for continuous imaging of premature newborns to detect hemorrhages or ischemia. This system is based on a combination of a new generation of magnetic sensors based on spin electronics, optimized MR acquisition sequences (based on the SPARKLING patent, Inria-CEA MIND team at NeuroSpin) and a open and compatible system with an incubator that will allow to achieve an image resolution of 1mm on a whole baby body in a short scan time. This project is a partnership of three academic partners and two hospital departments. The different stages of the project are the finalization of the hardware development and software system, preclinical validation on small animals and clinical validation. Kumari Pooja has been hired in January 2022 as research engineer in MIND to interact with the coordinator of this ANR project, Claude Fermon and design new accelerated acquisition methods for verly low field MRI. Preliminary encouraging results allow us to retrospectively accelerate MRI acquisition by a factor of 10 without degrading image quality at 2mm isotropic resolution.
KARAIB AI CHAIR
-
Title:
KARAIB: Knowledge And RepresentAtion Integration on the Brain
-
Duration:
2020 ->
-
Coordinator:
Bertrand Thirion
-
Partners:
- INRIA MIND, Gif-sur-Yvette, France
-
Inria contact:
Bertrand Thirion
-
Summary:
Cognitive science describes mental operations, and functional brain imaging provides a unique window into the brain systems that support these operations. A growing body of neuroimaging research has provided significant insight into the relations between psychological functions and brain activity. However, the aggregation of cognitive neuroscience results to obtain a systematic mapping between structure and function faces the roadblock that cognitive concepts are ill-defined and may not map cleanly onto the computational architecture of the brain.
To tackle this challenge, we propose to leverage rapidly increasing data sources: text and brain locations described in neuroscientific publications, brain images and their annotations taken from public data repositories, and several reference datasets. Our aim here is to develop multi-modal machine learning techniques to bridge these data sources.
- Aim 1 develops representation techniques for noisy data to couple brain data with descriptions of behavior or diseases, in order to extract semantic structure.
- Aim 2 challenges these representations to provide explanations to the observed relationships, based on two frameworks: i) a statistical analysis framework; ii) integration into a domain-specific language.
- Aim 3 outputs readily-usable products for neuroimaging: atlases and ontologies and focuses on implementation, with contributions to neuroimaging web-based data sharing tools.site.
BrAIN AI CHAIR
-
Title:
BrAIN: Bridging Artificial Intelligence and Neuroscience
-
Duration:
2020 ->
-
Coordinator:
Alexandre Gramfort
-
Partners:
- INRIA MIND, Gif-sur-Yvette, France
-
Inria contact:
Alexandre Gramfort
-
Summary:
The BrAIN project investigates learning tasks from multivariate EEG and MEG time series. In clinical or cognitive neuroscience, electromagnetic signals emitted by synchronously firing neurons are collected by electroencephalography (EEG) or magnetoencephalography (MEG). Such data, typically sampled at millisecond resolution, are routinely used for clinical applications such as anesthesia monitoring, sleep medicine, epilepsy or disorders of consciousness. Low cost EEG devices are also becoming commodities with hardware startups such as DREEM in France or InteraXon in Canada that have collected hundred of thousands of neural recordings. The field of neuroscience urgently needs algorithms that can learn from such large and poorly labeled datasets. The general objectives of BrAIN is to develop ML algorithms that can learn with weak or no supervision on neural time series. It requires contributions to self-supervised learning, domain adaptation and data augmentation techniques, exploiting the known underlying physical mechanisms that govern the data generating process of neurophysiological signals.
The BrAIN project is organized around four objectives:
- Learn with no-supervision on noisy and complex multivariate signals
- Learn end-to-end predictive systems from limited data exploiting physical constraints
- Learn from data coming from many different source domains
- Develop high-quality software tools that can reach clinical research
9 Dissemination
Participants: Demian Wassermann, Bertrand Thirion, Philippe Ciuciu, Alexandre Gramfort, Thomas Moreau.
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
Member of the organizing committees
-
P. Ciuciu
June-July 2022: Co-organizer of the summer school AI4SIP (Artificial Intelligence for Signal Processing) at the Paris-Saclay University, with the support of the Institut Pascal and the DataIA institute.
-
B.Thirion
June-July 2022: Co-organizer of the summer school AI4SIP (Artificial Intelligence for Signal Processing) at the Paris-Saclay University, with the support of the Institut Pascal and the DataIA institute.
9.1.2 Scientific events: selection
-
P. Ciuciu
Member (Representative of the IEEE Signal Processing Society) of the steering committee of the IEEE International Symposium on Biomedical Imaging. I participated in selecting the bids for 2022 (Kolkata, IN) 2023 (Cartagena de Indias , CO) and 2024 (Athens, GR).
Member of the conference program committees
-
P. Ciuciu
Area chair for the BISA track in EUSIPCO 2022 as Past-vice chair of this technical committee.
-
B. Thirion
Area chair for NeurIPS 2022.
-
A. Gramfort
Area chair for ICML 2022, NeurIPS 2022, ICLR 2022.
9.1.3 Journal
Member of the editorial boards
-
P. Ciuciu
Associate Editor (AE) for IEEE Transactions on Medical Imaging (TMI), Senior Area Editor for IEEE Open Journal on Signal Processing, AE for Frontiers in Neuroscience, section Brain Imaging Methods.
-
B. Thirion
Associate Editor (AE) for Medical Image Analysis (MIA), Aperture and Transactions on Machine Learning Research.
- A. Gramfort
Reviewer - reviewing activities
-
P. Ciuciu
IEEE TMI (Bronze reviewer award in 2022), IEEE Signal Processing Magazine, Magnetic Resonance in Medicine, NeuroImage, MIA, SIAM Imaging Science
-
D. Wassermann
NeuroImage, Brain Structure and Function, Pattern Analysis and Machine Intelligence (IEEE PAMI), MIA,
-
T. Moreau
Transactions on Signal Processing, Signal Processing, ICML (outstanding reviewer, top 10%), NeurIPS.
-
B. Thirion
NeuroImage, Nature Human Behavior, MEdIA, IEEE Transactions on Medical Imaging, Brain Structure and Function, Human Brain Mapping, Nature Communications.
-
B. Thirion
NeuroImage, Journal of Neural Engineering, Data In Brief
9.1.4 Invited talks
-
P. Ciuciu
- June 2022: LIONS lab at EPFL (Lausanne, CH)
- July 2022: Plenary speaker at the 13th FORTH scientific retreat (Heraklion, GR)
-
D. Wassermann
- Johns Hopkins University, USA
- Stanford University, USA
-
T. Moreau
- March 2022: LJK seminar at UGA (Grenoble, France)
- June 2022: CSD seminar at ENS Paris (Paris, France)
- Invited talk at Curves and Surfaces (Arcachon, France)
- July 2022: invited talk for AI4SIP workshop at Institut Pascal (Orsay, France)
-
B.Thirion
- March 2022: SousSoucis Days, Institut Mathématique de Toulouse
- May 2022: HBP WP1 conference, Paris
- November 2022: ML for Life Science, Montpellier
- December 2022: plenary talk at MAIN conference, Montreal
-
A.Gramfort
- March 2022: Invited talk, UCL ML seminar, London
- June 2022: Brain and Spine Institute (ICM) symposium “Computational and mathematical approaches for neuroscience”, Paris, France
- July 2022: invited talk for AI4SIP workshop at Institut Pascal (Orsay, France)
- August 2022: Invited talk Biomag conference, Birmingham, UK
9.1.5 Scientific expertise
-
P. Ciuciu
: European expert reviewer for the European Innovation Council Accelerator actions (main track: AI and health).
-
A. Gramfort
: External reviewer for the European Research Council (ERC).
9.1.6 Research administration
-
P. Ciuciu
- Member of the Board of Directors at NeuroSpin (CEA).
- Member of the steering committee of the CEA cross-disciplinary research program on numerical simulation and AI.
-
B. Thirion
- Délégué Scientifique of Inria Saclay Center
- Member of ENS Paris-Saclay Scientific Council
- Member of Inria Commission évaluation
-
A. Gramfort
- Membre du comité des programmes de l'Institut de Henry Poincaré (IHP)
- Membre du pôle B de l'école doctorale de l'Université Paris-Saclay
- Responsable du Center for Data Science (CDS) de l'institut DataIA en charge des data challenges
- Représentant Inria au sein du comité opérationnel du cendre d'IA Hi!Paris d'IP Paris
9.2 Teaching - Supervision - Juries
-
P. Ciuciu
- Instructor at the 14th IEEE EMBS summer school on Biomedical Imaging (St Jacut de la Mer, FR) on Computational MRI.
- Instructor at the AI4SIP summer school (Orsay, FR) on Computational MRI.
- Lecturer at the M2 ATSI (CentraleSupelec, ENS Paris-Saclay): Medical imaging course
- Lecturer at the Institut d'Optique Graduate School (3rd year, Signal & Images major).
-
D. Wassermann
- Master MVA (École Polytechnique, École Normale Superiore, Centrale Supelec): Graphical Models
- Master in Biomedical Engineering (Université Paris Descartes): Quantification in NeuroImaging
-
T. Moreau
- Master Data Science (IPP): Datacamp.
-
B.Thirion
- MVA Master (École Polytechnique, École Normale Superiore, Centrale Supelec): Brain Function
- NeuroEngineering Master (UPSaclay): fMRI data analysis
- Instructor at the AI4SIP summer school (Orsay, FR)
- Instructor at MAIN 2022 conference Tutorial session
-
A.Gramfort
- Master: Optimization for Data Science, 23h, Msc 2 Data Science Master Ecole Polytechnique, France
- Master: DataCamp, 30h, Msc 2 Data Science Master Ecole Polytechnique, France
- Master: Source Imaging with EEG and MEG, 4h, Msc 2 in Biomedical Engineering at Université de Paris Cité
- Master: EEG and MEG data processing, 4h, Msc 2 in NeuroEngineering at UPSaclay, France
- Doctoral School: Machine learning for biosignals, 3h, Summer School Hi!Paris, Palaiseau, France
- Instructor at MAIN 2022 conference Tutorial session on machine learning for MEG/EEG
- Instructor at the AI4SIP summer school (Orsay, FR)
9.2.1 Supervision
-
P. Ciuciu
- Dr Z. Ramzi (with J.-L. Starch, CEA), PhD 2019-2022
- Dr G. Daval-Frérot (with A. Vignaud, CEA), PhD 2019-2022
- C. Giliyar Radhakrishna, PhD 2020-2023 (defense planned in April 2023)
- M. Dumeur (with M. Palva, Aalto Univ), PhD in cotutelle (4y), 2020-2024
- Z. Amor (with A. Vignaud, CEA) PhD 2019-2023
- A. Waguet (with T. Druet, CEA) PhD 2019-2023
- P.-A. Comby (with A. Vignaud, CEA), PhD 2021-2024
- Maja Pantic (with A. Vignaud, CEA), PhD resigned in Dec 2022 for personal reasons after obtaining an UDOPIA scholarship in June 2022.
- Serge Brosset, (with Z. Saghi, CEA) PhD 2022-2025
- W. Omezzine, M1 INSA Toulouse, (June - Sep 2022)
- Maja Pantic M2, Univ Paris-Saclay (Apr - Sep 2022)
-
D. Wassermann
- L. Rouillard, PhD 2021-2023
- M. Jallais, PhD 2019-2022
- G. Zanitti, PhD 2020-2023
- C. Fang (with J-R Li), PhD 2020-2023
- R. Meudec (with B. Thirion), PhD 2021-2023
- A. Le Bris, M2 Telecom ParisTech, 2022
-
T. Moreau
- B. Malézieux, PhD 2020-2023 (with M. Kowalski)
- C. Allain, PhD 2021-2024 (with A. Gramfort)
- M. Dagréou, PhD 2021-2024 (with S. Vaiter and P. Ablin)
- F. Michel, PhD 2022-2025 (with M. Kowalski)
- E. Lai, 3A Ecole Polytechnique, 2022 (with A. Gramfort and J.-C. Pesquet)
- M. Nargeot, L2 Université de Bordeaux, 2022
-
B. Thirion
- Alexandre Pasquiou, PhD 2020-2023 (with C.Pallier)
- Alexis Thual, PhD 2020-2023 (with S. Dehaene)
- Ahmad Chamma, PhD 2021-2023 (with D.Engemann)
- Raphael Meudec, PhD 2021-2024 (with D.Wassermann)
- Thomas Chapalain, PhD 2021-2024 (with E.Eger)
- Alexandre Balin, PhD 2021-2024 (with P.Neuvial)
-
A. Gramfort
- Charlotte Caucheteux, PhD 2020-2023 (with J.R. King)
- Omar Chehab, PhD 2020-2023 (with A. Hyvarinen)
- Cédric Allain, PhD 2021-2024 (with T.Moreau)
- Apolline Mellot, PhD 2021-2024 (with D.Engemann)
- Julia Linhart, PhD 2021-2024 (with P.Rogrigues)
- Theo Gnassounou, PhD 2022-2025 (with R.Flamary)
- Ambroise Heurtebise, PhD 2022-2025 (with P.Ablin)
9.2.2 Juries
-
P. Ciuciu
: External reviewer of the PhD thesis defended by Thomas Sanchez (EPFL, Lausanne, CH) in April 2022.
-
D. Wassermann
: Examinator for the PhD thesis defended by J. Ringard at École Polytechnique.
-
T. Moreau
: Examinator for the PhD thesis defended by L. Dragoni at Université Côte d'Azure (Nice, France) in May 2022.
-
B. Thirion
External reviewer of the PhD thesis defended by Frederico Bertoni (Sorbonne Université), in Febuary 2022
-
A. Gramfort
External reviewer of the PhD thesis defended by Martin Grignard (Université de Liège, Belgique), in September 2022
-
A. Gramfort
External reviewer of the PhD thesis defended by Jean-Yves Franceschi (Sorbonne Université), in Febuary 2022
-
A. Gramfort
External reviewer of the PhD thesis defended by Ali Hashemi (TU Berlin), in September 2022
-
A. Gramfort
External reviewer of the HdR defended by Levgen Redko (Université St Etienne), in July 2022
-
A. Gramfort
Examinator for the PhD thesis defended by Theo Desbordes (Sorbonne Université), in Dec 2022.
-
A. Gramfort
Examinator for the PhD thesis defended by Antoine Collas (Université Paris-Saclay), in Nov 2022.
9.3 Popularization
-
B.Thirion
Les Vendredi de Gif, March 2022 Où va l'intelligence artificielle ?
-
B.Thirion
L'université populaire d'Antony, November 2022, Où va l'intelligence artificielle ?
9.3.1 Internal or external Inria responsibilities
-
D. Wassermann
COERLE Scientific representative for Inria Saclay Île-de-France; Representative at the Graduate School in Computer Science of Université Paris-Saclay for Inria Saclay Île-de-France.
-
T. Moreau
President of the Inria Saclay CUMI; Representative for Inria Saclay in the commission for the development of the national computational resources.
-
A. Gramfort
Membre de la comission d'évaluation technologique (CDT) du centre de Saclay
-
A. Gramfort
Representant de l'Inria Saclay dans le comité opérationnel de Hi!Paris
10 Scientific production
10.1 Major publications
- 1 articleFunctional gradients in the human lateral prefrontal cortex revealed by a comprehensive coordinate-based meta-analysis.eLife2022
- 2 articleDeep language algorithms predict semantic comprehension from brain activity.Scientific ReportsSeptember 2022
- 3 inproceedingsA framework for bilevel optimization that enables stochastic and global variance reduction algorithms.Advances in Neural Information Processing Systems (NeurIPS)New Orleans, United StatesNovember 2022
- 4 articleOptimizing full 3D SPARKLING trajectories for high-resolution T2*-weighted Magnetic Resonance Imaging.IEEE Transactions on Medical ImagingAugust 2022
- 5 inproceedingsBenchopt: Reproducible, efficient and collaborative optimization benchmarks.NeurIPS 2022 - 36th Conference on Neural Information Processing SystemsNew Orleans, United StatesNovember 2022
- 6 articleNC-PDNet: a Density-Compensated Unrolled Network for 2D and 3D non-Cartesian MRI Reconstruction.IEEE Transactions on Medical ImagingJanuary 2022
- 7 articleData augmentation for learning predictive models on EEG: a systematic comparison.Journal of Neural EngineeringNovember 2022
10.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Reports & preprints
Other scientific publications
10.3 Cited publications
- 55 inproceedingsTensorFlow: A System for Large-Scale Machine Learning.12th USENIX Symposium on Operating Systems Design and Implementation OSDI2016, 265--283
- 56 articleFaster independent component analysis by preconditioning with Hessian approximations.IEEE Trans. Signal Process.66152018, 4040-4049
- 57 inproceedingsLearning Step Sizes for Unfolded Sparse Coding.Advances in Neural Information Processing Systems (NeurIPS)Vancouver, BC, Canada2019, 13100--13110
- 58 inproceedingsSuper-Efficiency of Automatic Differentiation for Functions Defined as a Minimum.International Conference on Machine Learning (ICML)July 2020
- 59 inproceedingsValidating Causal Inference Models via Influence Functions.Proceedings of the 36th International Conference on Machine Learning97Proceedings of Machine Learning ResearchLong Beach, California, USAPMLR09--15 Jun 2019, 191--201URL: http://proceedings.mlr.press/v97/alaa19a.html
- 60 articleExpressive Languages for Querying the Semantic Web.ACM Transactions on Database Systems433November 2018, 1--45
- 61 articleThe State of Applied Econometrics - Causality and Policy Evaluation.ArXiv e-printsJuly 2016, arXiv:1607.00699
- 62 inproceedingsFeature Grouping as a Stochastic Regularizer for High-Dimensional Structured Data.ICML2019, 385--394
- 63 articleDeclarative Probabilistic Programming with Datalog.ACM Transactions on Database Systems424October 2017, 1-35
- 64 articleMultimodal Machine Learning: A Survey and Taxonomy.IEEE Transactions on Pattern Analysis and Machine Intelligence412Feb 2019, 423-443
- 65 articleUncovering the structure of clinical EEG signals with self-supervised learning.Journal of Neural Engineering2020
- 66 articleThe Vadalog System: Datalog-Based Reasoning for Knowledge Graphs.Proceedings of the VLDB Endowment119May 2018, 975-987
- 67 articleRepresentation learning: A review and new perspectives.Pattern Analysis and Machine Intelligence352013, 1798
- 68 articleControlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing.Journal of the Royal Statistical Society Series B (Methodological)5711995, 289-300URL: http://dx.doi.org/10.2307/2346101
- 69 inproceedingsImplicit Differentiation of Lasso-Type Models for Hyperparameter Optimization.International Conference on Machine Learning (ICML)2002.08943onlineApril 2020, 3199--3210
- 70 articlePost hoc confidence bounds on false positives using reference families.Ann. Statist.48306 2020, 1281--1303URL: https://doi.org/10.1214/19-AOS1847
- 71 phdthesisMachine learning based on Hawkes processes and stochastic optimization.Université Paris Saclay (COmUE)CMAP, École Polytechnique2019
- 72 articleOn the generation of sampling schemes for magnetic resonance imaging.SIAM Journal on Imaging Sciences942016, 2039--2072
- 73 articlePanning for gold: ‘model-X’ knockoffs for high dimensional controlled variable selection.Journal of the Royal Statistical Society: Series B (Statistical Methodology)8032018, 551-577URL: https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/rssb.12265
- 74 articleSpatio-temporal wavelet regularization for parallel MRI reconstruction: application to functional MRI.Magnetic Resonance Materials in Physics, Biology and Medicine2762014, 509--529
- 75 articleGlobally optimized 3D SPARKLING trajectories for high-resolution T2*-weighted Magnetic Resonance Imaging.2020
- 76 inproceedingsA Deep Learning Architecture to Detect Events in EEG Signals During Sleep.2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP)Sept 2018, 1-6
- 77 articleA projection algorithm for gradient waveforms design in Magnetic Resonance Imaging.IEEE Transactions on Medical Imaging3592016, 2026--2039
- 78 articleThe Visual Word Form Area (VWFA) Is Part of Both Language and Attention Circuitry.Nature Communications101December 2019, 5601
- 79 inproceedingsAnalysis vs synthesis-based regularization for combined compressed sensing and parallel MRI reconstruction at 7 Tesla.2018 26th European Signal Processing Conference (EUSIPCO)IEEE2018, 36--40
- 80 articleMultivariate semi-blind deconvolution of fMRI time series.revised for publication to NeuroImageApril 2021
- 81 inproceedingsLearning to Solve TV Regularised Problems with Unrolled Algorithms.Advances in Neural Information Processing Systems (NeurIPS)online2020
- 82 inproceedingsStatistical Inference with Ensemble of Clustered Desparsified Lasso.MICCAIGrenade, Spain2018
- 83 articlePrediction of brain age suggests accelerated atrophy after traumatic brain injury.Annals of neurology7742015, 571--581
- 84 inproceedingsA unified architecture for natural language processing: Deep neural networks with multitask learning.ICML2008, 160
- 85 inproceedingsRandaugment: Practical automated data augmentation with a reduced search space.IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW)Seattle, WA, USAIEEEJune 2020, 3008--3017URL: https://ieeexplore.ieee.org/document/9150790/
- 86 unpublishedBeyond brain age: Empirically-derived proxy measures of mental health.October 2020, working paper or preprint
- 87 bookTheory of Max-Min and Its Application to Weapons Allocation Problems..OCLC: 953666019Berlin/HeidelbergSpringer Berlin Heidelberg1967
- 88 inproceedingsOff-resonance correction non-Cartesian SWI using internal field map estimation.29th Proc. of the ISMRM annual meetingvirtualMay 2021
- 89 incollectionWhat does classifying more than 10,000 image categories tell us?ECCV2010, 71
- 90 articleBERT: Pre-training of Deep Bidirectional Transformers for Language Understanding.CoRRabs/1810.048052018, URL: http://arxiv.org/abs/1810.04805
- 91 articleBrain topography beyond parcellations: local gradients of functional maps.NeuroImageJanuary 2021, 117706
- 92 articlePrediction of individual brain maturity using fMRI.Science32959972010, 1358--1361
- 93 inproceedingsMultivariate Convolutional Sparse Coding for Electromagnetic Brain Signals.Advances in Neural Information Processing Systems (NeurIPS)Montreal, Canada2018, 3296--3306
- 94 inproceedingsOnline MR image reconstruction for compressed sensing acquisition in T2* imaging.Wavelets and Sparsity XVIII11138International Society for Optics and Photonics2019, 1113819
- 95 articleCalibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization.Journal of Imaging732021, 58
- 96 inproceedingsSelf-calibrating nonlinear reconstruction algorithms for variable density sampling and parallel reception MRI.2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM)IEEE2018, 415--419
- 97 articleCombining magnetoencephalography with magnetic resonance imaging enhances learning of surrogate-biomarkers.eLife9may 2020, e54055URL: https://doi.org/10.7554/eLife.54055
- 98 articleRobust EEG-based cross-site and cross-protocol classification of states of consciousness.Brain141112018, 3179--3192
- 99 articlePySAP: Python Sparse Data Analysis Package for Multidisciplinary Image Processing.Astronomy and Computing322020, 100402
- 100 articleDeep Equilibrium Architectures for Inverse Problems in Imaging.arXiv preprint arXiv:2102.079442021
- 101 articleFunctional brain age prediction suggests accelerated aging in preclinical familial Alzheimer's disease, irrespective of fibrillar amyloid-beta pathology.bioRxiv2020
- 102 inproceedingsLearning Fast Approximations of Sparse Coding.Proceedings of the 27th International Conference on Machine Learning2010
- 103 articlePoint spectra of some mutually exciting point processes.Journal of the Royal Statistical Society: Series B (Methodological)3331971, 438--443
- 104 articleFReM -- scalable and stable decoding with fast regularized ensemble of models.NeuroImage2017, 1-16
- 105 inproceedingsComplex Coordinate-Based Meta-Analysis with Probabilistic Programming.Association for the Advancement of Artificial IntelligenceOnline, FranceFebruary 2021
- 106 inproceedingsCytoarchitecture Measurements in Brain Gray Matter using Likelihood-Free Inference.RøJune 2021
- 107 inproceedingsGroup Level MEG/EEG Source Imaging via Optimal Transport: Minimum Wasserstein Estimates.Information Processing in Medical ImagingChamSpringer International Publishing2019, 743--754
- 108 inproceedingsWasserstein regularization for sparse multi-task regression.AISTATS89Proceedings of Machine Learning ResearchPMLRApril 2019, 1407--1416URL: http://proceedings.mlr.press/v89/janati19a.html
- 109 inproceedingsLearning the Morphology of Brain Signals Using Alpha-Stable Convolutional Sparse Coding.Advances in Neural Information Processing Systems (NeurIPS)Long Beach, CA, USA2017, 1099--1108
- 110 articleConfidence Intervals and Hypothesis Testing for High-Dimensional Regression.151January 2014, 2869–2909
- 111 unpublishedOn the consistency of supervised learning with missing values.March 2019, working paper or preprint
- 112 articleWhy has it taken so long for biological psychiatry to develop clinical tests and what to do about it?Molecular Psychiatry17122012, 1174--1179
- 113 articleEncoding and Decoding Framework to Uncover the Algorithms of Cognition.The Cognitive Neurosciences VI, MIT Pressin press2020
- 114 articleData augmentation for deep-learning-based electroencephalography.Journal of Neuroscience Methods3462020, 108885URL: https://www.sciencedirect.com/science/article/pii/S0165027020303083
- 115 articleSPARKLING: variable-density k-space filling curves for accelerated T2*-weighted MRI.Magnetic Resonance in Medicine8162019, 3643--3661
- 116 article3D variable-density SPARKLING trajectories for high-resolution T2*-weighted Magnetic Resonance imaging.NMR in Biomedicine33e43492020, 1--12
- 117 inproceedingsData-driven Data Augmentation for Motor Imagery Brain-Computer Interface.2021 International Conference on Information Networking (ICOIN)ISSN: 1976-7684January 2021, 683--686
- 118 articlePredicting brain-age from multimodal imaging data captures cognitive impairment.NeuroImage1482017, 179--188
- 119 miscFast and Powerful Conditional Randomization Testing via Distillation.2020
- 120 articleSignal Processing Approaches to Minimize or Suppress Calibration Time in Oscillatory Activity-Based Brain-Computer Interfaces.Proc. of the IEEE10362015, 871-890
- 121 articleCausal Effect Inference with Deep Latent-Variable Models.arXiv e-printsMay 2017, arXiv:1705.08821
- 122 articleOnline Learning for Matrix Factorization and Sparse Coding.Journal of Machine Learning Research (JMLR)1112010, 19--60
- 123 inproceedingsCeler: a Fast Solver for the Lasso with Dual Extrapolation.Proceedings of the 35th International Conference on Machine Learning802018, 3321--3330URL: https://arxiv.org/abs/1802.07481
- 124 articleDual Extrapolation for Sparse GLMs.Journal of Machine Learning Research212342020, 1-33URL: http://jmlr.org/papers/v21/19-587.html
- 125 articleMicrostructural Organization of Human Insula Is Linked to Its Macrofunctional Circuitry and Predicts Cognitive Control.eLife9June 2020, e53470
- 126 inproceedingsLearning Neural Representations of Human Cognition across Many fMRI Studies.NIPSLong Beach, United StatesDecember 2017
- 127 articleStochastic Subsampling for Factorizing Huge Matrices.IEEE Transactions on Signal Processing661January 2018, 113--128
- 128 inproceedingsShuffle and learn: unsupervised learning using temporal order verification.ECCVSpringer2016, 527--544
- 129 articleDiCoDiLe: Distributed Convolutional Dictionary Learning.Transaction on Pattern Analysis and Machine Intelligence (TPAMI)in press2020
- 130 inproceedingsDICOD: Distributed Convolutional Sparse Coding.International Conference on Machine Learning (ICML)Stockohlm, SwedenPMLR (80)2018, 3626--3634
- 131 articleResults of the 2020 fastMRI challenge for machine learning mr image reconstruction.IEEE transactions on medical imaging4092021, 2306--2317
- 132 articleHuman Neocortical Neurosolver (HNN), a new software tool for interpreting the cellular and network origin of human MEG/EEG data.eLife9jan 2020, e51214URL: https://doi.org/10.7554/eLife.51214
- 133 inproceedingsAggregation of Multiple Knockoffs.ICML 2020 - 37th International Conference on Machine LearningProceedings of the ICML 37th International Conference on Machine Learning,119Vienne / Virtual, AustriaJuly 2020
- 134 inproceedingsECKO: Ensemble of Clustered Knockoffs for robust multivariate inference on MRI data.IPMIJune 2019
- 135 articleQuasi-Oracle Estimation of Heterogeneous Treatment Effects.ArXiv e-printsDecember 2017, arXiv:1712.04912
- 136 inproceedingsDeepDive: Web-scale Knowledge-base Construction using Statistical Learning and Inference..VLDS2012, 25
- 137 inproceedingsUnsupervised learning of visual representations by solving jigsaw puzzles.ECCVSpringer2016, 69--84
- 138 articleRepresentation learning with contrastive predictive coding.arXiv e-prints2018
- 139 miscLecture notes in Statistical analysis of neural data course: Chapter 2 -- Introduction to Point Processes.September 2019
- 140 articleData Augmentation with Manifold Exploring Geometric Transformations for Increased Performance and Robustness.arXiv e-printsJanuary 2019
- 141 inproceedingsPyTorch: An Imperative Style, High-Performance Deep Learning Library.Advances in Neural Information Processing Systems (NeurIPS)Vancouver, BC, Canada2019, 12
- 142 articleActive MR k-space Sampling with Reinforcement Learning.Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics)12262 LNCS2020, 23--33
- 143 articleSubject-specific segregation of functional territories based on deep phenotyping.Human Brain MappingDecember 2020
- 144 articleIndividual Brain Charting dataset extension, second release of high-resolution fMRI data for cognitive mapping.Scientific Data71October 2020
- 145 inproceedingsDensity Compensated Unrolled Networks for Non-Cartesian MRI Reconstruction.ISBI 2021 - International Symposium on Biomedical Imaging2021, URL: http://arxiv.org/abs/2101.01570
- 146 conferenceXPDNet for MRI Reconstruction: an application to the 2020 fastMRI challenge.ISMRM2021
- 147 inproceedingsHNPE: Leveraging Global Parameters for Neural Posterior Estimation.Advances in Neural Information Processing Systems (NeurIPS)December 2021
- 148 articleAll-Resolutions Inference for brain imaging.Neuroimage18111 2018, 786--796
- 149 articleDeep learning-based electroencephalography analysis: a systematic review.Journal of Neural Engineering165aug 2019, 051001URL: https://doi.org/10.1088/1741-2552/ab260c
- 150 articleEstimating causal effects of treatments in randomized and nonrandomized studies..Journal of educational Psychology6651974, 688
- 151 articleManifold-regression to predict from MEG/EEG brain signals without source modeling.arXiv preprint arXiv:1906.026872019
- 152 articlePredictive regression modeling with MEG/EEG: from source power to signals and cognitive states.NeuroImage2222020, 116893
- 153 articleThe Virtual Brain: a simulator of primate brain network dynamics.Frontiers in Neuroinformatics72013, 10URL: https://www.frontiersin.org/article/10.3389/fninf.2013.00010
- 154 articleEstimation of brain age delta from brain imaging.NeuroImage2019
- 155 articleHow old are you, really? Communicating chronic risk through ‘effective age’of your body and organs.BMC medical informatics and decision making1612016, 1--6
- 156 inproceedingsProbabilistic Databases for All.Proceedings of the 39th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database SystemsPortland OR USAACMJune 2020, 19--31
- 157 articleCP-Logic: A Language of Causal Probabilistic Events and Its Relation to Logic Programming.Theory and Practice of Logic Programming93May 2009, 245--308
- 158 articleThe White Matter Query Language: A Novel Approach for Describing Human White Matter Anatomy..Brain Structure and FunctionJanuary 2016
- 159 articleReducing Uncertainty in Undersampled MRI Reconstruction with Active Acquisition.February 2019, URL: http://arxiv.org/abs/1902.03051

