3.1.1 Efficient methods for testing and characterizing quantum systems

Obtaining an accurate mathematical characterization of the quantum systems that are prepared in the lab is a pressing question for quantum technologies. For this reason, there has been very important progress on such statistical questions in the last few years. This includes the answer to foundational questions such as the number of samples needed to characterize an unknown quantum state, improved methods for characterizing quantum devices, and very recently techniques that can very efficiently predict multiple relevant properties of quantum systems. We plan to contribute to these lines of work by considering several questions all going in the direction of better characterization of quantum systems.

First, we will consider basic statistical questions related to testing relevant properties of quantum states. In particular, given a description of an ideal target state $|\psi \rangle$, how to efficiently test whether the state prepared by the device complies with $|\psi \rangle$? Another question is how to test whether the state prepared by the device is entangled or not? These are fundamental questions and for some of them the best known algorithm is to learn the whole state by performing a complete quantum tomography. We believe that this is far from optimal and that a better understanding of the geometry of quantum states can be turned into a significantly more efficient testing algorithm. Techniques from high-dimensional convex geometry 32 are likely to play an important role.

Building on that, we will then develop tools to characterize the noise affecting quantum devices. As the number of parameters and samples required to characterize an arbitrary noisy process grows exponentially in the number of qubits  65, it is of paramount importance to devise protocols to find an effective ansatz for the underlying structure. The first step we will take in this direction will be to devise scalable protocols that are able to identify the correlation structure of the noise. By singling out on which parts of the device the noise acts independently and on which the noise is correlated it is possible to substantially reduce the number of parameters that are required to effectively describe it, bringing it to a tractable number. Although finding the conditional independence structure of a set of random variables to a high precision is a difficult problem even classically, we will generalize to the quantum setting efficient classical techniques that employ convex relaxations  47 to obtain good approximate solutions.

The next step will then be to devise protocols inspired from machine learning techniques that can exploit the knowledge of the underlying correlation structure to efficiently learn its parameters. This will be combined with randomized benchmarking techniques 56, 61, 57. Randomized benchmarking techniques are known to be robust and experimentally friendly, however current results either give very limited information or require stringent assumptions on the structure of the underlying noise. Thus, the goal of this part will be to overcome these two limitations, providing experimentalists with much needed tools to efficiently characterize large noisy quantum devices.

Such a line of research certainly also profits from inputs from experimentalists to test the algorithms on real quantum hardware. Thus, we plan to work with the local experimental group led by Benjamin Huard to test such methods on the devices they build. Moreover, it is invaluable to obtain input from experimentalists regarding what are the limitations and challenges they face in the lab when characterizing their devices.

An important aspect in this direction that we will consider is the design of measurements that can probe the physical property of interest without disturbing the state by much. This is the so-called quantum non-demolition measurement (QND) and is important when one has a continuous signal which one wants to measure, since one has to measure the same system repeatedly over time and, ideally, one wants the outcomes of later measurements to depend solely on the quantity one intends to measure, and not on any disturbances caused by prior measurements. QNDs have found usages in many areas, including quantum computing and, most prominently, proposals for gravitational wave detectors with improved sensitivity. We view the problem through the lens of quantum information theory, and in this way, it can be seen that the quantum system involved in the QND, is a quantum reference frame. What’s more, there is a one-to-one relation between the reference frame imperfections, and its ability to act as a system for QND measurements. In 36, 82, we gave a construction of a QND where the error is a function of energy and dimension. Going forward, our objective is to determine whether this construction is optimal, determine the optimal tradeoff between error and energy and dimension and assess the extent to which such constructions can lead to an advantage for quantum sensing.

3.1.2 Limitations on the computational power of noisy quantum devices

In order to establish a quantum advantage for noisy quantum computers, it is important to study when noisy quantum computers can be simulated classically. Intuitively, it is clear that the noise present in a quantum device imposes a limit on the circuit depth we can implement before the device loses its usefulness when compared to classical devices. In order to understand the potential of noisy quantum devices, it is crucial to develop tools to characterize when this happens given a problem and noise model. In the context of optimization, such bounds were achieved by our work 55. In short, the results of 55 show that sampling from the output of noisy quantum devices quickly becomes comparable to sampling from Gibbs states that are easy to simulate classically by giving stringent explicit bounds. This is showcased Figure 1, where we plot at which density of corrupted qubits the noisy quantum device loses advantage against classical methods.

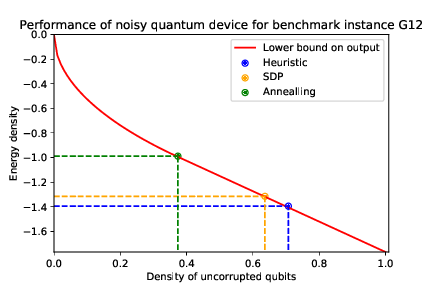
However, in their current version, our methods only allow for an analysis of the first moments. To extend the analysis and conclusions beyond optimization to other fields like quantum machine learning, it is imperative to obtain results for higher moments and concentration inequalities for the outputs of noisy quantum circuits. That is, to quantify how much noise a quantum system can tolerate before it behaves like a state that can be easily sampled from classically. To achieve this goal, we intend to resort to and further develop methods from the emerging field of quantum optimal transport  70, 48. Optimal transport techniques are by now a well-established method to show powerful concentration inequalities  75. They are known to combine well with other areas of expertise of the group, such as entropic and semigroup methods.

3.1.3 Efficient optimization using noisy quantum computers

Identifying good use cases for the noisy quantum devices expected to be available in the near future is one of the main current challenges faced by the quantum computing community. One possible candidate for such an application are quantum Gibbs state-sampling based methods. Quantum Gibbs states are at the core of powerful classical and quantum algorithms for optimization and machine learning based on mirror descent or the matrix multiplicative weight method  41, 38, 37. These iterative algorithms can be understood as a variation of simulated annealing, in which one starts with a (quantum) Gibbs state at infinite temperature and decreases the temperature to converge to the solution of an optimization problem. That is, we begin with a state that is supported everywhere on the state space and slowly zoom into regions that contain solutions to the problem of interest by tuning the Gibbs state. This intuitive picture conveys one feature of such methods: they are robust, especially at the first iterations, as we only need to ensure that we are zooming in the right direction. This robustness translates into them only requiring the preparation of states with relatively small precision to make progress.

On the other hand, this picture also showcases the issue noise imposes for such methods: after a while, the noise will make it impossible to zoom in further, imposing fundamental barriers onto how well we can characterize the region of solutions. Thus, it is expected that noisy quantum computers can offer useful advice as to which direction to go up to a level that naturally depends on the noise present in the device. Thus, we will design hybrid quantum-classical algorithms that explicitly take into account this limitation. They will only use the quantum computer to identify a region of a relatively small dimension that contains the solution.

At this stage, it is then possible to use powerful randomized linear algebra techniques to take advantage of the initial zooming in performed by the noisy quantum device. Techniques from randomized linear algebra offer significant speedups for basic operations under the promise that the involved matrices are supported on a small dimensional space  80. Thus, after doing the first iterations efficiently on the noisy quantum device and identifying a low-dimensional space that contains the solutions, a classical device takes over with this input and runs the later iterations much faster. Such a hybrid algorithm would lead to more efficient solvers for convex optimization problems. Although such problems can usually be solved in polynomial time, in practice it is still challenging to solve larger dimensional instances, impeding their more widespread use. Such a hybrid algorithm will increase the practicality of solving large-dimensional semidefinite programs, as the classical computer would only have to operate in the low-dimensional regime. It would also lead to provable speedups for quantum devices under noise, a goal that has so far remained elusive.

The main technical challenges that need to be overcome for the success of such an algorithm are threefold: first, carrying out a detailed analysis of the trade-offs as to when it becomes more efficient to transition from performing the optimization on the noisy quantum device to the classical computer. Second, the development of improved quantum Gibbs sampler for noisy devices to prepare the required states. Third, the identification of practically relevant problems that offer a good opportunity window for quantum speedups. The first and third challenges will profit from and are connected to the result of the previously discussed Goals 3.1.1 and 3.1.2. The second, the development of better quantum Gibbs samplers, as current proposals for Gibbs samplers require quantum circuits that are unlikely to be implementable in the near term, will certainly yield results that find applications in many other directions. Indeed, efficient classical Gibbs samplers are the bread the butter of most Monte Carlo techniques, and it is to be expected that quantum Gibbs samplers will find similar widespread application.

3.1.4 Certification of quantum devices

In the device-independent framework of quantum cryptography, protocols offer security by relying on minimal assumptions. Namely, they are secure even when the devices used within the protocol are completely untrusted or uncharacterized. The main idea behind many device-independent protocols, such as randomness expansion and quantum key distribution, is that there are certain correlations between multiple separate systems that ($i$) could only have been produced by entangled quantum systems and $\left(ii\right)$ are intrinsically random. The fundamental question underlying the analysis of such protocols is how to certify entanglement or randomness from the observed measurement statistics of the untrusted device?

This question of certification is recurrent when assessing the behaviour of quantum devices (and particularly of noisy ones), as highlighted by the issues that Goals 3.1.1 and 3.1.2 address. We plan to develop techniques to address the certification of quantum systems with minimal assumptions. Our objective is to first build mathematical tools in the continuity of the Entropy Accumulation Theorem 50 that allow us to make accurate statistical statements about large quantum systems. The second objective is to design computational methods 40 to certify in a quantitative way the relevant quantum properties that are consistent with the observed statistics.

For the context of device-independent cryptography, this will allow us to obtain protocols with improved noise tolerance and finite-length analysis to reach the realm of what can be done with current quantum technologies. But we believe these techniques will be applicable in the wider setting of certifying properties of quantum networks and quantum computing devices.

3.2.1 Optimal error correction tailored to noise model

Shannon's 1948 seminal theorem  72 modeled the problem of communication (or storage) over a given noisy channel and determined precisely its ultimate limit. Shannon's noisy coding theorem relates the maximum rate at which information can be transmitted reliably over a noisy channel ${𝒲}_{X\to Y}$ to a simple entropic expression $I(X:Y)$ measuring the correlations between the input and output of the channel. More precisely, it states that as $n\to \infty$, the maximum number of bits that can be sent using $n$ independent copies of ${𝒲}_{X\to Y}$ is asymptotically given by

where the right hand side is a maximization over distributions $P_X$ over the input of the channel and $I(X:Y)$ is a correlation measure, the exact definition of which we will omit in this document. Setting the fundamental limits for reliable communication, Shannon's theorem was instrumental in the discovery of good error correcting codes which are used in virtually every device or communication link today. One of the goals of the field of information theory is to characterize the optimal communication rates in the form (1) for various information processing tasks.

Devices that make use of the laws of quantum theory are also affected by noise, in fact even more so. Determining the optimal method in order to communicate (or store information) reliably over a noisy quantum channel is thus of fundamental importance in order to exploit the full potential of a quantum computer, or more generally a quantum device. However, despite the problem's importance and more than 40 years of efforts in quantum information theory  63, 79, it is fair to say that we do not have a quantum analogue of Shannon's theorem Eq. (1). Indeed, a formula analogous to Eq. (1) for quantum channels is known only in very special cases. As an illustration, even for the simplest possible quantum channel, called the qubit depolarizing channel, the asymptotic maximum rate of quantum communication is still unknown  49. The qubit depolarizing channel can be thought of as the quantum analogue of the channel that flips the input bit with some probability $f$.

The main difficulty in understanding the ability of a quantum channel in transmitting information is the non-additivity of the quantum entropic quantities having the form of the right hand side of Eq. (1)  49, 64, 62, 73. This challenge is due in many cases to the quantum property of entanglement and we believe that a new approach is needed to overcome this difficulty.

Faced with these difficulties, we propose a new framework for studying communication over noisy channels. Instead of trying to determine the optimal rate of communication asymptotically as the number of channel uses $n\to \infty$ (as in the left hand side of Eq. (1)), we assume we have a description of a finite channel ${\overline{𝒲}}_{\overline{X}\to \overline{Y}}$ (a particular case of which is ${\overline{𝒲}}_{\overline{X}\to \overline{Y}}={𝒲}_{X\to Y}^{\otimes n}$ for some finite $n$, but it could be much more general). Our objective is then to design an efficient algorithm that determines the maximum number of bits or qubits that can be sent reliably using ${\overline{𝒲}}_{\overline{X}\to \overline{Y}}$.

For the problem of classical communication over a classical channel, we have characterized this computational complexity precisely in our previous work 35 and this led to interesting connections between information theory and combinatorial optimization. The main objective here is to extend this approach to quantum channels, thereby designing algorithms that can find the best error correction schemes for a given noise model. These algorithms can naturally then be used on the noise models that are estimated using the methods developed in Axis 3.1.1. In particular, we will focus on relevant noise models that appear in current devices. For this we plan to collaborate with Benjamin Huard in the physics lab of ENS Lyon, and the presence of Cyril Élouard in the team significantly helps in this regard. To start in this direction, Cyril has given talks within the group to explain the mathematics of superconducting qubits and we are at the moment discussing specific dissipative models that can be reasonably implemented in hardware and for such different models compare their ability to store quantum information reliably.

3.2.2 Error correction and fault-tolerance with LDPC codes

Having a coding strategy for a given noise model with good performance is not enough: for a strategy to be applicable, it is important to be able to implement the error correction operations efficiently. An efficient decoding algorithm is not only important to establish fast and reliable communication networks but it is also crucial for fault-tolerant computing. In fact, the basic idea of fault-tolerant computing schemes is to perform computations on data encoded in an error correcting code. To prevent the errors that occurred during the computation from spreading, a decoding operation has to be regularly applied to correct these errors. For this reason, it is crucial for the decoding operation to be very fast to prevent the accumulation of errors. We focus here on an important class of quantum error correcting codes called Low-Density Parity-Check (LDPC) codes  42, 74 defined by two sparse binary parity-check matrices $H_X$ and $H_Z$ satisfying $H_X{H}_Z^T=0$. Our first objective is to design efficient decoding algorithms for quantum LDPC codes.

Quantum LDPC codes are particularly well suited to achieve fault-tolerant quantum computation. This is because the sparsity of the parity check matrices allows us to bound the error rate of the syndrome measurements. In fact, currently the leading candidate error correcting code to be used in future quantum computers is the surface code, a special kind of LDPC code. Even though the surface code can be embedded on a surface with only nearest neighbour interactions, it suffers from a very poor encoding rate, and thus using it for fault-tolerant constructions incurs a very large memory overhead. Our previous work 54 shows that in principle the memory overhead can be significantly reduced by using constant-rate LDPC codes based on expander graphs. The general idea of using constant-rate codes is illustrated in Figure 2. Our objective is to make fault-tolerant constructions with LDPC codes practical by finding fault-tolerant gadgets for such codes and using decoding algorithms with better performance.

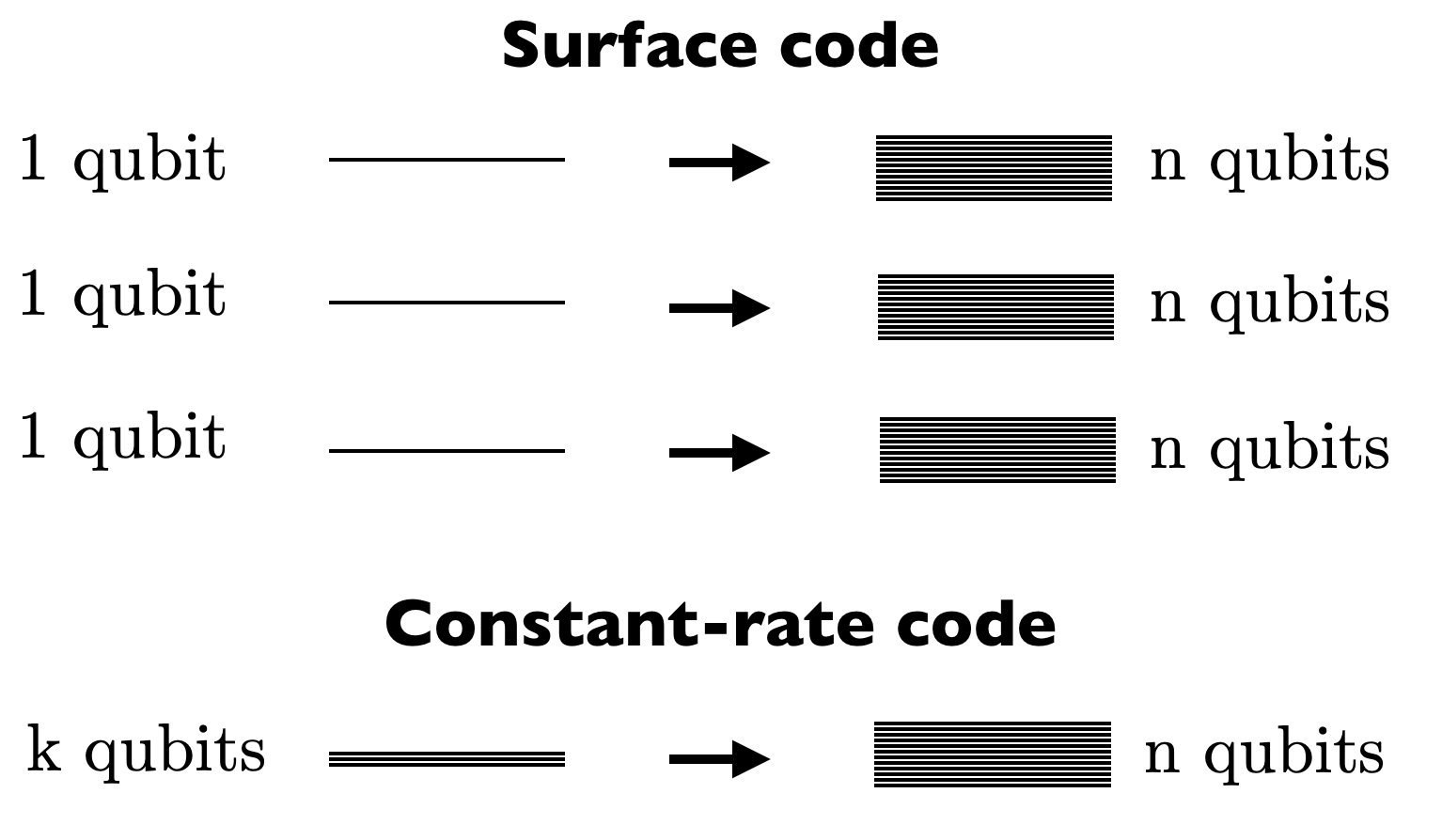
3.2.3 New approaches for fault-tolerance

As mentioned before, the currently leading approach for fault-tolerance is using surface codes. In contrast to the previous goal 3.2.2, our objective here is to explore radically different approaches to fault-tolerance that could provide new avenues towards achieving fault-tolerance. In particular, we will look at one based on quantum polar codes and the other one based on quantum reference frames.

The class of quantum polar codes that has recently been proposed in 51 can be promising candidates for fault-tolerant quantum computing. The construction relies on a channel combining and splitting procedure, where a two-qubit gate randomly chosen from the Clifford group is used to combine two single-qubit channels. Applied recursively, this procedure allows synthesizing a set of so-called virtual channels from several instances of the quantum channel. When the code length goes to infinity, the virtual channels polarize, in the sense that they tend to become either noiseless or completely noisy. Interestingly, polar codes feature several extremely desirable properties: they protect a high number of logical qubits, and they have efficient decoding algorithms. In addition, logical Clifford operations can be easily performed by using code deformation like techniques. However, there are a number of challenging issues to be addressed in the fault-tolerant computing context. First, quantum channel polarization needs to be investigated by taking into account the fact that Clifford gates used for channel-combining are faulty. Second, we need to construct a universal set of fault-tolerant gates, which can be tackled by using magic state distillation. For this approach, we plan to collaborate closely with Mehdi Mhalla (CNRS, LIG).

The second approach we consider here is based one a way of circumventing the famous Eastin-Knill theorem. In the early days of quantum computing, one of the key ideas for building a quantum computer whose errors can be corrected, was the notion of transversal logic gates. The idea was to devise a scheme in which all the gates needed for universal quantum computation could be applied on non-overlapping subspaces in such a way that all the locally occurring errors were correctable. More specifically, the objective is to find an encoding $ℰ$ mapping the logical space to the physical space such that for any unitary $𝒱$ acting on the logical space, there exist unitaries ${𝒱}_1,\cdots ,{𝒱}_n$ acting on the physical space such that

This scheme would allow for errors in the implementation of the gates to be corrected before they have propagated through the computation and rendered its results useless. Unfortunately, transversality of all the gates needed for universal computation and local correctability within the blocks cannot both be simultaneously satisfied for finite dimensional codes. This was proven by Eastin and Knill in a landmark paper in 2009  52. Subsequently, workarounds have been found. For example, one of the current frontrunner approaches is to apply all but one of the gates needed for universal computation transversally, while the remaining gate is applied in a non-transversal way using other costly techniques.

We have developed in a series of two papers 81, 83, a new method for quantum error correction which is not based on this approach. In this technique, all of the gates in the set needed for universal computation are treated on an equal footing. More precisely, rather than circumventing the Eastin-Knill theorem by having one non-transversal gate, all gates from the universal set can be applied transversally, and local errors corrected, but at the price of an error in the decoding. As long as the error in the decoding is kept small, it will not disrupt the computation and is thus not significant from a practical point of view. To do so, it uses quantum reference frames and randomness to encode the information about which gate was applied during the computation. As the quality of the reference frame increases, the error in the decoding approaches zero. The concept of a quantum reference frame was introduced in the field of quantum foundations in the context of sharing so-called “unspeakable information”, such as the relative orientation of two distant observes. While it has been used over the years in various problems in quantum information theory, its use in quantum error correction has yet to be fully explored.

While this work on the circumvention of the Eastin-Knill theorem has attracted a lot of attention and follow up work by other research groups (see e.g. Refs.  67, 84, 76 and 66), it is not yet ready for primetime. The reason for this, it that while the encoded states are readily fault tolerant (due to the transversality of its gates), the current protocol for applying the encoding and decoding channels are not fault tolerant. This is down to the method in which the quantum reference frames are constructed. However, we believe that finding protocols for implementing the encoder and decoder in a fault tolerant way is a surmountable challenge. We plan to use a recent construction of unitary $t$-designs that use a constant number of non-Clifford gates. Implementing the Clifford gates in the circuit can be done in a transversal way and for the non-Clifford gates, a constant number of magic states can be used. This is analogous in some ways to the entanglement needed to perform magic state distillation 39, which is the building block of one of the leading proposals for fault tolerant quantum computation. However, there are many potential benefits to the proposed use of the initial entanglement resource over that of the magic state distillation approach — it is these benefits, which are the key to why this approach could become the chosen method to implement error correction. This includes the fact that the amount of entanglement needed is independent of the computation as well as the high adaptability of this method.

3.3.1 Quantum control in quantum information processing

One of the intrinsic limitations of the standard quantum circuit model is that the structure of the circuit, and hence of the flow of information, is fixed prior to computation; quantum circuits do not allow for the possibility of a “quantum if-statement”. In this research goal we study new models to quantum computation that, in contrast, have explicit quantum control structures. These models, in particular, have the potential to provide new approaches to mitigate noise can lead to stronger quantum advantages in certain applications.

To study quantum control structures we work within the framework of higher-order quantum operations  43, 69, which formalise the types of ways quantum circuits or channels can themselves be transformed within quantum theory. This approach has developed rapidly in recent years 77 since it was first used to show that one can indeed formulate quantum computations in which the order of two quantum gates is superposed with the help of a quantum control system, a gadget known as the quantum switch  44 (see Fig. 3).

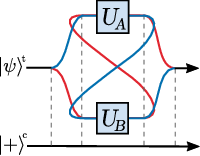
The quantum switch and related computations have since been shown to provide new types of quantum advantages in several information-theoretical tasks  46, 31, 60, where they outperform even “standard” quantum circuits. Moreover, its relevance for improving noise tolerance has recently come to light in a number of works showing how quantum control can be used to improve communication over noisy quantum channels 53, 45,30.

This progress emphasises the potential benefits in studying such models of quantum information processing, and motivates a more systematic study of quantum control models in this context. In a first step in this direction we recently formalised a computational model strictly generalising quantum circuits, called quantum circuits with quantum control of causal order (QC-QC) that incorporate – and generalise – quantum control structures 78. This model will serve as the base for a systematic study of the computational power of quantum computations exploiting quantum control, allowing us to understand the types of advantages this new resource of quantum control can provide.

With a better understanding of quantum computations with quantumly controlled operations, we will aim to develop algorithms for several problems where quantum control appears to be a promising problem. Of particular interest, we will look to use it to provide new algorithms for quantum metrology and parameter estimation – both key problems that are seen as near-to-mid-term applications for quantum information – that are more efficient than existing approaches and, in particular, are more robust in the noisy versions of these problems. An important first step we are undertaking in this direction is to generalise existing advantages obtainable with quantum circuits with quantum control of causal order from problems in a noiseless regime – where the controlled operations are unitary – to a noisy regime, where the controlled operations are noisy quantum channels.

In order to obtain such results, the mathematical tools being studied and developed in the other research axes of the proposed team, most notably convex optimisation, will be of utmost importance (e.g., Goals 3.1.3, 3.1.4 and 3.2.1). These research goals also build on existing collaborations on quantum control of causal order with physicists at the Institut Néel in Grenoble (including on the development of QC-QCs 78), in order to transfer physical insight on quantum control towards new application for information processing. We likewise plan to collaborate with the CAPP team at LIG to study diagrammatic calculi to understand how these new types of computations can be composed and compiled, building on existing collaborations with Mehdi Mhalla on quantum control 30.

The quantum control of quantum operations has potential as a resource throughout quantum information processing: not just for quantum computation but, e.g., also for quantum communication  60. As an example, it can be used to send messages through a quantum network in a superposition of different paths, amounting to a novel extension of quantum Shannon theory  45. By doing so, it has recently been shown in a simple, proof-of-principle setting, that one can notably reduce the effect of noise on the message as it traverses a network5330 and the effect experimentally verified 71. We will study this possibility further, looking at how it can be extended to practical network topologies and aim to show how it can be exploited to improve quantum communication protocols and lead to novel approaches for quantum cryptography.

One can also generalize the model of computation one step further. In causally indefinite models of computations such as QC-QCs the relative order between gates is rendered indefinite through the use of quantum control systems. Nonetheless, the computation itself still proceeds in the presence of a fixed, causal clock or external control. We will seek to go one step further in the quantum-classical divide and allow for this external control to also be quantum and autonomous. This would require the addition of another quantum system implementing the quantum gates themselves. In the case of a fixed causal order, this autonomous device needs its own internal notion of time, hence it should also be an accurate quantum clock 82. Since it is quantum, this clock which controls the interactions can be prepared in a superposition of different time states, leading to new types of non-casually implemented gates and potentially novel applications.

3.3.2 Multipartite entanglement and its applications

Multipartite entanglement plays an important role in quantum protocols and in quantum games, and is likewise a key resource for measurement-based quantum computing. Nonetheless, our understanding of multipartite entanglement as a resource is much less developed than for the simpler, but important, case of bipartite entanglement. The objective of this task is develop our understanding of multipartite entanglement, how it can contribute to reducing the effect of noise in communication, computation and more generally how it can improve coordination in multipartite scenarios.

In particular, we plan consider communication problems over noisy classical networks and quantify the extent to which multipartite nonlocality can improve the transmission rates  68. Focussing on relevant classical network communication scenarios, we will ask whether entanglement between some of the involved parties significantly improve the rates.

In a related direction, we plan to study game-theoretic settings with players with divergent interests and the advantage that can be achieved by using multipartite entangled states and, in particular, quantum graph states  59. In collaboration with Mehdi Mhalla, we will aim to use such advantages to provide new approaches to certify multipartite entangled states, and in particular to self-test quantum graph states – important resources in certain quantum computational models – by certifying them solely from the correlations they produce  34, 33. We plan to use progress towards Goal 3.1.4 to provide a finer analysis of the problem.

Techniques for learning the parameters of the evolution of a quantum system

We developed in 27 new protocols to learn the dynamics governing a quantum system. Our protocols are the first ones to be able to characterize both dissipative and Hamiltonian dynamics efficiently under minimal assumptions. More precisely, our protocols do not require evolutions by short-times and a number of measurements that scales logarithmic in the number of qubits. Furthermore, it only requires a very mild locality from the interactions: it can even characterize interactions that are algebraically decaying in the distance between qubits. Such techniques are essential to characterize quantum devices.

New bounds on the performance of noisy quantum devices:

We developed novel results that allow to understand the promise that noisy quantum devices hold before the advent of fault-tolerant quantum devices. In the absence of error correction, these devices can only reliably implement very shallow circuits or comparatively deeper circuits at the expense of a nontrivial density of errors. In 25 we developped concentration inequalities that bound the performance of noisy quantum devices. In the noisy regime with local depolarizing noise $p$, we prove that depth $p^{-1}$ it is exponentially unlikely that the outcome of a noisy quantum circuit outperforms efficient classical algorithms for combinatorial optimization problems. Similarly, we show that for certain instances constant depth quantum circuits cannot outperform efficient classical algorithms. Our results are based on newly developed quantum entropic and concentration inequalities, which constitute a homogeneous toolkit of theoretical methods from the quantum theory of optimal mass transport whose potential usefulness goes beyond the study of variational quantum algorithms. These results put into question if solving combinatorial optimization problems is a good application for noisy quantum devices.

Furthermore, in 26 we show that accurately estimating the expectation value of an observable of the output of a noiseless circuit given access to copies of a noisy circuit is a fundamentally inefficient task. More precisely, we show that if we go slightly beyond constant depth circuits, namely at depths polylogarithmic in the number of qubits, the number of copies required for this task scales superpolynomially in the worst case. These results rely on constructing quantum circuits that are maximally sensitive to noise. Furthermore, they put into question whether current error mitigation techniques for the use of noisy quantum devices, are a viable path for quantum advantage.

Techniques for certifying security in quantum cryptography

  We developped in 11 a new tool, called generalised entropy accumulation, for computing lower bounds on the min-entropy produced by a sequential process. Concretely, we consider a sequential process in which each step outputs a system $A_i$ and updates a side information register $E$. We prove that if this process satisfies a natural “non-signalling” condition between past outputs and future side information, the min-entropy of the outputs $A_1,\cdots ,A_n$ conditioned on the side information $E$ at the end of the process can be bounded from below by a sum of von Neumann entropies associated with the individual steps. This tool generalises our original version introduced in 2016. Due to its more general model of side-information, our generalised entropy accumulation theory can be applied more easily and to a broader range of cryptographic protocols. In particular, it is the first general tool that is applicable to mistrustful device-independent cryptography. To demonstrate this, we give the first security proof for blind randomness expansion against general adversaries. Furthermore, our generalised EAT can be used to give improved security proofs for quantum key distribution.

In addition, in 15, we introduced a numerical method to compute lower bounds on the rates device-independent (DI) quantum protocols. We derive a sequence of optimization problems that converge to the conditional von Neumann entropy. Applying our method to compute the rates of DI randomness expansion and DI quantum key distribution protocols, we find substantial improvements over all previous numerical techniques, demonstrating significantly higher rates.

In a similar direction, we derived in 20 a new hierarchy of semidefinite programs that can certify a lower bounds on the squashed entanglement.

Quantum cryptography protocols with weakened assumptions

We developed a new protocol for quantum key distribution (QKD) that strikes to seek a balance between standard QKD protocols, in which one assumes full knowledge of how one's devices function, and device-independent QKD, the gold standard in which no assumptions are made, but which is extremely challenging to implement. Our protocol 5, which we call receiver-device-independent QKD, assumes only that the sender's device is partially characterised in that the states generated have a bounded overlap (distinguishability), while no assumptions at all are made about the receiver's device. The protocol is secure against standard attacks such as blinding attacks, and can achieve positive key rates in the presence of much more noise (and thus over longer distances) than device-independent QKD. In collaboration with experimentalists at the University of Geneva, a proof-of-principle demonstration was performed and analysed 4, demonstrating positive key rate over $4.8$km.

Semi-device-independent certification of causal indefiniteness

To certify quantum devices or resources one must make use over other devices, e.g. to prepare probe states or perform measurements. In many scenarios, it is desirable to certify resources while making use of devices that are noisy, uncharacterised or untrusted. One approach is to use device-independent (DI) methods based on Bell inequality violation, but this is demanding and unable to certify many resources, while semi-DI approaches strive for a middle ground. In the context of causal indefiniteness – a new quantum resource we have been studying – we introduce a new semi-DI approach and show that this can be used to certify all bipartite causally nonseparable resources 3. Our approach only assumes the ability to prepare certain quantum states accurately, without assuming any characterised measurements or transformations. We make use of a novel assumption on the bipartite nature of these states. This new assumption has potential as a useful semi-DI method in other domains and applications of quantum information.

Quantum correlations to improve communication over networks

In 9, we addressed the problem of coding for classical multiple-access channels (MACs) with the assistance of non-signaling correlations between parties. It is well-known that non-signaling assistance does not change the capacity of classical point-to-point channels. However, it was recently observed that one can construct MACs from two-player non-local games while relating the winning probability of the game to the capacity of the MAC. By considering games for which entanglement (a special kind of non-signaling correlation) increases the winning probability (e.g., the Magic Square game), this shows that for some specific kinds of channels, entanglement between the senders can increase the capacity. Here, we show that the increase in capacity from non-signaling assistance goes beyond such special channels and applies even to a simple deterministic MAC: the binary adder channel. In particular, using non-signaling assistance, the sum-rate $\frac{{log}_2\left(72\right)}{4}\simeq 1.5425$ can be reached even with zero error, which beats the maximum sum-rate capacity of $1.5$ in the unassisted case.

A lower bound on the space overhead of fault-tolerant quantum computation

The threshold theorem is a fundamental result in the theory of fault-tolerant quantum computation stating that arbitrarily long quantum computations can be performed with a polylogarithmic overhead provided the noise level is below a constant level. It was recently shown that the space overhead can be asymptotically reduced to a constant independent of the circuit provided we only consider circuits with a length bounded by a polynomial in the width. In 10, using a minimal model for quantum fault tolerance, we establish a general lower bound on the space overhead required to achieve fault tolerance.

More specifically, for any non-unitary qubit channel $𝒩$ and any quantum fault tolerance schemes against $\mathrm{i}.\mathrm{i}.\mathrm{d}.$ noise modeled by $𝒩$, we prove a lower bound of $max\{\mathrm{Q}{\left(𝒩\right)}^{-1}n,{\alpha }_{𝒩}logT\}$ on the number of physical qubits, for circuits of length $T$ and width $n$. Here, $\mathrm{Q}\left(𝒩\right)$ denotes the quantum capacity of $𝒩$ and ${\alpha }_{𝒩}>0$ is a constant only depending on the channel $𝒩$. In our model, we allow for qubits to be replaced by fresh ones during the execution of the circuit and we allow classical computation to be free and perfect. This improves upon results that assumed classical computations to be also affected by noise, and that sometimes did not allow for fresh qubits to be added. Along the way, we prove an exponential upper bound on the maximal length of fault-tolerant quantum computation with amplitude damping noise resolving a conjecture by Ben-Or, Gottesman and Hassidim (2013).

A new type of Knill-Laflamme-like error-correction conditions for protection of temporal information

In 18, we introduce and study a fundamental trade-off which relates the amount by which noise reduces the accuracy of a quantum clock to the amount of information about the energy of the clock that leaks to the environment. Specifically, we consider an idealized scenario in which a party Alice prepares an initial pure state of the clock, allows the clock to evolve for a time that is not precisely known, and then transmits the clock through a noisy channel to a party Bob. Meanwhile, the environment (Eve) receives any information about the clock that is lost during transmission. We prove that Bob’s loss of quantum Fisher information about the elapsed time is equal to Eve’s gain of quantum Fisher information about a complementary energy parameter. We also prove a similar, but more general, trade-off that applies when Bob and Eve wish to estimate the values of parameters associated with two non-commuting observables. We derive the necessary and sufficient conditions for the accuracy of the clock to be unaffected by the noise, which form a subset of the Knill-Laflamme error-correction conditions. A state and its local time evolution direction, if they satisfy these conditions, are said to form a metrological code. We provide a scheme to construct metrological codes in the stabilizer formalism. We show that there are metrological codes that cannot be written as a quantum error-correcting code with similar distance in which the Hamiltonian acts as a logical operator, potentially offering new schemes for constructing states that do not lose any sensitivity upon application of a noisy channel. We discuss applications of the trade-off relation to sensing using a quantum many-body probe subject to erasure or amplitude-damping noise.

Computational advantages from quantum control of causal order

One of the primary directions we are exploring in this axis is the use of quantum system to control the order in which operations are applied in a computation or a process, creating a form of "causal indefiniteness" between operations. The potential advantages of this use of quantum control are not yet well understood, and we have been exploring several possible applications.

In 22 we analyse the canonical such resource, the so-called quantum switch, from an energetic perspective. We show that a certain task – discriminating between different properties of noisy quantum operations – can be performed more efficiently (in terms of energetic requirements) than using a standard fixed-order protocol. We use this energetic approach to shed light on a recent debate about the status of proof-of-principle implementations of the quantum switch and simulations thereof. Our approach shows that (in the specific physical setting we consider) faithful implementations can be distinguished from naive "four-box" simulations, and perform better (for a fixed energy budget) than these simulations. This work opens a new path to explore the energetic advantages of causally indefinite protocols.

We have also been exploring other advantages of quantum control of causal order. In a paper in preparation, we show study its use in protocols for quantum metrology. Several recent works have claimed that the quantum switch can provide advantages in the metrological problem of estimating a parameter characterising a noisy quantum channel. However, we show that these works fail to properly compare their results against all possible standard metrological protocols, and that these advantages do not hold up to scrutiny. By developing convex optimisation techniques to compute the relevant metrological quantity, the "quantum Fisher information", we are able to optimise the performance of protocols using quantum control of causal order, and compare it to all protocols that have a fixed causal order. We find that, for certain classes of noisy channels, this resource can provide metrological advantages, but that it is necessary to consider protocols other than the quantum switch for this. A key ingredient for these advantages appears to be so-called dynamical quantum control.

Finally, in a further paper in preparation we study the computational advantages of causal indefiniteness in query complexity problems. Using semi-definite programming approaches, we are able to calculate the exact query complexity of different types of computations for small input sizes (4-bit Boolean functions with 2 queries to the oracle): standard quantum circuits, circuits with quantum control of causal order, and more general causally indefinite supermaps. We find that, for certain functions, causally indefinite supermaps can provide an advantage in query complexity, uncovering a new computational advantage of causal indefiniteness that, in contrast to previously known advantages, is formulated in a more standard complexity-theoretic setting. However, we prove that the class of quantum circuits with quantum control of causal order is unable to improve upon standard quantum circuits in this query complexity setting.

Multipartite entanglement and different forms of quantum resource

Entanglement is one of the primary quantum resources behind many quantum advantages, but many applications focus on bipartite entanglement shared between only two parties, in part due to the simplicity of this setting. In 12 we studied multipartite entanglement in the context of non-collaborative game theory, to understand how it can be used as a resource in tasks where there are conflicts of interest. We showed how quantum entanglement can lead to higher "social welfare" – a measure of the quality of a Nash equilibrium – than could be obtained with classical resources. Moreover, this setting allowed us to uncover surprising and nuanced differences between having direct access to quantum resources, and indirect access via some idealised black boxes.

Multi-party computation within a Wigner's friend scenarios

It is natural to expect a complete physical theory to have the ability to consistently model agents as physical systems of the theory. In 58, Frauchiger and Renner (FR) claim to show that when agents in quantum theory reason about each other's knowledge in a certain Wigner's friend scenario, they arrive at a logical contradiction. It was suggested that, among other things, that this posed a problem for computation as different agents would conclude different outcomes of a computation. In light of this, Renner often poses the challenge: provide a set of reasoning rules that can be used to program quantum computers that may act as agents, which are (a) logically consistent (b) generalise to arbitrary Wigner's friend scenarios (c) efficiently programmable and (d) consistent with the temporal order of the protocol. In 29 we develop a general framework where we show that every logical Wigner's friend scenario (LWFS) can be mapped to a single temporally ordered quantum circuit, which allows agents in any LWFS to reason in a way that meets all four criteria of the challenge. Importantly, our framework achieves this general resolution without modifying classical logic or unitary quantum evolution or the Born rule, while allowing agents' perspectives to be fundamentally subjective. We analyse the FR protocol in detail, showing how the apparent paradox is resolved there. We show that apparent logical contradictions in any LWFS only arise when ignoring the choice of Heisenberg cut in scenarios where this choice does matter, and taking this dependence into account will always resolve the apparent paradox. Our results establish that universal applicability of quantum theory does not pose any threat to multi-agent logical reasoning and we discuss the implications of these results for FR's claimed no-go theorem.

Thermodynamic constraints on arbitrary quantum systems

  We developed in  17 (accepted in Physical Review X Quantum) a new framework which expresses constraints on the energy transfers between two or more arbitrary quantum systems. The constraints take the same form as the laws of thermodynamics, but are extended to any quantum system (whatever their size or initial state). On one hand, our framework identifies an effective temperature associated with the von Neumann entropy of a quantum state, and deduces from it the energy flows that are uncontrolled (i.e the heat). On the other hand, we identified the general type of resources in the quantum states that must be consumed to control energy flows (e.g. to reverse the direction of a heat flow as in a refrigerator, or to power an engine). The versatility of our framework allows us to explore limitations on the performances of quantum devices based on the systems used to implement them, as well as new directions to store and recover useful energy at the nanoscale.

In  17 we investigated direct proof-of-principle applications of the formalism to the smallest possible quantum machines based on two interacting qubits. A collaboration with the group of Benjamin Huard (ENS Lyon), an experimentalis specialized in superconducting circuits setups, is ongoing so as to test these results experimentally. In a collaboration with the group of Karyn le Hur (Ecole Polytechnique) 14, we have investigated another manifestation of our findings, which is the ability of the environment of a quantum system to store work rather than heat, providing new potential mechanism for efficient energy transfers.

6.1.1 Horizon Europe

6.1.2 H2020 projects

PEPR DIQKD

• Title:
  Device-independent quantum key distribution
• Program:
  PEPR on Quantum Technologies
• Contact Inria:
  O. Fawzi
• Partners:
  CEA (coordinator), CNRS, Université Côte D’Azur, Sorbonne Université
• Duration:
  July 1, 2022 - June 30 2026

PEPR NISQ2LSQ

Participants: Omar Fawzi, Mischa Woods.

• Title:
  From NISQ to LSQ: Bosonic and LDPC codes
• Program:
  PEPR on Quantum Technologies
• Contact Inria:
  A. Leverrier (team COSMIQ)
• Contact QInfo:
  O. Fawzi
• Partners:
  Inria (coordinator), CNRS, CEA
• Duration:
  January 1, 2022 - December 2026

PEPR EPIQ

Participants: Alastair Abbott, Guillaume Aubrun, Omar Fawzi, Daniel Stilck Franca.

• Title:
  Study of the quantum stack: Algorithm, models, and simulation for quantum computing
• Program:
  PEPR on Quantum Technologies
• Contact Inria:
  S. Perdrix (team MOCQUA)
• Contact QInfo:
  O. Fawzi
• Partners:
  Inria (coordinator), CNRS, CEA
• Duration:
  January 1, 2022 - December 2026

PEPR HQI

• Title:
  Hybrid HPC Quantum Initiative
• Program:
  PEPR on Quantum Technologies
• Contact QInfo:
  D. Stilck Franca
• Partners:
  Inria, CPU, GENCI, CNRS, CEA (coordinator)
• Duration:
  April 1, 2023 - March 2028

ANR TaQC

• Title:
  Taming Quantum Causality
• Program:
  AAP Générique 2022
• Contact QInfo:
  A. Abbott
• Partners:
  CNRS (Institut Néel; coordinator), Inria QINFO, Inria QUACS, CEA (IRFU/LARSIM)
• Duration:
  January 1, 2023 - December 2026

ANR QSTEAM

• Title:
  Quantum Stochastic Thermodynamics of Entanglement and Measurement
• Program:
  T-ERC2020
• PI:
  C. Elouard
• Duration:
  March 1, 2021 - February 2023

IDEX UGA CIQup

• Title:
  Causally Indefinite Quantum Protocols: From Complexity to Applications
• Program:
  IRGA Projet Nouvel Arrivant 2021
• PI:
  A. Abbott
• Partners:
  Inria QINFO, LIG (CNRS), Institut Néel (CNRS)
• Duration:
  July 1, 2021 - December 2022

7.1.1 Scientific events: organisation

7.1.2 Scientific events: selection

7.1.3 Journal

7.1.4 Invited talks

• A. Abbott, Causal indefiniteness from quantum control of processes, "Ateliers du LKB" seminar series, Paris, France, October 13, 2022
• M. Woods, Quantum clocks: from mathematical formulation to quantum advantage, Workshop Quantum Information and the Frontiers of Quantum Theory, Lyon, France, June 27 to 30, 2022
• D. Stilck Franca Concentration properties of shallow quantum circuits and applications to variational quantum algorithms, Journées Informatique Quantique 2022, Paris, France, Novemember 14, 2022
• D. Stilck Franca Mixing properties of tensor network states, AGATES kickoff workshop at Banach Center, Warsaw, Poland, September 19, 2022
• D. Stilck Franca, Limitations of noisy quantum annealers, Adiabatic Quantum Computing Conference 2022, Trieste, Italy, June 20, 2022
• D. Stilck Franca, Tomography of many-body quantum states from a few copies through optimal transport, Quantum Information Theory and Mathematical Physics 2022, Budapest University of Technology and Economics, Budapest, Hungary, June 14, 2022.
• D. Stilck Franca, Limitations of variational quantum algorithms: a quantum optimal transport approach, Workshop Quantum Information and the Frontiers of Quantum Theory, Lyon, France, June 27 to 30, 2022
• O. Fawzi, Variational expressions for quantum divergences and applications, Quantum Information Theory and Mathematical Physics 2022, Budapest University of Technology and Economics, Budapest, Hungary, June 14, 2022
• O. Fawzi, A chain rule for quantum conditional Rényi entropy, Mathematics of Quantum Information and Many-Body systems, Cambridge, UK, October 21, 2022

7.1.5 Leadership within the scientific community

• A. Abbott is a member of the governing board of the QuantAlps research federation and, in 2022, was in the steering committee of QuantAlps
• O. Fawzi is a member of the steering committee of the annual conference Quantum Information Processing (QIP)

7.1.6 Scientific expertise

• 2022 Jury d'admissibilité Inria de Paris CRCN/ISFP (O. Fawzi)
• A. Abbott was a member of the jury for the Quantum Hackathon by QuantX, October 1 to 2, 2022

7.2.1 Teaching

• Master: A. Abbott, Fundamental Computer Science. M1 MOSIG/M1 INFO UGA, 24 hours.
• Master: M. Woods, Quantum Sensing and Metrology Theory. ETH Zurich, 30 hours lectures + tutorials (worth 6 ECTS credits).
• Master: O. Fawzi, Quantum Information Theory. Master ICFP, 10 hours.
• Master: D. Stilck Franca, Quantum Computer Science. Master CS ENS Lyon, 40 hours lectures (worth 6 ECTS credits).

7.2.2 Supervision

• PhD: Hoang Ta, Asymptotic properties of hypergraphs and channels, July 11, 2022 (O. Fawzi)
• PhD: Lucien Grouès, Decoding of quantum LDPC codes, July 11, 2022 (O. Fawzi, with A. Leverrier)
• PhD in progress: Pierre Pocreau, Implications of causal indefiniteness for quantum communication, since October 2022 (A. Abbott, with M. Mhalla)
• PhD in progress: Raphaël Mothe, Causal superpositions in quantum information and thermodynamics, since October 2021 (A. Abbott, with C. Brianciard)
• PhD in progress: Aadil Oufkir, Testing properties of quantum states and channels (O. Fawzi, with A. Garivier)
• PhD in progress: Paul Fermé, Algorithmic aspects of optimal channel coding (O. Fawzi)
• PhD in progress: Emily Beatty, Applications of quantum optimal transport to quantum information theory (G. Aubrun and D. Stilck Franca)
• Master (M2): Pierre Pocreau, Query complexity for higher order quantum computation (A. Abbott, with M. Mhalla)
• Master (M1): Elliot Renel, Computational advantages with causally indefinite quantum circuits (A. Abbott)
• Master: Arman Pour Tak Dost, Ultra regular spontaneous emission (M. Woods)
• Master: Tristan Malleville, On the weak simulation of Matrix Product States (D. Stilck Franca with C. Rouze and I. Bardet)

7.2.3 Juries

• HDR: Nicolas Sangouard, Bell test: a compelling certification tool for quantum communication technologies, Université Paris-Saclay, September 28, 2022 (O. Fawzi reviewer)
• PhD: Daniel Szilagyi, Toward efficient algorithms for optimization and sampling, Université Paris-Cité, 20 October 2022 (O. Fawzi examiner)
• PhD: Adien Suau, Implémentation, analyse et améliorations bas-niveau d’algorithmes quantiques pour le calcul scientifique, Université de Montpellier, 27 October, 2022 (O. Fawzi reviewer)
• PhD: Harshit Verma, Quantum control in probing relativistic effects and thermodynamics, University of Queensland, Australia (M. Woods on examination board)
• PhD: Jeongrak Son, catalysis in thermodynamic resource theories, Nanyang Technological University, Singapore (M. Woods on thesis advisory committee)

7.3.1 Articles and contents

• O. Fawzi, La mécanique quantique, clé de la sécurité des échanges, POUR LA SCIENCE N° 543
• D. Stilck Franca, Conquering the challenge of quantum optimization, Physics World February 2022
• A. Abbott, Interview for the podcast series Decode quantum, animated by O. Ezratty and F. Bouton, October 27, 2022

International journals

• 1 articleG.Guillaume Aubrun and A.Alexander Müller-Hermes. Annihilating Entanglement Between Cones.Communications in Mathematical PhysicsDecember 2022
  HALDOI
• 2 articleG.Giulio Chiribella, K. R.Kenneth R. Davidson, V. I.Vern I. Paulsen and M.Mizanur Rahaman. Counterexamples to the extendibility of positive unital norm-one maps.Linear Algebra Appl.2023
  HAL
• 3 articleH.Hippolyte Dourdent, A. A.Alastair A. Abbott, N.Nicolas Brunner, I.Ivan Šupić and C.Cyril Branciard. Semi-device-independent Certification of Causal Nonseparability with Trusted Quantum Inputs.Physical Review Letters1299August 2022, 090402
  HALDOIback to text
• 4 articleM.Marie Ioannou, M. A.Maria Ana Pereira, D.Davide Rusca, F.Fadri Grünenfelder, A.Alberto Boaron, M.Matthieu Perrenoud, A. A.Alastair A. Abbott, P.Pavel Sekatski, J.-D.Jean-Daniel Bancal, N.Nicolas Maring, H.Hugo Zbinden and N.Nicolas Brunner. Receiver-Device-Independent Quantum Key Distribution.Quantum6May 2022, 718
  HALDOIback to text
• 5 articleM.Marie Ioannou, P.Pavel Sekatski, A. A.Alastair A. Abbott, D.Denis Rosset, J.-D.Jean-Daniel Bancal and N.Nicolas Brunner. Receiver-device-independent quantum key distribution protocols.New Journal of Physics2462022, 063006
  HALDOIback to text
• 6 article M. P.Mischa P. Woods and M.Michał Horodecki. Autonomous quantum devices: When are they realizable without additional thermodynamic costs? Physical Review X 2023
  HAL

International peer-reviewed conferences

• 7 inproceedingsM.Matthias Christandl, O.Omar Fawzi, H.Hoang Ta and J.Jeroen Zuiddam. Larger Corner-Free Sets from Combinatorial Degenerations.13th Innovations in Theoretical Computer Science Conference (ITCS 2022)Berkeley, United StatesJanuary 2022
  HALDOI
• 8 inproceedingsJ.Julien Devevey, O.Omar Fawzi, A.Alain Passelègue and D.Damien Stehlé. On Rejection Sampling in Lyubashevsky's Signature Scheme.ASIACRYPT 2022 - 28th Annual International Conference on the Theory and Application of Cryptology and Information SecurityTaipei, TaiwanDecember 2022
  HAL
• 9 inproceedingsO.Omar Fawzi and P.Paul Fermé. Beating the Sum-Rate Capacity of the Binary Adder Channel with Non-Signaling Correlations.ISIT 2022 - IEEE International Symposium on Information TheoryEspoo, FinlandJune 2022
  HALback to text
• 10 inproceedingsO.Omar Fawzi, A.Alexander Müller-Hermes and A.Ala Shayeghi. A lower bound on the space overhead of fault-tolerant quantum computation.13th Innovations in Theoretical Computer Science Conference (ITCS 2022)Berkeley, United StatesJanuary 2022
  HALDOIback to text
• 11 inproceedingsT.Tony Metger, O.Omar Fawzi, D.David Sutter and R.Renato Renner. Generalised entropy accumulation.2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS)Denver, United StatesOctober 2022
  HALDOIback to text

Reports & preprints

• 12 miscA. A.Alastair A. Abbott, M.Mehdi Mhalla and P.Pierre Pocreau. Improving social welfare in non-cooperative games with different types of quantum resources.November 2022
  HALback to text
• 13 miscG.Guillaume Aubrun, A.Alexander Müller-Hermes and M.Martin Plávala. Monogamy of entanglement between cones.July 2022
  HAL
• 14 miscE.Ephraim Bernhardt, C.Cyril Elouard and K. L.Karyn Le Hur. A topologically protected quantum dynamo effect in a driven spin-boson model.August 2022
  HALback to text
• 15 miscP.Peter Brown, H.Hamza Fawzi and O.Omar Fawzi. Device-independent lower bounds on the conditional von Neumann entropy.February 2022
  HALback to text
• 16 miscG.Giulio Chiribella, K. R.Kenneth R. Davidson, V. I.Vern I. Paulsen and M.Mizanur Rahaman. Positive maps and entanglement in real Hilbert spaces.August 2022
  HAL
• 17 miscC.Cyril Elouard and C. L.Camille Lombard Latune. Extending the laws of thermodynamics for autonomous, arbitrary quantum systems.January 2023
  HALback to textback to text
• 18 miscP.Philippe Faist, M. P.Mischa P. Woods, V. V.Victor V. Albert, J. M.Joseph M. Renes, J.Jens Eisert and J.John Preskill. Time-energy uncertainty relation for noisy quantum metrology.2022
  HALback to text
• 19 miscH.Hamza Fawzi, O.Omar Fawzi and S. O.Samuel O. Scalet. A subpolynomial-time algorithm for the free energy of one-dimensional quantum systems in the thermodynamic limit.November 2022
  HAL
• 20 miscH.Hamza Fawzi and O.Omar Fawzi. Semidefinite programming lower bounds on the squashed entanglement.August 2022
  HALback to text
• 21 miscO.Omar Fawzi, L.Li Gao and M.Mizanur Rahaman. Asymptotic Equipartition Theorems in von Neumann algebras.January 2023
  HAL
• 22 miscM.Marco Fellous-Asiani, R.Raphaël Mothe, L.Léa Bresque, H.Hippolyte Dourdent, P. A.Patrice A. Camati, A. A.Alastair A. Abbott, A.Alexia Auffèves and C.Cyril Branciard. Comparing the quantum switch and its simulations with energetically-constrained operations.August 2022
  HALback to text
• 23 miscV.Victor Gitton and M. P.Mischa P. Woods. On the system loophole of generalized noncontextuality.September 2022
  HAL
• 24 miscM.Maria Maffei, C.Cyril Elouard, B. O.Bruno O. Goes, B.Benjamin Huard, A. N.Andrew N. Jordan and A.Alexia Auffèves. Anomalous energy exchanges and Wigner function negativities in a single qubit gate.October 2022
  HAL
• 25 miscG.Giacomo de Palma, M.Milad Marvian, C.Cambyse Rouzé and D.Daniel Stilck Franca. Limitations of variational quantum algorithms: a quantum optimal transport approach.January 2023
  HALback to text
• 26 miscY.Yihui Quek, D. S.Daniel Stilck França, S.Sumeet Khatri, J. J.Johannes Jakob Meyer and J.Jens Eisert. Exponentially tighter bounds on limitations of quantum error mitigation.December 2022
  HALback to text
• 27 miscD.Daniel Stilck Franca, L. A.Liubov A. Markovich, V. V.V. V. Dobrovitski, A. H.Albert H. Werner and J.Johannes Borregaard. Efficient and robust estimation of many-qubit Hamiltonians.January 2023
  HALback to text
• 28 miscM.Masaaki Tokieda, C.Cyril Elouard, A.Alain Sarlette and P.Pierre Rouchon. Complete Positivity Violation in Higher-order Quantum Adiabatic Elimination.November 2022
  HAL
• 29 miscV.V. Vilasini and M. P.Mischa P. Woods. A general framework for consistent logical reasoning in Wigner's friend scenarios: subjective perspectives of agents within a single quantum circuit.September 2022
  HALback to text