Keywords
Computer Science and Digital Science
- A1.1.11. Quantum architectures
- A4.2. Correcting codes
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.3. Discrete Modeling (multi-agent, people centered)
- A6.1.4. Multiscale modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.3. Probabilistic methods
- A6.2.6. Optimization
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
- A6.3.3. Data processing
- A6.3.4. Model reduction
- A6.4. Automatic control
- A6.4.1. Deterministic control
- A6.4.2. Stochastic control
- A6.4.3. Observability and Controlability
- A6.4.4. Stability and Stabilization
Other Research Topics and Application Domains
- B5.3. Nanotechnology
- B5.4. Microelectronics
- B6.5. Information systems
- B9.10. Privacy
1 Team members, visitors, external collaborators
Research Scientists
- Mazyar Mirrahimi [Team leader, INRIA, Senior Researcher, HDR]
- Philippe Campagne Ibarcq [INRIA, Researcher]
- Alain Sarlette [INRIA, Researcher, HDR]
Faculty Members
- Zaki Leghtas [Mines Paris, Professor, HDR]
- Tudor-Alexandru Petrescu [Mines Paris]
- Pierre Rouchon [Mines Paris, Professor, HDR]
- Antoine Tilloy [Mines Paris]
Post-Doctoral Fellows
- Yousra Bouasria [Inria, from Apr 2022]
- Vincent Lienhard [ENS PARIS]
- Mathys Rennela [Inria, until Aug 2022]
- Remi Robin [ARMINES, from Oct 2022]
- Masaaki Tokieda [INRIA]
PhD Students
- Thiziri Aissaoui [ALICE ET BOB]
- Camille Berdou [ARMINES]
- Adrien Bocquet [ALICE ET BOB, from Sep 2022]
- Alvise Borgognoni [ENS Paris]
- Michiel Burgelman [INRIA, until May 2022]
- Leon Carde [ALICE ET BOB, from Sep 2022]
- Ronan Gautier [INRIA]
- Linda Greggio [INRIA, from Oct 2022]
- Pierre Guilmin [ALICE ET BOB, from Feb 2022]
- François-Marie Le Regent [ALICE ET BOB]
- Matthieu Praquin [ENS PARIS]
- Angela Riva [INRIA, from Oct 2022]
- Erwan Roverc'h [ENS Paris]
- Diego Ruiz [ALICE ET BOB, from Sep 2022]
- Ulysse Réglade [Alice&Bob]
- Lev-Arcady Sellem [ARMINES]
- Christian Siegele [INRIA]
- Karanbir Tiwana [ARMINES, from Nov 2022]
- Aron Vanselow [INRIA]
- Marius Villiers [ENS Paris]
Interns and Apprentices
- Jason Akoun [Inria, from Apr 2022 until Jul 2022]
- Louis Paletta [INRIA, until Jul 2022]
Administrative Assistant
- Derya Gok [INRIA]
External Collaborator
- Jeremie Guillaud [ALICE ET BOB]
2 Overall objectives
2.1 Overall objectives
The research activities of QUANTIC team lie at the border between theoretical and experimental efforts in the emerging field of quantum systems engineering. Our research topics are in direct continuation of a historic research theme of INRIA, classical automatic control, while opening completely new perspectives toward quantum control: by developing a new mathematical system theory for quantum circuits, we will realize the components of a future quantum information processing unit.
One of the unique features of our team concerns the large spectrum of our subjects going from the mathematical analysis of the physical systems (development of systematic mathematical methods for control and estimation of quantum systems), and the numerical analysis of the proposed solutions, to the experimental implementation of the quantum circuits based on these solutions. This is made possible by the constant and profound interaction between the applied mathematicians and the physicists in the group. Indeed, this close collaboration has already brought a significant acceleration in our research efforts. In a long run, this synergy should lead to a deeper understanding of the physical phenomena behind these emerging technologies and the development of new research directions within the field of quantum information processing.
Towards this ultimate task of practical quantum digital systems, the approach of the QUANTIC team is complementary to the one taken by teams with expertise in quantum algorithms. Indeed, we start from the specific controls that can be realistically applied on physical systems, to propose designs which combine them into hardware shortcuts implementing robust behaviors useful for quantum information processing. Whenever a significant new element of quantum engineering architecture is developed, the initial motivation is to prove an enabling technology with major impact for the groups working one abstraction layer higher: on quantum algorithms but also on e.g. secure communication and metrology applications.
3 Research program
3.1 Hardware-efficient quantum information processing
In this scientific program, we will explore various theoretical and experimental issues concerning protection and manipulation of quantum information. Indeed, the next, critical stage in the development of Quantum Information Processing (QIP) is most certainly the active quantum error correction (QEC). Through this stage one designs, possibly using many physical qubits, an encoded logical qubit which is protected against major decoherence channels and hence admits a significantly longer effective coherence time than a physical qubit. Reliable (fault-tolerant) computation with protected logical qubits usually comes at the expense of a significant overhead in the hardware (up to thousands of physical qubits per logical qubit). Each of the involved physical qubits still needs to satisfy the best achievable properties (coherence times, coupling strengths and tunability). More remarkably, one needs to avoid undesired interactions between various subsystems. This is going to be a major difficulty for qubits on a single chip.
The usual approach for the realization of QEC is to use many qubits to obtain a larger Hilbert space of the qubit register 99, 103. By redundantly encoding quantum information in this Hilbert space of larger dimension one make the QEC tractable: different error channels lead to distinguishable error syndromes. There are two major drawbacks in using multi-qubit registers. The first, fundamental, drawback is that with each added physical qubit, several new decoherence channels are added. Because of the exponential increase of the Hilbert's space dimension versus the linear increase in the number of decay channels, using enough qubits, one is able to eventually protect quantum information against decoherence. However, multiplying the number of possible errors, this requires measuring more error syndromes. Note furthermore that, in general, some of these new decoherence channels can lead to correlated action on many qubits and this needs to be taken into account with extra care: in particular, such kind of non-local error channels are problematic for surface codes. The second, more practical, drawback is that it is still extremely challenging to build a register of more than on the order of 10 qubits where each of the qubits is required to satisfy near the best achieved properties: these properties include the coherence time, the coupling strengths and the tunability. Indeed, building such a register is not merely only a fabrication task but rather, one requirers to look for architectures such that, each individual qubit can be addressed and controlled independently from the others. One is also required to make sure that all the noise channels are well-controlled and uncorrelated for the QEC to be effective.
We have recently introduced a new paradigm for encoding and protecting quantum information in a quantum harmonic oscillator (e.g. a high-Q mode of a 3D superconducting cavity) instead of a multi-qubit register 71. The infinite dimensional Hilbert space of such a system can be used to redundantly encode quantum information. The power of this idea lies in the fact that the dominant decoherence channel in a cavity is photon damping, and no more decay channels are added if we increase the number of photons we insert in the cavity. Hence, only a single error syndrome needs to be measured to identify if an error has occurred or not. Indeed, we are convinced that most early proposals on continuous variable QIP 68, 61 could be revisited taking into account the design flexibilities of Quantum Superconducting Circuits (QSC) and the new coupling regimes that are provided by these systems. In particular, we have illustrated that coupling a qubit to the cavity mode in the strong dispersive regime provides an important controllability over the Hilbert space of the cavity mode 70. Through a recent experimental work 110, we benefit from this controllability to prepare superpositions of quasi-orthogonal coherent states, also known as Schrödinger cat states.
In this Scheme, the logical qubit is encoded in a four-component Schrödinger cat state. Continuous quantum non-demolition (QND) monitoring of a single physical observable, consisting of photon number parity, enables then the tractability of single photon jumps. We obtain therefore a first-order quantum error correcting code using only a single high-Q cavity mode (for the storage of quantum information), a single qubit (providing the non-linearity needed for controllability) and a single low-Q cavity mode (for reading out the error syndrome). An earlier experiment on such QND photon-number parity measurements 104 has recently led to a first experimental realization of a full quantum error correcting code improving the coherence time of quantum information 7. As shown in Figure 1, this leads to a significant hardware economy for realization of a protected logical qubit. Our goal here is to push these ideas towards a reliable and hardware-efficient paradigm for universal quantum computation.
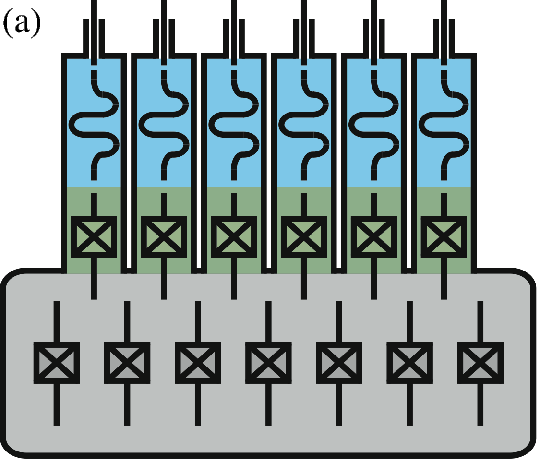
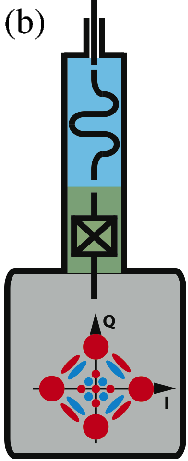
3.2 Reservoir (dissipation) engineering and autonomous stabilization of quantum systems
Being at the heart of any QEC protocol, the concept of feedback is central for the protection of quantum information, enabling many-qubit quantum computation or long-distance quantum communication. However, such a closed-loop control which requires a real-time and continuous measurement of the quantum system has been for long considered as counter-intuitive or even impossible. This thought was mainly caused by properties of quantum measurements: any measurement implies an instantaneous strong perturbation to the system's state. The concept of quantum non-demolition (QND) measurement has played a crucial role in understanding and resolving this difficulty 41. In the context of cavity quantum electro-dynamics (cavity QED) with Rydberg atoms 64, a first experiment on continuous QND measurements of the number of microwave photons was performed by the group at Laboratoire Kastler-Brossel (ENS) 62. Later on, this ability of performing continuous measurements allowed the same group to realize the first continuous quantum feedback protocol stabilizing highly non-classical states of the microwave field in the cavity, the so-called photon number states 9 (this ground-breaking work was mentioned in the Nobel prize attributed to Serge Haroche). The QUANTIC team contributed to the theoretical work behind this experiment 52, 30, 102, 32. These contributions include the development and optimization of the quantum filters taking into account the quantum measurement back-action and various measurement noises and uncertainties, the development of a feedback law based on control Lyapunov techniques, and the compensation of the feedback delay.
In the context of circuit quantum electrodynamics (circuit QED) 50, recent advances in quantum-limited amplifiers 92, 107 have opened doors to high-fidelity non-demolition measurements and real-time feedback for superconducting qubits 65. This ability to perform high-fidelity non-demolition measurements of a quantum signal has very recently led to quantum feedback experiments with quantum superconducting circuits 107, 91, 43. Here again, the QUANTIC team has participated to one of the first experiments in the field where the control objective is to track a dynamical trajectory of a single qubit rather than stabilizing a stationary state. Such quantum trajectory tracking could be further explored to achieve metrological goals such as the stabilization of the amplitude of a microwave drive 79.
While all this progress has led to a strong optimism about the possibility to perform active protection of quantum information against decoherence, the rather short dynamical time scales of these systems limit, to a great amount, the complexity of the feedback strategies that could be employed. Indeed, in such measurement-based feedback protocols, the time-consuming data acquisition and post-treatment of the output signal leads to an important latency in the feedback procedure.
The reservoir (dissipation) engineering 86 and the closely related coherent feedback 76 are considered as alternative approaches circumventing the necessity of a real-time data acquisition, signal processing and feedback calculations. In the context of quantum information, the decoherence, caused by the coupling of a system to uncontrolled external degrees of freedom, is generally considered as the main obstacle to synthesize quantum states and to observe quantum effects. Paradoxically, it is possible to intentionally engineer a particular coupling to a reservoir in the aim of maintaining the coherence of some particular quantum states. In a general viewpoint, these approaches could be understood in the following manner: by coupling the quantum system to be stabilized to a strongly dissipative ancillary quantum system, one evacuates the entropy of the main system through the dissipation of the ancillary one. By building the feedback loop into the Hamiltonian, this type of autonomous feedback obviates the need for a complicated external control loop to correct errors. On the experimental side, such autonomous feedback techniques have been used for qubit reset 60, single-qubit state stabilization 80, and the creation 35 and stabilization 69, 75, 98 of states of multipartite quantum systems.
Such reservoir engineering techniques could be widely revisited exploring the flexibility in the Hamiltonian design for QSC. We have recently developed theoretical proposals leading to extremely efficient, and simple to implement, stabilization schemes for systems consisting of a single, two or three qubits 60, 73, 48, 51. The experimental results based on these protocols have illustrated the efficiency of the approach 60, 98. Through these experiments, we exploit the strong dispersive interaction 96 between superconducting qubits and a single low-Q cavity mode playing the role of a dissipative reservoir. Applying continuous-wave (cw) microwave drives with well-chosen fixed frequencies, amplitudes, and phases, we engineer an effective interaction Hamiltonian which evacuates the entropy of the system interacting with a noisy environment: by driving the qubits and cavity with continuous-wave drives, we induce an autonomous feedback loop which corrects the state of the qubits every time it decays out of the desired target state. The schemes are robust against small variations of the control parameters (drives amplitudes and phase) and require only some basic calibration. Finally, by avoiding resonant interactions between the qubits and the low-Q cavity mode, the qubits remain protected against the Purcell effect, which would reduce the coherence times. We have also investigated both theoretically and experimentally the autonomous stabilization of non-classical states (such as Schrodinger cat states and Fock states) of microwave field confined in a high-Q cavity mode 94, 666, 4.
3.3 System theory for quantum information processing
In parallel and in strong interactions with the above experimental goals, we develop systematic mathematical methods for dynamical analysis, control and estimation of composite and open quantum systems. These systems are built with several quantum subsystems whose irreversible dynamics results from measurements and/or decoherence. A special attention is given to spin/spring systems made with qubits and harmonic oscillators. These developments are done in the spirit of our recent contributions 93, 30, 101, 95, 102, 328 resulting from collaborations with the cavity quantum electrodynamics group of Laboratoire Kastler Brossel.
3.4 Stabilization by measurement-based feedback
The protection of quantum information via efficient QEC is a combination of (i) tailored dynamics of a quantum system in order to protect an informational qubit from certain decoherence channels, and (ii) controlled reaction to measurements that efficiently detect and correct the dominating disturbances that are not rejected by the tailored quantum dynamics.
In such feedback scheme, the system and its measurement are quantum objects whereas the controller and the control input are classical. The stabilizing control law is based on the past values of the measurement outcomes. During our work on the LKB photon box, we have developed, for single input systems subject to quantum non-demolition measurement, a systematic stabilization method 32: it is based on a discrete-time formulation of the dynamics, on the construction of a strict control Lyapunov function and on an explicit compensation of the feedback-loop delay. Keeping the QND measurement assumptions, extensions of such stabilization schemes will be investigated in the following directions: finite set of values for the control input with application to the convergence analysis of the atomic feedback scheme experimentally tested in 111; multi-input case where the construction by inversion of a Metzler matrix of the strict Lyapunov function is not straightforward; continuous-time systems governed by diffusive master equations; stabilization towards a set of density operators included in a target subspace; adaptive measurement by feedback to accelerate the convergence towards a stationary state as experimentally tested in 83. Without the QND measurement assumptions, we will also address the stabilization of non-stationary states and trajectory tracking, with applications to systems similar to those considered in 65, 43.
3.5 Filtering, quantum state and parameter estimations
The performance of every feedback controller crucially depends on its online estimation of the current situation. This becomes even more important for quantum systems, where full state measurements are physically impossible. Therefore the ultimate performance of feedback correction depends on fast, efficient and optimally accurate state and parameter estimations.
A quantum filter takes into account imperfection and decoherence and provides the quantum state at time from an initial value at and the measurement outcomes between 0 and . Quantum filtering goes back to the work of Belavkin 37 and is related to quantum trajectories 44, 49. A modern and mathematical exposure of the diffusive models is given in 34. In 63 a first convergence analysis of diffusive filters is proposed. Nevertheless the convergence characterization and estimation of convergence rate remain open and difficult problems. For discrete time filters, a general stability result based on fidelity is proven in 93, 101. This stability result is extended to a large class of continuous-time filters in 31. Further efforts are required to characterize asymptotic and exponential stability. Estimations of convergence rates are available only for quantum non-demolition measurements 38. Parameter estimations based on measurement data of quantum trajectories can be formulated within such quantum filtering framework 55, 81.
We will continue to investigate stability and convergence of quantum filtering. We will also exploit our fidelity-based stability result to justify maximum likelihood estimation and to propose, for open quantum system, parameter estimation algorithms inspired of existing estimation algorithms for classical systems. We will also investigate a more specific quantum approach: it is noticed in 42 that post-selection statistics and “past quantum” state analysis 56 enhance sensitivity to parameters and could be interesting towards increasing the precision of an estimation.
3.6 Stabilization by interconnections
In such stabilization schemes, the controller is also a quantum object: it is coupled to the system of interest and is subject to decoherence and thus admits an irreversible evolution. These stabilization schemes are closely related to reservoir engineering and coherent feedback 86, 76. The closed-loop system is then a composite system built with the original system and its controller. In fact, and given our particular recent expertise in this domain 898, 60, this subsection is dedicated to further developing such stabilization techniques, both experimentally and theoretically.
The main analysis issues are to prove the closed-loop convergence and to estimate the convergence rates. Since these systems are governed by Lindblad differential equations (continuous-time case) or Kraus maps (discrete-time case), their stability is automatically guaranteed: such dynamics are contractions for a large set of metrics (see 85). Convergence and asymptotic stability is less well understood. In particular most of the convergence results consider the case where the target steady-state is a density operator of maximum rank (see, e.g., 33[chapter 4, section 6]). When the goal steady-state is not full rank very few convergence results are available.
We will focus on this geometric situation where the goal steady-state is on the boundary of the cone of positive Hermitian operators of finite trace. A specific attention will be given to adapt standard tools (Lyapunov function, passivity, contraction and Lasalle's invariance principle) for infinite dimensional systems to spin/spring structures inspired of 8, 698, 60 and their associated Fokker-Planck equations for the Wigner functions.
We will also explore the Heisenberg point of view in connection with recent results of the INRIA project-team MAXPLUS (algorithms and applications of algebras of max-plus type) relative to Perron-Frobenius theory 59, 58. We will start with 97 and 89 where, based on a theorem due to Birkhoff 39, dual Lindblad equations and dual Kraus maps governing the Heisenberg evolution of any operator are shown to be contractions on the cone of Hermitian operators equipped with Hilbert's projective metric. As the Heisenberg picture is characterized by convergence of all operators to a multiple of the identity, it might provide a mean to circumvent the rank issues. We hope that such contraction tools will be especially well adapted to analyzing quantum systems composed of multiple components, motivated by the facts that the same geometry describes the contraction of classical systems undergoing synchronizing interactions 106 and by our recent generalized extension of the latter synchronizing interactions to quantum systems 78.
Besides these analysis tasks, the major challenge in stabilization by interconnections is to provide systematic methods for the design, from typical building blocks, of control systems that stabilize a specific quantum goal (state, set of states, operation) when coupled to the target system. While constructions exist for so-called linear quantum systems 82, this does not cover the states that are more interesting for quantum applications. Various strategies have been proposed that concatenate iterative control steps for open-loop steering 109, 74 with experimental limitations. The characterization of Kraus maps to stabilize any types of states has also been established 40, but without considering experimental implementations. A viable stabilization by interaction has to combine the capabilities of these various approaches, and this is a missing piece that we want to address.
3.6.1 Perturbation methods
With this subsection we turn towards more fundamental developments that are necessary in order to address the complexity of quantum networks with efficient reduction techniques. This should yield both efficient mathematical methods, as well as insights towards unravelling dominant physical phenomena/mechanisms in multipartite quantum dynamical systems.
In the Schrödinger point of view, the dynamics of open quantum systems are governed by master equations, either deterministic or stochastic 64, 57. Dynamical models of composite systems are based on tensor products of Hilbert spaces and operators attached to the constitutive subsystems. Generally, a hierarchy of different timescales is present. Perturbation techniques can be very useful to construct reliable models adapted to the timescale of interest.
To eliminate high frequency oscillations possibly induced by quasi-resonant classical drives, averaging techniques are used (rotating wave approximation). These techniques are well established for closed systems without any dissipation nor irreversible effect due to measurement or decoherence. We will consider in a first step the adaptation of these averaging techniques to deterministic Lindblad master equations governing the quantum state, i.e. the system density operator. Emphasis will be put on first order and higher order corrections based on non-commutative computations with the different operators appearing in the Lindblad equations. Higher order terms could be of some interest for the protected logical qubit of figure 1b. In future steps, we intend to explore the possibility to explicitly exploit averaging or singular perturbation properties in the design of coherent quantum feedback systems; this should be an open-systems counterpart of works like 72.
To eliminate subsystems subject to fast convergence induced by decoherence, singular perturbation techniques can be used. They provide reduced models of smaller dimension via the adiabatic elimination of the rapidly converging subsystems. The derivation of the slow dynamics is far from being obvious (see, e.g., the computations of page 142 in 45 for the adiabatic elimination of low-Q cavity). Conversely to the classical composite systems where we have to eliminate one component in a Cartesian product, we here have to eliminate one component in a tensor product. We will adapt geometric singular perturbations 53 and invariant manifold techniques 46 to such tensor product computations to derive reduced slow approximations of any order. Such adaptations will be very useful in the context of quantum Zeno dynamics to obtain approximations of the slow dynamics on the decoherence-free subspace corresponding to the slow attractive manifold.
Perturbation methods are also precious to analyze convergence rates. Deriving the spectrum attached to the Lindblad differential equation is not obvious. We will focus on the situation where the decoherence terms of the form are small compared to the conservative terms . The difficulty to overcome here is the degeneracy of the unperturbed spectrum attached to the conservative evolution . The degree of degeneracy of the zero eigenvalue always exceeds the dimension of the Hilbert space. Adaptations of usual perturbation techniques 67 will be investigated. They will provide estimates of convergence rates for slightly open quantum systems. We expect that such estimates will help to understand the dependence on the experimental parameters of the convergence rates observed in 60, 98, 73.
As particular outcomes for the other subsections, we expect that these developments towards simpler dominant dynamics will guide the search for optimal control strategies, both in open-loop microwave networks and in autonomous stabilization schemes such as reservoir engineering. It will further help to efficiently compute explicit convergence rates and quantitative performances for all the intended experiments.
3.7 On-chip microwave engineering
The rapid development of circuitQED over the past 20 years was enabled by commercially available microwave components such as filters, switches and circulators, which allow experimentalists to shape and route measurement and control signals in and out of quantum systems. However, these components are intrinsically bulky, lossy and are imperfectly impedance-matched, leading to spurious reflections at their ports. In order to implement a full-scale quantum computer based on superconducting circuits, it is crucial that these functionalities be enabled reliably on-chip.
On-chip filters commonly used in circuitQED experiments are far from the level of variety and refinement of commercially available components. The near exclusive strategy known as "Purcell-filtering" 90 consists in placing stubs 87 on all feed lines. This cancels the admittance of the environment seen by a superconducting qubit at its resonance frequency, inhibiting spontaneous relaxation. An issue with this strategy is that given the modest width of the stub stopband, performances are degraded as soon as the qubit is not perfectly in resonance. Moreover, this approach is not suited for multiplexed control and measurements, in which a single feed line addresses simultaneously several qubits. Notable alternatives include highpass waveguide filters only available in 3D circuitQED 88, and a recent implementation of a bandpass filter 54.
On-chip non-reciprocal elements, such as isolators, circulators and gyrators are at a very early stage of development. So far, the most promising approach to break reciprocity without resorting to strong magnetic fields—which are incompatible with superconducting circuit technology—relies on the differential phase impinged on a signal during parametric down-conversion with respect to the reverse process of up-conversion. Combining coherently several conversion paths with well-chosen phases, one obtains a constructive forward interference, and a destructive backward one. In circuitQED, frequency conversion is enabled by a non-linear Josephson circuit 100, 47, 29, or by electromechanical coupling to nanoresonators 36, 84. A serious drawback of this approach is that it relies on a destructive interference effect to obtain the reverse isolation, which limits the operational bandwidth: the highest value reported so far is a 23 dB isolation over a 8 MHz band 29. For completeness, we mention a recent implementation of a forward amplifier based on resistively shunted Josephson junctions 105 that reaches a 100 MHz bandwidth at the cost of added noise, and the long term prospect of harnessing the anomalous Hall effect to implement a gyrator 108, 77.
In this project, we propose to develop novel on-chip filters and isolators based on 1D photonic crystals, which could reach unprecedented bandwidth, tunable range and on/off or forward/backward transmission ratios. The central idea is that a microwave transmission line with periodically modulated electrical properties behaves as a robust stopband filter, with attenuation scaling exponentially with the line length.
By fabricating lines whose properties are modulated by design, we plan to demonstrate the efficiency of this novel type of stopband filters. These lines will be fabricated in a high-kinetic inductance material (such as chains of Josephson junctions or granular aluminium), we will overcome the main weakness of this approach, which is the large on-chip footprint required when fabricating with conventional superconductors. Extending the numerical simulation methods developed in thsi work, we plan to design other types of filters (bandpass, highpass, lowpass) based on a similar technology.
We will then change perspective and modulate a line properties parametrically instead of by design to implement non-reciprocal elements. The idea is to design a line that possesses two traveling mode 1 and 2, with different propagation phase-velocity . If a low-frequency pump wave propagates on 1 modulates the electrical properties of the mode 2 thanks to shared non-linear inductance—for instance Josephson junction participating in both modes inductance—we obtain a situation in which mode 2 has spatially modulated electrical properties, with the phase of this modulation slowly evolving in time with at the pump period. A stopband appears in the transmission of a probe signal on mode 2, whose central frequency depends on whether the probe propagates in the same direction as the pump or not. It is then straightforward to turn this non-reciprocal filter into an isolator on circulator.
4 Application domains
4.1 Quantum engineering
A new field of quantum systems engineering has emerged during the last few decades. This field englobes a wide range of applications including nano-electromechanical devices, nuclear magnetic resonance applications, quantum chemical synthesis, high resolution measurement devices and finally quantum information processing devices for implementing quantum computation and quantum communication. Recent theoretical and experimental achievements have shown that the quantum dynamics can be studied within the framework of estimation and control theory, but give rise to new models that have not been fully explored yet.
The QUANTIC team's activities are defined at the border between theoretical and experimental efforts of this emerging field with an emphasis on the applications in quantum information, computation and communication. The main objective of this interdisciplinary team is to develop quantum devices ensuring a robust processing of quantum information.
On the theory side, this is done by following a system theory approach: we develop estimation and control tools adapted to particular features of quantum systems. The most important features, requiring the development of new engineering methods, are related to the concept of measurement and feedback for composite quantum systems. The destructive and partial 1 nature of measurements for quantum systems lead to major difficulties in extending classical control theory tools. Indeed, design of appropriate measurement protocols and, in the sequel, the corresponding quantum filters estimating the state of the system from the partial measurement record, are themselves building blocks of the quantum system theory to be developed.
On the experimental side, we develop new quantum information processing devices based on quantum superconducting circuits. Indeed, by realizing superconducting circuits at low temperatures and using microwave measurement techniques, the macroscopic and collective degrees of freedom such as the voltage and the current are forced to behave according to the laws of quantum mechanics. Our quantum devices are aimed to protect and process quantum information through these integrated circuits.
5 Highlights of the year
- Antoine Tilloy has obtained an ERC starting grant entitled QFT.zip "Compressing many-body quantum states in continuous space-time with tensor networks".
- Successful defence of Zaki Leghtas for his Professorship position at Mines Paris.
- Launch of two PEPR projects RobustSuperQ and NISQ2LSQ in which Quantic is involved.
- Successful PhD defence of Michiel Burgelman on July 1st 18.
6 New results
6.1 Structurally stable subharmonic regime of a driven quantum Josephson circuit
Participants: Michiel Burgelman, Pierre Rouchon, Alain Sarlette, Mazyar Mirrahimi
Driven quantum nonlinear oscillators, while essential for quantum technologies, are generally prone to complex chaotic dynamics that fall beyond the reach of perturbative analysis. By focusing on subharmonic bifurcations of a harmonically driven oscillator, in 12, we provide a recipe for the choice of the oscillator's parameters that ensures a regular dynamical behavior independently of the driving strength. We show that this suppression of chaotic phenomena is compatible with a strong quantum nonlinear effect reflected by the confinement rate in the degenerate manifold spanned by stable subharmonic orbits. This analysis and proof of possible and impossible dynamical bifurcations is one of the main results of the thesis of M. Burgelman.
6.2 Quantum dynamical decoupling by shaking the close environment
Participants: Michiel Burgelman, Alain Sarlette
Quantum dynamical decoupling is a procedure to cancel the effective coupling between two systems by applying sequences of fast actuations, under which the coupling Hamiltonian averages out to leading order(s). One of its prominent uses is to drive a target system in such a way as to decouple it from a less protected one. The paper 11 investigates the dual strategy: acting on a noisy "environment" subsystem such as to decouple it from a target system. The potential advantages are that actions on the environment commute with system operations, and that imprecisions in the decoupling actuation are harmless to the target. We consider two versions of environment-side decoupling: adding an imprecise Hamiltonian drive which stirs the environment components; and, increasing the decoherence rates on the environment. The latter can be viewed as driving the environment with pure noise and our conclusions establish how, maybe counterintuitively, isolating the environment from noise sources as much as possible is often not the best option. We explicitly analyze the induced decoherence on the target system and establish how it is influenced by the parameters in both cases. The analysis combines Lindbladian derivation, adiabatic elimination, and Floquet modeling in a way that may be of independent interest.
6.3 Correlation functions for realistic continuous quantum measurement
Participants: Pierre Guilmin, Pierre Rouchon, Antoine Tilloy
In 23, we propose a self-contained and accessible derivation of a formula for the n-point correlation functions of the signal measured when continuously observing a quantum system. The expression depends on the initial quantum state and on the Stochastic Master Equation (SME) governing the dynamics. This derivation applies to both jump and diffusive evolutions and takes into account common imperfections of realistic measurement devices. We show how these correlations can be efficiently computed numerically for commonly filtered and integrated signals available in practice.
6.4 Symmetries and field tensor network states
Participants: Antoine Tilloy
In 21, we study the interplay between symmetry representations of the physical and virtual space on the class of tensor network states for critical spins systems known as field tensor network states (fTNS). These are by construction infinite dimensional tensor networks whose virtual space is described by a conformal field theory (CFT). We can represent a symmetry on the physical index as a commutator with the corresponding CFT current on the virtual space. By then studying this virtual space representation we can learn about the critical symmetry protected topological properties of the state, akin to the classification of symmetry protected topological order for matrix product states. We use this to analytically derive the critical symmetry protected topological properties of the two ground states of the Majumdar-Ghosh point with respect to the previously defined symmetries.
6.5 A study of the quantum Sinh-Gordon model with relativistic continuous matrix product states
Participants: Antoine Tilloy
In 26, we study the Sine-Gordon (SG) and Sinh-Gordon (ShG) quantum field theories with a recently introduced variational method, the relativistic continuous matrix product states (RCMPS). The main advantage is to work directly in the thermodynamic limit, and without any UV regulator. The SG model is well understood and integrable, which provides a convenient benchmark for the variational method and serves as a warm-up. RCMPS approximate the ground state of the SG model arbitrary well up to the free Fermion point (b=1/sqrt(2)), where the ground energy collapses to minus infinity, and some renormalized ansatz would be needed. The ShG model, while integrable, is less understood and its strong coupling regime is subject to some controversy. RCMPS also fit the ground state of the ShG model up to approximately b=1/sqrt(2), after which their predictions start to deviate substantially from the "exact" results. This is more puzzling as nothing is expected to happen physically for the ShG model at that point (eg, the ground energy density does not diverge). Either the "exact" ShG results are not exact (the analytic continuation of the SG Bethe Ansatz solution is unwarranted), or, more likely, the physical structure of the ShG ground state changes in such a way that it becomes out of reach of the RCMPS manifold for reasonable bond dimensions.
6.6 Exponential convergence of a dissipative quantum system towards finite-energy grid states of an oscillator
Participants: Lev-Arcady Sellem, Philippe Campagne-Ibarcq, Mazyar Mirrahimi, Pierre Rouchon
This result (published in 17) proposes a dissipative quantum system with explicit decoherence operators to stabilize grid-states of a quantum harmonic oscillator (GKP states). Based on the stabilizer formalism underlying Quantum Error Correction (QEC), the design of an original Lindblad master equation for the density operator of a quantum harmonic oscillator is proposed. This Lindblad dynamics stabilizes exactly the finite-energy grid states introduced in 2001 by Gottesman, Kitaev and Preskill for quantum computation. Stabilization results from an exponential Lyapunov function with an explicit lower-bound on the convergence rate. Numerical simulations indicate the potential interest of such autonomous QEC in presence of non-negligible photon losses.
6.7 Magnifying quantum phase fluctuations with Cooper-pair pairing
Participants: M. Villiers, P. Campagne-Ibarcq, Z. Leghtas
Remarkably, complex assemblies of superconducting wires, electrodes, and Josephson junctions are compactly described by a handful of collective phase degrees of freedom that behave like quantum particles in a potential. The inductive wires contribute a parabolic confinement, while the tunnel junctions add a cosinusoidal corrugation. Usually, the ground state wavefunction is localized within a single potential well – that is, quantum phase fluctuations are small – although entering the regime of delocalization holds promise for metrology and qubit protection. A direct route is to loosen the inductive confinement and let the ground state phase spread over multiple Josephson periods, but this requires a circuit impedance vastly exceeding the resistance quantum and constitutes an ongoing experimental challenge. In 16, we take a complementary approach and fabricate a generalized Josephson element that can be tuned in situ between one- and two-Cooper-pair tunneling, doubling the frequency of the corrugation and thereby magnifying the number of wells probed by the ground state. We measure a tenfold suppression of flux sensitivity of the first transition energy, implying a twofold increase in the vacuum phase fluctuations.
6.8 One hundred second bit-flip time in a two-photon dissipative oscillator
Participants: Camille Berdou, Ulysse Réglade, Marius Villiers, Lev-Arcady Sellem, Pierre Rouchon, Alain Sarlette, Mazyar Mirrahimi, Philippe Campagne-Ibarcq, Zaki Leghtas
Current implementations of quantum bits (qubits) continue to undergo too many errors to be scaled into useful quantum machines. An emerging strategy is to encode quantum information in the two meta-stable pointer states of an oscillator exchanging pairs of photons with its environment, a mechanism shown to provide stability without inducing decoherence. Adding photons in these states increases their separation, and macroscopic bit-flip times are expected even for a handful of photons, a range suitable to implement a qubit. However, previous experimental realizations have saturated in the millisecond range. In this experimental work 19, we aim for the maximum bit-flip time we could achieve in a two-photon dissipative oscillator. To this end, we design a Josephson circuit in a regime that circumvents all suspected dynamical instabilities, and employ a minimally invasive fluorescence detection tool, at the cost of a two-photon exchange rate dominated by single-photon loss. We attain bit-flip times of the order of 100 seconds for states pinned by two-photon dissipation and containing about 40 photons. This experiment lays a solid foundation from which the two-photon exchange rate can be gradually increased, thus gaining access to the preparation and measurement of quantum superposition states, and pursuing the route towards a logical qubit with built-in bit-flip protection.
6.9 Dynamically enhancing qubit-photon interactions with anti-squeezing
Participants: Marius Villiers, Alexandru Petrescu, Alvise Borgognoni, Alain Sarlette, Mazyar Mirrahimi, Philippe Campagne-Ibarcq, Zaki Leghtas
The interaction strength of an oscillator to a qubit grows with the oscillator's vacuum field fluctuations. The well known degenerate parametric oscillator has revived interest in the regime of strongly detuned squeezing, where its eigenstates are squeezed Fock states. Owing to these amplified field fluctuations, it was recently proposed that squeezing this oscillator would dynamically boost qubit-photon interactions. In a superconducting circuit experiment, we observe a two-fold increase in the dispersive interaction between a qubit and an oscillator at 5.5 dB of squeezing, demonstrating in-situ dynamical control of qubit-photon interactions 28.
6.10 Complete positivity violation in higher-order quantum adiabatic elimination
Participants: Masaaki Tokieda, Alain Sarlette, Pierre Rouchon
When a composite Lindblad system consists of weakly coupled sub-systems with fast and slow timescales, the description of slow dynamics can be simplified by discarding fast degrees of freedom. This model reduction technique is called adiabatic elimination. While second-order perturbative expansion with respect to the timescale separation has revealed that the evolution of a reduced state is completely positive, in 27, we present an example exhibiting complete positivity violation in the fourth-order expansion. Despite the non-uniqueness of slow dynamics parametrization, we prove that complete positivity cannot be ensured in any parametrization. The violation stems from correlation in the initial state.
6.11 Two-photon driven Kerr quantum oscillator with multiple spectral degeneracies
Participants: Diego Ruiz, Ronan Gautier, Jérémie Guillaud, Mazyar Mirrahimi
Kerr nonlinear oscillators driven by a two-photon process are promising systems to encode quantum information and to ensure a hardware-efficient scaling towards fault-tolerant quantum computation. In 25, we show that an extra control parameter, the detuning of the two-photon drive with respect to the oscillator resonance, plays a crucial role in the properties of the defined qubit. At specific values of this detuning, we benefit from strong symmetries in the system, leading to multiple degeneracies in the spectrum of the effective confinement Hamiltonian. Overall, these degeneracies lead to a stronger suppression of bit-flip errors. We also study the combination of such Hamiltonian confinement with colored dissipation to suppress leakage outside of the bosonic code space. We show that the additional degeneracies allow us to perform fast and high-fidelity gates while preserving a strong suppression of bit-flip errors.
6.12 High-performance repetition cat code using fast noisy operations
Participants: François-Marie Le Regent, Camille Berdou, Zaki Leghtas, Jérémie Guillaud, Mazyar Mirrahimi
Bosonic cat qubits stabilized by two-photon driven dissipation benefit from exponential suppression of bit-flip errors and an extensive set of gates preserving this protection. These properties make them promising building blocks of a hardware-efficient and fault-tolerant quantum processor. In 24, we propose a performance optimization of the repetition cat code architecture using fast but noisy CNOT gates for stabilizer measurements. This optimization leads to high thresholds for the physical figure of merit, given as the ratio between intrinsic single-photon loss rate of the bosonic mode and the engineered two-photon loss rate, as well as a very interesting scaling below threshold of the required overhead, to reach an expected level of logical error rate. Relying on the specific error models for cat qubit operations, this optimization exploits fast parity measurements, using accelerated low-fidelity CNOT gates, combined with fast ancilla parity-check qubits. The significant enhancement in the performance is explained by: 1- the highly asymmetric error model of cat qubit CNOT gates with a major component on control (ancilla) qubits, and 2- the robustness of the error correction performance in presence of the leakage induced by fast operations. In order to demonstrate these performances, we develop a method to sample the repetition code under circuit-level noise that also takes into account cat qubit state leakage.
6.13 Dynamics of Transmon Ionization
Participants: Alexandru Petrescu
In 15, together with R. Shillito, J. Cohen, and A. Blais, and within a larger collaboration with the quantum many-body theory group of G. Vidal at Google Quantum AI, we numerically explored the dynamics of a driven transmon-resonator system under strong and nearly resonant measurement drives, and found clear signatures of transmon ionization where the qubit escapes out of its cosine potential. Using a semiclassical model, we interpreted this ionization as resulting from resonances occurring at specific resonator photon populations. We found that the photon populations at which these spurious transitions occur are strongly parameter dependent and that they can occur at low resonator photon populations, something which may explain the experimentally observed degradation in measurement fidelity.
6.14 Reminiscence of classical chaos in driven transmons
Participants: Alexandru Petrescu
In 20, together with J. Cohen, R. Shillito, and A. Blais, we showed that off-resonant drives, in regimes routinely used in experiments, can cause strong modifications to the structure of the transmon spectrum rendering a large part of it chaotic. Accounting for the full nonlinear dynamics of the transmon in a Floquet-Markov formalism, we found that these chaotic states, often neglected through the hypothesis that the anharmonicity is weak, strongly impact the lifetime of the transmon's computational states. In particular, we observe that chaos-assisted quantum phase slips greatly enhance band dispersions. In the presence of a measurement resonator, we find that approaching chaotic behavior correlates with strong transmon-resonator hybridization, and an average resonator response centered on the bare resonator frequency. These results lead to a photon number threshold characterizing the appearance of chaos-induced quantum demolition effects during strong-drive operations such as dispersive qubit readout. The phenomena described are expected to be present in all circuits based on low-impedance Josephson-junctions.
6.15 A tutorial introduction to quantum stochastic master equations based on the qubit/photon system
Participants: Pierre Rouchon
This is an elementary introduction to stochastic master equations from discrete to continuous time for the control engineering community (published in Annual Reviews of Control 14).
From the key composite quantum system made of a two-level system (qubit) and a harmonic oscillator (photon) with resonant or dispersive interactions, one derives the corresponding quantum Stochastic Master Equations (SME) when either the qubits or the photons are measured. Starting with an elementary discrete-time formulation based on explicit formulae for the interaction propagators, one shows how to include measurement imperfections and decoherence. This qubit/photon quantum system illustrates the Kraus-map structure of general discrete-time SME governing the dynamics of an open quantum system subject to measurement backaction and decoherence induced by the environment. Then, on the qubit/photon system, one explains the passage to a continuous-time mathematical model where the measurement signal is either a continuous real value signal (typically homodyne or heterodyne signal) or a discontinuous and integer-value signal obtained from a photo-counter. During this derivation, the Kraus map formulation is preserved in an infinitesimal way. Such a derivation provides also an equivalent Kraus map formulation to the continuous-time SME usually expressed as stochastic differential equations driven either by Wiener or Poisson processes. From such Kraus map formulation, simple linear numerical integration schemes are derived that preserve the positivity and the trace of the density operator, i.e. of the quantum state.
6.16 A tutorial on quantum computation with cat qubits
Participants: Mazyar Mirrahimi
These are the lecture notes from the 2019 Les Houches Summer School on "Quantum Information Machines". After a brief introduction to quantum error correction and bosonic codes, we focus on the case of cat qubits stabilized by a nonlinear multi-photon driven dissipation process. We argue that such a system can be seen as a self-correcting qubit where bit-flip errors are robustly and exponentially suppressed. Next, we provide some experimental directions to engineer such a multi-photon driven dissipation process with superconducting circuits. Finally, we analyze various logical gates that can be implemented without re-introducing bit-flip errors. This set of bias-preserving gates pave the way towards a hardware-efficient and fault-tolerant quantum processor. These lecture notes should soon appear in 'Quantum Information Machines; Lecture Notes of the Les Houches Summer School 2019', eds. M. Devoret, B. Huard, and I. Pop, Scipost Lecture notes 22.
7 Bilateral contracts and grants with industry
7.1 Bilateral contracts with industry
- New PhD contracts with Alice&Bob for 3 new students: L. Carde, D. Ruiz, A. Bocquet.
- Inria-Microsoft lab funding to further study "quantum random walks". This funding led to the hiring of Mathys Rennela. The postdoc and funding ended on August 2022. A forthcoming paper will present the results of this collaboration.
8 Partnerships and cooperations
8.1 European initiatives
8.1.1 Horizon Europe
DANCINGFOOL
DANCINGFOOL project on cordis.europa.eu
-
Title:
High-impedance Superconducting Circuits Enabling Fault-tolerant Quantum Computing by Wideband Microwave Control
-
Duration:
From December 1, 2022 to November 30, 2027
-
Partners:
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE (INRIA), France
- ECOLE NORMALE SUPERIEURE (ENS), France
-
Inria contact:
Philippe Campagne-Ibarcq
-
Coordinator:
Philippe Campagne-Ibarcq
-
Summary:
A physical system implementing a quantum bit (qubit) is never perfectly isolated from an uncontrolled environment. The system dynamics is thus noisy, modifying randomly the qubit state. This phenomenon of decoherence is the main roadblock to build a stable quantum computing platform. In order to mitigate decoherence, quantum error correction employs only a few code states within a much larger informational space, so that noise-induced dynamics can be detected and corrected before the encoded information gets corrupted. Unfortunately, most known protocols require to control dauntingly complex systems, with a degree of coherence currently out of reach. Our project is to build autonomously error-corrected qubits encoded in high-impedance superconducting circuits. In our protocol, a qubit is encoded in the vast phase-space of the quantum oscillator implemented by each circuit, in the form of Gottesman-Kitaev-Preskill (GKP) states. The novelty is that the GKP states are fully stabilized by a modular dissipation, induced by the coherent tunneling of charges through a stroboscopically biased Josephson junction. The coherence of the encoded qubit is expected to exceed that of existing superconducting qubits by orders of magnitude. Furthermore, we propose to perform protected logical gates between encoded qubits by varying adiabatically the parameters of the modular dissipation, paving the way toward fault-tolerant quantum computing. The major experimental challenge of our protocol resides in the exquisite level of control needed over a wide band in the microwave range. We propose to address this challenge by developing novel on-chip filters, tunable couplers and isolators based on periodically modulated, high-impedance, transmission lines. These on-chip components would find a wide range of applications in quantum technologies, and favor the advent of large-scale quantum computing platforms.
QFT.zip
QFT.zip project on cordis.europa.eu
-
Title:
Compressing many-body quantum states in continuous space-time with tensor networks
-
Duration:
From January 1, 2023 to December 31, 2027
-
Partners:
- ARMINES, France
- INRIA, France
-
Coordinator:
Antoine Tilloy
-
Summary:
Many-body quantum systems with strong correlations are particularly difficult to understand in the continuum, where non-perturbative techniques are in scarce supply. Direct diagonalization methods are not available, since the Hilbert space is simply too large to be manageable. This inhibits progress in high energy physics, nuclear physics, and in the study of exotic topological phases of matter. On the lattice, tensor network states, a variational class of wavefunctions coming from quantum information theory, have allowed to compress exponentially large Hilbert spaces down to a smaller numerically manageable corner. This has allowed substantial theoretical and numerical advance on the many-body problem on the lattice. This project will develop continuous tensor network states, a new framework to extend the recent lattice progress to the continuum and quantum field theory (QFT). The originality of the approach is that it will not rely on any discretization of space-time. We will work directly in the continuum, without any cutoff. Low energy states of quantum field theories, which a priori live in a continuously infinite dimensional Hilbert space, will be compressed down to a finite and small number of parameters. This will then allow to solve numerically very generic (non-integrable) strongly coupled theories in a fully non-perturbative manner. Such a compression was long thought to be impossible, in particular in the relativistic case, but we overcame crucial theoretical hurdles in the past year, making the proposal particularly timely. We will construct this framework with 3 main applications in mind: i) non-relativistic problems in 2 space dimensions and more, including e.g. fractional quantum Hall states, ii) relativistic QFT, starting with 1+1 dimensional toy model and gradually increasing complexity to get closer to nonabelian gauge theories, iii) critical quantum systems (and classical statistical mechanics).
8.1.2 H2020 projects
ERC Starting Grant ECLIPSE
- Program: H2020
- Type: ERC
- Project acronym: ECLIPSE
- Project title: Exotic superconducting circuits to probe and protect quantum states of light and matter
- Duration: 2019-2024
- Coordinator: Zaki Leghtas, Mines Paristech
- Abstract: Quantum systems can occupy peculiar states, such as superposition or entangled states. These states are intrinsically fragile and eventually get wiped out by inevitable interactions with the environment. Protecting quantum states against decoherence is a formidable and fundamental problem in physics, which is pivotal for the future of quantum computing. The theory of quantum error correction provides a solution, but its current envisioned implementations require daunting resources: a single bit of information is protected by encoding it across tens of thousands of physical qubits. This project intend to encode quantum information in an entirely new type of qubit with two key specificities. First, it will be encoded in a single superconducting circuit resonator whose infinite dimensional Hilbert space can replace large registers of physical qubits. Second, this qubit will be rf-powered, continuously exchanging photons with a reservoir. This approach challenges the intuition that a qubit must be isolated from its environment. Instead, the reservoir acts as a feedback loop which continuously and autonomously corrects against errors. This correction takes place at the level of the quantum hardware, and reduces the need for error syndrome measurements which are resource intensive. The circuits I will develop manipulate quantum states of light, whose utility transcends the long term goal of quantum computing, and can readily be used to probe fundamental properties of matter. In mesoscopic physics where a large number of particles exhibit collective quantum phenomena, the measurement tools to characterize subtle quantum effects are often lacking. Here, the project proposes to measure the spin entanglement of a single Cooper pair, by coupling a superconductor to a circuit composed of microwave resonators and a carbon nanotube. The spin entanglement can be swapped into microwave photons, which can be detected by deploying the arsenal of quantum limited microwave measurement devices.
ERC Advanced Grant Q-Feedback
- Program: H2020
- Type: ERC
- Project acronym: Q-Feedback
- Project title: Quantum feedback Engineering
- Duration: 2020-2025
- Coordinator: Pierre Rouchon, Mines Paristech
-
Abstract : Quantum technologies, such as quantum computers and simulators, have the potential of revolutionizing our computational speed, communication security and measurement precision.The power of the quantum relies on two key but fragile resources: quantum coherence and entanglement. This promising field is facing a major open question: how to design machines which exploit quantum properties on a large scale, and efficiently protect them fromexternal perturbations (decoherence), which tend to suppress the quantum advantage?
Making a system robust and stable to the influence of external perturbations is one of the core problems in control engineering. The goal of this project is to address the above question from the angle of control systems. The fundamental and scientific ambition is to elaborate theoretical control methods to analyse and design feedback schemes for protecting and stabilizing quantum information. Q-Feedback develops mathematical methods to harness the inherently stochastic aspects of quantum measurements. Relying on the development of original mathematical perturbation techniques specific to open quantum systems, Q-Feedback proposes a new hierarchical strategy for quantum feedback modeling, design and analysis.
The building block of a quantum machine is the quantum bit (qubit), a system which can adopt two quantum states. Despite major progress, qubits remain fragile and lose their quantum properties before a meaningful task can be accomplished. For this reason, a qubit must be both protected against external perturbations, and manipulated to perform a task. Today, no such qubit has been built. In collaboration with experimentalists, the practical ambition is to design, relying on the control tools developed here, qubits readily integrable in a quantum processing unit. The physical platform will be Josephson superconducting circuits. Q-Feedback is expected to demonstrate the crucial role of control engineering in emerging quantum technologies.
Quantera Grant QuCos
- Program: H2020
- Type: Quantera
- Project acronym: QuCos
- Project title: Quantum Computation with Schrödinger cat states
- Duration: 2019-2023
- Coordinator: Gerhard Kirchmair, University of Innsbruck, Austria.
- Inria contacts: Zaki Leghtas and Mazyar Mirrahimi
- Other partners: ENS Lyon (France), Karlsruhe Institut of Technology (Germany), Quantum Machines (Israel), National Institute for Research and Development of Isotopic and Molecular Technologies, Romania.
- Abstract: This project seeks to establish a radically new, alternative approach to realizing the fundamental building blocks of quantum computers with superconducting qubits. In the next 3 years, we plan to employ only a handful of realistic components to realize robust error-corrected logical quantum bits. We aim to demonstrate the same level of protection provided by a few hundreds of qubits (with properties beyond the state of the art) in today’s mainstream approach of the so-called surface code architecture. Our alternative approach is known as cat codes, because it employs multiple interconnected high coherence cavity modes with non-linear dissipation, to encode a qubit in superpositions of Schrödinger cat states. Our project combines realizing the quantum processor architecture as well as the control system and the protocols that drive it, building towards a full-stack error-corrected quantum computer. The partners in our collaboration form a strong synergetic group that has the full range of expertise needed to design and realize these systems, and to obtain these challenging goals. Furthermore, all partners of our project, including both industry and academia, have worked together and published works in the fields of quantum computing and quantum information processing. We aim to implement error protected qubits, fault tolerant operations, and demonstrate the scalability of this approach by realizing a repetition code. Our project will enable quantum experiments towards the ambitious and well-defined goal of constructing a logical qubit, on which we can perform gates, and most importantly, quantum error-correction (QEC).
8.2 National initiatives
- PEPR NISQ2LSQ: Quantic is a PI and the coordinator of WP1 of this PEPR project which started in 2022. The goal is to accelerate French research on the topic of bosonic and LDPC codes for preparing the ground for hardware-efficient and fault-tolerant quantum computation.
- PEPR RobustSuperQ: Quantic is a PI and the coordinator of WP1 of this PEPR project which started in 2022. The goal is to accelerate French research on the topic of high quality, noise resilient, superconducting qubits.
- ANR project HAMROQS: In the framework of the ANR program JCJC, Alain Sarlette has received a funding for his research program "High-accuracy model reduction for open quantum systems". This grant of 212k euros started on april 2019 and will run for 4 years.
- ANR project SYNCAMIL: In the framework of the ANR program JCJC, Philippe Campagne-Ibarcq received a funding for his research program "Synthetic Non-Local Hamiltonians for the protection of quantum information". This grant of 380k euros has allowed us to purchase the experimental equipment to perform an experiment on stabilization of GKP grid states at ENS Paris, and to hire a postdoctoral associate, Vincent Lienhard, for 2 years. The project started in December 2020 for 48 months. This project was however stopped on Nov 30th following the start of the ERC-Dancingfool project, as these two sources of funding are mutually exclusive.
- ANR project Mecaflux: Alain Sarlette is a PI of this ANR Grant that started in 2022 and runs for 4 years. This project aims to couple mechanical oscillators with superconduncting circuits at the quantum level, using a new circuit architecture allowing near-resonant coupling. The project is coordinated by mechanical oscillators expert Samuel Deléglise (LKB, U.Sorbonne), other project PIs are Alain Sarlette and Zaki Leghtas (QUANTIC project-team), Emmanuel Flurin and Hélène LeSueur (CEA Saclay). Our new recruit Antoine Tilloy may join with quantum gravity expertise if the level of control attains the objective where those effects become significant. The PhD thesis of Angela Riva is funded on this ANR.
- ANR project OCTAVES: Mazyar Mirrahimi is a PI of this ANR Grant that started in 2022 and will run for 4 years. This project aims in studying the measurement problem in circuit QED (non QND effects in presence of probe drives) as well as limitations to the parametric driving for cat qubit stabilization. The project is coordinated by Olivier Buisson (Institut Néel, Grenoble) and other project PIs are Benjamin Huard (ENS Lyon), Mazyar Mirrahimi (Quantic project-team), and Dima Shepelyansky (LPT, Toulouse). The PhD thesis of Linda Greggio is funded on this ANR.
8.3 Regional initiatives
- PSL Jeune Equipe Grant: Antoine Tilloy obtained a PSL grant to start his activity as an associate professor in 2021.
9 Dissemination
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
Member of the organizing committees
- Mazyar Mirrahimi and Pierre Rouchon were co-organizers of a one-week workshop "Mathematical methods for quantum hardware" at IMSI, university of Chicago: July 11-15.
9.1.2 Scientific events: selection
Reviewer
- Pierre Rouchon has been a reviewer for IEEE and IFAC inetrnational conferences.
9.1.3 Journal
Member of the editorial boards
- Pierre Rouchon is a member of the editorial board of Annual Reviews in Control.
Reviewer - reviewing activities
- Philippe Campagne-Ibacq has been a reviewer for Physical Review Letters.
- Zaki Leghtas has been a reviewer for Physical Review Letters, Physical Review X, and Nature Physics.
- Pierre Rouchon has been a reviewer for Journal of differential equation and Physical Review X.
- Alex Petrescu reviewed for Physical Review, and Nature Communications.
9.1.4 Invited talks
- Zaki Leghtas at Sorbonne Université.
- Zaki Leghtas at Laboratoire Jacques Louis Lions.
- Zaki Leghtas at Journées X/ENS.
- Zaki Leghtas at ENSTA.
- Zaki Leghtas at Quantum innovation, Tokyo (online).
- Zaki Leghtas at APS March Meeting, Chicago (online).
- Mazyar Mirrahimi at APS March Meeting, Chicago (online).
- Mazyar Mirrahimi at Journée DIM Quantip.
- Mazyar Mirrahimi at Journée Quantique at Académie des Sciences.
- Alex Petrescu at Chicago IMSI Workshop Mathematical Methods for Quantum Hardware.
- Alex Petrescu at Helsinki SQA Conference.
- Alex Petrescu gave an invited seminar at the Walther Meissner Institut, München.
- Alex Petrescu gave an invited seminar at U Mass Lowell.
- Alex Petrescu at ENS Balades Quantiques.
- Pierre Rouchon at inauguration of Laboratoire QTech, ONERA.
- Piere Rouchon at IHP workshop Q-coast: Estimation and control of open quantum systems, Institut Henri Poincaré.
- Pierre Rouchon was a plenary speaker at GRETSI 2022, Nancy.
- Alain Sarlette at IHP workshop Q-coast: Estimation and control of open quantum systems, Institut Henri Poincaré.
9.1.5 Leadership within the scientific community
- Alain Sarlette is a board member of the new DIM "QUANTIP" (Quantum Technologies in Paris Region), which has been successfully submitted and launched in 2022.
9.1.6 Scientific expertise
- Philippe Campagne-Ibarcq was a member of the Inria-Scalay CRCN/ISFP admissibility jury.
- Pierre Rouchon and Alain Sarlette are members of ANR Comité d'Evaluation Scientifique on Quantum Technologies.
- Alain Sarlette was a member of the selection committees for various calls of the DIM QUANTIP.
- Philippe Campagne-Ibarcq, Zaki Leghtas and Mazyar Mirrahimi are members of the scientific board of Alice and Bob company.
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
- Zaki Leghtas: Cycle Ingénieur at Mines Paris, Quantum Computing, 30 hours.
- Mazyar Mirrahimi: Automatic Control at Ecole Polytechnique (16 hours), Optimization and Control at Ecole Polytechnique (40 hours), Ecole Polytechnique bachelor program thesis instructor (20 hours).
- Alex Petrescu Automatics at Mines ParisTech (12 hours).
- Alexandru Petrescu and Pierre Rouchon: M1 course (Mathematical method for quantum engineering) of the new PSL Master Quantum Engineering, 20 hours.
- Pierre Rouchon is a member of the steering commitee of PSL master of Quantum Engineering with ENS-Paris.
- Pierre Rouchon is in charge of the "Mathematics and Automatics" specialty within the ISMME-621 doctoral school.
- Pierre Rouchon: Lake Como School of Advanced Studies, September 19-23, Quantum characterization and control of quantum complex systems.
- Pierre Rouchon: Esquisses summer school at Porquerolles, July 4-9.
- Antoine Tilloy: Mines Paris, TDs of Optimisation, TDs of Introduction to quantum mechanics.
- Alain Sarlette and Antoine Tilly: M1 Course (Introduction to quantum computing) of the new PSL Master Quantum Engineering, 20 hours.
- Alain Sarlette: Robotics at Ghent university (24 hours).
9.2.2 Supervision
-
PhD in progress
Marius Villiers. Enhancing qubit-photon interactions with anti-squeezing. Supervision Zaki Leghtas.
-
PhD in progress
Camille Berdou. Cat-qubit: macroscopic bit-flip times. Supervision of Zaki Leghtas.
-
PhD in progress
Alvise Borgognoni. Non-local quantum dynamics. Supervision of Zaki Leghtas.
-
PhD in progress
Ulysse Réglade. 3D cat-qubit. Supervision of Zaki Leghtas and Raphaël Lescanne.
-
PhD in progress
Adrien Bocquet. Cat-qubit: quantum coherence and macroscopic bit-flip times. Supervision of Zaki Leghtas and Raphaël Lescanne.
-
PhD in progress
Erwan Roverch’. Protected qubits. Supervision of Zaki Leghtas.
-
PhD in progress
Angela Riva. Dynamics and control of a mechanical quantum oscillator quasi-resonantly coupled to a Heavy Fluxonium qubit. Supervision of Alain Sarlette.
-
PhD in progress
Christian Siegele. Quantum error correction with grid states of light. Supervision of Philippe Campagne-Ibarcq and Mazyar Mirrahimi.
-
PhD in progress
Aron Vanselow. Autonomous stabilization of GKP grid states in high impedance circuits. Supervision of Philippe Campagne-Ibarcq and Mazyar Mirrahimi.
-
PhD defended in 2022
: Michiel Burgelman. A systematic study of strongly driven and dissipative quantum systems towards high-accuracy quantum control designs. Supervision of Pierre Rouchon and Alain Sarlette.
-
PhD in progress
François-Marie Le Régent. Quantum computing architecture with cat-qubits. Supervision of Mazyar Mirrahimi and Jérémie Guillaud
-
PhD in progress
Ronan Gautier. Efficient protection and fast gates in bosonic quantum codes. Supervision of Alain Sarlette.
-
PhD in progress
Lev-Arcady Sellem. Mathematical methods for simulation and control of open quantum systems. Supervision of Claude Le Bris and Pierre Rouchon.
-
PhD in progress
Thiziei Aissaoui. On-chip biasing of superconducting circuits. Supervision of Alain Sarlette and Anil Murani.
-
PhD in progress
Matthieu Praquin, Reconfigurable microwave photonics crystals based on granular superconductors. Supervision of Philippe Campagne-Ibarcq and Zaki Leghtas.
-
PhD in progress
Linda Greggio. Strong drive effects in quantum superconducting circuits. Supervision of Alexandru Petrescu and Mazyar Mirrahimi.
-
PhD in progress
Diego Ruiz. Scaling up a bosonic quantum processor. Supervision of Mazyar Mirrahimi and Jérémie Guillaud.
-
PhD in progress
Louis Paletta. Autonomous quantum error correction with cat qubits. Supervision of Mazyar Mirrahimi, Anthony Leverrier, Christophe Vuillot and Alain Sarlette.
-
PhD in progress
Pierre Guilmin. Quantum estimation and control of cat-qubit. Supervision of Pierre Rouchon and Antoine Tilloy.
-
PhD in progress
Leon Carde. Control and fast preparation of cat qubits, supervision of Joachim Cohen, Alexandru Petrescu, Pierre Rouchon.
-
PhD in progress
Karanbir Singh Tiwana. Tensor networks for quantum field theory. Supervision of Antoine Tilloy.
9.2.3 Juries
- Zaki Leghtas was in the PhD committee of Catherine Leroux, Université de Sherbrooke.
- Zaki Leghtas was in the PhD committee of Guilliam Butseraen, Institut Néel Grenoble.
- Pierre Rouchon was in the HDR jury of Nina Amini.
- Pierre Rouchon was referee for the PhD thesis of Remi Robin at Sorbonne University.
9.3 Popularization
9.3.1 Articles and contents
- Antoine Tilloy: L’ordinateur quantique ne se résume pas à une course aux qubits (interview by Sean Bailly for la Science, June 2022)
- Antoine Tilloy: Décrire le monde grâce à la mécanique quantique, la Recherche, Oct-Dec 2022.
9.3.2 Education
- Our PhD students received middle school students during half a day and presented the context of our activities and life and profession of a researcher.
10 Scientific production
10.1 Major publications
- 1 articleQuantum Fast-Forwarding: Markov chains and graph property testing.Quantum Information & ComputationApril 2019
- 2 articleQuantum error correction of a qubit encoded in grid states of an oscillator.Nature584Text and figures edited for clarity. The claims of the paper remain the same. Author list fixedAugust 2020
- 3 articleRepetition Cat Qubits for Fault-Tolerant Quantum Computation.Physical Review Xhttps://arxiv.org/abs/1904.09474 - 22 pages, 11 figuresDecember 2019
- 4 articleConfining the state of light to a quantum manifold by engineered two-photon loss.Science3476224February 2015, 853-857
- 5 articleExponential suppression of bit-flips in a qubit encoded in an oscillator.Nature PhysicsMarch 2020
- 6 articleDynamically protected cat-qubits: a new paradigm for universal quantum computation.New Journal of Physics164apr 2014, 045014
- 7 articleExtending the lifetime of a quantum bit with error correction in superconducting circuits.Nature5362016, 5
- 8 articleStabilization of nonclassical states of the radiation field in a cavity by reservoir engineering.Phys. Rev. Lett.1070104022011
- 9 articleReal-time quantum feedback prepares and stabilizes photon number states.Nature4772011, 73--77
- 10 articleMagnifying quantum phase fluctuations with Cooper-pair pairing.Physical Review X122April 2022, 021002
10.2 Publications of the year
International journals
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
10.3 Cited publications
- 29 articleOn-chip single-pump interferometric Josephson isolator for quantum measurements.arXiv preprint arXiv:2006.019182020
- 30 articleStabilization of a delayed quantum system: the Photon Box case-study.IEEE Trans. Automatic Control5782012, 1918--1930
- 31 articleStability of continuous-time quantum filters with measurement imperfections.Russian Journal of Mathematical Physics212014, 297--315
- 32 articleFeedback stabilization of discrete-time quantum systems subject to non-demolition measurements with imperfections and delays.Automatica4992013, 2683--2692
- 33 bookS.S. AttalA.A. JoyeC.-A.C.-A. PilletOpen Quantum Systems III: Recent Developments.Springer, Lecture notes in Mathematics 18802006
- 34 bookQuantum Trajectories and Measurements in Continuous Time: the Diffusive Case.Springer Verlag2009
- 35 articleAn open-system quantum simulator with trapped ions.Nature4704862011
- 36 articleMechanical on-chip microwave circulator.Nature communications812017, 1--7
- 37 articleQuantum stochastic calculus and quantum nonlinear filtering.Journal of Multivariate Analysis4221992, 171--201
- 38 articleLarge Time Behavior and Convergence Rate for Quantum Filters Under Standard Non Demolition Conditions.Communications in Mathematical Physics2014, 1-21URL: http://dx.doi.org/10.1007/s00220-014-2029-6
- 39 articleExtensions of Jentzch's theorem.Trans. Amer. Math. Soc.851957, 219--227
- 40 articleEngineering stable discrete-time quantum dynamics via a canonical QR decomposition.IEEE Trans. Autom. Control552010
- 41 bookQuantum Measurements.Cambridge University Press1992
- 42 articleObserving Interferences between Past and Future Quantum States in Resonance Fluorescence.Phys. Rev. Lett.11218040218May 2014, URL: http://link.aps.org/doi/10.1103/PhysRevLett.112.180402
- 43 articlePersistent Control of a Superconducting Qubit by Stroboscopic Measurement Feedback.Phys. Rev. X30210082013
- 44 bookAn Open Systems Approach to Quantum Optics.Springer-Verlag1993
- 45 bookStatistical Methods in Quantum Optics 2: Non-Classical Fields.Spinger2007
- 46 bookApplication of Center Manifold Theory.Springer1981
- 47 articleWidely tunable on-chip microwave circulator for superconducting quantum circuits.Physical Review X742017, 041043
- 48 articleDissipation-induced continuous quantum error correction for superconducting circuits.Phys. Rev. A902014, 062344
- 49 articleWave-function approach to dissipative processes in quantum optics.Phys. Rev. Lett.6851992, 580--583
- 50 miscSuperconducting Qubits: A Short Review.arXiv:cond-mat/04111742004
- 51 articleRemote entanglement stabilization and concentration by quantum reservoir engineering.Physical Review Ahttps://arxiv.org/abs/1703.03379 - 5 pages, 4 figuresJuly 2018
- 52 articleQuantum feedback by discrete quantum non-demolition measurements: towards on-demand generation of photon-number states.Physical Review A80: 013805-0138132009
- 53 articleGeometric singular perturbation theory for ordinary differential equations.J. Diff. Equations311979, 53--98
- 54 articleCollapse and Revival of an Artificial Atom Coupled to a Structured Photonic Reservoir.arXiv preprint arXiv:2001.032402020
- 55 articleState and dynamical parameter estimation for open quantum systems.Phys. Rev. A644042105September 2001, URL: http://link.aps.org/doi/10.1103/PhysRevA.64.042105
- 56 articlePast Quantum States of a Monitored System.Phys. Rev. Lett.11116160401October 2013, URL: http://link.aps.org/doi/10.1103/PhysRevLett.111.160401
- 57 bookQuantum Noise.Springer2010
- 58 articleChecking the strict positivity of Kraus maps is NP-hard.arXiv:1402.14292014
- 59 articleThe contraction rate in Thompson's part metric of order-preserving flows on a cone - Application to generalized Riccati equations.Journal of Differential Equations2568April 2014, 2902--2948URL: http://www.sciencedirect.com/science/article/pii/S0022039614000424
- 60 articleDemonstrating a Driven Reset Protocol of a Superconducting Qubit.Phys. Rev. Lett.1101205012013
- 61 articleEncoding a qubit in an oscillator.Phys. Rev. A640123102001
- 62 articleProgressive field-state collapse and quantum non-demolition photon counting.Nature4482007, 889-893
- 63 articleThe stability of quantum Markov filters.Infin. Dimens. Anal. Quantum Probab. Relat. Top.122009, 153--172
- 64 bookExploring the Quantum: Atoms, Cavities and Photons.Oxford University Press2006
- 65 articleQuantum back-action of an individual variable-strength measurement.Science3392013, 178--181
- 66 articleSingle-photon-resolved cross-Kerr interaction for autonomous stabilization of photon-number states.Phys. Rev. Lett.1152015, 180501
- 67 bookPerturbation Theory for Linear Operators.Springer1966
- 68 articleA scheme for efficient quantum computation with linear optics.Nature409462001
- 69 articleEntanglement Generated by Dissipation and Steady State Entanglement of Two Macroscopic Objects.Phys. Rev. Lett.1070805032011
- 70 articleDeterministic protocol for mapping a qubit to coherent state superpositions in a cavity.Phys. Rev. A870423152013
- 71 articleHardware-efficient autonomous quantum memory protection.Phys. Rev. Lett.1111205012013
- 72 articleAdiabatic passage and ensemble control of quantum systems.J. Phys. B441540172011
- 73 articleStabilizing a Bell state of two superconducting qubits by dissipation engineering.Phys. Rev. A880238492013
- 74 articleEnsemble control of Bloch equations.IEEE Trans. Autom. Control542009, 528--536
- 75 articleDissipative production of a maximally entangled steady state of two quantum bits.Nature5042013, 415--418
- 76 articleCoherent quantum feedback.Phys. Rev. A620221082000
- 77 articleZero-field edge plasmons in a magnetic topological insulator.Nature communications812017, 1--7
- 78 articleConsensus for quantum networks: from symmetry to gossip iterations.IEEE Trans. Automat. Controlin press2014
- 79 conferenceStrong measurement and quantum feedback for persistent Rabi oscillations in circuit QED experiments.IEEE Conference on Decision and ControlIEEE Conference on Decision and Control2012
- 80 articleCavity-assisted quantum bath engineering.Phys. Rev. Lett.1091836022012
- 81 articleEstimation of classical parameters via continuous probing of complementary quantum observables.New Journal of Physics15121250022013, URL: http://stacks.iop.org/1367-2630/15/i=12/a=125002
- 82 articleCoherent quantum LQG control.Automatica452009, 1837--1846
- 83 articleAdaptive Quantum Nondemolition Measurement of a Photon Number.Phys. Rev. Lett.1128080401Feb 2014, URL: http://link.aps.org/doi/10.1103/PhysRevLett.112.080401
- 84 articleDemonstration of efficient nonreciprocity in a microwave optomechanical circuit.Physical Review X732017, 031001
- 85 articleMonotone Metrics on matrix spaces.Linear Algebra and its Applications2441996, 81--96
- 86 articleQuantum Reservoir Engineering with Laser Cooled Trapped Ions.Phys. Rev. Lett.77231996, 4728--4731
- 87 bookMicrowave engineering.John wiley & sons2011
- 88 articleQuantum memory with millisecond coherence in circuit QED.Physical Review B9412016, 014506
- 89 articleHilbert's projective metric in quantum information theory.Journal of Mathematical Physics528082201August 2011, URL: http://dx.doi.org/10.1063/1.3615729
- 90 articleFast reset and suppressing spontaneous emission of a superconducting qubit.Applied Physics Letters96202010, 203110
- 91 articleInitialization by measurement of a superconducting quantum bit circuit.Phys. Rev. Lett.1090505072012
- 92 articleWidely tunable, non-degenerate three-wave mixing microwave device operating near the quantum limit.Phys. Rev. Lett.1081477012012
- 93 articleFidelity is a Sub-Martingale for Discrete-Time Quantum Filters.IEEE Transactions on Automatic Control56112011, 2743--2747
- 94 articleContinuous generation and stabilization of mesoscopic field superposition states in a quantum circuit.Phys. Rev. A912015, 013810
- 95 articleStabilization of nonclassical states of one- and two-mode radiation fields by reservoir engineering.Phys. Rev. A860121142012
- 96 articleResolving photon number states in a superconducting circuit.Nature4452007, 515--518
- 97 inproceedingsConsensus in non-commutative spaces.Decision and Control (CDC), 2010 49th IEEE Conference on2010, 6596--6601
- 98 articleAutonomously stabilized entanglement between two superconducting quantum bits.Nature5042013, 419--422
- 99 articleScheme for reducing decoherence in quantum memory.Phys. Rev. A521995, 2493--2496
- 100 articleReconfigurable Josephson circulator/directional amplifier.Physical Review X542015, 041020
- 101 inproceedingsDesign and Stability of Discrete-Time Quantum Filters with Measurement Imperfections.American Control Conference2012, 5084--5089
- 102 articleApproximate stabilization of infinite dimensional quantum stochastic system.Reviews in Mathematical Physics2513500012013
- 103 articleError Correcting Codes in Quantum Theory.Phys. Rev. Lett7751996
- 104 articleTracking photon jumps with repeated quantum non-demolition parity measurements.Nature5112014, 444--448
- 105 articleReverse isolation and backaction of the SLUG microwave amplifier.Physical Review Applied852017, 054007
- 106 articleProblems in decentralized decision making and computation.PhD Thesis, MIT1984
- 107 articleStabilizing Rabi oscillations in a superconducting qubit using quantum feedback.Nature4902012, 77--80
- 108 articleHall effect gyrators and circulators.Physical Review X422014, 021019
- 109 articleDynamical decoupling of open quantum system.Phys. Rev. Lett.821999, 2417-2421
- 110 articleDeterministically encoding quantum information using 100-photon Schrödinger cat states.Science3422013, 607--610
- 111 articleField locked to Fock state by quantum feedback with single photon corrections.Physical Review Letter1082436022012

