Keywords
Computer Science and Digital Science
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.6. Optimization
- A8.2. Optimization
- A8.9. Performance evaluation
Other Research Topics and Application Domains
- B4.3. Renewable energy production
- B5.2. Design and manufacturing
1 Team members, visitors, external collaborators
Research Scientists
- Anne Auger [Team leader, INRIA, Senior Researcher, HDR]
- Dimo Brockhoff [INRIA, Researcher]
- Nikolaus Hansen [INRIA, Senior Researcher, HDR]
PhD Students
- Paul Dufossé [Thales, Cifre PhD]
- Mohamed Gharafi [Inria]
- Armand Gissler [LIX]
- Eugénie Marescaux [Ecole Polytechnique, until Nov 2022]
Administrative Assistants
- Marie Enee [INRIA]
- Julienne Moukalou [Inria, from May 2022]
2 Overall objectives
2.1 Scientific Context
Critical problems of the 21st century like the search for highly energy efficient or even carbon-neutral, and cost-efficient systems, or the design of new molecules against extensively drug-resistant bacteria crucially rely on the resolution of challenging numerical optimization problems. Such problems typically depend on noisy experimental data or involve complex numerical simulations where derivatives are not useful or not available and the function is considered as a black-box.
Many of those optimization problems are in essence multiobjective—one needs to optimize simultaneously several conflicting objectives like minimizing the cost of an energy network and maximizing its reliability—and most of the challenging black-box problems are non-convex and non-smooth and they combine difficulties related to ill-conditioning, non-separability, and ruggedness (a term that characterizes functions that can be non-smooth but also noisy or multi-modal). Additionally, the objective function can be expensive to evaluate, that is, one function evaluation can take several minutes to hours (it can involve for instance a CFD simulation).
In this context, the use of randomness combined with proper adaptive mechanisms that notably satisfy certain invariance properties (affine invariance, invariance to monotonic transformations) has proven to be one key component for the design of robust global numerical optimization algorithms 54, 39.
The field of adaptive stochastic optimization algorithms has witnessed some important progress over the past 15 years. On the one hand, subdomains like medium-scale unconstrained optimization may be considered as “solved” (particularly, the CMA-ES algorithm, an instance of Evolution Strategy (ES) algorithms, stands out as state-of-the-art method) and considerably better standards have been established in the way benchmarking and experimentation are performed. On the other hand, multiobjective population-based stochastic algorithms became the method of choice to address multiobjective problems when a set of some best possible compromises is sought after. In all cases, the resulting algorithms have been naturally transferred to industry (the CMA-ES algorithm is now regularly used in companies such as Bosch, Total, ALSTOM, ...) or to other academic domains where difficult problems need to be solved such as physics, biology 59, geoscience 47, or robotics 50).
ES algorithms also attracted quite some attention in Machine Learning with the OpenAI article Evolution Strategies as a Scalable Alternative to Reinforcement Learning. It is shown that the training time for difficult reinforcement learning benchmarks could be reduced from 1 day (with standard RL approaches) to 1 hour using ES 56.1 Already ten years ago, another impressive application of CMA-ES, how “Computer Sim Teaches Itself To Walk Upright” (published at the conference SIGGRAPH Asia 2013) was presented in the press in the UK.
Several of these important advances around adaptive stochastic optimization algorithms rely to a great extent on works initiated or achieved by the founding members of RandOpt, particularly related to the CMA-ES algorithm and to the Comparing Continuous Optimizer (COCO) benchmarking platform.
Yet, the field of adaptive stochastic algorithms for black-box optimization is relatively young compared to the “classical optimization” field that includes convex and gradient-based optimization. For instance, the state-of-the art algorithms for unconstrained gradient based optimization like quasi-Newton methods (e.g. the BFGS method) date from the 1970s 38 while the stochastic derivative-free counterpart, CMA-ES dates from the early 2000s 40. Consequently, in some subdomains with important practical demands, not even the most fundamental and basic questions are answered:
- This is the case of constrained optimization where one needs to find a solution minimizing a numerical function while respecting a number of constraints typically formulated as for . Only somewhat recently, the fundamental requirement of linear convergence2, as in the unconstrained case, has been clearly stated 30.
- In multiobjective optimization, most of the research so far has been focusing on how to select candidate solutions from one iteration to the next one. The difficult question of how to generate effectively new solutions is not yet answered in a proper way and we know today that simply applying operators from single-objective optimization may not be effective with the current best selection strategies. As a comparison, in the single-objective case, the question of selection of candidate solutions was already solved in the 1980s and 15 more years were needed to solve the trickier question of an effective adaptive strategy to generate new solutions.
- With the current demand to solve larger and larger optimization problems (e.g. in the domain of deep learning), optimization algorithms that scale linearly (in terms of internal complexity, memory and number of function evaluations to reach an -ball around the optimum) with the problem dimension are nowadays in increasing demand. Not long ago, first proposals of how to reduce the quadratic scaling of CMA-ES have been made without a clear view of what can be achieved in the best case in practice. These later variants apply to optimization problems with thousands of variables. The question of designing randomized algorithms capable to handle problems with one or two orders of magnitude more variables effectively and efficiently is still largely open.
- For expensive optimization, standard methods are so called Bayesian optimization (BO) algorithms often based on Gaussian processes. Commonly used examples of BO algorithms are EGO 44, SMAC 42, Spearmint 57, or TPE 33 which are implemented in different libraries. Yet, our experience with a popular method like EGO is that many important aspects to come up with a good implementation rely on insider knowledge and are not standard across implementations. Two EGO implementations can differ for example in how they perform the initial design, which bandwidth for the Gaussian kernel is used, or which strategy is taken to optimize the expected improvement.
Additionally, the development of stochastic adaptive methods for black-box optimization has been mainly driven by heuristics and practice—rather than a general theoretical framework—validated by intensive computational simulations. Undoubtedly, this has been an asset as the scope of possibilities for design was not restricted by mathematical frameworks for proving convergence. In effect, powerful stochastic adaptive algorithms for unconstrained optimization like the CMA-ES algorithm emerged from this approach. At the same time, naturally, theory strongly lags behind practice. For instance, the striking performances of CMA-ES empirically observed contrast with how little is theoretically proven on the method. This situation is clearly not satisfactory. On the one hand, theory generally lifts performance assessment from an empirical level to a conceptual one, rendering results independent from the problem instances where they have been obtained. On the other hand, theory typically provides insights that change perspectives on some algorithm components. Also theoretical guarantees generally increase the trust in the reliability of a method and facilitate the task to make it accepted by wider communities.
Finally, as discussed above, the development of novel black-box algorithms strongly relies on scientific experimentation, and it is quite difficult to conduct proper and meaningful experimental analysis. This is well known for more than two decades now and summarized in this quote from Johnson in 1996
“the field of experimental analysis is fraught with pitfalls. In many ways, the implementation of an algorithm is the easy part. The hard part is successfully using that implementation to produce meaningful and valuable (and publishable!) research results.” 43
Since then, quite some progress has been made to set better standards in conducting scientific experiments and benchmarking. Yet, some domains still suffer from poor benchmarking standards and from the generic problem of the lack of reproducibility of results. For instance, in multiobjective optimization, it is (still) not rare to see comparisons between algorithms made by solely visually inspecting Pareto fronts after a fixed budget. In Bayesian optimization, good performance seems often to be due to insider knowledge not always well described in papers.
In the context of black-box numerical optimization previously described, the scientific positioning of the RandOpt ream is at the intersection between theory, algorithm design, and applications. Our vision is that the field of stochastic black-box optimization should reach the same level of maturity than gradient-based convex mathematical optimization. This entails major algorithmic developments for constrained, multiobjective and large-scale black-box optimization and major theoretical developments for analyzing current methods including the state-of-the-art CMA-ES.
The specificity in black-box optimization is that methods are intended to solve problems characterized by "non-properties"—non-linear, non-convex, non-smooth, non-Lipschitz. This contrasts with gradient-based optimization and poses on the one hand some challenges when developing theoretical frameworks but also makes it compulsory to complement theory with empirical investigations.
On the practical side, our ultimate goal is to provide software that is suitable for researchers and industry that need to solve practical optimization problems. We see theory also as a means for this end (rather than only an end in itself) and we also firmly belief that parameter tuning is part of the algorithm designer's task.
This shapes, on the one hand, four main scientific objectives for our team:
- develop novel theoretical frameworks for guiding (a) the design of novel black-box methods and (b) their analysis, allowing to
- provide proofs of key features of stochastic adaptive algorithms including the state-of-the-art method CMA-ES: linear convergence and learning of second order information.
- develop stochastic numerical black-box algorithms following a principled design in domains with a strong practical need for much better methods namely constrained, multiobjective, large-scale and expensive optimization. Implement the methods such that they are easy to use. And finally, to
- set new standards in scientific experimentation, performance assessment and benchmarking both for optimization on continuous or combinatorial search spaces. This should allow in particular to advance the state of reproducibility of results of scientific papers in optimization.
On the other hand, the above motivates our objectives with respect to dissemination and transfer:
- develop software packages that people can directly use to solve their problems. This means having carefully thought out interfaces, generically applicable setting of parameters and termination conditions, proper treatment of numerical errors, catching properly various exceptions, etc.;
- have direct collaborations with industrials;
- publish our results both in applied mathematics and computer science bridging the gap between very often disjoint communities.
3 Research program
The lines of research we intend to pursue is organized along four axes namely developing novel theoretical framework, developing novel algorithms, setting novel standards in scientific experimentation and benchmarking and applications.
3.1 Developing Novel Theoretical Frameworks for Analyzing and Designing Adaptive Stochastic Algorithms
Stochastic black-box algorithms typically optimize non-convex, non-smooth functions. This is possible because the algorithms rely on weak mathematical properties of the underlying functions: the algorithms do not use the derivatives—hence the function does not need to be differentiable—and, additionally, often do not use the exact function value but instead how the objective function ranks candidate solutions (such methods are sometimes called function-value-free). (To illustrate a comparison-based update, consider an algorithm that samples (with an even integer) candidate solutions from a multivariate normal distribution. Let in denote those candidate solutions at a given iteration. The solutions are evaluated on the function to be minimized and ranked from the best to the worse:
In the previous equation denotes the index of the sampled solution associated to the -th best solution. The new mean of the Gaussian vector from which new solutions will be sampled at the next iteration can be updated as
The previous update moves the mean towards the best solutions. Yet the update is only based on the ranking of the candidate solutions such that the update is the same if is optimized or where is strictly increasing. Consequently, such algorithms are invariant with respect to strictly increasing transformations of the objective function. This entails that they are robust and their performances generalize well.)
Additionally, adaptive stochastic optimization algorithms typically have a complex state space which encodes the parameters of a probability distribution (e.g. mean and covariance matrix of a Gaussian vector) and other state vectors. This state-space is a manifold. While the algorithms are Markov chains, the complexity of the state-space makes that standard Markov chain theory tools do not directly apply. The same holds with tools stemming from stochastic approximation theory or Ordinary Differential Equation (ODE) theory where it is usually assumed that the underlying ODE (obtained by proper averaging and limit for learning rate to zero) has its critical points inside the search space. In contrast, in the cases we are interested in, the critical points of the ODEs are at the boundary of the domain.
Last, since we aim at developing theory that on the one hand allows to analyze the main properties of state-of-the-art methods and on the other hand is useful for algorithm design, we need to be careful not to use simplifications that would allow a proof to be done but would not capture the important properties of the algorithms. With that respect one tricky point is to develop theory that accounts for invariance properties.
To face those specific challenges, we need to develop novel theoretical frameworks exploiting invariance properties and accounting for peculiar state-spaces. Those frameworks should allow researchers to analyze one of the core properties of adaptive stochastic methods, namely linear convergence on the widest possible class of functions.
We are planning to approach the question of linear convergence from three different complementary angles, using three different frameworks:
- the Markov chain framework where the convergence derives from the analysis of the stability of a normalized Markov chain existing on scaling-invariant functions for translation and scale-invariant algorithms 32. This framework allows for a fine analysis where the exact convergence rate can be given as an implicit function of the invariant measure of the normalized Markov chain. Yet it requires the objective function to be scaling-invariant. The stability analysis can be particularly tricky as the Markov chain that needs to be studied writes as where are independent identically distributed and is typically discontinuous because the algorithms studied are comparison-based. This implies that practical tools for analyzing a standard property like irreducibility, that rely on investigating the stability of underlying deterministic control models 51, cannot be used. Additionally, the construction of a drift to prove ergodicity is particularly delicate when the state space includes a (normalized) covariance matrix as it is the case for analyzing the CMA-ES algorithm.
- The stochastic approximation or ODE framework. Those are standard techniques to prove the convergence of stochastic algorithms when an algorithm can be expressed as a stochastic approximation of the solution of a mean field ODE 35, 34, 48. What is specific and induces difficulties for the algorithms we aim at analyzing is the non-standard state-space since the ODE variables correspond to the state-variables of the algorithm (e.g. for step-size adaptive algorithms, where denotes the set of positive definite matrices if a covariance matrix is additionally adapted). Consequently, the ODE can have many critical points at the boundary of its definition domain (e.g. all points corresponding to are critical points of the ODE) which is not typical. Also we aim at proving linear convergence, for that it is crucial that the learning rate does not decrease to zero which is non-standard in ODE method.
- The direct framework where we construct a global Lyapunov function for the original algorithm from which we deduce bounds on the hitting time to reach an -ball of the optimum. For this framework as for the ODE framework, we expect that the class of functions where we can prove linear convergence are composite of where is differentiable and is strictly increasing and that we can show convergence to a local minimum.
We expect those frameworks to be complementary in the sense that the assumptions required are different. Typically, the ODE framework should allow for proofs under the assumptions that learning rates are small enough while it is not needed for the Markov chain framework. Hence this latter framework captures better the real dynamics of the algorithm, yet under the assumption of scaling-invariance of the objective functions. Also, we expect some overlap in terms of function classes that can be studied by the different frameworks (typically convex-quadratic functions should be encompassed in the three frameworks). By studying the different frameworks in parallel, we expect to gain synergies and possibly understand what is the most promising approach for solving the holy grail question of the linear convergence of CMA-ES. We foresee for instance that similar approaches like the use of Foster-Lyapunov drift conditions are needed in all the frameworks and that intuition can be gained on how to establish the conditions from one framework to another one.
3.2 Algorithmic developments
We are planning on developing algorithms in the subdomains with strong practical demand for better methods of constrained, multiobjective, large-scale and expensive optimization.
Many of the algorithm developments, we propose, rely on the CMA-ES method. While this seems to restrict our possibilities, we want to emphasize that CMA-ES became a family of methods over the years that nowadays include various techniques and developments from the literature to handle non-standard optimization problems (noisy, large-scale, ...). The core idea of all CMA-ES variants—namely the mechanism to adapt a Gaussian distribution—has furthermore been shown to derive naturally from first principles with only minimal assumptions in the context of derivative-free black-box stochastic optimization 54, 39. This is a strong justification for relying on the CMA-ES premises while new developments naturally include new techniques typically borrowed from other fields. While CMA-ES is now a full family of methods, for visibility reasons, we continue to refer often to “the CMA-ES algorithm”.
3.2.1 Constrained optimization
Many (real-world) optimization problems have constraints related to technical feasibility, cost, etc. Constraints are classically handled in the black-box setting either via rejection of solutions violating the constraints—which can be quite costly and even lead to quasi-infinite loops—or by penalization with respect to the distance to the feasible domain (if this information can be extracted) or with respect to the constraint function value 36. However, the penalization coefficient is a sensitive parameter that needs to be adapted in order to achieve a robust and general method 37. Yet, the question of how to handle properly constraints is largely unsolved. Previous constraints handling for CMA-ES were ad-hoc techniques driven by many heuristics 37. Also, only somewhat recently it was pointed out that linear convergence properties should be preserved when addressing constraint problems 30.
Promising approaches though, rely on using augmented Lagrangians 30, 31. The augmented Lagrangian, here, is the objective function optimized by the algorithm. Yet, it depends on coefficients that are adapted online. The adaptation of those coefficients is the difficult part: the algorithm should be stable and the adaptation efficient. We believe that the theoretical frameworks developed (particularly the Markov chain framework) will be useful to understand how to design the adaptation mechanisms. Additionally, the question of invariance will also be at the core of the design of the methods: augmented Lagrangian approaches break the invariance to monotonic transformation of the objective functions, yet understanding the maximal invariance that can be achieved seems to be an important step towards understanding what adaptation rules should satisfy.
3.2.2 Large-scale Optimization
In the large-scale setting, we are interested to optimize problems with the order of to variables. For one to two orders of magnitude more variables, we will talk about a “very large-scale” setting.
In this context, algorithms with a quadratic scaling (internal and in terms of number of function evaluations needed to optimize the problem) cannot be afforded. In CMA-ES-type algorithms, we typically need to restrict the model of the covariance matrix to have only a linear number of parameters to learn such that the algorithms scale linearly in terms of internal complexity, memory and number of function evaluations to solve the problem. The main challenge is thus to have rich enough models for which we can efficiently design proper adaptation mechanisms. Some first large-scale variants of CMA-ES have been derived. They include the online adaptation of the complexity of the model 29, 28. Yet, the type of Hessian matrices they can learn is restricted and not fully satisfactory. Different restricted families of distributions are conceivable and it is an open question which can be effectively learned and which are the most promising in practice.
Another direction, we want to pursue, is exploring the use of large-scale variants of CMA-ES to solve reinforcement learning problems 56.
Last, we are interested to investigate the very-large-scale setting. One approach consists in doing optimization in subspaces. This entails the efficient identification of relevant spaces and the restriction of the optimization to those subspaces.
3.2.3 Multiobjective Optimization
Multiobjective optimization, i.e., the simultaneous optimization of multiple objective functions, differs from single-objective optimization in particular in its optimization goal. Instead of aiming at converging to the solution with the best possible function value, in multiobjective optimization, a set of solutions 3 is sought. This set, called Pareto-set, contains all trade-off solutions in the sense of Pareto-optimality—no solution exists that is better in all objectives than a Pareto-optimal one. Because converging towards a set differs from converging to a single solution, it is no surprise that we might lose many good convergence properties if we directly apply search operators from single-objective methods. However, this is what has typically been done so far in the literature. Indeed, most of the research in stochastic algorithms for multiobjective optimization focused instead on the so called selection part, that decides which solutions should be kept during the optimization—a question that can be considered as solved for many years in the case of single-objective stochastic adaptive methods.
We therefore aim at rethinking search operators and adaptive mechanisms to improve existing methods. We expect that we can obtain orders of magnitude better convergence rates for certain problem types if we choose the right search operators. We typically see two angles of attack: On the one hand, we will study methods based on scalarizing functions that transform the multiobjective problem into a set of single-objective problems. Those single-objective problems can then be solved with state-of-the-art single-objective algorithms. Classical methods for multiobjective optimization fall into this category, but they all solve multiple single-objective problems subsequently (from scratch) instead of dynamically changing the scalarizing function during the search. On the other hand, we will improve on currently available population-based methods such as the first multiobjective versions of the CMA-ES. Here, research is needed on an even more fundamental level such as trying to understand success probabilities observed during an optimization run or how we can introduce non-elitist selection (the state of the art in single-objective stochastic adaptive algorithms) to increase robustness regarding noisy evaluations or multi-modality. The challenge here, compared to single-objective algorithms, is that the quality of a solution is not anymore independent from other sampled solutions, but can potentially depend on all known solutions (in the case of three or more objective functions), resulting in a more noisy evaluation as the relatively simple function-value-based ranking within single-objective optimizers.
3.2.4 Expensive Optimization
In the so-called expensive optimization scenario, a single function evaluation might take several minutes or even hours in a practical setting. Hence, the available budget in terms of number of function evaluation calls to find a solution is very limited in practice. To tackle such expensive optimization problems, it is needed to exploit the first few function evaluations in the best way. To this end, typical methods couple the learning of a surrogate (or meta-model) of the expensive objective function with traditional optimization algorithms.
In the context of expensive optimization and CMA-ES, which usually shows its full potential when the number of variables is not too small (say larger than 3) and if the number of available function evaluations is about or larger, several research directions emerge. The two main possibilities to integrate meta-models into the search with CMA-ES type algorithms are (i) the successive injection of the minimum of a learned meta-model at each time step into the learning of CMA-ES's covariance matrix and (ii) the use of a meta-model to predict the internal ranking of solutions. While for the latter, first results exist, the former idea is entirely unexplored for now. In both cases, a fundamental question is which type of meta-model (linear, quadratic, Gaussian Process, ...) is the best choice for a given number of function evaluations (as low as one or two function evaluations) and at which time the type of the meta-model shall be switched.
3.3 Setting novel standards in scientific experimentation and benchmarking
Numerical experimentation is needed as a complement to theory to test novel ideas, hypotheses, the stability of an algorithm, and/or to obtain quantitative estimates. Optimally, theory and experimentation go hand in hand, jointly guiding the understanding of the mechanisms underlying optimization algorithms. Though performing numerical experimentation on optimization algorithms is crucial and a common task, it is non-trivial and easy to fall in (common) pitfalls as stated by J. N. Hooker in his seminal paper 41.
In the RandOpt team we aim at raising the standards for both scientific experimentation and benchmarking.
On the experimentation aspect, we are convinced that there is common ground over how scientific experimentation should be done across many (sub-)domains of optimization, in particular with respect to the visualization of results, testing extreme scenarios (parameter settings, initial conditions, etc.), how to conduct understandable and small experiments, how to account for invariance properties, performing scaling up experiments and so forth. We therefore want to formalize and generalize these ideas in order to make them known to the entire optimization community with the final aim that they become standards for experimental research.
Extensive numerical benchmarking, on the other hand, is a compulsory task for evaluating and comparing the performance of algorithms. It puts algorithms to a standardized test and allows to make recommendations which algorithms should be used preferably in practice. To ease this part of optimization research, we have been developing the Comparing Continuous Optimizers platform (COCO) since 2007 which allows to automatize the tedious task of benchmarking. It is a game changer in the sense that the freed time can now be spent on the scientific part of algorithm design (instead of implementing the experiments, visualization, statistical tests, etc.) and it opened novel perspectives in algorithm testing. COCO implements a thorough, well-documented methodology that is based on the above mentioned general principles for scientific experimentation.
Also due to the freely available data from 300+ algorithms benchmarked with the platform, COCO became a quasi-standard for single-objective, noiseless optimization benchmarking. It is therefore natural to extend the reach of COCO towards other subdomains (particularly constrained optimization, many-objective optimization) which can benefit greatly from an automated benchmarking methodology and standardized tests without (much) effort. This entails particularly the design of novel test suites and rethinking the methodology for measuring performance and more generally evaluating the algorithms. Particularly challenging is the design of scalable non-trivial testbeds for constrained optimization where one can still control where the solutions lies. Other optimization problem types, we are targeting are expensive problems (and the Bayesian optimization community in particular, see our AESOP project), optimization problems in machine learning (for example parameter tuning in reinforcement learning), and the collection of real-world problems from industry.
Another aspect of our future research on benchmarking is to investigate the large amounts of benchmarking data, we collected with COCO during the years. Extracting information about the influence of algorithms on the best performing portfolio, clustering algorithms of similar performance, or the automated detection of anomalies in terms of good/bad behavior of algorithms on a subset of the functions or dimensions are some of the ideas here.
Last, we want to expand the focus of COCO from automatized (large) benchmarking experiments towards everyday experimentation, for example by allowing the user to visually investigate algorithm internals on the fly or by simplifying the set up of algorithm parameter influence studies.
4 Application domains
Applications of black-box algorithms occur in various domains. Industry but also researchers in other academic domains have a great need to apply black-box algorithms on a daily basis. Generally, we do not target a specific application domain and are interested in black-box applications stemming from various origins. This is to us intrinsic to the nature of the methods we develop that are general purpose algorithms. Hence our strategy with respect to applications can be considered as opportunistic and our main selection criteria when approached by colleagues who want to develop a collaboration around an application is whether we find the application interesting and valuable: that means the application brings new challenges and/or gives us the opportunity to work on topics we already intended to work on, and it brings, in our judgement, an advancement to society in the application domain.
The concrete applications related to industrial collaborations we are currently dealing with are:
- With Thales for the theses of Konstantinos Varelas and Paul Dufossé (DGA-CIFRE theses) related to the design of radars (shape optimization of the wave form). They investigate more specifically the development of large-scale variants of CMA-ES and constrained-handling for CMA-ES, respectively.
- With Storengy, a subsidiary of the ENGIE group, specialized in gas storage for the theses of Cheikh Touré and Mohamed Gharafi. Different multiobjective applications are considered in this context but the primary motivation of Storengy is to get at their disposal a better multiobjective variant of CMA-ES which is the main objective of the developments within the theses.
5 Social and environmental responsibility
5.1 Footprint of research activities
We are concerned about CO2 footprint and discourage oversea conferences when far away. After the situation with respect to Covid went back to normal with respect to be able to travel, we are still dedicated to travel less than in the past and attend some conferences online.
5.2 Impact of research results
We develop general purpose optimization methods that apply in difficult optimization contexts where little is required on the function to be optimized. Application domains include optimization and design of renewable systems and climate change.
Our main method CMA-ES is transferred and widely used. The code stemming from the team is frequently downloaded (see Section 7). Among the usage of our method and our code, we find naturally problems in the domain of energy to capture carbon dioxide 52, 49, 53, solar energy 45, 46, or wind-thermal power systems 55.
Those publications witness the impact of our research results with respect to research questions and engineering design related to climate change and renewable energy.
6 Highlights of the year
- Publication in three major venues in applied mathematics (SIAM Journal on Optimization, Stochastic Processes and their Applications, Journal of Global Optimization) of important results on the theory of Evolution Strategies and mathematical methodology (ODE method) to analyze Evolution Strategies: 13, 14, 17.
- Release of the first constraint test suite of the COCO platform.
7 New software and platforms
The RandOpt team maintains and further develops the two software libraries, CMA-ES and COCO, with more than 300 commits in 2022.
As an indicator of the impact of the libraries, Figure 1 shows weekly downloads from the Python Package Index (PyPI) since the second half of 2021 of software packages developed by the RandOpt team and of the cmaes package developed by Masashi Shibata (the package is directly derived from RandOpt's cma package but more tailored to machine learning applications). The cma module has currently about 30–40,000 weekly downloads, the cmaes module over 300,000.
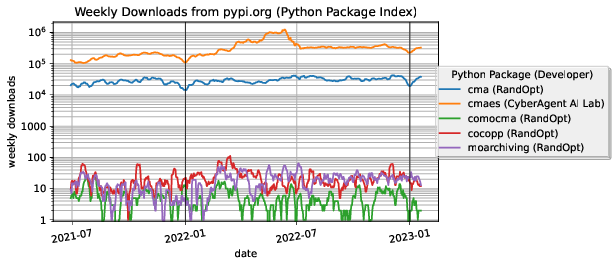
Downloads of five packages, cma, cmaes, comocma, cocopp and morarchiving over time since mid 2021
Weekly downloads from PyPI of RandOpt related Python software packages since mid 2021.
Comparing the second half of 2022 with the second half of the year before, we find an increase of 28% for the cma module which was downloaded more than 1.6 million times in 2022. Overall, the packages developed by the team have been downloaded more than 3.8 million times from PyPI.
7.1 New software
7.1.1 COCO
-
Name:
COmparing Continuous Optimizers
-
Keywords:
Benchmarking, Numerical optimization, Black-box optimization, Stochastic optimization
-
Scientific Description:
COmparing Continuous Optimisers (COCO) is a tool for benchmarking algorithms for black-box optimisation. COCO facilitates systematic experimentation in the field of continuous optimization. COCO provides: (1) an experimental framework for testing the algorithms, (2) post-processing facilities for generating publication quality figures and tables, including the easy integration of data from benchmarking experiments of 300+ algorithm variants, (3) LaTeX templates for scientific articles and HTML overview pages which present the figures and tables.
The COCO software is composed of two parts: (i) an interface available in different programming languages (C/C++, Java, Matlab/Octave, Python, external support for R) which allows to run and log experiments on several function test suites (unbounded noisy and noiseless single-objective functions, unbounded noiseless multiobjective problems, mixed-integer problems, constrained problems) and (ii) a Python tool for generating figures and tables that can be looked at in every web browser and that can be used in the provided LaTeX templates to write scientific papers.
-
Functional Description:
The COCO platform aims at supporting the numerical benchmarking of blackbox optimization algorithms in continuous domains. Benchmarking is a vital part of algorithm engineering and a necessary path to recommend algorithms for practical applications. The COCO platform releases algorithm developers and practitioners alike from (re-)writing test functions, logging, and plotting facilities by providing an easy-to-handle interface in several programming languages. The COCO platform has been developed since 2007 and has been used extensively within the “Blackbox Optimization Benchmarking (BBOB)” workshop series since 2009. Overall, 300+ algorithms and algorithm variants by contributors from all over the world have been benchmarked on the platform's supported test suites so far. The most recent extensions have been towards large-scale as well as mixed-integer problems.
- URL:
-
Contact:
Dimo Brockhoff
-
Participants:
Anne Auger, Asma Atamna, Dejan Tusar, Dimo Brockhoff, Marc Schoenauer, Nikolaus Hansen, Ouassim Ait Elhara, Raymond Ros, Tea Tusar, Thanh-Do Tran, Umut Batu, Konstantinos Varelas
-
Partners:
Charles University Prague, Jozef Stefan Institute (JSI)
7.1.2 CMA-ES
-
Name:
Covariance Matrix Adaptation Evolution Strategy
-
Keywords:
Numerical optimization, Black-box optimization, Stochastic optimization
-
Scientific Description:
The CMA-ES is considered as state-of-the-art in evolutionary computation and has been adopted as one of the standard tools for continuous optimisation in many (probably hundreds of) research labs and industrial environments around the world. The CMA-ES is typically applied to unconstrained or bound-constrained optimization problems and search space dimension between three and a few hundred. Recent versions can also handle nonlinear constraints. The method should be applied, if derivative based methods, e.g. quasi-Newton BFGS or conjugate gradient, (supposedly) fail due to a rugged search landscape, e.g. discontinuities, sharp bends or ridges, noise, local optima, outliers. If second order derivative based methods are successful, they are usually much faster than the CMA-ES: on purely convex-quadratic functions, BFGS (Matlabs function fminunc) is typically faster by a factor of about ten (in number of objective function evaluations assuming that gradients are not available) and on the most simple quadratic functions by a factor of about 30.
-
Functional Description:
The CMA-ES is an evolutionary algorithm for difficult non-linear non-convex black-box optimisation problems in continuous domain.
- URL:
-
Contact:
Nikolaus Hansen
-
Participant:
Nikolaus Hansen
7.1.3 COMO-CMA-ES
-
Name:
Comma Multi-Objective Covariance Matrix Adaptation Evolution Strategy
-
Keywords:
Black-box optimization, Global optimization, Multi-objective optimisation
-
Scientific Description:
The CMA-ES is considered as state-of-the-art in evolutionary computation and has been adopted as one of the standard tools for continuous optimisation in many (probably hundreds of) research labs and industrial environments around the world. The CMA-ES is typically applied to unconstrained or bounded constraint optimization problems, and search space dimensions between three and a hundred. COMO-CMA-ES is a multi-objective optimization algorithm based on the standard CMA-ES using the Uncrowded Hypervolume Improvement within the so-called Sofomore framework.
-
Functional Description:
The COMO-CMA-ES is an evolutionary algorithm for difficult non-linear non-convex black-box optimisation problems with several (two) objectives in continuous domain.
- URL:
-
Contact:
Nikolaus Hansen
7.1.4 MOarchiving
-
Name:
Multiobjective Optimization Archiving Module
-
Keywords:
Mathematical Optimization, Multi-objective optimisation
-
Scientific Description:
Multi-objective optimization relies on the maintenance of a set of non-dominated (and hence incomparable) solutions. Performance indicator computations and in particular the computation of the hypervolume indicator is based on this solution set. The hypervolume computation and the update of the set of non-dominated solutions are generally time critical operations. The module computes the bi-objective hypervolume in linear time and updates the non-dominated solution set in logarithmic time.
-
Functional Description:
The module implements a bi-objective non-dominated archive using a Python list as parent class. The main functionality is heavily based on the bisect module. The class provides easy and fast access to the overall hypervolume, the contributing hypervolume of each element, and to the uncrowded hypervolume improvement of any given point in objective space.
- URL:
-
Contact:
Nikolaus Hansen
8 New results
8.1 Analysis of Adaptive Stochastic Search Algorithms
Participants: Anne Auger, Nikolaus Hansen, Cheikh Touré, Armand Gissler.
External collaborators: Youhei Akimoto (Tsukuba University), Tobias Glasmachers (Ruhr University, Bochum)
We published the article where we prove the global linear convergence of the (1+1)-ES with one-fifth success rule as step-size adaptation on a class of functions that embed smooth strongly convex functions and positively homogeneous functions. Because of the invariance to monotonic transformations, the study holds for non-continuous and non-convex functions. Arguably, our study provides the first proof of the linear convergence of an adaptive evolution strategy without modifying its underlying updates (to make a proof work) on such a wide class of functions 13.
We have analyzed the linear convergence of a step-size adaptive -ES on continuously differentiable scaling invariant functions 17. The study constitutes the first convergence analysis of this class of algorithm which is the underlying algorithmic scheme of the CMA-ES algorithms while we assume here only step-size adaptation. This study has been using the methodology based on Markov chain that we have been developing. We published our research on extending ODE theory (that connects convergence of a stochastic algorithm to the statility of an underlying ODE obtained when taking the limit for learning rate to zero) in order to prove the geometric convergence of an algorithm 14. We illustrate how to apply the theory to prove the linear convergence of a step-size adaptive ES.
We investigated theoretically and numerically the possible benefit of adapting the learning rate on the mean in adaptive Evolution Strategies 20, 27. We quantified in particular convergence rates under the assumption of optimal learning rate.
8.2 Multi-objective optimization
Participants: Eugénie Marescaux, Anne Auger, Dimo Brockhoff, Nikolaus Hansen.
Motivated by the incremental version of the previously designed COMO-CMA-ES algorithm 58 in order to obtain an algorithm that converges to the entire Pareto front, Eugénie Marescaux in her thesis studied the convergence of the ensuing solver from a theoretical standpoint 22. It was then proven, under the assumption of perfect single-objective search and convex, bilipschitz Pareto front, that the algorithm converges towards the entire Pareto front 23. In addition the best possible algorithm decreases the hypervolume gap in the order of after meta-iterations of optimal search.8.3 Benchmarking: methodology and the Comparing Continuous Optimziers Platform (COCO)
Participants: Anne Auger, Dimo Brockhoff, Paul Dufossé, Nikolaus Hansen.
External collaborators: Olaf Mersmann (TH Köln), Tea Tušar (Jozef Stefan Institute)
Benchmarking is an important task in optimization in order to assess and compare the performance of algorithms as well as to motivate the design of better solvers. We are leading the benchmarking of derivative free solvers in the context of difficult problems: we have been developing methodologies and testbeds as well as assembled this into a platform automatizing the benchmarking process. This is a continuing effort that we are pursuing in the team.
The COCO platform, developed at Inria first in the TAO team and then in Randopt since 2007, aims at automatizing numerical benchmarking experiments and the visual presentation of their results. The platform consists of an experimental part to generate benchmarking data (in various programming languages) and a postprocessing module (in python), see Figure 2. At the interface between the two, we provide data sets from numerical experiments of 300+ algorithms and algorithm variants from various fields (quasi-Newton, derivative-free optimization, evolutionary computing, Bayesian optimization) and for various problem characteristics (noiseless/noisy optimization, single-/multi-objective optimization, continuous/mixed-integer, ...).
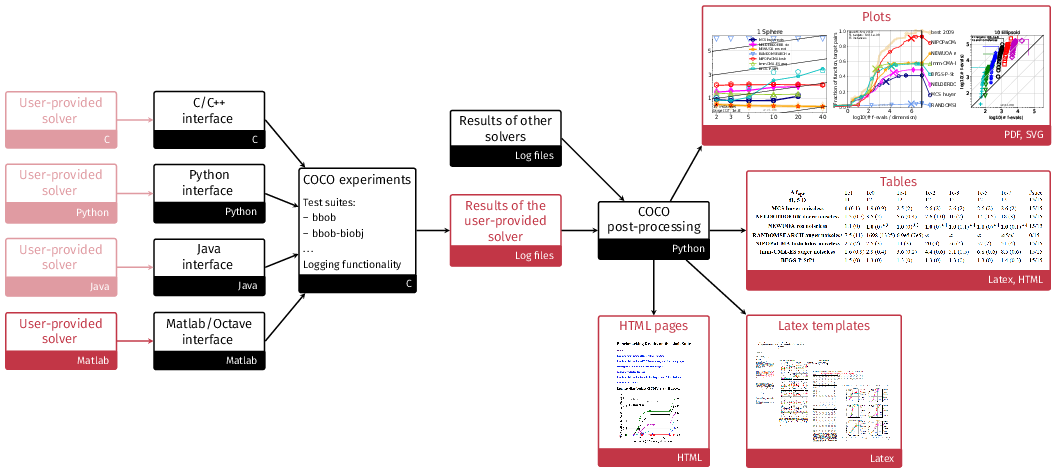
Visual overview of the COCO platform
Structural overview of the COCO platform. COCO provides all black parts while users only have to connect their solver to the COCO interface in the language of interest, here for instance Matlab, and to decide on the test suite the solver should run on. The other red components show the output of the experiments (number of function evaluations to reach certain target precisions) and their post-processing and are automatically generated.
We have been using the platform in the past to initiate workshop papers during the ACM-GECCO conference as well as to collect algorithm data sets from the entire optimization community (300+ so far over the different test suites). The next workshop in this series is going to take place in 2023 and we also held a workshop in 2022.
In this context, we constantly improve and extend the software and provide additional data from benchmarking experiments. In 2022, 14 new data sets on the existing test suites have been collected from the BBOB-2022 participants and 6 through continuous submissions. All of which are available via the COCO postprocessing module. Our own contribution was a comparison of diagonal decoding versions of CMA-ES 19.
After several years of development, we released the first constrained test suite 21 for COCO in 2022 and used it for the BBOB-2022 workshop. Overall, 9 data sets have been collected so far on this new test suite. We contributed by comparing different versions of the augmented Lagrangian version of CMA-ES 18.
Journal articles describing the bbob-biobj test suite 15 and the general performance assessment methodology within COCO 16 have been published in 2022, too.
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
- Contract with the company Storengy funding the PhD thesis of Mohamed Gharafi in the context of the CIROQUO project (2021–2024)
- Contract with Thales for the CIFRE PhD thesis of Paul Dufossé (2018–2022)
- Contract with Thales for the CIFRE PhD thesis of Tristan Marty (2023–2025)
10 Partnerships and cooperations
10.1 National initiatives
- CIROQUO ("Consortium Industriel de Recherche en Optimisation et QUantification d'incertitudes pour les données Onéreuses"), participation as Inria Saclay/Ecole Polytechnique, together with six other academic and five industrial partners (2021–2024)
11 Dissemination
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
- Anne Auger, Dimo Brockhoff, Paul Dufossé, Nikolaus Hansen: co-organizer of the Blackbox Optimization Benchmarking workshop at the GECCO 2022 conference, together with Konstantin Dietrich, Tobias Glasmachers, Olaf Mersmann, Petr Pošik, and Tea Tušar
- A. Auger: co-organizer of the Dagstuhl seminar 22081 Theory of Randomized Optimization Heuristics in 2022
- A. Auger: co-organizer of the Dagstuhl seminar 23251 Challenges in Benchmarking Optimization Heuristics in 2023
- D. Brockhoff: co-editor of the book “Many-Criteria Optimization and Decision Analysis”, based on the 2019 Lorentz Center workshop of the same name, Springer, to appear in 2023
11.1.2 Scientific events: selection
Chair of conference program committees
- D. Brockhoff: GECCO 2023 track chair for the EMO track, together with Hiroyuki Sato
Reviewer
- D. Brockhoff: reviewer for the conferences GECCO 2022 and EMO 2023
11.1.3 Journal
Member of the editorial boards
- A. Auger and N. Hansen member of the editorial board of Evolutionary Computation Journal since 2009
- D. Brockhoff and N. Hansen: Associate Editors for ACM Transactions on Evolutionary Learning and Optimization since 2019
Reviewer - reviewing activities
- The three permanent members are frequent reviewers for major journals in Evolutionary Computation. Anne Auger is a frequent reviewer of mathematical optimization journal (JOGO, SIAM OPT). We additionally review papers in Machine Learning related to optimization for JMLR, Machine Learning.
11.1.4 Invitations
- A. Gissler and N. Hansen were invited to the Dagstuhl seminar "Theory of Randomized Optimization Heuristics", February 2022
- N. Hansen were invited to give an introductory talk A Gentle Introduction to Information-Geometric Optimization at the Dagstuhl Seminar 22182 "Estimation-of-Distribution Algorithms: Theory and Applications", May 2022
- D. Brockhoff and N. Hansen were invited to the Lorentz Center seminar "Benchmarked: Optimization Meets Machine Learning", May-June 2022
11.1.5 Leadership within the scientific community
- A. Auger: elected member of the ACM SIVEVO board
- A. Auger: member of the business committee of the ACM SIGEVO board
11.1.6 Research administration
- A. Auger: member of the conseil de laboratoire of the CMAP
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Master: A. Auger, “Derivative-free Optimization”, 22.5h ETD, niveau M2 (Optimization Master of Paris-Saclay)
- Master: D. Brockhoff, “Algorithms and Complexity”, 36h ETD, niveau M1 (joint MSc with ESSEC “Data Sciences & Business Analytics”, CentraleSupelec, France
- Master: D. Brockhoff, “Advanced Optimization”,36h ETD, niveau M2 (joint MSc with ESSEC “Data Sciences & Business Analytics”), CentraleSupelec, France
- Master: A. Auger and D. Brockhoff, “Optimization in Machine Learning”, formerly “Introduction to Optimization”, 22.5h ETD, niveau M2 (Master Artificial Intelligence), U. Paris-Saclay, France
Tutorials
- A (Biased) Introduction to Benchmarking, tutorial at the GECCO conference in 2022 (A. Auger and N. Hansen)
- Benchmarking Multiobjective Optimizers 2.0, tutorial at the GECCO conference in 2022 as well as at EMO'2023 (D. Brockhoff and T. Tušar)
- CMA-ES and Advanced Adaptation Mechanisms, tutorial at the GECCO conference in 2022 (Y. Akimoto and N. Hansen)
11.2.2 Supervision
- PhD: Paul Dufossé, "Constrained Optimization and Radar Applications", (Oct. 2018–Dec. 2022), supervisor: Nikolaus Hansen
- PhD: Eugénie Marescaux, Theoretical Analysis of convergence of multi-objective solvers (2019–2022), supervisor: Anne Auger
- PhD in progress: Armand Gissler, "Analysis of covariance matrix adaptation methods for randomized derivative free optimization" (2021–), supervisors: Anne Auger and Nikolaus Hansen
- PhD in progress: Mohamed Gharafi (Jan. 2022–), supervisors: Nikolaus Hansen and Dimo Brockhoff
- PhD in progress: Tristan Marty (Jan. 2023–), supervisors: Anne Auger and Nikolaus Hansen
11.2.3 Juries
- A. Auger member of the CRCN/ISFP hiring committee of Inria Saclay
- A. Auger president of the PhD defense jury of Ashley Hill
11.2.4 Internal or external Inria responsibilities
- D. Brockhoff: member of the CDT in Saclay
- A. Auger: member of the BCEP of Inria Saclay
12 Scientific production
12.1 Major publications
- 1 articleGlobal Linear Convergence of Evolution Strategies on More Than Smooth Strongly Convex Functions.SIAM Journal on OptimizationJune 2022
- 2 articleAn ODE Method to Prove the Geometric Convergence of Adaptive Stochastic Algorithms.Stochastic Processes and their Applications1452022, 269-307
- 3 articleDiagonal Acceleration for Covariance Matrix Adaptation Evolution Strategies.Evolutionary Computation2832020, 405-435
- 4 articleA SIGEVO impact award for a paper arising from the COCO platform.ACM SIGEVOlution134January 2021, 1-11
- 5 articleUsing Well-Understood Single-Objective Functions in Multiobjective Black-Box Optimization Test Suites.Evolutionary Computation2022
- 6 articleVerifiable Conditions for the Irreducibility and Aperiodicity of Markov Chains by Analyzing Underlying Deterministic Models.Bernoulli251December 2018, 112-147
- 7 inproceedingsA Global Surrogate Assisted CMA-ES.GECCO 2019 - The Genetic and Evolutionary Computation ConferenceACMPrague, Czech RepublicJuly 2019, 664-672
- 8 articleCOCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting.Optimization Methods and Software361ArXiv e-prints, arXiv:1603.087852020, 114-144
- 9 articleInformation-Geometric Optimization Algorithms: A Unifying Picture via Invariance Principles.Journal of Machine Learning Research18182017, 1-65
- 10 articleGlobal linear convergence of Evolution Strategies with recombination on scaling-invariant functions.Journal of Global Optimization2022
- 11 articleScaling-invariant functions versus positively homogeneous functions.Journal of Optimization Theory and ApplicationsSeptember 2021
- 12 inproceedingsUncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework.GECCO 2019 - The Genetic and Evolutionary Computation ConferencePart of this research has been conducted in the context of a research collaboration between Storengy and InriaPrague, Czech RepublicJuly 2019
12.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
Reports & preprints
Other scientific publications
12.3 Cited publications
- 28 inproceedingsOnline model selection for restricted covariance matrix adaptation.International Conference on Parallel Problem Solving from NatureSpringer2016, 3--13
- 29 inproceedingsProjection-based restricted covariance matrix adaptation for high dimension.Proceedings of the 2016 on Genetic and Evolutionary Computation ConferenceACM2016, 197--204
-
30
inproceedingsTowards au Augmented Lagrangian Constraint Handling Approach for the
-ES.Genetic and Evolutionary Computation ConferenceACM Press2015, 249-256 - 31 inproceedingsLinearly Convergent Evolution Strategies via Augmented Lagrangian Constraint Handling.Foundation of Genetic Algorithms (FOGA)2017
- 32 articleLinear Convergence of Comparison-based Step-size Adaptive Randomized Search via Stability of Markov Chains.SIAM Journal on Optimization2632016, 1589-1624
- 33 inproceedingsAlgorithms for Hyper-Parameter Optimization.Neural Information Processing Systems (NIPS 2011)2011
- 34 articleThe O.D.E. Method for Convergence of Stochastic Approximation and Reinforcement Learning.SIAM Journal on Control and Optimization382January 2000
- 35 bookletStochastic approximation: a dynamical systems viewpoint.Cambridge University Press2008
- 36 inproceedingsConstraint-handling techniques used with evolutionary algorithms.Proceedings of the 2008 Genetic and Evolutionary Computation ConferenceACM2008, 2445--2466
- 37 inproceedingsCovariance Matrix Adaptation Evolution Strategy for Multidisciplinary Optimization of Expendable Launcher Families.13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Proceedings2010
- 38 bookNumerical Methods for Unconstrained Optimization and Nonlinear Equations.Englewood Cliffs, NJPrentice-Hall1983
- 39 incollectionPrincipled design of continuous stochastic search: From theory to practice.Theory and principled methods for the design of metaheuristicsSpringer2014, 145--180
- 40 articleCompletely Derandomized Self-Adaptation in Evolution Strategies.Evolutionary Computation922001, 159--195
- 41 articleTesting heuristics: We have it all wrong.Journal of heuristics111995, 33--42
- 42 inproceedingsAn Evaluation of Sequential Model-based Optimization for Expensive Blackbox Functions.GECCO (Companion) 2013Amsterdam, The NetherlandsACM2013, 1209--1216
- 43 articleA theoretician’s guide to the experimental analysis of algorithms.Data structures, near neighbor searches, and methodology: fifth and sixth DIMACS implementation challenges592002, 215--250
- 44 articleEfficient global optimization of expensive black-box functions.Journal of Global optimization1341998, 455--492
- 45 articleA hybrid CMA-ES and HDE optimisation algorithm with application to solar energy potential.Applied Soft Computing922009, 738--745
- 46 articleOptimisation of building form for solar energy utilisation using constrained evolutionary algorithms.Energy and Buildings4262010, 807--814
- 47 articleCalibrating a global three-dimensional biogeochemical ocean model (MOPS-1.0).Geoscientific Model Development1012017, 127
- 48 bookStochastic approximation and recursive algorithms and applications.Applications of mathematicsNew YorkSpringer2003
- 49 inproceedingsOptimal Design of CO2 Sequestration with Three-Way Coupling of Flow-Geomechanics Simulations and Evolution Strategy.SPE Reservoir Simulation ConferenceOnePetro2019
- 50 inproceedingsDesign and Optimization of an Omnidirectional Humanoid Walk: A Winning Approach at the RoboCup 2011 3D Simulation Competition.Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence (AAAI)Toronto, Ontario, CanadaJuly 2012
- 51 bookMarkov Chains and Stochastic Stability.New YorkSpringer-Verlag1993
- 52 inproceedingsWell placement optimization for carbon dioxide capture and storage via CMA-ES with mixed integer support.Proceedings of the Genetic and Evolutionary Computation Conference Companion2018, 1696--1703
- 53 inproceedingsDevelopment of a high speed optimization tool for well placement in Geological Carbon dioxide Sequestration.5th ISRM Young Scholars' Symposium on Rock Mechanics and International Symposium on Rock Engineering for Innovative FutureOnePetro2019
- 54 articleThe Journal of Machine Learning Research1812017, 564--628
- 55 articleEnergy and spinning reserve scheduling for a wind-thermal power system using CMA-ES with mean learning technique.International Journal of Electrical Power & Energy Systems532013, 113--122
- 56 articleEvolution strategies as a scalable alternative to reinforcement learning.arXiv preprint arXiv:1703.038642017
- 57 inproceedingsPractical bayesian optimization of machine learning algorithms.Neural Information Processing Systems (NIPS 2012)2012, 2951--2959
- 58 inproceedingsUncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework.GECCO 2019 - The Genetic and Evolutionary Computation ConferencePart of this research has been conducted in the context of a research collaboration between Storengy and InriaPrague, Czech RepublicJuly 2019
- 59 articleLong-term model predictive control of gene expression at the population and single-cell levels.Proceedings of the National Academy of Sciences109352012, 14271--14276

