Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.1.4. Functional programming
- A2.1.6. Concurrent programming
- A2.1.10. Domain-specific languages
- A2.1.11. Proof languages
- A2.4.2. Model-checking
- A2.4.3. Proofs
- A6.2.1. Numerical analysis of PDE and ODE
- A7.2. Logic in Computer Science
- A7.2.1. Decision procedures
- A7.2.2. Automated Theorem Proving
- A7.2.3. Interactive Theorem Proving
- A7.2.4. Mechanized Formalization of Mathematics
- A8.10. Computer arithmetic
Other Research Topics and Application Domains
- B5.2.2. Railway
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B6.1. Software industry
- B9.5.1. Computer science
- B9.5.2. Mathematics
1 Team members, visitors, external collaborators
Research Scientists
- Claude Marché [Team leader, INRIA, Senior Researcher, HDR]
- Sylvie Boldo [INRIA, Senior Researcher, HDR]
- Jean-Christophe Filliâtre [CNRS, Senior Researcher, HDR]
- Armaël Guéneau [INRIA, Researcher]
- Guillaume Melquiond [INRIA, Senior Researcher, HDR]
Faculty Members
- Sylvain Conchon [UNIV PARIS SACLAY, Professor, HDR]
- Andriy Paskevych [UNIV PARIS SACLAY, Associate Professor]
PhD Students
- Léo Andrès [OCamlPro, CIFRE, CIFRE grant by OCamlPro Company]
- Xavier Denis [UNIV PARIS SACLAY]
- Antoine Lanco [UNIV PARIS SACLAY, ATER, from Oct 2022]
- Antoine Lanco [INRIA, until Sep 2022]
- Josué Moreau [INRIA, PhD grant from ERC Fresco]
- Houda Mouhcine [INRIA, PhD grant from ERC Alpines-EMC2]
- Clément Pascutto [TARIDES, CIFRE grant funded by Tarides company]
Technical Staff
- Paul Bonnot [INRIA, Engineer, from Sep 2022, Funded by ProofInUse Consortium]
- Yacine El Haddad [INRIA, Engineer, until May 2022]
- Paul Geneau De Lamarlière [INRIA, Engineer, from Sep 2022, Funded by ProofInUse Consortium]
- Solene Moreau [INRIA, Engineer, from Mar 2022, Funded by ProofInUse Consortium]
Interns and Apprentices
- Paul Geneau De Lamarlière [ENS DE LYON, Intern, from Feb 2022 until Jul 2022]
- Josue Moreau [LMF, Intern, from Mar 2022 until Jul 2022]
Administrative Assistant
- Alexandra Merlin [INRIA, until Apr 2022]
External Collaborators
- Thibaut Balabonski [UNIV PARIS SACLAY, Associate Professor]
- Jacques-Henri Jourdan [CNRS, Research Scientist]
- Chantal Keller [UNIV PARIS SACLAY, Associate Professor]
2 Overall objectives
2.1 Presentation
The general objective of the Toccata project is to promote formal specification and computer-assisted proof in the development of software that requires high assurance in terms of safety and correctness with respect to its intended behavior. Such safety-critical software appears in many application domains like transportation (e.g., aviation, aerospace, railway, and more and more in cars), communication (e.g., internet, smartphones), health devices, etc. The number of tasks performed by software is quickly increasing, together with the number of lines of code involved. Given the need of high assurance of safety in the functional behavior of such applications, the need for automated (i.e., computer-assisted) methods and techniques to bring guarantee of safety became a major challenge. In the past and at present, the most widely used approach to check safety of software is to apply heavy test campaigns, which take a large part of the costs of software development. Yet they cannot ensure that all the bugs are caught, and remaining bugs may have catastrophic causes (e.g., the Heartbleed bug in OpenSSL library discovered in 2014).
Generally speaking, software verification approaches pursue three goals: (1) verification should be sound, in the sense that no bugs should be missed, (2) verification should not produce false alarms, or as few as possible, (3) it should be as automatic as possible. Reaching all three goals at the same time is a challenge. A large class of approaches emphasizes goals (2) and (3): testing, run-time verification, symbolic execution, model checking, etc. Static analysis, such as abstract interpretation, emphasizes goals (1) and (3). Deductive verification emphasizes (1) and (2). The Toccata project is mainly interested in exploring the deductive verification approach, although we also consider the other ones in some cases.
In the past decade, significant progress has been made in the domain of deductive program verification. This is emphasized by some success stories of application of these techniques on industrial-scale software. For example, the Atelier B system was used to develop part of the embedded software of the Paris metro line 14 41 and other railway-related systems; a formally proved C compiler was developed using the Coq proof assistant 69; the L4-verified project developed a formally verified micro-kernel with high security guarantees, using analysis tools on top of the Isabelle/HOL proof assistant 68. A bug in the JDK implementation of TimSort was discovered using the KeY environment 64 and a fixed version was proved sound. Another sign of recent progress is the emergence of deductive verification competitions (e.g., VerifyThis 44). Finally, recent trends in the industrial practice for development of critical software is to require more and more guarantees of safety, e.g., the new DO-178C standard for developing avionics software adds to the former DO-178B the use of formal models and formal methods. It also emphasizes the need for certification of the analysis tools involved in the process.
3 Research program
Panorama of Deductive Verification
There are two main families of approaches for deductive verification. Methods in the first family build on top of mathematical proof assistants (e.g., Coq, Isabelle) in which both the model and the program are encoded; the proof that the program meets its specification is typically conducted in an interactive way using the underlying proof construction engine. Methods from the second family proceed by the design of standalone tools taking as input a program in a particular programming language (e.g., C, Java) specified with a dedicated annotation language (e.g., ACSL 35, JML 51) and automatically producing a set of mathematical formulas (the verification conditions) which are typically proved using automatic provers (e.g., Z3 71, Alt-Ergo 54, CVC4 34).
The first family of approaches usually offers a higher level of assurance than the second, but also demands more work to perform the proofs (because of their interactive nature) and makes them less easy to adopt by industry. Moreover, they generally do not allow to directly analyze a program written in a mainstream programming language like Java or C. The second kind of approaches has benefited in the past years from the tremendous progress made in SAT and SMT solving techniques, allowing more impact on industrial practices, but suffers from a lower level of trust: in all parts of the proof chain (the model of the input programming language, the VC generator, the back-end automatic prover), potential errors may appear, compromising the guarantee offered. Moreover, while these approaches are applied to mainstream languages, they usually support only a subset of their features.
Overall Goals of the Toccata Project
One of our original skills is the ability to conduct proofs by using automatic provers and proof assistants at the same time, depending on the difficulty of the program, and specifically the difficulty of each particular verification condition. We thus believe that we are in a good position to propose a bridge between the two families of approaches of deductive verification presented above. Establishing this bridge is one of the goals of the Toccata project: we want to provide methods and tools for deductive program verification that can offer both a high amount of proof automation and a high guarantee of validity. Indeed, an axis of research of Toccata is the development of languages, methods and tools that are themselves formally proved correct. Recent advances in the foundations of deductive verification include various aspects such as reasoning efficiently on bitvector programs 60 or providing counterexamples when a proof does not succeed 55.
A specifically challenging aspect of deductive verification methods is how does one deal with memory mutation in general, an issue that appear under various similar forms such the reasoning on mutable data structures or on concurrent programs, with the common denominator of the tracking of memory change on shared data. The ability to track aliasing is also a key for the ability of specifying programs and conduct proofs using the advanced notion of ghost code58, notion that can be push forward very far as demonstrated by our work on ghost monitors 534.
In industrial applications, numerical calculations are very common (e.g. control software in transportation). Typically they involve floating-point numbers. Some of the members of Toccata have an internationally recognized expertise on deductive program verification involving floating-point computations. Our past work includes a new approach for proving behavioral properties of numerical C programs using Frama-C/Jessie 33, various examples of applications of that approach 49, the use of the Gappa solver for proving numerical algorithms 57, an approach to take architectures and compilers into account when dealing with floating-point programs 50, 73. We contributed to the CompCert verified compiler, regarding the support for floating-point operations 48. We also contributed to the Handbook of Floating-Point Arithmetic 72. A representative case study is the analysis and the proof of both the method error and the rounding error of a numerical analysis program solving the one-dimension acoustic wave equation 4645. We published a reference book on the verification of floating-point algorithms with Coq 2. Our experience led us to a conclusion that verification of numerical programs can benefit a lot from combining automatic and interactive theorem proving 47, 49, 61. Verification of numerical programs is another main axis of Toccata.
Deductive program verification methods are built upon theorem provers to decide whether a expected proof obligation on a program is a valid mathematical proposition, hence working on deductive verification requires a certain amount of work on the aspect of design of theorem provers. We are involved in particular in the Alt-Ergo SMT solver, for which we designed an original approach for reasoning on arithmetic facts 510 ; the Gappa tool dedicated to reasoning on rounding errors in floating-point computations 70; and the interval tactic to reason about real approximations 8. Proof by reflection is also a powerful approach for advanced reasoning about programs 9.
In the past, we have been more and more involved in the development of significantly large case studies and applications, such as for example the verification of matrix multiplication algorithms 3, the design of verified OCaml librairies 52, the realization of a platform for verification of shell scripts 39 1, or the correct-by-construction design of an efficient library for arbitrary-precision arithmetic 9.
Our scientific programme detailed below is structured into four axes:
- Foundations and spreading of deductive program verification;
- Reasoning on mutable memory in program verification;
- Verification of Computer Arithmetic;
- Spreading Formal Proofs.
Let us conclude with more general considerations about our agenda of current four years period 2019-2013: we want to keep on
- with general audience actions;
- industrial transfer, in particular through an extension of the perimeter of the ProofInUse joint lab.
3.1 Foundations and spreading of deductive program verification
Permanent researchers: S. Conchon, J.-C. Filliâtre, A. Guéneau C. Marché, G. Melquiond, A. Paskevich
This axis covers the central theme of the team: deductive verification, from the point of view of its foundations but also our will to spread its use in software development. The general motto we want to defend is “deductive verification for the masses”. A non-exhaustive list of subjects we want to address is as follows.
- The verification of general-purpose algorithms and data structures: the challenge is to discover adequate invariants to obtain a proof, in the most automatic way as possible, in the continuation of the current VOCaL project and the various case studies presented in Axis 4 below.
- Uniform approaches to obtain correct-by-construction programs and libraries, in particular by automatic extraction of executable code (in OCaml, C, CakeML, etc.) from verified programs, and including innovative general methods like advanced ghost code, ghost monitoring, etc.
- Automated reasoning dedicated to deductive verification, so as to improve proof automation; improved combination of interactive provers and fully automated ones, proof by reflection.
- Improved feedback in case of proof failures: based on generation of counterexamples, or symbolic execution, or possibly randomized techniques à la quickcheck.
- Reduction of the trusted computing base in our toolchains: production of certificates from automatic proofs, for goal transformations (like those done by Why3), and from the generation of VCs
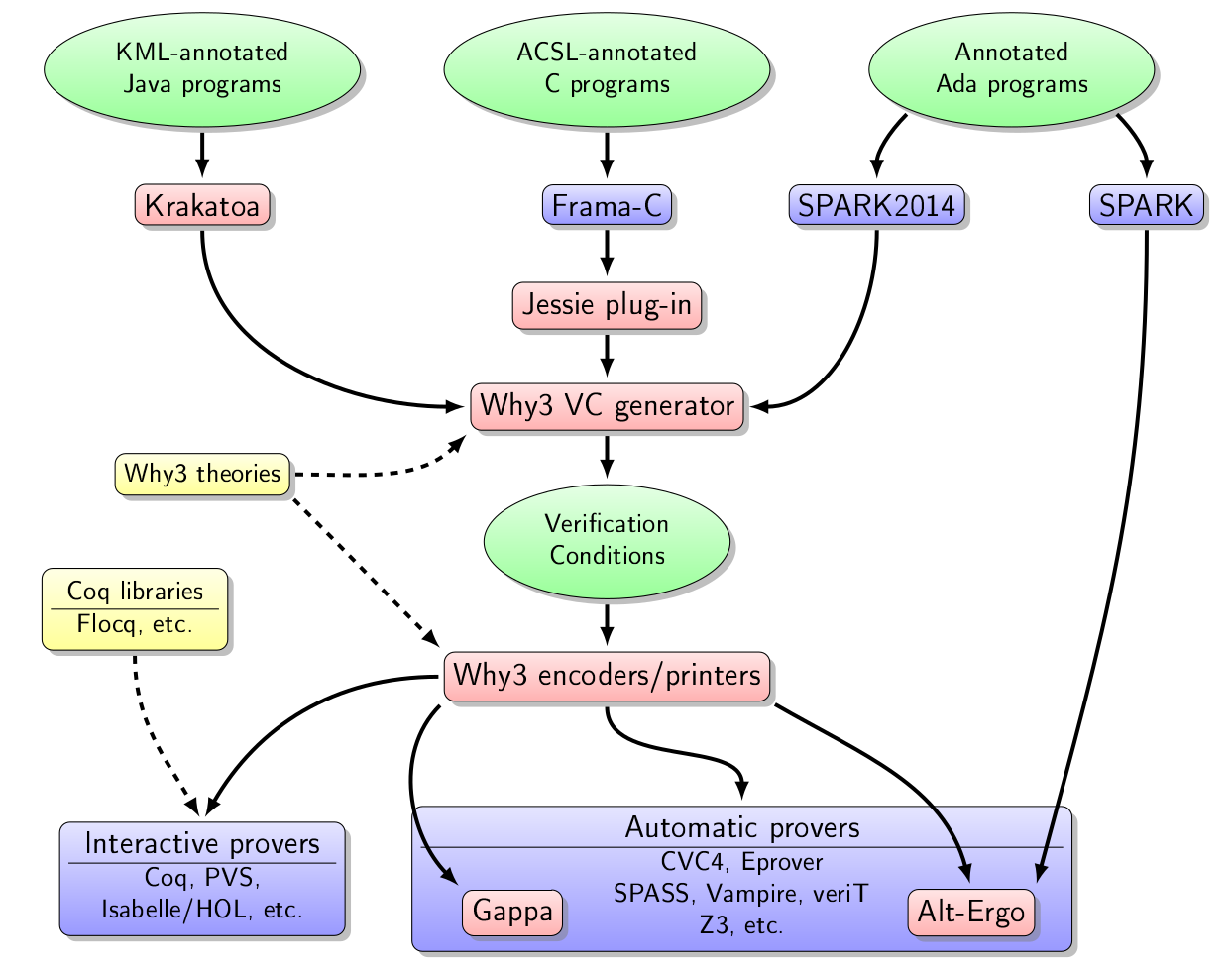
A significant part of the work achieved in this axis is related to the Why3 toolbox and its ecosystem, displayed on Figure 1. The boxes in red background correspond to the tools we develop in the Toccata team. A recent representative publication is a report on abstraction and genericity features of Why3 659.
3.2 Reasoning on mutable memory in program verification
Permanent researchers: J.-C. Filliâtre, A. Guéneau, C. Marché, G. Melquiond, A. Paskevich
This axis concerns specifically the techniques for reasoning on programs where aliasing is the central issue. It covers the methods based on type-based alias analysis and related memory models, on specific program logics such as separation logics, and extended model-checking. It concerns the application on analysis of C or C++ codes, on Ada codes involving pointers, but also concurrent programs in general. The main topics planned are:
- The study of advanced type systems dedicated to verification, for controlling aliasing, and their use for obtaining easier-to-prove verification conditions. Modern typing systems in the style of Rust, involving ownership and borrowing, are considered.
- The design of front-ends of Why3 for the proofs of programs where aliasing cannot be fully controlled statically, via adequate memory models, aiming in particular at extraction to C; and also for concurrent programs.
- The continuation of fruitful work on concurrent parameterized systems, and its corresponding specific SMT-based model-checking.
- Concurrent programming on weak memory models, on one hand as an extension of parameterized systems above, but also in the specific context of OCaml multicore.
- In particular in the context of the ProofInUse consortium, design methods for Ada, C, C++ or Java using memory models involving fine-grain analysis of pointers. Rust programs are considered as well.
3.3 Verification of Computer Arithmetic
Permanent researchers: S. Boldo, C. Marché, G. Melquiond
We of course want to keep this axis which is a major originality of Toccata. The main topics are:
- Fundamental studies concerning formalization of floating-point computations, algorithms, and error analysis. Related to numerical integration, we will develop the relationships between mathematical stability and floating-point stability of numerical schemes.
- A significant effort dedicated to verification of numerical programs written in C, Ada, C++. This involves combining specifications in real numbers and computation in floating-point, and underlying automated reasoning techniques with floating-point numbers and real numbers. A new approach we have in mind concerns some variant of symbolic execution of both code and specifications involving real numbers.
- We have not yet studied embedded systems. Our approach is first to tackle numerical filters. This requires more results on fixed-point arithmetic and a careful study of overflows.
3.4 Spreading Formal Proofs
Permanent researchers: S. Boldo, S. Conchon, J.-C. Filliâtre, A. Guéneau, C. Marché, G. Melquiond, A. Paskevich
This axis covers applications in general. The applications we currently have in mind are:
- Hybrid Systems, i.e., systems mixing discrete and continuous transitions. This theme covers many aspects such as general techniques for formally reasoning of differential equations, and extending SMT-based reasoning. The challenge is to support both abstract mathematical reasoning and concrete program execution (e.g., using floating-point representation). Hybrid systems will be a common effort with other members of the future laboratory joint with LSV of ENS Cachan.
- Applied mathematics, in the continuation of the current efforts towards verification of Finite Element Method. It has only been studied in the mathematical point of view during this period. We plan to also consider their floating-point behavior and a demanding application is that of molecular simulation exhibited in the new EMC2 project. The challenge here is both in the mathematics to be formalized, in the numerical errors that have never been studied (and that may be huge in specific cases), and in the size of the programs, which requires that our tools scale.
- Continuation of our work on analysis of shell scripts. The challenge is to be able to analyze a large number of scripts (more than 30,000 in the corpus of Debian packages installation scripts) in an automatic manner. An approach that will be considered is some form of symbolic execution.
- Explore proof tools for mathematics, in particular automated reasoning for real analysis (application: formalization of the weak Goldbach conjecture), and in number theory.
- Obtain and distribute verified OCaml libraries, as expected outcome of the VOCaL project.
- Formalization of abstract interpretation and WP calculi: in the continuation of the former project Verasco, and an ongoing project proposal joint with CEA List. The difficulty of achieving full verification of such tools will be mitigated by use of certificate techniques.
4 Application domains
The application domains we target involve safety-critical software, that is where a high-level guarantee of soundness of functional execution of the software is wanted. Currently our industrial collaborations or impact mainly belong to the domain of transportation: aerospace, aviation, railway, automotive.
Generally speaking, we believe that our increasing industrial impact is a representative success for our general goal of spreading deductive verification methods to a larger audience, and we are firmly engaged into continuing such kind of actions in the future.
4.1 Safety-Critical Software in Transportation
-
Transfer to aeronautics: Airbus France
Development of the control software of Airbus planes historically includes advanced usage of formal methods. A first aspect is the usage of the CompCert verified compiler for compiling C source code. Our work in cooperation with Gallium team for the safe compilation of floating-point arithmetic operations 48 is directly in application in this context. A second aspect is the usage of the Frama-C environment for static analysis to verify the C source code. In this context, both our tools Why3 and Alt-Ergo are indirectly used to verify C code.
-
Transfer to the community of Atelier B
In the former ANR project BWare, we investigated the use of Why3 and Alt-Ergo as an alternative back-end for checking proof obligations generated by Atelier B, whose main applications are railroad-related. The transfer effort continues nowadays through the FUI project LCHIP.
-
ProofInUse joint lab: transfer to the community of Ada
development
Through the creation of the ProofInUse joint lab in 2014, with AdaCore company, we have a growing impact on the community of industrial development of safety-critical applications written in Ada. See the web page for a an overview of AdaCore's customer projects, in particular those involving the use of the SPARK Pro tool set. This impact involves both the use of Why3 for generating VCs on Ada source codes, and the use of Alt-Ergo for performing proofs of those VCs.
The impact of ProofInUse can also be measured in term of job creation: the first two ProofInUse engineers, D. Hauzar and C. Fumex, employed initially on Inria temporary positions, have now been hired on permanent positions in AdaCore company. It is also interesting to notice that this effort allowed AdaCore company to get new customers, in particular the domains of application of deductive formal verification went beyond the historical domain of aerospace: application in automotive, cyber-security, health (artificial heart).
4.2 Formal Analysis of Debian packages
Impactful results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A first important step was the version 2 of the design of the CoLiS language done by B. Becker, C. Marché and other co-authors 40, that includes a modified formal syntax, a extended formal semantics, together with the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following the initial approach for the concrete interpreter published in 2018 65 and an approach for symbolic interpretation 39), and finally extracted to OCaml code.
To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 67, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library is documented in details in a research report 66.
A third result is a large verification campaign running the CoLiS toolbox on all the packages of the current Debian distribution. The results of this campaign were reported in another article 38 that was submitted to TACAS conference in 2020, and finally presented in the 2021 edition. The most visible side effect of this experiment is the discovery of bugs: more than 150 bug reports have been filled against various Debian packages.
4.3 From the ProofInUse Joint Lab to the ProofInUse Consortium
The current continuation of the ProofInUse joint lab is under the form of a ProofInUse Consortium with an extension at a larger perimeter than Ada applications, that continue in collaboration with AdaCore company. We are collaborating with the TrustInSoft company for the verification of C and C++ codes, including in the recent past the use of Why3 to design verified and reusable C libraries (CIFRE PhD thesis). We also collaborate with Mitsubishi Electric R&D Centre Europe in Rennes for a specific usage of Why3 for verifying embedded devices (logic controllers). The recent best paper award at the FMICS conference 742 is a result of this last collaboration. These three collaboration share similar interests in he consortium, in particular via similar usage of Why3, and in particular for the generation of counterexamples when proofs fail. Plenary meetings are organized to encourage discussions and collaborations. These meetings are open to other friends of the Consortium, such as the CEA-list which develops the Frama-C environment, that uses Why3, and OCamlPro which maintains the solver Alt-Ergo.
5 Social and environmental responsibility
5.1 Footprint of research activities
Our research activities make use of standard computers for developing software and developing formal proofs. We have no use of specific large size computing resources. Though, we are making use of external services for continuous integration. A continuous integration methodology for mature software like Why3 is indeed mandatory for ensuring a safe software engineering process for maintenance and evolution. We make the necessary efforts to keep the energy consumption of such a continuous integration process as low as possible.
Ensuring the reproducibility of proofs in formal verification is essential. It is thus mandatory to replay such proofs regularly to make sure that our changes in our software do not loose existing proofs. For example, we need to make sure that the case studies in formal verification that we present in our gallery are reproducible. We also make the necessary efforts to keep the energy consumption for replaying proofs low, by doing it only when necessary.
As widely accepted nowadays, the major sources of environmental impact of research is travel to international conferences by plane, and renewal of electronic devices. The number of travels we made in 2022 remained very low with respect to previous years, of course because of the Covid pandemic, and the fact that many conferences were now proposed online participation. We intend to continue limiting the environmental impact of our travels. Concerning renewal of electronic devices, that is mainly laptops and monitors, we have always been careful on keeping them usable for as long time as possible.
5.2 Impact of research results
Our research results aims at improving the quality of software, in particular in mission-critical contexts. As such, making software safer is likely to reduce the necessity for maintenance operations and thus reducing energy costs.
Our efforts are mostly towards ensuring the safety of functional behavior of software, but we also increasingly consider the verification of their time or memory consumption. Reducing those would naturally induce a reduction in energy consumption.
Our research never involve any processing of personal data, and consequently we have no concern about preserving individual privacy, and no concern with respect to the RGPD (Règlement Général sur la Protection des Données).
6 Highlights of the year
6.1 Agrégation d'Informatique
In the past years, increasingly more Computer Science topics have been introduced in the high school curricula. This evolution resulted in an increasing need for teachers with high skills in that domain. The French ministry of education has decided in 2021 to create a new discipline in the concours de l'agrégation, which is the most selective competition for recruiting high school teachers. To prepare the first round of this recruiting competition that took place in 2022, Sylvie Boldo has been nominated as president of the competition committee. Notice that she was the only full-time researcher to chair an agrégation committee this year. She will continue to chair the recruiting committee in 2023.
6.2 Awards
-
PLDI 2022, Distinguished Paper Award
Xavier Denis, Jacques-Henri Jourdan and their co-authors Yusuke Matsushita and Derek Dreyer received a Distinguished Paper Award for their contribution RustHornBelt: A semantic foundation for functional verification of Rust programs with unsafe code at PLDI 2022, the 43rd ACM SIGPLAN Conference on Programming Language Design and Implementation.
6.3 Institutional Life
The team wishes to thank the Inria Evaluation Committee (Commission d'Évaluation) for its outstanding efforts, in 2022 as in previous years, in defending the interests of the research community, keeping us thoroughly informed about topics relevant to the scientific life, and upholding the moral and intellectual values we are collectively proud of and which define our institute.
7 New software and platforms
7.1 New software
7.1.1 Alt-Ergo
-
Name:
Automated theorem prover for software verification
-
Keywords:
Software Verification, Automated theorem proving
-
Functional Description:
Alt-Ergo is an automatic solver of formulas based on SMT technology. It is especially designed to prove mathematical formulas generated by program verification tools, such as Frama-C for C programs, or SPARK for Ada code. Initially developed in Toccata research team, Alt-Ergo's distribution and support are provided by OCamlPro since September 2013.
-
Release Contributions:
the "SAT solving" part can now be delegated to an external plugin, new experimental SAT solver based on mini-SAT, provided as a plugin. This solver is, in general, more efficient on ground problems, heuristics simplification in the default SAT solver and in the matching (instantiation) module, re-implementation of internal literals representation, improvement of theories combination architecture, rewriting some parts of the formulas module, bugfixes in records and numbers modules, new option "-no-Ematching" to perform matching without equality reasoning (i.e. without considering "equivalence classes"). This option is very useful for benchmarks coming from Atelier-B, two new experimental options: "-save-used-context" and "-replay-used-context". When the goal is proved valid, the first option allows to save the names of useful axioms into a ".used" file. The second one is used to replay the proof using only the axioms listed in the corresponding ".used" file. Note that the replay may fail because of the absence of necessary ground terms generated by useless axioms (that are not included in .used file) during the initial run.
- URL:
-
Contact:
Sylvain Conchon
-
Participants:
Alain Mebsout, Évelyne Contejean, Mohamed Iguernelala, Stéphane Lescuyer, Sylvain Conchon
-
Partner:
OCamlPro
7.1.2 CoqInterval
-
Name:
Interval package for Coq
-
Keywords:
Interval arithmetic, Coq
-
Functional Description:
CoqInterval is a library for the proof assistant Coq.
It provides several tactics for proving theorems on enclosures of real-valued expressions. The proofs are performed by an interval kernel which relies on a computable formalization of floating-point arithmetic in Coq.
The Marelle team developed a formalization of rigorous polynomial approximation using Taylor models in Coq. In 2014, this library has been included in CoqInterval.
- URL:
- Publications:
-
Contact:
Guillaume Melquiond
-
Participants:
Assia Mahboubi, Érik Martin-Dorel, Guillaume Melquiond, Jean-Michel Muller, Laurence Rideau, Laurent Théry, Micaela Mayero, Mioara Joldes, Nicolas Brisebarre, Thomas Sibut-Pinote
7.1.3 Coquelicot
-
Name:
The Coquelicot library for real analysis in Coq
-
Keywords:
Coq, Real analysis
-
Functional Description:
Coquelicot is library aimed for supporting real analysis in the Coq proof assistant. It is designed with three principles in mind. The first is the user-friendliness, achieved by implementing methods of automation, but also by avoiding dependent types in order to ease the stating and readability of theorems. This latter part was achieved by defining total function for basic operators, such as limits or integrals. The second principle is the comprehensiveness of the library. By experimenting on several applications, we ensured that the available theorems are enough to cover most cases. We also wanted to be able to extend our library towards more generic settings, such as complex analysis or Euclidean spaces. The third principle is for the Coquelicot library to be a conservative extension of the Coq standard library, so that it can be easily combined with existing developments based on the standard library.
- URL:
-
Contact:
Sylvie Boldo
-
Participants:
Catherine Lelay, Guillaume Melquiond, Sylvie Boldo
7.1.4 Cubicle
-
Name:
The Cubicle model checker modulo theories
-
Keywords:
Model Checking, Software Verification
-
Functional Description:
Cubicle is an open source model checker for verifying safety properties of array-based systems, which corresponds to a syntactically restricted class of parametrized transition systems with states represented as arrays indexed by an arbitrary number of processes. Cache coherence protocols and mutual exclusion algorithms are typical examples of such systems.
- URL:
-
Contact:
Sylvain Conchon
-
Participants:
Alain Mebsout, Sylvain Conchon
7.1.5 Flocq
-
Name:
The Flocq formalization of floating-point arithmetic for the Coq proof assistant
-
Keywords:
Floating-point, Arithmetic code, Coq
-
Functional Description:
The Flocq library for the Coq proof assistant is a comprehensive formalization of floating-point arithmetic: core definitions, axiomatic and computational rounding operations, high-level properties. It provides a framework for developers to formally verify numerical applications.
Flocq is currently used by the CompCert verified compiler to support floating-point computations.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Guillaume Melquiond, Pierre Roux, Sylvie Boldo
7.1.6 Gappa
-
Name:
The Gappa tool for automated proofs of arithmetic properties
-
Keywords:
Floating-point, Arithmetic code, Software Verification, Constraint solving
-
Functional Description:
Gappa is a tool intended to help formally verifying numerical programs dealing with floating-point or fixed-point arithmetic. It has been used to write robust floating-point filters for CGAL and it is used to verify elementary functions in CRlibm. While Gappa is intended to be used directly, it can also act as a backend prover for the Why3 software verification plateform or as an automatic tactic for the Coq proof assistant.
- URL:
- Publications:
-
Contact:
Guillaume Melquiond
-
Participant:
Guillaume Melquiond
7.1.7 Why3
-
Name:
The Why3 environment for deductive verification
-
Keywords:
Formal methods, Trusted software, Software Verification, Deductive program verification
-
Functional Description:
Why3 is an environment for deductive program verification. It provides a rich language for specification and programming, called WhyML, and relies on external theorem provers, both automated and interactive, to discharge verification conditions. Why3 comes with a standard library of logical theories (integer and real arithmetic, Boolean operations, sets and maps, etc.) and basic programming data structures (arrays, queues, hash tables, etc.). A user can write WhyML programs directly and get correct-by-construction OCaml programs through an automated extraction mechanism. WhyML is also used as an intermediate language for the verification of C, Java, or Ada programs.
- URL:
-
Contact:
Claude Marche
-
Participants:
Andriy Paskevych, Claude Marche, François Bobot, Guillaume Melquiond, Jean-Christophe Filliâtre, Levs Gondelmans, Martin Clochard
-
Partners:
CNRS, Université Paris-Sud
7.1.8 Coq
-
Name:
The Coq Proof Assistant
-
Keywords:
Proof, Certification, Formalisation
-
Scientific Description:
Coq is an interactive proof assistant based on the Calculus of (Co-)Inductive Constructions, extended with universe polymorphism. This type theory features inductive and co-inductive families, an impredicative sort and a hierarchy of predicative universes, making it a very expressive logic. The calculus allows to formalize both general mathematics and computer programs, ranging from theories of finite structures to abstract algebra and categories to programming language metatheory and compiler verification. Coq is organised as a (relatively small) kernel including efficient conversion tests on which are built a set of higher-level layers: a powerful proof engine and unification algorithm, various tactics/decision procedures, a transactional document model and, at the very top an integrated development environment (IDE).
-
Functional Description:
Coq provides both a dependently-typed functional programming language and a logical formalism, which, altogether, support the formalisation of mathematical theories and the specification and certification of properties of programs. Coq also provides a large and extensible set of automatic or semi-automatic proof methods. Coq's programs are extractible to OCaml, Haskell, Scheme, ...
-
Release Contributions:
Coq version 8.14 integrates many usability improvements, as well as an important change in the core language. The main changes include:
- The internal representation of match has changed to a more space-efficient and cleaner structure, allowing the fix of a completeness issue with cumulative inductive types in the type-checker. The internal representation is now closer to the user-level view of match, where the argument context of branches and the inductive binders "in" and "as" do not carry type annotations.
- A new "coqnative" binary performs separate native compilation of libraries, starting from a .vo file. It is supported by coq_makefile.
- Improvements to typeclasses and canonical structure resolution, allowing more terms to be considered as classes or keys.
- More control over notation declarations and support for primitive types in string and number notations.
- Removal of deprecated tactics, notably omega, which has been replaced by a greatly improved lia, along with many bug fixes.
- New Ltac2 APIs for interaction with Ltac1, manipulation of inductive types and printing.
Many changes and additions to the standard library in the numbers, vectors and lists libraries. A new signed primitive integers library Sint63 is available in addition to the unsigned Uint63 library.
-
News of the Year:
Coq version 8.14 integrates many usability improvements, as well as an important change in the core language. See the changelog at https://coq.inria.fr/refman/changes.html#version-8-14 for an overview of the new features and changes, along with the full list of contributors.
- URL:
-
Contact:
Matthieu Sozeau
-
Participants:
Yves Bertot, Frederic Besson, Tej Chajed, Cyril Cohen, Pierre Corbineau, Pierre Courtieu, Maxime Denes, Jim Fehrle, Julien Forest, Emilio Jesús Gallego Arias, Gaetan Gilbert, Georges Gonthier, Benjamin Grégoire, Jason Gross, Hugo Herbelin, Vincent Laporte, Olivier Laurent, Assia Mahboubi, Kenji Maillard, Érik Martin-Dorel, Guillaume Melquiond, Pierre-Marie Pedrot, Clément Pit-Claudel, Kazuhiko Sakaguchi, Vincent Semeria, Michael Soegtrop, Arnaud Spiwack, Matthieu Sozeau, Enrico Tassi, Laurent Théry, Anton Trunov, Li-Yao Xia, Theo Zimmermann
-
Partners:
CNRS, Université Paris-Sud, ENS Lyon, Université Paris-Diderot
7.1.9 creusot
-
Name:
Creusot
-
Keywords:
Rust, Specification language, Deductive program verification
-
Functional Description:
Creusot is a tool for deductive verification of Rust code. It allows you to annotate your code with specifications, invariants and assertions and then verify them formally and automatically, proving, mathematically, that your code satisfies your specifications.
Creusot works by translating Rust code to WhyML, the verification and specification language of Why3. Users can then leverage the full power of Why3 to (semi)-automatically discharge the verification conditions.
-
Release Contributions:
This is the first version, providing the main process to go from a Rust program annotated with Pearlite specifications to a set of verifications conditions to be discharged by external SMT solvers.
- URL:
- Publications:
-
Contact:
Xavier Denis
-
Participants:
Xavier Denis, Jacques-Henri Jourdan, Claude Marche
-
Partners:
Université Paris-Saclay, CNRS
7.1.10 coq-num-analysis
-
Name:
Numerical analysis Coq library
-
Keywords:
Coq, Numerical analysis, Real analysis
-
Scientific Description:
These Coq developments are based on the Coquelicot library for real analysis. Version 1.0 includes the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
-
Functional Description:
Formal developments and proofs in Coq of numerical analysis problems. The current long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
-
News of the Year:
Opam package (version 1.0). In progress: formalization of the concept of finite element.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Sylvie Boldo, François Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
-
Partners:
LIPN (Laboratoire d'Informatique de l'Université Paris Nord), LMAC (Laboratoire de Mathématiques Appliquées de Compiègne)
8 New results
8.1 Foundations and Spreading of Deductive Program Verification
Participants: Andrei Paskevich, Antoine Lanco, Claude Marché, Clément Pascutto, Guillaume Melquiond, Jean-Christophe Filliâtre, Léo Andrès, Quentin Garchery, Solène Moreau, Sylvain Conchon, Xavier Denis.
-
Certificates for Logic Transformations
In a context of formal program verification, using automatic provers, the trusted code base of verification environments is typically very broad. An environment such as Why3 implements many complex procedures: generation of verification conditions, logical transformations of proof tasks, and interactions with external provers. Considering only the logical transformations of Why3, their implementation already amounts to more than 17,000 lines of OCaml code. In order to increase our confidence in the correction of such a verification tool, Q. Garchery proposed a mechanism of certifying transformations, producing certificates that can be validated by an external tool, according to the skeptical approach. He explored two methods to validate certificates: one based on a dedicated verifier developed in OCaml, the other based on the universal proof checker Dedukti. A specificity of these certificates is to be “small grains” and composable, which makes the approach incremental, allowing to gradually add new certifying transformations 63. Among the new results in that topics, the approach is now supporting built-in theories such as equality and integer arithmetic. It is even possible to check certificates for proofs by strong induction on integers 62. Q. Garchery defended his thesis in 2022 25.
-
Explaining and Categorizing Counterexamples with
Giant-Step Assertion Checking
Identifying the cause of a proof failure during deductive verification of programs is hard: it may be due to an incorrectness in the program, an incompleteness in the program annotations, or an incompleteness of the prover. The changes needed to resolve a proof failure depend on its category, but the prover cannot provide any help on the categorization. When using an SMT solver to discharge a proof obligation, that solver can propose a model from a failed attempt, from which a possible counterexample can be derived. But the counterexample may be invalid, in which case it may add more confusion than help. To check the validity of a counterexample and to categorise the proof failure, B. Becker, C. Lourenço and C. Marché propose the comparison between the run-time assertion-checking (RAC) executions under two different semantics, using the counterexample as an oracle. The first RAC execution follows the normal program semantics, and a violation of a program annotation indicates an incorrectness in the program. The second RAC execution follows a novel “giant-step” semantics 37, 36 that does not execute loops nor function calls but instead retrieves return values and values of modified variables from the oracle. A violation of the program annotations only observed under giant-step execution characterizes an incompleteness of the program annotations. The approach was implemented in Why3 and evaluated it using examples from prior literature 74. S. Moreau worked on the application of this approach to Why3 front-ends, in particular in the Spark/Ada environment developed in collaboration with AdaCore.
-
Continuation Passing as an Abstract Syntax for Deductive
Verification
Continuation-passing style allows us to devise an extremely economical abstract syntax for a generic algorithmic language. This syntax is flexible enough to naturally express conditionals, loops, (higher-order) function calls, and exception handling. It is type-agnostic and state-agnostic, which means that we can combine it with a wide range of type and effect systems.
In this work 31, Paskevich shows how programs written in the continuation-passing style can be augmented in a natural way with specification annotations, ghost code, and side-effect discipline. He defines the rules of verification condition generation for this syntax, and shows that the resulting formulas are nearly identical to what traditional approaches, like the weakest precondition calculus, produce for the equivalent algorithmic constructions. This amounts to a minimalistic yet versatile abstract syntax for annotated programs for which one can compute verification conditions without sacrificing their size, legibility, and amenability to automated proof, compared to more traditional methods. This makes it an excellent candidate for internal code representation in program verification tools.
8.2 Reasoning on mutable memory in program verification
Participants: Andrei Paskevich, Armaël Guéneau, Claude Marché, Clément Pascutto, Guillaume Melquiond, Jean-Christophe Filliâtre, Léo Andrès, Sylvain Conchon, Xavier Denis.
-
Deductive program verification for a language with a
Rust-like typing discipline
Rust is a fairly recent programming language for system programming, bringing static guarantees of memory safety through a strong ownership policy. This feature opens promising advances for deductive verification of Rust code. The project underlying the PhD thesis of X. Denis, supervised by J.-H. Jourdan and C. Marché, is to propose techniques for the verification of Rust program, using a translation to a purely-functional language. The challenge of this translation is the handling of mutable borrows: pointers which control of aliasing in a region of memory. To overcome this, we used a technique inspired by prophecy variables to predict the final values of borrows 56. The underlying foundations for safety of this approach was published by X. Denis and J.-H. Jourdan, in a collaborative work with U. Saarbrücken 19.
This method is implemented in a new standalone tool called Creusot 17. The specification language of Creusot features the notion of prophecy mentioned above, which is central for the specification of behavior of programs performing memory mutation. Prophecies also permit efficient automated reasoning for verifying about such programs. Moreover, Rust provides advanced abstraction features based on a notion of traits, extensively used in the standard library and in user code. The support for traits is another main feature of Creusot, because it is at the heart of its approach, in particular for providing complex abstraction of the functional behavior of programs 17.
An important step to take further in the applicability of Creusot on a wide variety of Rust code is to support iterators, which are ubiquitous and in fact idiomatic in Rust programming (for example, every for loop is in fact internally desugared into an iterator). X. Denis and J.-H. Jourdan proposed a new approach to simplify the specifications of Rust code in presence of iterators, and to make the proofs more automatic also 28.
-
Capability Machines
A capability machine is a type of CPU allowing fine-grained privilege separation using capabilities, machine words that represent certain kinds of authority. We present a mathematical model and accompanying proof methods that can be used for formal verification of functional correctness of programs running on a capability machine, even when they invoke and are invoked by unknown (and possibly malicious) code. We use a program logic called Cerise for reasoning about known code, and an associated logical relation, for reasoning about unknown code. The logical relation formally captures the capability safety guarantees provided by the capability machine. The Cerise program logic, logical relation, and all the examples considered in the paper have been mechanized using the Iris program logic framework in the Coq proof assistant. We have submitted for publication at the Journal of the ACM an in-depth, pedagogical introduction to this methodology 29. We start from minimal examples and work our way up to new results involving sophisticated object-capability patterns, demonstrating that the methodology scales to such reasoning.
In subsequent work, we show that this approach enables the formal verification of full-system security properties under multiple attacker models: different security objectives of the full system can be verified under a different choice of trust boundary (i.e. under a different attacker model) 20. The proposed verification approach is modular, and is robust: code outside the trust boundary for a given security objective can be arbitrary, unverified attacker-provided code. We instantiate the approach concretely by extending an existing capability machine model with support for memory-mapped I/O and we obtain full system, machine-verified security properties about external effect traces while limiting the manual verification effort to a small trusted computing base relevant for the specific property under study.
-
Separation Arithmetic
In this work 23, Paskevich and Filliâtre propose an approach that helps to improve automation of proofs for certain classes of pointer-manipulating programs. It consists in mapping a recursive data structure onto a numerical domain, in such a way that ownership and separation properties can be expressed in terms of simple arithmetic inequalities. In addition to making the proof simpler, this provides for a clearer and more natural specification. This is illustrated with the classical example of in-place list reversal.
8.3 Verification of Computer Arithmetic
Participants: Claude Marché, Guillaume Melquiond, Houda Mouhcine, Josué Moreau, Paul Bonnot, Paul Geneau de Lamarlière, Sylvie Boldo.
-
Round-Off Errors and Hydrodynamics
Numerical simulations are carefully-written programs, and their correctness is based on mathematical results. Nevertheless, those programs rely on floating-point arithmetic and the corresponding round-off errors are often ignored. L. Ben Salem-Knapp, S. Boldo and W. Weens studied a specific simple scheme applied to advection, that is a particular equation from hydrodynamics dedicated to the transport of a substance. Their work shows a tight bound on the round-off error of the 1-dimensional and 2-dimensional upwind schemes, with an error roughly proportional to the number of steps. The error bounds are generic with respect to the floating-point format and exceptional behaviors are taken into account. Some experiments give an insight of the quality of the bounds 13.
-
Formalization of Integration
Integration, just as much as differentiation, is a fundamental calculus tool that is widely used in many scientific domains. Formalizing the mathematical concept of integration and the associated results in a formal proof assistant helps in providing the highest confidence on the correctness of numerical programs involving the use of integration, directly or indirectly. By its capability to extend the (Riemann) integral to a wide class of irregular functions, and to functions defined on more general spaces than the real line, the Lebesgue integral is perfectly suited for use in mathematical fields such as probability theory, numerical mathematics, and real analysis. In this article, we present the Coq formalization of -algebras, measures, simple functions, and integration of non-negative measurable functions, up to the full formal proofs of the Beppo Levi Theorem (monotone convergence) and Fatou's Lemma. More than a plain formalization of the known literature, we present several design choices made to balance the harmony between mathematical readability and usability of Coq theorems 14.
Once the Lebesgue integral is formally defined and the first lemmas are proved, the question of the convenience of the formalization naturally arises. To check it, a useful extension is Tonelli's theorem, stating that the (double) integral of a nonnegative measurable function of two variables can be computed by iterated integrals, and allowing to switch the order of integration. This requires the formal definition and proof in Coq of product sigma-algebras, product measures and their uniqueness, the construction of iterated integrals, up to Tonelli's theorem. We also advertise the Lebesgue induction principle provided by an inductive type for nonnegative measurable functions cite 27, 16.
The Bochner integral is a generalization of the Lebesgue integral, for functions taking their values in a Banach space. Therefore, both its mathematical definition and its formalization in the Coq proof assistant are more challenging 26.
8.4 Spreading Formal Proofs
Participants: Andrei Paskevich, Antoine Lanco, Armaël Guéneau, Claude Marché, Clément Pascutto, Guillaume Melquiond, Houda Mouhcine, Jean-Christophe Filliâtre, Josué Moreau, Léo Andrès, Paul Bonnot, Paul Geneau de Lamarlière, Solène Moreau, Sylvain Conchon, Sylvie Boldo, Xavier Denis, Yacine El Haddad.
-
Formally Verified Arbitrary-Precision Arithmetic
The WhyMP library implements some algorithms of the GNU Multi-Precision library (GMP), the state-of-the-art C library for performing computations on arbitrary-precision integers. WhyMP is written in WhyML, the programming language offered by the Why3 software verification framework, and the functional correctness of the algorithms is formally verified. The WhyML code is then extracted as a C library that is binary-compatible with GMP and can be substituted to it in existing programs. Performance-wise, it is competitive with the no-assembly version of GMP, for small and medium-sized inputs 15.
-
Verification of Ladder programs
Programmable Logic Controllers (PLCs) are industrial digital computers used as automation controllers in manufacturing processes. The Ladder language is a programming language used to develop PLC software. The aim of this work is to prove that a given Ladder program conforms to an expected temporal behavior given as a timing chart, describing scenarios of execution. C. Lourenço and C. Marché, in collaboration with Mitsubishi Electric R&D Centre Europe 43, 42, developed an approach to translate the Ladder code and the timing chart into a program for the Why3 environment. The ultimate goal is two-fold: first, by obtaining a complete proof, one can verify the conformance of the Ladder code with respect to the timing chart with a high degree of confidence. Second, when the proof is not fully completed, one can obtain a counterexample, illustrating a possible execution scenario of the Ladder code which does not conform to the timing chart. An extended paper in this work was published in a journal 12. Y. El Haddad and C. Marché are continuing this collaborative work MERCE by designing a new engine for inference of loop invariants, with dedicated features to Boolean variables, which are ubiquitous in Ladder programs.
-
Runtime Assertion Checking for OCaml
In behavioural specifications of imperative languages, postconditions may refer to the prestate of the function, usually with an old operator. Therefore, code performing runtime verification has to record prestate values required to evaluate the postconditions, typically by copying part of the memory state, which causes severe verification overhead, both in memory and CPU time.
In this work 18, Filliâtre and Pascutto consider the problem of efficiently capturing prestates in the context of Ortac, a runtime assertion checking tool for OCaml. Their contribution is a postcondition transformation that reduces the subset of the prestate to copy. They formalize this transformation, and they provide proof that it is sound and improves the performance of the instrumented programs. They illustrate the benefits of this approach with a maze generator. Benchmarks show that unoptimized instrumentation is not practicable, while their transformation restores performances similar to the program without any runtime check.
-
Formal Analysis of Debian packages
Several results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A new language was designed by B. Becker, C. Marché and other co-authors 40, including a formal syntax, a formal semantics, and the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following initial approaches for the concrete interpreter 65 and symbolic interpretation 39), and finally extracted to OCaml code.
To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 67, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library was documented in details in a research report 66.
An important result is a large verification campaign running the CoLiS toolbox on all the packages of the Debian distribution. Preliminary results of this campaign were reported in an article 38 presented at TACAS conference in 2021. The most visible side effect of this experiment is the discovery of bugs: more than 150 bugs report have been filled against various Debian packages. A journal paper reporting updated experimental results using an improved implementation of the platform, and on the new Debian stable distribution, was published in 2022 11.
-
Blockchains and Smart Contracts
In collaboration with the Nomadic Labs company, S. Conchon designed a new tool called Mitten, aiming at finely describing and playing scenarios on an implementation of Tenderbake. The latter is the next consensus protocol at the pBFT of the Tezos blockchain. Mitten is configurable so as to filter and examine messages according to particular scenarios written in a DSL built on top of OCaml. Thanks to Mitten, they were able to write and simulate subtle scenarios to reproduce behaviors that are difficult to achieve in normal times. They were also able to simulate situations allowing to exhibit bugs in the current implementation and to test proposed fixes 22.
-
Software Heritage
Software Heritage is a project initiated by Inria to archive the set of free software available online. In this work 21, Léo Andrès et al. present Software Heritage and describe their work in connection to the OCaml ecosystem, opam and Software Heritage. This includes extending Software Heritage with modules to archive opam packages, the development of an OCaml library to manipulate Software Heritage identifiers, a way for opam to download packages from Software Heritage (when not available through opam anymore), and finally the repair of opam repository when packages are missing. As of today, 3516 opam packages are already archived at Software Heritage.
-
Verified Computer Algebra
The Fresco project aims at turning the Coq proof assistant into a competitive tool for doing verified computer algebra. To do so, a two-language architecture is envisioned. First, there is an interpreted high-level language, with a functional mindset, which is the main programming language used by the users to input their queries. Second, there is a compiled low-level imperative language, so that experts can implement high-performance basic blocks. A proof-of-concept of this low-level language was built upon the CompCert compiler and the preservation of semantics during compilation was formally proven in Coq 30.
9 Bilateral contracts and grants with industry
We have bilateral contracts which are closely related to a joint effort called the ProofInUse consortium. The objective of ProofInUse is to provide verification tools, based on mathematical proof, to industry users. These tools are aimed at replacing or complementing the existing test activities, whilst reducing costs.
This consortium is a follow-up of the former LabCom ProofInUse between Toccata and the SME AdaCore, funded by the ANR programme “Laboratoires communs”, from April 2014 to March 2017.
9.1 ProofInUse-AdaCore Collaboration
Participants: Claude Marché [contact], Jean-Christophe Filliâtre, Andrei Paskevich, Guillaume Melquiond, Solène Moreau.
This collaboration is a joint effort of the Inria project-team Toccata and the AdaCore company which provides development tools for the Ada programming language. It is funded by a 5-year bilateral contract from Jan 2019 to Dec 2023.
The SME AdaCore is a software publisher specializing in providing software development tools for critical systems. A previous successful collaboration between Toccata and AdaCore enabled Why3 technology to be put into the heart of the AdaCore-developed SPARK technology.
The objective of ProofInUse-AdaCore is to significantly increase the capabilities and performances of the Spark/Ada verification environment proposed by AdaCore. It aims at integration of verification techniques at the state-of-the-art of academic research, via the generic environment Why3 for deductive program verification developed by Toccata.
9.2 ProofInUse-MERCE Collaboration
Participants: Claude Marché [contact], Guillaume Melquiond, Paul Bonnot, Paul Geneau de Lamarlière.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company Mitsubishi Electric R&D (MERCE) in Rennes. It is funded by a bilateral contract of 3 years and 6 months from Nov 2019 to April 2023.
MERCE has strong and recognized skills in the field of formal methods. In the industrial context of the Mitsubishi Electric Group, MERCE has acquired knowledge of the specific needs of the development processes and meets the needs of the group in different areas of application by providing automatic verification and demonstration tools adapted to the problems encountered.
The objective of ProofInUse-MERCE is to significantly improve on-going MERCE tools regarding the verification of Programmable Logic Controllers and also regarding the verification of numerical C codes.
9.3 ProofInUse-TrustInSoft Collaboration
Participants: Claude Marché [contact], Guillaume Melquiond, Raphaël Rieu-Helft, Paul Bonnot.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company TrustInSoft in Paris. It is funded by a bilateral contract of 24 months from Dec 2020 to Nov 2022.
TrustInSoft is an SME that offers the TIS-Analyzer environment for analysis of safety and security properties of source codes written in C and C++ languages. A version of TIS-Analyzer is available online, under the name TaaS (TrustInSoft as a Service).
The objective of ProofInUse-TrustInSoft is to integrate Deductive Verification in the platform TIS-Analyzer, under the form of a new plug-in called J-cube. One specific interest resides in the generation of counterexample to help the user in case of proof failure.
9.4 Action “Plan de relance” Toccata-TrustInSoft
Participants: Claude Marché [contact], Raphaël Rieu-Helft.
Toccata and the company TrustInSoft set up a research action in the context of the national “plan de relance”. It is funded for 24 months from January 2022 to December 2023. The funding covers the leave of R. Rieu-Helft for 80% time as an invited researcher in Toccata.
The objective of this action is to extend the ProofInUse-TrustInSoft collaboration towards two axes: a refinement of the J-cube memory model incorporating a static separation analysis, and the support of the C++ language.
9.5 CIFRE contract with Tarides company
Participants: Jean-Christophe Filliâtre [contact], Clément Pascutto.
Clément Pascutto started a CIFRE PhD in June 2020, under the supervision of Jean-Christophe Filliâtre (at Toccata) and Thomas Gazagnaire (at Tarides). The subject of the PhD is the dynamic and deductive verification of OCaml programs and its application to distributed data structures.
9.6 CIFRE contract with OCamlPro company
Participants: Jean-Christophe Filliâtre [contact], Léo Andrès.
Léo Andrès started a CIFRE PhD in October 2021, under the supervision of Jean-Christophe Filliâtre (at Toccata) and Pierre Chambart and Vincent Laviron (at OCamlPro). The subject of the PhD is the design, formalization, and implementation of a garbage collector for WebAssembly.
10 Partnerships and cooperations
10.1 International initiatives
10.1.1 Visits to international teams
Research stays abroad
Armaël Guéneau
-
Visited institution:
Aarhus University
-
Country:
Denmark
-
Dates:
From October 10, 2022 to October 23, 2022
-
Context of the visit:
Scientific collaboration on verification in Separation Logic for OCaml/C interoperability
-
Mobility program:
research stay
10.2 European initiatives
10.2.1 H2020 projects
EMC2, ERC Synergy project
EMC2 project on cordis.europa.eu
-
Title:
Extreme-scale Mathematically-based Computational Chemistry
-
Duration:
From September 1, 2019 to February 28, 2026
-
Partners:
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE (INRIA), France
- ECOLE NATIONALE DES PONTS ET CHAUSSEES (ENPC), France
- CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE CNRS (CNRS), France
- SORBONNE UNIVERSITE, France
-
Inria contact:
Laura GRIGORI (Alpines)
- Coordinator:
-
Summary:
Molecular simulation has become an instrumental tool in chemistry, condensed matter physics, molecular biology, materials science, and nanosciences. It will allow to propose de novo design of e.g. new drugs or materials provided that the efficiency of underlying software is accelerated by several orders of magnitude.
The ambition of the EMC2 project is to achieve scientific breakthroughs in this field by gathering the expertise of a multidisciplinary community at the interfaces of four disciplines: mathematics, chemistry, physics, and computer science. It is motivated by the twofold observation that, i) building upon our collaborative work, we have recently been able to gain efficiency factors of up to 3 orders of magnitude for polarizable molecular dynamics in solution of multi-million atom systems, but this is not enough since ii) even larger or more complex systems of major practical interest (such as solvated biosystems or molecules with strongly-correlated electrons) are currently mostly intractable in reasonable clock time. The only way to further improve the efficiency of the solvers, while preserving accuracy, is to develop physically and chemically sound models, mathematically certified and numerically efficient algorithms, and implement them in a robust and scalable way on various architectures (from standard academic or industrial clusters to emerging heterogeneous and exascale architectures).
EMC2 has no equivalent in the world: there is nowhere such a critical number of interdisciplinary researchers already collaborating with the required track records to address this challenge. Under the leadership of the 4 PIs, supported by highly recognized teams from three major institutions in the Paris area, EMC2 will develop disruptive methodological approaches and publicly available simulation tools, and apply them to challenging molecular systems. The project will strongly strengthen the local teams and their synergy enabling decisive progress in the field.
FRESCO, ERC Consolidator project
-
Title:
Fast and Reliable Symbolic Computation
-
Duration:
November 2021 – October 2026
-
Coordinator:
Assia Mahboubi
- Website
Using computers to formulate conjectures and consolidate proof steps pervades all mathematics fields, even the most abstract. Most computer proofs are produced by symbolic computations, using computer algebra systems. However, these systems suffer from severe, intrinsic flaws, rendering computational correction and verification challenging. The FRESCO project aims to shed light on whether computer algebra could be both reliable and fast. Researchers will disrupt the architecture of proof assistants, which serve as the best tools for representing mathematics in silico, enriching their programming features while preserving their compatibility with their logical foundations. They will also design novel mathematical software that should feature a high-level, performance-oriented programming environment for writing efficient code to boost computational mathematics.
10.3 National initiatives
10.3.1 ANR NuSCAP
Participants: Guillaume Melquiond [contact], Sylvie Boldo.
The last twenty years have seen the advent of computer-aided proofs in mathematics and this trend is getting more and more important. They request various levels of numerical safety, from fast and stable computations to formal proofs of the computations. Hovewer, the necessary tools and routines are usually ad hoc, sometimes unavailable, or inexistent. On a complementary perspective, numerical safety is also critical for complex guidance and control algorithms, in the context of increased satellite autonomy. We plan to design a whole set of theorems, algorithms and software developments, that will allow one to study a computational problem on all (or any) of the desired levels of numerical rigor. Key developments include fast and certified spectral methods and polynomial arithmetic, with subsequent formal verifications. There will be a strong feedback between the development of our tools and the applications that motivate it.
The project led by École Normale Supérieure de Lyon (LIP) has started in February 2021 and lasts for 4 years. Partners: Inria (teams Aric, Galinette, Lfant, Marelle, Toccata), École Polytechnique (LIX), Sorbonne Université (LIP6), Université Sorbonne Paris Nord (LIPN), CNRS (LAAS).
10.3.2 ANR GOSPEL
Participants: Jean-Christophe Filliâtre [contact], Andrei Paskevich, Armaël Guéneau.
A specification language extends a programming language by allowing code and specifications to be written in a single document. Examples include SparkAda, JML, and ACSL, which extend Ada, Java, and C with syntax for specifications.
By offering a specification language to programmers, one encourages them to document, test, and verify their code as they write it, not as a separate step that is too easily postponed. From a technical point of view, the presence of specifications makes it possible to test or verify each module independently and is the key to scalability. From a pragmatic point of view, embedding specifications in the code allows them to be automatically distributed (via a package management system) to every programmer; this is the key to practical adoption.
The GOSPEL project proposes to develop Gospel, a specification language that extends the programming language OCaml; to develop an ecosystem of tools based on Gospel; and to demonstrate and validate these tools via several case studies.
The project led by Inria Paris has started in October 2022 and lasts for 4 years. Partners: Inria Paris (team Cambium), Université Paris-Saclay (LMF), Tarides, Nomadic Labs.
10.3.3 Project “SecurEval” of PEPR Cybersécurité
Participants: Sylvain Conchon [contact].
The SecureVal project aims to design new tools, benefiting from new digital technologies, to verify the absence of hardware and software vulnerabilities, and carry out the proof of compliance required.
The project is led by CEA-List, it started in 2022 and lasts for 5 years.
11 Dissemination
Participants: Andrei Paskevich, Antoine Lanco, Armaël Guéneau, Claude Marché, Guillaume Melquiond, Houda Mouhcine, Jean-Christophe Filliâtre, Josué Moreau, Sylvain Conchon, Sylvie Boldo, Xavier Denis.
11.1 Administration, Collective Responsibilities
- S. Boldo was nominated president of the (first) concours de l'agrégation d'informatique that recruited French computer science teachers for high school in 2022. She gave a talk about it at the PhD Day organized by SIF (société informatique de France) on Dec 13.
- S. Boldo, member of the council of the Computer Science Graduate School of Université Paris-Saclay (and co-head for open science).
- S. Boldo, member of the (national) Inria IES commission (”commission pour l'information et l'édition scientifique”) about scientific edition and publication models.
- S Boldo, member of the CLFP (“commission locale de formation permanente”).
- G. Melquiond, member of the scientific commission of Inria Saclay, in charge of selecting candidates for PhD grants, Post-doc grants, temporary leaves from universities (“délégations”).
- G. Melquiond, elected member of the ED STIC doctoral school of Université Paris-Saclay, in charge of selecting candidates for PhD grants and monitoring PhD students.
- G. Melquiond, member of Inria's MissionJC (Jeunes Chercheurs), in charge of funding thematic research schools.
- G. Melquiond, responsible of Inria Saclay's FpR (Formation par la Recherche), in charge of funding participation of PhD students to thematic research schools.
- G. Melquiond, member of the CCUPS (“commission consultative de l'Université Paris-Saclay”) of Université Paris-Saclay, section 27.
- G. Melquiond, representing Inria at the COPOD (“Conseil de la Politique Doctorale”), in charge of setting the major orientations of the doctoral schools of Université Paris-Saclay.
- A. Paskevich, member of the CCUPS (“commission consultative de l'Université Paris-Saclay”) of Université Paris-Saclay, section 27.
11.2 Promoting scientific activities
Member of the organizing committees
- G. Melquiond, finance chair of the 29th IEEE Symposium on Computer Arithmetic, ARITH'2022
Member of the conference program committees
- S. Boldo, 29th IEEE Symposium on Computer Arithmetic, ARITH'2022
- S. Boldo, 14th NASA Formal Methods Symposium, NFM'2022
- S. Boldo, Certified Programs and Proofs, CPP'2022
- S. Boldo, 13th International Conference on Interactive Theorem Proving, ITP'2022
- G. Melquiond, 29th IEEE Symposium on Computer Arithmetic, ARITH'2022
11.2.1 Journal
Member of the editorial boards
- J.-C. Filliâtre, member of the editorial board of Journal of Functional Programming.
- G. Melquiond, member of the editorial board of Reliable Computing.
- A. Paskevich, member of the editorial board of Formal Methods in System Design.
11.2.2 Invited talks
- X. Denis, “Advanced verification of Rust programs with Creusot”, Workshop RustVerify, Apr 3, 2022.
- G. Melquiond, “Computing and Verifying Bounds on Mathematical Expressions”, Workshop on Machine-Checked Mathematics, Mar 2-4, 2022.
- G. Melquiond, “Formal Proofs and Numerical Computations”, 45th Congress on Numerical Analysis CANUM, June 13-17, 2022.
- G. Melquiond, “Formal Proofs and Numerical Computations”, 13th Rencontres Arithmétiques du GDR IM RAIM, Nov 2-4, 2022.
- G. Melquiond, “Numerical Computations and Formal Proofs”, Mathematical Components Workshop, Dec 7, 2022.
11.2.3 Leadership within the scientific community
- S. Boldo, elected chair of the ARITH working group of the GDR-IM (a CNRS subgroup of computer science) with L.-S. Didier (Univ. Toulon).
- S. Boldo, steering committee member of the IEEE International Symposium on Computer Arithmetic.
- J.-C. Filliâtre, chair of IFIP WG 1.9/2.15 verified Software.
11.2.4 Scientific expertise
- J.-C. Filliâtre, member of the jury of the concours de l'agrégation d'informatique, 2022.
- C. Marché, member of a recruitment committee for an associate professor position in computer science at the School ENSEIRB-MATMECA of the Institut National Polytechnique de Bordeaux.
- G. Melquiond, grading the entrance examination at X/ENS (“option informatique”).
- G. Melquiond, member of a recruitment committee for a full professor position in computer science at the École Normale Supérieure Paris Saclay.
11.3 Teaching - Supervision - Juries
11.3.1 Teaching
- S. Conchon and J.-C. Filliâtre, DIU Enseigner l'Informatique au Lycée, 2 weeks, rectorat de Versailles (together with T. Balabonski and K. Nguyen).
- J.-C. Filliâtre, Langages de programmation et compilation, 25h, L3, École Normale Supérieure, France.
- J.-C. Filliâtre, Les bases de l'algorithmique et de la programmation, 15h, L3, École Polytechnique, France.
- J.-C. Filliâtre, Compilation, 18h, M1, École Polytechnique, France.
- A. Guéneau, Programmation avancée, 12h, L3, ENS Paris-Saclay, France.
- A. Lanco, Introduction à l'informatique, 24h, L1, Université Paris-Saclay, France.
- A. Lanco, Programmation fonctionnelle, 24h, L2, Université Paris-Saclay, France.
- A. Lanco, Projet, 20h, L3, Université Paris-Saclay, France.
- A. Lanco, Sécurité des systèmes d'information, 24h, M1, Université Paris-Saclay, France.
- C. Marché, Proofs of Programs, 12h, M2, Master Parisien de Recherche en Informatique (MPRI).
- G. Melquiond, Initiation à la recherche, 12h, M1, MPRI, École Normale Supérieure Paris-Saclay, France.
- J. Moreau, Algorithmique, 16h, L3, Université Paris-Saclay, France.
- A. Paskevich, Vérification Déductive, 12h, M1, MPRI, Université Paris-Saclay, France.
- A. Paskevich, Programmation système, 56h, BUT2, IUT d'Orsay, Université Paris-Saclay, France.
11.3.2 Supervision
- PhD: Q. Garchery, “Certification de la transformation de tâches de preuve”, since Oct. 2018, supervised by C. Keller, C. Marché and A. Paskevich, defended in January 2022 25.
- PhD in progress: A. Lanco, “Stratégies pour la réduction forte”, since Oct. 2019, supervised by T. Balabonski and G. Melquiond.
- PhD in progress: C. Pascutto, “Runtime and Deductive Verification of OCaml programs and applications to Mergeable Data Structures”, since June 2020, supervised by J.-C. Filliâtre.
- PhD in progress: X. Denis, “Deductive program verification for Rust”, since Oct. 2020, supervised by J.-H. Jourdan and C. Marché.
- PhD in progress: L. Andrès, “Formalization of a garbage collector for WebAssembly”, since Oct. 2021, supervised by J.-C. Filliâtre.
- PhD in progress: H. Mouhcine, “Preuves formelles en mathématiques appliquées: vérification d'un générateur de formules de quadrature”, since Oct 2021, supervised by S. Boldo, F. Clément, and M. Mayero.
- PhD in progress: J. Moreau, “A low-level programming language for formally verified computer algebra”, since Oct. 2022, supervised by G. Melquiond.
- PhD in progress: P. Geneau de Lamarlière, “Design of formally verified floating-point components”, since Sep. 2022, supervised by G. Melquiond.
11.3.3 Juries
- S. Boldo, president of the jury of the PhD defense of Hugo Mlodecki (U. Paris-Saclay, 8 Dec 2022)
- S. Boldo, member of the jury of the PhD defense of Lucien Rakotomalala (ISAE Toulouse, 15 Feb 2022)
- S. Boldo, member of the jury of the HDR defense of Pascal Véron (U. Toulon, 6 April 2022)
- C. Marché, reviewer of the PhD of Dara Ly and member of the jury for the defense (U. d'Orléans, 5 Dec 2022)
- C. Marché, reviewer of the PhD of Junaid Ali Rasheed and member of the jury for the viva examination (Aston University in Birmingham, UK, 15 Dec 2022)
- J.-C. Filliâtre, reviewer of the PhD of Louis Noizet and member of the jury of the defense (U. Rennes 1, 29 Sep 2022)
- J.-C. Filliâtre, president of the jury of the PhD defense of Dara Ly (U. d'Orléans 1, 5 Dec 2022)
11.4 Popularization
11.4.1 Articles and contents
- S. Boldo, N. Brisebarre, and J.-M. Muller published a popularization article in the well-known journal La Recherche32.
11.4.2 Education
- S. Conchon and J.-C. Filliâtre are co-authors, with T. Balabonski, K. Nguyen and L. Sartre, of Informatique - MP2I/MPI - CPGE 1re et 2e années - Cours et exercices corrigés 24 (Ellipses, Sep 2022), a 1116 page book targeting the students of the brand new curriculum MP2I/MPI in the French CPGE.
11.4.3 Interventions
- S. Boldo, gave a talk for high school female students during the RJMI (Rencontres des Jeunes Mathématiciennes et Informaticiennes) organized online by Inria Saclay (Feb 22)
- S. Boldo gave a talk at high school students at Lycée Blaise Pascal, Orsay (May 16)
- S. Boldo, animation of a stand for the Fête de la science (Oct 7)
12 Scientific production
12.1 Major publications
- 1 inproceedingsAnalysing installation scenarios of Debian packages.Tools and Algorithms for the Construction and Analysis of SystemsTACAS 2020 - 26th International Conference on Tools and Algorithms for the Construction and Analysis of Systems12079Lecture Notes in Computer ScienceThe conference took place on-line, because it couldn't be held in Dublin, IrelandApril 2020, 235-253
- 2 bookComputer Arithmetic and Formal Proofs: Verifying Floating-point Algorithms with the Coq System.ISTE Press - ElsevierDecember 2017, URL: https://hal.inria.fr/hal-01632617
- 3 articleThe Matrix Reproved.Journal of Automated Reasoning6032018, 365--383URL: https://hal.inria.fr/hal-01617437
- 4 inproceedingsDeductive Verification with Ghost Monitors.POPL 2020 - 47th ACM SIGPLAN Symposium on Principles of Programming LanguagesNew Orleans, United States2020
- 5 inproceedingsA Three-tier Strategy for Reasoning about Floating-Point Numbers in SMT.Computer Aided Verification2017, URL: https://hal.inria.fr/hal-01522770
- 6 inproceedingsAbstraction and Genericity in Why3.ISoLA 2021 - 9th International Symposium On Leveraging Applications of Formal Methods, Verification and Validation12476Rhodes, Greece2020
- 7 inproceedingsAutomated Verification of Temporal Properties of Ladder Programs.FMICS 2021 - Formal Methods for Industrial Critical Systems12863Lecture Notes in Computer ScienceParis, France2021
- 8 articleFormally Verified Approximations of Definite Integrals.Journal of Automated Reasoning622February 2019, 281-300
- 9 inproceedingsA Why3 Framework for Reflection Proofs and its Application to GMP's Algorithms.9th International Joint Conference on Automated ReasoningLecture Notes in Computer ScienceOxford, United KingdomJuly 2018, URL: https://hal.inria.fr/hal-01699754
- 10 inproceedingsA Non-linear Arithmetic Procedure for Control-Command Software Verification.24th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS)Thessalonique, GreeceApril 2018, URL: https://hal.science/hal-01737737
12.2 Publications of the year
International journals
International peer-reviewed conferences
National peer-reviewed Conferences
Scientific books
Doctoral dissertations and habilitation theses
Reports & preprints
12.3 Other
Scientific popularization
12.4 Cited publications
- 33 inproceedingsMulti-Prover Verification of Floating-Point Programs.Fifth International Joint Conference on Automated Reasoning6173Lecture Notes in Artificial IntelligenceEdinburgh, ScotlandSpringerJuly 2010, 127--141URL: http://hal.inria.fr/inria-00534333
- 34 inproceedingsCVC4.Computer Aided Verification6806Lecture Notes in Computer ScienceSpringer2011, 171--177
- 35 manualACSL: ANSI/ISO C Specification Language, version 1.4.2009
- 36 inproceedingsExplaining Counterexamples with Giant-Step Assertion Checking.6th Workshop on Formal Integrated Development Environments (F-IDE 2021)Electronic Proceedings in Theoretical Computer ScienceMay 2021, URL: https://hal.inria.fr/hal-03217393
- 37 techreportGiant-step Semantics for the Categorisation of Counterexamples.RR-9407InriaApril 2021, URL: https://hal.inria.fr/hal-03213438
- 38 inproceedingsAnalysing installation scenarios of Debian packages.Tools and Algorithms for the Construction and Analysis of Systems12079Lecture Notes in Computer Science2020, 235--253URL: https://hal.science/hal-02355602
- 39 inproceedingsGhost Code in Action: Automated Verification of a Symbolic Interpreter.Verified Software: Tools, Techniques and Experiments12031Lecture Notes in Computer ScienceNew York, United StatesJuly 2019, URL: https://hal.inria.fr/hal-02276257
- 40 techreportRevision 2 of CoLiS language: formal syntax, semantics, concrete and symbolic interpreters.HAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321743
- 41 inproceedingsMETEOR : A successful application of B in a large project.Proceedings of FM'99: World Congress on Formal MethodsLecture Notes in Computer Science (Springer-Verlag)Springer VerlagSeptember 1999, 369--387
- 42 inproceedingsAutomated Verification of Temporal Properties of Ladder Programs.Formal Methods for Industrial Critical Systems12863Lecture Notes in Computer Science2021, 21--38URL: https://hal.inria.fr/hal-03281580
- 43 techreportFormal Analysis of Ladder Programs using Deductive Verification.RR-9402InriaApril 2021, URL: https://hal.inria.fr/hal-03199464
- 44 articleLet's Verify This with Why3.International Journal on Software Tools for Technology Transfer (STTT)1762015, 709--727
- 45 inproceedingsFormal Proof of a Wave Equation Resolution Scheme: the Method Error.Proceedings of the First Interactive Theorem Proving Conference6172LNCSEdinburgh, ScotlandSpringerJuly 2010, 147--162URL: http://hal.inria.fr/inria-00450789/
- 46 articleWave Equation Numerical Resolution: a Comprehensive Mechanized Proof of a C Program.Journal of Automated Reasoning504April 2013, 423--456URL: http://hal.inria.fr/hal-00649240/en/
- 47 inproceedingsCombining Coq and Gappa for Certifying Floating-Point Programs.16th Symposium on the Integration of Symbolic Computation and Mechanised Reasoning5625Lecture Notes in Artificial IntelligenceGrand Bend, CanadaSpringerJuly 2009, 59--74
- 48 articleVerified Compilation of Floating-Point Computations.Journal of Automated Reasoning542February 2015, 135-163URL: https://hal.inria.fr/hal-00862689
- 49 articleFormal verification of numerical programs: from C annotated programs to mechanical proofs.Mathematics in Computer Science542011, 377--393URL: http://hal.inria.fr/hal-00777605
- 50 articleProofs of numerical programs when the compiler optimizes.Innovations in Systems and Software Engineering722011, 151--160URL: http://hal.inria.fr/hal-00777639
- 51 articleAn overview of JML tools and applications.International Journal on Software Tools for Technology Transfer (STTT)73June 2005, 212--232
- 52 inproceedingsGOSPEL --- Providing OCaml with a Formal Specification Language.FM 2019 23rd International Symposium on Formal MethodsPorto, PortugalOctober 2019, URL: https://hal.inria.fr/hal-02157484
- 53 inproceedingsDeductive Verification with Ghost Monitors.Principles of Programming LanguagesNew Orleans, United States2020, URL: https://hal.inria.fr/hal-02368284
- 54 inproceedingsAlt-Ergo 2.2.SMT Workshop: International Workshop on Satisfiability Modulo TheoriesOxford, United KingdomJuly 2018
- 55 articleInstrumenting a Weakest Precondition Calculus for Counterexample Generation.Journal of Logical and Algebraic Methods in Programming992018, 97--113URL: https://hal.inria.fr/hal-01802488
- 56 techreportDeductive program verification for a language with a Rust-like typing discipline.Université de ParisSeptember 2020, URL: https://hal.science/hal-02962804
- 57 articleCertifying the floating-point implementation of an elementary function using Gappa.IEEE Transactions on Computers6022011, 242--253URL: http://hal.inria.fr/inria-00533968/en/
- 58 articleThe Spirit of Ghost Code.Formal Methods in System Design4832016, 152--174URL: https://hal.science/hal-01396864v1
- 59 inproceedingsAbstraction and Genericity in Why3.9th International Symposium On Leveraging Applications of Formal Methods, Verification and Validation (ISoLA)12476Lecture Notes in Computer ScienceRhodes, GreeceSpringerOctober 2020, 122--142URL: https://hal.inria.fr/hal-02696246
- 60 inproceedingsSpecification and Proof of High-Level Functional Properties of Bit-Level Programs.8th NASA Formal Methods Symposium9690Lecture Notes in Computer ScienceMinneapolis, MN, USASpringerJune 2016, 291--306URL: https://hal.inria.fr/hal-01314876
- 61 inproceedingsAutomating the Verification of Floating-Point Programs.Verified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/hal-01534533/
- 62 inproceedingsA Framework for Proof-carrying Logical Transformations.Proof eXchange for Theorem Proving336Electronic Proceedings in Theoretical Computer ScienceJuly 2021, 5--23URL: https://hal.science/hal-03349223
- 63 inproceedingsDes transformations logiques passent leur certicat.Trente-et-unièmes Journées Francophones des Langages ApplicatifsGruissan, FranceJanuary 2020, URL: https://hal.inria.fr/hal-02384946
- 64 inbookOpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case.Computer Aided Verification: 27th International Conference, CAV 2015, San Francisco, CA, USA, July 18-24, 2015, Proceedings, Part ID.Daniel KroeningC. S.Corina S. PăsăreanuChamSpringer International Publishing2015, 273--289
- 65 inproceedingsA Formally Verified Interpreter for a Shell-like Programming Language.Verified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/hal-01534747
- 66 techreportSpecification of UNIX Utilities.HAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321691
- 67 inproceedingsDeciding the First-Order Theory of an Algebra of Feature Trees with Updates.9th International Joint Conference on Automated ReasoningOxford, United KingdomJuly 2018, URL: https://hal.science/hal-01807474
- 68 articleseL4: Formal verification of an OS kernel.Communications of the ACM536June 2010, 107--115
- 69 articleA formally verified compiler back-end.Journal of Automated Reasoning4342009, 363--446URL: http://hal.inria.fr/inria-00360768/en/
- 70 articleProving Tight Bounds on Univariate Expressions with Elementary Functions in Coq.Journal of Automated Reasoning2016, URL: https://hal.inria.fr/hal-01086460
- 71 inproceedingsZ3, An Efficient SMT Solver.TACAS4963Lecture Notes in Computer ScienceSpringer2008, 337--340
- 72 bookHandbook of Floating-point Arithmetic (2nd edition).Birkhäuser BaselJuly 2018
- 73 inproceedingsHardware-Dependent Proofs of Numerical Programs.Certified Programs and ProofsLecture Notes in Computer ScienceSpringerDecember 2011, 314--329URL: http://hal.inria.fr/hal-00772508
- 74 articleHow testing helps to diagnose proof failures.Formal Aspects Comput.3062018, 629--657

