Keywords
Computer Science and Digital Science
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.4.1. Deterministic control
- A6.4.3. Observability and Controlability
- A6.4.4. Stability and Stabilization
- A6.4.5. Control of distributed parameter systems
- A6.4.6. Optimal control
- A6.5.1. Solid mechanics
- A6.5.4. Waves
Other Research Topics and Application Domains
- B3.3.1. Earth and subsoil
- B5.2.1. Road vehicles
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B5.4. Microelectronics
- B5.6. Robotic systems
- B7.1.2. Road traffic
- B9.5.2. Mathematics
- B9.5.5. Mechanics
- B9.11.1. Environmental risks
1 Team members, visitors, external collaborators
Research Scientists
- Vincent Acary [Team leader, INRIA, Senior Researcher, HDR]
- Franck Bourrier [INRAE, Researcher, HDR]
- Bernard Brogliato [INRIA, Senior Researcher, HDR]
- Olivier Goury [INRIA, Researcher]
- Félix A. Miranda Villatoro [INRIA, ISFP]
- Mohammad Rasool Mojallizadeh [INRIA, Starting Research Position]
- Arnaud Tonnelier [INRIA, Researcher, HDR]
Faculty Members
- Paul Armand [UNIV LIMOGES, Professor, from Feb 2022, HDR]
- Guillaume James [GRENOBLE INP, Professor, HDR]
Post-Doctoral Fellow
- Nicholas Anton Collins-Craft [INRIA]
PhD Students
- Hoang Minh Nguyen [INRIA]
- Quang Hung Pham [UNIV LIMOGES, from Oct 2022]
- Quang Hung Pham [GRENOBLE INP, from Jul 2022]
- Benoit Viano [INRIA]
- Aya Younes [UGA]
Technical Staff
- Franck Pérignon [CNRS, Engineer]
Interns and Apprentices
- Quang Hung Pham [GRENOBLE INP, from Feb 2022 until Jul 2022]
Administrative Assistant
- Diane Courtiol [INRIA]
External Collaborator
- Christophe Prieur [CNRS]
2 Overall objectives
2.1 Introduction
The joint research team, TRIPOP, between INRIA Grenoble Rhône–Alpes, Grenoble INP and CNRS, part of the Laboratoire Jean Kuntzmann (LJK UMR 5224) is mainly concerned with the modeling, the mathematical analysis, the simulation and the control of nonsmooth dynamical systems, with a strong application to modeling natural environmental risks in mountains.
Nonsmooth dynamics concerns the study of the time evolution of systems that are not smooth in the mathematical sense, i.e. systems that are characterized by a lack of differentiability, either of the mappings in their formulations, or of their solutions with respect to time. In mechanics, the main instances of nonsmooth dynamical systems are multibody systems with Signorini unilateral contact, set-valued (Coulomb-like) friction and impacts. In electronics, examples are found in switched electrical circuits with ideal components (diodes, switches, transistors). In control, nonsmooth systems arise in the sliding mode control theory and in optimal control. Many examples can also be found in cyber-physical systems (hybrid systems), in transportation sciences, in mathematical biology or in finance. For the next four years, the team is organized along two research axes: 1) nonsmooth simulation and numerical modeling for natural gravitational risks in mountains and 2) modeling, simulation and control of nonsmooth dynamical systems. The idea of this restructuring is to put forward a strong application axis for which there is a strong academic research dynamic in the Grenoble region and a network of socio-economic actors very interested in an industrial transfer of digital science methods on these subjects. The second axis takes up the main themes of the former axes of the TRIPOP project by updating them after the first four years.
2.2 General scope and motivations
Nonsmooth dynamics concerns the study of the time evolution of systems that are not smooth in the mathematical sense, i.e., systems that are characterized by a lack of differentiability, either of the mappings in their formulations, or of their solutions with respect to time. The class of nonsmooth dynamical systems recovers a large variety of dynamical systems that arise in many applications. The term “nonsmooth”, like the term “nonlinear”, does not precisely define the scope of the systems we are interested in but, and most importantly, they are characterized by the mathematical and numerical properties that they share. To give more insight into nonsmooth dynamical systems, we give in the following a very brief introduction of their salient features. For more details, we refer to 63, 35, 50, 77, 45, 66.
As we have indicated there are many applications to the methods of nonsmooth dynamics. We have chosen a strong particular application for this technique of nonsmooth dynamics which is that of natural gravity risk in the mountains. The choice of this application is particularly motivated by global climate change which has increased the number of rockfall and landslide events very significantly in recent decades. Especially, the effects of melting permafrost, increased rainfall and rapid temperature changes means that alpine regions are particularly at risk 87, 75. Another important interest is the strong academic research dynamics in the Grenoble region and a network of socio-economic actors very interested in an industrial transfer of digital science methods on these subjects. The team will conduct research on the mechanical modeling and simulation of natural hazards in mountains (floods and debris flows, block falls, glacial hazards), bringing new software development in a high performance computing (HPC) framework.
2.3 A flavor of nonsmooth dynamical systems
As a first illustration, let us consider a linear finite-dimensional system described by its state over a time-interval :
subjected to a set of inequality (unilateral) constraints:
If the constraints are physical constraints, a standard modeling approach is to augment the dynamics in (1) by an input vector that plays the role of a Lagrange multiplier vector. The multiplier restricts the trajectory of the system in order to respect the constraints. Furthermore, as in the continuous optimization theory, the multiplier must be signed and must vanish if the constraint is not active. This is usually formulated as a complementarity condition:
which models the one-sided effect of the inequality constraints. The notation holds component–wise and means . All together we end up with a Linear Complementarity System (LCS) of the form,
where is the matrix that models the input generated by the constraints. In a more general way, the constraints may also involve the Lagrange multiplier,
leading to a general definition of LCS as
[ scale=5,
axis/.style= ->, >=stealth',
important line/.style=very thick,
dashed line/.style=dashed, thin,
pile/.style=thick, ->, >=stealth', shorten <=2pt, shorten >=2pt,
every node/.style=color=black,
soldot/.style=only marks,mark=*,
holdot/.style=fill=white,only marks,mark=*
]
[axis] (-0.1,0) – (0.6,0) node(xline)[right] ;
[axis] (0,-0.1) – (0,0.6) node(yline)[right] ;
[important line] (0.0,0.5) – (0.0,.0) – (0.5,0.0);
The complementarity condition, illustrated in Figure 1 is the archetype of a nonsmooth graph that we extensively use in nonsmooth dynamics. The mapping is a multi-valued (set-valued) mapping, that is nonsmooth at the origin. It has many interesting mathematical properties and reformulations that come mainly from convex analysis and variational inequality theory. Let us introduce the indicator function of as
This function is convex, proper and can be sub-differentiated 69. The definition of the subdifferential of a convex function is defined as:
A basic result of convex analysis is
that gives a first functional meaning to the set-valued mapping . Another interpretation of is based on the normal cone to a closed and nonempty convex set :
It is easy to check that and it follows that
Finally, the definition of the normal cone yields a variational inequality:
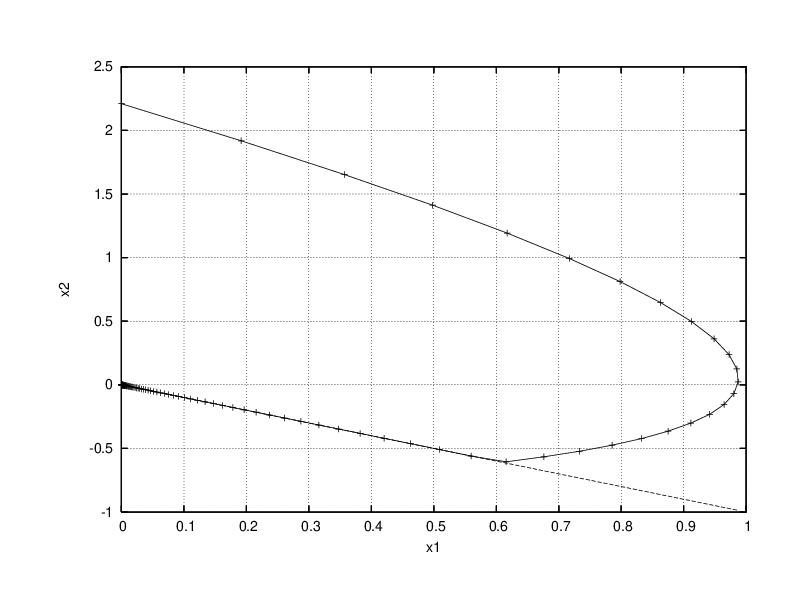
The relations (11) and (12) allow one to formulate the complementarity system with as a differential inclusion based on a normal cone (see (15)) or as a differential variational inequality. By extending the definition to other types of convex functions, possibly nonsmooth, and using more general variational inequalities, the same framework applies to the nonsmooth laws depicted in Figure 2 that includes the case of piecewise smooth systems.
The mathematical concept of solutions depends strongly on the nature of the matrix quadruplet in (6). If is a positive definite matrix (or a -matrix), the Linear Complementarity problem
admits a unique solution which is a Lipschitz continuous mapping. It follows that the Ordinary Differential Equation (ODE)
is a standard ODE with a Lipschitz right-hand side with a solution for the initial value problem. If , the system can be written as a differential inclusion in a normal cone as
that admits a solution that is absolutely continuous if is a definite positive matrix and the initial condition satisfies the constraints. The time derivative and the multiplier may have jumps and are generally considered as functions of bounded variations. If , the order of nonsmoothness increases and the Lagrange multiplier may contain Dirac atoms and must be considered as a measure. Higher–order index, or higher relative degree systems yield solutions in terms of distributions and derivatives of distributions 33.
A lot of variants can be derived from the basic form of linear complementarity systems, by changing the form of the dynamics including nonlinear terms or by changing the complementarity relation by other multivalued maps. In particular the nonnegative orthant may be replaced by any convex closed cone leading to complementarity over cones
where its dual cone given by
In Figure 2, we illustrate some other basic maps that can be used for defining the relation between and . The saturation map, depicted in Figure 2(a) is a single valued continuous function which is an archetype of a piece-wise smooth map. In Figure 2(b), the relay multi-function is illustrated. If the upper and the lower limits of are respectively equal to 1 and , we obtain the multivalued sign function defined as
Using again convex analysis, the multivalued sign function may be formulated as an inclusion into a normal cone as
More generally, any system of the type,
can reformulated in terms of the following set-valued system
The system (21) appears in a lot of applications; among them, we can cite the sliding mode control, electrical circuits with relay and Zener diodes 28, or mechanical systems with friction 35.
[Saturation] [ scale=5, axis/.style= ->, >=stealth', important line/.style=very thick, dashed line/.style=dashed, thin, pile/.style=thick, ->, >=stealth', shorten <=2pt, shorten >=2pt, every node/.style=color=black ] [axis] (-0.4,0) – (0.4,0) node(xline)[right] ; [axis] (0,-0.4) – (0,0.4) node(yline)[above] ; [important line] (-0.4,-0.3) – (-.1,-.3) –(0.1,0.3) –(.4,.3) ;
[Relay]
[ scale=5,
axis/.style= ->, >=stealth',
important line/.style=very thick,
dashed line/.style=dashed, thin,
pile/.style=thick, ->, >=stealth', shorten <=2pt, shorten >=2pt,
every node/.style=color=black,
soldot/.style=only marks,mark=*,
holdot/.style=fill=white,only marks,mark=* ]
[axis] (-0.4,0) – (0.4,0) node(xline)[right] ;
[axis] (0,-0.4) – (0,0.4) node(yline)[above] ;
[important line] (-0.4,-0.3) – (-.0,-.3);
[important line] (-0.0,-0.3) – (-.0,.3);
[important line](0.0,0.3) –(.4,.3) ;
[Relay with dead zone]
[ scale=5,
axis/.style= ->, >=stealth',
important line/.style=very thick,
dashed line/.style=dashed, thin,
pile/.style=thick, ->, >=stealth', shorten <=2pt, shorten >=2pt,
every node/.style=color=black,
soldot/.style=only marks,mark=*,
holdot/.style=fill=white,only marks,mark=* ]
[axis] (-0.4,0) – (0.4,0) node(xline)[right] ;
[axis] (0,-0.4) – (0,0.4) node(yline)[above] ;
[important line] (-.4,-.3) – (-0.1,-0.3) ;
[important line] (-0.1, 0.0) – (0.1,0.0);
[important line] (0.1,0.3) – (0.4,0.3);
[important line] (-0.1,-0.3) – (-0.1,0.0);
[important line] (0.1,-0.0) – (0.1,0.3);
Though this class of systems seems to be rather specific, it includes as well more general dynamical systems such as piecewise smooth systems and discontinuous ordinary differential equations. Indeed, the system (20) for scalars and can be viewed as a discontinuous differential equation:
One of the most well-known mathematical frameworks to deal with such systems is the Filippov theory 63 that embeds the discontinuous differential equations into a differential inclusion. In the case of a single discontinuity surface given in our example by , the Filippov differential inclusion based on the convex hull of the vector fields in the neighborhood of is equivalent to the use of the multivalued sign function in (20). Conversely, as it has been shown in 39, a piecewise smooth system can be formulated as a nonsmooth system based on products of multivalued sign functions.
2.4 Nonsmooth Dynamical systems in the large
Generally, the nonsmooth dynamical systems we propose to study mainly concern systems that possess the following features:
- A nonsmooth formulation of the constitutive/behavioral laws that define the system. Examples of nonsmooth formulations are piecewise smooth functions, multi–valued functions, inequality constraints, yielding various definitions of dynamical systems such as piecewise smooth systems, discontinuous ordinary differential equations, complementarity systems, projected dynamical systems, evolution or differential variational inequalities and differential inclusions (into normal cones). Fundamental mathematical tools come from convex analysis 88, 68, 69, complementarity theory 58, and variational inequalities theory 62.
- A concept of solutions that does not require continuously differentiable functions of time. For instance, absolutely continuous, Lipschitz continuous functions or functions of local bounded variation are the basis for solution concepts. Measures or distributions are also solutions of interest for differential inclusions or evolution variational inequalities.
2.5 Nonsmooth systems versus hybrid systems
The nonsmooth dynamical systems we are dealing with, have a nonempty intersection with hybrid systems and cyber-physical systems, as is briefly discussed in Sect. 3.3.1. Like in hybrid systems, nonsmooth dynamical systems define continuous-time dynamics that can be identified with modes separated by guards, defined by the constraints. However, the strong mathematical structure of nonsmooth dynamical systems allows us to state results on the following points:
- Mathematical concept of solutions: well-posedness (existence, and possibly, uniqueness properties, (dis)continuous dependence on initial conditions).
- Dynamical systems theoretic properties: existence of invariants (equilibria, limit cycles, periodic solutions,...) and their stability, existence of oscillations, periodic and quasi-periodic solutions and propagation of waves.
- Control theoretic properties: passivity, controllability, observability, stabilization, robustness.
These latter properties, that are common for smooth nonlinear dynamical systems, distinguish the nonsmooth dynamical systems from the very general definition of hybrid or cyber-physical systems 43, 67. Indeed, it is difficult to give a precise mathematical concept of solutions for hybrid systems since the general definition of hybrid automata is usually too loose.
2.6 Numerical methods for nonsmooth dynamical systems
To conclude this brief exposition of nonsmooth dynamical systems, let us recall an important fact related to numerical methods. Beyond their intrinsic mathematical interest, and the fact that they model real physical systems, using nonsmooth dynamical systems as a model is interesting, because there exists a large set of robust and efficient numerical techniques to simulate them. Without entering into the finer details, let us give two examples of these techniques:
- Numerical time integration methods: convergence, efficiency (order of consistency, stability, symplectic properties). For the nonsmooth dynamical systems described above, there exist event-capturing time-stepping schemes with strong mathematical results. These schemes have the ability to numerically integrate the initial value problem without performing an event location, but by capturing the event within a time step. We call an event, or a transition, every change into the index set of the active constraints in the complementarity formulation or in the normal cone inclusion. Hence these schemes are able to simulate systems with a huge number of transitions or even with finite accumulation of events (Zeno behavior). Furthermore, the schemes do not suffer from the weaknesses of the standard schemes based on a regularization (smoothing) of the multi-valued mapping resulting in stiff ordinary differential equations. For the time-integration of the initial value problem (IVP), or Cauchy problem, a lot of improvements of the standard time-stepping schemes for nonsmooth dynamics (Moreau–Jean time-stepping scheme) have been proposed in the last decade, in terms of accuracy and dissipation properties 38, 41, 89, 90, 37, 57, 52, 92, 54. A significant number of these schemes have been developed by members of the BIPOP team and have been implemented in the Siconos software.
- Numerical solution procedure for the time–discretized problem, mainly through well-identified problems studied in the optimization and mathematical programming community. Another very interesting feature is the fact that the discretized problem that we have to solve at each time–step is generally a well-known problem in optimization. For instance, for LCSs, we have to solve a linear complementarity problem 58 for which there exist efficient solvers in the literature. Compared to the brute force algorithm with exponential complexity that consists of enumerating all the possible modes, the algorithms for linear complementarity problem have polynomial complexity when the problem is monotone.
3 Research program
3.1 Introduction
In this section, we develop our scientific program. In the framework of nonsmooth dynamical systems, the activities of the project–team will be focused on the following research axes:
- Axis 1: Nonsmooth simulation and numerical modeling for natural gravitational risk in mountains. (detailed in Sect. 3.2).
- Axis 2: Modeling, simulation and control (detailed in Sect. 3.3).
These research axes will be developed with a strong emphasis on the software development and the industrial transfer.
3.2 Axis 1: Nonsmooth simulation and numerical modeling for natural gravitational risk in mountains.
In this research axis, we propose, on the one hand, to extend existing methods of simulation in mechanics of complex flows in a nonsmooth framework, which allows us to simplify the models by decreasing the physical parameters, and to make more robust the numerical simulations and thus to make possible the construction of reduced models or meta-models. On the other hand, the so-called "data-driven modeling" methods will be explored for gravity flows and prevention structures. The aim is to make the most of laboratory and observational data in order to build and calibrate the models, to evaluate their sensitivity, to improve their predictive character, i.e. to control and take into account the uncertainties, thanks to variational, statistical and AI methods.
This work will be conducted in close collaboration with the UR ETNA of INRAE as well as other researchers from INRIA (AIRSEA, LEMON). More generally, our collaboration with INRAE opens new long term perspectives on granular flow applications such as debris and mud flows, granular avalanches and the design of structural protections. The numerical methods that go with these new modeling approaches will be implemented in our software Siconos).
This research is also part of the more general context of a digital platform on environmental risk in the mountains, including intensive and cloud computing.
3.2.1 Rockfall trajectory modeling
Trajectory analysis of falling rocks during rockfall events is limited by the currently unrefined modeling of the impact phase 48, 47, 76. The goal of this axis is to improve reliability of simulation techniques.
- Rock fracturing: When a rock falls from a steep cliff, it stores a large amount of kinetic energy that is partly dissipated though the impact with the ground. If the ground is composed of rocks and the kinetic energy is sufficiently high, the probability of the fracture of the rock is high and yields an extra amount of dissipated energy but also an increase of the number of blocks that fall. In this topic, we want to use the capability of the nonsmooth dynamical framework for modeling cohesion and fracture 74, 40 to propose new cohesive zone models with contact and friction.
- Rock/forest interaction: To prevent damage and incidents to infrastructure, a smart use of the forest is one of the ways to control trajectories (decrease of the run-out distance, jump heights and the energy) of the rocks that fall under gravity 59, 61. From the modeling point of view and to be able to improve the protective function of the forest, an accurate modeling of impacts between rocks and trees is required. Due to the aspect ratio of the trees, they must be considered as flexible bodies that may be damaged by the impact. This new aspect offers interesting modeling research perspectives, especially, building rockfall simulation method with mechanical models of trees including damage, fracture and plasticity.
- Experimental validation: The participation of INRAE with F. Bourrier makes possible the experimental validation of models and simulations through comparisons with real data. INRAE has extensive experience of lab and in-situ experiments for rockfall trajectory modeling 48, 47. It is a unique opportunity to strengthen our model and to prove that nonsmooth modeling of impacts is reliable for such experiments and forecasting of natural hazards.
3.2.2 Modeling and simulation of gravity hazards (debris flows, avalanches and large-scale rock flows)
Different modeling approaches are used in the literature depending on the type of hazard.
For rockfalls and dense snow avalanches, methods that explicitly model the particles of granular materials (notably Discrete Element Methods - DEM) are preferred, whereas for flows (debris flows, avalanches and large-scale rockfalls), methods that assimilate the large number of individual constituents to materials with complex rheology are more commonly used (notably Material Point Method - MPM, Smoothed-Particle Hydrodynamics - SPH, Shallow Water models - SWM). It should be noted that these methods are most often explicit and regularize the constraints of inequalities and thresholds.
This research item will develop the following points:
- Rethinking DEM, MPM, SPH and SWM methods in the nonsmooth framework. This will allow a simple and efficient modeling of threshold and inequality phenomena (one-sided contact, impact with Coulomb friction, threshold behavior laws such as plasticity, damage or fracture, Bingham-type fluids) in order to develop new, implicit and robust numerical methods, where the most important physical features of frictional cohesive materials are well-modeled neglecting the second order phenomena. In a context of data utilization and prediction, these methods seem particularly well suited as our first experiments on block trajectography and rock flows have already shown.
- Couple these methods to integrate the "multi-scale (micro/meso/macro)" character of these problems or, more simply, to spatially couple at the same scale several physical phenomena better taken into account by different methods, for example a debris flow containing a material with complex rheology (MPM or SPH) and large size particles (DEM)
- Use “data-driven mechanics” approaches when behavioral models are not reliable and faithful to the observed physical phenomena. These techniques can also be used to model “sub-mesh” phenomena, which are not or only slightly taken into account in large-scale phenomenological models.
3.2.3 Data-driven modelling for prediction and mitigation of gravity hazards
The objective is to develop simplified models that can be used extensively for the development of calibration and uncertainty quantification methods that allow for the joint use of data from various sources to evaluate and improve the predictive capacity of gravity hazard models.
The following points will be developed:
- Statistical models integrating various types of data and the hazard models developed in the previous section. The identification of the parameters of these hazard models, in particular using Bayesian approaches, will also allow the calibration and quantification of the uncertainties associated with the hazard models.
- Model reduction approaches (POD, PGD,...) or construction of substitution models (Sparse Polynomial Chaos, Gaussian Processes,...) to build simplified models usable in this context.
- Application of different data assimilation techniques (particle filters or variational methods) on the models described in the first axis and the reduced order models.
3.3 Axis 2: Modeling, simulation and control of non-smooth dynamical systems.
This axis is dedicated to the modeling and the mathematical analysis of nonsmooth dynamical systems. It consists of two main directions: 1) Modeling, analysis and numerical methods and 2) Automatic control.
3.3.1 Modeling, analysis and numerical methods
Multibody vibro-impact systems
- Multiple impacts with or without friction (short-term): there are many different approaches to model collisions, especially simultaneous impacts (so-called multiple impacts) 83. One of our objectives is on one hand to determine the range of application of the models (for instance, when can one use “simplified” rigid contact models relying on kinematic, kinetic or energetic coefficients of restitution?) on typical benchmark examples (chains of aligned beads, rocking block systems). On the other hand, we will try to take advantage of the new results on nonlinear wave phenomena, to better understand multiple impacts in 2D and 3D granular systems. The study of multiple impacts with (unilateral) nonlinear visco-elastic models (Simon–Hunt–Crossley, Kuwabara–Kono), or visco-elasto-plastic models (assemblies of springs, dashpots and dry friction elements), is also a topic of interest, since these models are widely used.
- Artificial or manufactured or ordered granular crystals, meta-materials (short-term): Granular metamaterials (or more general nonlinear mechanical metamaterials) offer many perspectives for the passive control of waves originating from impacts or vibrations. The analysis of waves in such systems is delicate due to spatial discreteness, nonlinearity and non-smoothness of contact laws 86, 73, 72, 78. We will use a variety of approaches, both theoretical (e.g. bifurcation theory, modulation equations) and numerical, in order to describe nonlinear waves in such systems, with special emphasis on energy localization phenomena (excitation of solitary waves, fronts, breathers).
- Systems with clearances, modeling of friction (long-term): joint clearances in kinematic chains deserve specific analysis, especially concerning friction modeling 42. Indeed contacts in joints are often conformal, which involve large contact surfaces between bodies. Lubrication models should also be investigated.
- Painlevé paradoxes (long-term): the goal is to extend the results in 65, which deal with single-contact systems, to multi-contact systems. One central difficulty here is the understanding and the analysis of singularities that may occur in sliding regimes of motion.
As a continuation of the work in the BIPOP team, our software Siconos will be our favored software platform for the integration of these new modeling results.
Systemic risk
- The high consumption of natural resources by our society puts in question its long-term sustainability. The decrease of natural resources results in a deterioration of human welfare with a risk of society instability. Recently, a simple nature-society interrelations model, called the HANDY model (Human And Nature DYnamics), has been proposed by Montesharrei et al (2014) to address this concern with a special emphasis on the role of the stratification of the society. The Handy model is a four dimensional nonlinear dynamical system that describes the evolution of population, resources and accumulated wealth. We analyse the dynamics of this model and we explore the influence of two parameters: the nature depletion rate and the inequality factor. We characterize the asymptotic states of the system through a bifurcation analysis and we derive several quantitative results on the trajectories. We show that some collapses are irreversible and, depending on the wealth production factor, a bistability regime between a sustainable equilibrium and cycles of collapse-and-regeneration can be obtained. We discuss possible policies to avoid dramatic scenarios.
Cyber-physical systems (hybrid systems)
Participants: V. Acary, B. Brogliato, C. Prieur, A. Tonnelier
Nonsmooth systems have a non-empty intersection with hybrid systems and cyber–physical systems. However, nonsmooth systems enjoy strong mathematical properties (concept of solutions, existence and uniqueness) and efficient numerical tools. This is often the result of the fact that nonsmooth dynamical systems are models of physical systems, and so can take advantage of their intrinsic properties (conservation or dissipation of energy, passivity, stability). A standard example is a circuit with ideal diodes. From the hybrid point of view, this circuit is a piecewise smooth dynamical system with modes, that can be quite cumbersome to enumerate in order to determinate the current mode. As a nonsmooth system, this circuit can be formulated as a complementarity system for which there exist efficient time-stepping schemes and polynomial time algorithms for the computation of the current mode. The key idea of this research action is to benefit from this observation to improve hybrid system modeling tools.
Structural analysis of multimode DAE : When a hybrid system is described by a Differential Algebraic Equation (DAE) with different differential indices in each continuous mode, the structural analysis has to be completely rethought. In particular, the re-initialization rule, when a switching occurs from one mode to another, has to be consistently designed. We propose in this action to use our knowledge in complementarity and (distribution) differential inclusions 33 to design consistent re-initialization rules for systems with nonuniform relative degree vector and .
Cyber–physical in hybrid systems modeling languages : Nowadays, some hybrid modeling languages and tools are widely used to describe and to simulate hybrid systems (modelica, simulink, and see 55 for references therein). Nevertheless, the compilers and the simulation engines behind these languages and tools suffer from several serious weaknesses (failure, nonsensical output or extreme sensitivity to simulation parameters), especially when some components, that are standard in nonsmooth dynamics, are introduced (piecewise smooth characteristic, unilateral constraints and complementarity condition, relay characteristic, saturation, dead zone, ...). One of the main reasons is the fact that most of the compilers reduce the hybrid system to a set of smooth modes modeled by differential algebraic equations and some guards and reinitialization rules between these modes. Sliding mode and Zeno-type behaviour are extremely difficult for hybrid systems and relatively simple for nonsmooth systems. With B. Caillaud (Inria HYCOMES) and M. Pouzet (Inria PARKAS), we propose to improve this situation by implementing a module able to identify/describe nonsmooth elements and to efficiently handle them with siconos as the simulation engine. They have already carried out a first implementation 53 in Zelus, a synchronous language for hybrid systems Zelus. Removing the weaknesses related to the nonsmoothness of solutions should improve hybrid systems towards robustness and certification.
A general solver for piecewise smooth systems This direction is the continuation of the promising result on modeling and the simulation of piecewise smooth systems 39. As for general hybrid automata, the notion or concept of solutions is not rigorously defined from the mathematical point of view. For piecewise smooth systems, multiplicity of solutions can happen and sliding solutions are common. The objective is to recast general piecewise smooth systems in the framework of differential inclusions with Aizerman–Pyatnitskii extension 39, 63. This operation provides a precise meaning to the concept of solutions. Starting from this point, the goal is to design and study an efficient numerical solver (time-integration scheme and optimization solver) based on an equivalent formulation as mixed complementarity systems of differential variational inequalities. We are currently discussing the issues in the mathematical analysis. The goal is to prove the convergence of the time-stepping scheme to get an existence theorem. With this work, we should also be able to discuss the general Lyapunov stability of stationary points of piecewise smooth systems.
Numerical optimization for discrete nonsmooth problems
- Second Order Cone Complementarity Problems (SOCCP) for discrete frictional systems (short-term): After some extensive comparisons of existing solvers on a large collection of examples 32, 29, the numerical treatment of constraint redundancy by the proximal point technique and the augmented Lagrangian formulation seems to be a promising path for designing new methods. From the comparison results, it appears that the redundancy of constraints prevents the use of second order methods such as semi-smooth Newton methods or interior point methods. With P. Armand (XLIM, U. de Limoges), we propose to adapt recent advances for regularizing constraints for the quadratic problem 64 for the second-order cone complementarity problem.
- The other question is the improvement of the efficiency of the algorithms by using accelerated schemes for the proximal gradient method that come from large-scale machine learning and image processing problems. Learning from the experience in large-scale machine learning and image processing problems, the accelerated version of the classical gradient algorithm 82 and the proximal point algorithm 44, and many of their further extensions, could be of interest for solving discrete frictional contact problems. Following the visit of Y. Kanno (University of Tokyo) and his preliminary experience on frictionless problems, we will extend its use to frictional contact problem. When we face large-scale problems, the main available solvers is based on a Gauss–Seidel strategy that is intrinsically sequential. Accelerated first-order methods could be a good alternative to benefit from distributed scientific computing architectures.
3.3.2 Automatic Control
This last item is dedicated to the automatic control of nonsmooth dynamical systems, or the nonsmooth control of smooth systems. The first research direction concerns the discrete-time sliding mode control and differentiation. The second research direction concerns multibody systems with unilateral constraint, impacts and set-valued friction. The third research direction concerns a class of dynamics which is an extension of linear complementarity systems (or, equivalently, of differential algebraic equations).
Discrete-time Sliding-Mode Control (SMC), State Observers (SMSO) and Differentiators (SMD)
- SMC with output feedback: Output feedback can take different forms, like the use of observers/differentiators in the loop (specific dynamic output feedback), or the design of static or dynamic output feedback (without state observation). The time-discretization of such feedback systems and its analysis remains largely open.
- Unifying algorithm for discrete-time SMC and SMD: maximal monotone operators, proximal algorithms.
Control of nonsmooth discrete Lagrangian systems
- Linear Complementarity Systems (LCS): the PhD thesis of Aya Younes is dedicated to the trajectory tracking control in LCS. In particular the cases with uncertainties and with state jumps are carefully analysed. The PhD thesis of Quang-Hung Pham focuses on networks of LCS. In both cases passivity is a central tool for the analysis.
- Optimal control: the optimal control of mechanical systems with unilateral constraints and impacts, largely remains an open issue. Through a collaboration with Moritz Diehl (Freiburg University) the problem has been tackled using a suitable dynamics transformation of Lagrangian complementarity systems into a Filippov "classical" differential inclusion with absolutely continuous solutions. The results are restricted to a single unilateral frictionless constraint. The global objective is to enlarge it to multiple unilateral constraints (hence multiple impacts) and friction.
- Cable-driven systems: these systems are typically different from the cable-car systems, and are closer in their mechanical structure to so-called tensegrity structures. The objective is to actuate a system via cables supposed in the first instance to be flexible (slack mode) but non-extensible in their longitudinal direction. This gives rise to complementarity conditions, one big difference with usual complementarity Lagrangian systems being that the control actions operate directly in one of the complementary variables (and not in the smooth dynamics as in cable-car systems). Therefore both the cable models and the control properties are expected to differ a lot from what we may use for cableway systems (for which guaranteeing a positive cable tension is usually not an issue, hence avoiding slack modes, but the deformation of the cables due to the nacelles and cables weights, is an important factor). Tethered systems are a close topic.
- Robot-object underactuated dynamical systems: such systems are made of a controlled part (called the robot) and an uncontrolled part (called the object). Both are linked by Lagrange multipliers which represent the contact forces. The object can be controlled only through the multipliers, which are in turn a function of the system's state. Examples are bipeds which walk, run, jump, juggling, tapping, pushing robots, prehensile and non-prehensile tasks, some cable-driven systems, and some circuits with nonsmooth set-valued components. A global approach consists in a backstepping-like control strategy. The goal is to derive a unifying framework which can be easily adapted to all these various systems and tasks.
Switching LCS and DAEs
- We have gained a strong experience in the field of complementarity systems and distribution differential inclusions 33, 51, that may be seen as some kind of switching DAEs. More recently we have obtained preliminary results on the analysis of so-called differential-algebraic linear complementarity systems (DALCS) and descriptor-variable LCS (DVLCS), as well as on switching DAEs with state-dependent swithing bilateral constraints. These systems can be seen as DAEs with added complementarity constraints, or as LCS with added equality constraints, or as DAEs with nonsmooth equality constraints. Their well-posedness (existence and uniqueness of solutions to the one-step nonsmooth problem of the implicit Euler scheme, existence and uniqueness of solutions to the continuous-time system) is non-trivial. The case of systems with state-jumps also requires careful analysis.
- A closely related subject is that of interconnections of LCSs or extensions of these (like differential inclusions with maximal monotone properties). The stability of the interconnected system is a topic of interest, as well as, the resulting collective behavior.
Dynamics of complex nonlinear networks, set-valued couplings
- The interconnections of uncertain dynamical systems is a topic of broad interest within the control community. For the case of nonlinear agents with set-valued coupling laws, many questions remain open regarding the resulting behavior of the network, as well as, their robustness properties against parametric uncertainties and external disturbances. The PhD thesis of Quang-Hung Pham focuses on such issues within the context of robust synchronization of LCSs.
- Recently, novel extensions of the concept of passivity have been studied for the analysis of systems away from equilibrium 14. However, their relevance in the context of networks remains largely unexplored.
- Two-dimensional networks of oscillators with set-valued generalized Coulomb friction laws arise challenging questions regarding their dynamics (nonlinear oscillations, localized waves, excitability), with applications in earthquake dynamics and friction control.
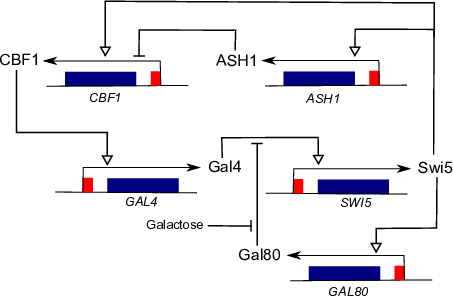
- G. James has recently introduced in collaboration with F. Karbou (Centre d'Etudes de la Neige, Grenoble) a nonsmooth dynamical system on a network suitable for segmenting wet snow areas in SAR (synthetic-aperture radar) satellite images. The network corresponds to a large ensemble of pixels of a grayscale image, whose evolutions are coupled or uncoupled depending on their distance and local topography given by a digital elevation model. This yields an excitable dynamical system that tends to create domain walls surrounding snowy areas. The system provides very good identification results and arises nontrivial questions regarding its theoretical analysis, optimization (parameters, complexity) and generalizations.
4 Application domains
4.1 Domain 1
Nonsmooth dynamical systems arise in many application fields. We briefly highlight here some applications that have been treated in the BIPOP team and that we will continue in the TRIPOP team, as a validation for the research axes and also in terms of transfer.
In mechanics, the main instances of nonsmooth dynamical systems are multibody systems with Signorini's unilateral contact, set-valued (Coulomb-like) friction and impacts, or in continuum mechanics, ideal plasticity, fracture or damage. Some illustrations are given in Figure 4(a-f). Other instances of nonsmooth dynamical systems can also be found in electrical circuits with ideal components (see Figure 4(g)) and in control theory, mainly with sliding mode control and variable structure systems (see Figure 4(h)). More generally, every time a piecewise, possibly set–valued, model of systems is invoked, we end up with a nonsmooth system. This is the case, for instance, for hybrid systems in nonlinear control or for piecewise linear modeling of gene regulatory networks in mathematical biology (see Figure 4(i)). Another common example of nonsmooth dynamics is also found when the vector field of a dynamical system is defined as a solution of an optimization problem under constraints, or a variational inequality. Examples of this kind are found in optimal control theory, in dynamic Nash equilibrium or in the theory of dynamic flows over networks.
[Rockfall 48, 47, 61, granular and debris flows]


[Frictional interface and solitary waves in the Burridge-Knopoff model 81]
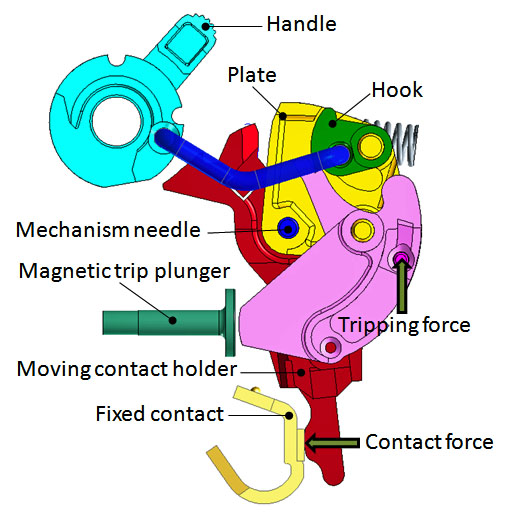
[Circuit breakers mechanisms 42 and Robots (ESA ExoMars Rover 31)]


[Switched electrical circuits (delta-sigma converter) 28]
[Sliding mode control 34, 36, 70, 71, 79]
[Gene regulatory networks 39]
5 Social and environmental responsibility
As for the environmental footprint, we have already decided to drastically reduce our air travel and our participation in international conferences. For instance, trips of less than 10 hours by train should not be made by plane. International conferences should be coupled with a visit to colleagues or other scientific events. Concerning the computer equipment, it is not replaced before 5 years and we try to keep the office machines between 7 and 10 years.
Regarding the social impact, the emergence of the research axis 1 on natural gravitational hazards in relation to climate change and studies on systemic risk are a way to focus research on the major concerns of societies. Industrial collaborations are now also evaluated according to the social and environmental responsibility efforts of the partners.
The question of the social and environmental footprint and impact of our research will be discussed in more detail at our next team seminar.
6 New software and platforms
6.1 New software
6.1.1 SICONOS
-
Name:
Modeling, simulation and control of nonsmooth dynamical systems
-
Keywords:
NSDS, MEMS, DCDC, SD, Collision, Friction, Mechanical multi-body systems
-
Scientific Description:
The aim of this work is to provide a common platform for the simulation, modeling, analysis and control of abstract nonsmooth dynamical systems. Besides usual quality attributes for scientific computing software, we want to provide a common framework for various scientific fields, to be able to rely on the existing developments (numerical algorithms, description and modeling software), to support exchanges and comparisons of methods, to disseminate the know-how to other fields of research and industry, and to take into account the diversity of users (end-users, algorithm developers, framework builders) in building expert interface in Python. After the requirements elicitation phase, the Siconos Software project has been divided into 5 work packages which are identified to software products:
• SICONOS/NUMERICS This library contains a set of numerical algorithms, already well identified, to solve non smooth dynamical systems. This library is written in low-level languages (C,F77) in order to ensure numerical efficiency and the use of standard libraries (Blas, Lapack, . . . )
• SICONOS/KERNEL This module is an object-oriented structure (C++) for the modeling and the simulation of abstract dynamical systems. It provides the users with a set of classes to describe their nonsmooth dynamical system (dynamical systems, interactions, nonsmooth laws, . . . ) and to perform a numerical time integration and solving.
• SICONOS/FRONT-END. This module is mainly an auto-generated wrapper in Python which provides a user-friendly interface to the Siconos libraries. A scilab interface is also provided in the Front-End module.
• SICONOS/CONTROL This part is devoted to the implementation of control strategies of non smooth dynamical systems.
• SICONOS/MECHANICS. This part is dedicated to the modeling and the simulation of multi-body systems with 3D contacts, impacts and Coulomb’s friction. It uses the Siconos/Kernel as simulation engine but relies on a industrial CAD library (OpenCascade and pythonOCC) to deal with complex body geometries and to compute the contact locations and distances between B-Rep description and on Bullet for contact detection between meshes.
-
Functional Description:
Siconos is an open-source scientific software primarily targeted at modeling and simulating nonsmooth dynamical systems in C++ and in Python:
- Mechanical systems (rigid or solid) with unilateral contact and Coulomb friction and impact (nonsmooth mechanics, contact dynamics, multibody systems dynamics or granular materials).
- Switched Electrical Circuit such as electrical circuits with ideal and piecewise linear components: power converter, rectifier, Phase-Locked Loop (PLL) or Analog-to-Digital converter.
- Sliding mode control systems.
- Biology (Gene regulatory network). Other applications are found in Systems and Control (hybrid systems, differential inclusions, optimal control with state constraints), Optimization (Complementarity systems and Variational inequalities), Fluid Mechanics, and Computer Graphics.
-
Release Contributions:
Main changes:
[numerics] add sparse linear solver with a sparse rhs based on csparse [numerics] new implementation of NM_LU_solve and NM_Cholesky_solve [kernel] new implementation of linear solvers in SimpleMatrix The class SimpleMatrix owns a internal NumericsMatrix thats is used for linear system solving, based on Siconos/Numerics [numerics] add balancing matrice framework [numerics] add freezing contacts in Gauss seidel solvers [externals] add LDL support [mechanics] modify broadphase for Bullet [numerics] render the truncation in NM_entry [numerics] add matrix versioning [misc] automates the generation of docker end-user images 'siconos-ready' [misc] build with ninja
- URL:
-
Contact:
Vincent Acary
-
Participants:
Franck Pérignon, Maurice Bremond, Vincent Acary
7 New results
7.1 Numerical Modeling for natural risk in mountains
7.1.1 Numerical modeling of rockfall trajectory
Participants: Vincent Acary, Franck Bourrier.
Rockfall propagation models are routinely used for the quantitative assessment of rockfall hazard. Their capacities and limitations remain difficult to assess due to the limited amount of exhaustive experimental data at the slope scale.
The article 49 presents experiments of block propagation performed in a quarry located in Authume (France). A total of more than one hundred blocks were released on two propagation paths. The propagation of the blocks was assessed by measuring the block stopping points as well as their kinematics at specific locations of the paths, called evaluation screens. Significant variability of the stopping points and of the block kinematics at the evaluation screens was observed and preferential transit and deposit zones were highlighted. The analysis of the results showed predominant effect of topography, in particular that related to topographical discontinuities. Significant influence of local and small scale parameters (e.g. block orientation, local topography) was also highlighted. These conclusions are of particular interest for researchers or practitioners who would like to assess the relevance of propagation modelling tools considering this complex study site. In this configuration, the quality of block propagation simulations should notably rely on the accuracy of digital terrain models, and on the integration of local conditions effects using physically based approaches.
Complementary with the research held in 49, the predictive capabilities of block propagation models after a preliminary calibration phase is investigated. It is focused on models integrating the shape of blocks since, despite their sound physical bases, they remain less used than lumped-mass approaches due to their more recent popularisation. We first performed an expert-based calibration based on the use of the 2D model and, second, evaluated the predictive capabilities of the calibrated model in 2D and in 3D using the remaining part of the experimental results. The calibrated model simulations predict the main characteristics of the propagation : after a calibration phase on sufficient amount of soil types, the model may be used in a predictive manner. The adequacy between 2D and 3D simulations also favors applicability of the model since easier and faster calibrations based on 2D simulations only can be envisaged. As classically observed for block propagation models, the model is not sufficient to predict the details of the velocity and stopping points but provides accurate prediction of the global ranges of these quantities, in particular of the extreme values. To lift these limitations in terms of predictive capabilities, more advanced calibration procedures based on optimization techniques can constitute a promising perspective as it is studied in 4.
7.1.2 Numerical modeling of fracture in solids
Participants: Vincent Acary, Franck Bourrier, Nicholas Collins-Craft.
In 11, a new extrinsic cohesive model is developed together with a consistent time–stepping scheme to simulate fracture in quasi-brittle material like rock or concrete. An extrinsic cohesive zone model with a novel unload-reload behaviour is developed in the framework of non-smooth mechanics. The model is extended to include the effects of dynamics with impact, and is discretised in such a way that it can be written as a Linear Complementarity Problem (LCP). This LCP is proved to be well-posed, and to respect the discrete energy balance of the system. Finally, the LCP system is validated numerically, in both statics and dynamics, by simple test cases, and more involved finite element simulations that correspond to standard test geometries in the literature. The results correspond well with those of other authors, while also demonstrating the simulations’ ability to resolve with relatively large time steps while respecting the energetic balance. We are now working on the development of a model taking into account the tangential cohesion coupled with the Coulomb friction. The objective is to propose a model coupled with hydro-thermal freezing and thawing phenomena in rock interfaces, which will be used to simulate the stability of cliffs in connection with the thawing of permafrost.
7.1.3 Numerical modeling of flexible barriers
Participants: Franck Bourrier.
The research held in 13 addresses the use of mechanical similitudes for the design of flexible barriers. A particular focus is placed on flexible barriers aimed at containing flow-driven solid materials. A set of five parameters is proposed to serve as similitude criteria relevant to this application. These refer to the flow velocity and to the dimensions and mechanical characteristics of the barrier components. The validity of this set of five criteria is assessed considering a simple barrier exposed to hydro-dynamic loading. In this purpose, a discrete element model is used to conduct simulations at various scales. In a second time, a real barrier with complex features is scaled for conducting flume experiments. This scaled barrier is printed from selected polymers, so that the mechanical characteristics of the barrier components meet the similitude criterion. For validation purpose, the barrier model is tested under hydro-static loading and its deformation is compared with that of the barrier at the real scale simulated with a discrete element model of the barrier.
7.2 Systemic risk
Participants: Arnaud Tonnelier, Vincent Acary.
The overexploitation of natural resources questions the long-term sustainability of our society. Recently, a simple nature-society interrelations model, called the HANDY model (Human And Nature DYnamics), has been proposed by Montesharrei et al (2014) to address this concern with a special emphasis on the role of the stratification of the society. We analyze the dynamics of this model and we explore the influence of two parameters: the nature depletion rate and the inequality factor. We characterize the asymptotic states of the system through a bifurcation analysis and we derive several quantitative results on the trajectories. We examine the possible collapses, sustainable equilibria and oscillations. We show that some collapses are irreversible and, depending on the wealth production factor, a bistability regime between a sustainable equilibrium and cycles of collapse-and-regeneration can be obtained. We discuss the possible applications of the model for the description of the collapse of pre-industrial societies and present the policies to avoid these dramatic fates. Results have been presented in a paper that is currently under review 26.7.3 Hybrid Differential Algebraic equations
Participants: Vincent Acary, Bernard Brogliato, Alexandre Rocca.
This concerns a class of nonsmooth dynamical systems, which can be interpreted in different ways (DAEs with nonsmooth or switching eauqlity constraints, or DAEs with complementarity constraints, or LCS with equality constraints). In 56 and in 9, we study classes of differential-algebraic linear complementarity systems which possess some passivity properties. These can be seen as an extension of DAEs in semi-explicit form, or of LCS with added equality constraints involving the algebraic and differential states, as well as the complementarity constraints multiplier. Specifically, the implicit Euler time-discretisation is analysed: the one-step nonsmooth problem's wellposedness is shown, then the convergence of the discrete solutions is studied. Examples are in circuits with nonsmooth components (like ideal diodes), as well as in some classes of switching DAEs (with state-dependent switches). For the moment the results apply mainly to systems with time-continuous solutions, however numerical simulations show that subtle mechanisms can appear which imply state jumps in both the algebraic and the differential states.7.4 Numerical analysis of multibody mechanical systems with constraints
Participants: Vincent Acary, Maurice Brémond, Paul Armand, Franck Bourrier, Charlélie Bertrand.
This scientific theme concerns the numerical analysis of mechanical systems with bilateral and unilateral constraints, with or without friction 1. They form a particular class of dynamical systems whose simulation requires the development of specific methods for analysis and dedicated simulators 60.
7.4.1 Numerical solvers for frictional contact problems.
Participants: Vincent Acary, Maurice Brémond, Paul Armand.
In 30, we review several formulations of the discrete frictional contact problem that arises in space and time discretized mechanical systems with unilateral contact and three-dimensional Coulomb’s friction. Most of these formulations are well–known concepts in the optimization community, or more generally, in the mathematical programming community. To cite a few, the discrete frictional contact problem can be formulated as variational inequalities, generalized or semi–smooth equations, second–order cone complementarity problems, or as optimization problems such as quadratic programming problems over second-order cones. Thanks to these multiple formulations, various numerical methods emerge naturally for solving the problem. We review the main numerical techniques that are well-known in the literature and we also propose new applications of methods such as the fixed point and extra-gradient methods with self-adaptive step rules for variational inequalities or the proximal point algorithm for generalized equations. All these numerical techniques are compared over a large set of test examples using performance profiles. One of the main conclusion is that there is no universal solver. Nevertheless, we are able to give some hints to choose a solver with respect to the main characteristics of the set of tests.Recently, new developments have been carried out on applications of well-known numerical methods in optimization. With the visit of Paul Armand, Université de Limoges, we co-supervise a M2 internship, Maksym Shpakovych on the application of interior point methods for quadratic problem with second-order cone constraints. The results are encouraging 91, 84, 27. A first publicawiton on rolling friction has been published 17 and another publication 18 is under review.
7.4.2 Finite element modeling of cable structures
Participants: Vincent Acary, Charlélie Bertrand.
Standard finite element discretization for cable structures suffer from several drawbacks. The first one is related to the mechanical assumption that the cable can not support compression. Standard formulations do not take into account this assumption. The second drawback comes from the high stiffness of the cable model when we deal with large lengths with high Young modulus such as cable ropeways installations. In this context, standard finite element applications cannot avoid compressive solutions and have huge difficulties to converge. In a forthcoming paper, we propose to a formulation based on a piecewise linear modeling of the cable constitutive behavior where the elasticity in compression is canceled. Furthermore, a dimensional analysis help us to formulate a problem that is well-balanced and the conditioning of the problem is diminished. The finite element discretization of this problem yields a robust method where convergence is observed with the number of elements and the nonlinear solver based on nonsmooth Newton strategy is converging up to tight tolerances. The convergence with the number of element allows one to refine the mesh as much as we want that will be of utmost importance for applications with contact and friction. Indeed, a fine discretization with respect to the whole length of the cable will be possible in the contact zone. This work has been the object of the following publication 46. In 3, consistent reduced order modeling has been proposed and comparisons with the model developped in 46 has been performed.
7.5 Analysis and Control of Set-Valued Systems
Participants: Bernard Brogliato, Christophe Prieur, Vincent Acary, Mohammad Rasool Mojallizadeh, Félix Miranda-Villatoro.
7.5.1 Discrete-time sliding-mode differentiators
In 24, the experimental analysis of discrete-time differentiators implemented in closed-loop control systems is achieved. To this end, two laboratory setups, namely an electro-pneumatic system and a rotary inverted pendulum have been used to implement 25 different differentiators. Since the selected laboratory setups behave differently in the case of dynamic response and noise characteristics, it is expected that the results remain valid for a wide range of control applications. The validity of several theoretical results, which have been already reported in the literature using mathematical analysis and numerical simulations, has been investigated, and several comments are provided to allow one to select an appropriate differentiation scheme in practical closed-loop control systems.
7.5.2 Discrete-time implicit Euler sliding-mode control
We continue our study on the discretization in time for set-valued sliding-mode controllers in 12. A nonsmooth model of hydraulic actuator has been derived elsewhere by Kikuuwe and co-authors. In this work the issue of robust control of such nonsmooth models is tackled using set-valued sliding-mode first-order controller. The well-posedness is carefully taken care of, and the implicit discretization is studied. Many simulations illustrate the theoretical results. In 15 it is proposed an upgrade of the PID controller using a switching strategy between a linear and a set-valued inputs. Several nonsmooth controllers, including a first-order sliding-mode one implicitly discretized, are compared experimentally on a rotary pendulum available at INRIA Lille, Valse team.
7.5.3 Optimal control of Lagrangian complementarity systems
In 85 we study the optimal control of Lagrangian complementarity systems. Such systems are nonsmooth (with impacts and set-valued friction) and undergo varying dimensions (due to the unilateral constraints and the complementarity constraints). The analysis is based on the transformation of the system with impacts, into a system without impacts, using an equivalent Filippov's differential inclusion with absolutely continuous solutions. The difficulty is in the correct design of the sliding surface so that the post-impact velocity is computed correctly. A specific numerical scheme developed by Nurkanovic and Diehl at Frieburg university is used for the numerical simulations on a jumping robot.
7.5.4 Bifurcations of equilibria in LCS
It is well-known that linear complementarity systems (LCSs) can undergo bifurcations at which multiple equilibria, limit cycle, or chaotic solutions might appear, dissappear or change stability. From a control viewpoint, it is important to know the range of parameters for which such changes take place. The work 80 addresses this issue by proposing a novel notion of equivalence between LCPs (linear complementarity problems) that permits to make a classification of steady-state bifurcations in dynamic LCS. The proposed approach takes advantage of the geometric structure of the problem and allows to closely mimic the bifurcation theory of smooth maps. This type of results allows us, for instance, to design LCSs with asymptotic behaviors showing multiple steady states, as is the case in negative resistance circuits, as well as, quantify the structural stability of a given LCP via structural stability margins. In addition, a full classification of stable and instable LCPs is provided for the planar case.
7.5.5 Nonlinear networks with set-valued coupling
The work 23 explores the use of maximal monotone set-valued couplings for achieving robust synchronization in networks of agents with external disturbances and/or model uncertainties. It is shown that perfect synchronization is achievable with bounded set-valued coupling laws under the affections of persistent disturbances. Moreover, if the coupling is done via the full-state, then finite-time synchronization is guaranteed. The work also proposes practical ways of realizing the set-valued coupling law via electrical circuits. Such regularized coupling law can be simulated in a digital computer using implicit methods 28 and it is detached from the dynamics of the individual agents. Moreover an estimation of the ultimate bound is given in function of the regularization index of the implemented coupling.
7.5.6 Dissipative systems
This activity mainly concerns the analysis of DALCS (differential algebraic linear complementarity systems) and DVLCS (descriptor variable linear complementarity systems) as done in 56 and in 9. It is shown that the passivity of some operators associated with the system's constraints (bilateral and complementarity constraints) allows one to guarantee the well-posedness of the discretization (existence and uniqueness of the nonsmooth one-step problem) as well as some convergence properties of the discrete-time solutions towards limits which are solutions of the continuous-time dynamics. Passivity is also at the core of the systems presented in the pedagogical article 7, which proposes an introduction to set-valued Lur'e systems which satisfy some passivity constraints. An erratum for the third edition of our book on dissipative systems has been published in 20. Notice that a corrected version of the third edition has been released in 2022. Incidentally an erratum for our book on nonsmooth circuits simulation has been updated in 19.
7.5.7 Robot-object underactuated nonsmooth dynamical systems
In 8 we propose a tutorial survey about an important class of Lagrangian complementarity systems (hence with impacts and set-valued friction) which possess a specific structure that can be split into two main parts: a controlled part (named the "robot") and an uncontrolled part (named the "object") which can be acted upon only through the Lagrange multipliers associated with the constraints (bilateral or/and unilateral) and the friction. This class comprises many well-known robotic systems like bipeds which walk, jump, run, juggling, tapping, hopping, pushing robots, prehensile of non-prehensile manipulation systems, some cable-driven systems, and some electrical circuits with nonsmooth set-valued components. The main message is that a backstepping-like control strategy should be followed to get a unified approach for the feedback control of all these underactuated systems.
7.5.8 Modelling and control of overhead cranes (OC)
This is a subject that we studied in the framework of the IRT project Levage, in collaboration with Schneider Electric. In 16, 21, 25 we have reviewed different modeling approaches for OCs in 2D and 3D, with detailed dynamical equations for single and double-pendulums. Many controllers have been reviewed, and a toolbox has been developed which allows to test numerically the controllers. A comparative work has been performed over typical open-loop and closed-loop controllers, including passivity-based, sliding-mode, feedback linearization, etc, for regulation and for trajectory tracking.
7.6 Impact modelling
Participants: Bernard Brogliato, Guillaume James, Abhishek Chatterjee.
In 56,10, we study the derivation of approximations of the coefficient of restitution associated with a class of nonlinear spring/dashpot contact/impact models (the most well-known being the so-called Simon-Hunt-Crossley, and Kuwabara-Kono models). The originality of our work (compared to previous results obtained by authors like Poschel and Brilliantov) is that the external load which acts on the system during the collision, is taken into account. This load can influence the restitution coefficient. The approximated expressions are obtained by careful analysis of suitable expansions. A piece of code which allows one to calculate the coefficients has been developed.8 Bilateral contracts and grants with industry
Participants: Vincent Acary, Bernard Brogliato, Christophe Prieur.
8.1 Bilateral grants with industry
Schneider Electric
This action started in 2001 with the post-doc of V. Acary co–supported by Schneider Electric and CNRS. With some brief interruptions, this action is still active and should further continue. It concerns mainly the simulation and modeling of multi–body systems with contact, friction and impacts with the application for the virtual prototyping of electrical circuit breakers.
During these years, various forms of collaborations have been held. Two PhD thesis have been granted by Schneider Electric (D.E. Taha and N. Akhakdar) accompanied with research contracts between INRIA and Schneider Electric. Schneider Electric participated also the ANR project Saladyn as a main partner.
Without going into deep details of the various actions over the years, the major success of this collaboration is the statistical tolerance analysis of the functional requirements of the circuit breakers with respect to clearance in joints and geometrical tolerances on the parts. Starting from the geometrical descriptions (CAD files) of a mechanism with prescribed tolerances on the manufacturing process, we perform worst-case analysis and Monte–Carlo simulations of the circuit breaker with Siconos and we record the variations in the functional requirements. The difficulty in such simulations are the modeling of contact with friction that models the joints with clearances. The results of these analysis enable Schneider Electric to define the manufacturing precision that has a huge impact of the production cost (Schneider Electric produces several millions of C60-type circuit breaker per year). Note that it is not possible to perform such simulations with the existing software codes of the market.
At the beginning, our interlocutor at Schneider Electric was the innovation (R&D) department. Now, we are working and discussing with the business unit, Division Power and Dinnov (M. Abadie, E. Boumediene, X. Herreros) in charge of designing and producing the circuit–breakers. The targeted users are the R&D engineers of Schneider Electric that use simulation tools for designing new models or improving existing circuit breakers. This collaboration continues with new modeling and simulation challenges (flexible parts, multiple impact laws) with the CIFRE PhD of Rami Sayoud.
STRMTG. Service Technique des remontées mécaniques et des transports guidés.
We have started with STRMTG a research contract about modelling, simulation and control of cable-transport systems. In such systems, the question of the coupling between the nonlinear dynamics of cables and their supports with unilateral contact and friction appears now to be determinant in order to increase the performances of the cableway systems, especially for urban transportation systems.
9 Partnerships and cooperations
Participants: Vincent Acary, Franck Bourrier, Bernard Brogliato, Félix Miranda Villatoro, Nicholas Collins Craft.
9.1 European initiatives
9.1.1 Horizon Europe
LEMMA
LEMMA project on cordis.europa.eu
-
Title:
Landslide and avalanchE Mechanics with Multiphysical datA
-
Duration:
From September 1, 2022 to August 31, 2024
-
Partners:
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE (INRIA), France
- ECOLE POLYTECHNIQUE FEDERALE DE LAUSANNE (EPFL), Switzerland
- UNIVERSITE GRENOBLE ALPES (UGA), France
-
Inria contact:
Vincent Acary
- Coordinator:
-
Summary:
Landslides and avalanches jointly cause approximately 150 deaths and €4.9 billion economic losses each year, with the impacts predicted to become more severe due to climate change. Mitigation and prevention of disasters requires accurate predictions of these phenomena, which due to their scale is only achievable via modelling and simulation. Accurate models of landslides in permafrost or avalanches must account for micro-scale (<1mm) processes such as cracks and shear bands that also involve thermal and hydrological effects that will be exacerbated by climate change. Such models do not currently exist. Further, this level of refinement is not computationally viable when modelling an entire mountainside, and so a new approach must be adopted.
This project will: 1) Develop new models for permafrost and snow subject to climate-change-induced loadings; 2) Use the new data-driven mechanics framework to transfer information from these models to the scale of the mountainside; and 3) Simulate the effects of climate change on the Mont-Blanc massif at Chamonix. This will combine the researcher's experience with shear band models with the supervisor's expertise in crack models and optimisation techniques. A secondment at a group specialising in simulating landslides and avalanches will provide the expertise to implement the simulation on a real mountainside.
This interdisciplinary project will ideally set the researcher for a career in academia in Europe, while benefiting the community at Chamonix, in particular the guide's association, as they will be able to plan adaptations and mitigations for the effects of climate change, ensuring their tourism industry remains viable. Specialised multiphysical models that are adapted to permafrost and snow will advance the state-of-the-art significantly, and the implementation of optimisation techniques in data-driven mechanics has wide applicability throughout civil and mechanical engineering, geology and environmental science.
9.2 National initiatives
ANR project Digitslid
B. Brogliato coordinated the ANR project Digitslid (PRC, ANR-18-CE40-0008-01), Differentiateurs et commandes homogenes par modes glissants en temps discret: l'approche implicite. Partners: LS2N (Ecole Centrale de Nantes), INRIA Lille Nord Europe (team Non-A-Post), and Tripop. October 2018-September 2021. 12 participants overall (3 post-doc students recruited by the project, 3 Ph.D. students supported by other means). Total financial support by the ANR: 338 362 euros (100 762 for Tripop, 18 months of post-doc).
FUI Modeliscale
Participants: Vincent Acary, Bernard Brogliato.
The ModeliScale FUI focuses on the modeling, simulation and analysis of large cyber-physical systems. It federates the research activities of several teams, covering a broad spectrum of topics, namely hybrid systems modeling & verification, numerical analysis, programming language design and automatic control. Our research agenda includes the following tracks:
- New compilation techniques for Modelica modelers: structural analysis of multimode DAE (Differential Algebraic Equations) systems, modular compilation, combining state-machines and non-smooth dynamical systems (complementarity dynamical systems and Filippov differential inclusions), contract-based specification of cyber-physical systems requirements, requirements capture using under-/over-determined DAE systems.
- Simulation of large cyber-physical systems: distributed simulation, discretization methods for non-smooth dynamical systems, space-/time-adaptive discretization methods for multimode DAE systems, quantized state solvers (QSS).
- Guaranteed numerics: guaranteed simulation of non-smooth and hybrid dynamical systems, numerical methods preserving invariant properties of hybrid systems, contract-based reasoning methods.
Project Levage, IRT NanoElec, Grenoble
This project deals with the modeling and control of overhead cranes, in collaboration with Schneider Electric. It involves M.R. Mojallizadeh (two-year contract funded by the IRT), B. Brogliato and C. Prieur. The major objective is to better understand how to minimize sway effects that may be created during operation. The major issues for modeling are how to choose in the set of finite-dimensional (pendulum-like), infinite-dimensional (string or wave equations), and finite-element-method based, models. One major issue for feedback control, concerns the choice of the measured cable angles. This is an ”Institut de Recherche Technologique NanoElec” project, founded by the french program ”Investissement d’Avenirs” ANR-10- AIRT-05, from 01/03/2021 to 28/02/2023 (due to the resignation of Rasool Mojallizadeh the project ended on 30/11/2022).
Project SsONDS LabEx PERSIVAL ANR-15-IDEX-02 and ANR-11-LABX-0025-01
Self-sustained Oscillations in Nonsmooth Dynamical Systems. October 2021 - September 2024. INRIA Grenoble TRIPOP team (F. Miranda-Villatoro, B. Brogliato) and Gipsa-Lab UGA (F. Ferrante). Coordinated by F. Miranda-Villatoro. The SsONDS project aims at developing theoretical methods for the analysis, design, and control of systems with robust self-sustained oscillations in environments with uncertainties (as for instance, lack of knowledge of certain parameters of the model, or the presence of external disturbances). Potential applications include the design of central pattern generators (CPGs) for motion control, and mathematical analysis of models from computational biology. Total fundings for TRIPOP = 99 keuros.
ANR SPECULAR
Simulation of Percutaneous Liver tumor Ablation in virtual Reality. The goal of this project is to develop an immersive simulation of needle-based procedures. Olivier Goury is responsible of Work Package 2 in collaboration with DEFROST at Inria Lille where the focus will be to speed up the numerical simulation using reduced-order modeling techniques and parallel programming. This project is coordinated by Stéphane Cotin at Inria Nancy and Hadrien Courtecuisse at Strasbourg University.
9.3 Regional initiatives
Smart Protect
The project aims to develop and test an innovative structure for protection against natural hazards. It is funded by the Auvergne Rhône-Alpes region as part of the R&D operation BOOSTER 2019. The partnerships (GEOLITHE INNOV, GEOLITHE, MYOTIS, INRIA and INRAE) and the operational solutions and tools developed as part of the "Smart-Protect" project will constitute major advances in the methods and means for the natural risk management, both nationally and internationally. GEOLITHE INNOV is leader of the SMART-PROTECT collaborative project. The financial support for INRIA is devoted to the post-doc of Nicholas Collins Craft for the study and the development of cohesive zone model for fracture mechanics simulation.
OCIRN
The OCIRN Project is supported and accompanied by the Auvergne Rhône-Alpes Region. The partners of the project are Géolithe, CAN, INRIA, department of Isère, Halias Technologies and INDURA cluster. The general ambition of the OCIRN project is to support the development of the natural gravity hazards sector in the development and integration of new digital practices. Natural gravity hazards are a growing concern in the context of global warming generating an increase in the frequency and intensity of events, combined with the reduction of societal and economic tolerance of these risks. A functional ambition of the project is to contribute to the integrated and reasoned management of natural gravitational risks, coordinated with the projects of development of the territories, in order to allow important progress in the reduction of the risks, the continuity of service of the installations and the optimization of the operations of mitigation and protection. The OCIRN project aims at 3 major objectives:
- The capitalization of data and the improvement of information flows between the actors of natural risks via the digital platform.
- The sharing of the uses of innovative software of simulation and modeling via the software bricks of simulation and modeling on digital platform.
- The homogenization and standardization of practices through the application of methods chosen by the sector (C2ROP) via the methodological software bricks on the digital platform.
These three objectives are addressed through access to shared tools on a scalable and collaborative digital platform made available to the sector. In addition, related training, data collection and processing services will be set up.
10 Dissemination
Participants: Vincent Acary, Franck Bourrier, Bernard Brogliato, Paul Armand, Félix Miranda Villatoro.
10.1 Promoting scientific activities
10.1.1 Scientific events: selection
Member of the conference program committees
- Bernard Brogliato was a member of the National Steering Commitee of the 10th European Nonlinear Dynamics Conference ENOC2022, 17-22 July 2022, Lyon.
- V. Acary organized a mini-symposium at ENOC 2022 (Lyon, July 2022).
Reviewer
- Olivier Goury is a regular reviewer of the conferences IEEE International Conference on Robotics and Automation (ICRA) and Robosoft.
10.1.2 Journal
Reviewer - reviewing activities
- Bernard Brogliato is a regular reviewer for Multibody Systems Dynamics, Mechanism and Machine Theory, Automatica, IEEE Transactions on Automatic Control, SIAM Journal on Control and Optimization, Systems and Control Letters, etc.
- Félix Miranda Villatoro is a regular reviewer of Automatica, IEEE Transactions on Automatic Control, and IEEE Control Systems Letters.
- Olivier Goury is a regular reviewer of Soft Robotics (SoRo) and IEEE Robotics and Automation Letters (RA-L).
- Vincent Acary is a regular reviewer for Multibody Systems Dynamics, IEEE Transactions on Automatic Control, SIAM Journal on Control and Optimization, Computational Methods in Applied and Mechanical Engineering, Mechanical Systems and Signal Processing, International Journal for Numerical Methods in Engineering.
10.1.3 Invited talks
- Félix Miranda-Villatoro. A nested set-valued controller for robust output regulation. 9th Annual Symposium of the European Network for Nonsmooth Dynamics. Toulouse, France. September 2022.
- Félix Miranda-Villatoro. Robust synchronization of networks via maximal monotone couplings. Seminar talk at Gipsa Lab, UGA. October 2022.
- Vincent Acary. Keynote lecture. Time-integration methods for nonsmooth contact dynamics : beyond the seminal Moreau-Jean scheme. CMIS 2022 Contact Mechanics international symposium. Chexbres. Switzerland. May 23-25, 2022
- Guillaume James, hybrid workshop "Nonlinear waves in discrete and continuum systems", Department of Mathematics, University of Pittsburgh, June 2022. Invited talk.
- Guillaume James, workshop "Spatial dynamics and related approaches", Institut für Analysis, Dynamik and Modellierung, Univ. Stuttgart, Sept. 2022. Invited speaker and overview talk (center manifolds for discrete systems).
10.1.4 Leadership within the scientific community
10.1.5 Scientific expertise
- Olivier Goury was reviewer for the ANR (appel à projets générique)
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- Licence : G. James, Introduction to Numerical Methods, 31 hETD, L3, Grenoble INP - Pagora (1st year).
- Licence : G. James, Normed Vector Spaces, 26 hETD, L2, Prépa INP, Grenoble.
- Master : G. James, Numerical Methods, 91 hETD, M1, Grenoble INP - Ensimag (1st year).
- Master : G. James, Dynamical Systems, 45 hETD, M1, Grenoble INP - Ensimag (2nd year).
- Master : Vincent Acary, 17H éq TD Systèmes dynamiques, ENSIMAG 2A.
- Licence : Franck Bourrier, 30H éq TD Slope Stabilitiy, IUT GCCD 2nd year, Université Grenoble Alpes.
- Master : Franck Bourrier, 5H éq TD Modélisation des chutes de blocs, Master GAIA, Université Savoie Mont-Blanc.
- Master : Franck Bourrier, 30H éq TD Slope Stabilitiy, Polytech’ Grenoble 4th year, Université Grenoble Alpes.
- Master : Félix Miranda-Villatoro, 32 H TD, Numerical Optimization, 1st year, Grenoble INP, Université Grenoble Alpes
10.2.2 Supervision
- Bernard Brogliato and Félix Miranda-Villatoro are supervising the PhD thesis of Aya Younes (start 01/10/2021).
- Bernard Brogliato and Félix Miranda-Villatoro are supervising the PhD thesis of Quang-Hung Pham (start 01/12/2022).
- V. Acary, F. Bourrier and Olivier Goury supervise the Ph.D. thesis of Louis Guillet (start 01/01/2023).
- V. Acary and P. Armand supervise the Ph.D. thesis of Hoand Minh Nguyen (start 01/10/2021).
- V. Acary and F. Bourrier supervise the post-doc intern of Nicholas Collins Craft.
10.2.3 Juries
- Bernard Brogliato was referee for the Habilitation degree of Dr Richard Seeber (Graz university, Austria).
- Vincent Acary was member for the PhD thesis of Maksym Shpakovych (Univ. Limoges 12/2022) and referee for the PhD thesis of Xiashu Ma (Univ Aix-Marseille, 06/2022)
10.3 Popularization
10.3.1 Internal or external Inria responsibilities
- Bernard Brogliato is a member of the commission consultative paritaire "scientifique" CCP1.
11 Scientific production
11.1 Major publications
- 1 bookNumerical methods for nonsmooth dynamical systems. Applications in mechanics and electronics.Lecture Notes in Applied and Computational Mechanics 35. Berlin: Springer. xxi, 525~p. 2008
- 2 bookNonsmooth mechanics.Communications and Control Engineering SeriesModels, dynamics and controlSpringer, [Cham]2016, xxii+629URL: http://dx.doi.org/10.1007/978-3-319-28664-8
11.2 Publications of the year
International journals
International peer-reviewed conferences
Reports & preprints
Other scientific publications
11.3 Cited publications
- 28 bookNonsmooth modeling and simulation for switched circuits..Springer Netherlands2011
- 29 inbookAdvanced Topics in Nonsmooth Dynamics..Advanced Topics in Nonsmooth DynamicsTo appearSpringer International Publishing2018, On solving frictional contact problems: formulations and comparisons of numerical methods.375--457
- 30 incollectionOn solving contact problems with Coulomb friction: formulations and numerical comparisons.Advanced Topics in Nonsmooth Dynamics - Transactions of the European Network for Nonsmooth DynamicsJune 2018, 375-457
- 31 inproceedingsMechanical simulation of the Exomars rover using Siconos in 3DROV.ASTRA 2013 - 12th Symposium on Advanced Space Technologies in Robotics and AutomationESA/ESTECNoordwijk, Netherlands2013
- 32 techreportFCLIB: a collection of discrete 3D Frictional Contact problems.RT-0444INRIA2014, 34
- 33 articleHigher order Moreau's sweeping process: mathematical formulation and numerical simulation.Mathematical Programming11312008, 133--217
- 34 articleImplicit Euler numerical scheme and chattering-free implementation of sliding mode systems.Systems & Control Letters595doi:10.1016/j.sysconle.2010.03.0022010, 284--293
- 35 bookNumerical methods for nonsmooth dynamical systems. Applications in mechanics and electronics..Lecture Notes in Applied and Computational Mechanics 35. Berlin: Springer. xxi, 525~p. 2008
- 36 articleChattering-Free Digital Sliding-Mode Control With State Observer and Disturbance Rejection.IEEE Transactions on Automatic Control5752012, 1087--1101
- 37 articleEnergy conservation and dissipation properties of time-integration methods for the nonsmooth elastodynamics with contact.ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik9652016, 585--603
- 38 articleHigher order event capturing time--stepping schemes for nonsmooth multibody systems with unilateral constraints and impacts..Applied Numerical Mathematics62102012, 1259--1275
- 39 articleNumerical Simulation of Piecewise-Linear Models of Gene Regulatory Networks Using Complementarity Systems Theory.Physica D: Nonlinear Phenomena2692013, 103--119
- 40 techreportNonsmooth fracture dynamics using a cohesive zone approach.RR-6032INRIA2006, 56
- 41 articleProjected event-capturing time-stepping schemes for nonsmooth mechanical systems with unilateral contact and Coulomb's friction.Computer Methods in Applied Mechanics and Engineering2562013, 224--250
- 42 articleMultibody systems with 3D revolute joint clearance, modelling, numerical simulation and experimental validation: an industrial case study.Multibody System Dynamics4232017, 249--282
- 43 articleThe algorithmic analysis of hybrid systems..Theoretical Computer Science13811995, 3--34
- 44 articleA Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems.SIAM Journal on Imaging Sciences212009, 183--202
- 45 bookPiecewise-smooth dynamical systems : theory and applications.Applied mathematical sciencesLondonSpringer2008
- 46 articleA robust and efficient numerical finite element method for cables.International Journal for Numerical Methods in Engineering12118September 2020, 4157-4186
- 47 articleRockfall rebound: comparison of detailed field experiments and alternative modelling approaches.Earth Surface Processes and Landforms3762012, 656--665
- 48 articleToward objective rockfall trajectory simulation using a stochastic impact model.Geomorphology1103-42009, 68--79
- 49 articleExperimental investigations on complex block propagation for the assessment of propagation models quality.Landslides182February 2021, 639-654
- 50 bookNonsmooth mechanics.Communications and Control Engineering SeriesModels, dynamics and controlSpringer International Publishing2016, 241--370
- 51 articleExistence and uniqueness of solutions for non-autonomous complementarity dynamical systems.J. Convex Anal.173-42010, 961--990
-
52
articleSimultaneous enforcement of constraints at position and velocity levels in the nonsmooth generalized-
scheme.Computer Methods in Applied Mechanics and Engineering2812014, 131--161 -
53
miscHybrid vs. nonsmooth dynamical systems.
http://synchron2014.inria.fr/wp-content/uploads/sites/13/2014/12/Caillaud-nsds.pdf 2014 - 54 articleTime finite element based Moreau‐type integrators.International Journal for Numerical Methods in Engineering11432018, 215--231
- 55 articleLanguages and tools for hybrid systems design.Foundations and Trends in Electronic Design Automation11/22006, 1--193
- 56 techreportApproximate analytical coefficient of restitution formulation for single bead impact with external load, using nonlinear visco-elastic models.INRIA Grenoble - Rhone-AlpesDecember 2021, 1-50
-
57
articleA nonsmooth generalized-
scheme for flexible multibody systems with unilateral constraints.International Journal for Numerical Methods in Engineering9682013, 487--511 - 58 bookThe Linear Complementarity Problem.Boston, MAAcademic Press, Inc.1992
- 59 articleState of the art in rockfall – forest interactions.Schweizerische Zeitschrift fur Forstwesen15862007, 128--141
- 60 articleThe Contact Dynamics method: A nonsmooth story .Comptes Rendus Mécanique3463March 2018, 247-262
- 61 articleNovel quantitative indicators to characterize the protective effect of mountain forests against rockfall.Ecological Indicators672016, 98--107
- 62 bookFinite-dimensional Variational Inequalities and Complementarity Problems. I & IISpringer Series in Operations ResearchSpringer New York2003
- 63 bookDifferential Equations with Discontinuous Right Hand Sides.Dordrecht, the NetherlandsKluwer1988
- 64 articleA primal--dual regularized interior-point method for convex quadratic programs.Mathematical Programming Computation412012, 71--107
- 65 articleNew results on Painlevé Paradoxes.European Journal of Mechanics - A/Solids1841999, 653--677
- 66 bookComplementarity and Variational Inequalities in Electronics.Academic Press2017
- 67 inproceedingsThe Theory of Hybrid Automata.Verification of Digital and Hybrid SystemsSpringer Berlin Heidelberg1996, 265--292
- 68 bookConvex Analysis and Minimization Algorithms.I and IISpringer Berlin Heidelberg1993
- 69 bookFundamentals of Convex Analysis.Springer Berlin Heidelberg2001
- 70 articleImplicit discrete-time twisting controller without numerical chattering: analysis and experimental results.Control Engineering Practice462016, 129--141
- 71 incollectionExperimental results on implicit and explicit time-discretization of equivalent-control-based sliding-mode control.Recent Trends in Sliding Mode ControlInstitution of Engineering and Technology2016, 207--235
- 72 articleBreathers in oscillator chains with Hertzian interactions.Physica D: Nonlinear Phenomena2512013, 39--59
- 73 articlePeriodic travelling waves and compactons in granular chains.Journal of Nonlinear Science2252012, 813--848
- 74 articleNon Smooth Contact dynamics approach of cohesive materials.Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences35917892001, 2497--2518
- 75 articleClimate change and geomorphological hazards in the eastern European Alps.Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences36819192010, 2461--2479
- 76 articleSimulation of rockfall trajectories with consideration of rock shape.Multibody System Dynamics3222014, 241--271
- 77 bookStability and Convergence of Mechanical Systems with Unilateral Constraints.36Lecture Notes in Applied and Computational MechanicsSpringer Verlag2008
- 78 articleNonlinear waves in a strongly resonant granular chain.Nonlinearity29112016, 3496--3527
- 79 articleMultivalued Robust Tracking Control of Lagrange Systems: Continuous and Discrete--Time Algorithms.IEEE Transactions on Automatic Control6292017, 4436--4450
- 80 unpublishedEquivalence of Linear Complementarity Problems: Theory and Application to Nonsmooth Bifurcations.August 2021, working paper or preprint
- 81 techreportSolitary waves in the excitable Burridge-Knopoff model.RR-8996To appear in Wave Motion.INRIA Grenoble - Rhône-Alpes2016, 103--121
-
82
articleA method of solving a convex programming problem with convergence rate
.Soviet Mathematics Doklady2721983, 372--376 - 83 bookMultiple Impacts in Dissipative Granular Chains.72Lecture Notes in Applied and Computational MechanicsXXII, 234 p. 109 illus.Springer Verlag2014
- 84 mastersthesisNumerical optimization for rolling frictional contact problems.MA ThesisUniversité de LimogesSeptember 2021
- 85 unpublishedThe Time-Freezing Reformulation for Numerical Optimal Control of Complementarity Lagrangian Systems with State Jumps.November 2021, working paper or preprint
- 86 articleGranular crystals: Nonlinear dynamics meets materials engineering.Physics Today68112015, 44--50
- 87 phdthesisHydrothermal processes within the active layer above alpine permafrost in steep scree slopes and their influence on slope stability.University of Zurich2007
- 88 bookConvex Analysis.Princeton University Press1970
- 89 articleTimestepping schemes for nonsmooth dynamics based on discontinuous Galerkin methods: Definition and outlook.Mathematics and Computers in Simulation952013, 180--199
- 90 articleHalf-explicit timestepping schemes on velocity level based on time-discontinuous Galerkin methods.Computer Methods in Applied Mechanics and Engineering290152015, 250--276
- 91 mastersthesisNumerical optimization for frictional contact problems.MA ThesisUniversité de LimogesSeptember 2019
- 92 bookNumerics of Unilateral Contacts and Friction. -- Modeling and Numerical Time Integration in Non-Smooth Dynamics.47Lecture Notes in Applied and Computational MechanicsSpringer Verlag2009

