2023Activity reportProject-TeamECUADOR
RNSR: 201421213B- Research center Inria Centre at Université Côte d'Azur
- Team name: Program transformations for scientific computing
- Domain:Applied Mathematics, Computation and Simulation
- Theme:Numerical schemes and simulations
Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.2.1. Static analysis
- A2.5. Software engineering
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.2.6. Optimization
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.3.2. Data assimilation
Other Research Topics and Application Domains
- B1.1.2. Molecular and cellular biology
- B3.2. Climate and meteorology
- B3.3.2. Water: sea & ocean, lake & river
- B3.3.4. Atmosphere
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B9.6.3. Economy, Finance
1 Team members, visitors, external collaborators
Research Scientists
- Laurent Hascoët [Team leader, INRIA, Senior Researcher, HDR]
- Alain Dervieux [INRIA, Emeritus, HDR]
PhD Student
- Bastien Sauvage [INRIA]
Administrative Assistant
- Christine Claux [INRIA]
External Collaborators
- Bruno Koobus [UNIV MONTPELLIER]
- Stephen Wornom [UNIV MONTPELLIER]
2 Overall objectives
Team Ecuador studies Algorithmic Differentiation (AD) of computer programs, blending :
- AD theory: We study software engineering techniques, to analyze and transform programs mechanically. Algorithmic Differentiation (AD) transforms a program P that computes a function , into a program P' that computes analytical derivatives of . We put emphasis on the adjoint mode of AD, a sophisticated transformation that yields gradients for optimization at a remarkably low cost.
- AD application to Scientific Computing: We adapt the strategies of Scientific Computing to take full advantage of AD. We validate our work on real-size applications.
We aim to produce AD code that can compete with hand-written sensitivity and adjoint programs used in the industry. We implement our algorithms into the tool Tapenade, one of the most popular AD tools at present.
Our research directions :
- Efficient adjoint AD of frequent dialects e.g. Fixed-Point loops.
- Development of the adjoint AD model towards Dynamic Memory Management.
- Evolution of the adjoint AD model to keep in pace with modern programming languages constructs.
- Optimal shape design and optimal control for steady and unsteady simulations. Higher-order derivatives for uncertainty quantification.
- Adjoint-driven mesh adaptation.
3 Research program
3.1 Algorithmic Differentiation
Participants: Laurent Hascoët.
- algorithmic differentiation (AD, aka Automatic Differentiation) Transformation of a program, that returns a new program that computes derivatives of the initial program, i.e. some combination of the partial derivatives of the program's outputs with respect to its inputs.
- adjoint Mathematical manipulation of the Partial Differential Equations that define a problem, obtaining new differential equations that define the gradient of the original problem's solution.
- checkpointing General trade-off technique, used in adjoint AD, that trades duplicate execution of a part of the program to save some memory space that was used to save intermediate results.
Algorithmic Differentiation (AD) differentiates programs. The input of AD is a source program that, given some , returns some , for a differentiable . AD generates a new source program that, given , computes some derivatives of 4.
Any execution of amounts to a sequence of instructions, which is identified with a composition of vector functions. Thus, if
where each is the elementary function implemented by instruction . AD applies the chain rule to obtain derivatives of . Calling the values of all variables after instruction , i.e. and , the Jacobian of is
which can be mechanically written as a sequence of instructions . This can be generalized to higher level derivatives, Taylor series, etc. Combining the with the control of yields , and therefore this differentiation is piecewise.
The above computation of , albeit simple and mechanical, can be prohibitively expensive on large codes. In practice, many applications only need cheaper projections of such as:
-
Sensitivities, defined for a given direction in the input space as:
3This expression is easily computed from right to left, interleaved with the original program instructions. This is the tangent mode of AD.
-
Adjoints, defined after transposition (), for a given weighting of the outputs as:
4This expression is most efficiently computed from right to left, because matrixvector products are cheaper than matrixmatrix products. This is the adjoint mode of AD, most effective for optimization, data assimilation 34, adjoint problems 27, or inverse problems.
Adjoint AD builds a very efficient program 29, which computes the gradient in a time independent from the number of parameters . In contrast, computing the same gradient with the tangent mode would require running the tangent differentiated program times.
However, the are required in the inverse of their computation order. If the original program overwrites a part of , the differentiated program must restore before it is used by . Therefore, the central research problem of adjoint AD is to make the available in reverse order at the cheapest cost, using strategies that combine storage, repeated forward computation from available previous values, or even inverted computation from available later values.
Another research issue is to make the AD model cope with the constant evolution of modern language constructs. From the old days of Fortran77, novelties include pointers and dynamic allocation, modularity, structured data types, objects, vectorial notation and parallel programming. We keep developing our models and tools to handle these new constructs.
3.2 Static Analysis and Transformation of programs
Participants: Laurent Hascoët.
- abstract syntax tree Tree representation of a computer program, that keeps only the semantically significant information and abstracts away syntactic sugar such as indentation, parentheses, or separators.
- control flow graph Representation of a procedure body as a directed graph, whose nodes, known as basic blocks, each contain a sequence of instructions and whose arrows represent all possible control jumps that can occur at run-time.
- abstract interpretation Model that describes program static analysis as a special sort of execution, in which all branches of control switches are taken concurrently, and where computed values are replaced by abstract values from a given semantic domain. Each particular analysis gives birth to a specific semantic domain.
- data flow analysis Program analysis that studies how a given property of variables evolves with execution of the program. Data Flow analysis is static, therefore studying all possible run-time behaviors and making conservative approximations. A typical data-flow analysis is to detect, at any location in the source program, whether a variable is initialized or not.
The most obvious example of a program transformation tool is certainly a compiler. Other examples are program translators, that go from one language or formalism to another, or optimizers, that transform a program to make it run better. AD is just one such transformation. These tools share the technological basis that lets them implement the sophisticated analyses 19 required. In particular there are common mathematical models to specify these analyses and analyze their properties.
An important principle is abstraction: the core of a compiler should not bother about syntactic details of the compiled program. The optimization and code generation phases must be independent from the particular input programming language. This is generally achieved using language-specific front-ends, language-independent middle-ends, and target-specific back-ends. In the middle-end, analysis can concentrate on the semantics of a reduced set of constructs. This analysis operates on an abstract representation of programs made of one call graph, whose nodes are themselves flow graphs whose nodes (basic blocks) contain abstract syntax trees for the individual atomic instructions. To each level are attached symbol tables, nested to capture scoping.
Static program analysis can be defined on this internal representation, which is largely language independent. The simplest analyses on trees can be specified with inference rules 22, 30, 20. But many data-flow analyses are more complex, and better defined on graphs than on trees. Since both call graphs and flow graphs may be cyclic, these global analyses will be solved iteratively. Abstract Interpretation 23 is a theoretical framework to study complexity and termination of these analyses.
Data flow analyses must be carefully designed to avoid or control combinatorial explosion. At the call graph level, they can run bottom-up or top-down, and they yield more accurate results when they take into account the different call sites of each procedure, which is called context sensitivity. At the flow graph level, they can run forwards or backwards, and yield more accurate results when they take into account only the possible execution flows resulting from possible control, which is called flow sensitivity.
Even then, data flow analyses are limited, because they are static and thus have very little knowledge of actual run-time values. Far before reaching the very theoretical limit of undecidability, one reaches practical limitations to how much information one can infer from programs that use arrays 38, 24 or pointers. Therefore, conservative over-approximations must be made, leading to derivative code less efficient than ideal.
3.3 Algorithmic Differentiation and Scientific Computing
Participants: Alain Dervieux, Laurent Hascoët, Bruno Koobus, Stephen Wornom.
- linearization In Scientific Computing, the mathematical model often consists of Partial Differential Equations, that are discretized and then solved by a computer program. Linearization of these equations, or alternatively linearization of the computer program, predict the behavior of the model when small perturbations are applied. This is useful when the perturbations are effectively small, as in acoustics, or when one wants the sensitivity of the system with respect to one parameter, as in optimization.
- adjoint state Consider a system of Partial Differential Equations that define some characteristics of a system with respect to some parameters. Consider one particular scalar characteristic. Its sensitivity (or gradient) with respect to the parameters can be defined by means of adjoint equations, deduced from the original equations through linearization and transposition. The solution of the adjoint equations is known as the adjoint state.
Scientific Computing provides reliable simulations of complex systems. For example it is possible to simulate the steady or unsteady 3D air flow around a plane that captures the physical phenomena of shocks and turbulence. Next comes optimization, one degree higher in complexity because it repeatedly simulates and applies gradient-based optimization steps until an optimum is reached. The next sophistication is robustness, that detects undesirable solutions which, although maybe optimal, are very sensitive to uncertainty on design parameters or on manufacturing tolerances. This makes second derivatives come into play. Similarly Uncertainty Quantification can use second derivatives to evaluate how uncertainty on the simulation inputs imply uncertainty on its outputs.
To obtain this gradient and possibly higher derivatives, we advocate adjoint AD (cf. 3.1) of the program that discretizes and solves the direct system. This gives the exact gradient of the discrete function computed by the program, which is quicker and more sound than differentiating the original mathematical equations 27. Theoretical results 26 guarantee convergence of these derivatives when the direct program converges. This approach is highly mechanizable. However, it requires careful study and special developments of the AD model 31, 36 to master possibly heavy memory usage. Among these additional developments, we promote in particular specialized AD models for Fixed-Point iterations 28, 21, efficient adjoints for linear algebra operators such as solvers, or exploitation of parallel properties of the adjoint code.
4 Application domains
4.1 Algorithmic Differentiation
Algorithmic Differentiation of programs gives sensitivities or gradients, useful for instance for :
- optimum shape design under constraints, multidisciplinary optimization, and more generally any algorithm based on local linearization,
- inverse problems, such as parameter estimation and in particular 4Dvar data assimilation in climate sciences (meteorology, oceanography),
- first-order linearization of complex systems, or higher-order simulations, yielding reduced models for simulation of complex systems around a given state,
- adaptation of parameters for classification tools such as Machine Learning systems, in which Adjoint Differentiation is also known as backpropagation.
- mesh adaptation and mesh optimization with gradients or adjoints,
- equation solving with the Newton method,
- sensitivity analysis, propagation of truncation errors.
4.2 Multidisciplinary optimization
A CFD program computes the flow around a shape, starting from a number of inputs that define the shape and other parameters. On this flow one can define optimization criteria e.g. the lift of an aircraft. To optimize a criterion by a gradient descent, one needs the gradient of the criterion with respect to all inputs, and possibly additional gradients when there are constraints. Adjoint AD is the most efficient way to compute these gradients.
4.3 Inverse problems and Data Assimilation
Inverse problems aim at estimating the value of hidden parameters from other measurable values, that depend on the hidden parameters through a system of equations. For example, the hidden parameter might be the shape of the ocean floor, and the measurable values of the altitude and velocities of the surface. Figure 1 shows an example of an inverse problem using the glaciology code ALIF (a pure C version of ISSM 33) and its AD-adjoint produced by Tapenade.
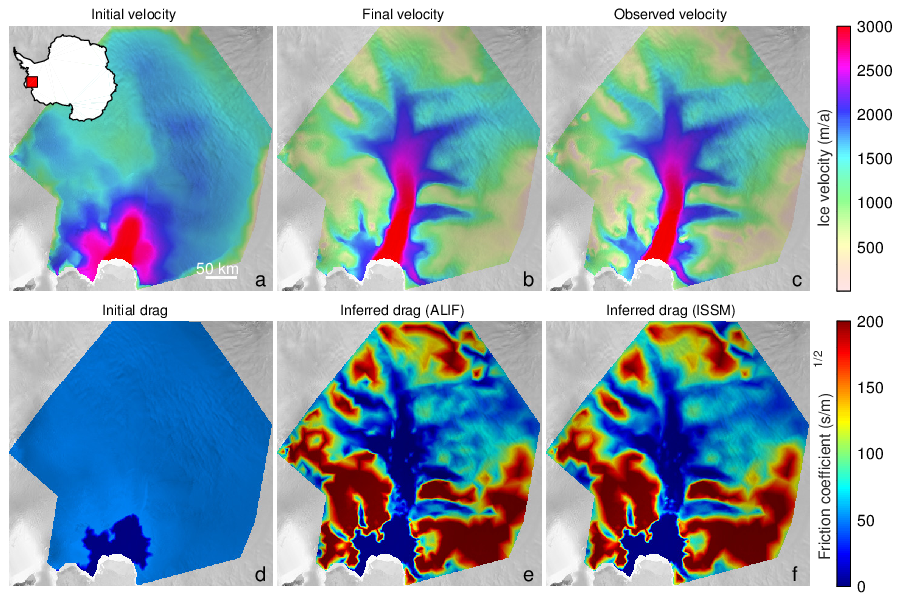
Six plots of fields of physical values on Pine Island Glacier, West Antarctica, showing resolution of an inverse problem
One particular case of inverse problems is data assimilation 34 in weather forecasting or in oceanography. The quality of the initial state of the simulation conditions the quality of the prediction. But this initial state is not well known. Only some measurements at arbitrary places and times are available. A good initial state is found by solving a least squares problem between the measurements and a guessed initial state which itself must verify the equations of meteorology. This boils down to solving an adjoint problem, which can be done though AD 37. The special case of 4Dvar data assimilation is particularly challenging. The 4th dimension in “4D” is time, as available measurements are distributed over a given assimilation period. Therefore the least squares mechanism must be applied to a simulation over time that follows the time evolution model. This process gives a much better estimation of the initial state, because both position and time of measurements are taken into account. On the other hand, the adjoint problem involved is more complex, because it must run (backwards) over many time steps. This demanding application of AD justifies our efforts in reducing the runtime and memory costs of AD adjoint codes.
4.4 Linearization
Simulating a complex system often requires solving a system of Partial Differential Equations. This can be too expensive, in particular for real-time simulations. When one wants to simulate the reaction of this complex system to small perturbations around a fixed set of parameters, there is an efficient approximation: just suppose that the system is linear in a small neighborhood of the current set of parameters. The reaction of the system is thus approximated by a simple product of the variation of the parameters with the Jacobian matrix of the system. This Jacobian matrix can be obtained by AD. This is especially cheap when the Jacobian matrix is sparse. The simulation can be improved further by introducing higher-order derivatives, such as Taylor expansions, which can also be computed through AD. The result is often called a reduced model.
4.5 Mesh adaptation
Some approximation errors can be expressed by an adjoint state. Mesh adaptation can benefit from this. The classical optimization step can give an optimization direction not only for the control parameters, but also for the approximation parameters, and in particular the mesh geometry. The ultimate goal is to obtain optimal control parameters up to a precision prescribed in advance.
5 Social and environmental responsibility
5.1 Impact of research results
Our research has an impact on environmental research: in Earth sciences, our gradients are used in inverse problems, to determine key properties in oceanography, glaciology, or climate models. For instance they determine basal friction coefficients of glaciers that are necessary to simulate their future evolution. Another example is to locate sources and sinks of CO2 by coupling atmospheric models and remote measurements.
6 New software, platforms, open data
6.1 New software
6.1.1 AIRONUM
-
Keywords:
Computational Fluid Dynamics, Turbulence
-
Functional Description:
Aironum is an experimental software that solves the unsteady compressible Navier-Stokes equations with k-epsilon, LES-VMS and hybrid turbulence modelling on parallel platforms, using MPI. The mesh model is unstructured tetrahedrization, with possible mesh motion.
- URL:
-
Contact:
Alain Dervieux
-
Participant:
Alain Dervieux
6.1.2 TAPENADE
-
Name:
Tapenade Automatic Differentiation Engine
-
Keywords:
Static analysis, Optimization, Compilation, Gradients
-
Scientific Description:
Tapenade implements the results of our research about models and static analyses for AD. Tapenade can be downloaded and installed on most architectures. Alternatively, it can be used as a web server. Higher-order derivatives can be obtained through repeated application.
Tapenade performs sophisticated data-flow analysis, flow-sensitive and context-sensitive, on the complete source program to produce an efficient differentiated code. Analyses include Type-Checking, Read-Write analysis, and Pointer analysis. AD-specific analyses include the so-called Activity analysis, Adjoint Liveness analysis, and TBR analysis.
-
Functional Description:
Tapenade is an Algorithmic Differentiation tool that transforms an original program into a new program that computes derivatives of the original program. Algorithmic Differentiation produces analytical derivatives, that are exact up to machine precision. Adjoint-mode AD can compute gradients at a cost which is independent from the number of input variables. Tapenade accepts source programs written in Fortran77, Fortran90, or C. It provides differentiation in the following modes: tangent, vector tangent, adjoint, and vector adjoint.
-
News of the Year:
Major speedup of the static data-flow analysis components. Automatic and asynchronous file offload and prefetching of the adjoint data stack. Improvements of the adjoint differentiation of fixed-point loops. Continued refactoring and bug fixes.
- URL:
-
Contact:
Laurent Hascoët
-
Participants:
Laurent Hascoët, Jan Hueckelheim, Michael Vossbeck
7 New results
7.1 Asynchronous file offload of the AD stack
Participants: Laurent Hascoët, Jan Hueckelheim [Argonne National Lab. (Illinois, USA)].
Data-Flow inversion is at the heart of the computation of gradients through AD. This amounts to providing (many of) the intermediate values computed at run-time, in reverse order. Most approaches use a stack, whose size may grow dramatically. Earth science applications such as climatology run on meshes of several million cells on thousands of time steps, yielding challenging stack sizes. Even using classical storage/recomputation tradeoffs, stack size may exceed the available main memory.
Most tools deal with this in an ad-hoc manner, identifying locations that consume a large part of the stack size, typically the “snapshots” taken before selected time steps. These snapshots are then stored in a specific way, i.e. directly on file. The way Tapenade's stack is organized allows for a more general and transparent approach. All storage needed by data-flow inversion goes to a unique stack. Without any intervention at the application level, this stack internally detects that its size becomes excessive, which triggers offloading of the deepest part of the stack to distant memory. Conversely, the stack is restored from the distant memory when needed. Offloading and restoring are triggered by the status of the stack, and are implemented in an asynchronous manner, allowing for time overlap between offloading/restoring on one hand, and derivative computation with elementary stack push/pop on the other hand.
We implemented an experimental version of this mechanism and started to use it on the adjoint of Dan Goldberg's “halfpipe-streamice” test case in the MIT GCM (Global Circulation Model). The much larger stack size permitted lets us experiment with different checkpointing patterns, with the effect of a significant speedup. More experiments are needed to validate this promising improvement.
In parallel, Jan Hueckelheim is looking at this asynchronous stack, written in C using POSIX pthreads and mutex'es, to experiment a code analysis tool to detect potential conflicts and data races in multithreaded C codes.
7.2 Frontiers of the AD model
Participants: Laurent Hascoët, Jan Hueckelheim [Argonne National Lab. (Illinois, USA)].
AD suffers from numerous limitations. Some limitations come from the constraints of application languages, or from coding styles adverse to AD or at least that make it inefficient. In this category of programming-related limitations, we have studied the question of data-flow reversal in languages with Garbage Collection (GC). Data-flow reversal means in particular restoring structures that have been deallocated. This is hard in presence of addresses, pointers, and even C pointer arithmetic. In a language with GC, how can we detect and undo a deallocation when it is done in a hidden manner and asynchronously? We proposed an extension of the AD model that deals with GC, we validated it on a simple Navier-Stokes solver application, and measured its performance. The article 13 describing this model and experiment has been published this year by ACM TOMS journal.
Other limitations are of a more abstract nature, and may come for instance from the mathematical equations underlying the code, or from the fundamental difference between computer's float numbers and real numbers. Categorizing these limitations is difficult, and a (very long) catalogue may prove useless. Jan Hueckelheim considered the question of what one can reasonably expect from AD. The assumption is that problematic cases are often not about AD producing wrong derivatives, but rather meaningful derivatives, only for a model different from what the user has in mind. Accurate knowledge of the context in which AD derivatives are meaningful will help users build a realistic expectation for AD tools. A joint article “Understanding Automatic Differentiation Pitfalls” is in preparation. A poster has been presented at the ICML 2023 workshop “Differentiable Almost Everything” in June.
7.3 Application to large industrial codes
Participants: Laurent Hascoët, Sébastien Bourasseau [ONERA], Cedric Content [ONERA], Bruno Maugars [ONERA], Stefano Carli [KU Leuwen], Shreyas Gaikwad [U. of Texas, Austin, USA], Sri Hari Krishna Narayanan [Argonne National Lab. (Illinois, USA)], Daniel Goldberg [University of Edinburgh, UK], Michael Vossbeck [The Inversion Lab, Hamburg, Germany].
We support users of Algorithmic Differentiation of large codes, mostly on CFD and Earth science.
In CFD, we continue support for the use of Tapenade to provide gradient computations in the Onera Platform “SoNice”. SoNice is a new CFD platform developed at ONERA by Bourasseau, Maugars, Content and colleagues, as a successor to Elsa. In the modular architecture of SoNice, Tapenade is used to build the differentiated counterpart of each module or operator. The implementation of each module is devised to be platform-independent, eventually targetting several multithreaded architectures through e.g. OpenMP or Cuda. This imposes technical constraints on the language differentiated by Tapenade, at various abstraction levels that range from AD models for multithreaded code, down to ways of handling fpp and cpp directives and automatically setting entry points and labels in a differentiated code to allow for some necessary post-processing.
We also continued support for Tapenade differentiation of the plasma Magneto-Hydro-Dynamic code SOLPS-ITER with Stefano Carli of KU Leuwen. A joint article 11 that describes this work was accepted this year for JCP.
In Earth science, this year main application is addressed by Shreyas Gaikwad, University of Texas at Austin, PhD student supervised by Patrick Heimbach, with support from Krishna Narayanan from Argonne. The goal is to produce the adjoint/gradient of all applications based on the MIT GCM code. These applications range from atmospheric to oceanic and glaciology. Last year's successful tangent and adjoint differentiation of MIT GCM was extended to several new validation test cases, and this year's work was to improve performance of the resulting differentiated code by carefully using the code optimization options of Tapenade. Still on MIT GCM, Dan Goldberg, University of Edinburgh, applies Tapenade to the glaciology test case “halfpipe-streamice”. Successful adjoint differentiation required improvements and extensions to Tapenade's handling of fixed-point loops. We are now working on performance improvement (in memory usage and CPU time) by exploring the available options for “checkpointing”, a classical storage/recomputation tradeoff of AD. This will also serve as an application for our new asynchronous stack save/restore mechanism (see section 7.1).
An article 12 was published in JOSS (Journal of Open Source Software) describing last year's application of Tapenade to SICOPOLIS, another similar glaciology code.
Still on Earth science, we support adjoint differentiation of the BEPS 32 code, a “biosphere” simulation model taking vegetation into account. This code is developed in part by the small company The Inversion Lab in Hamburg, Germany. We collaborate with Michael Vossbeck, engineer with The Inversion Lab, to provide the adjoint of BEPS by Tapenade. Differentiation with Tapenade is becoming a strategic part of the business of The Inversion Lab. Michael Vossbeck is progressively getting acquainted with the source code of Tapenade, with the objective of contributing to Tapenade development, and of being able to maintain it. This year, Michael Vossbeck improved the flexibility of the built-in auto-validation tool of Tapenade.
7.4 Aeroacoustics
Participants: Alain Dervieux, Bastien Sauvage, Bruno Koobus [IMAG, U. of Montpellier], Florian Miralles [IMAG, U. of Montpellier], Stephen Wornom [IMAG, U. of Montpellier], Tanya Kozubskaya [CAALAB, Moscow].
The progress in highly accurate schemes for compressible flows on unstructured meshes (together with advances in massive parallelization of these schemes) allows to solve problems previously out of reach. The four-years programme Norma, associating:
- IMAG of Montpellier University (B. Koobus, coordinator),
- Computational AeroAcoustics Laboratory (CAALAB) of Keldysh Institute of Moscow (T. Kozubskaya, head), and
- Ecuador of INRIA Sophia-Antipolis.
is supported by the French ANR and by the Russian Science Foundation, and is active till september 2024. Norma is a cooperation on the subject of extending Computational AeroAcoustics methods to simulate the noise emited by rotating machines (helicopters, aerial vehicles, unmanned aerial vehicles, wind turbines...). A detailed description with progress reports is available at this location.
Sections 7.5, 7.6, 7.7, 7.8 describe the 2023 contributions of Ecuador to the Norma programme.
7.5 Turbulence models
Participants: Bastien Sauvage, Alain Dervieux, Bruno Koobus [IMAG, U. of Montpellier], Florian Miralles [IMAG, U. of Montpellier], Stephen Wornom [IMAG, U. of Montpellier], Tanya Kozubskaya [CAALAB, Moscow].
Modelling turbulence is an essential aspect of CFD. The purpose of our work in hybrid RANS/LES (Reynolds Averaged Navier-Stokes / Large Eddy Simulation) is to develop new approaches for industrial applications of LES-based analyses. In the applications targeted (aeronautics, hydraulics), the Reynolds number can be as high as several tens of millions, far too high for pure LES models. However, certain regions in the flow can be predicted better with LES than with usual statistical RANS (Reynolds averaged Navier-Stokes) models. These are mainly vortical separated regions as assumed in one of the most popular hybrid models, the Detached Eddy Simulation (DES) model. Here, “hybrid” means that a blending is applied between LES and RANS. The development of hybrid models, in particular DES in the litterature, has raised the question of the domain of validity of these models. According to theory, these models should not be applied to flows involving laminar boundary layers (BL). But industrial flows are complex flows and often combine in a single flow regions of laminar BL, regions of fully developed turbulent BL, and regions of non-equilibrium vortical BL. It is then mandatory for industrial use that the new hybrid models give a reasonable prediction for all these types of flow. We concentrated on evaluating the behavior of hybrid models for laminar BL and for vortical wakes. While less predictive than pure LES on laminar BL, some hybrid models still give reasonable predictions for rather low Reynolds numbers.
An important result for this year is the proposal by Florian Miralles of a novel intermittency-based statistical two-equation model, and its extension to a novel intermittency-based hybrid RANS-LES model. The new model predicts accurately a larger class of turbulent flow, as demonstrated by its ability to predict (using relatively coarse grids) the drag crisis and the increase in Strouhal number when applied to the simulation of the flow around a circular cylinder from sub-critical to super-critical flow regimes (cf. 35). This work is a part of the PhD thesis of Florian Miralles, supported by the Norma programme and defended in november 2023 at university of Montpellier.
The Montpellier-Sophia team has been studying this new model in combination with the mesh adaptation method developed by Bastien Sauvage, for higher Reynolds number and wing geometries. A Norma report and a paper are in preparation.
7.6 Rotating machines
Participants: Alain Dervieux, Didier Chargy [Lemma, Sophia-Antipolis], Bastien Sauvage, Bruno Koobus [IMAG, U. of Montpellier], Florian Miralles [IMAG, U. of Montpellier], Stephen Wornom [IMAG, u. of Montpellier], Tanya Kozubskaya [CAALAB, Moscow], Ilya Abalakin [CAALAB, Moscow], Vladimir Bobkov [CAALAB, Moscow], Valentina Tsvetkova [CAALAB, Moscow].
The physical problem addressed by Norma involves a computational domain made of at least two components having different rotative motions. The numerical problem of their combination gave birth to many specialized schemes, such as the so-called sliding method, chimera method, immersed boundary method (IBM). The Ecuador team is studying a novel Chimera method, in cooperation with Lemma engineering (Sophia-Antipolis).
In 2023, B. Sauvage and Didier Chargy made progress in the computation of the Caradonna-Tung rotor, with a new adapted calculation on 3 million vertices. Results were presented in 15.
7.7 High order approximations
Participants: Alain Dervieux, Bastien Sauvage, Didier Chargy [Lemma, Sophia-Antipolis].
Thanks to anisotropic mesh adaptation, high-fidelity industrial calculations can be made to converge at second-order (in the steady case), even for rather singular cases, and convergence error can be evaluated. We are investigating the way to extend this to higher order. Our research relies on a fourth-order accurate three-dimensional vertex-centered Central Essentially Non Oscillating (CENO) scheme. In 2023, the consolidation and validation of the fourth-order accurate CENO in a mesh-adaptive version of NiceFlow has been advanced. A theory is being developped for proposing a h-p approach (a simultaneous adaptation of the mesh and of the truncation order) combining the CENO scheme and our anisotropic mesh adaption approach.
7.8 Control of approximation errors
Participants: Alain Dervieux, Adrien Loseille [Gamma3 team, INRIA-Saclay], Frédéric Alauzet [Gamma3 team, INRIA-Saclay].
Reducing approximation errors as much as possible by modifying the mesh is a particular kind of optimal control problem. We formulate it exactly this way when we look for the optimal metric of the mesh, which minimizes a user-specified functional (goal-oriented mesh adaptation). In that case, the usual methods of optimal control apply, using adjoint states that can be produced by Algorithmic Differentiation.
The second volume of the book 25 on mesh adaptation by Alauzet, Loseille, Koobus and Dervieux has been published by Wiley this year.
7.9 Space-time mesh adaptation
Participants: Bastien Sauvage, Alain Dervieux, Frédéric Alauzet [GammaO, INRIA, Saclay].
The INRIA teams GammaO (Saclay) and Ecuador (Sophia-Antipolis) have continued to study the application of anisotropic mesh adaptation to unsteady flow simulation. The baseline approach is the Global Fixed Point algorithm combined with a timestep relying on Courant-type stability condition for explicit time-advancing. This remains the best approach for many transient flows. For many unsteady turbulent flows at high Reynolds number, this is however inefficient, since very small cells in the boundary layer impose a very small explicit time step. Implicit timestepping is compulsory. Indeed, the time steps which can be used are notably larger than those permitted with an explicit time advancing. Large time steps bring a higher CPU efficiency, but the time approximation accuracy becomes an issue. Too large time steps degrade the prediction, too small time steps increases the computational cost. The new development focuses on obtaining directly the space-time discretization that minimizes the global error, under the constraint of a prescribed space-time discretization complexity. Application to vortex shedding flows (see figure 2) illustrate the interest of this novel method (cf. 18, 14, and B. Sauvage, F. Alauzet, A. Dervieux, “A space and time fixed point mesh adaptation method”, in preparation).
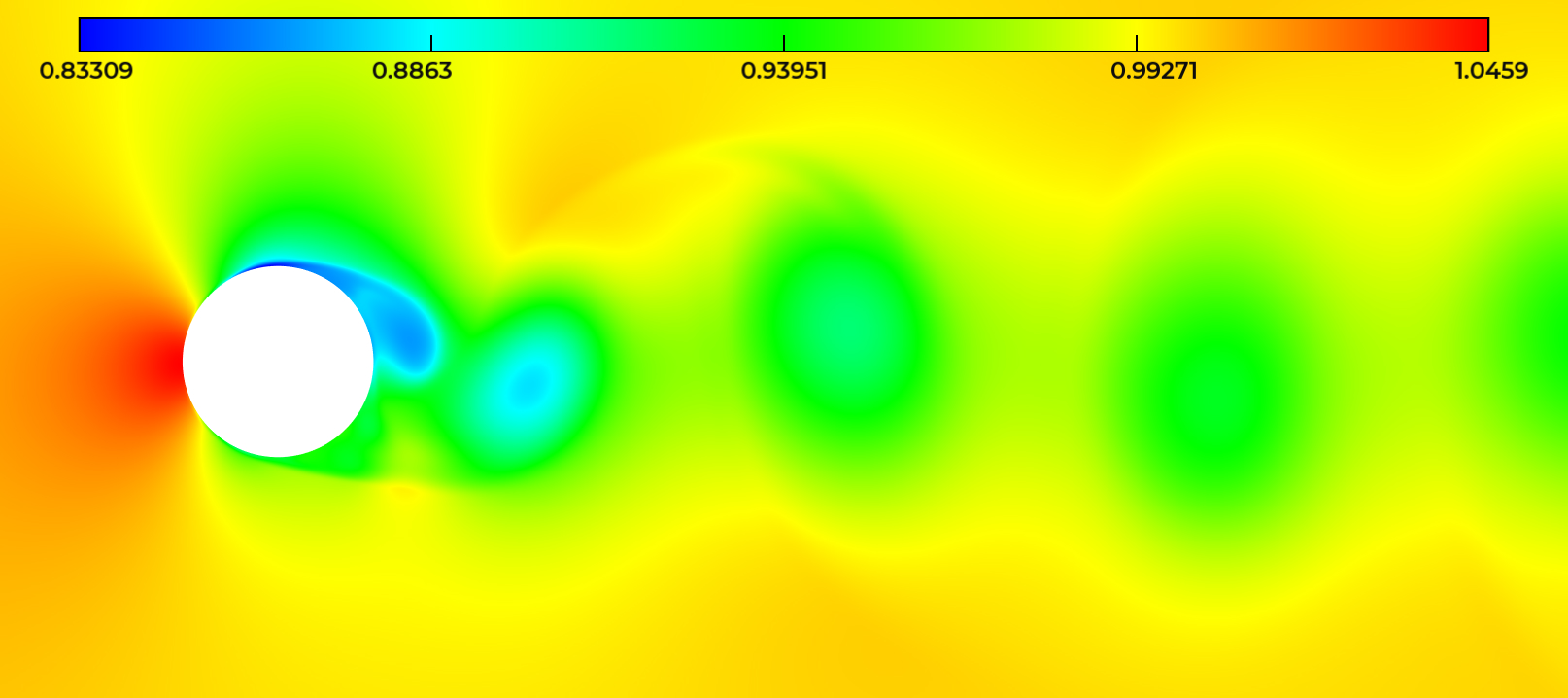
Vortices in the flow around a cylinder
Vortices in the flow around a cylinder
7.10 Mesh adaptation for LES
Participants: Bastien Sauvage, Alain Dervieux, Bruno Koobus [IMAG, u. of Montpellier],, Frédéric Alauzet [GammaO, INRIA, Saclay].
With statistical turbulence models, only a part of turbulent industrial flows can be predicted at an affordable cost. The rest may involve large detached regions which cannot be accurately described by statistical modelling, or vortices producing noise that the engineer wants to predict accurately. The Large Eddy Simulation (LES) is a model which predicts a part of the vortices of industrial interest. LES relies on filtering too small vortices and on modeling their effect on the larger ones. But this approach is one or two orders of magnitude more computer intensive than statistical modeling and therefore cannot be routinely used by engineers. Germano proposed an analysis using two different filters in order to measure the efficiency of a family of LES models. Recently, Toosi and Larsson demonstrated that the Germano analysis in fact deals with the source term of LES modeling error. We introduce this error term in our mesh adaptation process for RANS flow in order to obtain an approach for adapting the mesh to hybrid RANS/LES flow calculations. Applications to vortex shedding flows are being performed (cf. B. Sauvage, B. Koobus, F. Alauzet, A. Dervieux, “A metric-based mesh adaptation for hybrid RANS/LES flow calculations”, in preparation).
7.11 Control of errors in optimization
Participants: Alain Dervieux, Didier Chargy [Lemma, Sophia-Antipolis], Frédéric Alauzet [GammaO team, INRIA-Saclay].
It appears today that with the new algorithms for mesh adaptation, new efficient and accurate automatic tools are available for maximizing the quality of high-fidelity prediction. In the near future, the advantages of these tools will probably make them mandatory in industrial practice. For design optimization, automatic tools are already available. However, these tools today rely on a generation of non- adaptative or poorly adaptative CFD. It is important to propose (see 16 and figure 3) a composite algorithm which nicely combines the novel mesh adaptation technology with the most recent design optimization loops.
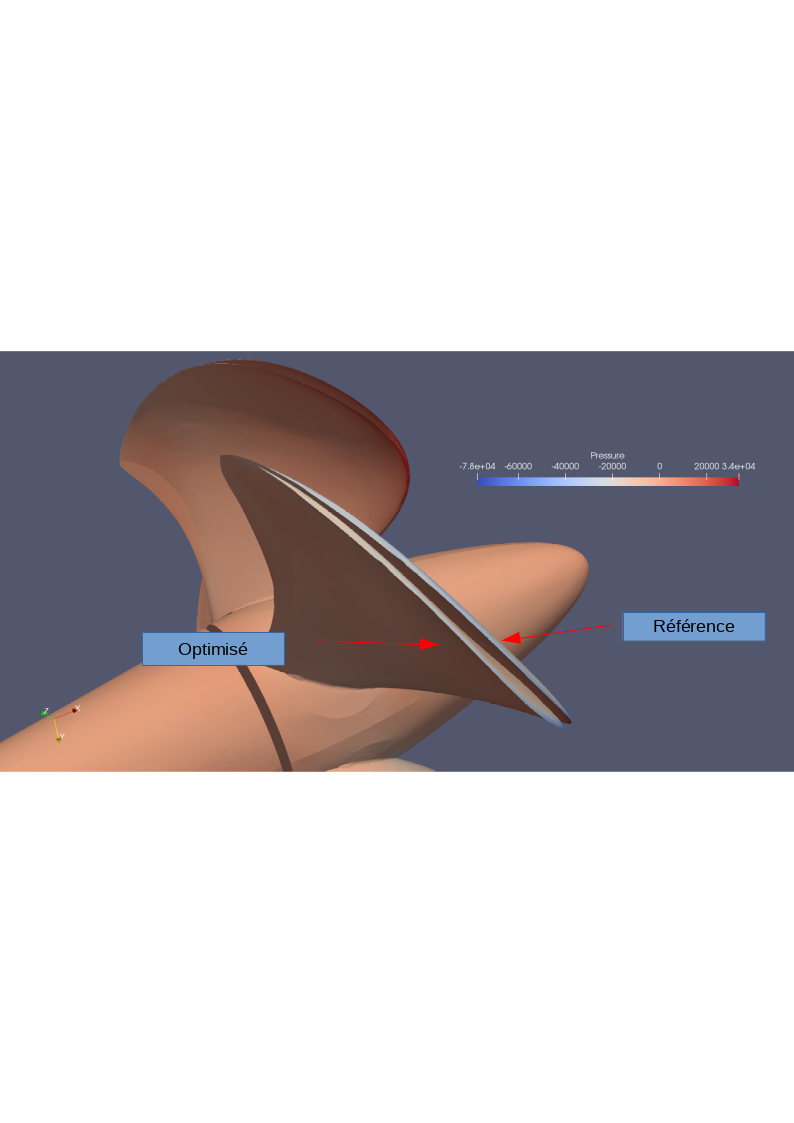
Image of a propeller and its pressure contours
8 Partnerships and cooperations
8.1 International initiatives
8.1.1 Associate Teams in the framework of an Inria International Lab or in the framework of an Inria International Program
JLESC
Participants: Laurent Hascoët, Paul Hovland [Argonne National Lab], Jan Hueckelheim [Argonne National Lab], Sri Hari Krishna [.
Ecuador participates in the Joint Laboratory for Exascale Computing (JLESC) together with colleagues at Argonne National Laboratory.
9 Dissemination
Participants: Laurent Hascoët, Alain Dervieux.
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
The team organized the 25th EuroAD workshop, at INRIA Sophia-Antipolis, June 13-14, 2023.
Member of organizing committees
- Laurent Hascoët is on the organizing commitee of the EuroAD series of workshops on Algorithmic Differentiation , taking place one or twice a year since 2005.
- Laurent Hascoët is on the organizing commitee and program commitee of the coming AD2024 conference on Algorithmic Differentiation, Northwestern U. at Evanston Illinois, USA, September 16-20 2024.
9.1.2 Invited talks
- Laurent Hascoët gave an invited talk at the 2023 EnzymeCon workshop, Boulder, Colorado, February 22-24, on “A survey of Tapenade in contrast with Enzyme”.
- Laurent Hascoët was invited at the MIAPbP seminar “Differentiable and Probabilistic Programming for Fundamental Physics”, which took place in Garching, Germany, 19-30 June. On this occasion he gave an invited talk on “Data-flow reversal and Garbage Collection” preceded by a general introduction on Source-Transformation AD.
9.1.3 Scientific expertise
Alain Dervieux is Scientific Director for the LEMMA company.
10 Scientific production
10.1 Major publications
- 1 articleReverse automatic differentiation for optimum design: from adjoint state assembly to gradient computation.Optimization Methods and Software1852003, 615-627
- 2 inproceedingsThe Data-Flow Equations of Checkpointing in reverse Automatic Differentiation.International Conference on Computational Science, ICCS 2006, Reading, UK2006
- 3 articleAn optimized treatment for algorithmic differentiation of an important glaciological fixed-point problem.Geoscientific Model Development952016, 27HAL
- 4 incollectionAdjoints by Automatic Differentiation.Advanced data assimilation for geosciencesOxford University Press2014, URL: https://hal.inria.fr/hal-01109881back to text
- 5 article``To Be Recorded'' Analysis in Reverse-Mode Automatic Differentiation.Future Generation Computer Systems2182004
- 6 articleThe Tapenade Automatic Differentiation tool: Principles, Model, and Specification.ACM Transactions On Mathematical Software3932013, URL: http://dx.doi.org/10.1145/2450153.2450158
- 7 articleCheaper Adjoints by Reversing Address Computations.Scientific Programming1612008, 81--92
- 8 articleProgramming language features, usage patterns, and the efficiency of generated adjoint code.Optimization Methods and Software312016, 885--903HALDOI
- 9 articleA Framework for Adjoint-based Shape Design and Error Control.Computational Fluid Dynamics Journal1642008, 454-464
- 10 articleAlgorithmic differentiation of code with multiple context-specific activities.ACM Transactions on Mathematical Software2016HAL
10.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
10.3 Cited publications
- 19 bookCompilers: Principles, Techniques and Tools.Addison-Wesley1986back to text
- 20 techreportA language and an integrated environment for program transformations.3313INRIA1997, URL: http://hal.inria.fr/inria-00073376back to text
- 21 articleReverse accumulation and implicit functions.Optimization Methods and Software941998, 307--322back to text
- 22 articleNatural semantics on the computer.Proceedings, France-Japan AI and CS Symposium, ICOTAlso, Information Processing Society of Japan, Technical Memorandum PL-86-6. Also INRIA research report # 4161986, 49-89URL: http://hal.inria.fr/inria-00076140back to text
- 23 articleAbstract Interpretation.ACM Computing Surveys2811996, 324-328back to text
- 24 articleInterprocedural Array Region Analyses.International Journal of Parallel Programming2461996, 513--546back to text
- 25 bookMesh adaptation for computational fluid dynamics.Wiley2022back to text
- 26 articleAutomatic differentiation and iterative processes.Optimization Methods and Software11992, 13--21back to text
- 27 inproceedingsAdjoint methods for aeronautical design.Proceedings of the ECCOMAS CFD ConferenceSwansea, U.K.2001back to textback to text
- 28 articleReduced Gradients and Hessians from Fixed Point Iteration for State Equations.Numerical Algorithms30(2)2002, 113--139back to text
- 29 bookEvaluating Derivatives: Principles and Techniques of Algorithmic Differentiation.SIAM, Other Titles in Applied Mathematics2008back to text
- 30 phdthesisTransformations automatiques de spécifications sémantiques: application: Un vérificateur de types incremental.Université de Nice Sophia-Antipolis1987back to text
- 31 techreportAutomatic Differentiation of Navier-Stokes computations.MCS-P687-0997Argonne National Laboratory1997back to text
- 32 article Modelling multi-year coupled carbon and water fluxes in a boreal aspen forest.Agric. For. Meteorol.1401-42006, 136--151DOIback to text
- 33 articleInferred basal friction and surface mass balance of the Northeast Greenland Ice Stream using data assimilation of ICESat (Ice Cloud and land Elevation Satellite) surface altimetry and ISSM (Ice Sheet System Model).Cryosphere862014, 2335-2351URL: http://www.the-cryosphere.net/8/2335/2014/DOIback to text
- 34 articleVariational algorithms for analysis and assimilation of meteorological observations: theoretical aspects.Tellus38A1986, 97-110back to textback to text
- 35 articleSimulation of the flow past a circular cylinder from sub-critical to super-critical Reynolds numbers using an intermittency-based hybrid model.Journal of Fluids and Structures1232023back to text
- 36 articlePractical application to fluid flows of automatic differentiation for design problems.Von Karman Lecture Series1997back to text
- 37 phdthesisDifférentiation Automatique: application à un problème d'optimisation en météorologie.université de Nice Sophia-Antipolis1993back to text
- 38 inproceedingsSymbolic Bounds Analysis of Pointers, Array Indices, and Accessed Memory Regions.Proceedings of the ACM SIGPLAN'00 Conference on Programming Language Design and ImplementationACM2000back to text

