2023Activity reportProject-TeamMATHNEURO
RNSR: 201622008G- Research center Inria Centre at Université Côte d'Azur
- In partnership with:CNRS, Université Côte d'Azur
- Team name: Mathematics for Neuroscience
- In collaboration with:Laboratoire Jean-Alexandre Dieudonné (JAD)
- Domain:Digital Health, Biology and Earth
- Theme:Computational Neuroscience and Medicine
Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.4. Multiscale modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.3. Probabilistic methods
- A6.3. Computation-data interaction
- A6.3.4. Model reduction
Other Research Topics and Application Domains
- B1. Life sciences
- B1.2. Neuroscience and cognitive science
- B1.2.1. Understanding and simulation of the brain and the nervous system
- B1.2.2. Cognitive science
1 Team members, visitors, external collaborators
Research Scientists
- Mathieu Desroches [Team leader, INRIA, Researcher, until Sep 2023, HDR]
- Mathieu Desroches [Team leader, INRIA, Senior Researcher, from Oct 2023, HDR]
- Emre Baspinar [INRIA, Researcher, from Oct 2023]
- Fabien Campillo [INRIA, Senior Researcher, HDR]
- Anton Chizhov [INRIA, Advanced Research Position]
- Pascal Chossat [CNRS, Emeritus, HDR]
- Maciej Krupa [UNIV COTE D'AZUR, Senior Researcher, until Aug 2023, HDR]
Post-Doctoral Fellow
- Mattia Sensi [INRIA, Post-Doctoral Fellow, until Feb 2023]
PhD Students
- Guillaume Girier [BCAM]
- Jordi Penalva Vadell [University of the Balearic Islands (Spain), from Nov 2023 until Nov 2023]
Administrative Assistant
- Marie-Cecile Lafont [INRIA]
External Collaborators
- Frederic Lavigne [UNIV COTE D'AZUR, from Oct 2023]
- Frederic Lavigne [UNIV COTE D'AZUR, until Sep 2023]
- Serafim Rodrigues [BCAM, from Mar 2023]
2 Overall objectives
MathNeuro focuses on the applications of multi-scale dynamics to neuroscience. This involves the modeling and analysis of systems with multiple time scales and space scales, as well as stochastic effects. We look both at single-cell models, microcircuits and large networks. In terms of neuroscience, we are mainly interested in questions related to synaptic plasticity and neuronal excitability, in particular in the context of pathological states such as epileptic seizures and neurodegenerative diseases such as Alzheimer.
Our work is quite mathematical but we make heavy use of computers for numerical experiments and simulations. We have close ties with several top groups in biological neuroscience. We are pursuing the idea that the "unreasonable effectiveness of mathematics" can be brought, as it has been in physics, to bear on neuroscience.
Modeling such assemblies of neurons and simulating their behavior involves putting together a mixture of the most recent results in neurophysiology with such advanced mathematical methods as dynamical systems theory, bifurcation theory, probability theory, stochastic calculus, theoretical physics and statistics, as well as the use of simulation tools.
We conduct research in the following main areas:
- Neural networks dynamics
- Mean-field and stochastic approaches
- Neural fields
- Slow-fast dynamics in neuronal models
- Modeling neuronal excitability
- Synaptic plasticity
- Memory processes
- Visual neuroscience
3 Research program
3.1 Neural networks dynamics
The study of neural networks is certainly motivated by the long term goal to understand how brain is working. But, beyond the comprehension of brain or even of simpler neural systems in less evolved animals, there is also the desire to exhibit general mechanisms or principles at work in the nervous system. One possible strategy is to propose mathematical models of neural activity, at different space and time scales, depending on the type of phenomena under consideration. However, beyond the mere proposal of new models, which can rapidly result in a plethora, there is also a need to understand some fundamental keys ruling the behaviour of neural networks, and, from this, to extract new ideas that can be tested in real experiments. Therefore, there is a need to make a thorough analysis of these models. An efficient approach, developed in our team, consists of analyzing neural networks as dynamical systems. This allows to address several issues. A first, natural issue is to ask about the (generic) dynamics exhibited by the system when control parameters vary. This naturally leads to analyze the bifurcations 57 58 occurring in the network and which phenomenological parameters control these bifurcations. Another issue concerns the interplay between the neuron dynamics and the synaptic network structure.
3.2 Mean-field and stochastic approaches
Modeling neural activity at scales integrating the effect of thousands of neurons is of central importance for several reasons. First, most imaging techniques are not able to measure individual neuron activity (microscopic scale), but are instead measuring mesoscopic effects resulting from the activity of several hundreds to several hundreds of thousands of neurons. Second, anatomical data recorded in the cortex reveal the existence of structures, such as the cortical columns, with a diameter of about 50 to 1, containing of the order of one hundred to one hundred thousand neurons belonging to a few different species. The description of this collective dynamics requires models which are different from individual neurons models. In particular, when the number of neurons is large enough, averaging effects appear, and the collective dynamics is well described by an effective mean-field, summarizing the effect of the interactions of a neuron with the other neurons, and depending on a few effective control parameters. This vision, inherited from statistical physics requires that the space scale be large enough to include a large number of microscopic components (here neurons) and small enough so that the region considered is homogeneous.
Our group is developing mathematical methods allowing to produce dynamic mean-field equations from the physiological characteristics of neural structure (neurons type, synapse type and anatomical connectivity between neurons populations). These methods use tools from advanced probability theory such as the theory of Large Deviations 46 and the study of interacting diffusions 4.
3.3 Neural fields
Neural fields are a phenomenological way of describing the activity of population of neurons by delayed integro-differential equations. This continuous approximation turns out to be very useful to model large brain areas such as those involved in visual perception. The mathematical properties of these equations and their solutions are still imperfectly known, in particular in the presence of delays, different time scales and noise.
Our group is developing mathematical and numerical methods for analyzing these equations. These methods are based upon techniques from mathematical functional analysis, bifurcation theory 23, 59, equivariant bifurcation analysis, delay equations, and stochastic partial differential equations. We have been able to characterize the solutions of these neural fields equations and their bifurcations, apply and expand the theory to account for such perceptual phenomena as edge, texture 40, and motion perception. We have also developed a theory of singular perturbations for neural fields equations 2, based in particular on center manifold and normal forms ideas 3.
3.4 Slow-fast dynamics in neuronal models
Neuronal rhythms typically display many different timescales, therefore it is important to incorporate this slow-fast aspect in models. We are interested in this modeling paradigm where slow-fast point models, using Ordinary Differential Equations (ODEs), are investigated in terms of their bifurcation structure and the patterns of oscillatory solutions that they can produce. To gain insight into the dynamics of such systems, we use a mix of theoretical techniques — such as geometric desingularization and centre manifold reduction 50 — and numerical methods such as pseudo-arclength continuation 44. We are interested in families of complex oscillations generated by both mathematical and biophysical models of neurons. In particular, so-called mixed-mode oscillations (MMOs)15, 42, 49, which represent an alternation between subthreshold and spiking behaviour, and bursting oscillations43, 48, also corresponding to experimentally observed behaviour 41; see Figure 1. We are working on extending these results to spatio-temporal neural models 2.
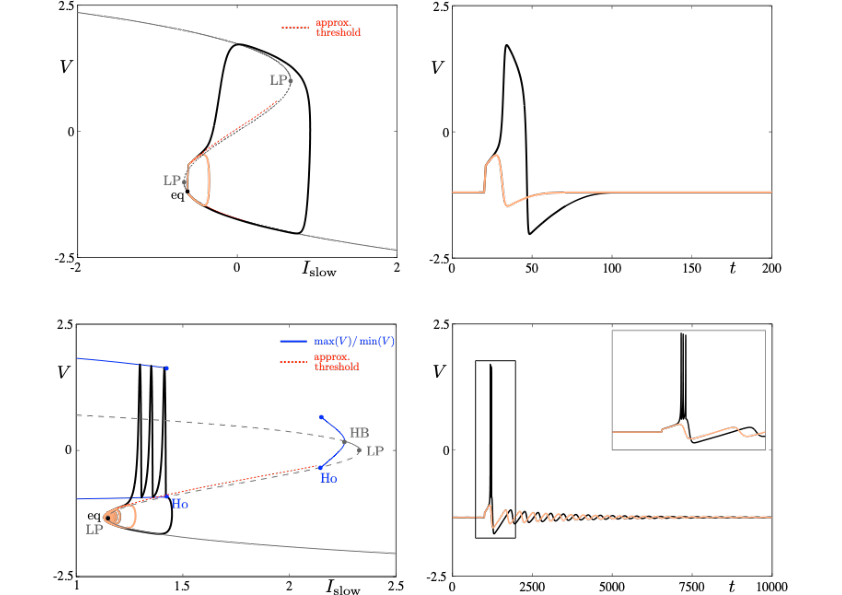
Excitability threshold as slow manifolds in a simple spiking model, namely the FitzHugh-Nagumo model, (top panels) and in a simple bursting model, namely the Hindmarsh-Rose model (bottom panels).
3.5 Modeling neuronal excitability
Excitability refers to the all-or-none property of neurons 45, 47. That is, the ability to respond nonlinearly to an input with a dramatic change of response from “none” — no response except a small perturbation that returns to equilibrium — to “all” — large response with the generation of an action potential or spike before the neuron returns to equilibrium. The return to equilibrium may also be an oscillatory motion of small amplitude; in this case, one speaks of resonator neurons as opposed to integrator neurons. The combination of a spike followed by subthreshold oscillations is then often referred to as mixed-mode oscillations (MMOs) 42. Slow-fast ODE models of dimension at least three are well capable of reproducing such complex neural oscillations. Part of our research expertise is to analyze the possible transitions between different complex oscillatory patterns of this sort upon input change and, in mathematical terms, this corresponds to understanding the bifurcation structure of the model. In particular, we also study possible combinations of different scenarios of complex oscillations and their relevance to revisit unexplained experimental data, e.g. in the context of bursting oscillations 43. In all case, the role of noise 39 is important and we take it into consideration, either as a modulator of the underlying deterministic dynamics or as a trigger of potential threshold crossings. Furthermore, the shape of time series of this sort with a given oscillatory pattern can be analyzed within the mathematical framework of dynamic bifurcations; see section 3.4. The main example of abnormal neuronal excitability is hyperexcitability and it is important to understand the biological factors which lead to such excess of excitability and to identify (both in detailed biophysical models and reduced phenomenological ones) the mathematical structures leading to these anomalies. Hyperexcitability is one important trigger for pathological brain states related to various diseases such as chronic migraine 53, epilepsy 55 or even Alzheimer's Disease 51. A central axis of research within our group is to revisit models of such pathological scenarios, in relation with a combination of advanced mathematical tools and in partnership with biological labs.
3.6 Synaptic Plasticity
Neural networks show amazing abilities to evolve and adapt, and to store and process information. These capabilities are mainly conditioned by plasticity mechanisms, and especially synaptic plasticity, inducing a mutual coupling between network structure and neuron dynamics. Synaptic plasticity occurs at many levels of organization and time scales in the nervous system 38. It is of course involved in memory and learning mechanisms, but it also alters excitability of brain areas and regulates behavioral states (e.g., transition between sleep and wakeful activity). Therefore, understanding the effects of synaptic plasticity on neurons dynamics is a crucial challenge.
Our group is developing mathematical and numerical methods to analyze this mutual interaction. On the one hand, we have shown that plasticity mechanisms 13, 21, Hebbian-like or Spike Timing Dependent Plasticity (STDP), have strong effects on neuron dynamics complexity, such as dynamics complexity reduction, and spike statistics.
3.7 Memory processes
The processes by which memories are formed and stored in the brain are multiple and not yet fully understood. What is hypothesized so far is that memory formation is related to the activation of certain groups of neurons in the brain. Then, one important mechanism to store various memories is to associate certain groups of memory items with one another, which then corresponds to the joint activation of certain neurons within different subgroup of a given population. In this framework, plasticity is key to encode the storage of chains of memory items. Yet, there is no general mathematical framework to model the mechanism(s) behind these associative memory processes. We are aiming at developing such a framework using our expertise in multi-scale modeling, by combining the concepts of heteroclinic dynamics, slow-fast dynamics and stochastic dynamics.
The general objective that we wish to pursue in this project is to investigate non-equilibrium phenomena pertinent to storage and retrieval of sequences of learned items. In previous work by team members 12, 1, 17, it was shown that with a suitable formulation, heteroclinic dynamics combined with slow-fast analysis in neural field systems can play an organizing role in such processes, making the model accessible to a thorough mathematical analysis. Multiple choice in cognitive processes require a certain flexibility in the neural network, which has recently been investigated in the submitted paper 18.
Our goal is to contribute to identify general processes under which cognitive functions can be organized in the brain.
4 Application domains
The project underlying MathNeuro revolves around pillars of neuronal behaviour –excitability, plasticity, memory– in link with the initiation and propagation of pathological brain states in diseases such as cortical spreading depression (in link with certain forms of migraine with aura) 11, epileptic seizures 20 and Alzheimer’s Disease 6. Our work on memory processes can also potentially be applied to studying mental disorders such as schizophrenia 56 or obsessive disorder troubles 54.
5 Highlights of the year
Mathieu Desroches, MathNeuro team leader, was promoted to Directeur de Recherche. Furthermore, a new permament researcher, Emre Baspinar, was recruited as Chargé de Recherche. He will consolidate the MathNeuro research line on multiscale modeling in Neuroscience, while bringing to the team the new thematic of Neurogeometry5.
6 New results
6.1 Mean field theory and stochastic processes
6.1.1 The Gauss-Galerkin approximation method in nonlinear filtering
Participants: Fabien Campillo.
This is a translation in English of an article published by Fabien Campillo in 1986.
We study an approximation method for the one-dimensional nonlinear filtering problem, with discrete time and continuous time observation. We first present the method applied to the Fokker-Planck equation. The convergence of the approximation is established. We finally present a numerical example..
This work is available as 37.
6.2 Neural fields theory
6.2.1 A neural field model for ignition and propagation of cortical spreading depression
Participants: Emre Baspinar, Daniele Avitabile [VU Amsterdam and external collaborator of MathNeuro], Mathieu Desroches, Massimo Mantegazza [Institute of Molecular and Cellular Pharmacology (IPMC) and Inserm].
We propose a new neural field model for migraine-related cortical spreading depression (CSD). The model follows the Wilson-Cowan-Amari formalism. It is based on an excitatory-inhibitory neuron population pair which is coupled to a potassium concentration variable. This model is spatially extended to a cortical layer. Therefore, it can model both the ignition and propagation of CSD. It controls the propagation speed via connection weights and contribution weight of each population activity to the potassium accumulation in the extracellular matrix. The simulation results regarding the propagation speed are in coherence with the experiment results provided in Chever et al. (2021).
This work is available as 33.
6.3 Slow-fast dynamics in Neuroscience
6.3.1 From integrator to resonator neurons: A multiple-timescale scenario
Participants: Guillaume Girier [BCAM, Spain], Mathieu Desroches, Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
This work has been partially done during stays of Serafim Rodrigues and Guillaume Girier in MathNeuro.
Neuronal excitability manifests itself through a number of key markers of the dynamics and it allows to classify neurons into different groups with identifiable voltage responses to input currents. In particular, two main types of excitability can be defined based on experimental observations, and their underlying mathematical models can be distinguished through separate bifurcation scenarios. Related to these two main types of excitable neural membranes, and associated models, is the distinction between integrator and resonator neurons. One important difference between integrator and resonator neurons, and their associated model representations, is the presence in resonators, as opposed to integrators, of subthreshold oscillations following spikes. Switches between one neural category and the other can be observed and/or created experimentally, and reproduced in models mostly through changes of the bifurcation structure. In the present work, we propose a new scenario of switch between integrator and resonator neurons based upon multiple-timescale dynamics and the possibility to force an integrator neuron with a specific time-dependent slowly-varying current. The key dynamical object organizing this switch is a so-called folded-saddle singularity. We also showcase the reverse switch via a folded-node singularity and propose an experimental protocol to test our theoretical predictions.
This work has been published in Nonlinear Dynamics and is available as 26.
6.3.2 Entry-exit functions in fast-slow systems with intersecting eigenvalues
Participants: Panagiotis Kaklamanos [The University of Edinburgh, UK], Christian Kuehn [TU Munich, Germany], Nikola Popovic [The University of Edinburgh, UK], Mattia Sensi.
We study delayed loss of stability in a class of fast-slow systems with two fast variables and one slow one, where the linearization of the fast vector field along a one-dimensional critical manifold has two real eigenvalues which intersect before the accumulated contraction and expansion are balanced along any individual eigendirection. That interplay between eigenvalues and eigendirections renders the use of known entry-exit relations unsuitable for calculating the point at which trajectories exit neighbourhoods of the given manifold. We illustrate the various qualitative scenarios that are possible in the class of systems considered here, and we propose novel formulae for the entry-exit functions that underlie the phenomenon of delayed loss of stability therein.
This work was published in Journal of Dynamics and Differential Equations and is available as 27.
6.4 Mathematical modelling of neuronal excitability
6.4.1 Observing hidden neuronal states in experiments
Participants: Dmitry Amakhin [Sechenov Institute of Evolutionary Physiology and Biochemistry of RAS, Russia], Anton Chizhov, Guillaume Girier [BCAM, Spain], Mathieu Desroches, Jan Sieber [University of Exeter, UK], Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
This work was partially done during a stay of Serafim Rodrigues in MathNeuro.
We construct systematically experimental steady-state bifurcation diagrams for entorhinal cortex neurons. A slowly ramped voltage-clamp electrophysiology protocol serves as closed-loop feedback controlled experiment for the subsequent current-clamp open-loop protocol on the same cell. In this way, the voltage-clamped experiment determines dynamically stable and unstable (hidden) steady states of the current-clamp experiment. The transitions between observable steady states and observable spiking states in the current-clamp experiment reveal stability and bifurcations of the steady states, completing the steady-state bifurcation diagram.
This work has been submitted for publication and is available as 32.
6.4.2 Single-compartment model of a pyramidal neuron, fitted to recordings with current and conductance injection
Participants: Anton Chizhov, Dmitry Amakhin [Sechenov Institute of Evolutionary Physiology and Biochemistry of RAS, Russia], A. Erdem Sagtekin [Istanbul Technical University, Turkey], Mathieu Desroches.
For single neuron models, reproducing characteristics of neuronal activity such as the firing rate, amplitude of spikes, and threshold potentials as functions of both synaptic current and conductance is a challenging task. In the present work, we measure these characteristics of regular spiking cortical neurons using the dynamic patch-clamp technique, compare the data with predictions from the standard Hodgkin-Huxley and Izhikevich models, and propose a relatively simple five-dimensional dynamical system model, based on threshold criteria. The model contains a single sodium channel with slow inactivation, fast activation and moderate deactivation, as well as, two fast repolarizing and slow shunting potassium channels. The model quantitatively reproduces characteristics of steady-state activity that are typical for a cortical pyramidal neuron, namely firing rate not exceeding 30 Hz; critical values of the stimulating current and conductance which induce the depolarization block not exceeding 80 mV and 3 times the resting input conductance, respectively; extremum of hyperpolarization close to the midpoint between spikes. The analysis of the model reveals that the spiking regime appears through a saddle-node-on-invariant-circle bifurcation, and the depolarization block is reached through a saddle-node bifurcation of cycles. The model can be used for realistic network simulations, and it can also be implemented within the so-called mean-field, refractory density framework.
This work was published in Biological Cybernetics and is available as 24.
6.4.3 Complex excitability and "flipping" of granule cells: an experimental and computational study
Participants: Joanna Danielewicz [BCAM, Bilbao], Guillaume Girier [BCAM, Bilbao], Anton Chizhov, Mathieu Desroches, Juan Manuel Encinas [Achucarro Center for Neuroscience, Spain], Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
This work was partially done during a stay of Serafim Rodrigues in MathNeuro.
In response to prolonged depolarizing current steps, different classes of neurons display specific firing characteristics (i.e. excitability class), such as a regular train of action potentials with more or less adaptation, delayed responses, or bursting. In general, one or more specific ionic transmembrane currents underlie the different firing patterns. Here we sought to investigate the influence of artificial sodium-like (Na channels) and slow potassium-like (KM channels) voltage-gated channels conductances on firing patterns and transition to depolarization block (DB) in Dentate Gyrus granule cells with dynamic clamp - a computer-controlled real-time closed-loop electrophysiological technique, which allows to couple mathematical models simulated in a computer with biological cells. Our findings indicate that the addition of extra Na/KM channels significantly affects the firing rate of low frequency cells, but not in high frequency cells. Moreover, we have observed that 44 percent of recorded cells exhibited what we have called a “flipping” behavior. This means that these cells were able to overcome the DB and generate trains of action potentials at higher current injections steps. We have developed a unified mathematical model of flipping cells to explain this phenomenon. Based on our computational model, we conclude that the appearance of flipping is linked to the number of states for the sodium channel of the model.
This work was submitted for publication and is available as 35.
6.4.4 Idealized multiple-timescale model of cortical spreading depolarization initiation and pre-epileptic hyperexcitability caused by NaV1.1/SCN1A mutations
Participants: Louisiane Lemaire [Humbolt University, Berlin, Germany], Mathieu Desroches, Martin Krupa, Massimo Mantegazza [Institute of Molecular and Cellular Pharmacology (IPMC) and Inserm].
NaV1.1 (SCN1A) is a voltage-gated sodium channel mainly expressed in GABAergic neurons. Loss of function mutations of NaV1.1 lead to epileptic disorders, while gain of function mutations cause a migraine in which cortical spreading depolarizations (CSDs) are involved. It is still debated how these opposite effects initiate two different manifestations of neuronal hyperactivity: epileptic seizures and CSD. To investigate this question, we previously built a conductance-based model of two neurons (GABAergic and pyramidal), with dynamic ion concentrations 20. When implementing either NaV1.1 migraine or epileptogenic mutations, ion concentration modifications acted as slow processes driving the system to the corresponding pathological firing regime. However, the large dimensionality of the model complicated the exploitation of its implicit multi-timescale structure. Here, we substantially simplify our biophysical model to a minimal version more suitable for bifurcation analysis. The explicit timescale separation allows us to apply slow-fast theory, where slow variables are treated as parameters in the fast singular limit. In this setting, we reproduce both pathological transitions as dynamic bifurcations in the full system. In the epilepsy condition, we shift the spike-terminating bifurcation to lower inputs for the GABAergic neuron, to model an increased susceptibility to depolarization block. The resulting failure of synaptic inhibition triggers hyperactivity of the pyramidal neuron. In the migraine scenario, spiking-induced release of potassium leads to the abrupt increase of the extracellular potassium concentration. This causes a dynamic spike-terminating bifurcation of both neurons, which we interpret as CSD initiation.
This work was published in Journal of Mathematical Biology and is available as 28.
6.5 Multiscale modelling of synaptic plasticity
6.5.1 Slow-fast dynamics in a neurotransmitter release model: delayed response to a time-dependent input signal
Participants: Mattia Sensi, Mathieu Desroches, Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
We propose a generalization of the neurotransmitter release model proposed in Rodrigues et al. (PNAS, 2016). We increase the complexity of the underlying slow-fast system by considering a degree-four polynomial as parametrization of the critical manifold. We focus on the possible transient and asymptotic dynamics, exploiting the so-called entry-exit function to describe slow parts of the dynamics. We provide extensive numerical simulations, complemented by numerical bifurcation analysis.
This work was published in Physica D and is available as 30.
6.5.2 Synchronization in STDP-driven memristive neural networks with time-varying topology
Participants: Marius Yamakou [University of Erlangen-Nuremberg, Germany], Mathieu Desroches, Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
Synchronization is a widespread phenomenon in the brain. Despite numerous studies, the specific parameter configurations of the synaptic network structure and learning rules needed to achieve robust and enduring synchronization in neurons driven by spike-timing-dependent plasticity (STDP) and temporal networks subject to homeostatic structural plasticity (HSP) rules remain unclear. Here, we bridge this gap by determining the configurations required to achieve high and stable degrees of complete synchronization (CS) and phase synchronization (PS) in time-varying small-world and random neural networks driven by STDP and HSP. In particular, we found that decreasing P (which enhances the strengthening effect of STDP on the average synaptic weight) and increasing F (which speeds up the swapping rate of synapses between neurons) always lead to higher and more stable degrees of CS and PS in small-world and random networks, provided that the network parameters such as the synaptic time delay , the average degree , and the rewiring probability have some appropriate values. When , , and are not fixed at these appropriate values, the degree and stability of CS and PS may increase or decrease when F increases, depending on the network topology. It is also found that the time delay can induce intermittent CS and PS whose occurrence is independent F . Our results could have applications in designing neuromorphic circuits for optimal information processing and transmission via synchronization phenomena.
This work was published in Journal of Biological Physics and is available as 31.
6.6 Studies on ageing
6.6.1 Viruses - a major cause of amyloid deposition in the brain
Participant: Tamas Fülöp [Université de Sherbrooke, Canada], Charles Ramassamy [INRS-IAF, Canada], Simon Lévesque [Centre hospitalo-universitaire de Sherbrooke, Canada], Eric Frost [Université de Sherbrooke, Canada], Benoît Laurent [University of Sherbrooke, Canada], Guy Lacombe [University of Sherbrooke, Canada], Abdelouahed Khalil [University of Sherbrooke, Canada], Anis Larbi [University of Sherbrooke, Canada], Katsuiku Hirokawa [Tokyo Medical and Dental University, Japan], Mathieu Desroches, Serafim Rodrigues [BCAM, Spain, and external collaborator of MathNeuro].
This work was partially done during a stay of Serafim Rodrigues in MathNeuro.
Clinically, Alzheimer's disease (AD) is a syndrome with a spectrum of various cognitive disorders. There is a complete dissociation between the pathology and the clinical presentation. Therefore, we need a disruptive new approach to be able to prevent and treat AD. In this review, we extensively discuss the evidence why the amyloid beta is not the pathological cause of AD which makes therefore the amyloid hypothesis not sustainable anymore. We review the experimental evidence underlying the role of microbes, especially that of viruses, as a trigger/cause for the production of amyloid beta leading to the establishment of a chronic neuroinflammation as the mediator manifesting decades later by AD as a clinical spectrum. In this context, the emergence and consequences of the infection/antimicrobial protection hypothesis are described. The epidemiological and clinical data supporting this hypothesis are also analyzed. For decades, we have known that viruses are involved in the pathogenesis of AD. This discovery was ignored and discarded for a long time. Now we should accept this fact, which is not a hypothesis anymore, and stimulate the research community to come up with new ideas, new treatments, and new concepts.
This work was published in Expert Review of Neurotherapeutics and is available as 25.
6.6.2 Topological Data Analysis of Human Brain Data
Participant: Ufuk Cem Birbiri [Université Côte d'Azur and MathNeuro].
This work is a research report written by Ufuk Cem Birbiri out of the report of his master 2 internship done under the supervision of Mathieu Desroches in 2022. This project has also involved Serafim Rodrigues (BCAM, Spain) and Fernando Santos (University of Amsterdam and Institute for Advanced Study, The Netherlands). It is available as 34. The work finds its place within our research line on using advanced data-scientific methods, such as Topological Data Analysis, to study biomarkers of aging.
6.7 Numerics
6.7.1 The one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering
Participant: Samuel Nyobe [University of Yaoundé, Cameroon], Fabien Campillo, Serge Moto [University of Yaoundé, Cameroon], Vivien Rossi [Cirad and University of Yaoundé, Cameroon].
Sequential Monte Carlo methods have been a major breakthrough in the field of numerical signal processing for stochastic dynamical state-space systems with partial and noisy observations. However, these methods still present certain weaknesses. One of the most fundamental is the degeneracy of the filter due to the impoverishment of the particles: the prediction step allows the particles to explore the state-space and can lead to the impoverishment of the particles if this exploration is poorly conducted or when it conflicts with the following observation that will be used in the evaluation of the likelihood of each particle. In this article, in order to improve this last step within the framework of the classic bootstrap particle filter, we propose a simple approximation of the one step fixed- lag smoother. At each time iteration, we propose to perform additional simulations during the prediction step in order to improve the likelihood of the selected particles.
7 Partnerships and cooperations
7.1 International research visitors
7.1.1 Visits of international scientists
Other international visits to the team
Serafim Rodrigues
-
Status:
researcher
-
Institution of origin:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
8-31 March, 4-11 May, 5-15 June and 18 Oct.-1 Nov. 2023
-
Context of the visit:
Collaboration with Mathieu Desroches on mathematical aspects of neuronal excitability; collaboration with Fabien Campillo and Mathieu Desroches on the modeling of Dravet Syndrome; collaboration with Anton Chizhov and Mathieu Desroches on the excitability of newborn neurons.
-
Mobility program/type of mobility:
research stays
Guillaume Girier
-
Status:
PhD
-
Institution of origin:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
1-30 September 2023
-
Context of the visit:
Collaboration with Mathieu Desroches , who is his second supervisor, on advancing his thesis a manuscript.
-
Mobility program/type of mobility:
research stay
Vivien Kirk
-
Status:
researcher
-
Institution of origin:
The University of Auckland
-
Country:
New Zealand
-
Dates:
16 October to 3 November 2023
-
Context of the visit:
Collaboration with Mathieu Desroches on multiple-timescale bursting dynamics, in the context of the PhD project of Morgan Meertens (also visitor).
-
Mobility program/type of mobility:
research stay
Morgan Meertens
-
Status:
PhD
-
Institution of origin:
The University of Auckland
-
Country:
New Zealand
-
Dates:
16 October to 3 November 2023
-
Context of the visit:
Collaboration with Mathieu Desroches on multiple-timescale bursting dynamics, in the context of her PhD project.
-
Mobility program/type of mobility:
research stay
Jordi Penalva Vadell
-
Status:
PhD
-
Institution of origin:
University of the Balearic Islands, Palma
-
Country:
Spain
-
Dates:
1-28 November 2023
-
Context of the visit:
Collaboration with Mathieu Desroches , who is his third supervisor, on finishing and submitting a manuscript and preparing for his PhD defence.
-
Mobility program/type of mobility:
research stay
7.1.2 Visits to international teams
Research stays abroad
Fabien Campillo
-
Visited institution:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
19-22 December 2023
-
Context of the visit:
Collaboration with Serafim Rodrigues on Bayesian inference in Neuroscience
-
Mobility program/type of mobility:
research stay
Mathieu Desroches
-
Visited institution:
VU Amsterdam
-
Country:
The Netherlands
-
Dates:
12-15 December 2023
-
Context of the visit:
Collaboration with Daniele Avitabile on multiple-timescale neural field models
-
Mobility program/type of mobility:
research stay
Mathieu Desroches
-
Visited institution:
Basque Center for Applied Mathematics, Bilbao
-
Country:
Spain
-
Dates:
03-20 Jan., 03-28 July, 16 Aug.-02 Sept., 28 Sept.-09 Oct., 05-12 Dec.
-
Context of the visit:
Collaboration with Serafim Rodrigues and PhD student Guillaume Girier on neuronal excitability.
-
Mobility program/type of mobility:
research stay
7.1.3 H2020 projects
HBP SGA3
Participants: Fabien Campillo, Mathieu Desroches.
HBP SGA3 project on cordis.europa.eu
-
Title:
Human Brain Project Specific Grant Agreement 3
-
Duration:
From April 1, 2020 to September 30, 2023
-
Inria contact:
Bertrand Thirion (Inria Saclay)
-
Coordinator:
Jan Bjaalie (Norway)
-
Summary:
The last of four multi-year work plans will take the HBP to the end of its original incarnation as an EU Future and Emerging Technology Flagship. The plan is that the end of the Flagship will see the start of a new, enduring European scientific research infrastructure, EBRAINS, hopefully on the European Strategy Forum on Research Infrastructures (ESFRI) roadmap. The SGA3 work plan builds on the strong scientific foundations laid in the preceding phases, makes structural adaptations to profit from lessons learned along the way (e.g. transforming the previous Subprojects and Co-Design Projects into fewer, stronger, well-integrated Work Packages) and introduces new participants, with additional capabilities.
7.2 National initiatives
7.2.1 ANR projects
HEBBIAN
-
Title:
Apprentissage hebbien de séquences
-
Duration:
From 1 October 2023 to 30 September 2027
-
Inria contact:
Mathieu Desroches
-
Coordinator:
Arnaud Rey (CNRS, Marseille)
-
Summary:
This project is articulated around three main research questions that are central to better understand sequence learning mechanisms: Q1) What is the relationship between the spacing between two repetitions of the same sequence and the development of a memory trace of that sequence? Q2) How does sequence encoding vary with sequence size, number, and learning context? Q3) How are small, regular sequences that are embedded in larger sequences, encoded (i.e., the parts and whole problem)? Our project is also based on two main research hypotheses. We first assume that the mechanisms supporting the learning of sequential information are based on elementary associative learning mechanisms that are evolutionarily ancient and shared by humans and non-human primates (Rey et al., 2012, 2019a, 2022). Our second main hypothesis assumes that these associative learning mechanisms are mainly supported by Hebbian learning principles (Brunel & Lavigne, 2009; Köksal Ersöz et al., 2020, 2022; Tovar & Westermann, 2023).
8 Dissemination
8.1 Promoting scientific activities
8.1.1 Scientific events: selection
-
Mathieu Desroches
was co-organiser of the two-part Mini-Symposium Multiple-Timescale Dynamics with a View Towards Biological Applications, at the SIAM Conference on Applications of Dynamical Systems (DS23), Portland (USA), 14-18 May 2023.
Member of the conference program committees
-
Mathieu Desroches
was program committee member of the 12th International Conference on Complex Networks and their Applications, Menton (France), 28-30 November 2023.
Member of the editorial boards
-
Fabien Campillo
is editorial board member of Revue Africaine de la Recherche en Informatique et Mathématiques Appliquées (ARIMA).
-
Mathieu Desroches
is co-founder and co-Editor-in-Chief of the SIAM book series on Mathematical Neuroscience. This new series will publish standard textbooks and monographs on Mathematical Neuroscience, hence filling a gap in the publishing landscape related to this young yet fast-growing research field. Furthermore, we will also put efforts on publishing short hands-on tutorials, with exercises, codes and multimedia content posted on a companion webpage hosted by SIAM.
-
Mathieu Desroches
is associate editor of the journal Frontiers in Physiology (impact factor 4.7).
Reviewer - reviewing activities
-
Fabien Campillo
acted as a reviewer for the Journal of Mathematical Biology.
-
Pascal Chossat
acted as a reviewer for the Journal of Computational Neuroscience.
-
Mathieu Desroches
acted as a reviewer for the journals Acta Applicandae Mathematicae, Applied Mathematical Modelling, Chaos, Journal of Nonlinear Science, Neural Computation, Nonlinear Dynamics and PLoS Computational Biology.
8.1.2 Invited talks
-
Fabien Campillo
gave an invited talk entitled “Nonlinear Filtering in Neuroscience” at the 21st INFORMS Applied Probability Society Conference, Nancy (France), 30 June 2023.
-
Anton Chizhov
gave an invited talk, jointly with Lyle Graham (CNRS, Université de Paris) entitled “Neurons and neuronal populations: From recordings in vivo to simulations of cortical tissue”, as a Neuromod mini-course, Inria centre at Université Côte d'Azur, 11 January 2023.
-
Mathieu Desroches
gave an invited talk entitled: “Classification of bursting patterns: Mind the slow variables” at the SIAM Conference on Applications of Dynamical Systems (DS23), Portland (USA), 17 May 2023.
-
Mathieu Desroches
gave an invited seminar talk entited “Classification of bursting patterns: Review & Extension” at the Institut de Neurosciences des Systèmes, Marseille (France), 14 September 2023.
8.1.3 Leadership within the scientific community
-
Fabien Campillo
is a founding member of the African scholarly Society on Digital Sciences (ASDS).
-
Mathieu Desroches
is member of the scientific committee of the Complex Systems Academy of the UCAJEDI IDEX.
8.1.4 Scientific expertise
-
Mathieu Desroches
has been reviewing grant proposals for the Agence Nationale de la Recherche (AAPG 2023).
-
Mathieu Desroches
has been reviewing grant proposals for the Complex Systems Academy of the UCAJEDI Idex.
8.1.5 Research administration
-
Fabien Campillo
is member of the “Inria Evaluation Committee (CE)”.
-
Fabien Campillo
is member of the “Health and Safety committee (CSHCT)” of the Inria centre at Université Côte d'Azur.
-
Mathieu Desroches
is supervising the PhD seminar at the Inria centre at Université Côte d'Azur.
8.2 Teaching - Supervision - Juries
8.2.1 Teaching
-
Master:
Mathieu Desroches, Modèles Mathématiques et Computationnels en Neuroscience (Lectures, example classes and computer labs), 18 hours (Feb. 2023), M1 (BIM), Sorbonne Université, Paris, France.
-
Master:
Mathieu Desroches, Multiple Timescale Dynamics in Neuroscience, (Lectures, example classes and computer labs), 9 hours (Jan. 2023) and 21 hours (Nov.-Dec. 2023), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
-
Masters and Engineer schools:
With the project to write a book, Fabien Campillo proposes a set of applications of particle filtering, developed in the context of lectures given during many years in Masters and Engineer schools. See the associated web page and git repository.
8.2.2 Supervision
-
PhD
Guillaume Girier, Basque Center for Applied Mathematics (BCAM, Bilbao, Spain) is doing a PhD on “A mathematical, computational and experimental study of neuronal excitability”, co-supervised by S. Rodrigues (BCAM) and Mathieu Desroches, in co-tutelle between the University of the Basque Country and Université Côte d'Azur.
-
PhD
Jordi Penalva Vadell, University of the Balearic Islands (UIB, Palma, Spain) is doing a PhD on “Neuronal piecewise linear models reproducing bursting dynamics”, co-supervised by A. E. Teruel (UIB), C. Vich (UIB) and Mathieu Desroches.
-
Master 2 internship
Safaa Habib (Université Côte d’Azur - UCA, Nice), “Revisiting a Single-Neuron Model of Seizure-Like Events, Ictal Activity and Depolarization Block”, supervised by Mathieu Desroches, April - September 2023.
8.2.3 Juries
-
Fabien Campillo
was member of the jury and reviewer of the PhD of Jana Zaherddine, entitled “Modèles mathématiques de l’allocation dynamique des ressources dans une cellule de bactérie”, supervised by Philipe Robert (Inria Paris Research Centre) and Vincent Fromion (Inrae, Jouy-en-Josas), 19 December 2023.
-
Pascal Chossat
was member of the jury of the PhD of Maria Virginia Bolelli, entitled “Neurogeometry of stereo vision”, supervised by Giovanna Citti (University of Bologna, Italy) and Alessandro Sarti (EHESS, Paris, France), 27 March 2023.
-
Mathieu Desroches
was member of the jury and reviewer of the PhD of Lisa Blum Moyse, entitled “Computational neuroscience models at different levels of abstraction for synaptic plasticity, astrocyte modulation of synchronization and systems memory consolidation”, supervised by Hugues Berry (Inria Lyon Centre), 14 September 2023.
9 Scientific production
9.1 Major publications
- 1 articleLatching dynamics in neural networks with synaptic depression.PLoS ONE128August 2017, e0183710HALDOIback to text
- 2 articleSpatiotemporal canards in neural field equations.Physical Review E 954April 2017, 042205HALDOIback to textback to text
- 3 articleLocal theory for spatio-temporal canards and delayed bifurcations.SIAM Journal on Mathematical Analysis526November 2020, 5703–5747HALDOIback to text
- 4 articleMean-field description and propagation of chaos in networks of Hodgkin-Huxley neurons.The Journal of Mathematical Neuroscience21We derive the mean-field equations arising as the limit of a network of interacting spiking neurons, as the number of neurons goes to infinity. The neurons belong to a fixed number of populations and are represented either by the Hodgkin-Huxley model or by one of its simplified version, the FitzHugh-Nagumo model. The synapses between neurons are either electrical or chemical. The network is assumed to be fully connected. The maximum conductances vary randomly. Under the condition that all neurons~ initial conditions are drawn independently from the same law that depends only on the population they belong to, we prove that a propagation of chaos phenomenon takes place, namely that in the mean-field limit, any finite number of neurons become independent and, within each population, have the same probability distribution. This probability distribution is a solution of a set of implicit equations, either nonlinear stochastic differential equations resembling the McKean-Vlasov equations or non-local partial differential equations resembling the McKean-Vlasov-Fokker-Planck equations. We prove the wellposedness of the McKean-Vlasov equations, i.e. the existence and uniqueness of a solution. We also show the results of some numerical experiments that indicate that the mean-field equations are a good representation of the mean activity of a finite size network, even for modest sizes. These experiments also indicate that the McKean-Vlasov-Fokker-Planck equations may be a good way to understand the mean-field dynamics through, e.g. a bifurcation analysis.2012, URL: http://www.mathematical-neuroscience.com/content/2/1/10back to text
- 5 articleA sub-Riemannian model of the visual cortex with frequency and phase.The Journal of Mathematical Neuroscience101December 2020HALDOIback to text
- 6 articleInteraction Mechanism Between the HSV-1 Glycoprotein B and the Antimicrobial Peptide Amyloid-β.Journal of Alzheimer's Disease Reports61September 2022, 599-606HALDOIback to text
- 7 articleLinks between deterministic and stochastic approaches for invasion in growth-fragmentation-death models.Journal of mathematical biology736-72016, 1781--1821URL: https://hal.science/hal-01205467
- 8 articleWeak convergence of a mass-structured individual-based model.Applied Mathematics & Optimization7212015, 37--73URL: https://hal.inria.fr/hal-01090727
- 9 articleAnalysis and approximation of a stochastic growth model with extinction.Methodology and Computing in Applied Probability1822016, 499--515URL: https://hal.science/hal-01817824
- 10 articleEffect of population size in a predator--prey model.Ecological Modelling2462012, 1--10URL: https://hal.inria.fr/hal-00723793
- 11 articleInitiation of migraine-related cortical spreading depolarization by hyperactivity of GABAergic neurons and NaV1.1 channels.The Journal of clinical investigation13121November 2021, e142203HALDOIback to text
- 12 articleHeteroclinic cycles in Hopfield networks.Journal of Nonlinear ScienceJanuary 2016HALDOIback to text
- 13 articleShort-term synaptic plasticity in the deterministic Tsodyks-Markram model leads to unpredictable network dynamics.Proceedings of the National Academy of Sciences of the United States of America 110412013, 16610-16615HALback to text
- 14 articleModeling cortical spreading depression induced by the hyperactivity of interneurons.Journal of Computational NeuroscienceOctober 2019HALDOI
- 15 articleCanards, folded nodes and mixed-mode oscillations in piecewise-linear slow-fast systems.SIAM Review584accepted for publication in SIAM Review on 13 August 2015November 2016, 653-691HALDOIback to text
- 16 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106HALDOI
- 17 articleNeuronal mechanisms for sequential activation of memory items: Dynamics and reliability.PLoS ONE1542020, 1-28HALDOIback to text
- 18 articleDynamic branching in a neural network model for probabilistic prediction of sequences.Journal of Computational Neuroscience504August 2022, 537-557HALDOIback to text
- 19 unpublishedCanard-induced complex oscillations in an excitatory network.November 2018, working paper or preprintHAL
- 20 articleModeling NaV1.1/SCN1A sodium channel mutations in a microcircuit with realistic ion concentration dynamics suggests differential GABAergic mechanisms leading to hyperexcitability in epilepsy and hemiplegic migraine.PLoS Computational Biology177July 2021, e1009239HALDOIback to textback to text
- 21 articleTime-coded neurotransmitter release at excitatory and inhibitory synapses.Proceedings of the National Academy of Sciences of the United States of America 1138February 2016, E1108-E1115HALDOIback to text
- 22 articleA Center Manifold Result for Delayed Neural Fields Equations.SIAM Journal on Mathematical Analysis4532013, 1527-1562HALDOI
- 23 articleA center manifold result for delayed neural fields equations.SIAM Journal on Applied Mathematics (under revision)RR-8020July 2012HALback to text
9.2 Publications of the year
International journals
Reports & preprints
Other scientific publications
9.3 Cited publications
- 38 articleTheory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex.The Journal of Neuroscience211982, 32--48back to text
- 39 articleThe non linear dynamics of retinal waves.Physica D: Nonlinear Phenomena4392022, 133436back to text
- 40 articleHyperbolic planforms in relation to visual edges and textures perception.PLoS Computational Biology5122009, e1000625back to text
- 41 articleA role for fast rhythmic bursting neurons in cortical gamma oscillations in vitro.Proceedings of the National Academy of Sciences of the United States of America101182004, 7152--7157back to text
- 42 articleMixed-Mode Oscillations with Multiple Time Scales.SIAM Review542May 2012, 211-288HALDOIback to textback to text
- 43 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106HALDOIback to textback to text
- 44 articleThe geometry of slow manifolds near a folded node.SIAM Journal on Applied Dynamical Systems742008, 1131--1162back to text
- 45 bookMathematical foundations of neuroscience.35Springer2010back to text
- 46 articleA large deviation principle and an expression of the rate function for a discrete stationary gaussian process.Entropy16122014, 6722--6738back to text
- 47 bookDynamical systems in neuroscience.MIT press2007back to text
- 48 articleNeural excitability, spiking and bursting.International Journal of Bifurcation and Chaos10062000, 1171--1266back to text
- 49 articleMixed-mode oscillations in a three time-scale model for the dopaminergic neuron.Chaos: An Interdisciplinary Journal of Nonlinear Science1812008, 015106back to text
- 50 articleRelaxation oscillation and canard explosion.Journal of Differential Equations17422001, 312--368back to text
- 51 articleAmyloid precursor protein: from synaptic plasticity to Alzheimer's disease.Annals of the New York Academy of Sciences104812005, 149--165back to text
- 52 articleThe one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering.HAL hal-034649872023, URL: https://hal.inria.fr/hal-03464987back to text
- 53 articlePathophysiology of migraine.Annual review of physiology752013, 365--391back to text
- 54 articleGlutamate, obsessive--compulsive disorder, schizophrenia, and the stability of cortical attractor neuronal networks.Pharmacology Biochemistry and Behavior10042012, 736--751back to text
- 55 articleDynamical diseases of brain systems: different routes to epileptic seizures.IEEE transactions on biomedical engineering5052003, 540--548back to text
- 56 articleAssociative semantic network dysfunction in thought-disordered schizophrenic patients: direct evidence from indirect semantic priming.Biological psychiatry34121993, 864--877back to text
- 57 articleA Markovian event-based framework for stochastic spiking neural networks.Journal of Computational Neuroscience30April 2011back to text
- 58 articleNeural Mass Activity, Bifurcations, and Epilepsy.Neural Computation2312December 2011, 3232--3286back to text
- 59 articleLocal/Global Analysis of the Stationary Solutions of Some Neural Field Equations.SIAM Journal on Applied Dynamical Systems93August 2010, 954--998URL: http://arxiv.org/abs/0910.2247DOIback to text

