2023Activity reportProject-TeamMOKAPLAN
RNSR: 201321083P- Research center Inria Paris Centre
- In partnership with:Université Paris-Dauphine, CNRS
- Team name: Advances in Numerical Calculus of Variations
- In collaboration with:CEREMADE
- Domain:Applied Mathematics, Computation and Simulation
- Theme:Numerical schemes and simulations
Keywords
Computer Science and Digital Science
- A5.3. Image processing and analysis
- A5.9. Signal processing
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.6. Optimization
- A6.3.1. Inverse problems
- A8.2.3. Calculus of variations
- A8.12. Optimal transport
- A9. Artificial intelligence
Other Research Topics and Application Domains
- B9.5.2. Mathematics
- B9.5.3. Physics
- B9.5.4. Chemistry
- B9.6.3. Economy, Finance
1 Team members, visitors, external collaborators
Research Scientists
- Vincent Duval [Team leader, INRIA, Senior Researcher, HDR]
- Jean-David Benamou [INRIA, Senior Researcher, HDR]
- Antonin Chambolle [CNRS, Senior Researcher, HDR]
- Thomas Gallouët [INRIA, Researcher]
- Flavien Leger [INRIA, Researcher]
- Irène Waldspurger [CNRS, Researcher]
Faculty Members
- Guillaume Carlier [DAUPHINE PSL, Professor, HDR]
- Paul Pegon [DAUPHINE PSL, Associate Professor, from Sep 2023]
- Paul Pegon [DAUPHINE PSL, Associate Professor Delegation, until Aug 2023]
- François-Xavier Vialard [UNIV GUSTAVE EIFFEL, Professor Delegation, from Feb 2023 until Jul 2023]
Post-Doctoral Fellow
- Adrien Vacher [INRIA, Post-Doctoral Fellow, from Dec 2023]
PhD Students
- Guillaume Chazareix [BNP, CIFRE]
- Hugo Malamut [DAUPHINE PSL]
- Joao Pinto Anastacio Machado [DAUPHINE PSL]
- Faniriana Rakoto Endor [CNRS, from Oct 2023]
- Erwan Stampfli [UNIV PARIS SACLAY]
- Maxime Sylvestre [DAUPHINE PSL]
Administrative Assistant
- Derya Gok [INRIA]
External Collaborators
- Yann Brenier [CNRS]
- François-Xavier Vialard [UNIV GUSTAVE EIFFEL, from Sep 2023]
2 Overall objectives
2.1 Introduction
The last decade has witnessed a remarkable convergence between several sub-domains of the calculus of variations, namely optimal transport (and its many generalizations), infinite dimensional geometry of diffeomorphisms groups and inverse problems in imaging (in particular sparsity-based regularization). This convergence is due to (i) the mathematical objects manipulated in these problems, namely sparse measures (e.g. coupling in transport, edge location in imaging, displacement fields for diffeomorphisms) and (ii) the use of similar numerical tools from non-smooth optimization and geometric discretization schemes. Optimal Transportation, diffeomorphisms and sparsity-based methods are powerful modeling tools, that impact a rapidly expanding list of scientific applications and call for efficient numerical strategies. Our research program shows the important part played by the team members in the development of these numerical methods and their application to challenging problems.
2.2 Static Optimal Transport and Generalizations
Optimal Transport, Old and New.
Optimal Mass Transportation is a mathematical research topic which started two centuries ago with Monge's work on the “Théorie des déblais et des remblais" (see 104). This engineering problem consists in minimizing the transport cost between two given mass densities. In the 40's, Kantorovich 113 introduced a powerful linear relaxation and introduced its dual formulation. The Monge-Kantorovich problem became a specialized research topic in optimization and Kantorovich obtained the 1975 Nobel prize in economics for his contributions to resource allocations problems. Since the seminal discoveries of Brenier in the 90's 67, Optimal Transportation has received renewed attention from mathematical analysts and the Fields Medal awarded in 2010 to C. Villani, who gave important contributions to Optimal Transportation and wrote the modern reference monographs 137, 138, arrived at a culminating moment for this theory. Optimal Mass Transportation is today a mature area of mathematical analysis with a constantly growing range of applications. Optimal Transportation has also received a lot of attention from probabilists (see for instance the recent survey 117 for an overview of the Schrödinger problem which is a stochastic variant of the Benamou-Brenier dynamical formulation of optimal transport). The development of numerical methods for Optimal Transportation and Optimal Transportation related problems is a difficult topic and comparatively underdeveloped. This research field has experienced a surge of activity in the last five years, with important contributions of the Mokaplan group (see the list of important publications of the team). We describe below a few of recent and less recent Optimal Transportation concepts and methods which are connected to the future activities of Mokaplan :
Brenier's theorem 70 characterizes the unique optimal map as the gradient of a convex potential. As such Optimal Transportation may be interpreted as an infinite dimensional optimisation problem under “convexity constraint": i.e. the solution of this infinite dimensional optimisation problem is a convex potential. This connects Optimal Transportation to “convexity constrained" non-linear variational problems such as, for instance, Newton's problem of the body of minimal resistance. The value function of the optimal transport problem is also known to define a distance between source and target densities called the Wasserstein distance which plays a key role in many applications such as image processing.
Monge-Ampère Methods.
A formal substitution of the optimal transport map as the gradient of a convex potential in the mass conservation constraint (a Jacobian equation) gives a non-linear Monge-Ampère equation. Caffarelli 74 used this result to extend the regularity theory for the Monge-Ampère equation. In the last ten years, it also motivated new research on numerical solvers for non-linear degenerate Elliptic equations 9612160 59 and the references therein. Geometric approaches based on Laguerre diagrams and discrete data 124 have also been developed. Monge-Ampère based Optimal Transportation solvers have recently given the first linear cost computations of Optimal Transportation (smooth) maps.
Generalizations of OT.
In recent years, the classical Optimal Transportation problem has been extended in several directions. First, different ground costs measuring the “physical" displacement have been considered. In particular, well posedness for a large class of convex and concave costs has been established by McCann and Gangbo 103. Optimal Transportation techniques have been applied for example to a Coulomb ground cost in Quantum chemistry in relation with Density Functional theory 90. Given the densities of electrons Optimal Transportation models the potential energy and their relative positions. For more than more than 2 electrons (and therefore more than 2 densities) the natural extension of Optimal Transportation is the so called Multi-marginal Optimal Transport (see 129 and the references therein). Another instance of multi-marginal Optimal Transportation arises in the so-called Wasserstein barycenter problem between an arbitrary number of densities 44. An interesting overview of this emerging new field of optimal transport and its applications can be found in the recent survey of Ghoussoub and Pass 128.

Example of color transfer between two images, computed using the method developed in 57, see also 133. The image framed in red and blue are the input images. Top and middle row: adjusted image where the color of the transported histogram has been imposed. Bottom row: geodesic (displacement) interpolation between the histogram of the chrominance of the image.
Numerical Applications of Optimal Transportation.
Optimal transport has found many applications, starting from its relation with several physical models such as the semi-geostrophic equations in meteorology 108, 93, 92, 55, 120, mesh adaptation 119, the reconstruction of the early mass distribution of the Universe 101, 68 in Astrophysics, and the numerical optimisation of reflectors following the Optimal Transportation interpretation of Oliker 73 and Wang 139. Extensions of OT such as multi-marginal transport has potential applications in Density Functional Theory , Generalized solution of Euler equations 69 (DFT) and in statistics and finance 53, 102 .... Recently, there has been a spread of interest in applications of OT methods in imaging sciences 63, statistics 61 and machine learning 94. This is largely due to the emergence of fast numerical schemes to approximate the transportation distance and its generalizations, see for instance 57. Figure 1 shows an example of application of OT to color transfer. Figure 2 shows an example of application in computer graphics to interpolate between input shapes.

Example of barycenter between shapes computed using optimal transport barycenters of the uniform densities inside the 3 extremal shapes, computed as detailed in 133. Note that the barycenters are not in general uniform distributions, and we display them as the surface defined by a suitable level-set of the density.
2.3 Diffeomorphisms and Dynamical Transport
Dynamical transport.
While the optimal transport problem, in its original formulation, is a static problem (no time evolution is considered), it makes sense in many applications to rather consider time evolution. This is relevant for instance in applications to fluid dynamics or in medical images to perform registration of organs and model tumor growth.
In this perspective, the optimal transport in Euclidean space corresponds to an evolution where each particule of mass evolves in straight line. This interpretation corresponds to the Computational Fluid Dynamic (CFD) formulation proposed by Brenier and Benamou in 54. These solutions are time curves in the space of densities and geodesics for the Wasserstein distance. The CFD formulation relaxes the non-linear mass conservation constraint into a time dependent continuity equation, the cost function remains convex but is highly non smooth. A remarkable feature of this dynamical formulation is that it can be re-cast as a convex but non smooth optimization problem. This convex dynamical formulation finds many non-trivial extensions and applications, see for instance 56. The CFD formulation also appears to be a limit case of Mean Fields games (MFGs), a large class of economic models introduced by Lasry and Lions 115 leading to a system coupling an Hamilton-Jacobi with a Fokker-Planck equation. In contrast, the Monge case where the ground cost is the euclidan distance leads to a static system of PDEs 64.
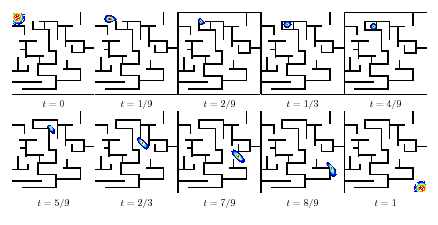
Examples of displacement interpolation (geodesic for optimal transport) according to a non-Euclidean Riemannian metric (the mass is constrained to move inside a maze) between to input Gaussian distributions. Note that the maze is dynamic: its topology change over time, the mass being “trapped” at time .
Gradient Flows for the Wasserstein Distance.
Another extension is, instead of considering geodesic for transportation metric (i.e. minimizing the Wasserstein distance to a target measure), to make the density evolve in order to minimize some functional. Computing the steepest descent direction with respect to the Wasserstein distance defines a so-called Wasserstein gradient flow, also known as JKO gradient flows after its authors 112. This is a popular tool to study a large class of non-linear diffusion equations. Two interesting examples are the Keller-Segel system for chemotaxis 111, 82 and a model of congested crowd motion proposed by Maury, Santambrogio and Roudneff-Chupin 123. From the numerical point of view, these schemes are understood to be the natural analogue of implicit scheme for linear parabolic equations. The resolution is however costly as it involves taking the derivative in the Wasserstein sense of the relevant energy, which in turn requires the resolution of a large scale convex but non-smooth minimization.
Geodesic on infinite dimensional Riemannian spaces.
To tackle more complicated warping problems, such as those encountered in medical image analysis, one unfortunately has to drop the convexity of the functional involved in defining the gradient flow. This gradient flow can either be understood as defining a geodesic on the (infinite dimensional) group of diffeomorphisms 52, or on a (infinite dimensional) space of curves or surfaces 140. The de-facto standard to define, analyze and compute these geodesics is the “Large Deformation Diffeomorphic Metric Mapping” (LDDMM) framework of Trouvé, Younes, Holm and co-authors 52, 107. While in the CFD formulation of optimal transport, the metric on infinitesimal deformations is just the norm (measure according to the density being transported), in LDDMM, one needs to use a stronger regularizing metric, such as Sobolev-like norms or reproducing kernel Hilbert spaces (RKHS). This enables a control over the smoothness of the deformation which is crucial for many applications. The price to pay is the need to solve a non-convex optimization problem through geodesic shooting method 125, which requires to integrate backward and forward the geodesic ODE. The resulting strong Riemannian geodesic structure on spaces of diffeomorphisms or shapes is also pivotal to allow us to perform statistical analysis on the tangent space, to define mean shapes and perform dimensionality reduction when analyzing large collection of input shapes (e.g. to study evolution of a diseases in time or the variation across patients) 75.
2.4 Sparsity in Imaging
Sparse regularization.
Beside image warping and registration in medical image analysis, a key problem in nearly all imaging applications is the reconstruction of high quality data from low resolution observations. This field, commonly referred to as “inverse problems”, is very often concerned with the precise location of features such as point sources (modeled as Dirac masses) or sharp contours of objects (modeled as gradients being Dirac masses along curves). The underlying intuition behind these ideas is the so-called sparsity model (either of the data itself, its gradient, or other more complicated representations such as wavelets, curvelets, bandlets 122 and learned representation 141).
The huge interest in these ideas started mostly from the introduction of convex methods to serve as proxy for these sparse regularizations. The most well known is the norm introduced independently in imaging by Donoho and co-workers under the name “Basis Pursuit” 87 and in statistics by Tibshirani 134 under the name “Lasso”. A more recent resurgence of this interest dates back to 10 years ago with the introduction of the so-called “compressed sensing” acquisition techniques 78, which make use of randomized forward operators and -type reconstruction.
Regularization over measure spaces.
However, the theoretical analysis of sparse reconstructions involving real-life acquisition operators (such as those found in seismic imaging, neuro-imaging, astro-physical imaging, etc.) is still mostly an open problem. A recent research direction, triggered by a paper of Candès and Fernandez-Granda 77, is to study directly the infinite dimensional problem of reconstruction of sparse measures (i.e. sum of Dirac masses) using the total variation of measures (not to be mistaken for the total variation of 2-D functions). Several works 76, 98, 97 have used this framework to provide theoretical performance guarantees by basically studying how the distance between neighboring spikes impacts noise stability.

|

|

|

|
| Segmentation input | output | Zooming input | output |
Two example of application of the total variation regularization of functions. Left: image segmentation into homogeneous color regions. Right: image zooming (increasing the number of pixels while keeping the edges sharp).
Low complexity regularization and partial smoothness.
In image processing, one of the most popular methods is the total variation regularization 132, 71. It favors low-complexity images that are piecewise constant, see Figure 4 for some examples on how to solve some image processing problems. Beside applications in image processing, sparsity-related ideas also had a deep impact in statistics 134 and machine learning 48. As a typical example, for applications to recommendation systems, it makes sense to consider sparsity of the singular values of matrices, which can be relaxed using the so-called nuclear norm (a.k.a. trace norm) 47. The underlying methodology is to make use of low-complexity regularization models, which turns out to be equivalent to the use of partly-smooth regularization functionals 118, 136 enforcing the solution to belong to a low-dimensional manifold.
2.5 Mokaplan unified point of view
The dynamical formulation of optimal transport creates a link between optimal transport and geodesics on diffeomorphisms groups. This formal link has at least two strong implications that Mokaplan will elaborate on: (i) the development of novel models that bridge the gap between these two fields ; (ii) the introduction of novel fast numerical solvers based on ideas from both non-smooth optimization techniques and Bregman metrics.
In a similar line of ideas, we believe a unified approach is needed to tackle both sparse regularization in imaging and various generalized OT problems. Both require to solve related non-smooth and large scale optimization problems. Ideas from proximal optimization has proved crucial to address problems in both fields (see for instance 54, 131). Transportation metrics are also the correct way to compare and regularize variational problems that arise in image processing (see for instance the Radon inversion method proposed in 57) and machine learning (see 94).
3 Research program
Since its creation, the Mokaplan team has made important contributions in Optimal Transport both on the theoretical and the numerical side, together with applications such as fluid mechanics, the simulation biological systems, machine learning. We have also contributed to to the field of inverse problems in signal and image processing (super-resolution, nonconvex low rank matrix recovery). In 2022, the team was renewed with the following research program which broadens our spectrum and addresses exciting new problems.
3.1 OT and related variational problems solvers encore et toujours
Participants: Flavien Léger, Jean-David Benamou, Guillaume Carlier, Thomas Gallouët, François-Xavier Vialard, Guillaume Chazareix , Adrien Vacher , Paul Pegon.
-
Asymptotic analysis of entropic OT
for a small entropic parameter is well understood for regular data on compact manifolds and standard quadratic ground cost 88, the team will extend this study to more general settings and also establish rigorous asymptotic estimates for the transports maps. This is important to provide a sound theoretical background to efficient and useful debiasing approaches like Sinkhorn Divergences 99. Guillaume Carlier , Paul Pegon and Luca Tamanini are investigating speed of convergence and quantitative stability results under general conditions on the cost (so that optimal maps may not be continuous or even fail to exist). Some sharp bounds have already been obtained, the next challenging goal is to extend the Laplace method to a nonsmooth setting and understand what entropic OT really selects when there are several optimal OT plans.
- High dimensional - Curse of dimensionality
-
Back-and-forth
The back-and-forth method 110, 109 is a state-of-the-art solver to compute optimal transport with convex costs and 2-Wasserstein gradient flows on grids. Based on simple but new ideas it has great potential to be useful for related problems. We plan to investigate: OT on point clouds in low dimension, the principal-agent problem in economics and more generally optimization under convex constraints 114, 126.
-
Transport and diffusion
The diffusion induced by the entropic regularization is fixed and now well understood. For recent variations of the OT problem (Martingale OT, Weak OT see 49) the diffusion becomes an explicit constraint or the control itself 105. The entropic regularisation of these problems can then be understood as metric/ground cost learning 79 (see also 130) and offers a tractable numerical method.
- Wasserstein Hamiltonian systems
-
Nonlinear fourth-order diffusion equations
such as thin-films or (the more involved) DLSS quantum drift equations are WGF. Such WGF are challenging both in terms of mathematical analysis (lack of maximum principle...) and of numerics. They are currently investigated by Jean-David Benamou , Guillaume Carlier in collaboration with Daniel Matthes. Note also that Mokaplan already contributed to a related topic through the TV-JKO scheme 80.
-
Lagrangian approaches for fluid mechanics
More generally we want to extend the design and implementation of Lagrangian numerical scheme for a large class of problem coming from fluids mechanics (WHS or WGF) using semi-discrete OT or entropic regularization. We will also take a special attention to link this approaches with problems in machine/statistical learning. To achieve this part of the project we will join forces with colleagues in Orsay University: Y. Brenier, H. Leclerc, Q. Mérigot, L. Nenna.
-
optimal transport
is a variant of OT where we want to minimize the maximal displacement of the transport plan, instead of the average distance. Following the seminal work of 86, and more recent developments 95, Guillaume Carlier , Paul Pegon and Luigi De Pascale are working on the description of restrictable solutions (which are cyclically -monotone) through some potential maps, in the spirit of Mange-Kantorovich potentials provided by a duality theory. Some progress has been made to partially describe cyclically quasi-motonone maps (related in some sense to cyclically -monotone maps), through quasi-convex potentials.
3.2 Application of OT numerics to non-variational and non convex problems
Participants: Flavien Léger, Guillaume Carlier, Jean-David Benamou, François-Xavier Vialard.
-
Market design
Z-mappings form a theory of non-variational problems initiated in the '70s but that has been for the most part overlooked by mathematicians. We are developing a new theory of the algorithms associated with convergent regular splitting of Z-mappings. Various well-established algorithms for matching models can be grouped under this point of view (Sinkhorn, Gale–Shapley, Bertsekas' auction) and this new perspective has the potential to unlock new convergence results, rates and accelerated methods.
-
Non Convex inverse problems
The PhD 142 provided a first exploration of Unbalanced Sinkhorn Divergence in this context. Given enough resources, a branch of PySit, a public domain software to test misfit functions in the context of Seismic imaging will be created and will allow to test other signal processing strategies in Full Waveform Inversion. Likewise the numerical method tested for 1D reflectors in 58 coule be develloped further (in particular in 2D).
-
Equilibrium and transport
Equilibrium in labor markets can often be expressed in terms of the Kantorovich duality. In the context of urban modelling or spatial pricing, this observation can be fruitfully used to compute equilibrium prices or densities as fixed points of operators involving OT, this was used in 51 and 50. Quentin Petit, Guillaume Carlier and Yves Achdou are currently developing a (non-variational) new semi-discrete model for the structure of cities with applications to tele-working.
-
Non-convex Principal-Agent problems
Guillaume Carlier , Xavier Dupuis, Jean-Charles Rochet and John Thanassoulis are developing a new saddle-point approach to non-convex multidimensional screening problems arising in regulation (Barron-Myerson) and taxation (Mirrlees).
3.3 Inverse problems with structured priors
Participants: Irène Waldspurger, Antonin Chambolle, Vincent Duval, Robert Tovey , Romain Petit .
-
Off-the-grid reconstruction of complex objects
Whereas, very recently, some methods were proposed for the reconstruction of curves and piecewise constant images on a continuous domain (66 and 81), those are mostly proofs of concept, and there is still some work to make them competitive in real applications. As they are much more complex than point source reconstruction methods, there is room for improvements (parametrization, introduction of several atoms...). In particular, we are currently working on an improvement of the algorithm 66 for inverse problems in imaging which involve Optimal Transport as a regularizer (see 135 for preliminary results). Moreover, we need to better understand their convergence and the robustness of such methods, using sensitivity analysis.
-
Correctness guarantees for Burer-Monteiro methods
Burer-Monteiro methods work well in practice and are therefore widely used, but existing correctness guarantees 65 hold under unrealistic assumptions only. In the long term, we aim at proposing new guarantees, which would be slightly weaker but would hold in settings more relevant to practice. A first step is to understand the “average” behavior of Burer-Monteiro methods, when applied to random problems, and could be the subject of a PhD thesis.
3.4 Geometric variational problems, and their interactions with transport
Participants: Vincent Duval, Paul Pegon, Antonin Chambolle, Joao-Miguel Machado .
-
Approximation of measures with geometric constraints
Optimal Transport is a powerful tool to compare and approximate densities, but its interaction with geometric constraints is still not well understood. In applications such as optimal design of structures, one aims at approximating an optimal pattern while taking into account fabrication constraints 62. In Magnetic Resonance Imaging (MRI), one tries to sample the Fourier transform of the unknown image according to an optimal density but the acquisition device can only proceed along curves with bounded speed and bounded curvature 116. Our goal is to understand how OT interacts with energy terms which involve, e.g. the length, the perimeter or the curvature of the support... We want to understand the regularity of the solutions and to quantify the approximation error. Moreover, we want to design numerical methods for the resolution of such problems, with guaranteed performance.
-
Discretization of singular measures
Beyond the (B)Lasso and the total variation (possibly off-the-grid), numerically solving branched transportation problems requires the ability to faithfully discretize and represent 1-dimensional structures in the space. The research program of A. Chambolle consists in part in developing the numerical analysis of variational problems involving singular measures, such as lower-dimensional currents or free surfaces. We will explore both phase-field methods (with P. Pegon, V. Duval) 83, 127 which easily represent non-convex problems, but lack precision, and (with V. Duval) precise discretizations of convex problems, based either on finite elements (and relying to the FEM discrete exterior calculus 46, cf 84 for the case of the total variation), or on finite differences and possibly a clever design of dual constraints as studied in 89, 85 again for the total variation.
-
Transport problems with metric optimization
In urban planning models, one looks at building a network (of roads, metro or train lines, etc.) so as to minimize a transport cost between two distributions, penalized by the cost for building the network, usually its length. A typical transport cost is Monge cost with a metric which is modified as a fraction of the euclidean metric on the network . We would like to consider general problems involving a construction cost to generate a conductance field (having in mind 1-dimensional integral of some function of ), and a transport cost depending on this conductance field. The afore-mentioned case studied in 72 falls into this category, as well as classical branched transport. The biologically-inspired network evolution model of 106 seems to provide such an energy in the vanishing diffusivity limit, with a cost for building a 1-dimensional permeability tensor and an congested transport cost with associated resistivity metric ; such a cost seems particularly relevant to model urban planning. Finally, we would like to design numerical methods to solve such problems, taking advantage of the separable structure of the whole cost.
4 Application domains
4.1 Natural Sciences
FreeForm Optics, Fluid Mechanics (Incompressible Euler, Semi-Geostrophic equations), Quantum Chemistry (Density Functional Theory), Statistical Physics (Schroedinger problem), Porous Media.
4.2 Signal Processing and inverse problems
Full Waveform Inversion (Geophysics), Super-resolution microscopy (Biology), Satellite imaging (Meteorology)
4.3 Social Sciences
Mean-field games, spatial economics, principal-agent models, taxation, nonlinear pricing.
5 Highlights of the year
Antonin Chambolle gave a plenary talk at the International Congress on Industrial and Applied Mathematics (ICIAM) 2023.
6 New software, platforms, open data
- Antonin Chambolle has implemented a new version of the fast and exact proximal operator of the Graph Total variation, built upon Boykov and Kolmogorov's maxflow-v3.04 algorithm (available on his web page and soon on plmlab), this is used to implement efficient methods for computing crystalline mean curvature flows.
7 New results
7.1 Entropic Optimal Transport Solutions of the Semigeostrophic Equations
Participants: Jean-David Benamou, Colin Cotter, Hugo Malamut.
The Semigeostrophic equations are a frontogenesis model in atmospheric science. Existence of solutions both from the theoretical and numerical point of view is given under a change of variable involving the interpretation of the pressure gradient as an Optimal Transport map between the density of the fluid and its push forward. Thanks to recent advances in numerical Optimal Transportation, the computation of large scale discrete approximations can be envisioned. We study in 25 the use of Entropic Optimal Transport and its Sinkhorn algorithm companion.
7.2 Wasserstein gradient flow of the Fisher information from a non-smooth convex minimization viewpoint
Participants: Jean-David Benamou, Guillaume Carlier, Daniel Matthes.
Motivated by the Derrida-Lebowitz-Speer-Spohn (DLSS) quantum drift equation, which is the Wasserstein gradient flow of the Fisher information, we study in 27 in details solutions of the corresponding implicit Euler scheme. We also take advantage of the convex (but non-smooth) nature of the corresponding variational problem to propose a numerical method based on the Chambolle-Pock primal-dual algorithm.
7.3 Total variation regularization with Wasserstein penalization
Participants: Antonin Chambolle, Vincent Duval, Joao-Miguel Machado.
In 20, a new derivation of the Euler-Lagrange equation of a total-variation regularization problem with a Wasserstein penalization is obtained, it is interesting as on easily deduces some regularity of the Lagrange multiplier for the non-negativity constraint. A numerical implementation is also described.
7.4 1D approximation of measures in Wasserstein spaces
Participants: Antonin Chambolle, Vincent Duval, Joao-Miguel Machado.
We propose in 32 a variational approach to approximate measures with measures uniformly distributed over a 1 dimensional set. The problem consists in minimizing a Wasserstein distance as a data term with a regularization given by the length of the support. As it is challenging to prove existence of solutions to this problem, we propose a relaxed formulation, which always admits a solution. In the sequel we show that if the ambient space is , under technical assumptions, any solution to the relaxed problem is a solution to the original one. Finally we prove that any optimal solution to the relaxed problem, and hence also to the original, is Ahlfors regular.
7.5 Exact recovery of the support of piecewise constant images via total variation regularization
Participants: Yohann De Castro, Vincent Duval, Romain Petit.
This work 23, 30 is concerned with the recovery of piecewise constant images from noisy linear measurements. We study the noise robustness of a variational reconstruction method, which is based on total (gradient) variation regularization. We show that, if the unknown image is the superposition of a few simple shapes, and if a non-degenerate source condition holds, then, in the low noise regime, the reconstructed images have the same structure: they are the superposition of the same number of shapes, each a smooth deformation of one of the unknown shapes. Moreover, the reconstructed shapes and the associated intensities converge to the unknown ones as the noise goes to zero.
7.6 A geometric Laplace method
Participants: Flavien Léger, François-Xavier Vialard.
A classical tool for approximating integrals is the Laplace method. The first-order, as well as the higher-order Laplace formula is most often written in coordinates without any geometrical interpretation. In 9, motivated by a situation arising, among others, in optimal transport, we give a geometric formulation of the first-order term of the Laplace method. The central tool is the Kim–McCann Riemannian metric which was introduced in the field of optimal transportation. Our main result expresses the first-order term with standard geometric objects such as volume forms, Laplacians, covariant derivatives and scalar curvatures of two different metrics arising naturally in the Kim–McCann framework. Passing by, we give an explicitly quantified version of the Laplace formula, as well as examples of applications.
7.7 Convergence rate of general entropic optimal transport costs
Participants: Guillaume Carlier, Paul Pegon, Luca Tamanini, Luca Nenna.
We investigate in 15 the convergence rate of the optimal entropic cost to the optimal transport cost as the noise parameter . For a large class of cost functions (for which optimal plans are not necessarily unique or induced by a transport map), we establish lower and upper bounds on the difference with the unregularized cost that depends on the dimensions of the marginals and on the ground cost, but not on the optimal transport plans themselves. Upper bounds are obtained by a block approximation strategy and an integral variant of Alexandrov's theorem. Under a non-degeneracy condition on the cost function (invertibility of the cross-derivative) we get the lower bound by establishing a quadratic detachment of the duality gap in dimensions thanks to Minty's trick. These results were improved and extended to the multi-marginal setting in 40. In particular, we establish lower bounds for costs defined on the product of submanifolds satisfying some signature condition on the mixed second derivatives that may include degenerate costs. We obtain in particular matching bounds in some typical situations where the optimal plan is deterministic, including the case of Wasserstein barycenters.
7.8 A geometric approach to apriori estimates for optimal transport maps
Participants: Simon Brendle, Flavien Leger, Robert J. McCann, Cale Rankin.
A key inequality which underpins the regularity theory of optimal transport for costs satisfying the Ma–Trudinger–Wang condition is the Pogorelov second derivative bound. This translates to an apriori interior C1 estimate for smooth optimal maps. Here we give a new derivation of this estimate which relies in part on Kim, McCann and Warren's observation that the graph of an optimal map becomes a volume maximizing spacelike submanifold when the product of the source and target domains is endowed with a suitable pseudo-Riemannian geometry that combines both the marginal densities and the cost.
7.9 Gradient descent with a general cost
Participants: Flavien Leger, Pierre-Cyril Aubin.
We present a new class of gradient-type optimization methods that extends vanilla gradient descent, mirror descent, Riemannian gradient descent, and natural gradient descent. Our approach involves constructing a surrogate for the objective function in a systematic manner, based on a chosen cost function. This surrogate is then minimized using an alternating minimization scheme. Using optimal transport theory we establish convergence rates based on generalized notions of smoothness and convexity. We provide local versions of these two notions when the cost satisfies a condition known as nonnegative cross-curvature. In particular our framework provides the first global rates for natural gradient descent and the standard Newton's method.
7.10 Second-order methods for Burer-Monteiro factorization
Participants: Florentin Goyens, Clément Royer, Irène Waldspurger.
The Burer-Monteiro factorization is a classical reformulation of optimization problems where the unknown is a matrix, when this matrix is known to have low rank. Rigorous analysis has been provided for this reformulation, when solved with first-order algorithms, but second-order algorithms oftentimes perform better in practice. We have established convergence rates for a representative second-order algorithm in a simplified setting. An article is in preparation.
7.11 Optimization for imaging and machine learning, analysis of inverse problems
Participants: Antonin Chambolle.
In 31, is analysed a stochastic primal-dual hybrid gradient for large-scale inverse problems (with application mostly to medical imaging), which was proposed some years ago by A. Chambolle and collaborators. The new result describes how the parameters can be modified/updated at each iteration in a way which still ensures (almost sure) convergence, and proposes some heuristic rules which fit into the framework and effectively improve the rate of convergence in practical experiments. The proceeding 21, in collaboration with U. Bordeaux, shows some convergence guarantees for a particular implementation of a “plug-and-play” image restoration method, where the regularizer for inverse problems is based on a denoising neural network. A more developed journal version has been submitted 39.
The proceeding 22, in collaboration with the computer imaging group at TU Graz (Austria), implements as a toy model a stochastic diffusion equation for sampling image priors based on Gaussian Mixture models, with exact formulas.
In a different direction, the proceeding 19, also with TU Graz, considers the issue of parameters learning for a better discretization of variational regularizers allowing for singularities (the “total-generalized-variation” of Bredies, Kunisch and Pock). A theoretical analysis of this model and of more standard total-variation regularization models is found in the new preprint 37, which introduces a novel approach (and much simpler than the previous ones) for studying the stability of the discontinuity sets in elementary denoising models.
7.12 Free discontinuity problems, fractures and shape optimization
Participants: Antonin Chambolle.
The publications 14, 17, 16, 33 are related to “free discontinuity problems” in materials science, with application to fracture growth or shape optimisation. In 17, 16 we discuss compactness for functionals which appear in the variational approach to fracture, in particular 16 is a new, very general, and in some sense more natural proof of compactness with respect to the previous results. The preprint 33 was submitted to the proceedings of the ICIAM conference, and it contains in an appendix a relatively simple presentation (in a simpler case) of the proof of Poincaré / Poincaré-Korn inequalities with small jump set developped in the past 10 years by A. Chambolle.
An application to shape optimization (of an object dragged in a Stokes flow) is presented in 14, while 34, 35 address other type of shape optimization problems in a more classical framework.
7.13 Interface evolution problems
Participants: Antonin Chambolle.
The new article 18 of Chambolle, DeGennaro, Morini generalizes to non-homogeneous flows an implicit approach for mean curvature flow of surfaces introduced in the 1990's by Luckhaus and Sturzenhecker, and Almgren, Taylor and Wang. Current developments in the fully discrete case are under study, with striking results which should appear in 2024, in the meantime, a short description of the possible anisotropies (or surface tension) which arise on discrete lattices was published in 13.
A different dynamics of interfaces, based on gradient flow instead of -type, is studied in 36.
7.14 Optimal quantization via branched optimal transport distance
Participants: Paul Pegon, Mircea Petrache.
In 41 we consider the problem of optimal approximation of a target measure by an atomic measure with atoms, in branched optimal transport distance. This is a new branched transport version of optimal quantization problems. New difficulties arise, as in previously known Wasserstein semi-discrete transport results the interfaces between cells associated with neighboring atoms had Voronoi structure and satisfied an explicit description. This description is missing for our problem, in which the cell interfaces are thought to have fractal boundary. We study the asymptotic behaviour of optimal quantizers for absolutely continuous measures as the number of atoms grows to infinity. We compute the limit distribution of the corresponding point clouds and show in particular a branched transport version of Zador's theorem. Moreover, we establish uniformity bounds of optimal quantizers in terms of separation distance and covering radius of the atoms, when the measure is -Ahlfors regular. A crucial technical tool is the uniform in Hölder regularity of the landscape function, a branched transport analog to Kantorovich potentials in classical optimal transport.
7.15 From geodesic extrapolation to a variational BDF2 scheme for Wasserstein gradient flows
Participants: Thomas Gallouët, Andrea Natale, Gabriele Todeschi.
We introduce a time discretization for Wasserstein gradient flows based on the classical Backward Differentiation Formula of order two. The main building block of the scheme is the notion of geodesic extrapolation in the Wasserstein space, which in general is not uniquely defined. We propose several possible definitions for such an operation, and we prove convergence of the resulting scheme to the limit PDE, in the case of the Fokker-Planck equation. For a specific choice of extrapolation we also prove a more general result, that is convergence towards EVI flows. Finally, we propose a variational finite volume discretization of the scheme which numerically achieves second order accuracy in both space and time.
7.16 Regularity theory and geometry of unbalanced optimal transport
Participants: Thomas Gallouët, Roberta Ghezzi, Francois-Xavier Vialard.
Using the dual formulation only, we show that regularity of unbalanced optimal transport also called entropy-transport inherits from regularity of standard optimal transport. We then provide detailed examples of Riemannian manifolds and costs for which unbalanced optimal transport is regular.Among all entropy-transport formulations, Wasserstein-Fisher-Rao metric, also called Hellinger-Kantorovich, stands out since it admits a dynamic formulation, which extends the Benamou-Brenier formulation of optimal transport. After demonstrating the equivalence between dynamic and static formulations on a closed Riemannian manifold, we prove a polar factorization theorem, similar to the one due to Brenier and Mc-Cann. As a byproduct, we formulate the Monge-Ampère equation associated with Wasserstein-Fisher-Rao metric, which also holds for more general costs.
7.17 Entropic approximation of optimal transport problems
Participants: Camilla Brizzi, Guillaume Carlier, Luigi De-Pascale.
We propose an entropic approximation approach for optimal transportation problems with a supremal cost. We establish -convergence for suitably chosen parameters for the entropic penalization and that this procedure selects cyclically monotone plans at the limit. We also present some numerical illustrations performed with Sinkhorn's algorithm.
7.18 Quantitative Stability of the Pushforward Operation by an Optimal Transport Map
Participants: Guillaume Carlier, Alex Delalande, Quentin Mérigot.
We study the quantitative stability of the mapping that to a measure associates its pushforward measure by a fixed (non-smooth) optimal transport map. We exhibit a tight Hölder-behavior for this operation under minimal assumptions. Our proof essentially relies on a new bound that quantifies the size of the singular sets of a convex and Lipschitz continuous function on a bounded domain.
7.19 Quantitative Stability of Barycenters in the Wasserstein Space
Participants: Guillaume Carlier, Alex Delalande, Quentin Mérigot.
Wasserstein barycenters define averages of probability measures in a geometrically meaningful way. Their use is increasingly popular in applied fields, such as image, geometry or language processing. In these fields however, the probability measures of interest are often not accessible in their entirety and the practitioner may have to deal with statistical or computational approximations instead. In this article, we quantify the effect of such approximations on the corresponding barycenters. We show that Wasserstein barycenters depend in a Hölder-continuous way on their marginals under relatively mild assumptions. Our proof relies on recent estimates that quantify the strong convexity of the dual quadratic optimal transport problem and a new result that allows to control the modulus of continuity of the push-forward operation under a (not necessarily smooth) optimal transport map.
7.20 Wasserstein medians: robustness, PDE characterization and numerics
Participants: Guillaume Carlier, Enis Chenchene, Katharina Eichinger.
We investigate the notion of Wasserstein median as an alternative to the Wasserstein barycenter, which has become popular but may be sensitive to outliers. In terms of robustness to corrupted data, we indeed show that Wasserstein medians have a breakdown point of approximately 1 2. We give explicit constructions of Wasserstein medians in dimension one which enable us to obtain estimates (which do not hold in higher dimensions). We also address dual and multimarginal reformulations. In convex subsets of , we connect Wasserstein medians to a minimal (multi) flow problem à la Beckmann and a system of PDEs of Monge-Kantorovich-type, for which we propose a p-Laplacian approximation. Our analysis eventually leads to a new numerical method to compute Wasserstein medians, which is based on a Douglas-Rachford scheme applied to the minimal flow formulation of the problem.
8 Bilateral contracts and grants with industry
Participants: Jean-David Benamou, Gregoire Loeper.
CIFRE PhD thesis scholarship (Guillaume Chazareix ) with BNP. Main supervisor Jean-David Benamou , co-supervision with Guillaume Carlier (Inria Mokaplan) and Gregoire Loeper (BNP). This contract is handled by Dauphine University.
9 Partnerships and cooperations
9.1 International research visitors
9.1.1 Visits of international scientists
Other international visits to the team
Participants: Pankaj Gautam.
-
Status
Postdoc
-
Institution of origin:
Norvegian University of Science and Technology (NTNU)
-
Country:
Norway
-
Dates:
November 13th to November 17th
-
Context of the visit:
The ERCIM postdoctoral fellowship program requires the students to spend one week in one of the institutions of the ERCIM program (Inria is one of them). Pankaj Gautam has given a lecture, attended several seminars, and discussed with the members of our team.
-
Mobility program/type of mobility:
research stay and lecture
Participants: Luigi De Pascale.
-
Status
Researcher
-
Institution of origin:
University of Florence
-
Country:
Italy
-
Dates:
May 2023
-
Context of the visit:
Luigi De Pascale was invited by Paul Pegon and Guillaume Carlier through the Invited Professors Program of Université Paris-Dauphine to work on a project on supremal optimal transport. As a regular visitor and collaborator of the team, he interacted with several other members of our team.
-
Mobility program/type of mobility:
research stay
9.1.2 Visits to international teams
Research stays abroad
- Jean-David Benamou has visited Pr. Colin Cotter (ICL) during the fall under a Nelder (ICL) fellowship.
- Paul Pegon has visited Pr. Mircea Petrache (PUC, Chile) for two weeks in March 2023
9.2 National initiatives
-
PRAIRIE chair
: Irène Waldspurger .
-
ANR CIPRESSI
(2019-2024) is a JCJC grant (149k€) carried by Vincent Duval . Its aim is to develop off-the-grid methods for inverse problems involving the reconstruction of complex objects.
-
PDE AI
(2023-2027) Antonin Chambolle is the main coordinator of the PDE-AI project, funded by the PEPR IA (France 2030, ANR) and gathering 10 groups throughout France working on PDEs and nonlinear analysis for artificial intelligence.
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
- Jean-David Benamou co-organized a Workshop on Numerical Optimal Transport at FOCM conference, Paris June.
- Jean-David Benamou co-organized an Ecole des Houches conference on Optimal Transport Theory : Applications to Physics, March.
- Guillaume Carlier co-organized a workshop at Lagrange Center.
- Vincent Duval was the main organizer of the Workshop on Off-the-Grid methods for Optimization and Inverse Problems in Imaging ( 60 participants) at Institut Henri Poincaré (November 21st and 22nd).
Member of the organizing committees
- Guillaume Carlier co-organized the séminaire Parisien d’Optimisation.
- Vincent Duval co-organized the Julia and Optimization Days 2023 ( 140 participants) at Conservatoire National des Arts et Métiers (October 4th, 5th and 6th).
- Vincent Duval co-organizes the monthly seminar Imaging in Paris.
- Antonin Chambolle co-organizes the monthly seminar "Séminaire Parisien d'Optimisation"
- Paul Pegon co-organizes the regular seminar of Calculus of Variations GT CalVa (until June 2023)
10.1.2 Scientific events: selection
Reviewer
- Vincent Duval has reviewed contributions to the GRETSI and SSVM conferences.
- Antonin Chambolle has reviewed contributions for SSVM and AISTATS 24
10.1.3 Journal
Member of the editorial boards
- Vincent Duval is associate editor at the Journal of Mathematical Imaging and Vision (JMIV)
-
Antonin Chambolle is associate editor at:
- Inverse Problems and Imaging (AIMS)
- Journal of Mathematical Imaging and Vision (JMIV, Springer)
- IPOL (Image Processing On Line),
- ESAIM : Mathematical Modelling and Numerical Analysis(M2AN, Cambridge UP),
- Applied Mathematics and Optimization (AMO, Springer),
- IMA journal of numerical analysis (Oxford)
- Journal of the European Math. Society (JEMS, EMS Publishing).
He is also one of the 4 editors of “Interfaces and Free Boundaries”.
- Irène Waldspurger is associate editor for the IEEE Transactions on Signal Processing.
-
Guillaume Carlier
is associate editor at:
- Journal de l'Ecole Polytechnique
- Applied Mathematics an Optimization
- J. Math. Analysis and Appl.
- J. Dynamics and Games
Reviewer - reviewing activities
- Vincent Duval has reviewed contributions to the journal of Foundations of Computational Mathematics (FoCM), Journal of NonSmooth Analysis and Optimization (JNSAO) and SIAM Journal on Imaging Sciences (SIIMS). He has also written reviews for the AMS: Mathematical Reviews.
- Antonin Chambolle is a reviewer for many journals including Arch. Rational Mech. Anal., Journal of the European Math. Society, Math. Programming, Calc. Var. PDE., etc.
- Irène Waldspurger has reviewed contributions to the Compte-rendus de l'académie des sciences (CRAS), to Applied and Computational Harmonic Analysis (ACHA), to Foundations of Computational Mathematics (FoCM) and to the Journal de mathématiques pures et appliquées (JMPA).
- Paul Pegon has reviewed contributions to ESAIM: Mathematical Modelling and Numerical Analysis (M2AN) and ESAIM: Control, Optimisation and Calculus of Variations (COCV).
- Flavien Leger has reviewed contributions to Journal of Convex Analysis and Advances in Mathematics.
- Thomas Gallouët has reviewed contributions to Analysis & PDE and other journals.
10.1.4 Invited talks
- Vincent Duval gave invited talks at the SIGOPT conference (Cottbus, Germany), Applied Inverse Problems (AIP) conference (Göttingen, Germany) and the colloquium 30 years of mathematics for optical imaging in Marseille. He was also invited at the local seminar "Modélisation, Analyse et Calcul Scientifique" in Université de Lyon.
- Antonin Chambolle was an invited speaker at ICIAM 2023 (Tokyo) (August 2023), and an invited speaker at the 3rd Alps-Adriatic Inverse Problems workshop, July 2023. He was also invited speaker at the conference in honor of the 60th birthday of Prof. Luigi Ambrosio, ETH, Zurich, Sept 2023.
- Flavien Leger gave invited talks at the "Machine Learning and Signal Processing seminar" (ENS Lyon), the "Geometric Analysis Seminar" (Iowa State University), the "Analysis and Applied Mathematics Seminar Series" (Bocconi University), the "PGMO Days" (EDF Lab, Saclay) and the "Séminaire Parisien d’Optimisation" (Institut Henri Poincaré).
- Irène Waldspurger gave an invited talk at the conference for Stéphane Mallat's 60th birthday, "A multiscale tour of harmonic analysis and machine learning".
- Paul Pegon gave invited talks at the "Analysis and Geometry seminar" of the Pontifical Catholic University of Chile (Santiago, Chile), at the June 2023 meeting of the "GdR Calva" (Université Paris-Cité) and the "PGMO Days" (EDF Lab, Saclay).
- Guillaume Carlier gave talks at the GT transport optimal, Orsay; the Analysis and Applied Mathematics seminar, Bocconi, Milan; The Financial math. seminar, ETH Zurich; PGMO Days, session transport optimal; workshop Optimal Transport and the Calculus of Variations, ICMS Edinburgh.
- Thomas Gallouët gave talks at the worshop on Optimal Transport and the Calculus of Varia- tions, Edinburgh, Scotland. The FoCM workshop on Opptimal Transport in Paris, France. The conference on Optimal Transport Theory And Applications to Physics, Centre de physique des Houches, France. A seminar for the journée de rentrée of the ANEDP team of the Laboratoire de Mathématique d’Orsay, Université de Paris- Saclay, Orsay.
10.1.5 Scientific expertise
- Vincent Duval was a member of the selection committee for a Chaire de Professeur Junior (CPJ) at Sorbonne Université.
- Antonin Chambolle was the head of the hiring comittee for a "maitre de conférence" in nonlinear analysis at Univ. Paris-Dauphine.
- Irène Waldspurger was a member of the selection committee for a "maître de conférence" position at Université Côte d'Azur.
- Thomas Gallouët was the vice-president of the hiring comittee for a "maitre de conférence" in nonlinear analysis at Univ. Paris-Dauphine.
10.1.6 Research administration
- Antonin Chambolle represents France in the IFIP TC7 group system modeling and optimization,
- Antonin Chambolle is member of the scientific comittee and of the board of the PGMO (programme Gaspard Monge pour l'Optimisation et la Recherche Opérationnelle) (FMJH - EDF).
- Irène Waldspurger is a member of the SMAI-MODE group.
- Vincent Duval was a member of the Comité de suivi doctoral (CSD) until June, 2023.
- Vincent Duval was a member of the Commission Emplois Scientifiques (CES) 2023 of the Paris research center.
- Vincent Duval has been "Délégué Scientifique Adjoint" (DSA) since September, 1st.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- Jean-David Benamou has given a serie of Lectures on Optimal Transport at Imperial College London. October and November.
- Master: Antonin Chambolle Optimisation Continue, 24h, niveau M2, Université Paris Dauphine-PSL, FR
- Master : Vincent Duval , Problèmes Inverses, 22,5 h équivalent TD, niveau M1, Université PSL/Mines ParisTech, FR
- Master : Vincent Duval , Optimization for Machine Learning, 9h, niveau M2, Université PSL/ENS, FR
- Licence : Irène Waldspurger , Pré-rentrée raisonnement, 31,2 h équivalent TD, niveau L1, Université Paris-Dauphine, FR
- Master : Irène Waldspurger , Optimization for Machine Learning, 9h, niveau M2, Université PSL/ENS, FR
- Master : Irène Waldspurger , Introduction à la géométrie différentielle et aux équations différentielles, 29,25 h équivalent TD, niveau M1, Université Paris Dauphine, FR
- Master : Irène Waldspurger , Non-convex inverse problems, 27 h d'équivalent TD, niveau M2, Université Paris Dauphine, FR
- Licence : Guillaume Carlier , algebre 1, L1 78h, Dauphine, FR
- Master : Guillaume Carlier Variational and transport methods in economics, M2 Masef, 27h, Dauphine, FR
- Agregation : Thomas Gallouët , Optimisation, Analyse numérique, 48h équivalent TD, niveau M2, Université d'Orsay), FR
- Guillaume Carlier : Licence Algèbre 1, Dauphine 70h, M2 Masef: Variatioanl and transport problems in economics, 18h
- Flavien Léger : Graduate course, two lectures in ‘math+econ+code’ masterclass on equilibrium transport and matching models in economics, NYU Paris. 5h.
10.2.2 Supervision
- PhD in progress: Joao-Miguel Machado , Transport optimal et structures géométriques, 01/10/2021, Co-supervised by Vincent Duval and Antonin Chambolle .
- PhD in progress : Chazareix Guillaume 1/08/2021, Non Linear Parabolic equations and Volatility Calibration. Co-supervised by Jean-David Benamou and Grégoire Loeper .
- PhD in progress : Hugo Malamut 1/09/2022, Régularisation Entropique et Transport Optimal Généralisé. Co-supervised by Jean-David Benamou and Guillaume Carlier .
- PhD in progress : Maxime Sylvestre 01/09/2002 on Hybrid methods fot Optimal Transport. Supervised by Guillaume Carlier and Alfred Galichon .
- PhD: Faniriana Rakoto Endor started a PhD on Burer-Monteiro methods, under the supervision of Antonin Chambolle and Irène Waldspurger .
- Postdoc: Adrien Vacher started a postdoc in December 2023 under the supervision of Flavien Léger .
- Phd in progress: Erwan Stämplfi , 01/09/2021, on singular limit for multiphase flow, co supervised with Yann Brenier
- Phd in progress: Siwan Boufadene , 01/09/2022, on energy distance flow, co supervised with Francois-Xavier Vialard
10.2.3 Juries
- Jean-David Benamou participated to the PhD Juries of Rodrigue Lelotte, Adrien Seguret.
- Vincent Duval was a referee for the PhD manuscripts of Adrien Frigerio (Université de Dijon, September) and Thu-Le Tran (Université de Rennes, December)
- Vincent Duval was an examiner in the PhD committee of Bastien Laville (Inria Sophia-Antipolis, September).
- Irène Waldspurger was an examiner in the PhD committees of Adrien Vacher (Université Gustave Eiffel) and Gaspar Rochette (ENS Paris).
- Guillaume Carlier was a member of the PhD comittee of Raphael Prunier (Sorbonne Université); Quentin Jacquet (Ecole Polytechnique).
- Guillaume Carlier was a member of the HdR comittee of Thibaut Le Gouic (Université de Aix-Marseille).
11 Scientific production
11.1 Major publications
- 1 inproceedingsMirror Descent with Relative Smoothness in Measure Spaces, with application to Sinkhorn and EM.NeurIPS 2022 - Thirty-sixth Conference on Neural Information Processing SystemsNew Orleans, United States2022HAL
- 2 articleIterative Bregman Projections for Regularized Transportation Problems.SIAM Journal on Scientific Computing2372015, A1111-A1138HALDOI
- 3 articleSecond order models for optimal transport and cubic splines on the Wasserstein space.Foundations of Computational MathematicsOctober 2019HALDOI
- 4 articleOn Representer Theorems and Convex Regularization.SIAM Journal on Optimization292May 2019, 1260–1281HALDOI
- 5 articleA variational finite volume scheme for Wasserstein gradient flows.Numerische Mathematik14632020, pp 437 - 480HALDOI
- 6 articleConvergence of Entropic Schemes for Optimal Transport and Gradient Flows.SIAM Journal on Mathematical Analysis492April 2017HALDOI
- 7 miscConvergence rate of general entropic optimal transport costs.June 2022HAL
- 8 miscGradient descent with a general cost.December 2023HAL
- 9 miscA geometric Laplace method.December 2022HALback to text
- 10 articlePhase retrieval with random Gaussian sensing vectors by alternating projections.IEEE Transactions on Information Theory6452018, 3301-3312HAL
- 11 articleRank optimality for the Burer-Monteiro factorization.SIAM Journal on Optimization3032020, 2577-2602HALDOI
11.2 Publications of the year
International journals
International peer-reviewed conferences
National peer-reviewed Conferences
Reports & preprints
11.3 Cited publications
- 44 articleBarycenters in the Wasserstein space.SIAM J. Math. Anal.4322011, 904--924back to text
- 45 articleHamiltonian ODEs in the Wasserstein space of probability measures.Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences6112008, 18--53back to text
- 46 articleFinite element exterior calculus, homological techniques, and applications.Acta Numerica152006, 1–155DOIback to text
- 47 articleConsistency of Trace Norm Minimization.J. Mach. Learn. Res.9June 2008, 1019--1048URL: http://dl.acm.org/citation.cfm?id=1390681.1390716back to text
- 48 articleConsistency of the Group Lasso and Multiple Kernel Learning.J. Mach. Learn. Res.9June 2008, 1179--1225URL: http://dl.acm.org/citation.cfm?id=1390681.1390721back to text
- 49 miscApplications of weak transport theory.2020back to text
- 50 unpublishedA spatial Pareto exchange economy problem.December 2021, working paper or preprintHALback to text
- 51 articleA mean field game model for the evolution of cities.Journal of Dynamics and Games2021HALback to text
- 52 articleComputing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms.International Journal of Computer Vision612February 2005, 139--157URL: http://dx.doi.org/10.1023/B:VISI.0000043755.93987.aaback to textback to text
- 53 articleModel-independent bounds for option prices mass transport approach.Finance and Stochastics1732013, 477--501URL: http://dx.doi.org/10.1007/s00780-013-0205-8DOIback to text
- 54 articleA computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem.Numer. Math.8432000, 375--393URL: http://dx.doi.org/10.1007/s002110050002DOIback to textback to text
- 55 articleWeak existence for the semigeostrophic equations formulated as a coupled Monge-Ampère/transport problem.SIAM J. Appl. Math.5851998, 1450--1461back to textback to text
- 56 articleAugmented Lagrangian algorithms for variational problems with divergence constraints.JOTA2015back to text
- 57 articleIterative Bregman Projections for Regularized Transportation Problems.SIAM J. Sci. Comp.to appear2015back to textback to textback to text
- 58 articlePoint Source Regularization of the Finite Source Reflector Problem.Journal of Computational PhysicsMay 2022HALback to text
- 59 articleNumerical solution of the optimal transportation problem using the Monge--Ampere equation.Journal of Computational Physics2602014, 107--126back to text
- 60 articleTwo numerical methods for the elliptic Monge-Ampère equation.M2AN Math. Model. Numer. Anal.4442010, 737--758back to text
- 61 articleConsistent estimation of a population barycenter in the Wasserstein space.Preprint arXiv:1212.25622012back to text
- 62 articleAdditive manufacturing scanning paths optimization using shape optimization tools.Struct. Multidiscip. Optim.6162020, 2437--2466URL: https://doi.org/10.1007/s00158-020-02614-3DOIback to text
- 63 articleSliced and Radon Wasserstein Barycenters of Measures.Journal of Mathematical Imaging and Vision5112015, 22--45URL: http://hal.archives-ouvertes.fr/hal-00881872/back to text
- 64 articleCharacterization of optimal shapes and masses through Monge-Kantorovich equation.J. Eur. Math. Soc. (JEMS)322001, 139--168URL: http://dx.doi.org/10.1007/s100970000027DOIback to text
- 65 articleDeterministic guarantees for Burer-Monteiro factorizations of smooth semidefinite programs.preprinthttps://arxiv.org/abs/1804.020082018back to text
- 66 articleA generalized conditional gradient method for dynamic inverse problems with optimal transport regularization.arXiv preprint arXiv:2012.117062020back to textback to text
- 67 articleDécomposition polaire et réarrangement monotone des champs de vecteurs.C. R. Acad. Sci. Paris Sér. I Math.305191987, 805--808back to text
- 68 articleReconstruction of the early universe as a convex optimization problem.Mon. Not. Roy. Astron. Soc.3462003, 501--524URL: http://arxiv.org/pdf/astro-ph/0304214.pdfback to text
- 69 articleGeneralized solutions and hydrostatic approximation of the Euler equations.Phys. D23714-172008, 1982--1988URL: http://dx.doi.org/10.1016/j.physd.2008.02.026DOIback to text
- 70 articlePolar factorization and monotone rearrangement of vector-valued functions.Comm. Pure Appl. Math.4441991, 375--417URL: http://dx.doi.org/10.1002/cpa.3160440402DOIback to text
- 71 articleA guide to the TV zoo.Level-Set and PDE-based Reconstruction Methods, Springer2013back to text
- 72 bookOptimal Urban Networks via Mass Transportation.1961Lecture Notes in MathematicsBerlin, HeidelbergSpringer Berlin Heidelberg2009, URL: http://link.springer.com/10.1007/978-3-540-85799-0DOIback to text
- 73 incollectionOn the numerical solution of the problem of reflector design with given far-field scattering data.Monge Ampère equation: applications to geometry and optimization (Deerfield Beach, FL, 1997)226Contemp. Math.Providence, RIAmer. Math. Soc.1999, 13--32URL: http://dx.doi.org/10.1090/conm/226/03233DOIback to text
- 74 articleThe regularity of mappings with a convex potential.J. Amer. Math. Soc.511992, 99--104URL: http://dx.doi.org/10.2307/2152752DOIback to text
- 75 articleComputational Analysis of LDDMM for Brain Mapping.Frontiers in Neuroscience72013back to text
- 76 articleSuper-Resolution from Noisy Data.Journal of Fourier Analysis and Applications1962013, 1229--1254back to text
- 77 articleTowards a Mathematical Theory of Super-Resolution.Communications on Pure and Applied Mathematics6762014, 906--956back to text
- 78 articleAn Introduction to Compressive Sensing.IEEE Signal Processing Magazine2522008, 21--30back to text
- 79 unpublishedSISTA: Learning Optimal Transport Costs under Sparsity Constraints.October 2020, working paper or preprintHALback to text
- 80 articleOn the total variation Wasserstein gradient flow and the TV-JKO scheme.ESAIM: Control, Optimisation and Calculus of Variations2019HALback to text
- 81 articleTowards Off-the-grid Algorithms for Total Variation Regularized Inverse Problems.Journal of Mathematical Imaging and VisionJuly 2022HALDOIback to text
- 82 articleKinetic models for chemotaxis and their drift-diffusion limits.Monatsh. Math.1421-22004, 123--141URL: http://dx.doi.org/10.1007/s00605-004-0234-7DOIback to text
-
83
articleVariational approximation of size-mass energies for
-dimensional currents.ESAIM Control Optim. Calc. Var.252019, Paper No. 43, 39URL: https://doi.org/10.1051/cocv/2018027DOIback to text - 84 articleCrouzeix-Raviart approximation of the total variation on simplicial meshes.J. Math. Imaging Vision626-72020, 872--899URL: https://doi.org/10.1007/s10851-019-00939-3DOIback to text
- 85 articleLearning consistent discretizations of the total variation.SIAM J. Imaging Sci.1422021, 778--813URL: https://doi.org/10.1137/20M1377199DOIback to text
-
86
articleThe
-Wasserstein Distance: Local Solutions and Existence of Optimal Transport Maps.401January 2008, 1--20URL: https://epubs.siam.org/doi/10.1137/07069938XDOIback to text - 87 articleAtomic decomposition by basis pursuit.SIAM journal on scientific computing2011999, 33--61back to text
- 88 inproceedingsFaster Wasserstein Distance Estimation with the Sinkhorn Divergence.Neural Information Processing SystemsAdvances in Neural Information Processing SystemsVancouver, CanadaDecember 2020HALback to text
- 89 articleDiscrete total variation: new definition and minimization.SIAM J. Imaging Sci.1032017, 1258--1290URL: https://doi.org/10.1137/16M1075247back to text
- 90 articleDensity Functional Theory and Optimal Transportation with Coulomb Cost.Communications on Pure and Applied Mathematics6642013, 548--599URL: http://dx.doi.org/10.1002/cpa.21437DOIback to text
- 91 bookA Mathematical Theory of Large-Scale Atmosphere/Ocean Flow.Imperial College Press2006, URL: https://books.google.fr/books?id=JxBqDQAAQBAJback to text
- 92 articleThe semigeostrophic equations discretized in reference and dual variables.Arch. Ration. Mech. Anal.18522007, 341--363URL: http://dx.doi.org/10.1007/s00205-006-0040-6DOIback to text
- 93 articleGeneralised Lagrangian solutions for atmospheric and oceanic flows.SIAM J. Appl. Math.5111991, 20--31back to text
- 94 inproceedingsSinkhorn Distances: Lightspeed Computation of Optimal Transport.Proc. NIPS2013, 2292--2300back to textback to text
-
95
articleA Study of the Dual Problem of the One-Dimensional
-Optimal Transport Problem with Applications.27611June 2019, 3304--3324URL: https://www.sciencedirect.com/science/article/pii/S0022123619300643DOIback to text - 96 articleNumerical methods for fully nonlinear elliptic equations of the Monge-Ampère type.Comput. Methods Appl. Mech. Engrg.19513-162006, 1344--1386back to text
- 97 articleExact Support Recovery for Sparse Spikes Deconvolution.Foundations of Computational Mathematics2014, 1--41URL: http://dx.doi.org/10.1007/s10208-014-9228-6DOIback to text
- 98 articleSupport detection in super-resolution.Proc. Proceedings of the 10th International Conference on Sampling Theory and Applications2013, 145--148back to text
- 99 unpublishedInterpolating between Optimal Transport and MMD using Sinkhorn Divergences.October 2018, working paper or preprintHALback to text
- 100 articleBreaking the Curse of Dimension in Multi-Marginal Kantorovich Optimal Transport on Finite State Spaces.SIAM Journal on Mathematical Analysis5042018, 3996--4019URL: https://doi.org/10.1137/17M1150025DOIback to text
- 101 articleMonge-Ampère-Kantorovitch (MAK) reconstruction of the eary universe.Nature4172602002back to text
- 102 articleA stochastic control approach to No-Arbitrage bounds given marginals, with an application to Loopback options.submitted to Annals of Applied Probability2011back to text
- 103 articleThe geometry of optimal transportation.Acta Math.17721996, 113--161URL: http://dx.doi.org/10.1007/BF02392620DOIback to text
- 104 articleGaspard Monge, Le mémoire sur les déblais et les remblais.Image des mathématiques, CNRS2012, URL: http://images.math.cnrs.fr/Gaspard-Monge,1094.htmlback to text
-
105
articlePath Dependent Optimal Transport and Model Calibration on Exotic Derivatives.SSRN Electron.~J.Available at
doi:10.2139/ssrn.3302384 01 2018DOIback to text - 106 articleNotes on a PDE System for Biological Network Formation.138June 2016, 127--155URL: https://www.sciencedirect.com/science/article/pii/S0362546X15004344DOIback to text
- 107 articleSoliton dynamics in computational anatomy.NeuroImage232004, S170--S178back to text
- 108 incollectionThe mathematical theory of frontogenesis.Annual review of fluid mechanics, Vol. 14Palo Alto, CAAnnual Reviews1982, 131--151back to text
- 109 articleThe back-and-forth method for Wasserstein gradient flows.ESAIM: Control, Optimisation and Calculus of Variations272021, 28back to text
- 110 articleA fast approach to optimal transport: The back-and-forth method.Numer. Math.1462020, 513--544URL: https://doi.org/10.1007/s00211-020-01154-8DOIback to text
- 111 articleOn explosions of solutions to a system of partial differential equations modelling chemotaxis.Trans. Amer. Math. Soc.32921992, 819--824URL: http://dx.doi.org/10.2307/2153966DOIback to text
- 112 articleThe variational formulation of the Fokker-Planck equation.SIAM J. Math. Anal.2911998, 1--17back to text
- 113 articleOn the translocation of masses.C. R. (Doklady) Acad. Sci. URSS (N.S.)371942, 199--201back to text
- 114 articleMinimizing within convex bodies using a convex hull method.SIAM Journal on Optimization162January 2005, 368--379HALback to text
- 115 articleMean field games.Jpn. J. Math.212007, 229--260URL: http://dx.doi.org/10.1007/s11537-007-0657-8DOIback to text
- 116 articleOptimal Transport Approximation of 2-Dimensional Measures.SIAM Journal on Imaging Sciences122January 2019, 762--787URL: https://epubs.siam.org/doi/10.1137/18M1193736DOIback to text
- 117 articleA survey of the Schrödinger problem and some of its connections with optimal transport.Discrete Contin. Dyn. Syst.3442014, 1533--1574URL: http://dx.doi.org/10.3934/dcds.2014.34.1533DOIback to text
- 118 articleActive sets, nonsmoothness, and sensitivity.SIAM Journal on Optimization1332003, 702--725back to text
- 119 articleOptimal transportation meshfree approximation schemes for Fluid and plastic Flows.Int. J. Numer. Meth. Engng 83:1541--579832010, 1541--1579back to text
- 120 articleA fully nonlinear version of the incompressible Euler equations: the semigeostrophic system.SIAM J. Math. Anal.3832006, 795--823 (electronic)back to text
- 121 articleNumerical solution of the Monge-Ampére equation by a Newton's algorithm.C. R. Math. Acad. Sci. Paris34042005, 319--324back to text
- 122 bookA wavelet tour of signal processing.Elsevier/Academic Press, Amsterdam2009back to text
- 123 articleA macroscopic crowd motion model of gradient flow type.Math. Models Methods Appl. Sci.20102010, 1787--1821URL: http://dx.doi.org/10.1142/S0218202510004799DOIback to text
- 124 articleA multiscale approach to optimal transport.Computer Graphics Forum3052011, 1583--1592back to text
- 125 articleGeodesic Shooting for Computational Anatomy.Journal of Mathematical Imaging and Vision242March 2006, 209--228URL: http://dx.doi.org/10.1007/s10851-005-3624-0back to text
- 126 articleAdaptive, Anisotropic and Hierarchical cones of Discrete Convex functions.Numerische Mathematik132435 pages, 11 figures. (Second version fixes a small bug in Lemma 3.2. Modifications are anecdotic.)2016, 807--853HALback to text
- 127 articleA Modica-Mortola Approximation for Branched Transport and Applications.Archive for Rational Mechanics and Analysis2011July 2011, 115--142URL: http://link.springer.com/10.1007/s00205-011-0402-6DOIback to text
- 128 articleOptimal transport: From moving soil to same-sex marriage.CMS Notes452013, 14--15back to text
- 129 articleUniqueness and Monge Solutions in the Multimarginal Optimal Transportation Problem.SIAM Journal on Mathematical Analysis4362011, 2758--2775back to text
- 130 miscRegularized Optimal Transport is Ground Cost Adversarial.2020back to text
- 131 articleA Generalized Forward-Backward Splitting.SIAM Journal on Imaging Sciences632013, 1199--1226URL: http://hal.archives-ouvertes.fr/hal-00613637/DOIback to text
- 132 articleNonlinear total variation based noise removal algorithms.Physica D: Nonlinear Phenomena6011992, 259--268URL: http://dx.doi.org/10.1016/0167-2789(92)90242-Fback to text
- 133 articleConvolutional Wasserstein Distances: Efficient Optimal Transportation on Geometric Domains.ACM Transaction on Graphics, Proc. SIGGRAPH'15to appear2015back to textback to text
- 134 articleRegression shrinkage and selection via the Lasso.Journal of the Royal Statistical Society. Series B. Methodological5811996, 267--288back to textback to text
- 135 unpublishedDynamical Programming for off-the-grid dynamic Inverse Problems.December 2022, working paper or preprintHALback to text
- 136 articleModel Selection with Piecewise Regular Gauges.Information and Inferenceto appear2015, URL: http://hal.archives-ouvertes.fr/hal-00842603/back to text
- 137 bookOptimal transport.338Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]Old and newBerlinSpringer-Verlag2009, xxii+973URL: http://dx.doi.org/10.1007/978-3-540-71050-9DOIback to text
- 138 bookTopics in optimal transportation.58Graduate Studies in MathematicsAmerican Mathematical Society, Providence, RI2003, xvi+370back to text
- 139 articleOn the design of a reflector antenna. II.Calc. Var. Partial Differential Equations2032004, 329--341URL: http://dx.doi.org/10.1007/s00526-003-0239-4DOIback to text
- 140 articleA continuum mechanical approach to geodesics in shape space.International Journal of Computer Vision9332011, 293--318back to text
- 141 articleSparse representation for computer vision and pattern recognition.Proceedings of the IEEE9862010, 1031--1044back to text
- 142 phdthesisEntropic Unbalanced Optimal Transport: Application to Full-Waveform Inversion and Numerical Illustration.Université de ParisDecember 2021HALback to text

