2023Activity reportProject-TeamPIXEL
RNSR: 202023565G- Research center Inria Centre at Université de Lorraine
- In partnership with:Université de Lorraine, CNRS
- Team name: Structure geometrical shapes
- In collaboration with:Laboratoire lorrain de recherche en informatique et ses applications (LORIA)
- Domain:Perception, Cognition and Interaction
- Theme:Interaction and visualization
Keywords
Computer Science and Digital Science
- A5.5.1. Geometrical modeling
- A5.5.2. Rendering
- A6.2.8. Computational geometry and meshes
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
Other Research Topics and Application Domains
- B3.3.1. Earth and subsoil
- B5.1. Factory of the future
- B5.7. 3D printing
- B9.2.2. Cinema, Television
- B9.2.3. Video games
1 Team members, visitors, external collaborators
Research Scientists
- Laurent Alonso [INRIA, Researcher]
- Etienne Corman [CNRS, Researcher]
- Nicolas Ray [INRIA, Researcher]
Faculty Members
- Dmitry Sokolov [Team leader, UL, Associate Professor, HDR]
- Dobrina Boltcheva [UL, Associate Professor]
PhD Students
- Guillaume Coiffier [University of Lorraine]
- Yoann Coudert-Osmont [UL]
- David Desobry [INRIA]
- Mohamed-Yassir Nour [UL, ATER, from Sep 2023]
Technical Staff
- Benjamin Loillier [INRIA, Engineer, from Oct 2023]
Interns and Apprentices
- Matthieu Rios [INRIA, Intern, from May 2023 until Jul 2023]
Administrative Assistant
- Emmanuelle Deschamps [INRIA, from Mar 2023]
External Collaborator
- François Protais [SIEMENS IND.SOFTWARE, from Oct 2023]
2 Overall objectives
PIXEL is a research team stemming from team ALICE founded in 2004 by Bruno Lévy. The main scientific goal of ALICE was to develop new algorithms for computer graphics, with a special focus on geometry processing. From 2004 to 2006, we developed new methods for automatic texture mapping (LSCM, ABF++, PGP), that became the de-facto standards. Then we realized that these algorithms could be used to create an abstraction of shapes, that could be used for geometry processing and modeling purposes, which we developed from 2007 to 2013 within the GOODSHAPE StG ERC project. We transformed the research prototype stemming from this project into an industrial geometry processing software, with the VORPALINE PoC ERC project, and commercialized it (TotalEnergies, Dassault Systems, + GeonX and ANSYS currently under discussion). From 2013 to 2018, we developed more contacts and cooperations with the “scientific computing” and “meshing” research communities.
After a part of the team “spun off” around Sylvain Lefebvre and his ERC project SHAPEFORGE to become the MFX team (on additive manufacturing and computer graphics), we progressively moved the center of gravity of the rest of the team from computer graphics towards scientific computing and computational physics, in terms of cooperations, publications and industrial transfer.
We realized that geometry plays a central role in numerical simulation, and that “cross-pollinization” with methods from our field (graphics) will lead to original algorithms. In particular, computer graphics routinely uses irregular and dynamic data structures, more seldom encountered in scientific computing. Conversely, scientific computing routinely uses mathematical tools that are not well spread and not well understood in computer graphics. Our goal is to establish a stronger connection between both domains, and exploit the fundamental aspects of both scientific cultures to develop new algorithms for computational physics.
2.1 Scientific grounds
Mesh generation is a notoriously difficult task. A quick search on the NSF grant web page with “mesh generation AND finite element” keywords returns more than 30 currently active grants for a total of $8 million. NASA indicates mesh generation as one of the major challenges for 2030 38, and estimates that it costs 80% of time and effort in numerical simulation. This is due to the need for constructing supports that match both the geometry and the physics of the system to be modeled. In our team we pay a particular attention to scientific computing, because we believe it has a world changing impact.
It is very unsatisfactory that meshing, i.e. just “preparing the data” for the simulation, eats up the major part of the time and effort. Our goal is to change the situation, by studying the influence of shapes and discretizations, and inventing new algorithms to automatically generate meshes that can be directly used in scientific computing. This goal is a result of our progressive shift from pure graphics (“Geometry and Lighting”) to real-world problems (“Shape Fidelity”).
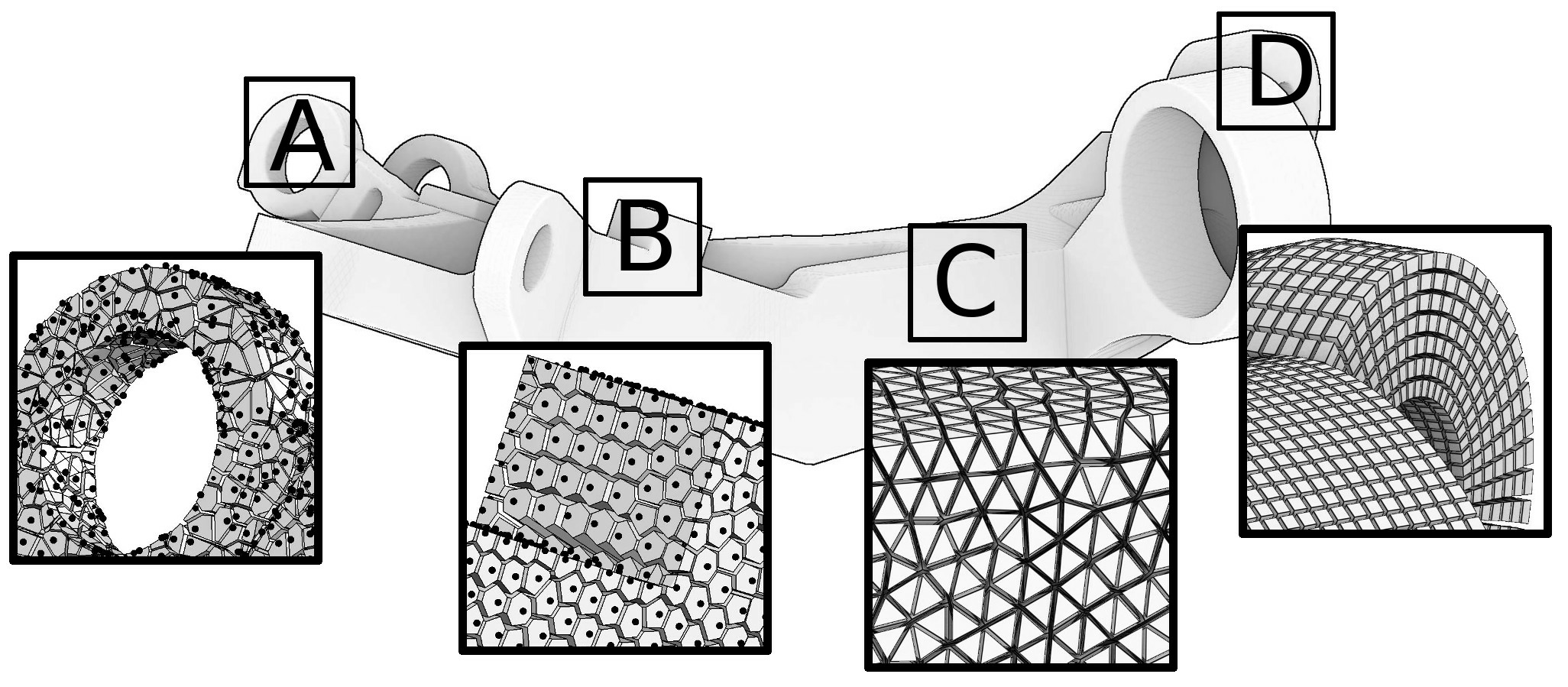
Meshing is central in geometric modeling because it provides a way to represent functions on the objects being studied (texture coordinates, temperature, pressure, speed, etc.). There are numerous ways to represent functions, but if we suppose that the functions are piecewise smooth, the most versatile way is to discretize the domain of interest. Ways to discretize a domain range from point clouds to hexahedral meshes; let us list a few of them sorted by the amount of structure each representation has to offer (refer to Figure 1).
-
At one end of the spectrum there are point clouds: they exhibit no structure at all (white noise point samples) or very little (blue noise point samples). Recent explosive development of acquisition techniques (e.g. scanning or photogrammetry) provides an easy way to build 3D models of real-world objects that range from figurines and cultural heritage objects to geological outcrops and entire city scans. These technologies produce massive, unstructured data (billions of 3D points per scene) that can be directly used for visualization purposes, but this data is not suitable for high-level geometry processing algorithms and numerical simulations that usually expect meshes. Therefore, at the very beginning of the acquisition-modeling-simulation-analysis pipeline, powerful scan-to-mesh algorithms are required.
During the last decade, many solutions have already been proposed 34, 18, 30, 29, 21, but the problem of building a good mesh from scattered 3D points is far from being solved. Beside the fact that the data is unusually large, the existing algorithms are challenged also by the extreme variation of data quality. Raw point clouds have many defects, they are often corrupted with noise, redundant, incomplete (due to occlusions): they all are uncertain.
-
Triangulated surfaces are ubiquitous, they are the most widely used representation for 3D objects. Some applications like 3D printing do not impose heavy requirements on the surface: typically it has to be watertight, but triangles can have an arbitrary shape. Other applications like texturing require very regular meshes, because they suffer from elongated triangles with large angles.
While being a common solution for many problems, triangle mesh generation is still an active topic of research. The diversity of representations (meshes, NURBS, ...) and file formats often results in a “Babel” problem when one has to exchange data. The only common representation is often the mesh used for visualization, that has in most cases many defects, such as overlaps, gaps or skinny triangles. Re-injecting this solution into the modeling-analysis loop is non-trivial, since again this representation is not well adapted to analysis.
-
Tetrahedral meshes are the volumic equivalent of triangle meshes, they are very common in the scientific computing community. Tetrahedral meshing is now a mature technology. It is remarkable that still today all the existing software used in the industry is built on top of a handful of kernels, all written by a small number of individuals 23, 36, 42, 25, 35, 37, 24, 46.
Meshing requires a long-term, focused, dedicated research effort that combines deep theoretical studies with advanced software development. We have the ambition to bring this kind of maturity to a different type of mesh (structured, with hexahedra), which is highly desirable for some simulations, and for which, unlike tetrahedra, no satisfying automatic solution exists. In the light of recent contributions, we believe that the domain is ready to overcome the principal difficulties.
-
Finally, at the most structured end of the spectrum there are hexahedral meshes composed of deformed cubes (hexahedra). They are preferred for certain physics simulations (deformation mechanics, fluid dynamics ...) because they can significantly improve both speed and accuracy. This is because (1) they contain a smaller number of elements (5-6 tetrahedra for a single hexahedron), (2) the associated tri-linear function basis has cubic terms that can better capture higher-order variations, (3) they avoid the locking phenomena encountered with tetrahedra 16, (4) hexahedral meshes exploit inherent tensor product structure and (5) hexahedral meshes are superior in direction dominated physical simulations (boundary layer, shock waves, etc). Being extremely regular, hexahedral meshes are often claimed to be The Holy Grail for many finite element methods 17, outperforming tetrahedral meshes both in terms of computational speed and accuracy.
Despite 30 years of research efforts and important advances, mainly by the Lawrence Livermore National Labs in the U.S. 41, 40, hexahedral meshing still requires considerable manual intervention in most cases (days, weeks and even months for the most complicated domains). Some automatic methods exist 28, 44, that constrain the boundary into a regular grid, but they are not fully satisfactory either, since the grid is not aligned with the boundary. The advancing front method 15 does not have this problem, but generates irregular elements on the medial axis, where the fronts collide. Thus, there is no fully automatic algorithm that results in satisfactory boundary alignment.
3 Research program
3.1 Point clouds
Currently, transforming the raw point cloud into a triangular mesh is a long pipeline involving disparate geometry processing algorithms:
- Point pre-processing: colorization, filtering to remove unwanted background, first noise reduction along acquisition viewpoint;
- Registration: cloud-to-cloud alignment, filtering of remaining noise, registration refinement;
- Mesh generation: triangular mesh from the complete point cloud, re-meshing, smoothing.
The output of this pipeline is a locally-structured model which is used in downstream mesh analysis methods such as feature extraction, segmentation in meaningful parts or building Computer-Aided Design (CAD) models.
It is well known that point cloud data contains measurement errors due to factors related to the external environment and to the measurement system itself 39, 33, 19. These errors propagate through all processing steps: pre-processing, registration and mesh generation. Even worse, the heterogeneous nature of different processing steps makes it extremely difficult to know how these errors propagate through the pipeline. To give an example, for cloud-to-cloud alignment it is necessary to estimate normals. However, the normals are forgotten in the point cloud produced by the registration stage. Later on, when triangulating the cloud, the normals are re-estimated on the modified data, thus introducing uncontrollable errors.
We plan to develop new reconstruction, meshing and re-meshing algorithms, with a specific focus on the accuracy and resistance to all defects present in the input raw data. We think that pervasive treatment of uncertainty is the missing ingredient to achieve this goal. We plan to rethink the pipeline with the position uncertainty maintained during the whole process. Input points can be considered either as error ellipsoids 43 or as probability measures 27. In a nutshell, our idea is to start by computing an error ellipsoid 45, 31 for each point of the raw data, and then to cumulate the errors (approximations) made at each step of the processing pipeline while building the mesh. In this way, the final users will be able to take the knowledge of the uncertainty into account and rely on this confidence measure for further analysis and simulations. Quantifying uncertainties for reconstruction algorithms, and propagating them from input data to high-level geometry processing algorithms has never been considered before, possibly due to the very different methodologies of the approaches involved. At the very beginning we will re-implement the entire pipeline, and then attack the weak links through all three reconstruction stages.
3.2 Parameterizations
One of the favorite tools we use in our team are parameterizations, and we have major contributions to the field: we have solved a fundamental problem formulated more than 60 years ago 2. Parameterizations provide a very powerful way to reveal structures on objects. The most omnipresent application of parameterizations is texture mapping: texture maps provide a way to represent in 2D (on the map) information related to a surface. Once the surface is equipped with a map, we can do much more than a mere coloring of the surface: we can approximate geodesics, edit the mesh directly in 2D or transfer information from one mesh to another.
Parameterizations constitute a family of methods that involve optimizing an objective function, subject to a set of constraints (equality, inequality, being integer, etc.). Computing the exact solution to such problems is beyond any hope, therefore approximations are the only resort. This raises a number of problems, such as the minimization of highly nonlinear functions and the definition of direction fields topology, without forgetting the robustness of the software that puts all this into practice.
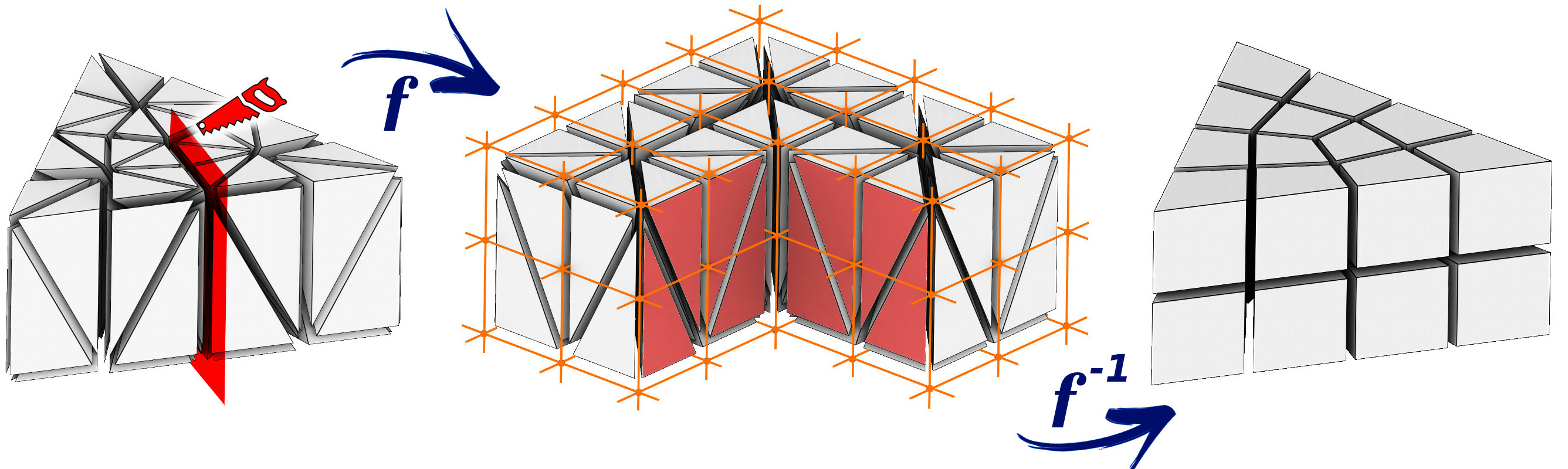
We are particularly interested in a specific instance of parameterization: hexahedral meshing. The idea 6, 4 is to build a transformation from the domain to a parametric space, where the distorted domain can be meshed by a regular grid. The inverse transformation applied to this grid produces the hexahedral mesh of the domain, aligned with the boundary of the object. The strength of this approach is that the transformation may admit some discontinuities. Let us show an example: we start from a tetrahedral mesh (Figure 2, left) and we want to deform it in a way that its boundary is aligned with the integer grid. To allow for a singular edge in the output (the valency 3 edge, Figure 2, right), the input mesh is cut open along the highlighted faces and the central edge is mapped onto an integer grid line (Figure 2, middle). The regular integer grid then induces the hexahedral mesh with the desired topology.
Current global parameterizations allow grids to be positioned inside geometrically simple objects whose internal structure (the singularity graph) can be relatively basic. We wish to be able to handle more configurations by improving three aspects of current methods:
- Local grid orientation is usually prescribed by minimizing the curvature of a 3D steering field. Unfortunately, this heuristic does not always provide singularity curves that can be integrated by the parameterization. We plan to explore how to embed integrability constraints in the generation of the direction fields. To address the problem, we already identified necessary validity criteria: for example, the permutation of axes along elementary cycles that go around a singularity must preserve one of the axes (the one tangent to the singularity). The first step to enforce this (necessary) condition will be to split the frame field generation into two parts: first we will define a locally stable vector field, followed by the definition of the other two axes by a 2.5D directional field (2D advected by the stable vector field).
- The grid combinatorial information is characterized by a set of integer coefficients whose values are currently determined through numerical optimization of a geometric criterion: the shape of the hexahedra must be as close as possible to the steering direction field. Thus, the number of layers of hexahedra between two surfaces is determined solely by the size of the hexahedra that one wishes to generate. In these settings, degenerate configurations arise easily, and we want to avoid them. In practice, mixed integer solvers often choose to allocate a negative or zero number of layers of hexahedra between two constrained sheets (boundaries of the object, internal constraints or singularities). We will study how to inject strict positivity constraints into these cases, which is a very complex problem because of the subtle interplay between different degrees of freedom of the system. Our first results for quad-meshing of surfaces give promising leads, notably thanks to motorcycle graphs 20, a notion we wish to extend to volumes.
- Optimization for the geometric criterion makes it possible to control the average size of the hexahedra, but it does not ensure the bijectivity (even locally) of the resulting parameterizations. Considering other criteria, as we did in 2D 26, would probably improve the robustness of the process. Our idea is to keep the geometry criterion to find the global topology, but try other criteria to improve the geometry.
3.3 Hexahedral-dominant meshing
All global parameterization approaches are decomposed into three steps: frame field generation, field integration to get a global parameterization, and final mesh extraction. Getting a full hexahedral mesh from a global parameterization means that it has positive Jacobian everywhere except on the frame field singularity graph. To our knowledge, there is no solution to ensure this property, but some efforts are done to limit the proportion of failure cases. An alternative is to produce hexahedral dominant meshes. Our position is in between those two points of view:
- We want to produce full hexahedral meshes;
- We consider as pragmatic to keep hexahedral dominant meshes as a fallback solution.
The global parameterization approach yields impressive results on some geometric objects, which is encouraging, but not yet sufficient for numerical analysis. Note that while we attack the remeshing with our parameterizations toolset, the wish to improve the tool itself (as described above) is orthogonal to the effort we put into making the results usable by the industry. To go further, our idea (as opposed to 32, 22) is that the global parameterization should not handle all the remeshing, but merely act as a guide to fill a large proportion of the domain with a simple structure; it must cooperate with other remeshing bricks, especially if we want to take final application constraints into account.
For each application we will take as an input domains, sets of constraints and, eventually, fields (e.g. the magnetic field in a tokamak). Having established the criteria of mesh quality (per application!) we will incorporate this input into the mesh generation process, and then validate the mesh by a numerical simulation software.
4 Application domains
4.1 Geometric Tools for Simulating Physics with a Computer
Numerical simulation is the main targeted application domain for the geometry processing tools that we develop. Our mesh generation tools will be tested and evaluated within the context of our cooperation with Hutchinson, experts in vibration control, fluid management and sealing system technologies. We think that the hex-dominant meshes that we generate have geometrical properties that make them suitable for some finite element analyses, especially for simulations with large deformations.
We also have a tight collaboration with a geophysical modeling specialists via the RING consortium. In particular, we produce hexahedral-dominant meshes for geomechanical simulations of gas and oil reservoirs. From a scientific point of view, this use case introduces new types of constraints (alignments with faults and horizons), and allows certain types of nonconformities that we did not consider until now.
Our cooperation with RhinoTerrain pursues the same goal: reconstruction of buildings from point cloud scans allows to perform 3D analysis and studies on insolation, floods and wave propagation, wind and noise simulations necessary for urban planification.
5 Highlights of the year
5.1 Awards
- Étienne Corman has received the Young Investigator Award from the Shape Modeling International society.
- Our software Geogram received the Symposium on Geometry Processing Software Award.
- François Protais received the second prize for his PhD from GdR IG-RV
5.2 Programming contests
- Yoann Coudert–Osmont finished second in the final of Tech Challenger, Tech Challenger 2023, a French algorithmic contest that attracted over 3'000 contestants. After four qualification rounds and a semi-final, 100 challengers gathered for a final in Paris. At each round, the participants have one hour to solve three algorithmic problems in as little time as possible.
- Yoann Coudert–Osmont received the Genius prize for the best student for the Master Dev de France 2023, a contest similar to Tech Challenger. The contest takes place on a single day with the format of five qualification round each one allowing 40 more participants to reach the final. The competition is attended by about 2000 participants.
- Yoann Coudert–Osmont won the first prize for the Meritis, Code on Time 2023. This contest lasts for 2 weeks. 332 French participants competed for the highest score by solving three exact problems and maximizing their scores with heuristics on a final NP-hard problem.
- Yoann Coudert–Osmont ranked second in the ICPC 2023 Online Spring Challenge powered by Huawei:.Few years ago, the ICPC foundation started to organize some regular challenges with their partner Huawei. The ICPC foundation organizes the International Collegiate Programming Contest (ICPC formerly ACM ICPC), the most prestigious algorithmic contest in the world. The 2023 Online Spring Challenge is the fifth one. The challenge lasted two weeks and gathered 1344 participants around the world. The goal of this edition was to design a buffer sharing algorithm for a multi-tenant database environment.
- ICPC Challenge Championship powered by Huawei: In August 2023, the ICPC foundation and Huawei invited 58 of the best contestants from the five previous ICPC challenges to a new onsite challenge in the Ox Horn campus, Dongguan, China. Participants came from 25 different countries. This new challenge, strongly inspired by the previous online challenge, lasted 5 hours and Yoann Coudert–Osmont came third out of the 58 contestants and about 100 participants from a training camp for the upcoming ICPC world finals which were taking place in the same time in Dongguan.
6 New software, platforms, open data
6.1 New software
6.1.1 ultimaille
-
Keyword:
Mesh
-
Functional Description:
Ultimaille is a lightweight mesh handling library. It does not contain any ready-to-execute remeshing algorithms. It simply provides a friendly way to manipulate a surface/volume mesh, it is meant to be used by external geometry processing software.
There are lots of mesh processing libraries in the wild, excellent specimens are: 1. geogram 2. libigl 3. pmp 4. CGAL
We are, however, not satisfied with either of those. At the moment of this writing, Geogram, for instance, has 847 thousand (sic!) of lines of code. We strive to make a library under 10K loc able to do common mesh handling tasks for surfaces and volumes. The idea is to propose a lightweight dependency for sharing geometry processing algorithms.
Another reason to create yet-another-mesh-library is the speed of development and debugging. We believe that explicit typing allows for an easier code maintenance, and we tend to avoid "auto" as long as it reasonable. In practice it means that we cannot use libigl for the simple reason that we do not know what this data represents:
Eigen::MatrixXd V, Eigen::MatrixXi F, Is it a polygonal surface or a tetrahedral mesh? If surface, is it triangulated or is it a generic polygonal mesh? Difficult to tell... Thus, ultimaille provides several classes that allow to represent meshes:
PointSet PolyLine Triangles, Quads, Polygons Tetrahedra, Hexahedra, Wedges, Pyramids You can not mix tetrahedra and hexahedra in a single mesh, we believe that it is confusing to do otherwise. If you need a mixed mesh, create a separate mesh for each cell type: these classes allow to share a common set of vertices via a std::shared_ptr.
This library is meant to have a reasonable performance. It means that we strive to make it as rapid as possible as long as it does not deteriorate the readability of the source code.
-
News of the Year:
All the library is built around STL containers (mainly std::vector<int>), pursuing our goal in explicit typing, last year we have added primitives and iterators. The primitives are very lightweight and can be casted to int. The compiler optimizes them away, but in the end we have a more readable and less error-prone code without compromising the efficiency. Another big feature of the last year is a completely redesigned connectivity interfaces for all kinds of meshes.
- URL:
-
Contact:
Dmitry Sokolov
6.1.2 stlbfgs
-
Name:
C++ L-BFGS implementation using plain STL
-
Keyword:
Numerical optimization
-
Functional Description:
Many problems can be stated as a minimization of some objective function. Typically, if we can estimate a function value at some point and the corresponding gradient, we can descend in the gradient direction. We can do better and use second derivatives (Hessian matrix). There is an alternative to this costly option: L-BFGS is a quasi-Newton optimization algorithm for solving large nonlinear optimization problems [1,2]. It employs function value and gradient information to search for the local optimum. It uses (as the name suggests) the BGFS (Broyden-Goldfarb-Fletcher-Shanno) algorithm to approximate the inverse Hessian matrix. The size of the memory available to store the approximation of the inverse Hessian is limited (hence L- in the name): in fact, we do not need to store the approximated matrix directly, but rather we need to be able to multiply it by a vector (most often the gradient), and this can be done efficiently by using the history of past updates.
Suprisingly enough, most L-BFGS solvers that can be found in the wild are wrappers/transpilation of the original Fortran/Matlab codes by Jorge Nocedal and Dianne O'Leary.
Such code is impossible to improve if, for example, we are working near the limits of floating point precision, therefore meet stlbfgs: a from-scratch modern C++ implementation. The project has zero external dependencies, no Eigen, nothing, plain standard library.
This implementation uses Moré-Thuente line search algorithm [3]. The preconditioning is performed using the M1QN3 strategy [5,6]. Moré-Thuente line search routine is tested against data [3] (Tables 1-6), and L-BFGS routine is tested on problems taken from [4].
[1] J. Nocedal (1980). Updating quasi-Newton matrices with limited storage. Mathematics of Computation, 35/151, 773-782. 3
[2] Dong C. Liu, Jorge Nocedal. On the limited memory BFGS method for large scale optimization. Mathematical Programming (1989).
[3] Jorge J. Moré, David J. Thuente. Line search algorithms with guaranteed sufficient decrease. ACM Transactions on Mathematical Software (1994)
[4] Jorge J. Moré, Burton S. Garbow, Kenneth E. Hillstrom, "Testing Unconstrained Optimization Software", ACM Transactions on Mathematical Software (1981)
[5] Gilbert JC, Lemaréchal C. The module M1QN3. INRIA Rep., version. 2006,3:21.
[6] Gilbert JC, Lemaréchal C. Some numerical experiments with variable-storage quasi-Newton algorithms. Mathematical Programming 45, pp. 407-435, 1989.
-
News of the Year:
Improved numerical stability of the preconditioner and a new linesearch routine.
- URL:
-
Contact:
Dmitry Sokolov
7 New results
Participants: Dmitry Sokolov, Nicolas Ray, Étienne Corman, Laurent Alonso, Guillaume Coiffier, David Desobry, Yoann Coudert-Osmont.
7.1 Integer seamless maps

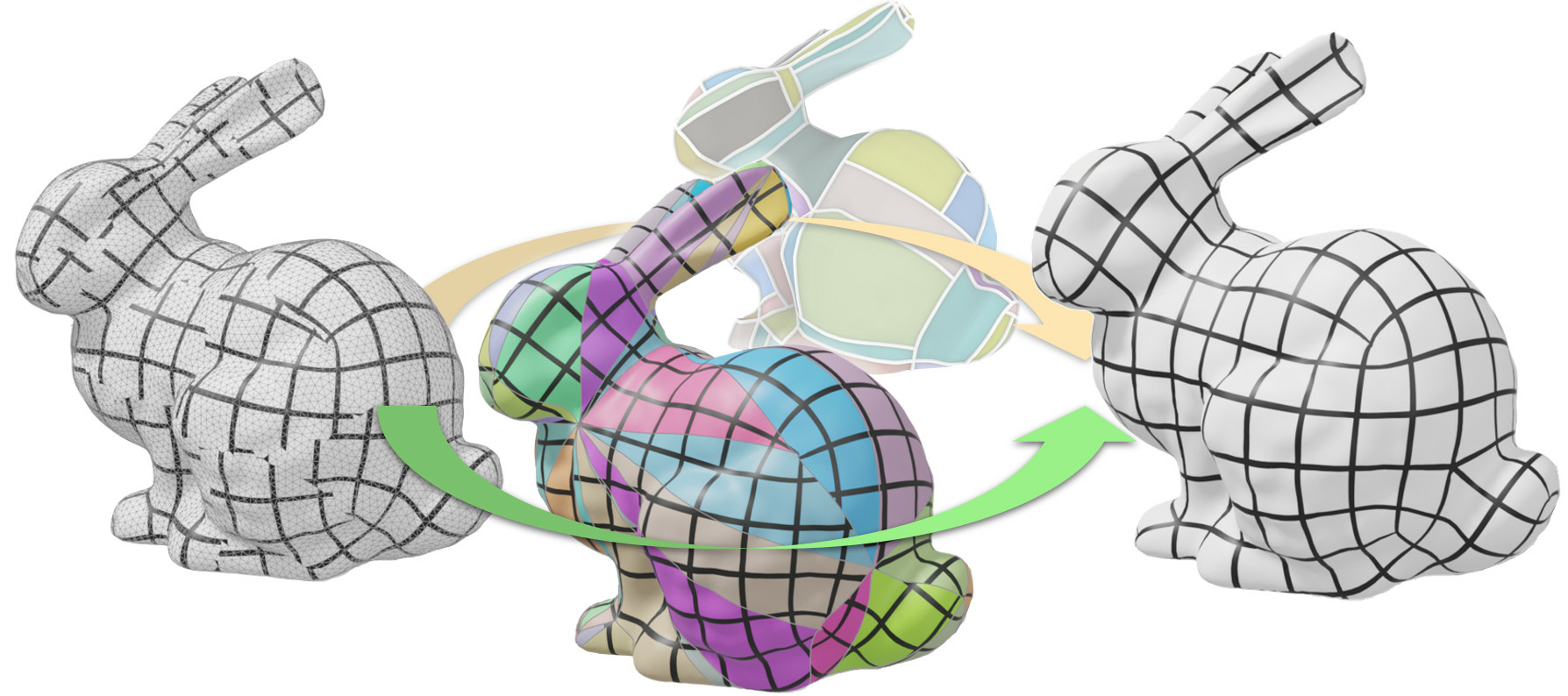
A large family of quadmeshing methods is based on a parametrization of the input surface. Intuitively, a quadmesh can be computed by first laying an input triangle mesh onto the plane using a parametrization technique, overlaying the uv-coordinates with an orthogonal grid of the plane and lifting the result back onto the surface. In other words, using a parametrization for quadmeshing boils down to applying a grid texture onto a surface and extracting the resulting connectivity, refer to Figure 3. However, one needs to be careful of what happens at the seams and the boundary of the input mesh in order to avoid discontinuities and retrieve complete and valid quads. Computing a global seamless parametrization is a challenging problem in geometry processing, mostly due to the fact that any attempt at solving it needs to determine two very different sets of variables. On the one hand, a seamless parametrization is defined by a discrete set of singular points (or cones) that concentrate all the curvature in multiples of . On the other hand, the actual mapping needs to be optimized to account for specific constraints depending on the application, such as alignment with feature edges or creases, local sizing of elements or controlled distortion. Yet, the mapping's topology is determined by the cone distribution, which can drastically alter its quality. In particular, finding cone positions minimizing the mapping's distortion is challenging and often leads to sophisticated optimization problems.
To overcome this apparent complexity a common approach is to decouple the problem into two independent subproblems: first computing a rotationally seamless parameterization, and then compute a truly seamless (integer seamless) map, refer to Figure 4 for an illustration. This year we contributed 7, 8 to both parts of the pipeline.

7.1.1 Rotationally seamless parameterization via moving frames
Even having relaxed a part of integer variables by targeting a rotationally seamless parameterization, we still face a hard problem. The common strategy is to choose the singularity locations using a cross field or other proxies and then compute a global rotationally seamless parametrization constrained to given singularity locations. This procedure, however, loosens the link between cone placement and the distortion of the final result. As a consequence, a quadmesh extracted from this parametrization can present quads that stray far away from squares because its connectivity was optimized almost independently of its geometry.
We proposed the first method 7 that keeps the connection between the rotational and positional variables. In differential geometry, Cartan's method of moving frames provides a rich theory to design and describe local deformations. This framework uses local frames as references, making local coordinates translation and rotation invariant. Furthermore, Cartan's first structure equation provides a necessary and sufficient condition to the existence of an embedded surface, as it describes how differential coordinates should change relative to the frame's motion, effectively removing all influence of the ambient coordinate systems on the deformation.
In this work, we extend Cartan's method to singular frame fields and we prove that any solution of the derived structure equations is a valid cone parametrization. Most importantly, we provide a vertex-based discretization of the smooth theory which provably preserves all its properties. The absence of a global coordinate system allows us to compute parametrizations without prior knowledge of the cut positions and to automatically place quantized cones optimizing for a given distortion energy. This makes the algorithm very versatile to user prescribed constraints such as feature or boundary alignment and forced cone locations. The algorithm takes the form of a single non-linear least-square problem minimized using quasi-Newton methods. We demonstrate its performance on a large dataset of models where we are able to output seamless parametrization that are less distorted than previous works.
7.1.2 Quad Mesh Quantization Without a T‐Mesh
As we have mentioned earlier, truly seamless maps can be obtained by solving a mixed integer optimization problem: real variables define the geometry of the charts and integer variables define the combinatorial structure of the decomposition. To make this optimization problem tractable, a common strategy is to ignore integer constraints at first by computing a rotationally seamless map, then to enforce them in a so-called quantization step.
Actual quantization algorithms exploit the geometric interpretation of integer variables to solve an equivalent problem: they consider that the final quadmesh is a subdivision of a T-mesh embedded in the surface, and optimize the number of subdivisions for each edge of this T-mesh (Fig. 5). We propose 8 to operate on a decimated version of the original surface instead of the T-mesh. One motivation for this work is the easiness of implementation adaptation to constraints such as free boundaries, complex feature curves network, etc. In addition to that, this approach is also very promising for its possible extensions to the 3D (hex meshing) case.
7.2 Non mesh-related results
This year we have also contributed to few topics not directly related to the core topic of the team.
7.2.1 One class classification
One class classification (OCC), or outlier detection, is the task of determining whether a sample belongs to a given distribution. We propose a new method, dubbed One Class Signed Distance Function (OCSDF), to perform One Class Classification by provably learning the Signed Distance Function (SDF) to the boundary of the support of a distribution, refer to Fig. 5. The distance to the support can be interpreted as a normality score, and its approximation using 1-Lipschitz neural networks provides robustness bounds against l2 adversarial attacks, an underexplored weakness of deep learning-based OCC algorithms. We show that OCSDF is competitive against concurrent methods on tabular and image data while being way more robust to adversarial attacks, illustrating its theoretical properties. Finally, as exploratory research perspectives, we theoretically and empirically show how OCSDF connects OCC with image generation and implicit neural surface parametrization.
7.2.2 PACE Solver Description: Touiouidth
We designed a twin-width solver 9 for the exact track of the 2023 PACE (Parameterized Algorithms and Computational Experiments) Challenge. Our solver is based on a simple branch and bound algorithm with search space reductions and is implemented in C++. The solver has been evaluated over a dataset composed of 20 graphs and it get ranked third out of twenty teams. The twin-width of an undirected graph is a natural number, used to study the parameterized complexity of graph algorithms. Intuitively, it measures how similar the graph is to a cograph, a type of graph that can be reduced to a single vertex by repeatedly merging together twins vertices that have the same neighbors. The twin-width is defined from a sequence of repeated mergers where the vertices are not required to be twins, but have nearly equal sets of neighbors.
7.2.3 Uniform random generations
We present a simple algorithm 13, 14 to help generate simple structures: 'Fibonacci words'(i.e., certain words that are enumerated by Fibonacci numbers), Motzkin words, Schröder trees of size n. It starts by choosing an initial integer with uniform probability (i.e., for some ), then uses a basic rejection method to accept or reject it. We show that at least for these structures, this leads to very simple and efficient algorithms with an average complexity of that only use small integers (integers smaller than ). More generally, for structures that satisfy a basic condition, we prove that this leads to an algorithm with an average complexity of . We then show that we can extend it to be more efficient if a distribution has a long 'trail' by showing how we can generate Partial Injections of size n in and Motzkin left factors of size n and final height h in .
8 Bilateral contracts and grants with industry
Participants: Dmitry Sokolov, Nicolas Ray, David Desobry.
8.1 Bilateral contracts with industry
Company: TotalEnergies
Duration: 01/10/2020 – 30/03/2024
Participants: Dmitry Sokolov, Nicolas Ray and David Desobry
Abstract: The goal of this project is to improve the accuracy of rubber behavior simulations for certain parts produced by TotalEnergies, notably gaskets. To do this, both parties need to develop meshing methods adapted to the simulation of large deformations in non-linear mechanics. The Pixel team has a strong expertise in hex-dominant meshing, TotalEnergies has a strong background in numerical simulation within an industrial context. This collaborative project aims to take advantage of both expertises.
David defended his PhD 12 on August 23, 2023.
9 Dissemination
Participants: Dmitry Sokolov, Étienne Corman, Dobrina Boltcheva, Nicolas Ray, Yoann Coudert-Osmont, Guillaume Coiffier.
9.1 Promoting scientific activities
9.1.1 Conference
Organization
This year we have hosted the 4th edition of the Frames workshop. The goal of the FRAMES is to gather both theoretical (computer science & applied mathematics) and practical (engineering & industry) specialists in the field of frame-based hex-meshing, in view of numerical computations.
Reviewer
Members of the team were reviewers for Eurographics, SIGGRAPH, SIGGRAPH Asia, ISVC, Pacific Graphics, and SPM.
9.1.2 Journal
Reviewer - reviewing activities
Members of the team were reviewers for Computer Aided Design (Elsevier), Computer Aided Geometric Design (Elsevier), Transactions on Visualization and Computer Graphics (IEEE), Transactions on Graphics (ACM), Computer Graphics Forum (Wiley), Computational Geometry: Theory and Applications (Elsevier) and Computers & Graphics (Elsevier).
9.1.3 Research administration
- Dmitry Sokolov is elected to the Inria Evaluation Committee.
- Dobrina Boltcheva participated to two Associate Professor hiring committees:
- Université de Lorraine: local organizer
- Université de Marseilles: exterior member
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
Dobrina Boltcheva is responsible of software engineering study program at IUT Saint-Die. Dmitry Sokolov is responsible for the 3d year of computer science license at the Université de Lorraine.
Members of the team have teached following courses:
- License: Guillaume Coiffier, Operations research, 20h, L3, École des Mines
- License: Guillaume Coiffier, Algorithms and complexity, 22h, L3, École des Mines
- Master: Étienne Corman, Analysis and Deep Learning on Geometric Data, 12h, M2, École Polytechnique
- BUT 2 INFO : Dobrina Boltcheva, Algorithmics, 20h, 2A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Software architecture, 20h, 2A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Software engineering, 20h, 2A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Computer Vision : Image processing, 20h, 2A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Advanced algorithmics, 20h, 3A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Graphical Application, 30h, 3A, IUT Saint-Dié-des-Vosges
- BUT 2 INFO : Dobrina Boltcheva, Advanced programming, 30h, 3A, IUT Saint-Dié-des-Vosges
- Master : Yoann Coudert–Osmont, Représentation des données visuelles, 6h, M1, Université de Lorraine
- Master : Yoann Coudert–Osmont, Système 1, 15h, L2, Université de Lorraine
- Master : Yoann Coudert–Osmont, Outils Système, 20h, L2, Université de Lorraine
- Master : Yoann Coudert–Osmont, Méthodologie de programmation et de conception avancée, 22h, L1, Université de Lorraine
- Master : Yoann Coudert–Osmont, NUMOC, 10h, L1, Université de Lorraine
- Master : Yoann Coudert–Osmont, Programmation compétitive (entraînement au SWERC) , 27h, Mines de Nancy and Télécom Nancy
- License : Dmitry Sokolov, Programming, 48h, 2A, Université de Lorraine
- License : Dmitry Sokolov, Logic, 30h, 3A, Université de Lorraine
- License : Dmitry Sokolov, Algorithmics, 25h, 3A, Université de Lorraine
- License : Dmitry Sokolov, Computer Graphics, 16h, M1, Université de Lorraine
- Master : Dmitry Sokolov, Logic, 22h, M1, Université de Lorraine
- Master : Dmitry Sokolov, Computer Graphics, 30h, M1, Université de Lorraine
- Master : Dmitry Sokolov, 3D data visualization, 15h, M1, Université de Lorraine
- Master : Dmitry Sokolov, 3D printing, 12h, M2, Université de Lorraine
- Master : Dmitry Sokolov, Numerical modeling, 12h, M2, Université de Lorraine
9.2.2 Supervision
- Yoann Coudert-Osmont, 2.5D Frame Fields for Hexahedral Meshing, started September 2021, advisors: Nicolas Ray, Dmitry Sokolov
PhD defenses
9.2.3 Juries
- Dmitry Sokolov participated in the PhD jury of Ali Fakih (Université de Haute-Alsace Mulhouse-Colmar) as a reviewer.
- Dmitry Sokolov participated in the PhD jury of Vladimir Bespalov (ITMO, Saint Petersburg, Russia) as a reviewer.
9.3 Popularization
9.3.1 Interventions
We have participated to different science popularization events:
- Guillaume Coiffier, lycée Notre Dame Saint Joseph, Épinal, 19/01/2023
- Guillaume Coiffier, Conférence fête de la science, lycée Louis Vincent, Metz, 12/10/2023
- Guillaume Coiffier, Fête de la science : Face à Face, Bouligny and Vandœuvre, 6/10/2023 and 11/10/2023
- Guillaume Coiffier, Les chercheurs passent le Grands Oral
- Dmitry Sokolov, Les chercheurs passent le Grands Oral, lycée Jean Zay, Jarny, 14/04/2023
10 Scientific production
10.1 Major publications
- 1 articleRestricted Power Diagrams on the GPU.Computer Graphics Forum402June 2021HALDOI
- 2 articleFoldover-free maps in 50 lines of code.ACM Transactions on GraphicsVolume 40issue 4July 2021, Article No.102, pp 1–16HALDOIback to text
- 3 articleMeshless Voronoi on the GPU.ACM Trans. Graph.376December 2018, 265:1--265:12URL: http://doi.acm.org/10.1145/3272127.3275092DOI
- 4 articlePractical 3D Frame Field Generation.ACM Trans. Graph.356November 2016, 233:1--233:9URL: http://doi.acm.org/10.1145/2980179.2982408DOIback to text
- 5 articleRobust Polylines Tracing for N-Symmetry Direction Field on Triangulated Surfaces.ACM Trans. Graph.333June 2014, 30:1--30:11URL: http://doi.acm.org/10.1145/2602145DOI
- 6 articleHexahedral-Dominant Meshing.ACM Transactions on Graphics3552016, 1 - 23HALDOIback to text
10.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
Reports & preprints
10.3 Cited publications
- 15 articleA frontal approach to hex-dominant mesh generation.Adv. Model. and Simul. in Eng. Sciences112014, 8:1--8:30URL: https://doi.org/10.1186/2213-7467-1-8DOIback to text
- 16 inproceedingsA Comparison of All-Hexahedral and All-Tetrahedral Finite Element Meshes for Elastic and Elasto-Plastic Analysis.International Meshing Roundtable conf. proc.1995back to text
- 17 inproceedingsMeeting the Challenge for Automated Conformal Hexahedral Meshing.9th International Meshing Roundtable2000, 11--20back to text
- 18 miscCloud Compare.http://www.danielgm.net/cc/release/back to text
- 19 articleMeasurement uncertainty on the circular features in coordinate measurement system based on the error ellipse and Monte Carlo methods.Measurement Science and Technology27122016, 125016URL: http://stacks.iop.org/0957-0233/27/i=12/a=125016back to text
- 20 inproceedingsMotorcycle Graphs: Canonical Quad Mesh Partitioning.Proceedings of the Symposium on Geometry ProcessingSGP '08Aire-la-Ville, Switzerland, SwitzerlandCopenhagen, DenmarkEurographics Association2008, 1477--1486URL: http://dl.acm.org/citation.cfm?id=1731309.1731334back to text
- 21 miscGRAPHITE.http://alice.loria.fr/software/graphite/doc/html/back to text
- 22 articleRobust Hex-Dominant Mesh Generation using Field-Guided Polyhedral Agglomeration.ACM Transactions on Graphics (Proceedings of SIGGRAPH)364July 2017DOIback to text
- 23 articleFully Automatic Mesh Generator for 3D Domains of Any Shape.IMPACT Comput. Sci. Eng.23December 1990, 187--218URL: http://dx.doi.org/10.1016/0899-8248(90)90012-YDOIback to text
- 24 articleGmsh: a three-dimensional finite element mesh generator.International Journal for Numerical Methods in Engineering79112009, 1309-1331back to text
- 25 inproceedingsReliable Isotropic Tetrahedral Mesh Generation Based on an Advancing Front Method.International Meshing Roundtable conf. proc.2004back to text
- 26 inproceedingsLeast squares conformal maps for automatic texture atlas generation.ACM transactions on graphics (TOG)21ACM2002, 362--371back to text
- 27 articleNotions of Optimal Transport theory and how to implement them on a computer.Computer and Graphics2018back to text
- 28 inproceedingsA New Approach to Octree-Based Hexahedral Meshing.International Meshing Roundtable conf. proc.2001back to text
- 29 miscMeshMixer.http://www.meshmixer.com/back to text
- 30 miscMeshlab.http://www.meshlab.net/back to text
- 31 inproceedingsUncertainty Propagation for Terrestrial Mobile Laser Scanner.SPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences2016back to text
- 32 articleCubeCover - Parameterization of 3D Volumes.Computer Graphics Forum3052011, 1397-1406URL: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-8659.2011.02014.xDOIback to text
- 33 miscSpatial Uncertainty Model for Visual Features Using a Kinect Sensor.2012back to text
- 34 miscPoint Cloud Library.http://www.pointclouds.org/downloads/back to text
- 35 articleNETGEN An advancing front 2D/3D-mesh generator based on abstract rules.Computing and visualization in science111997back to text
- 36 articleAutomatic three-dimensional mesh generation by the finite octree technique.International Journal for Numerical Methods in Engineering3241991back to text
- 37 articleTetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator.ACM Trans. on Mathematical Software4122015back to text
- 38 techreportCFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences.NASA/CR-2014-218178, NF1676L-183322014back to text
- 39 articleScanning geometry: Influencing factor on the quality of terrestrial laser scanning points.ISPRS Journal of Photogrammetry and Remote Sensing6642011, 389 - 399URL: http://www.sciencedirect.com/science/article/pii/S0924271611000098DOIback to text
- 40 inproceedingsUnconstrained Paving & Plastering: A New Idea for All Hexahedral Mesh Generation.International Meshing Roundtable conf. proc.2005back to text
- 41 articleThe whisker weaving algorithm.International Journal of Numerical Methods in Engineering1996back to text
- 42 articleEfficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints.International Journal for Numerical Methods in Engineering37121994, 2005--2039URL: http://dx.doi.org/10.1002/nme.1620371203DOIback to text
- 43 inproceedingsRobust and Practical Depth Map Fusion for Time-of-Flight Cameras.Image AnalysisChamSpringer International Publishing2017, 122--134back to text
- 44 inproceedingsAdaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data.International Meshing Roundtable conf. proc.2004back to text
- 45 articlePoint cloud uncertainty analysis for laser radar measurement system based on error ellipsoid model.Optics and Lasers in Engineering792016, 78 - 84URL: http://www.sciencedirect.com/science/article/pii/S0143816615002675DOIback to text
- 46 miscCgal, Computational Geometry Algorithms Library.http://www.cgal.orgback to text

