2023Activity reportProject-TeamQURIOSITY
RNSR: 202324386L- Research center Inria Saclay Centre at Institut Polytechnique de Paris
- In partnership with:Institut Polytechnique de Paris
- Team name: Quantum Information Processing and Communication
- In collaboration with:Laboratoire Traitement et Communication de l'Information
- Domain:Algorithmics, Programming, Software and Architecture
- Theme:Algorithmics, Computer Algebra and Cryptology
Keywords
Computer Science and Digital Science
- A3.4. Machine learning and statistics
- A4.2. Correcting codes
- A4.3. Cryptography
- A4.3.4. Quantum Cryptography
- A4.6. Authentication
- A5.9. Signal processing
- A6.1.2. Stochastic Modeling
- A6.5. Mathematical modeling for physical sciences
- A7.1. Algorithms
- A7.1.4. Quantum algorithms
Other Research Topics and Application Domains
- B5.11. Quantum systems
- B6.2. Network technologies
- B9.1. Education
- B9.10. Privacy
1 Team members, visitors, external collaborators
Research Scientist
- Cambyse Rouze [INRIA, ISFP, from Sep 2023]
Faculty Members
- Romain Alléaume [Team leader, Télécom Paris - IP Paris, Professor, HDR]
- Peter Brown [Télécom Paris, Associate Professor]
- Augustin Vanrietvelde [Télécom Paris, Associate Professor]
Post-Doctoral Fellow
- Thomas Van Himbeeck [Telecom Paris]
PhD Students
- Jan Kochanowski [IP Paris, from Nov 2023]
- Francesco Mazzoncini [Telecom Paris]
- Tristan Nemoz [Telecom Paris]
- Thomas Pousset [Télécom Paris]
- Guillaume Ricard [Telecom Paris]
- Pierre Enguerrand Verdier [Orange, CIFRE]
Interns and Apprentices
- Ali Almasi [IP Paris, from Sep 2023, PhD Track student]
- Evdokia Gneusheva [École Polytechnique, Intern, until Mar 2023]
Administrative Assistant
- Natalia Alves [Inria]
External Collaborators
- Pablo Arrighi [Université Paris-Saclay, Team Leader, Inria Team QuACS, HDR]
- Roger Colbeck [University of York, Professor, University of York, HDR]
- Nicolas Fabre [Telecom Paris]
- Omar Fawzi [Inria, Team Leader of QInfo at ENS Lyon, HDR]
- Sylvain Gigan [Ecole Normale Supérieure, HDR]
- Yves Jaouën [Telecom Paris, HDR]
- Robert König [Technical University Münich, Professor, HDR]
- David Peres Garcia [ Universidad Complutense de Madrid , Professor, HDR]
- Cambyse Rouze [Technical University Münich, from Apr 2023 until Aug 2023]
- Daniel Stilck França [Inria, Inria Research Scientist at QInfo, ENS Lyon]
- Simone Warzel [Technical University Münich, Professor, HDR]
- Mirjam Weilenmann [University of Geneva]
2 Overall objectives
Quriosity's ambition is to extend the application horizon of quantum information science by addressing novel questions positioned at the intersection between theoretical research in quantum information and the engineering of quantum devices, with a focus on approaches combining digital and quantum photonics technologies.
The overarching goal of the project-team will be to push forward our ability to harness and exploit high-dimensional complex quantum systems for quantum information processing and quantum communications purposes.
Leveraging a dual approach combining fundamental research in quantum information with quantum photonics expertise, Quriosity will strive to take advantage of and develop strong synergies with the unique quantum ecosystem of Saclay and to pursue objectives that have the potential to bring radical advances to several application domains of quantum technologies, ranging from cryptography to computing:
- Design quantum-enhanced cryptographic hardware, leveraging concepts based on computational hardness and quantum information.
- Conceive and engineer photonic-based processors and systems capable of achieving quantum advantage in computation or communication tasks.
- Develop efficient quantum information processing schemes implementable on near-term hardware and advance the theoretical framework to understand the fundamental limits of noisy quantum information processing.
3 Research program
The research program that we aim to lead in the Quriosity project-team intends to embrace a relatively wide area of theoretical questions, ranging from quantum cryptography, that we ambition to combine with complexity-based schemes and establish as a framework to enhance hardware security, to the mathematical foundations of quantum information and quantum computing. Conversely, we also intend to develop research capable of leveraging photonics and digital information processing technologies to design systems capable of producing high-dimensional and controllable quantum states of light in order to push forward the frontiers of quantum information processing advantage.
3.1 Research axis 1: Quantum cryptography complexity and hardware frontiers
This axis aims to identify and solve frontier research topics in quantum cryptography, from two main perspectives. First by exploring the interplay between security models - including computational ones - and theoretical quantum cryptography, allowing to build protocols with stronger security properties and lesser resource requirements. Second by laying a special emphasis on interplay between quantum cryptography and hardware security, with the need to develop extended techniques for quantum cryptographic hardware security certification, but also the idea to strengthen hardware security and its resilience to information leakage by resorting to quantum cryptographic constructions.
3.1.1 Everlasting security from a quantum-computational hybrid model
We proposed in 2015 a security model that we later coined a Quantum Computational Timelock (QCT) security model. It consists in assuming that computationally secure encryption may only be broken after time much longer than the coherence time of quantum memories available at the time of protocol execution. The QCT security model opens the possibility to propose new quantum cryptographic constructions and in particular to make use of encoding and security proof techniques that strongly depart from “traditional” quantum conjugate coding that is a central ingredient in most quantum cryptographic protocols.
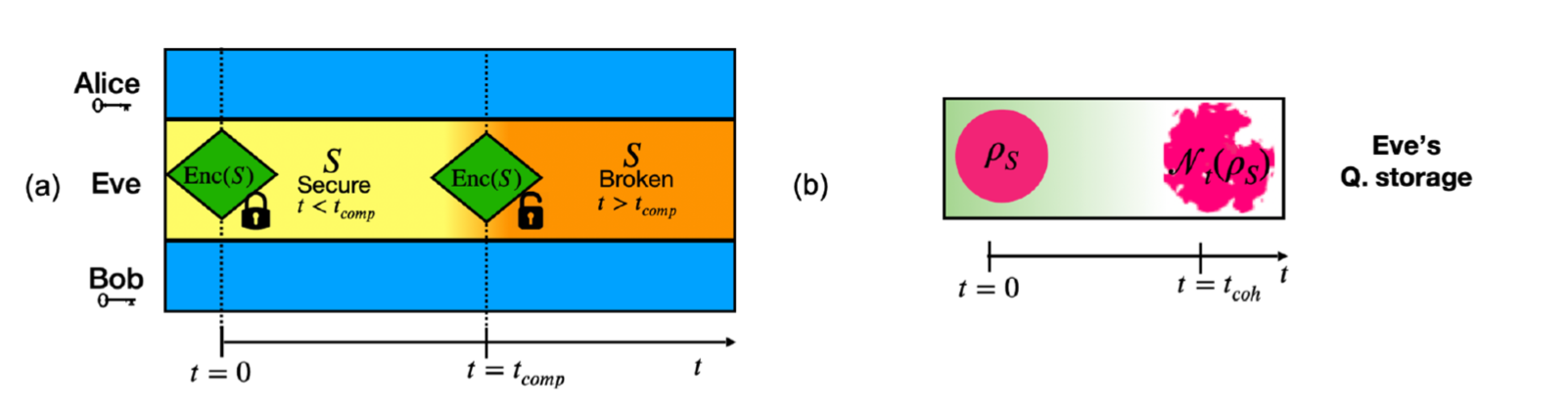
Description of the QCT security model
The QCT security model opens towards a rich variety of fascinating questions, that we have certainly not all identified. In the coming years we intend to push forward the theoretical analysis of several of these questions, that relate to the computational frontiers of quantum cryptography. One ongoing direction consists in studying key agreement constructions whose security can be reduced to distributed computational problems that exhibit an exponential separation in terms of quantum or classical communication complexity.
As an alternative way to build secure protocols in the QCT model, we also intend to investigate pseudo-random quantum states, which can be seen as a computational variant of a
3.1.2 Device-independent cryptography
Device-independent cryptography allows one to perform quantum cryptography with reduced or even no trust assumptions on the quantum hardware. It remains a challenge experimentally and pushing the performance (in terms of key rate, or trust reduction) of device-independent cryptography defines an active research frontier for quatum cryptography. Recent implementations of DI-QKD147, 57, 57 have shown that whilst it is now feasible, it has a relatively low rate and can only be executed over a short distance. By improving the theoretical methods for analyzing various protocols and security proofs and by improving the protocol design we can look to boost the rates of these protocols and push them towards a more viable technology. Examples of such improvements include protocol design modifications 51, 40 and improved methods to calculate rates 28, 29, 50. Our goals are to develop better designed protocols and security proofs (assessing their performance in experiments) and to investigate the fundamental limitations of DI protocol rates Overall pushing the practicality of DI forwards and improving our understanding of its limitations.
As a complementary line of research we will also investigate prospects of semi-device-independent protocols as a viable near-term alternative to device-independent security. Proposed protocols rely on assumptions of system energy 49, dimension bounds and bounded distrust 52 amongst others. We will investigate alternative assumptions and derive resulting protocols to be analyzed and subsequently implemented. We will also apply the semi-device-independent framework to the problem of hardware verification, designing tests to establish that the hardware is functioning correctly whilst placing limited trust on the components.
3.1.3 Quantum-enhanced leakage-resilience
We will also investigate some questions placed at the intersection between classical hardware security and quantum cryptography, namely how to prove the security of a cryptographic protocols when implemented using hardware, such as processors or storage, that may leak some of the security-sensitive information.
We intend to tackle leakage-resilience cryptography from a new viewpoint, that will consist in integrating quantum cryptographic constructions as a base layer within cryptographic systems, in order to obtain security guarantees even in presence of information leakage with strictly weaker assumptions than existing classical leakage-resilience protocols. We will first consider simple cryptographic protocols such as One-Time-Pad encryption or authentication protocols relying on Physically Uncloneable Functions PUFs. We intend for example to investigate how the use of hybrid classical-quantum cryptographic hardware, comprising quantum channels to interconnect processors or secure storage sites, can lead to cryptographic protocols with provable security under some realistic information leakage models.
3.1.4 Real-world quantum cryptography
40 year of quantum cryptography (QC) have lead to major theoretical and technological advances, with fundamental impact on the field of information security. Market adoption however remains limited, with major challenges that practical QC still needs to be overcome in order to become widely used in real-world applications. We identify in particular two main challenges: 1) cryptographic advantage, namely the design of protocols for which the use of QC in combination with classical cryptography gives a competitive edge over classical cryptography only; 2) security certification of quantum cryptographic implementations. Quriosity intends to actively contribute to lift these barriers and to foster the development of real-world quantum cryptography and in particular to the uptake of a French and European industry. The development of a QC industry is indeed becoming an important topic, with strategic investments from leading scientific countries (China, Korea, Japan, UK, etc. ) including also notably the EU27 supporthing the EuroQCI initiative. On the other hand, the adoption of quantum cryptography for real-world application remains often considered with skepticism by representatives of the cybersecurity community, stressing the dire need of cross-disciplinary vision combining best-in-class classical and quantum cryptography expertise.
Regarding cryptographic advantage, our conviction is that one should not aim at constructions where quantum cryptography would just functionally replace classical cryptography, but on the other hand to identify applications where the use of QC combined with post-quantum cryptography (PQC) can present strict security gain over PQC alone.
Regarding security certification, it has become a central challenge in particular in the context of the EuroQCI initiative aiming at developing a pan-European quantum communication infrastructure, together with an industry, in the next 10 years It constitutes a complex task, requiring the collaboration of experts from different fields. In future years, we intend to tackle this question from different angles: on the theory side, we intend to propose a shift in the security objective towards everlasting security, and demonstrate how this can make the security certification of key establishment based on QKD combined with ephemeral post-quantum cryptography primitives much more tractable. On the system engineering side and in resonance with Section 3.2, we intend to identify and close implementation security gaps in modern CV-QKD systems relying on digital signal processing, notably the complex interplay between calibration procedure and finite-size security, but also between Nyquist pulse shaping and leakage.
3.2 Research axis 2: Multimode photonic systems for quantum information processing and communications
Building a quantum processor that we could use to solve real-world problems with practical benefits might constitute one of the most burning scientific and technological challenges of the beginning of the 21st century. Very interestingly, recent results indicate that quantum optical circuits constitute a very promising approach for quantum information processing, in particularly high-dimensional linear optics systems, which can form a (weaker) non-universal quantum computing platform, and yet efficiently perform tasks intractable for a classical computer, such as Boson Sampling 17.
We will actively investigate new theoretical questions related to quantum information processing with high-dimensional photonic system, and their interplay with technology and experiments.
3.2.1 Quantum coherent communications and digital signal processing
Quantum Key Distribution (QKD) systems are among the most advanced quantum communications technologies available today. QKD therefore provides an ideal platform to test novel system designs and validate quantum communication technology over real networks Leveraging essential features of modern optical communication systems, and in particular high sampling rates and digital signal processing 43, quantum coherent communications systems constitute a recent and promising route towards high-rates, highly integrated and cost-effective quantum communication systems. They rely on two central ingredients: -Spectrally efficient modulation formats and coherent detection, exploiting phase and intensity information and able to operate a very high rates (> GHz) even with shot-noise limited receivers. - Digital signal processing that takes advantage of the high sampling rates to digitally evaluate and compensate many impairments of the communications such as optical carrier phase noise or polarization mode dispersion, using dedicated algorithms.
In collaboration with Prof. Yves Jaouen from the GTO team of Telecom Paris,and working on a state-of-the-art experimental platform, Quriosity has designed and demonstrated for the first time DSP-enhanced quantum communications, with noise control performances that allow to successfully run QKD over metropolitan distances while being jointly deployed over classical coherent optical link 21. We have also filed a patent about this general concept and our inventive system design.
In the future, we then aim to leverage digital signal processing and machine learning (ML) techniques to characterize and mitigate noise in order to push further our ability to operate quantum communications over existing optical fibers, in coexistence with classical signals.
As a complementary line of research, we intend to theoretically study multimode quantum coherent communications using multimode shaping of the local oscillator, taking inspiration from 30. We also intend to explore the possibility to rely on CV multimode encoding as a way to experimentally implement new quantum cryptographic constructions in the hybrid quantum computational security models introduced in Section 3.1.
3.2.2 Quantum information processing with a programmable frequency processor
In collaboration with the teams of Nadia Belabas and Pascale Senellart at C2N and in the context of the ParisQCI project, we study how to combine high-dimensional photonic gates in the frequency domain, to efficiently synthesize high-dimensional unitary transformations. Leveraging on the possibility to parallelize single-qubit unitaries, that we have recently analyzed 5 we intend to study how such systems could be leveraged for optical quantum information processing, and in particular for quantum metrology. In the future, we will also investigate how to scale the platform to perform information processing with high-dimensional quantum states, opening the possibility to achieve quantum computational advantage, but also implementation routes for the hybrid quantum-computational cryptographic protocols in the QCT model, studied in Section 3.1
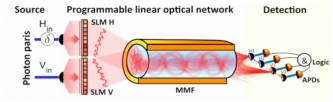
Multimode programmable linear optical circuit and associated experimental devices (Spatial Light Modulators: SLM, Multimode fibers: MMF, Detection of single photons multipixel APDs).
3.2.3 Quantum information processing using multimode programmable linear circuits
In collaboration with the team of Sylvain Gigan at ENS Ulm, and in the context of Francesco Mazzoncini's PhD that we co-supervise, we aim to use a multimode programmable linear circuit, built around a multimode fiber (cf. Figure 2) to perform some fundamental tests and demonstrations of quantum communication advantage, related to fundamental problems such as the Vector in a Subspace 48.
The prospects of this work are very promising: first they could lead to the first experimental demonstration of a exponential communication complexity gap between one-way quantum communication and two-way classical communications and may also open towards the possibility for experimentally robust Bell inequality violations 45, with applications for quantum cryptography and also in quantum computing.
3.3 Research axis 3: Mathematical foundations of quantum information
Quantum information and computation are built upon the mathematical frameworks of functional analysis and information theory. Developing our understanding of the mathematical underpinnings of these theories can in turn lead to new insights and applications. At Quriosity, one of our aims is to explore quantum information theory through the lens of the underlying mathematics. In a nutshell, we will parallelly develop new analytic and numerical tools for the study of quantum entropic quantities and complex quantum systems made of spin or bosonic degrees of freedom. We will in turn consider these systems to design new, physically motivated models of noise-robust quantum computing.
3.3.1 Convex relaxations of quantum optimization problems
Convex optimization concerns the optimization of convex functions over convex sets. This family of optimization problems has several particularly nice properties, including the guarantee of global optima, which makes them particularly appealing from both the perspective of the mathematics and the applications. They are widely applicable to many domains of science but in particular they arise rather naturally in the context of quantum theory as many of the relevant objects (states, channels and measurements) form convex sets.
We will aim to develop and apply techniques in convex optimization theory to problems within quantum information and quantum computing. Recent examples of our work in this area include 28, 29 where we developed semidefinite programming relaxations for entropic optimization problems relevant to device independent cryptography. Continuing this line of research we aim to extend these techniques to other entropic quantities beyond the relative entropy, for instance to the Petz and sandwiched families of Rényi divergences. We also have the ambitious goal of understanding and characterizing what classes of functions, relevant in the context of quantum theory, are amenable to such semidefinite programming approximations. In other words, what optimization problems in quantum information theory and quantum computing can we approximate?
A well-known example concerns strengthenings of the monotonicity of the relative entropy under the action of a quantum channel or a Markovian evolution known as strong data processing and modified logarithmic Sobolev inequalities. These fundamental inequalities are known to be hard to prove analytically, even for simple random walks on
3.3.2 Fundamental properties of entropies
Entropies are fundamental quantities in quantum information theory, obtaining operational meanings in terms of rates of various tasks 36. By improving our understanding of these quantities, we can in turn gain new insights into the various applications in which they appear.
For example, new chain rules for Rényi entropies 35 led to a versatile framework for cryptographic security proofs 20. The result, known as the entropy accumulation theorem, effectively gives sufficient conditions under which the entropy of a large system can be accurately described by the entropy of its individual systems. At QURIOSITY we aim to understand under which conditions does entropy accumulate in this manner? By understanding the minimal requirements for entropy to accumulate we can understand the minimal requirements under which a randomness based cryptographic protocol functions securely. Moreover, we aim to investigate the connection between the entropy accumulation theorem and the related works of the quantum probability estimation framework 56. This is an alternative method to break large entropies down into smaller quantities and reports several advantages over the entropy accumulation theorem. Understanding how advantages from one technique can be transferred to the other will lead to much stronger theoretical results and would have immediate applications to improve security proofs and rates of cryptographic protocols, leading to more practical technologies.
Other types of decompositions of entropic quantities of interacting complex systems into smaller components involving marginals over subsystems include generalizations of the famous strong subadditivity of the relative entropy known as approximate tensor-stability of the relative entropy. These are at the core of most successful methods for finding the speed of convergence of Gibbs sampling algorithms based on the modified logarithmic Sobolev inequality. In previous work, we successfully extended these notions to the quantum realm 38 and applied them to problems in network quantum information theory 25, 33 and open complex quantum systems 31, 22. Extensions and refinements of these concepts will lead to new breakthroughs in both fields (see Sections 3.3.3 and 3.3.4).
3.3.3 Complexity and entanglement properties of quantum Gibbs states
A complexity theoretical definition of the quantum phase of a state
In the setting of classical Gibbs measures, analogous questions have been intensively studied from the perspective of Markov chain Monte Carlo algorithms (MCMC). On regular lattices, the analysis of the speed of convergence of MCMC for lattice spin systems is by now well-understood through the study of correlations at equilibrium. The generalization to general interaction graphs is still a very active field of research in theoretical computer science, probability theory and mathematical physics 32. The problem becomes even harder in the quantum regime, where purely quantum mechanical effects, e.g. long-range entanglement, may cause the quantum Markov chain to slow down in an unpredicted manner. For the important case of commuting interactions, which include most hitherto studied Hamiltonians for the purpose of quantum error-correction, and for physical dynamics generated by the weak coupling of the system with a large environment (Davies dynamics), general results were obtained through spectral methods. However the latter are not powerful enough to distinguish evolutions generating topologically ordered states from rapidly mixing ones. Instead, more involved techniques, e.g. entropic inequalities, are needed. In 24, 31, 23, 22, we were able to prove rapid mixing by extending one of the most successful classical approaches to prove rapid mixing based on the modified logarithmic Sobolev inequality and the approximate tensor-stability of the relative entropy (cf Section 3.3.2). Extending this novel powerful approach, we plan to conduct a systematic joint study of mixing times and thermal stability of topological quantum order in low lattice dimensions. We will conduct this research in collaboration with Daniel Stilck França from QINFO with whom we co-authored 31. We also see a clear connection with the research focus of Daniel Malz who was recently recruited as a junior professor at Inria Saclay, the mathematical and theoretical condensed matter physicists at CPhT, as well as the team PEIPS at CMAP (X).
3.3.4 Mathematical analysis of quantum memories
In parallel to the previous research plan, we will conduct a mathematical analysis on the storage of quantum information and the concept of self-correction in complex quantum systems. Early work on the storage time of candidates of self-correcting quantum memories relied on the connection to the energy barrier of the system, that is the energy the system must reach for a logical error to occur, via an empirical principle called the Arrhenius law. More recently, the energy barrier was rigorously related to spectral properties of the evolution, whereas some no-go theorems showed the impossibility of an exact mathematical formulation of the Arrhenius law. Here instead, we plan to relate the memory lifetime of a device directly to properties of its thermal equilibrium state. We currently work on this research direction in the setting of lattice spin systems with Anthony Leverrier and Ivan Bardet from the team COSMIQ through the development of spectral methods, and plan to extend our framework to lattices with bosonic degrees of freedom in the near future. We also plan to initiate a dialogue with Jean-René Chazottes from CPhT (X) on refinements of our techniques using concentration and entropic inequalities which already proved their usefulness in the study of hitting times of classical Markov chains and their metastability. One of our long–term goals is to find systems with thermally stable entanglement, both stable against thermal fluctuations and robust against local perturbations. Such a theoretical result would be of very high practical interest since experimental implementations are inevitably subject to noise and errors.
3.3.5 Tomography of complex quantum systems
As the size of quantum devices continues to increase beyond what can be easily simulated classically, new challenges have appeared concerning the robust and efficient characterization of their states. This often necessitates the preparation and destructive measurement of exponentially many copies of the quantum system, as well as the storage of measurement outcomes in a classical memory. Recently, new methods of tomography have been proposed which precisely leverage this important simplification to develop efficient state learning algorithms. One highly relevant development in this direction is that of classical shadows 41, 42. In we propose a better solution by combining classical shadows with new insights from the emerging field of quantum optimal transport. Our current first step only applies to topologically trivial quantum states such as high-temperature Gibbs states or outputs of shallow quantum circuits, and more effort is needed to adapt and generalize our algorithm to non-trivial phases. We envision three new major contributions: First, we will develop constrained versions of concentration inequalities in order to develop efficient tomography algorithms of complex quantum states, assuming the prior knowledge of their phase. This line of research is original even in the classical setting where works on constrained entropic inequalities only very recently appeared in the literature. The expertise of Jean-René Chazottes from CPhT (X) will prove crucial to the success of this project. Second, we will extend the framework of shadow tomography to CV quantum systems. The main difficulties here are two-fold: first, CV systems are infinite-dimensional in nature, and hence some physical constraints need to be imposed on the states that one can hope to learn, such as their energy. Moreover, the set of measurements (homodyne/heterodyne) available in photonic experiments further limits the type of observables that one can hope to predict. In order to ensure the wide applicability of the method and test the resulting algorithm, we will rely on the already established interactions of IQA with the groups of experimentalists at IP Paris and Saclay, and initiate a fruitful dialogue with start-up like Quandela and Pasqal. In the future, we will use these methods to devise hardware-oriented noise-learning algorithms for many-body systems. For this, we plan to get in touch with the experts on statistical learning among IP Paris, and in particular at LIX.
3.3.6 Formal tools for higher-order quantum computation
The theoretical study of quantum computation and its advantages has, in the past decade, opened to a new perspective: higher-order quantum computation, i.e. the way in which one can transform black-box quantum gates by inserting them into computation architectures. This is useful to study the ways in which one can query subroutines in quantum computation, a pratice that is bound to become ubiquitous, for example in delegated quantum computing. The study of higher-order quantum computation has already led to promising as well as disconcerting results, such as about the difficulty of formally defining a quantum version of the computational `if' clause 19, or the fact that one might be able to query two unknown gates in a `superposed order of application', using a computation architecture called the quantum switch 34. Using the latter leads to computational advantages for certain tasks 18. However, the mathematical study of higher-order quantum processes quickly encounters thorny formal issues related to their non-trivial compositional structure.
Overcoming these issues would require the development of a specific and robust type system, stipulating which inputs a given higher-order quantum process admits and which output it produces. Despite recent advances 44, currently available type systems are not detailed enough to provide a fully compositional view of higher-order quantum computation. Our work thus focuses on refining them, through the encoding of sectorial structure, i.e. information about how quantum channels behave with respect to certain direct-sum decompositions of their input and output spaces, using the recently developed framework of routed quantum circuits 53, 54. Progress in this direction will pave the way to computer manipulation of complex higher-order processes, for instance to numerically optimise the advantage they yield.
3.3.7 Causal structure in quantum theory
Many of the peculiarities of quantum theory can be tracked down to it not matching our classical notion of causal structure 55; this leads to the question of how one could develop a quantum notion of causal structure, on which some progress has been achieved recently 26. Exploring quantum theory from a causal perspective yields potential progress in understanding its structure and potential applications, in particular for the aforementioned higher-order quantum processes, whose performances are directly connected to their causal structure. In that regard, a particularly important conjecture to prove is that of causal decompositions46, which puts forward a tentative equivalence between a unitary channel's causal structure (operational data about which of its inputs can affect which of its outputs) and its compositional structure (mathematical data about how it can be written as the composition of sub-channels). If such a conjecture (which has not been proven yet in the general case) were to be true, it would yield a remarkable mathematical lever on the relationship between the operational and formal sides of quantum theory. We investigate this conjecture mathematically with the aim to prove it in more and more general cases; this involves abstract mathematical methods employing C* algebras. More generally, we explore how the latter might provide a useful formal basis for considerations of causality in a quantum context.
4 Application domains
Quriosity positions its activity at the - fruitfull - frontier between theoretical research in quantum computer science and mathematics, and quantum technology engineering and applications.
We in particular believe that useful quantum inventions and technologies are going to emerge from the current investments in quantum information sciences and technologies, much before large scale (and error corrected) quantum computers can be built.
Our research programs opens in particular towards such perspective, on different aspects:
- The development of more efficient and higher security quantum cryptographic protocols.
- The ability to leverage quantum cryptography principles and tecnnologies to strengthen hardware security.
- The design of cost-effective quantum communications systems that can tightly integrated into modern communication infrastructures, making them widely deployable.
- The design of better quantum memories and therefore larger quantum computer as well as quantum networks.
5 Social and environmental responsibility
5.1 Footprint of research activities
Quriosity members are individually, and collectively making efforts to reduce their carbon footprint, in particular by taking the plane much less than before the Covid period. Augustin Vanrietvelde and Peter Brown will moreover act as carbon footprint delegates for Quriosity, and report to a working group at LTCI level, whose objective will be to increase the global awareness on carbon footprint, and steer the discussions to help decide on collective regulatory measures.
5.2 Impact of research results
Scientific publication
Quriosity aims at publishing high-impact papers in high profile journals such as Nature, Science, Physical Review, Quantum, IEEE Transactions on Information Theory, as well as top conferences in our field such as QIP, QCrypt, TQC as well as Crypto, EuroCrypt, CHES.
Innovation
Telecom Paris currently holds 5 granted patents: 3 on hybrid quantum computational cryptography (axis 3.1) and 2 on quantum coherent communications (axis 3.2). We plan to patent technological innovations, including foundamental proposals for which we see a clear implementation route and possible exploitation paths.
Teaching
Quriosity intends to play a vigorous role in the training of the future generation of quantum engineers and researchers. IQA and Romain Alléaume have been at the forefront of such development by opening the Quantum Engineering M2 Program in 2017. At Saclay level, and in collaboration notably with the QuACs Inria team but also with active Saclay quantum industry, we have the mid-term ambition to launch a master program on quantum computer science and engineering.
6 Highlights of the year
6.1 Five papers selected at QIP 2024
After less than a year of existence Quriosity has obtained oustanding results at QIP 2024 in terms of selected contributions, with 4 members of Quriosity that are co-authors of 5 accepted papers:
- Thomas van Himbeeck and Peter Brown. A tight and general finite-size security proof for quantum key distribution.
- Jan Kochanowski, Alvaro Alhambra, Ángela Capel and Cambyse Rouzé. Spectral gap implies rapid mixing for commuting Hamiltonians
- Robert König and Cambyse Rouzé. Limitations of local update recovery in stabilizer-GKP codes: a quantum optimal transport approach.
- Emilio Onorati, Cambyse Rouzé, Daniel Stilck Franca and James Watson. Efficient learning of ground and thermal states within phases of matter.
- Emilio Onorati, Cambyse Rouzé, Daniel Stilck França and James Watson. Provably Efficient Learning of Phases of Matter
6.2 Awards and Grants
Starting Packages
Cambyse Rouzé, Mirjam Weilenmann and Augustin Vanrietvelde have each been awarded a starting package in the context of the ANR ExcellenceS Program, on the STEP2 project sucessfully presented by IP Paris.
Best Poster Award
Tristan Nemoz has been granted the Best Poster Award (category Information Communication Electronics) at IP PAris PhD Day, on December 10 2023.
6.3 Quantum Hardware Security Workshop
The 2-day workshop held at University of Edinburgh on Novepber 23-24 and organized between Quriosity (Romain Alléaume, Peter Brown, Francesco Mazzoncini, Tristan Nemoz) and the team of Elham Kashefi at Quantum Software Lab (Elham Kashefi, Mina Doosti, Myrto Arapinis, Yao Ma, Abbas Poshtvan, Chrirag Wadhwa) has been extremly fruitful both scientifically and in the quality and friendlyness of the exchanges. We can see strong convergence, and possible synergies and collaborations, between our visions of the role that Quantum Cryptography can play in Hardware Security, as also expressed in 3.1 )
7 New results
7.1 Research axis 1: Quantum cryptography complexity and hardware frontiers
7.1.1 Prove the security of hybrid quantum-computational cryptographic protocols by a reduction to a quantum to classical communication complexity gap
Participants: Romain Alléaume, Peter Brown, Francesco Mazzoncini.
In 11, we introduce an explicit construction for a key distribution protocol in the Quantum Computational Timelock (QCT) security model, where one assumes that computationally secure encryption may only be broken after a time much longer than the coherence time of available quantum memories.
Taking advantage of the QCT assumptions, we build a key distribution protocol called HM-QCT from the Hidden Matching problem for which there exists an exponential gap in one-way communication complexity between classical and quantum strategies.
We establish that the security of HM-QCT against arbitrary i.i.d. attacks can be reduced to the difficulty of solving the underlying Hidden Matching problem with classical information. Legitimate users, on the other hand, can use quantum communication, which gives them the possibility of sending multiple copies of the same quantum state while retaining an information advantage. This leads to an everlasting secure key distribution scheme over n bosonic modes. Such a level of security is unattainable with purely classical techniques. Remarkably, the scheme remains secure with up to
7.1.2 New self-testing constructions for device-independent cryptography
Participants: Lewis Wooltorton, Peter Brown, Roger Colbeck.
In 16, 15 we developed new constructions to certify properties of quantum systems using Bell-tests. In 16 we provide a method to stitch together bipartite Bell-inequalties to construct useful multipartite Bell-inequalities. We show that these new inequalities inherit certain self-testing prop erties of the original inequalities and we use this to produce protocols that achieve maximal device-independent randomness generation. In 15 we explore the complicated relationship between nonlocality and secret-key, showing that perfect secret key-rates can be achieved in device-independent quantum key distribution protocols with correlations that are arbitrarily close to classical. This involves developing a compact expression of a parameterized Bell-inequality that represents all possible self-tests of the maximally entangled state
7.1.3 Tight finite-size security proof for quantum key distribution protocols
Participants: Thomas Van Himbeeck, Peter Brown.
We have developed a new security proof framework for standard quantum key-distribution (QKD) protocols. The framework is: (i) generic, applying to all possible round based QKD protocols; (ii) tight, providing key-rates that are optimal for any given finite number of rounds up to leading order correction and (iii) computable, we develop convex optimization methods to compute the key-rates. This is achieved in part through the development of new entropic quantities that enable tight accounting of finite-size corrections. We expect the work to have significant impact on the future development of QKD protocols and security proofs.
7.2 Research axis 2: Multimode photonic systems for quantum information processing and communications
7.2.1 Quantum Coherent Communication and Digital Signal Processing
Participants: Romain Alléaume, Gjuillaume Ricard, Nicolas Fabre, Thomas Pousset, Yves Jaouën.
Building up on 21, we are performing a systematic analysis and model of excess noise in a quantum coherent communication channel, jointly operated with a classical coherent channel, taking into account the effect of digital signal processing. We are moreover validating our results with digital simulation along with experimental system demonstration. We are moreover studying how Kramers-Krönig coherent detection can be used in quantum communications.
7.2.2 Parallelizable Synthesis of Arbitrary Single-Qubit Gates with Linear Optics and Time-Frequency Encoding
Participants: Romain Alléaume, Guillaume Ricard, Antoine Henry, Nadia Belabas.
In 5, we propose novel methods for the exact synthesis of single-qubit unitaries with high success probability and gate fidelity, considering both time-bin and frequency-bin encodings. The proposed schemes are experimentally implementable with a spectral linear-optical quantum computation (S- LOQC) platform, composed of electro-optic phase modulators and phase-only programmable filters (pulse shapers). We further investigate the parallelization of arbitrary single-qubit gates over multiple qubits with a compact experimental setup, both for spectral and temporal encodings. Our analysis positions spectral S-LOQC as a promising platform to conduct massively parallel single qubit operations, with potential applications to quantum metrology and quantum tomography.
7.2.3 Limitations of GKP-LDPC concatenated codes
Participants: Robert König, Cambyse Rouze.
In 10, we established an analytic upper bound on the fault-tolerance threshold for concatenated GKP-stabilizer codes with local update recovery. Our bound applies to noise channels that are tensor products of one-mode beamsplitters with arbitrary environment states, capturing, in particular, photon loss occurring independently in each mode. It shows that for loss rates above a threshold given explicitly as a function of the locality of the recovery maps, encoded information is lost at an exponential rate.
7.3 Research axis 3: Mathematical foundations of quantum information
7.3.1 Higher-Order quantum computation
Participants: Augustin Vanrietvelde, Octave Mestoudjian.
We are developing fine-grained type systems for the certification of quantum computation architectures, in particular those involving quantum control (quantum versions of the "if" clause) and indefinite causal order (application of operations in a superposed order).
7.3.2 Causal models in quantum theory
Participants: Augustin Vanrietvelde, Pablo Arrighi, Octave Mestoudjian.
We are investigating the relationship (and in particular the potential equivalence) between the causal structure of quantum dynamics and their compositional structure. We are finishing a proof (to be published soon) that there is an equivalence between the two in the case of local dynamics over a 1D array of quantum systems, at any range.
7.3.3 Learning complex quantum states
Participants: Marco Fanizza, Niklas Galke, Josep Lumbreras, Cambyse Rouzé, Andreas Winter, Emilio Onorati, Daniel Stilck França, James D Watson, Tim Möbus, Andreas Bluhm, Matthia C Caro, Abert H Werner, Cambyse Rouzé.
In 12, 12, 13, 27, we have developed robust, sample and computationally efficient quantum algorithms for tomography and learning of states and noise on many-body discrete and continuous variables quantum systems, including thermal and ground states of spin and Bosonic Hamiltonians, finitely correlated states, and Pauli noise channels with unknown underlying local structure.
7.3.4 Complexity of quantum Gibbs states
Participants: Ivan Bardet, Ángela Capel, Li Gao, Angelo Lucia, David Peres-García, Cambyse Rouzé, Jan Kochanowski, Alvaro Alhambra, Paul Gondolf.
We have kept on working on the complexity of Gibbs sampling algorithms and its applications to the stability of quantum simulation and the characterization of self-correcting quantum memories 22, 23. In particular, we have extended our previous result on the rapid mixing of Gibbs samplers from 2-local to k-local interacting systems (the article is being finalized). In particular, we resolved an old open problem, namely whether the existence of a dissipative gap implies rapid mixing of the thermalization process. As regards to applications to quantum memories, our result implies that the entire class of quantum double models (including the 2D Toric code) reaches thermal equilibrium in logarithmic time, while the previous best thermalization time scaled linearly with the system size.
7.3.5 Improved quantum algorithm design from polynomial optimization
Participants: Thomas Van Himbeeck, Peter Brown.
A recently developed quantum algorithm known as the Quantum Singular Value Transform (QSVT) was shown to encompass the standard quantum algorithms, Shor/Grover etc., as special cases. Using the fact that the QSVT provides a correspondence between polynomials and certain families of quantum circuits, we develop methods to optimize these circuits (and hence the resulting algorithms) in terms of polynomial optimization and its resulting SDP relaxations. We also show to scale up these optimizations to large-scale circuits, demonstrating its usefulness at scales necessary for quantum advantage.
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
Orange Innvovation
Participants: Romain Alléaume, Yves Jaouën, Guillaume Ricard, Pierre-Enguerrand Verdier.
- CIFRE with Orange Innovation (Chatillon) on Discrete Variable Quantum Key Distribution and Time Multiplexing, PhD Student: Pierre-Enguerrand Verdier.
- CIFRE with Orange Innovation (Lannion) on Continous Variable Quantum Key Distribution and Wavelenght Division Multiplexing, PhD student: Marco Andersohn.
8.2 Grants with industry
Paris Region PhD Grant, collaboration with Quandela
Doctoral project of Guillaume Ricard, on Quatum Coherent Communications and Digital Signal Processing, Funded by Paris funded by Paris Region (region Ile-de France) in the context of the Paris Region PhD call, with a planned collaboration with Quandela on noise mitigation in optical coherent quantum communications.
9 Partnerships and cooperations
9.1 European initiatives
9.1.1 Horizon Europe
Quantum Secure Network Partnership
Participants: Romain Alléaume, Peter Brown, Tristan Nemoz, Francesco Mazzoncini, Guillaume Ricard, Thomas Van Himbeeck, Thomas Pousset, Nicolas Fabre, Yves Jaouën.
-
Partner Institutions:
The Quantum Secure Networks Partnership (QSNP) aims at creating a sustainable European ecosystem in quantum cryptography and communication. Its 42 partners are world-leading academic groups, research and technology organizations (RTOs), quantum component and system spin-offs, cybersecurity providers, integrators, and telecommunication operators. The Partnership thus has the expertise in all technology development phases, from new designs to field deployment, making it ideal to carry out the future Specific Grant Agreement (SGA) projects.
- ICFO-The Institute of Photonic Sciences, Spain, (Coordinator)
- Centre National de la Recherche Scientifique, France
- Institut Polytechnique de Paris, France
- Technical University of Denmark, Denmark
- Universidad Politécnica de Madrid, Spain
- Friedrich-Alexander University Erlangen-Nuremberg, Germany
- QuTech, at the Technical University Delft, Netherlands
- Università di Padova, Italy
- AIT Austrian Institute of Technology, Austria
- Palacky University Olomouc, Czech Rep.
- Instituto Superior Técnico, Portugal
- Universidade de Vigo, Spain
- Katholieke Universiteit Leuven, Belgium
- Universität Wien, Austria
- Université libre de Bruxelles, Belgium
- University of Warsaw, Poland
- University of Malta, Malta
- Institute of Communications and Computer Systems, Greece
- Universität Paderborn, Germany
- Inria Cosmiq team, France
- National and Kapodistrian University of Athens (NKUA),Greece
- Instituto De Telecomunicacoes, Portugal
- Politecnico di Bari, Italy,
- Fraunhofer Heinrich-Hertz-Institut, Germany
- Commissariat à l’Energie Atomique et aux Energies Alternatives, France
- Technische Universiteit Eindhoven, Netherland
- Interuniversity Microelectronics Centre, Belgium
- University College Cork, Ireland
- QuSide, Spain
- LuxQuanta, Spain
- Micro Photon Devices, Italy
- ThinkQuantum, Italy
- VPIphotonics GmbH, Germany
- Alea Quantum Technologies ApS, Denmark
- Q*Bird, Nertherlands
- Cryptonext Security, France
- Nokia Bell Labs, France
- Nextworks, Italy
- Deutsche Telekom, Germany
- Telefónica, Spain
- TIM S.p.A, Italy
- Orange SA,France
-
Contract ID:
HORIZON-CL4-2022-QUANTUM-04-SGA
-
Information on the Contract:
Special Grant Agreement in the context of a Federated Grant Agreement related to the Quantum Communications Pillar of the European Quantum Technology Flagship.
-
Duration:
March 2023 – August 2026
-
Description:
The Quantum Secure Networks Partnership (QSNP) is structured around three main Science and Technology (ST) pillars. The first two pillars, “Next Generation Protocols” and “Integration”, focus on frontier research and innovation led mostly by academic partners and RTOs. The third ST pillar “Use cases and Applications” aims at expanding the industrial and economic impact of QSN technologies and is mostly driven by companies. In order to achieve the specific objectives within each pillar and ensure that know-how transfer and synergy between them are coherent and effective, QSNP has established ST activities corresponding to the three main layers of the technology value chain, “Components and Systems”, “Networks” and “Cryptography and Security”. Future SGA projects will be able to efficiently rely on this framework, in such a way that the ultimate objective of developing quantum communication technology for critical European infrastructures, such as EuroQCI, and private information and communication market sectors, will be achieved. QSNP will contribute to achieving European sovereignty in quantum technology for cybersecurity. At the same time, it will generate significant economic benefits to the whole society, including training a new generation of scientists and engineers, and the creation of high-tech jobs in the rapidly growing quantum industry.
-
Role of Quriosity:
Quriosity has important participations on Quantum Coherent Communications System Design (WP2), Theory of Quantum Cryptography and in particular on Device-Independent Quantum Crypography (WP3), Hybrid Quantum-Computational Cryptography (WP4 and WP6).
- Romain Alléaume leads one of the 3 pillars of the project, devoted to Integration (at hardware, middleware and cryptographic applications levels) and is member of the Executive Board of QSNP
- Romain Alléaume leads WP6 on Quantum and Classical Cryptography Integration.
- Romain Alléaume leads IP Paris contribution to WP4 on Quantum Cryptographic Protocols beyond QKD.
- Peter Brown leads IP Paris contribution to WP3 on Device-Independent QKD and QRNG.
- Several teams from IP Paris participates to the project: Quriosity, GTO, C2 at Telecom Paris and GRACE at LIX/Ecole Polytechnique.
9.1.2 Digital Europe
FranceQCI
Participants: Romain Alléaume, Peter Brown, Tristan Nemoz, Francesco Mazzoncini, Guillaume Ricard, Thomas Van Himbeeck.
-
Partner Institutions:
- Orange SA,France (Coordinator)
- Institut-Mines-Telecom (IMT), France
- Airbus Defense and Space, France
- Thales SIX, France
- CryptoNext Security, France
- CNRS, France
- Thales Alenia Space, France
- CNRS Université Cote d'Azur, France
- Sorbonne Université, France
- WeLinQ SAS, France
- VeriQloud, France
- Direction des Services de la Navigation Aérienne, DSNA, France
-
Contract ID:
Project: 101091675 — FranceQCI — DIGITAL-2021-QCI-01
-
Information on the Contract:
Call DIGITAL-2021-QCI-01-DEPLOY-NATIONAL, Topic 1 from the Digital Europe Call on Quantum Communication Infrastructures.
-
Duration:
January 2023 – June 2025
-
Description:
The objective of the project is to test use cases of quantum communication technologies and to deploy advanced national quantum systems with existing communication networks in support of national QCI initiatives.
-
Role of Quriosity:
Quriosity, represented as IMT, contributes to network design and deployment (WP2), to security studies (WP3), and leads the activity on training (WP7) by coordinating the first executive education training offfer (in France) on quantum communication and cryptography, in collaboration with Sorbonne University and Orange Innovation.
9.1.3 Other european programs/initiatives
PETRUS
Participants: Romain Alléaume.
-
Partner Institutions:
- Deutsche Telekom
- Airbus Defense and Space, France
- Thales SIX, France
- Austrian Institute of Technology, AIT, Austria
-
Contract ID:
DIGITAL-2021-QCI-01 Digital European Program under grant agreement no. PETRUS 101091719.
-
Information on the Contract:
PETRUS is the Coordination and Support Action for the national Quantum Communication Infrastructures.
-
Duration:
July 2023 – December 2025
-
Description:
The European Quantum Communication Infrastructure (EuroQCI)is to be rolled out in the EU Member States over the coming years. PETRUS supports the Digital Europe Program projects that aim to form the basis for a European industrial ecosystem for secure quantum technologies. PETRUS brings together former consortium leaders of the most relevant studies and projects on EuroQCI, bundles their experience and expertise and includes top experts from industry and the academic quantum community.
-
Role of Quriosity:
Romain Alléaume acts as Scientific Expert for the project.
9.2 National initiatives
PEPR QCommTestbed
Participants: Romain Alléaume, Peter Brown, Nicolas Fabre, Yves Jaouën, Tristan Nemoz, Thomas Pousset, Thomas Van Himbeeck.
-
Partner Institutions:
- Institut-Mines-Telecom (IMT), France
- CNRS Université Cote d'Azur, France
- Sorbonne Université, France
- CEA Leti, France
- C2N, France
- Université Paris-Cité, France
-
Contract ID:
PC 4.3 « QCommTestbed » (Quantum communication testbeds)
-
Duration:
01/07/2022 – 30/06/2027
-
Description:
The objective of the QcommTestbed project is to lay the foundations for fiber optic and free-space quantum networks on a regional and longer-term national scale, making it possible to connect systems including quantum elements (transmitters and receivers, processors, sensors) via repeater nodes. The project also aims to make decisive advances in the TRL of quantum communication systems, and also in their security evaluation and testing, to pave the way for their wider adoption and ubiquituous deployment.
-
Role of Quriosity:
- Demonstration of ITS secure communication over a single fiber, based on joint CV-QKD and classical communication integration.
- Performance and Cost of Long-Term Secure Storage based on CV-QKD
- Vulnerability analysis of a QKD (VAN) system. Definition of an evaluation methodology (based on the Common Criteria.
- Experimental Demonstration of Mulimode Frequency-encoded Key Distribution in the QCT model
9.3 Regional initiatives
ParisRegionQCI
Participants: Romain Alléaume, Francesco Mazzoncini, Thomas Van Himbeeck.
-
Partner Institutions:
- Orange SA,France (Coordinator)
- LTCI, Telecom Paris, France
- Thales SIX, France
- Thales Research and Technology (TRT), France
- CryptoNext Security, France
- CNRS, France
- LIP6, Sorbonne Université, France
- VeriQloud, France
- NOKIA Bell Labs, France
- Kets Quantum, UK
- Laboratoire Charles Fabry, France
-
Information on the Contract:
Project funded as a SIRTEQ Synergy action, funded by Paris Region
-
Duration:
January 2021 – Dec 2023
-
Description:
The ParisRegionQCI project revolves around the development and operation of a fiber network quantum in Paris Region (Île-de-France ). The creation of such a network is envisaged as part of the project H2020 “OpenQKD”, which is a precursor of the “European Quantum Communication Infrastructure”, EuroQCI, planned as part of the next framework program of the European Commission, and which will include terrestrial and space segments.
-
Role of Quriosity:
Quriosity, as part of Telecom Paris has been to contributes to network design and deployment, and to lead the security study, with a focus on the security advantage that could (or could not) be achieved using QKD, in different cryptographic constructions aiming to ensure secure communication security services.
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
Member of the organizing committees
- Romain Alléaume member of the organization committee of the LTCI Research Day, Nov 24 2023.
- Romain Alléaume co-organized the Quantum Hardware Security Workshop at Edinburgh, with the Quantum Software Lab, 22-23 November 2023.
10.1.2 Scientific events: selection
Member of the conference program committees
- Romain Alléaume TPC of TPC IEEE ICC'23 - SAC-11 QCIT Track
- Cambyse Rouzé TPC of QIP 2024
Reviewer
- Romain Alléaume for TQC (subreviewer)
10.1.3 Journal
Reviewer - reviewing activities
- Romain Alléaume for Science Advances
10.1.4 Invited talks
- Peter Brown , Tight finite-size security proof of QKD, 5th edition of security of QKD workshop, IQC Waterloo, Canada. (September 2023).
- Peter Brown , On the computation of device-independent quantities, 5th edition of security of QKD workshop, IQC Waterloo, Canada. (September 2023).
- Peter Brown , Tight finite-size security proof of QKD, Workshop on Gaussian and non-Gaussian Quantum Correlations, Copenhagen Denmark (November 2023).
- Romain Alléaume , Quantum Secure Network Partnership Integration Pillar, CLP Days, ICFO, Barcelona (25 Mai 2023).
- Romain Alléaume , Slow Information, Workshop On Quantum Ecology, Leyzin Switzerland (July 2023).
10.1.5 Leadership within the scientific community
- Romain Alléaume is one of the 3 Pillar Leaders, WP6 Leader and a member of the Executive Board of the Quantum Secure Network Partnership Flagship Project.
10.1.6 Scientific expertise
- Romain Alléaume , Member of the Alliance Quantum Evaluation Committee, at NSERC, in charge of scientific evaluation of Canada Quantum Grants Applications (4 sessions per year).
- Romain Alléaume , Member of the Evaluation Committee attributing the Plan Quantique PHD Grants, for the Paris Centre for Quantum Technologies (Sorbonne University, March 14 2023).
- Romain Alléaume , Member of the Evaluation Committee for IP Paris PhD Track in Qauntum Science and Technology, February, 14 2023.
- Romain Alléaume , Member of the Evaluation Committee for the admission of Polytecniciens, at Telecom Paris (double degree)
- Romain Alléaume , Member of the recruitement committee for the position at Ecole Polytechnique, Professor Monge in Quantum Computing, May 17, 2023
- Romain Alléaume , Member of the recruitement committee for the Assistant/Associate Professor position in Quantum Computing and Quantum Information Procesing at Telecom Paris, May 9, 2023
10.1.7 Research administration
- Romain Alléaume , Member of Comité Directeur of the Network and Computer Science Departement of Telecom Paris (Infres), acting as Infres Research Delegate, (2023-)..
- Romain Alléaume , Deputy director of Laboratoire de Traitement and Communication de l'Information LTCI and member of LTCI board (bureau) (2023-).
- Romain Alléaume , Member of Conseil Scientifique du LTCI (2023-).
- Romain Alléaume , Member of Conseil du LTCI (2021-).
- Romain Alléaume , Member of IP Paris IDIA Department bureau, (2023-).
- Romain Alléaume , Member of the Committee in charge of supervising STEP2 program (ANR ExcellenceS program) funding allocation in Foundation of Computer Science (including Quantum Computer Science).
- Romain Alléaume is (2020–) an executive committee member of the Quantum center of Saclay. The center coordinates the French strategy for quantum technologies at the scale of Univ. Paris-Saclay and Institut Polytechnique de Paris.
10.2 Teaching - Supervision - Juries
All teaching durations are given in hetd = "heures équivalent TD".
10.2.1 Teaching
L3 courses, at Telecom Paris
-
Romain Alléaume
is teaching in PHY101: Introduction to Quantum Technologies. Courses: 9 hetd
- Peter Brown , Francesco Mazzoncini, Tristan Nemoz, Thomas Van Himbeeck, Programming a real quantum computer, 6+6+6+6 hetd, 9 students.
M1 courses at Telecom Paris
-
Peter Brown
, Continuous Optimization and Numerical Analysis,
-
Peter Brown
and Romain Alléaume
, Introduction to quantum information and quantum computing,
M2 courses in the Quantum Engineering Program at Telecom Paris, (in collaboration with ARTeQ, ENS Paris-Saclay)
- Romain Alléaume coordinates (2017-) the Quantum Engineering Program, a Access PhD Program (M2 level) on Quantum Maths and TCS, and Quantum Technologies, that is currently held in collaboration with ARTeQ (ENS Paris-Saclay) and M2 QDCS (Université Paris-Saclay).
-
Peter Brown
and Romain Alléaume
, Quantum information tutorials,
-
Peter Brown
and Romain Alléaume
, Quantum information and quantum cryptography, M2 QEng Telecom Paris and ARTeQ,
- Cambyse Rouzé has started a new Quantum Computing course for the students of QEng and ARTeQ.
- This course on the exploration of near-term quantum advantage delves into contemporary advancements in the theory of quantum computing and quantum information processing. It covers a spectrum of topics, ranging from demonstrating quantum advantage in sampling tasks with a specific focus on BosonSampling experiments, to exploring variational quantum algorithms tailored for solving constrained satisfaction problems and their interplay with adiabatic quantum algorithms. Additionally, participants were introduced to quantum state tomography, with the study of cutting-edge shadow tomography algorithms.
- Taught 16 hetd, for
Teaching in other contexts and programs
-
Romain Alléaume
taught a short course on Quantum Cryptography Theory in the M1 Quantum Technologies atCentrale-Supélec 4,5 hetd, to
- Peter Brown gave an Invited lecture at Padova QCOMMS summer school (May 2023) on Device-independent quantum key distribution.
- Thomas Van Himbeeck gave an Invited lecture at Padova QCOMMS summer school (May 2023) on Finite-size effects in quantum key distribution.
10.2.2 Supervision
PhD Supervisions
- Tristan Nemoz, Computational models in quantum cryptography (Romain Alléaume and Peter Brown ), (2022-)
- Tristan Le Roy Deloison, Device-independent Quantum Key Distribution (Omar Fawzi [QINFO] and Peter Brown ), (2023-)
- Guillaume Ricard, Quantum Coherent Communications and Digital Signal Processing, (Romain Alléaume and Yves Jaouën), (2021-)
- Francesco Mazzoncini, Communications quantiques multimodes et cryptographie hybride, (Romain Alléaume and Sylvain Gigan [ENS Paris]), (2020-).
- Pierre-Enguerrand Verdier, Cryptographie quantique à variables discrètes : caractérisation de systèmes, déploiement opérationnel sur réseaux télécom et applications, (Thomas Rivera [Orange] and Romain Alléaume ), (2022-).
- Thomas Pousset, Protocoles de communications quantiques en variables temps-fréquence, (Nicolas Fabre and Romain Alléaume ), (2023-).
- Octave Mestoudjian, La notion de sous-système en informatique quantique, (Pablo Arrighi (équipe Inria Quacs) and Augustin Vanrietvelde ), (2023-).
- Jan Kochanowski, Analytic and algorithmic approaches on strong data processing in complex quantum systems, (Omar Fawzi [QINFO] and Cambyse Rouzé ), (2023-)
Master, PhD Track and L3 Students supervisions
- Rola Saidi, Evaluating crosstalk on quantum computers, QEng PRIM M2 project, (Peter Brown ).
- Kriss Lady Stephanie Gutierrez Anco, Rényi intrinsic randomness, QEng PRIM M2 project, (Peter Brown ).
- Tristan Philippe, Ressource theory of quantum antecents to LWE, QEng PRIM M2 project, (Romain Alléaume ).
- Thomas Vinet, Distinguishing unitary gates using controlization, QEng PRIM M2 project, (Augustin Vanrietvelde )
- Idris Delsol, Quantum error correction using Cat Qubits, QEng PRIM M2 project, (Cambyse Rouzé)
- Ali Almasi, Positive but not completely positive maps, M1 PhD Track research project, (Peter Brown )
- Timothé Bramas, Programming a LDPC-based Error Correction stack for CV-QKD, ENSTA M1 research internship, (Romain Alléaume )
- Evdokia Gneusheva, Secret key-rates vs. entanglement, Polytechnique Bachelor L3 research internship, (Peter Brown )
10.2.3 Juries
PhD juries
(Apart from our own students PhD juries)
- Romain Alléaume , Rapporteur for the PhD Defense of Yao Ma, Quantum Hardware Security and Near-term Applications December 4 2023, Sorbonne University.
- Peter Brown , Examinator for the PhD Defense of Xavier Valcarce, Device independent certification: quantum resources and quantum key distribution, Université Paris Saclay, May 17 2023.
10.3 Popularization
10.3.1 Articles and contents
- Romain Alléaume , Peter Brown, Cambyse Rouzé contributed to the writing of a wide audience presentation article of Quriosity, for the Inria website.
- Romain Alléaume was interviewed by Isabelle Mauriac, for Telecom Paris Ideas, on the scaling of quantum advantage, leading to short video and a podcast .
10.3.2 Interventions
- Romain Alléaume gave a talk "Nouvelles Quantiques de Télécom Paris", and participated to an invited panel at the Prix des Technologlies Numériques, October 17, 2023.
- Romain Alléaume gave a presentation to a delegation from University of Hannover, on Quantum Research activites at Quriosity, on March 12, 2023.
- Romain Alléaume gave an invited talk, on Quriosity, at Telecom Paris Journées Partenaires Entreprises, on March 16, 2023;
- Romain Alléaume gave a talk on Quantum Computing to MEDEF Essonne, at ENS-Paris Saclay, on October 20, 2023.
11 Scientific production
11.1 Major publications
- 1 miscHybrid Quantum Cryptography from Communication Complexity.November 2023HAL
- 2 articleLimitations of variational quantum algorithms: a quantum optimal transport approach.PRX Quantum4January 2023, 010309HALDOI
- 3 miscDevice-independent quantum key distribution with arbitrarily small nonlocality.September 2023HAL
11.2 Publications of the year
International journals
- 4 articleCoarse Ricci curvature of quantum channels.Journal of Functional AnalysisJanuary 2024, 110336HALDOI
- 5 articleParallelizable Synthesis of Arbitrary Single-Qubit Gates with Linear Optics and Time-Frequency Encoding.Physical Review A1076June 2023, 062610HALDOIback to textback to text
- 6 articleQuantum Differential Privacy: An Information Theory Perspective.IEEE Transactions on Information Theory699September 2023, 5771-5787HALDOI
- 7 articleLimitations of variational quantum algorithms: a quantum optimal transport approach.PRX Quantum4January 2023, 010309HALDOI
Reports & preprints
- 8 miscInformation-theoretic generalization bounds for learning from quantum data.November 2023HAL
- 9 miscLearning finitely correlated states: stability of the spectral reconstruction.2023HAL
- 10 miscLimitations of local update recovery in stabilizer-GKP codes: a quantum optimal transport approach.2023HALDOIback to text
- 11 miscHybrid Quantum Cryptography from Communication Complexity.November 2023HALback to text
- 12 miscProvably Efficient Learning of Phases of Matter via Dissipative Evolutions.November 2023HALDOIback to textback to text
- 13 miscEfficient learning of the structure and parameters of local Pauli noise channels.2023HALDOIback to text
- 14 miscSemidefinite programming relaxations for quantum correlations.2023HAL
- 15 miscDevice-independent quantum key distribution with arbitrarily small nonlocality.September 2023HALback to textback to text
- 16 miscExpanding bipartite Bell inequalities for maximum multi-partite randomness.August 2023HALback to textback to text
11.3 Cited publications
- 17 inproceedingsThe computational complexity of linear optics.Proceedings of the forty-third annual ACM symposium on Theory of computing2011, 333--342back to text
- 18 articleComputational advantage from quantum-controlled ordering of gates.Physical review letters113252014, 250402DOIback to text
- 19 articleQuantum circuits cannot control unknown operations.New Journal of Physics1692014, 093026DOIback to text
- 20 articlePractical device-independent quantum cryptography via entropy accumulation.Nature communications912018, 459back to text
- 21 articleSymbiotic joint operation of quantum and classical coherent communications.arXiv preprint arXiv:2202.069422022back to textback to text
- 22 articleEntropy decay for Davies semigroups of a one dimensional quantum lattice.arXiv preprint arXiv:2112.006012021back to textback to textback to text
- 23 articleRapid thermalization of spin chain commuting Hamiltonians.arXiv preprint arXiv:2112.005932021back to textback to text
- 24 articleApproximate Tensorization of the Relative Entropy for Noncommuting Conditional Expectations.Annales Henri Poincaré2312021, 101--140back to text
- 25 articleGroup Transference Techniques for the Estimation of the Decoherence Times and Capacities of Quantum Markov Semigroups.IEEE Transactions on Information Theory6752021, 2878-2909DOIback to text
- 26 articleQuantum causal models.DOIback to text
- 27 articleClassical shadow tomography for continuous variables quantum systems.arXiv preprint arXiv:2211.075782022back to text
- 28 articleComputing conditional entropies for quantum correlations.Nature communications1212021, 1--12back to textback to text
- 29 articleDevice-independent lower bounds on the conditional von Neumann entropy.arXiv preprint arXiv:2106.136922021back to textback to text
- 30 articleMultimode entanglement in reconfigurable graph states using optical frequency combs.Nature communications812017, 1--9back to text
- 31 articleThe modified logarithmic Sobolev inequality for quantum spin systems: classical and commuting nearest neighbour interactions, (QIP talk, presented at ICMP).arXiv:2009.118172020back to textback to textback to text
- 32 inproceedingsOptimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expansion.Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of ComputingSTOC 2021New York, NY, USAVirtual, ItalyAssociation for Computing Machinery2021, 1537?1550URL: https://doi.org/10.1145/3406325.3451035DOIback to text
- 33 articleStrong Converse Bounds in Quantum Network Information Theory.IEEE Transactions on Information Theory6742021, 2269-2292DOIback to text
- 34 articleQuantum computations without definite causal structure.Physical Review A8822013, 022318DOIback to text
- 35 articleEntropy accumulation.Communications in Mathematical Physics3792020, 1--47back to text
- 36 articleThe Entropy Zoo.https://phfaist.com/entropyzooback to text
- 37 articleSum-of-Squares proofs of logarithmic Sobolev inequalities on finite Markov chains.arXiv preprint arXiv:2101.049882021back to text
- 38 articleComplete Entropic Inequalities for Quantum Markov Chains.Archive for Rational Mechanics and Analysis2451may 2022, 183--238URL: https://doi.org/10.1007%2Fs00205-022-01785-1DOIback to text
- 39 inproceedingsThe Entropy Photon-Number Inequality and its consequences.2008 Information Theory and Applications Workshop2008, 128-130DOIback to text
- 40 articleFidelity Bounds for Device-Independent Advantage Distillation.arXiv preprint arXiv:2105.032132021back to text
- 41 articlePredicting many properties of a quantum system from very few measurements.Nature Physics1610June 2020, 1050--1057URL: https://doi.org/10.1038/s41567-020-0932-7DOIback to text
- 42 articleProvably efficient machine learning for quantum many-body problems.arXiv preprint arXiv:2106.126272021back to text
- 43 articleFundamentals of Coherent Optical Fiber Communications.in Journal of Lightwave Technology vol. 34, N°12016back to text
- 44 articleA categorical semantics for causal structure.Logical Methods in Computer ScienceVolume 15, Issue 32019DOIback to text
- 45 articleRobust Bell inequalities from communication complexity.Quantum22018, 72back to text
- 46 articleCausal and compositional structure of unitary transformations.Quantum52021, 511DOIback to text
- 47 articleDevice-independent quantum key distribution.arXiv preprint arXiv:2109.146002021back to text
- 48 inproceedingsQuantum one-way communication can be exponentially stronger than classical communication.Proceedings of the forty-third annual ACM symposium on Theory of computing2011, 31--40back to text
- 49 articleSelf-testing quantum random-number generator based on an energy bound.Physical Review A10062019, 062338back to text
- 50 articleComputing secure key rates for quantum cryptography with untrusted devices.npj Quantum Information712021, 1--6back to text
- 51 articleImproved DIQKD protocols with finite-size analysis.arXiv preprint arXiv:2012.087142020back to text
- 52 articleSemi-device-independent framework based on restricted distrust in prepare-and-measure experiments.Physical Review Letters126212021, 210503back to text
- 53 articleRouted quantum circuits.Quantum5Jul 2021, 503DOIback to text
- 54 articleConsistent circuits for indefinite causal order.6 2022back to text
- 55 articleThe lesson of causal discovery algorithms for quantum correlations: causal explanations of Bell-inequality violations require fine-tuning.New Journal of Physics173March 2015, 033002URL: http://dx.doi.org/10.1088/1367-2630/17/3/033002DOIback to text
- 56 articleEfficient randomness certification by quantum probability estimation.Physical review research212020, 013016back to text
- 57 articleExperimental device-independent quantum key distribution between distant users.arXiv preprint arXiv:2110.005752021back to textback to text

