2023Activity reportProject-TeamRANDOPT
RNSR: 201622221N- Research center Inria Saclay Centre at Institut Polytechnique de Paris
- Team name: Randomized Optimization
- In collaboration with:Centre de Mathématiques Appliquées (CMAP)
- Domain:Applied Mathematics, Computation and Simulation
- Theme:Optimization, machine learning and statistical methods
Keywords
Computer Science and Digital Science
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.6. Optimization
- A8.2. Optimization
- A8.9. Performance evaluation
Other Research Topics and Application Domains
- B4.3. Renewable energy production
- B5.2. Design and manufacturing
1 Team members, visitors, external collaborators
Research Scientists
- Anne Auger [Team leader, INRIA, Senior Researcher, HDR]
- Dimo Brockhoff [INRIA, Researcher]
- Nikolaus Hansen [INRIA, Senior Researcher, HDR]
PhD Students
- Mohamed Gharafi [INRIA]
- Armand Gissler [Ecole Polytechnique (CMAP)]
- Tristan Marty [THALES]
Technical Staff
- Shan-Conrad Wolf [INRIA, Engineer, from Feb 2023 until May 2023]
Interns and Apprentices
- Zeidan Braik [INRIA, Intern, from May 2023 until Sep 2023]
- Lorenzo Consoli [INRIA, Intern, from Aug 2023]
- Oskar Lucien Girardin [INRIA, Intern, from Sep 2023]
Administrative Assistant
- Julienne Moukalou [INRIA]
2 Overall objectives
2.1 Scientific Context
Critical problems of the 21st century like the search for highly energy efficient or even carbon-neutral, and cost-efficient systems, or the design of new molecules against extensively drug-resistant bacteria crucially rely on the resolution of challenging numerical optimization problems. Such problems typically depend on noisy experimental data or involve complex numerical simulations where derivatives are not useful or not available and the function is considered as a black-box.
Many of those optimization problems are in essence multiobjective—one needs to optimize simultaneously several conflicting objectives like minimizing the cost of an energy network and maximizing its reliability—and most of the challenging black-box problems are non-convex and non-smooth and they combine difficulties related to ill-conditioning, non-separability, and ruggedness (a term that characterizes functions that can be non-smooth but also noisy or multi-modal). Additionally, the objective function can be expensive to evaluate, that is, one function evaluation can take several minutes to hours (it can involve for instance a CFD simulation).
In this context, the use of randomness combined with proper adaptive mechanisms that notably satisfy certain invariance properties (affine invariance, invariance to monotonic transformations) has proven to be one key component for the design of robust global numerical optimization algorithms 53, 38.
The field of adaptive stochastic optimization algorithms has witnessed some important progress over the past 15 years. On the one hand, subdomains like medium-scale unconstrained optimization may be considered as “solved” (particularly, the CMA-ES algorithm, an instance of Evolution Strategy (ES) algorithms, stands out as state-of-the-art method) and considerably better standards have been established in the way benchmarking and experimentation are performed. On the other hand, multiobjective population-based stochastic algorithms became the method of choice to address multiobjective problems when a set of some best possible compromises is sought after. In all cases, the resulting algorithms have been naturally transferred to industry (the CMA-ES algorithm is now regularly used in companies such as Bosch, Total, ALSTOM, ...) or to other academic domains where difficult problems need to be solved such as physics, biology 57, geoscience 46, or robotics 49).
ES algorithms also attracted quite some attention in Machine Learning with the OpenAI article Evolution Strategies as a Scalable Alternative to Reinforcement Learning. It is shown that the training time for difficult reinforcement learning benchmarks could be reduced from 1 day (with standard RL approaches) to 1 hour using ES 55.1 Already ten years ago, another impressive application of CMA-ES, how “Computer Sim Teaches Itself To Walk Upright” (published at the conference SIGGRAPH Asia 2013) was presented in the press in the UK.
Several of these important advances around adaptive stochastic optimization algorithms rely to a great extent on works initiated or achieved by the founding members of RandOpt, particularly related to the CMA-ES algorithm and to the Comparing Continuous Optimizer (COCO) benchmarking platform.
Yet, the field of adaptive stochastic algorithms for black-box optimization is relatively young compared to the “classical optimization” field that includes convex and gradient-based optimization. For instance, the state-of-the art algorithms for unconstrained gradient based optimization like quasi-Newton methods (e.g. the BFGS method) date from the 1970s 37 while the stochastic derivative-free counterpart, CMA-ES dates from the early 2000s 39. Consequently, in some subdomains with important practical demands, not even the most fundamental and basic questions are answered:
- This is the case of constrained optimization where one needs to find a solution minimizing a numerical function while respecting a number of constraints typically formulated as for . Only somewhat recently, the fundamental requirement of linear convergence2, as in the unconstrained case, has been clearly stated 28.
- In multiobjective optimization, most of the research so far has been focusing on how to select candidate solutions from one iteration to the next one. The difficult question of how to generate effectively new solutions is not yet answered in a proper way and we know today that simply applying operators from single-objective optimization may not be effective with the current best selection strategies. As a comparison, in the single-objective case, the question of selection of candidate solutions was already solved in the 1980s and 15 more years were needed to solve the trickier question of an effective adaptive strategy to generate new solutions.
- With the current demand to solve larger and larger optimization problems (e.g. in the domain of deep learning), optimization algorithms that scale linearly (in terms of internal complexity, memory and number of function evaluations to reach an -ball around the optimum) with the problem dimension are nowadays in increasing demand. Not long ago, first proposals of how to reduce the quadratic scaling of CMA-ES have been made without a clear view of what can be achieved in the best case in practice. These later variants apply to optimization problems with thousands of variables. The question of designing randomized algorithms capable to handle problems with one or two orders of magnitude more variables effectively and efficiently is still largely open.
- For expensive optimization, standard methods are so called Bayesian optimization (BO) algorithms often based on Gaussian processes. Commonly used examples of BO algorithms are EGO 43, SMAC 41, Spearmint 56, or TPE 31 which are implemented in different libraries. Yet, our experience with a popular method like EGO is that many important aspects to come up with a good implementation rely on insider knowledge and are not standard across implementations. Two EGO implementations can differ for example in how they perform the initial design, which bandwidth for the Gaussian kernel is used, or which strategy is taken to optimize the expected improvement.
Additionally, the development of stochastic adaptive methods for black-box optimization has been mainly driven by heuristics and practice—rather than a general theoretical framework—validated by intensive computational simulations. Undoubtedly, this has been an asset as the scope of possibilities for design was not restricted by mathematical frameworks for proving convergence. In effect, powerful stochastic adaptive algorithms for unconstrained optimization like the CMA-ES algorithm emerged from this approach. At the same time, naturally, theory strongly lags behind practice. For instance, the striking performances of CMA-ES empirically observed contrast with how little is theoretically proven on the method. This situation is clearly not satisfactory. On the one hand, theory generally lifts performance assessment from an empirical level to a conceptual one, rendering results independent from the problem instances where they have been obtained. On the other hand, theory typically provides insights that change perspectives on some algorithm components. Also theoretical guarantees generally increase the trust in the reliability of a method and facilitate the task to make it accepted by wider communities.
Finally, as discussed above, the development of novel black-box algorithms strongly relies on scientific experimentation, and it is quite difficult to conduct proper and meaningful experimental analysis. This is well known for more than two decades now and summarized in this quote from Johnson in 1996
“the field of experimental analysis is fraught with pitfalls. In many ways, the implementation of an algorithm is the easy part. The hard part is successfully using that implementation to produce meaningful and valuable (and publishable!) research results.” 42
Since then, quite some progress has been made to set better standards in conducting scientific experiments and benchmarking. Yet, some domains still suffer from poor benchmarking standards and from the generic problem of the lack of reproducibility of results. For instance, in multiobjective optimization, it is (still) not rare to see comparisons between algorithms made by solely visually inspecting Pareto fronts after a fixed budget. In Bayesian optimization, good performance seems often to be due to insider knowledge not always well described in papers.
In the context of black-box numerical optimization previously described, the scientific positioning of the RandOpt ream is at the intersection between theory, algorithm design, and applications. Our vision is that the field of stochastic black-box optimization should reach the same level of maturity than gradient-based convex mathematical optimization. This entails major algorithmic developments for constrained, multiobjective and large-scale black-box optimization and major theoretical developments for analyzing current methods including the state-of-the-art CMA-ES.
The specificity in black-box optimization is that methods are intended to solve problems characterized by "non-properties"—non-linear, non-convex, non-smooth, non-Lipschitz. This contrasts with gradient-based optimization and poses on the one hand some challenges when developing theoretical frameworks but also makes it compulsory to complement theory with empirical investigations.
On the practical side, our ultimate goal is to provide software that is suitable for researchers and industry that need to solve practical optimization problems. We see theory also as a means for this end (rather than only an end in itself) and we also firmly belief that parameter tuning is part of the algorithm designer's task.
This shapes, on the one hand, four main scientific objectives for our team:
- develop novel theoretical frameworks for guiding (a) the design of novel black-box methods and (b) their analysis, allowing to
- provide proofs of key features of stochastic adaptive algorithms including the state-of-the-art method CMA-ES: linear convergence and learning of second order information.
- develop stochastic numerical black-box algorithms following a principled design in domains with a strong practical need for much better methods namely constrained, multiobjective, large-scale and expensive optimization. Implement the methods such that they are easy to use. And finally, to
- set new standards in scientific experimentation, performance assessment and benchmarking both for optimization on continuous or combinatorial search spaces. This should allow in particular to advance the state of reproducibility of results of scientific papers in optimization.
On the other hand, the above motivates our objectives with respect to dissemination and transfer:
- develop software packages that people can directly use to solve their problems. This means having carefully thought out interfaces, generically applicable setting of parameters and termination conditions, proper treatment of numerical errors, catching properly various exceptions, etc.;
- have direct collaborations with industrials;
- publish our results both in applied mathematics and computer science bridging the gap between very often disjoint communities.
3 Research program
The lines of research we intend to pursue is organized along four axes namely developing novel theoretical framework, developing novel algorithms, setting novel standards in scientific experimentation and benchmarking and applications.
3.1 Developing Novel Theoretical Frameworks for Analyzing and Designing Adaptive Stochastic Algorithms
Stochastic black-box algorithms typically optimize non-convex, non-smooth functions. This is possible because the algorithms rely on weak mathematical properties of the underlying functions: the algorithms do not use the derivatives—hence the function does not need to be differentiable—and, additionally, often do not use the exact function value but instead how the objective function ranks candidate solutions (such methods are sometimes called function-value-free). (To illustrate a comparison-based update, consider an algorithm that samples (with an even integer) candidate solutions from a multivariate normal distribution. Let in denote those candidate solutions at a given iteration. The solutions are evaluated on the function to be minimized and ranked from the best to the worse:
In the previous equation denotes the index of the sampled solution associated to the -th best solution. The new mean of the Gaussian vector from which new solutions will be sampled at the next iteration can be updated as
The previous update moves the mean towards the best solutions. Yet the update is only based on the ranking of the candidate solutions such that the update is the same if is optimized or where is strictly increasing. Consequently, such algorithms are invariant with respect to strictly increasing transformations of the objective function. This entails that they are robust and their performances generalize well.)
Additionally, adaptive stochastic optimization algorithms typically have a complex state space which encodes the parameters of a probability distribution (e.g. mean and covariance matrix of a Gaussian vector) and other state vectors. This state-space is a manifold. While the algorithms are Markov chains, the complexity of the state-space makes that standard Markov chain theory tools do not directly apply. The same holds with tools stemming from stochastic approximation theory or Ordinary Differential Equation (ODE) theory where it is usually assumed that the underlying ODE (obtained by proper averaging and limit for learning rate to zero) has its critical points inside the search space. In contrast, in the cases we are interested in, the critical points of the ODEs are at the boundary of the domain.
Last, since we aim at developing theory that on the one hand allows to analyze the main properties of state-of-the-art methods and on the other hand is useful for algorithm design, we need to be careful not to use simplifications that would allow a proof to be done but would not capture the important properties of the algorithms. With that respect one tricky point is to develop theory that accounts for invariance properties.
To face those specific challenges, we need to develop novel theoretical frameworks exploiting invariance properties and accounting for peculiar state-spaces. Those frameworks should allow researchers to analyze one of the core properties of adaptive stochastic methods, namely linear convergence on the widest possible class of functions.
We are planning to approach the question of linear convergence from three different complementary angles, using three different frameworks:
- the Markov chain framework where the convergence derives from the analysis of the stability of a normalized Markov chain existing on scaling-invariant functions for translation and scale-invariant algorithms 30. This framework allows for a fine analysis where the exact convergence rate can be given as an implicit function of the invariant measure of the normalized Markov chain. Yet it requires the objective function to be scaling-invariant. The stability analysis can be particularly tricky as the Markov chain that needs to be studied writes as where are independent identically distributed and is typically discontinuous because the algorithms studied are comparison-based. This implies that practical tools for analyzing a standard property like irreducibility, that rely on investigating the stability of underlying deterministic control models 50, cannot be used. Additionally, the construction of a drift to prove ergodicity is particularly delicate when the state space includes a (normalized) covariance matrix as it is the case for analyzing the CMA-ES algorithm.
- The stochastic approximation or ODE framework. Those are standard techniques to prove the convergence of stochastic algorithms when an algorithm can be expressed as a stochastic approximation of the solution of a mean field ODE 33, 32, 47. What is specific and induces difficulties for the algorithms we aim at analyzing is the non-standard state-space since the ODE variables correspond to the state-variables of the algorithm (e.g. for step-size adaptive algorithms, where denotes the set of positive definite matrices if a covariance matrix is additionally adapted). Consequently, the ODE can have many critical points at the boundary of its definition domain (e.g. all points corresponding to are critical points of the ODE) which is not typical. Also we aim at proving linear convergence, for that it is crucial that the learning rate does not decrease to zero which is non-standard in ODE method.
- The direct framework where we construct a global Lyapunov function for the original algorithm from which we deduce bounds on the hitting time to reach an -ball of the optimum. For this framework as for the ODE framework, we expect that the class of functions where we can prove linear convergence are composite of where is differentiable and is strictly increasing and that we can show convergence to a local minimum.
We expect those frameworks to be complementary in the sense that the assumptions required are different. Typically, the ODE framework should allow for proofs under the assumptions that learning rates are small enough while it is not needed for the Markov chain framework. Hence this latter framework captures better the real dynamics of the algorithm, yet under the assumption of scaling-invariance of the objective functions. Also, we expect some overlap in terms of function classes that can be studied by the different frameworks (typically convex-quadratic functions should be encompassed in the three frameworks). By studying the different frameworks in parallel, we expect to gain synergies and possibly understand what is the most promising approach for solving the holy grail question of the linear convergence of CMA-ES. We foresee for instance that similar approaches like the use of Foster-Lyapunov drift conditions are needed in all the frameworks and that intuition can be gained on how to establish the conditions from one framework to another one.
3.2 Algorithmic developments
We are planning on developing algorithms in the subdomains with strong practical demand for better methods of constrained, multiobjective, large-scale and expensive optimization.
Many of the algorithm developments, we propose, rely on the CMA-ES method. While this seems to restrict our possibilities, we want to emphasize that CMA-ES became a family of methods over the years that nowadays include various techniques and developments from the literature to handle non-standard optimization problems (noisy, large-scale, ...). The core idea of all CMA-ES variants—namely the mechanism to adapt a Gaussian distribution—has furthermore been shown to derive naturally from first principles with only minimal assumptions in the context of derivative-free black-box stochastic optimization 53, 38. This is a strong justification for relying on the CMA-ES premises while new developments naturally include new techniques typically borrowed from other fields. While CMA-ES is now a full family of methods, for visibility reasons, we continue to refer often to “the CMA-ES algorithm”.
3.2.1 Constrained optimization
Many (real-world) optimization problems have constraints related to technical feasibility, cost, etc. Constraints are classically handled in the black-box setting either via rejection of solutions violating the constraints—which can be quite costly and even lead to quasi-infinite loops—or by penalization with respect to the distance to the feasible domain (if this information can be extracted) or with respect to the constraint function value 35. However, the penalization coefficient is a sensitive parameter that needs to be adapted in order to achieve a robust and general method 36. Yet, the question of how to handle properly constraints is largely unsolved. Previous constraints handling for CMA-ES were ad-hoc techniques driven by many heuristics 36. Also, only somewhat recently it was pointed out that linear convergence properties should be preserved when addressing constraint problems 28.
Promising approaches though, rely on using augmented Lagrangians 28, 29. The augmented Lagrangian, here, is the objective function optimized by the algorithm. Yet, it depends on coefficients that are adapted online. The adaptation of those coefficients is the difficult part: the algorithm should be stable and the adaptation efficient. We believe that the theoretical frameworks developed (particularly the Markov chain framework) will be useful to understand how to design the adaptation mechanisms. Additionally, the question of invariance will also be at the core of the design of the methods: augmented Lagrangian approaches break the invariance to monotonic transformation of the objective functions, yet understanding the maximal invariance that can be achieved seems to be an important step towards understanding what adaptation rules should satisfy.
3.2.2 Large-scale Optimization
In the large-scale setting, we are interested to optimize problems with the order of to variables. For one to two orders of magnitude more variables, we will talk about a “very large-scale” setting.
In this context, algorithms with a quadratic scaling (internal and in terms of number of function evaluations needed to optimize the problem) cannot be afforded. In CMA-ES-type algorithms, we typically need to restrict the model of the covariance matrix to have only a linear number of parameters to learn such that the algorithms scale linearly in terms of internal complexity, memory and number of function evaluations to solve the problem. The main challenge is thus to have rich enough models for which we can efficiently design proper adaptation mechanisms. Some first large-scale variants of CMA-ES have been derived. They include the online adaptation of the complexity of the model 27, 26. Yet, the type of Hessian matrices they can learn is restricted and not fully satisfactory. Different restricted families of distributions are conceivable and it is an open question which can be effectively learned and which are the most promising in practice.
Another direction, we want to pursue, is exploring the use of large-scale variants of CMA-ES to solve reinforcement learning problems 55.
Last, we are interested to investigate the very-large-scale setting. One approach consists in doing optimization in subspaces. This entails the efficient identification of relevant spaces and the restriction of the optimization to those subspaces.
3.2.3 Multiobjective Optimization
Multiobjective optimization, i.e., the simultaneous optimization of multiple objective functions, differs from single-objective optimization in particular in its optimization goal. Instead of aiming at converging to the solution with the best possible function value, in multiobjective optimization, a set of solutions 3 is sought. This set, called Pareto-set, contains all trade-off solutions in the sense of Pareto-optimality—no solution exists that is better in all objectives than a Pareto-optimal one. Because converging towards a set differs from converging to a single solution, it is no surprise that we might lose many good convergence properties if we directly apply search operators from single-objective methods. However, this is what has typically been done so far in the literature. Indeed, most of the research in stochastic algorithms for multiobjective optimization focused instead on the so called selection part, that decides which solutions should be kept during the optimization—a question that can be considered as solved for many years in the case of single-objective stochastic adaptive methods.
We therefore aim at rethinking search operators and adaptive mechanisms to improve existing methods. We expect that we can obtain orders of magnitude better convergence rates for certain problem types if we choose the right search operators. We typically see two angles of attack: On the one hand, we will study methods based on scalarizing functions that transform the multiobjective problem into a set of single-objective problems. Those single-objective problems can then be solved with state-of-the-art single-objective algorithms. Classical methods for multiobjective optimization fall into this category, but they all solve multiple single-objective problems subsequently (from scratch) instead of dynamically changing the scalarizing function during the search. On the other hand, we will improve on currently available population-based methods such as the first multiobjective versions of the CMA-ES. Here, research is needed on an even more fundamental level such as trying to understand success probabilities observed during an optimization run or how we can introduce non-elitist selection (the state of the art in single-objective stochastic adaptive algorithms) to increase robustness regarding noisy evaluations or multi-modality. The challenge here, compared to single-objective algorithms, is that the quality of a solution is not anymore independent from other sampled solutions, but can potentially depend on all known solutions (in the case of three or more objective functions), resulting in a more noisy evaluation as the relatively simple function-value-based ranking within single-objective optimizers.
3.2.4 Expensive Optimization
In the so-called expensive optimization scenario, a single function evaluation might take several minutes or even hours in a practical setting. Hence, the available budget in terms of number of function evaluation calls to find a solution is very limited in practice. To tackle such expensive optimization problems, it is needed to exploit the first few function evaluations in the best way. To this end, typical methods couple the learning of a surrogate (or meta-model) of the expensive objective function with traditional optimization algorithms.
In the context of expensive optimization and CMA-ES, which usually shows its full potential when the number of variables is not too small (say larger than 3) and if the number of available function evaluations is about or larger, several research directions emerge. The two main possibilities to integrate meta-models into the search with CMA-ES type algorithms are (i) the successive injection of the minimum of a learned meta-model at each time step into the learning of CMA-ES's covariance matrix and (ii) the use of a meta-model to predict the internal ranking of solutions. While for the latter, first results exist, the former idea is entirely unexplored for now. In both cases, a fundamental question is which type of meta-model (linear, quadratic, Gaussian Process, ...) is the best choice for a given number of function evaluations (as low as one or two function evaluations) and at which time the type of the meta-model shall be switched.
3.3 Setting novel standards in scientific experimentation and benchmarking
Numerical experimentation is needed as a complement to theory to test novel ideas, hypotheses, the stability of an algorithm, and/or to obtain quantitative estimates. Optimally, theory and experimentation go hand in hand, jointly guiding the understanding of the mechanisms underlying optimization algorithms. Though performing numerical experimentation on optimization algorithms is crucial and a common task, it is non-trivial and easy to fall in (common) pitfalls as stated by J. N. Hooker in his seminal paper 40.
In the RandOpt team we aim at raising the standards for both scientific experimentation and benchmarking.
On the experimentation aspect, we are convinced that there is common ground over how scientific experimentation should be done across many (sub-)domains of optimization, in particular with respect to the visualization of results, testing extreme scenarios (parameter settings, initial conditions, etc.), how to conduct understandable and small experiments, how to account for invariance properties, performing scaling up experiments and so forth. We therefore want to formalize and generalize these ideas in order to make them known to the entire optimization community with the final aim that they become standards for experimental research.
Extensive numerical benchmarking, on the other hand, is a compulsory task for evaluating and comparing the performance of algorithms. It puts algorithms to a standardized test and allows to make recommendations which algorithms should be used preferably in practice. To ease this part of optimization research, we have been developing the Comparing Continuous Optimizers platform (COCO) since 2007 which allows to automatize the tedious task of benchmarking. It is a game changer in the sense that the freed time can now be spent on the scientific part of algorithm design (instead of implementing the experiments, visualization, etc.) and it opened novel perspectives in algorithm testing. COCO implements a thorough, well-documented methodology that is based on the above mentioned general principles for scientific experimentation.
Also due to the freely available data from 350+ algorithms benchmarked with the platform, COCO became a quasi-standard for single-objective, noiseless optimization benchmarking. It is therefore natural to extend the reach of COCO towards other subdomains (particularly constrained optimization, many-objective optimization) which can benefit greatly from an automated benchmarking methodology and standardized tests without (much) effort. This entails particularly the design of novel test suites and rethinking the methodology for measuring performance and more generally evaluating the algorithms. Particularly challenging is the design of scalable non-trivial testbeds for constrained optimization where one can still control where the solutions lies. Other optimization problem types, we are targeting are expensive problems (and the Bayesian optimization community in particular), optimization problems in machine learning (for example parameter tuning in reinforcement learning), and the collection of real-world problems from industry.
Another aspect of our future research on benchmarking is to investigate the large amounts of benchmarking data, we collected with COCO during the years. Extracting information about the influence of algorithms on the best performing portfolio, clustering algorithms of similar performance, or the automated detection of anomalies in terms of good/bad behavior of algorithms on a subset of the functions or dimensions are some of the ideas here.
Last, we want to expand the focus of COCO from automatized (large) benchmarking experiments towards everyday experimentation, for example by allowing the user to visually investigate algorithm internals on the fly or by simplifying the set up of algorithm parameter influence studies.
4 Application domains
Applications of black-box algorithms occur in various domains. Industry but also researchers in other academic domains have a great need to apply black-box algorithms on a daily basis. Generally, we do not target a specific application domain and are interested in black-box applications stemming from various origins. This is to us intrinsic to the nature of the methods we develop that are general purpose algorithms. Hence our strategy with respect to applications can be considered as opportunistic and our main selection criteria when approached by colleagues who want to develop a collaboration around an application is whether we find the application interesting and valuable: that means the application brings new challenges and/or gives us the opportunity to work on topics we already intended to work on, and it brings, in our judgement, an advancement to society in the application domain.
The concrete applications related to industrial collaborations we are currently dealing with are:
- With Thales for the theses of Konstantinos Varelas, Paul Dufossé, and Tristan Marty (DGA-CIFRE theses). They investigate more specifically the development of large-scale variants of CMA-ES, constrained-handling for CMA-ES, and the handling of discrete variables within CMA-ES respectively.
- With Storengy, a subsidiary of the ENGIE group, specialized in gas storage for the theses of Cheikh Touré and Mohamed Gharafi. Different multiobjective applications are considered in this context but the primary motivation of Storengy is to get at their disposal a better multiobjective variant of CMA-ES which is the main objective of the developments within the theses.
5 Social and environmental responsibility
5.1 Footprint of research activities
We are concerned about CO footprint and discourage oversea conferences when far away. Since the situation with respect to Covid went back to normal with respect to travelling, we have been dedicated to travel less than in the past and attend some conferences online.
5.2 Impact of research results
We develop general purpose optimization methods that apply in difficult optimization contexts where little is required on the function to be optimized. Application domains include optimization and design of renewable systems and climate change.
Our main method CMA-ES is transferred and widely used. The code stemming from the team is frequently downloaded (see Section 6). Among the usage of our method and our code, we find naturally problems in the domain of energy to capture carbon dioxide 51, 48, 52, solar energy 44, 45, or wind-thermal power systems 54.
Those publications witness the impact of our research results with respect to research questions and engineering design related to climate change and renewable energy.
6 New software, platforms, open data
The RandOpt team maintains and further develops the two software libraries, CMA-ES and COCO.
As an indicator of the impact of the libraries, Figure 1 shows weekly downloads (without mirrors) from the Python Package Index (PyPI) since July 2021 of Python software packages developed by the RandOpt team and of the cmaes package developed by Masashi Shibata (the package is directly derived from RandOpt's cma package but tailored to machine learning applications). The cma package receives currently about 40,000 weekly downloads and, as of January 2024, has been downloaded more than six million times in total.
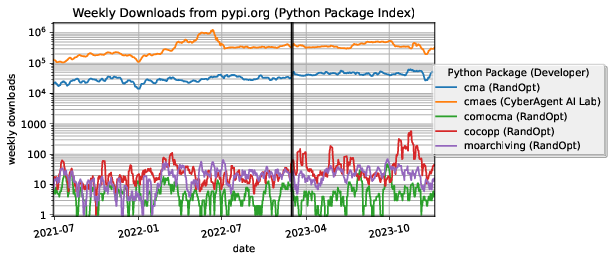
Weekly download numbers for Randopt's software packages.
Weekly download numbers from the Python Package Index (PyPI) of Python software created by the RANDOPT team or directly related to their scientific results (based on numbers from pepy.tech).
6.1 New software
6.1.1 COCO
-
Name:
COmparing Continuous Optimizers
-
Keywords:
Benchmarking, Numerical optimization, Black-box optimization, Stochastic optimization
-
Scientific Description:
COmparing Continuous Optimisers (COCO) is a tool for benchmarking algorithms for black-box optimisation. COCO facilitates systematic experimentation in the field of continuous optimization. COCO provides: (1) an experimental framework for testing the algorithms, (2) post-processing facilities for generating publication quality figures and tables, including the easy integration of data from benchmarking experiments of 350+ algorithm variants, (3) LaTeX templates for scientific articles and HTML overview pages which present the figures and tables.
The COCO software is composed of two parts: (i) an interface available in different programming languages (C/C++, Java, Matlab/Octave, Python, external support for R) which allows to run and log experiments on several function test suites (unbounded noisy and noiseless single-objective functions, unbounded noiseless multiobjective problems, mixed-integer problems, constrained problems) and (ii) a Python tool for generating figures and tables that can be looked at in every web browser and that can be used in the provided LaTeX templates to write scientific papers.
-
Functional Description:
The COCO platform aims at supporting the numerical benchmarking of blackbox optimization algorithms in continuous domains. Benchmarking is a vital part of algorithm engineering and a necessary path to recommend algorithms for practical applications. The COCO platform releases algorithm developers and practitioners alike from (re-)writing test functions, logging, and plotting facilities by providing an easy-to-handle interface in several programming languages. The COCO platform has been developed since 2007 and has been used extensively within the “Blackbox Optimization Benchmarking (BBOB)” workshop series since 2009. Overall, 350+ algorithms and algorithm variants by contributors from all over the world have been benchmarked on the platform's supported test suites so far. The most recent extensions has been towards constrained problems.
- URL:
-
Contact:
Dimo Brockhoff
-
Participants:
Anne Auger, Asma Atamna, Dejan Tusar, Dimo Brockhoff, Marc Schoenauer, Nikolaus Hansen, Ouassim Ait Elhara, Raymond Ros, Tea Tusar, Thanh-Do Tran, Umut Batu, Konstantinos Varelas
-
Partners:
Charles University Prague, Jozef Stefan Institute (JSI), Cologne University of Applied Sciences
6.1.2 CMA-ES
-
Name:
Covariance Matrix Adaptation Evolution Strategy
-
Keywords:
Numerical optimization, Black-box optimization, Stochastic optimization
-
Scientific Description:
The CMA-ES is considered as state-of-the-art in evolutionary computation and has been adopted as one of the standard tools for continuous optimisation in many (probably hundreds of) research labs and industrial environments around the world. The CMA-ES is typically applied to unconstrained or bound-constrained optimization problems and search space dimension between three and a few hundred. Recent versions can also handle nonlinear constraints. The method should be applied, if derivative based methods, e.g. quasi-Newton BFGS or conjugate gradient, (supposedly) fail due to a rugged search landscape, e.g. discontinuities, sharp bends or ridges, noise, local optima, outliers. If second order derivative based methods are successful, they are usually much faster than the CMA-ES: on purely convex-quadratic functions, BFGS (Matlabs function fminunc) is typically faster by a factor of about ten (in number of objective function evaluations assuming that gradients are not available) and on the most simple quadratic functions by a factor of about 30.
-
Functional Description:
The CMA-ES is an evolutionary algorithm for difficult non-linear non-convex black-box optimisation problems in continuous domain.
- URL:
-
Contact:
Nikolaus Hansen
-
Participant:
Nikolaus Hansen
6.1.3 COMO-CMA-ES
-
Name:
Comma Multi-Objective Covariance Matrix Adaptation Evolution Strategy
-
Keywords:
Black-box optimization, Global optimization, Multi-objective optimisation
-
Scientific Description:
The CMA-ES is considered as state-of-the-art in evolutionary computation and has been adopted as one of the standard tools for continuous optimisation in many (probably hundreds of) research labs and industrial environments around the world. The CMA-ES is typically applied to unconstrained or bounded constraint optimization problems, and search space dimensions between three and a hundred. COMO-CMA-ES is a multi-objective optimization algorithm based on the standard CMA-ES using the Uncrowded Hypervolume Improvement within the so-called Sofomore framework.
-
Functional Description:
The COMO-CMA-ES is an evolutionary algorithm for difficult non-linear non-convex black-box optimisation problems with several (two) objectives in continuous domain.
- URL:
-
Contact:
Nikolaus Hansen
6.1.4 MOarchiving
-
Name:
Multiobjective Optimization Archiving Module
-
Keywords:
Mathematical Optimization, Multi-objective optimisation
-
Scientific Description:
Multi-objective optimization relies on the maintenance of a set of non-dominated (and hence incomparable) solutions. Performance indicator computations and in particular the computation of the hypervolume indicator is based on this solution set. The hypervolume computation and the update of the set of non-dominated solutions are generally time critical operations. The module computes the bi-objective hypervolume in linear time and updates the non-dominated solution set in logarithmic time.
-
Functional Description:
The module implements a bi-objective non-dominated archive using a Python list as parent class. The main functionality is heavily based on the bisect module. The class provides easy and fast access to the overall hypervolume, the contributing hypervolume of each element, and to the uncrowded hypervolume improvement of any given point in objective space.
- URL:
-
Contact:
Nikolaus Hansen
6.2 Open data
The COCO platform allows to generate data sets by running an implementation of an optimization algorithm on a set of test functions. Those data sets contain a carefully chosen subset of all function evaluations that an algorithm performed during an experiment, on each test function from a COCO testbed, instance and dimension. Data sets can be loaded easily with the postprocessing module of COCO and used to compare the performance of different algorithms. We collect those data sets, curate them (check that they are clean, add meta-data, ...) and make them available to the community. Those data sets are maintained by Dimo Brockhoff from RandOpt.
In 2023, in total, 25 new algorithm data sets have been added to the publicly accessible database of COCO. Overall, we have collected 350+ data sets over the years.
7 New results
7.1 Analysis of Adaptive Stochastic Search Algorithms
Participants: Anne Auger, Nikolaus Hansen, Armand Gissler.
The main theoretical achievements of this year relate to our progress in the analysis of the (linear) convergence of CMA-ES. This theoretical question is open for more than 20 years and seen as the holy grail by many researchers. It is the main specific long term goal we have announced in our team proposal while recognizing its difficulty and the risk inherent to it. Following a methodology we have developed to analyze step-size adaptive ES 14, we solved theoretical challenges to achieve the analysis of the convergence of CMA-ES. In particular, we achieved the analysis of the irreducibility of underlying normalized chains, the analysis of the geometric ergodicity by finding an appropriate Lyapunov function as well as connecting affine-invariance of the algorithm to the linear convergence on convex-quadratic function. We are currently working on five publications to present the different parts of the proof. One of them is an extension of the theory of Markov chains to be able to analyze the irreducibility of Markov chains that are defined on smooth manifold, namely an extension of 34. We also derived a technical result to get asymptotic estimations of the eigenvalue and eigenvectors of the covariance matrix for large condition number as needed in the proof 13.
The proof that we intend to publish includes all the components of the CMA-ES algorithm: step-size adaptation, cumulation for the step-size and for the covariance matrix update. In order to better appraise the impact of each component on the performance of the algorithm as well as testing some modifications, an intensive benchmarking of different variants was undertaken 18.
7.2 Multi-objective optimization
Participants: Anne Auger, Dimo Brockhoff, Mohamed Gharafi, Nikolaus Hansen.
A central theme for the team is the design, analysis, and benchmarking of multiobjective optimization algorithms. In 2023, we have progressed on the following aspects.
In the context of our collaboration with the company Storengy for the PhD thesis of Mohamed Gharafi, we developed a surrogate-model-based version of our COMO-CMA-ES algorithm 12 in order to deal with the high evaluation time of solutions in many real-world problems. The integration of the single-objective lq-CMA-ES algorithm 7 into COMO-CMA-ES resulted in the COMO-lq-CMA-ES, presented in 17. Numerical experiments on simple, biobjective functions and on the bbob-biobj test suite of the COCO platform revealed an average improvement of 20-60% on the latter and a six times faster convergence rate on the double sphere function with default population size (and 20 times faster convergence with a four times larger population size).
After we co-organized the “Many-Criteria Optimization and Decision Analysis (MACODA)” workshop in 2019 at the Lorentz Center (The Netherlands), the plan arose to publish the results of the workshop's discussions in a book in order to “develop a vision for the next decade of MACODA research”. This book has been eventually published in 2023 with Springer under the title “Many-Criteria Optimization and Decision Analysis—State-of-the-Art, Present Challenges, and Future Perspectives” 20. Besides co-editing the book, we contributed to its introductory chapter in which we introduced the basic notations and definitions, wrote briefly about the state of the art in many-criteria optimization (i.e. when more than three objective functions or criteria have to be simultaneously optimized), and gave an overview of the history of the field's first two decades 21.
Related to the benchmarking aspects of multiobjective optimization, we gave two tutorials on benchmarking multiobjective algorithms at the EMO and GECCO conferences together with Tea Tušar 24. We also benchmarked the multiobjective Borg algorithm within a student project 15. Finally, our publicly available Python module for archiving and hypervolume calculcations (moarchiving), continues to get picked up after its release in 2020 with, on average, 5 downloads per day on PyPi, the python package index.
7.3 Benchmarking: methodology and the Comparing Continuous Optimziers Platform (COCO)
Participants: Anne Auger, Dimo Brockhoff, Lorenzo Consoli, Armand Gissler, Nikolaus Hansen, Tristan Marty.
Benchmarking is an important task in optimization in order to assess and compare the performance of algorithms as well as to motivate the design of better solvers. We are leading the benchmarking of derivative free solvers in the context of difficult problems: we have been developing methodologies and testbeds as well as assembled this into a platform automatizing the benchmarking process. This is a continuing effort that we are pursuing in the team.
The COCO platform, developed at Inria since 2007, aims at automatizing numerical benchmarking experiments and the visual presentation of their results. The platform consists of an experimental part to generate benchmarking data (in various programming languages) and a postprocessing module (in Python), see Figure 2. At the interface between the two, we provide data sets from numerical experiments of 300+ algorithms and algorithm variants from various fields (quasi-Newton, derivative-free optimization, evolutionary computing, Bayesian optimization) and for various problem characteristics (noiseless/noisy optimization, single-/multi-objective optimization, continuous/mixed-integer, ...).
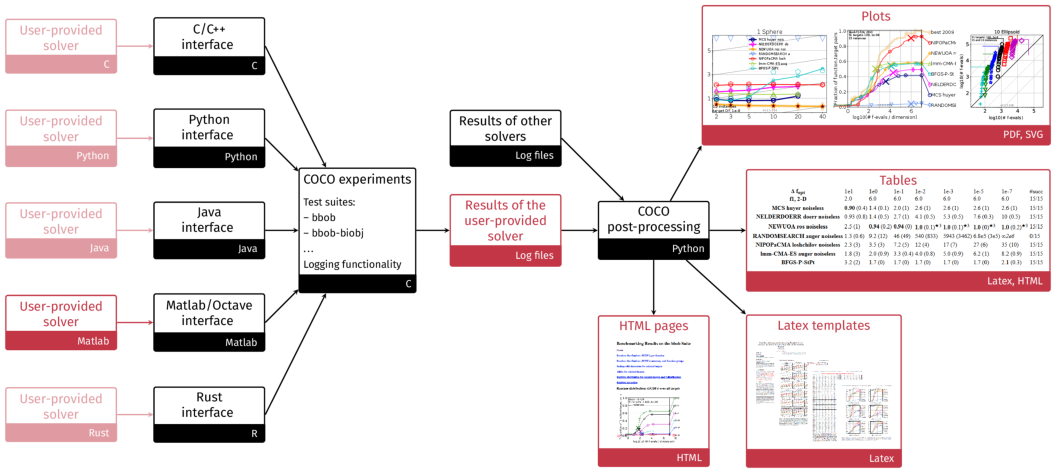
Visual overview of the COCO platform
Structural overview of the COCO platform. COCO provides all black parts while users only have to connect their solver to the COCO interface in the language of interest, here for instance Matlab, and to decide on the test suite the solver should run on. The other red components show the output of the experiments (number of function evaluations to reach certain target precisions) and their post-processing and are automatically generated.
We have been using the platform in the past to initiate workshop papers during the ACM-GECCO conference as well as to collect algorithm data sets from the entire optimization community (350+ so far over the different test suites). This was not different in 2023 with a new workshop held at the ACM-GECCO conference in Lisbon, Portugal where six workshop papers have been presented. Overall, 25 new data sets on the existing test suites have been collected in 2023 from the workshop participants. Our own contributions were as follows.
The first contribution, a comparison of the Borg algorithm on the multiobjective test suite 15 stems from a student project in our "Derivative-free Optimization" lecture. On the noiseless bbob suite, A. Gissler experimented with several variants of the CMA-ES algorithm to see how much certain simplifications, that help his theoretical analysis of the algorithm, affect the algorithm's performance in practice 18. In the context of the PhD thesis of Tristan Marty, we benchmarked the performance of the latest CMA-ES python implementation (pycma version 3.3.0) on COCO's bbob-mixint test suite 19. The results show substantial improvement since the last benchmarked version of pycma from 2019. The latest CMA-ES version is now competitive with other mixed integer algorithms.
After we released the first constrained test suite within COCO in 2022, a new box-constrained test suite has been introduced in 2023 by the organizers of the Workshop on Strict Box-Constrained Black-Box Optimization. We contributed to this workshop by benchmarking the two constraint-handling mechanisms of the CMA-ES algorithm, implemented in its python module, on this newly introduced sbox-cost suite and compared their performance on the classical, unconstrained bbob suite, which is the basis of the sbox-cost suite 16. To this end, the sbox-cost test suite has been made available with COCO.
In addition, Lorenzo Consoli worked on providing a C implementation of the bbob-noisy test suite for the current version of COCO. To assert the long-term maintenance of the platform, we further initiated our first in-person COCO code and documentation sprint which we held during one week in late October 2023 together with all main contributors of the platform. Our second sprint will take place on November 25–29, 2024 in Dagstuhl, Germany.
8 Bilateral contracts and grants with industry
Participants: Anne Auger, Dimo Brockhoff, Nikolaus Hansen, Tristan Marty, Mohamed Garafi.
8.1 Bilateral contracts with industry
- Contract with the company Storengy funding the PhD thesis of Mohamed Gharafi in the context of the CIROQUO project (2021–2024)
- Contract with Thales for the CIFRE PhD thesis of Tristan Marty (2023–2026)
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Visits of international scientists
Other international visits to the team
Olaf Mersmann
-
Status:
professor
-
Institution of origin:
Cologne University of Applied Sciences
-
Country:
Germany
-
Dates:
October 23–27, 2023
-
Context of the visit:
1st COCO code and documentation sprint
-
Mobility program/type of mobility:
research stay
Tea Tušar
-
Status:
researcher
-
Institution of origin:
Jozef Stefan Institute
-
Country:
Slovenia
-
Dates:
October 23–27, 2023
-
Context of the visit:
1st COCO code and documentation sprint
-
Mobility program/type of mobility:
research stay
9.2 European initiatives
9.2.1 Other european programs/initiatives
CA22137 - Randomised Optimisation Algorithms Research Network (ROAR-NET)
Participants: Anne Auger, Dimo Brockhoff, Nikolaus Hansen.
-
Title:
Randomised Optimisation Algorithms Research Network (ROAR-NET)
-
Partner Institution(s):
institutions from 30+ European countries
-
Date/Duration:
2023–2027
-
Additionnal info/keywords:
Randopt is involved in this EU COST action project (2023–2027) by participating in several working groups and by Anne Auger co-leading the working group on mixed-integer optimization.
9.3 National initiatives
CIROQUO
Participants: Dimo Brockhoff, Mohamed Gharafi, Nikolaus Hansen.
-
Title:
CIROQUO ("Consortium Industriel de Recherche en Optimisation et QUantification d'incertitudes pour les données Onéreuses")
-
Partner Institution(s):
six other academic and five industrial partners, including Storengy
-
Date/Duration:
2021–2024
-
Additionnal info/keywords:
Randopt is involved in the context of the PhD thesis of Mohamed Gharafi which is financed by the company Storengy.
10 Dissemination
Participants: Anne Auger, Dimo Brockhoff, Nikolaus Hansen.
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
General chair, scientific chair
- Anne Auger, Dimo Brockhoff, Nikolaus Hansen: co-organizer of the Blackbox Optimization Benchmarking workshop at the ACM-GECCO 2023 conference, together with Paul Dufossé, Olaf Mersmann, Petr Pošik, and Tea Tušar
- A. Auger co-organized the Dagstuhl seminar on benchmarking "Challenges in Benchmarking Optimization Heuristics"
- A. Auger, member of the scientific committee of the 21st French-German-Spanish Conference on Optimization (FGS2024)
- A. Auger: co-organizer of the Dagstuhl seminar 24271 Theory of Randomized Optimization Heuristics in June/July 2024, together with Tobias Glasmachers, Martin S. Krejca, and Johannes Lengler
- D. Brockhoff: co-organizer of the Lorentz Center workshop "Benchmarking in Multi-Criteria Optimization (BeMCO)", April 2024, Leiden, the Netherlands, together with Michael Emmerich, Boris Naujoks, Robin Purshouse, and Tea Tušar
Member of the organizing committees
- A. Auger member of the ACM SIGEVO board
- A. Auger elected member of the business committee of SIGEVO.
10.1.2 Scientific events: selection
Chair of conference program committees
- D. Brockhoff: GECCO 2024 track chair for the EMO track, together with Tapabrata Ray
- D. Brockhoff: GECCO 2023 track chair for the EMO track, together with Hiroyuki Sato
Reviewer
- D. Brockhoff: reviewer for the conferences GECCO and FOGA in 2023 and PPSN 2024
- A. Auger: reviewer at the conference GECCO and PPSN 2024.
10.1.3 Journal
Member of the editorial boards
- A. Auger and N. Hansen member of the editorial board of Evolutionary Computation Journal, since 2009
- D. Brockhoff and N. Hansen: Associate Editors for ACM Transactions on Evolutionary Learning and Optimization, since 2019
Reviewer - reviewing activities
The three permanent members are frequent reviewers for major journals in Evolutionary Computation. Anne Auger is a frequent reviewer of mathematical optimization journal (JOGO, SIAM OPT). We additionally review papers in Machine Learning related to optimization for JMLR, Machine Learning.
10.1.4 Invited talks
Keynote at ECTA 2023 "Assessment and Evaluation of Empirical and Scientific Data" 25
10.1.5 Scientific expertise
- Dimo Brockhoff: National Science Centre Poland
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- Master: A. Auger, “Derivative-free Optimization”, 22.5h ETD, niveau M2 (Optimization Master of Paris-Saclay)
- Master: D. Brockhoff, “Algorithms and Complexity”, 36h ETD, niveau M1 (joint MSc with ESSEC “Data Sciences & Business Analytics”), CentraleSupelec, France
- Master: D. Brockhoff, “Advanced Optimization”,36h ETD, niveau M2 (joint MSc with ESSEC “Data Sciences & Business Analytics”), CentraleSupelec, France
- Bachelor: A. Auger, "Convex Optimization and Control", Bachelor of Ecole Polytechnique, 3rd year.
Tutorials
- An Introduction to Scientific Experimentation and Benchmarking, tutorial at the GECCO conference in 2023 (A. Auger and N. Hansen) 23
- Benchmarking Multiobjective Optimizers 2.0, tutorial at the GECCO 2023 conference (D. Brockhoff and T. Tušar) 24
- Benchmarking Multiobjective Optimizers 2.0, tutorial at the EMO 2023 conference (D. Brockhoff and T. Tušar)
- CMA-ES and Advanced Adaptation Mechanisms, tutorial at the GECCO conference in 2023 (Y. Akimoto and N. Hansen) 22
10.2.2 Supervision
- PhD in progress: Armand Gissler, "Analysis of covariance matrix adaptation methods for randomized derivative free optimization" (2021–), supervisors: Anne Auger and Nikolaus Hansen
- PhD in progress: Mohamed Gharafi (Jan. 2022–), supervisors: Nikolaus Hansen and Dimo Brockhoff
- PhD in progress: Tristan Marty (Jan. 2023–), supervisors: Anne Auger and Nikolaus Hansen
10.2.3 Juries
- A. Auger member of the CRCN jury of Inria Saclay.
- A. Auger, president of the jury of Pablo JIMENEZ.
- A. Auger, member of the COS Professeur Université Calais.
10.3 Popularization
10.3.1 Internal or external Inria responsibilities
- A. Auger: member of the BCEP of Inria Saclay
- D. Brockhoff: member of the CDT in Saclay
- D. Brockhoff: member of the CUMI in Saclay
11 Scientific production
11.1 Major publications
- 1 articleGlobal Linear Convergence of Evolution Strategies on More Than Smooth Strongly Convex Functions.SIAM Journal on OptimizationJune 2022HAL
- 2 articleAn ODE Method to Prove the Geometric Convergence of Adaptive Stochastic Algorithms.Stochastic Processes and their Applications1452022, 269-307HALDOI
- 3 articleDiagonal Acceleration for Covariance Matrix Adaptation Evolution Strategies.Evolutionary Computation2832020, 405-435HALDOI
- 4 articleA SIGEVO impact award for a paper arising from the COCO platform.ACM SIGEVOlution134January 2021, 1-11HALDOI
- 5 articleUsing Well-Understood Single-Objective Functions in Multiobjective Black-Box Optimization Test Suites.Evolutionary Computation2022HALDOI
- 6 articleVerifiable Conditions for the Irreducibility and Aperiodicity of Markov Chains by Analyzing Underlying Deterministic Models.Bernoulli251December 2018, 112-147HALDOI
- 7 inproceedingsA Global Surrogate Assisted CMA-ES.GECCO 2019 - The Genetic and Evolutionary Computation ConferenceACMPrague, Czech RepublicJuly 2019, 664-672HALDOIback to text
- 8 articleCOCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting.Optimization Methods and Software361ArXiv e-prints, arXiv:1603.087852020, 114-144HALDOI
- 9 articleInformation-Geometric Optimization Algorithms: A Unifying Picture via Invariance Principles.Journal of Machine Learning Research18182017, 1-65HAL
- 10 articleGlobal linear convergence of Evolution Strategies with recombination on scaling-invariant functions.Journal of Global Optimization2022HALDOI
- 11 articleScaling-invariant functions versus positively homogeneous functions.Journal of Optimization Theory and ApplicationsSeptember 2021HAL
- 12 inproceedingsUncrowded Hypervolume Improvement: COMO-CMA-ES and the Sofomore framework.GECCO 2019 - The Genetic and Evolutionary Computation ConferencePart of this research has been conducted in the context of a research collaboration between Storengy and InriaPrague, Czech RepublicJuly 2019HALDOIback to text
11.2 Publications of the year
International journals
International peer-reviewed conferences
Scientific books
Scientific book chapters
Other scientific publications
11.3 Cited publications
- 26 inproceedingsOnline model selection for restricted covariance matrix adaptation.International Conference on Parallel Problem Solving from NatureSpringer2016, 3--13back to text
- 27 inproceedingsProjection-based restricted covariance matrix adaptation for high dimension.Proceedings of the 2016 on Genetic and Evolutionary Computation ConferenceACM2016, 197--204back to text
-
28
inproceedingsTowards au Augmented Lagrangian Constraint Handling Approach for the
-ES.Genetic and Evolutionary Computation ConferenceACM Press2015, 249-256back to textback to textback to text - 29 inproceedingsLinearly Convergent Evolution Strategies via Augmented Lagrangian Constraint Handling.Foundation of Genetic Algorithms (FOGA)2017back to text
- 30 articleLinear Convergence of Comparison-based Step-size Adaptive Randomized Search via Stability of Markov Chains.SIAM Journal on Optimization2632016, 1589-1624back to text
- 31 inproceedingsAlgorithms for Hyper-Parameter Optimization.Neural Information Processing Systems (NIPS 2011)2011HALback to text
- 32 articleThe O.D.E. Method for Convergence of Stochastic Approximation and Reinforcement Learning.SIAM Journal on Control and Optimization382January 2000back to text
- 33 bookletStochastic approximation: a dynamical systems viewpoint.Cambridge University Press2008back to text
- 34 articleVerifiable Conditions for the Irreducibility and Aperiodicity of Markov Chains by Analyzing Underlying Deterministic Models.Bernoulli(conditionally accepted)2016back to text
- 35 inproceedingsConstraint-handling techniques used with evolutionary algorithms.Proceedings of the 2008 Genetic and Evolutionary Computation ConferenceACM2008, 2445--2466back to text
- 36 inproceedingsCovariance Matrix Adaptation Evolution Strategy for Multidisciplinary Optimization of Expendable Launcher Families.13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Proceedings2010back to textback to text
- 37 bookNumerical Methods for Unconstrained Optimization and Nonlinear Equations.Englewood Cliffs, NJPrentice-Hall1983back to text
- 38 incollectionPrincipled design of continuous stochastic search: From theory to practice.Theory and principled methods for the design of metaheuristicsSpringer2014, 145--180back to textback to text
- 39 articleCompletely Derandomized Self-Adaptation in Evolution Strategies.Evolutionary Computation922001, 159--195back to text
- 40 articleTesting heuristics: We have it all wrong.Journal of heuristics111995, 33--42back to text
- 41 inproceedingsAn Evaluation of Sequential Model-based Optimization for Expensive Blackbox Functions.GECCO (Companion) 2013Amsterdam, The NetherlandsACM2013, 1209--1216back to text
- 42 articleA theoretician’s guide to the experimental analysis of algorithms.Data structures, near neighbor searches, and methodology: fifth and sixth DIMACS implementation challenges592002, 215--250back to text
- 43 articleEfficient global optimization of expensive black-box functions.Journal of Global optimization1341998, 455--492back to text
- 44 articleA hybrid CMA-ES and HDE optimisation algorithm with application to solar energy potential.Applied Soft Computing922009, 738--745back to text
- 45 articleOptimisation of building form for solar energy utilisation using constrained evolutionary algorithms.Energy and Buildings4262010, 807--814back to text
- 46 articleCalibrating a global three-dimensional biogeochemical ocean model (MOPS-1.0).Geoscientific Model Development1012017, 127back to text
- 47 bookStochastic approximation and recursive algorithms and applications.Applications of mathematicsNew YorkSpringer2003back to text
- 48 inproceedingsOptimal Design of CO2 Sequestration with Three-Way Coupling of Flow-Geomechanics Simulations and Evolution Strategy.SPE Reservoir Simulation ConferenceOnePetro2019back to text
- 49 inproceedingsDesign and Optimization of an Omnidirectional Humanoid Walk: A Winning Approach at the RoboCup 2011 3D Simulation Competition.Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence (AAAI)Toronto, Ontario, CanadaJuly 2012back to text
- 50 bookMarkov Chains and Stochastic Stability.New YorkSpringer-Verlag1993back to text
- 51 inproceedingsWell placement optimization for carbon dioxide capture and storage via CMA-ES with mixed integer support.Proceedings of the Genetic and Evolutionary Computation Conference Companion2018, 1696--1703back to text
- 52 inproceedingsDevelopment of a high speed optimization tool for well placement in Geological Carbon dioxide Sequestration.5th ISRM Young Scholars' Symposium on Rock Mechanics and International Symposium on Rock Engineering for Innovative FutureOnePetro2019back to text
- 53 articleThe Journal of Machine Learning Research1812017, 564--628back to textback to text
- 54 articleEnergy and spinning reserve scheduling for a wind-thermal power system using CMA-ES with mean learning technique.International Journal of Electrical Power & Energy Systems532013, 113--122back to text
- 55 articleEvolution strategies as a scalable alternative to reinforcement learning.arXiv preprint arXiv:1703.038642017back to textback to text
- 56 inproceedingsPractical bayesian optimization of machine learning algorithms.Neural Information Processing Systems (NIPS 2012)2012, 2951--2959back to text
- 57 articleLong-term model predictive control of gene expression at the population and single-cell levels.Proceedings of the National Academy of Sciences109352012, 14271--14276back to text

