2023Activity reportProject-TeamRAPSODI
RNSR: 201521771D- Research center Inria Centre at the University of Lille
- In partnership with:Université de Lille
- Team name: Reliable numerical approximations of dissipative systems
- In collaboration with:Laboratoire Paul Painlevé (LPP)
- Domain:Applied Mathematics, Computation and Simulation
- Theme:Numerical schemes and simulations
Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
Other Research Topics and Application Domains
- B3. Environment and planet
- B3.3. Geosciences
- B3.3.1. Earth and subsoil
- B3.4. Risks
- B3.4.2. Industrial risks and waste
- B4. Energy
- B4.2. Nuclear Energy Production
- B4.2.1. Fission
1 Team members, visitors, external collaborators
Research Scientists
- Clément Cancès [Team leader, Inria, Senior Researcher, HDR]
- Théophile Chaumont-Frelet [Inria, Researcher, from Sep 2023]
- Maxime Herda [Inria, Researcher]
- Simon Lemaire [Inria, Researcher]
- Andrea Natale [Inria, Researcher]
Faculty Members
- Caterina Calgaro [University of Lille, Associate Professor]
- Claire Chainais-Hillairet [University of Lille, Professor, HDR]
- Benoît Merlet [University of Lille, Professor, HDR]
- Marc Pegon [University of Lille, Associate Professor]
- Thomas Rey [University of Lille, Associate Professor, until Aug 2023, HDR]
Post-Doctoral Fellows
- Enrico Facca [Inria, until Mar 2023]
- Pierre Gervais [CNRS, Post-Doctoral Fellow, from Sep 2023]
- Silvano Pitassi [Inria/EDF, Post-Doctoral Fellow]
- Clément Sarrazin [Inria, Post-Doctoral Fellow, from Nov 2023]
PhD Students
- Jules Candau-Tilh [University of Lille]
- Robin Colombier [Université Polytechnique Hauts-de-France]
- Amélie Dupouy [Inria, from Oct 2023]
- Maxime Jonval [Inria/IFPEn]
- Tino Laidin [University of Lille]
- Julien Moatti [Inria, until Sep 2023]
Technical Staff
- Thoma Zoto [Inria, Engineer]
Interns and Apprentices
- Abdoul Aziz Diallo [Inria, Intern, from May 2023 until Jul 2023]
- Sam Dossin [INRAE, Intern, from Apr 2023 until Sep 2023]
- Abbas El Hajj [University of Lille, Intern, from May 2023 until Jul 2023]
- Ivan Tagliaferro De Oliveira Tezoto [Inria, Intern, from May 2023 until Jul 2023]
Administrative Assistants
- Isabelle Aslani [Inria, from Sep 2023]
- Aurore Dalle [Inria, until Aug 2023]
Visiting Scientist
- Jian-Guo Liu [Duke University (USA), from Jun 2023 until Jul 2023]
External Collaborators
- Matthieu Alfaro [University of Rouen Normandy, from Oct 2023, HDR]
- Emmanuel Creusé [Université Polytechnique Hauts-de-France, HDR]
- Juliette Venel [Université Polytechnique Hauts-de-France]
2 Overall objectives
Together with the diffusion of scientific computing, there has been a recent and impressive increase of the demand for numerical methods. The problems to be addressed are everyday more complex and require specific numerical algorithms. The quality of the results has to be accurately assessed, so that in-silico experiments results can be trusted. Nowadays, producing such reliable numerical results goes way beyond the abilities of isolated researchers, and must be carried out by structured teams.
The topics addressed by the RAPSODI project-team belong to the broad theme of numerical methods for the approximation of the solutions to systems of partial differential equations (PDEs). Besides standard convergence properties, a good numerical method for approximating a physical problem has to satisfy at least the following three criteria:
- preservation at the discrete level of some crucial features of the solution, such as positivity of solutions, conservation of prescribed quantities (e.g., mass), decay of physically motivated entropies, free energies, etc;
- provide accurate numerical approximations at a reasonable computational cost (and ultimately maximize the accuracy at a fixed computational effort);
- robustness with respect to physical conditions: the computational cost for a given accuracy should be essentially insensitive to a change in physical parameters.
We contribute to the development of methods fulfilling the above quality criteria for physical models which all display a dissipative behavior, and that are motivated by industrial collaborations or multidisciplinary projects.
Ideally, we should allow ourselves to design entirely new numerical methods. For some applications however (often in the context of industrial collaborations), the members of the team have to work with existing codes. The numerical algorithms have thus to be optimized under this constraint.
Some technological bottlenecks related to points (a)–(c) mentioned above are well identified. In particular, it appears that a good numerical method should handle general meshes, so that dynamic mesh adaptation strategies can be used in order to achieve (b). But it should also be of the highest possible order while remaining stable in the sense of (a), and robust in the sense of (c). There have been numerous research contributions on each point of (a)–(c) in the last decades, in particular for solving each difficulty separately, but combining them still leads to unsolved problems of crucial interest. Yet, before addressing the above points (a)–(c) concerning the design of nice numerical methods, one has to identify the structural properties of (and possibly modify) the continuous model to be discretized.
In a nutshell, our goal is to take advantage of and extend the most recent breakthroughs of the mathematical community to tackle in an efficient way some application-guided problems coming either from academics or from industrial partners. To this end, we focus on the following objectives, which are necessary for the applications we work on and which define the three research axes of our project:
- Study of the structural properties of continuous PDE models.
- Design and numerical analysis of structure-preserving numerical methods.
- Computational optimization of the numerical methods.
The originality of the RAPSODI research team is its holistic approach as illustrated on Figure 1.
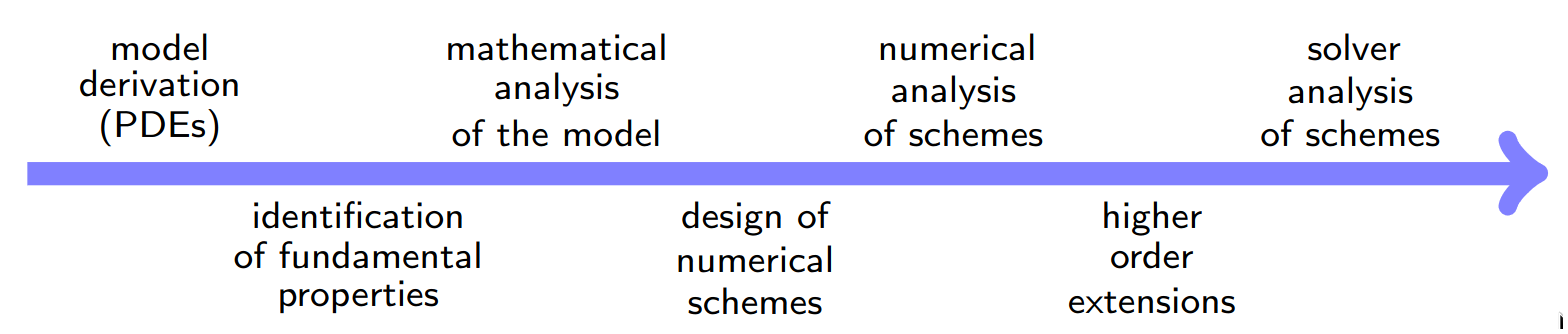
model derivation (PDEs), then identification of fundamental properties, then mathematical analysis of the model, then design of numerical schemes, then numerical analysis of the schemes, then higher order extensions and finally solver analysis of schemes
We consider the problem resolution in a global manner, starting from the model derivation (for instance based on physical principles) to the practical development of efficient numerical methods.
model derivation (PDEs), then identification of fundamental properties, then mathematical analysis of the model, then design of numerical schemes, then numerical analysis of the schemes, then higher order extensions and finally solver analysis of schemes
We consider the problem resolution in a global manner, starting from the model derivation (for instance based on physical principles) to the practical development of efficient numerical methods.
The study of the structural properties of the models under consideration helps in designing robust and accurate numerical schemes. It also helps in the design of efficient solvers. Our research program in these three axes, which constitute the core of the RAPSODI research project, is now going to be further detailed.
3 Research program
3.1 Axis 1: Study of the structural properties of continuous models
A well-behaved continuous (PDE based) model is a requisite to a reliable numerical approximation. The fine understanding of a continuous model is indeed a prior to the design of a numerical scheme in order to identify the structural properties to be preserved at the discrete level. Further, the mathematical analysis carried out on the continuous model often paves the way for the theoretical foundations of the numerical methods, hence our strong interest in this first research axis. Analyzing time-dependent PDE systems relying on their mathematical (Hamiltonian, gradient flow, ...) structure is very natural and unsurprisingly not new. However, the interest in this domain strongly increased in the last two decades. The focus of the RAPSODI project-team encompasses kinetic models, fluid mechanics, electromagnetism, multicomponent systems and applied calculus of variations. While carrying out theoretical analyses, we bear in mind that our results should be transposed to the discrete setting.
3.1.1 Thermodynamically consistent models for multi-component systems
Mathematical tools for the derivation and the mathematical analysis of models which are compatible with the second principle of thermodynamics and more specifically with Onsager's reciprocal principle 139 widely developed in the last decade. The general setting proposed in 133, 143 offers a powerful and robust framework for obtaining such models in configurations where inertia can be neglected.
This situation is typical of porous media flows in the Darcy regime. When rich physics are considered, like in presence of multiple phases and components within deformable and fractured matrices, the derivation of such thermodynamically consistent models is a timely problem 148, 149, 151. One of the goals of the RAPSODI project-team is to contribute to the mathematical understanding of such models 4.
Inertia is also commonly neglected in models for semi-conductors of van Roosbroeck type, as for instance in models for the corrosion of iron 75. In the latter framework, the geometry of the domain varies along time and is one of the unknowns of the problem. The reference model proposed in 75 is not built from thermodynamical considerations. The design, the simulation and the calibration of a mathematical model which is consistent with the second principle is an ongoing task addressed by our team (see 16 for preliminary results).
3.1.2 Variational models and optimal transport
Optimal transport has a long history. In Monge's seminal work “Théorie des déblais et des remblais” dating back to 1781 150, the problem was roughly stated the following way: how should one proceed to move piles of sand from one point to another in order to minimize the workload? This problem is now often referred to as “Monge problem”. It has stayed with no solution in the general case until the 1940s, when Kantorovich inserted it into a proper framework 126, which allowed eventually to tackle it and provide solutions. A major breakthrough was obtained by Brenier 84, who showed that under very broad assumptions, the general solution to the optimal transport problem had a very specific form and could be linked with the famous Monge–Ampère equation.
In recent years, optimal transport has become a very active field of research, due to the discovery of new and efficient algorithms 112 and to its wide range of applications, to economy, image processing, analysis of partial differential equations or data sciences (see e.g. references in 144).
One of the focus of our team is the use of optimal transport for understanding the formation of bi-layer cellular membranes thanks to a model introduced in 142. In this model, the global shape of micelles or liposomes should be the result of competing forces: a short-range attractive force given by the area of the boundary, and a non-local repulsive force of Wasserstein-type (that is, an optimal transport cost). Our aim is to explore numerically this problem and obtain theoretically the shape of the solutions in some asymptotic regimes.
3.1.3 Kinetic models of large particle systems and their asymptotic regimes
Nearly 150 years after Boltzmann paved the way to the kinetic representation of complex phenomena 83, this approach for modeling is more than ever active. This increasing interest is partially due to the development of computational facilities that make the numerical approximation of such models possible, but also to the great flexibility of the approach which can be applied in biology 147, economics 114 or social sciences 86, way beyond its original scope in physics of gases.
One focus of our team is the asymptotic analysis of these equations. The large-time limit of kinetic equations has been dealt with thanks to hypocoercivity techniques in 71 and new hydrodynamic limits have been derived from kinetic models for gases composed of macroscopic particles interacting via energy dissipative collisions 124, 101 and plasmas 123. A future concern will be the study of the long time dynamics of a kinetic model for relativistic electron bunches in storage rings 145 (see Section 4.6).
3.2 Axis 2: Design and analysis of structure-preserving numerical methods
The more complex is the PDE system to be discretized, the smaller is the chance that a naive discretization preserves at the discrete level its mathematical structure. Since this structure was the cornerstone of the mathematical analysis (typically by providing the well-posedness and the stability of the continuous system under consideration), its preservation at the discrete level will be key to get well-behaved and theoretically certified numerical methods. Our team concentrates a large part of its research effort on the design of provably convergent numerical methods, either based on the popular two-point flux approximation finite volume method, or on more flexible yet less natural structure preserving methods. We also pay attention to the fact that our schemes are robust with respect to the parameters and in the long time limit. The numerical approximation of complex (inhomogeneous or with low compressibility) flows is one of the topics we address.
3.2.1 Structure-preserving methods for systems of dissipative PDEs and variational models
A very important part of the activity of our team concerns the design of structure-preserving numerical methods for dissipative PDEs.
In this regard, two-point flux approximation (TPFA) finite volume schemes are very popular in industrial codes since they enjoy remarkable stability properties at a moderate computational price. Our team has a strong experience in the design of provably convergent entropy stable TPFA finite volume schemes for complex problems 66, 91, 96, 120, 100, 17, 90, 106, 94, 98, 100. Ongoing 95, 137 and future research directions are based on the discretization of some action functionals and their optimization to obtain so-called variational schemes based on TPFA finite volumes. We also mention the Lagrangian approach 118, for which the computation of some optimal tessellation based on semi-discrete optimal transportation shows subtle but deep similarities with Eulerian TPFA based methods.
The main drawback of TPFA finite volume schemes is that they (essentially) restrict to isotropic diffusion problems and to regular grids 117, 119. The strong constraints on the meshes and on the isotropic nature of the problems under consideration for TPFA schemes motivated in the last decades the development of more robust finite volume schemes, see for instance 115 for a review on this topic. These developments were particularly motivated by applications in geosciences, where anisotropic porous media are common and where (possibly poorly regular) meshes are often prescribed by data. Tuning such advanced methods, which do not enjoy monotonicity properties in general, to make them thermodynamically consistent is a key challenge for our team. An active research topic of our team is to propose new structure-preserving numerical schemes beyond TPFA. Our team has made important preliminary contributions on this topic through the design of structure-preserving control volume finite elements schemes 64, 65, vertex centered finite volume schemes 5, discrete duality finite volume schemes 93, finite element schemes 99 and hybrid finite volume schemes 104. The latter numerical method also constitutes a first step towards high-order methods (see Section 3.2.2).
We intend to pursue our contributions in the development of structure-preserving numerical methods, both based on simple TPFA finite volumes and on more advanced robust methods. We will keep working on always more complex porous media flows, more advanced semi-conductor devices, or on non-standard flow models.
3.2.2 High-order structure-preserving numerical methods
Taking advantage of our experience in the design of low-order structure-preserving numerical schemes, we intend to improve the accuracy of our numerical methods by going to high-order discretizations in the space and time variables.
There are important contributors in the community in these topics. For instance, the development of high-order in space methods allowing for general grids for diffusion problems was pushed forward in the last decade by several groups, for instance around Lourenço Beirão da Veiga and Franco Brezzi 78 for the Virtual Element Methods (VEM), around Daniele A. Di Pietro and Alexandre Ern 9, 113 for the Hybrid High-Order (HHO) methods, or around Bernardo Cockburn 110 for the Hybridizable Discontinuous Galerkin (HDG) methods.
Our team aims at designing high-order in space and entropy stable schemes based on the HHO technology. We also aim at developing high-order methods on general meshes for electromagnetism in the context of a collaboration with EDF (French electricity supply company), with application to the non-invasive control of nuclear plants (see Section 4.4).
Concerning the time discretization strategies, we take inspiration in the works by Giovanni Samaey 128 for projective integration schemes, and in those by Christophe Besse 80 and Jie Shen 88 for relaxation methods. It appears that (explicit) Strong Stability Preserving high-order time discretizations 122, which are very popular in the community working on hyperbolic systems, are not suitable for solving dissipation driven (and typically parabolic) systems for which implicit methods are commonly used.
At the moment most of our energy stable methods rely on merely first-order time discretizations, typically Backward Euler or minimizing movement schemes 125. The extension to higher order time discretizations is already the purpose of ongoing studies in our team. Two tracks have been identified so far and are already studied: (i) the variational BDF2 scheme 131 which generalizes to second order in time the minimizing movement scheme, and (ii) Runge-Kutta type schemes obtained after having changed of main variables. Both approaches have their pros and their cons: (i) is difficult to implement, whereas (ii) might lead to non-conservative methods. Our goal for the next years on this topic is to be able to overpass the difficulties of (at least one of) these methods and to get efficient implementation strategies as well as theoretical foundations.
3.2.3 Asymptotic-preserving and multiscale numerical methods
It has been understood around year 2000 that the fine quantification of the entropy dissipation allows one to deduce fine properties on the asymptotic behavior of the solutions to dissipative PDEs 69, 102. The extension to the discrete setting of this type of tools is more recent, see for instance 103, 82, 105. Our team is involved in the study of the long-time behavior of numerical schemes for drift-diffusion models 81, 92, 6, 104 and kinetic equations 2, 14. A future challenge is the study of the long time behavior properties for numerical schemes which can handle general meshes and high order accuracy (see Section 3.2.1 and Section 3.2.2).
We also contribute actively to the design and analysis of multiscale methods for highly heterogeneous (or highly oscillatory) diffusion problems. We have extended in 109 within the HHO framework the nonconforming multiscale method of 127 to arbitrary approximation orders (and its analysis also to the case of general meshes). We have also established in 107 an equivalence result between our multiscale HHO method and the MHM method of 68, improving in passing on both methods.
In the future we will continue our effort in the design of numerical schemes which enjoy accurate asymptotic properties in large time, extreme regimes of parameters and multiscale settings. This effort, which aims at increasing the robustness of our numerical methods, is strongly correlated with the preservation of energy or entropy dissipation structures at the discrete level (cf. Section 3.2.1), as explained above. A particular effort has begun in the investigation of asymptotic preserving schemes to pass from kinetic models to van Roosbroeck type models for semiconductor devices.
3.2.4 Numerical methods for optimal transport
In the last years optimal transport and its generalisations have proven to be a powerful tool to analyse a large class of models, exposing useful mathematical structures which are responsible of their properties 67, and guiding the conception of novel numerical schemes. Due to its geometrical and physical meanings, optimal transport has also emerged as a useful modelling tool in different contexts including economics, biology or social sciences 146.
Transportation problems can often be cast as global space-time optimisation problems such as in variational mean field games or optimal planning problems 79. Part of the activity of our team in this area is concerned with the analysis of such models in the discrete setting, which poses significant difficulties both in terms of the conception of schemes (which often passes through the definition of discrete variational problems) 137136, and of the devising of efficient optimization algorithms to compute their solutions 22.
As currently many of these problems are still intractable at the numerical level (due to their high dimensionality and lack of smoothness), our aim is to further improve the current approaches, for example by using unstructured meshes in space-time, which would pave the way for the development of adaptive refinement techniques. Importantly, such new schemes could be used as a building block to construct new discretisations for PDEs with a variational structure related to optimal transport (such as Wasserstein gradient flows 13852). In particular, this could represent an additional research path to reach our objectives mentioned in Section 3.2.1.
3.3 Axis 3: Computational optimization of the numerical methods
Good numerical methods shall enjoy strong theoretical foundations allowing to guarantee their behavior in very general situations. They shall also be highly efficient from a computational point of view, so that they can be used in practice for solving real-world problems.
To increase the efficiency and applicability of our methods, we work on three tracks. First, we aim at building a unified and optimized software platform to implement, test and diffuse our numerical methods. Second, since our methods often yield nonlinear systems, the improvement of the nonlinear solvers is also key to increase the efficiency of our methods. Finally, for high-dimensional models such as kinetic and particle systems, the curse of dimensionality makes numerical computations realistically feasible only if specific computationally efficient numerical strategies are deployed.
3.3.1 Development of the platform ParaSkel++
ParaSkel++77 is a C++ platform, conceived by S. Lemaire and mainly developed since December 2022 by T. Zoto (succeeding L. Beaude), which is freely distributed under LGPL v3.0. The ParaSkel++ platform aims at the high-performance, arbitrary-order, 2/3D numerical approximation of PDEs on general polytopal meshes using skeletal Galerkin methods (see 130).
A first version (v1, August 2021) of the platform is operational, featuring a sequential implementation of all the main skeletal methods (Lagrange FE, VEM and HHO). The next, already ongoing, crucial development steps are the parallelization on shared and distributed memory, and the implementation of efficient quadrature formulas on polytopal cells. Eventually, the ParaSkel++ platform is expected to possess five main assets with respect to other codes of the same nature from the community: (i) a unified 2/3D implementation, (ii) the native support of any type of DOF (vertex-, edge-, face-, and cell-based), (iii) an ultra-factorized architecture (with common-to-all-methods local elimination and global assembly steps), (iv) the use of efficient quadrature formulas on general polytopal cells (without the need for subtessellation), and (v) the embedding of parallel computation capabilities.
3.3.2 Design of robust nonlinear solvers
The entropy stable methods we build often yield nonlinear systems to be solved at each time step. It is therefore of paramount importance to have fast and robust nonlinear solvers at hand to address them, hence the increasing interest for so-called nonlinear preconditioning techniques. In 3, we proposed a strategy which consists in expressing the problem in terms of a new primary variable which, if well chosen, allows to remove the degeneracies of the system under consideration. This strategy has then been extended to the case of more complex systems arising in the context of porous media flows 74, 73. In the framework of a collaboration with IFPEn, we develop new solvers for the computation of chemical equilibria (see 44), with application to reactive transport. The methodology being developed in this framework will then be transposed to other contexts in an as generic as possible way.
3.3.3 Efficient numerical methods for high-dimensional systems
Physically-relevant problems usually involve regimes of validity. These regimes are characterized by the relative size of some dimensionless numbers. Developing numerical methods that are able to accurately reproduce the behaviors for such various regimes is then crucial when dealing with applications, whether theoretical or with an engineering goal. Nevertheless, because of the high dimensionality of the phase space in kinetic theory (up to 7 dimensions), this can become a real challenge to develop implicit methods able to deal with the different time scales of the problems.
A robust and fully explicit method that was developed and allows for time integration of (two-scale) stiff systems with arbitrary order of accuracy in time is called projective integration (PInt). It was proposed in 121 for stiff systems of ordinary differential equations with a clear gap in their eigenvalue spectrum. In 128, PInt was introduced and analyzed for linear kinetic equations with a diffusive scaling. It was then extended to the nonlinear Boltzmann equation in 132 and to gas mixtures in 72.
However, having robust numerical methods is not enough: one also needs these methods to be extremely accurate and implemented efficiently, in order to obtain relevant numerical results in reasonable time. Spectral methods based on the fast Fourier transform have been developed in this sense in the last two decades, and reached enough maturity to be incorporated in high performance computing codes 10. Equilibrium preserving extensions were also introduced and analyzed in the series of papers 141, 140. Finally, an extension to the more mathematically intricated quantum Boltzmann operator has been achieved in the code KINEBEC 134, which has been used to show Bose–Einstein condensation and Fermi–Dirac relaxation in 31.
4 Application domains
4.1 Subsurface CO2 storage
The capture and storage in the subsurface of carbon dioxide is commonly acknowledged as a promising solution to mitigate the emission of greenhouse gas from localized production sites, as for instance cement plants. The safety assessment of the subsurface sequestration sites requires advanced numerical tools building on theoretically certified numerical models and algorithms which remain valid in the long time limit. Among the numerous difficulties encountered in such a setting, let us mention the high level of coupling between the mechanics of the (solid) porous matrix 111, the multiphase and multicomponent character of the fluid which flows therein 76, and chemical reactions with a wide range of characteristic times 129. Despite important differences (at the level of chemistry especially), similar problems occur in the emerging topic of dihydrogen subsurface storage, or native dihydrogen (generated by the corrosion of iron in an aqueous environment) migration in the context of nuclear waste repository management.
Together with colleagues from applied research institutes and academics, the RAPSODI project-team contributes to the derivation of so-called thermodynamically consistent models, the stability of which in the long-time limit being guaranteed by the second principle. The team also contributes to the design and the analysis of numerical schemes for multiphase and multicomponent flows in complex geometries (possibly allowing for general meshes), and to the design of fast and robust solvers for chemical equilibria.
4.2 Material sciences
The team is interested in the theoretical and numerical analysis of mathematical models describing the degradation of materials, as concrete carbonation and corrosion. The study of such models is an important environmental and industrial issue. Atmospheric carbonation degrades reinforced concretes and limits the lifetime of civil engineering structures. Corrosion phenomena issues occur for instance in the reliability of nuclear power plants and the nuclear waste repository. The study of the long time evolution of these phenomena is of course fundamental in order to predict the lifetime of the structures.
4.3 Complex fluid flows
The team is interested in numerical methods for the simulation of systems of PDEs describing complex flows, like for instance mixture flows, granular gases, rarefied gases, or quantum fluids.
Variable-density, low-Mach flows have been widely studied in the recent literature because of their applicability in various phenomena such as flows in high-temperature gas reactors, meteorological flows, flows with convective and/or conductive heat transfer or combustion processes. In such cases, the resolution of the full compressible Navier–Stokes system is not adapted, because of the sound waves' speed. The Boussinesq incompressible model is not a better alternative for such low-speed phenomena, because the compressibility effects cannot be totally cancelled due to large variations of temperature and density. Consequently, some models have been formally derived, leading to the filtering of the acoustic waves by the use of some formal asymptotic expansions and two families of methods have been developed in the literature in order to compute these flows. We are interested in particular in the so-called pressure-based methods, which are more robust than density-based solvers, although their range of validity is in general more limited.
The kinetic theory of molecular gases models a gas as a system of elastically colliding spheres, conserving mechanical energy during impact. Once initialized, it takes to a molecular gas no more than a few collisions per particle to relax to its equilibrium state, characterized by a Maxwellian velocity distribution and a certain homogeneous density (in the absence of external forces). A granular gas is a system of dissipatively colliding, macroscopic particles (grains). This slight change in the microscopic dynamics (converting energy into heat) causes drastic changes in the behavior of the gas: granular gases are open systems, which exhibit self-organized spatio-temporal cluster formations, and have no equilibrium distribution. They can be used to model silos, avalanches, pollen or planetary rings.
Quantum models can be used to describe superfluids, quantum semiconductors, weakly interacting Bose gases, or quantum trajectories of Bohmian mechanics. They have attracted considerable attention in the last decades, due in particular to the development of nanotechnology applications. To describe quantum phenomena, there exists a large variety of models. In particular, there exist three different levels of description: microscopic, mesoscopic, and macroscopic. The quantum Navier–Stokes equations deal with a macroscopic description in which the quantum effects are taken into account through a third-order term called the quantum Bohm potential. This Bohm potential arises from the fluid dynamical formulation of the single-state Schrödinger equation. The nonlocality of quantum mechanics is approximated by the fact that the equations of state do not only depend on the particle density but also on its gradient. These equations were employed to model field emissions from metals and steady-state tunneling in metal-insulator-metal structures, and to simulate ultra-small semiconductor devices.
4.4 Electromagnetism for non-invasive control
The RAPSODI project-team works on the development of high-order polyhedral methods for electromagnetism. A well-known specificity in electromagnetism is that topology plays a crucial role in the well-posedness of the models. Dedicated analysis tools must then be deployed for their study 70. We are interested in the devising of HHO methods in the curl/curl setting 108. The mathematical analysis of HHO methods in this setting is particularly involved, as most of the needed discrete functional analysis tools are currently lacking. The design of (efficient and robust) multilevel linear solvers for statically condensed HHO approximations of electromagnetic models, as well as of computable (reliable and locally efficient) a posteriori error estimators on polyhedral cells are two other, still largely unexplored, aspects we are interested in. Our main target application, in the framework of a recently initiated collaboration with EDF, is the simulation of eddy current testing (ECT). ECT is used by EDF as a non-invasive control technique to assess the integrity of heat exchanger tubes in nuclear plants. The forward problem consists in solving the time-harmonic 3D Maxwell's equations in domains featuring more or less complex flaws. The use of high-order polyhedral methods is expected to yield improvements on two aspects. First, the support of polyhedral cells is expected to ease the full meshing process, and in particular enable to account for defects with complex geometries/topologies. Second, the increase in the approximation order is expected to yield a reduction of the noise on the computed control signal based on which the presence of a defect is inferred.
4.5 Large population models in epidemiology
Developing mathematical models to describe how infectious pathogens spread in animal populations is an essential step to identify the main biological mechanisms or environmental factors which contribute to the emergence of epidemics. When describing a pathogen spread at large scales, it is often relevant to model the distributions of hosts (which may represent individuals, animals or herds, for example) as spatially varying densities, and to model the pathogen dynamics via PDEs which describe the combined effect of neighbourhood interactions, large scale population dynamics, and environmental factors.
The team initiated a collaboration with INRAE (National Research Institute on Agriculture and Environment) on the modeling of different types of pathogen spread mechanisms in such continous models. A first focus of this collaboration is on neighbourhood interactions, which are a dominant factor in the infection dynamics of many pathogens (a specific example is the Bovine Viral Diarrhea Virus, an endemic disease present worldwide among industrial cattle herds, and causing annually large economic losses), and which at large scales may be described via non-local (convolution) terms. The analysis of the resulting model requires the development of dedicated mathematical tools, and will lead to a better understanding of the influence of neighborhood interactions on the spatial features of the epidemic dynamics. A second focus is on arboviruses, which are pathogens transmitted to mammals by the bite of arthropod vectors, mainly mosquitoes, and causing diseases such as the Zika virus, the Rift Valley fever and the West Nile virus. In this case, the aim is to produce a comprehensive description of the viral dynamics both in the vectors and in the hosts as well as to model their interaction in space (via diffusion processes and nonlocal interactions), which will then be used to identify the main mechanisms driving the virus spread.
4.6 Particle accelerators
Relativistic electron bunches are used in storage rings to produce intense radiation in various ranges of frequencies. The dynamics of these bunches is nonlinear because of interactions between electrons in the bunch. Moreover, these interactions occur in an asymmetric fashion because of the relativistic nature of the dynamics. The stability properties of the bunch (and thus the long-time properties of the dynamics) have been shown, both theoretically and experimentally, to be crucial in the understanding of the intensity of the emitted radiation 87, 116.
From a mathematical point of view, the dynamics of the electron density in the phase space can be described by a Vlasov–Fokker–Planck type equation 87 with a well suited mean-field self-interaction term 135. The mathematical understanding of the long time behavior of solutions to this equation and the design of adapted numerical schemes constitutes a challenging and physically important problem.
5 New software, platforms, open data
5.1 New software
5.1.1 ParaSkel++
-
Keywords:
PDEs, Polytopal meshes, High-order methods, HPC, C++
-
Functional Description:
ParaSkel++ is a C++ platform for the high-performance, arbitrary-order, 2/3D numerical approximation of PDEs on general polytopal meshes using skeletal Galerkin methods.
Skeletal Galerkin methods are a vast family of numerical methods for the approximation of PDE-based models that satisfy the following two building principles.
(1) The degrees of freedom (DOF) of the method split into (i) skeleton DOF, attached to the geometric entities (vertices, edges, faces) composing the mesh skeleton and common to all cells sharing the geometric entity in question, which prescribe the conformity properties of the underlying discrete functional space, and (ii) bulk DOF (if need be), attached to the interior of the cells, which play no role in the prescription of the conformity properties of the underlying discrete functional space.
(2) The global discrete bilinear form of the problem (potentially after linearization, if the problem is nonlinear) writes as the sum over the mesh cells of cell-wise (referred to as local) bilinear contributions.
The very structure underpinning skeletal methods grants them the property of being amenable to static condensation, i.e. locally to each cell, bulk DOF can be eliminated in terms of the local skeleton DOF by means of a Schur complement. The final global system to solve thus writes in terms of the skeleton DOF only. The skeletal family encompasses in particular standard FE methods and virtual-like Galerkin methods (VEM, HHO, HDG...). It does not contain (plain vanilla) DG methods.
ParaSkel++ offers a high-performance factorized C++ architecture for the implementation of arbitrary-order skeletal methods on general 2/3D polytopal meshes.
- URL:
- Publication:
-
Contact:
Simon Lemaire
6 New results
6.1 Modeling and numerical simulation of multi-component systems
In 34, C. Cancès, C. Chainais-Hillairet et al. propose a two-point flux approximation finite-volume scheme for the approximation of two cross-diffusion systems coupled by a free interface to account for vapor deposition. The moving interface is addressed with a cut-cell approach, where the mesh is locally deformed around the interface. The scheme preserves the structure of the continuous system, namely: mass conservation, nonnegativity, volume-filling constraints and decay of the free energy. Numerical results illustrate the properties of the scheme.
Multiphase poromechanics describes the evolution of multiphase flows in deformable porous media. Mathematical models for such multiphysics systems are inherently nonlinear, potentially degenerate and fully coupled systems of partial differential equations. In 45, C. Cancès et al. present a thermodynamically consistent multiphase poromechanics model falling into the category of Biot equations and obeying to a generalized gradient flow structure. It involves capillarity effects, degenerate relative permeabilities, and gravity effects. Contrary to established models it introduces a Lagrange multiplier associated to a bound constraint on the effective porosity in particular ensuring its positivity. They establish existence of global weak solutions under the assumption of a weak coupling strength, implicitly utilizing the gradient flow structure, as well as regularization, a Faedo-Galerkin approach and compactness arguments. This comprises the first global existence result for multiphase poromechanics accounting for degeneracies that are consistent with the multiphase nature of the flow.
In 46, C. Cancès, C. Chainais-Hillairet, B. Merlet, J. Venel et al. propose a new model to describe the evolution of the oxide layer covering iron in an aqueous environment. This model is an update of the original Diffusion Poisson Coupled Model (DPCM) proposed in 75 which is designed so that the Gibbs free energy is dissipated along time, making it consistent with the second principle of thermodynamics. The main changes with respect to the original model 75 are the use of nonlinear mobilities to represent the vacancy diffusion of iron cations and oxygen vacancies – these changes were already taken into account in the reduced model 16 –, and the fact that the oxide expansion is governed by the jump of grand canonical potential at the interfaces with the metal and the solution.
The presence of moving interfaces is a characteristic feature of corrosion phenomena. The evolution of these interfaces is governed by nonlinear laws and poses significant difficulties in the theoretical and numerical treatment of the models. B. Merlet, J. Venel et al. attack these difficulties in 60, namely, they show the existence of solutions to a 1D reduced corrosion model with a moving interface. Their method is based on a minimizing movement scheme for some modified Wasserstein metric.
In 35, C. Cancès, M. Herda et al. present two finite volume approaches for modeling the diffusion of charged particles, specifically ions, in constrained geometries using a degenerate Poisson-Nernst-Planck system with cross-diffusion and volume filling. Both methods utilize a two-point flux approximation and are part of the exponentially fitted scheme framework. The only difference between the two is the selection of a Stolarsky mean for the drift term originating from a self-consistent electric potential. The first version of the scheme, referred to as (SQRA), uses a geometric mean and is an extension of the squareroot approximation scheme studied in 19. The second scheme, (SG), utilizes an inverse logarithmic mean to create a generalized version of the Scharfetter-Gummel scheme. Both approaches ensure the decay of some discrete free energy. Classical numerical analysis results - existence of discrete solutions, convergence of the scheme as the grid size and the time step go to 0 - follow. Numerical simulations show that both schemes are effective for moderately small Debye lengths, with the (SG) scheme demonstrating greater robustness in the small Debye length regime.
In 17, C. Cancès et al. propose a provably convergent Finite Volume scheme for the so-called Stefan–Maxwell model, which describes the evolution of the composition of a multi-component mixture and reads as a cross-diffusion system. The proposed scheme relies on a Two-Point Flux Approximation, and preserves at the discrete level some fundamental theoretical properties of the continuous model, namely the non-negativity of the solutions, the conservation of mass, and the preservation of the volume-filling constraints. In addition, the scheme satisfies a discrete entropy-entropy dissipation relation, very close to the relation which holds at the continuous level. In this article, C. Cancès et al. present the scheme together with its numerical analysis, and finally illustrate its behavior with some numerical results.
In 23, J. Moatti et al. consider a drift-diffusion model for light emitting diode simulations with high carrier densities. Different finite volume discretisations of the system are introduced, and the case of non-Boltzmann statistics is discussed. Numerical results illustrate the importance of using a consistent flux discretisation (as the SEDAN one) in order to avoid unphysical behaviours.
In 24, J. Moatti et al. study an aluminium gallium nitride ((Al,Ga)N) LED device thanks to numerical simulations. The computations highlight that the fluctuations induced by the ((Al,Ga)N) alloy increase the non-radiative Auger recombination in comparison to the radiative process, which could lead to a degradation of the device. Thus, this indicates that a careful design (using for example wider wells) is required to improve the efficiency of deep UV light emitters.
In 62, J. Moatti et al. consider an (In,Ga)N/GaN semiconductor system with quantum wells. They introduce a model with accounts for random alloy fluctuations through an atomistic tight-binding model, where quantum corrections are introduced via a localization landscape theory and propose a numerical method to simulate the model at hand. They investigate the impact of the order of the wells on the device behaviour and compare the results of the simulations with existing simulation codes as well as with physical experimentations.
In 18, C. Cancès et al. prove the existence of weak solutions to a system of two diffusion equations that are coupled by a pointwise volume constraint. The time evolution is given by gradient dynamics for a free energy functional. Their primary example is a model for the demixing of polymers, the corresponding energy is the one of Flory, Huggins and de Gennes. Due to the nonlocality in the equations, the dynamics considered here is qualitatively different from the one found in the formally related Cahn–Hilliard equations. Their angle of attack stems from the theory of optimal mass transport, that is, they consider the evolution equations for the two components as two gradient flows in the Wasserstein distance with one joint energy functional that has the volume constraint built in. The main difference with their previous work 97 is the nonlinearity of the energy density in the gradient part, which becomes singular at the interface between pure and mixed phases.
6.2 Analysis and numerical simulation in electromagnetism
In 50, T. Chaumont-Frelet et al. analyse Nédélec finite element discretizations of the time-harmonic Maxwell's equation, and show that the discrete solution is asymptotically optimal.
In 59, S. Lemaire and S. Pitassi prove discrete versions of the first and second Weber inequalities on -like hybrid spaces spanned by polynomials attached to the faces and to the cells of a polyhedral mesh. The proven hybrid Weber inequalities are optimal in the sense that (i) they are formulated in terms of - and -like hybrid semi-norms designed so as to embed optimally (polynomially) consistent face penalty terms, and (ii) they are valid for face polynomials in the smallest possible stability-compatible spaces. The results are valid on domains with general, possibly non-trivial topology. In a second part are also proved, within a general topological setting, related discrete Maxwell compactness properties.
In 51, E. Creusé et al. propose an a posteriori goal-oriented error estimator for the harmonic (–) formulation arising in the modeling of eddy current problems, approximated by nonconforming finite element methods. It is based on the resolution of a dual problem associated with the initial one. For each of these two problems, a guaranteed equilibrated estimator is developed using some flux reconstructions. These fluxes also allow to obtain a goal-oriented error estimator that is fully computable and can be split in a principal part and a remainder one. Their theoretical results are illustrated by numerical experiments.
Volume integral methods for the solution of eddy current problems are very appealing in practice since they require meshing only the conducting regions. However, they require the assembly and storage of a dense stiffness matrix. With the objective of cutting down assembly time and memory occupation, low-rank approximation techniques like the Adaptive Cross Approximation (ACA) have been considered a major breakthrough. Recently, the VINCO framework has been introduced to reduce significantly memory occupation and computational time thanks to a novel factorization of the dense stiffness matrix. In 32, S. Pitassi et al. introduce a new matrix compression technique enabled by the VINCO framework. They compare the performance of VINCO framework approaches with state-of-the-art alternatives in terms of memory occupation, computational time and accuracy by solving benchmark eddy current problems at increasing mesh sizes; the comparisons are carried out using both direct and iterative solvers. The results clearly indicate that the so-called VINCO-FAIME approach which exploits the Fast Multipole Method (FMM) has the best performance.
6.3 Structural properties of dissipative models and their discretization
In 43, 33, C. Chainais-Hillairet, M. Alfaro et al. consider the so-called field-road diffusion model in a bounded domain and its approximation by a TPFA finite volume scheme. In both the continuous and the discrete settings, they prove the exponential decay of an entropy, and thus the long time convergence to the stationary state selected by the total mass of the initial data. Numerical simulations confirm and complete the analysis, and raise new issues.
In 36, C. Chainais-Hillairet et al. define, in the case of quasilinear convection-diffusion equations, an approximation of the numerical fluxes obtained by extending the Scharfetter and Gummel fluxes. They show that this approximation is compatible with the asymptotic thermal equilibrium on an application example.
Following 36, in 20, C. Chainais-Hillairet et al. propose a new numerical two-point flux for a quasilinear convection-diffusion equation. This numerical flux is shown to be an approximation of the numerical flux derived from the solution of a two-point Dirichlet boundary value problem for the projection of the continuous flux onto the line connecting neighboring collocation points. The later approach generalizes an idea first proposed by Scharfetter and Gummel for linear drift-diffusion equations. Convergence of the scheme is established, as well as relative entropy decay properties.
In 42, S. Lemaire et al. study the numerical approximation of sign-shifting problems of elliptic type. They fully analyze and assess the method briefly introduced in 63. The method, which is based on domain decomposition and optimization, is proved to be convergent as soon as, for a given loading, the continuous problem admits a unique solution of finite energy. Departing from the -coercivity approach, which relies on the use of geometrically fitted mesh families, the method works for arbitrary (interface-compliant) meshes. Moreover, it is shown convergent for a class of problems for which -coercivity is not applicable. A comprehensive set of test-cases complements the analysis.
In 30, J. Moatti considers an anisotropic drift-diffusion system for semiconductor models in exterior magnetic fields. Following the methodology introduced in 104, he introduces an Hybrid Finite Volume scheme and proves the existence of discrete solutions with bounds on the densities, as well as a long-time behaviour result. Numerical experiments illustrate the behaviour of the scheme.
In 37, J. Moatti et al. present two different low-order structure-preserving schemes for drift-diffusion systems on general meshes. The two schemes have an entropic structure, which ensures the positivity of the computed densities, and are respectively based on the Discrete Duality Finite Volume and Hybrid Finite Volume methods. Numerical results assert the robustness of the schemes and show that their behaviours are similar.
In 39, J. Moatti introduces a new nonlinear high-order scheme for advection-diffusion. The scheme is based on the Hybrid High-Order methodology, and is devised in order to preserve the entropy structure of the continuous equation, which ensures the positivity of the solutions. Numerical experiments show that the scheme converges at the expected order, while preserving positivity. Moreover, numerical results point out that the use of high-order approximation gives a better efficiency (accuracy for a given computational cost) than low-order methods.
Following 39, in 28, S. Lemaire and J. Moatti are interested in the high-order approximation of anisotropic, potential-driven advection-diffusion models on general polytopal partitions. They study two hybrid schemes, both built upon the Hybrid High-Order technology. The first one hinges on exponential fitting and is linear, whereas the second is nonlinear. The existence of solutions is established for both schemes. Both schemes are also shown to possess a discrete entropy structure, ensuring that the long-time behaviour of discrete solutions mimics the PDE one. For the nonlinear scheme, the positivity of discrete solutions is a built-in feature. In contrast, numerical evidence is displayed indicating that the linear scheme violates positivity, whatever the order. Finally, they verify numerically that the nonlinear scheme has optimal order of convergence, expected long-time behaviour, and that raising the polynomial degree results, also in the nonlinear case, in an efficiency gain.
In 13, C. Chainais-Hillairet, M. Herda et al. consider a drift-diffusion charge transport model for perovskite solar cells, where electrons and holes may diffuse linearly (Boltzmann approximation) or nonlinearly (e.g. due to Fermi-Dirac statistics). To incorporate volume exclusion effects, they rely on the Fermi-Dirac integral of order when modeling moving anionic vacancies within the perovskite layer which is sandwiched between electron and hole transport layers. After non-dimensionalization, they first prove a continuous entropy-dissipation inequality for the model. Then, they formulate a corresponding two-point flux finite volume scheme on Voronoi meshes and show an analogous discrete entropy-dissipation inequality. This inequality helps them to show the existence of a discrete solution to the nonlinear discrete system with the help of a corollary of Brouwer's fixed point theorem and the minimization of a convex functional. Finally, they verify the theoretically proven properties numerically, simulating a realistic device setup and showing exponential decay in time with respect to the -error as well as a physically and analytically meaningful relative entropy.
In 14, M. Herda et al. introduce and analyse numerical schemes for the homogeneous and the kinetic Lévy-Fokker-Planck equations. The discretizations are designed to preserve the main features of the continuous model such as conservation of mass, heavy-tailed equilibrium and (hypo)coercivity properties. They perform a thorough analysis of the numerical scheme and show exponential stability and convergence of the scheme. Along the way, they introduce new tools of discrete functional analysis, such as discrete nonlocal Poincaré and interpolation inequalities adapted to fractional diffusion. Their theoretical findings are illustrated and complemented with numerical simulations.
In 49, M. Herda et al. study a self-consistent Vlasov-Fokker-Planck equation which describes the longitudinal dynamics of an electron bunch in the storage ring of a synchrotron particle accelerator. They show existence and uniqueness of global classical solutions under physical hypotheses on the initial data. The proof relies on a mild formulation of the equation and hypoelliptic regularization estimates. They also address the problem of the long-time behavior of solutions. They prove the existence of steady states, called Haissinski solutions, given implicitly by a nonlinear integral equation. When the beam current (i.e. the nonlinearity) is small enough, they show uniqueness of steady state and local asymptotic nonlinear stability of solutions in appropriate weighted Lebesgue spaces. The proof is based on hypocoercivity estimates. Finally, they discuss the physical derivation of the equation and its particular asymmetric interaction potential.
Neuron models have attracted a lot of attention recently, both in mathematics and neurosciences. In 58, M. Herda et al. are interested in studying long-time and large-population emerging properties in a simplified toy model. From a mathematical perspective, this amounts to study the long-time behaviour of a degenerate reflected diffusion process. Using coupling arguments, the flow is proven to be a contraction of the Wasserstein distance for long times, which implies the exponential relaxation toward a (non-explicit) unique globally attractive equilibrium distribution. The result is extended to a McKean-Vlasov type non-linear variation of the model, when the mean-field interaction is sufficiently small. The ergodicity of the process results from a combination of deterministic contraction properties and local diffusion, the noise being sufficient to drive the system away from non-contractive domains.
In 26, M. Herda et al. analyse a finite volume scheme for a nonlocal version of the Shigesada-Kawazaki-Teramoto (SKT) cross-diffusion system. They prove the existence of solutions to the scheme, derive qualitative properties of the solutions and prove its convergence. The proofs rely on a discrete entropy-dissipation inequality, discrete compactness arguments, and on the novel adaptation of the so-called duality method at the discrete level. Finally, thanks to numerical experiments, they investigate the influence of the nonlocality in the system: on convergence properties of the scheme, as an approximation of the local system and on the development of diffusive instabilities.
In 15, C. Calgaro, C. Cancès and E. Creusé performed the convergence analysis of a finite volume scheme for a convection-diffusion equation involving a Joule effect term which was introduced in the former contribution 89 emanating from the team. The proof proposed in 15 relies on compactness arguments. In order to treat the Joule effect term, a second order discrete Gagliardo-Nirenberg inequality has been established by the authors. By going beyond the (nowadays usual) framework of discrete functional inequalities involving first order discrete differential operators, this contribution seems to be a genuine novelty in the field of discrete functional analysis.
6.4 Assessment and improvement of the efficiency of numerical methods
In 44, C. Cancès, M. Jonval et al. propose two numerical strategies to solve chemical equilibria in aqueous solutions. The first strategy can be thought as an extension of the parametrisation trick initially proposed in 85 to smoothen the stiff relation between molar fractions and chemical potential. In a second approach referred to as Cartesian representation, this relation is relaxed and only recovered at convergence. Numerical experiments show that our approaches allow to strongly improve the robustness of the Newton-Raphson algorithm with respect to state-of-the-art methods even without the adjunction of limitation strategies.
In 38, T. Laidin and T. Rey present an extension of the hybrid, model-adaptation method introduced in 27 for linear collisional kinetic equations in a diffusive scaling to the nonlinear mean-field Vlasov-Poisson-BGK model. The aim of the approach is to reduce the computational cost by taking advantage of the lower dimensionality of the asymptotic model. The authors show that the method offers a significant computational gain for the nonlinear model and illustrate properties such as mass conservation and long-time behaviour of the hybrid model.
In 21, E. Creusé et al. present a unified framework for goal-oriented estimates for elliptic and parabolic problems that combine the dual-weighted residual method with equilibrated flux reconstruction. This framework allows to analyze simultaneously different approximation schemes for the space discretization of the primal and the dual problems, such as conforming or nonconforming finite element methods, discontinuous Galerkin methods, or finite volume methods. Their main contribution is the splitting of the error on the quantity of interest into a fully computable estimator and a remainder that is bounded, up to an explicit constant, by the product of the fully computable estimators of the primal and dual problems. Some illustrative numerical examples that validate their theoretical results are presented.
6.5 Analysis and numerical simulation of variational models
In 47, C. Cancès et al. consider the convergence of a finite element discretization of a degenerate parabolic equation of -Laplace type with an additional external potential. The main novelty of the approach presented therein is that the authors use the underlying gradient flow structure in the -Wasserstein metric: from the abstract machinery of metric gradient flows, the convergence of the scheme is obtained solely on the basis of estimates that result naturally from the equation's variational structure. In particular, the limit is identified as the unique gradient flow solution without reference to monotonicity methods.
In 57, B. Merlet et al. introduce and study the notion of tensor rectifiable chains which form a two-dimensional chain complex of normed groups. They complete the theory of tensor flat chains in 53 by establishing a deformation theorem in this setting and by identifying isometrically some subgroups of tensor flat chains with corresponding subgroups of classical chains.
In 56, the same authors define and prove the existence of the decomposition in “connected components” for some objects which are very weak generalizations of surfaces (called flat chains). This result is used in the higher dimensional case of the previous paper to reduce the study of the jump set to the study of its “connected components” and then to understand their fine geometrical structure.
In 54, B. Merlet et al. study a variant of the Eikonal equation in 2D. The classical model arises in various physical models from the study of micromagnetism or liquid crystals and consists in the differential inclusion for functions . The regularity and even the dimension of the singular set of assuming that its entropy production is a finite measure is still an important unsolved problem. Here, the authors consider instead the differential inclusion or equivalently (the circle is replaced by the crossed formed by a vertical and a horizontal line). This model comes from anisotropic Ising models. In this variant, the regularity problem is easier and the authors show that the singular set is made of lines. They also establish similar results in higher dimension. This work introduces new lines of research for the study of the standard Eikonal equation.
In 55, B. Merlet, M. Pegon et al. establish a -regularity theorem for almost-minimizers of the functional , where , is the standard perimeter for Caccioppoli sets and is a nonlocal energy converging to the perimeter as vanishes. Their theorem provides a criterion for -regularity at a point of the boundary which is uniform as the parameter goes to 0. As a consequence they obtain that volume-constrained minimizers of are balls for any small enough. For small , this minimization problem corresponds to the large mass regime for a Gamow-type problem where the nonlocal repulsive term is given by an integrable kernel with sufficiently fast decay at infinity.
In 25, motivated by some models of pattern formation involving an unoriented director field in the plane, B. Merlet, M. Pegon et al. study a family of unoriented counterparts to the Aviles–Giga functional. They introduce a nonlinear curl operator for such unoriented vector fields as well as a family of even entropies which they call "trigonometric entropies". Using these tools they show two main theorems which parallel some results in the literature on the classical Aviles–Giga energy. The first is a compactness result for sequences of configurations with uniformly bounded energies. The second is a complete characterization of zero-states, that is, the limit configurations when the energies go to 0. Their methods provide alternative proofs in the classical Aviles–Giga context.
In 48, J. Candau-Tilh, B. Merlet et al. consider a variant of the optimal transport problem and investigate the existence and characterization of its maximizers. In particular, they show that among sets of any fixed volume, the ball is the unique solution up to translation of this problem.
In 61, A. Natale studies a class of discrete models in which a collection of particles evolves in time following the gradient flow of an energy depending on the cell areas of an associated Laguerre (i.e. a weighted Voronoi) tessellation. Using a modulated energy argument, it is proven that in the limit of a high number of particles, the discrete solutions converge towards smooth solutions of nonlinear diffusion PDEs of porous medium type.
In 52, A. Natale et al. introduce a time discretization for Wasserstein gradient flows based on the classical Backward Differentiation Formula of order two. The main building block of the scheme is the notion of geodesic extrapolation in the Wasserstein space, which in general is not uniquely defined. They propose several possible definitions for such an operation, and prove convergence of the resulting scheme to the limit PDE, in the case of the Fokker-Planck equation. For a specific choice of extrapolation they also prove a more general result, that is convergence towards EVI flows. Finally, they propose a variational finite volume discretization of the scheme which numerically achieves second order accuracy in both space and time.
In 22, E. Facca, A. Natale et al. address the numerical solution of the quadratic optimal transport problem in its dynamical form, the so-called Benamou-Brenier formulation. When solved using interior point methods, the main computational bottleneck is the solution of large saddle-point linear systems arising from the associated Newton-Raphson scheme. They compare different preconditioners to solve these linear systems via iterative methods, and they introduce a new one based on the partial commutation of the operators that compose the dual Schur complement of these saddle-point linear systems, which scales only slightly more than linearly with respect to the number of unknowns used to discretize the problem.
In 29, E. Facca et al. study the emergence of loop in complex networks in optimal transport problems with time-varying loads. The study includes both theoretical and experimental results, with a test-case defined on the Bordeaux bus network.
7 Bilateral contracts and grants with industry
7.1 Bilateral contracts with industry
A research collaboration contract has been signed in 2022 between RAPSODI and EDF R&D in the framework of the France Relance recovery plan. The contract follows the lines of the bilateral agreement between Inria and EDF. The research project is coordinated by S. Lemaire and involves S. Pitassi, whose 2-year post-doc position, which started in October 2022, has been funded in this framework ("Dispositif 4 de l'action de Préservation de l'Emploi de R&D"). The project concerns the development of high-order polyhedral methods for the numerical simulation of eddy current testing.
In 2023, the PRCE project HIPOTHEC (HIgh-order POlyhedral meTHods for Eddy Current testing simulations) has been funded in the generic ANR call. This project is coordinated by S. Lemaire, and is a collaboration between Inria, EDF, and 3 additional academic partners. The aim of the project is to pursue, within an enlarged academic consortium, the research efforts initiated in the framework of the France Relance collaboration between RAPSODI and EDF R&D. More details about the HIPOTHEC project can be found in Section 8.4.1.
The PhD thesis of M. Jonval (supervised by C. Cancès), that started in October 2021, is co-funded by Inria (salaries) and IFPEn (overhead costs). The contract follows the lines of the bilateral contract between Inria and IFPEn.
7.2 Bilateral grants with industry
CEA (Christian Bataillon) and ANDRA (Laurent Trenty) are involved in the EURAD project on corrosion modeling together with the RAPSODI project-team (C. Cancès, C. Chainais-Hillairet, and B. Merlet). More details on the project can be found in Section 8.3.1.
8 Partnerships and cooperations
8.1 International initiatives
8.1.1 PHC (Partenariats Hubert Curien)
C. Cancès has been the co-PI, with Jakub W. Both (Univ. Bergen, Norway), of the 2022-2023 Franco-Norwegian Aurora project GradFlowPoro funded ( 2k€/year) by Campus France. M. Jonval also took part to the project.
8.2 International research visitors
8.2.1 Visits of international scientists
Annamaria Massimini
-
Status:
PhD student
-
Institution of origin:
TU Vienna
-
Country:
Austria
-
Dates:
January 23-27
-
Context of the visit:
Numerical approximation of Generalized Poisson-Nernst-Planck models with cross diffusion.
-
Mobility program/type of mobility:
Research stay in the framework of an Amadeus Franco-Austrian project (46397PA) supported by Campus France.
Jian-Guo Liu
-
Status:
Professor
-
Institution of origin:
Duke University
-
Country:
USA
-
Dates:
June 5-23
-
Context of the visit:
Design and analysis of numerical schemes for the Cattaneo model.
-
Mobility program/type of mobility:
Invited professorship position funded by the LabEx CEMPI.
Federica Raimondi
-
Status:
Post-doctoral researcher
-
Institution of origin:
University of Salerno
-
Country:
Italy
-
Dates:
June 12-16
-
Context of the visit:
Mathematical and numerical analysis of models for the corrosion of iron.
-
Mobility program/type of mobility:
Research stay in the framework of the H2020 EJP EURAD project.
Stefan Portisch
-
Status:
PhD student
-
Institution of origin:
TU Vienna
-
Country:
Austria
-
Dates:
July 17-21
-
Context of the visit:
Analysis of a three-species model of Memristor.
-
Mobility program/type of mobility:
Research stay in the framework of the ERC project "Emerging Network Structures and Neuromorphic Applications".
Jakub W. Both, Omar Duran, Veljko Lipovak and Peter von Schultzendorff
-
Status:
Researcher / Researcher / PhD student /PhD student
-
Institution of origin:
University of Bergen
-
Country:
Norway
-
Dates:
November 20-24
-
Context of the visit:
Study of multiphase poromechanics systems.
-
Mobility program/type of mobility:
Research stay in the framework of the Aurora Franco-Norwegian project GradFlowPoro (2022–2023) supported by Campus France.
8.2.2 Visits of scientists from French institutions
Gaël Beaunée
-
Status:
INRAE researcher
-
Institution of origin:
INRAE Nantes
-
Dates:
June 13-14
-
Context of the visit:
Development of an epidemiological model to describe the intra-vector dynamics of arboviruses.
-
Mobility program/type of mobility:
Funded by the DIGIT-BIO MIDIIVEC INRAE project.
Gregor Gantner
-
Status:
Inria researcher (ISFP)
-
Institution of origin:
Inria Paris Centre
-
Dates:
September 18-22
-
Context of the visit:
Adaptive boundary element discretizations of time-harmonic wave propagation problems.
-
Mobility program/type of mobility:
Funded by the welcome package of Gregor Gantner.
Kevin Fourteau
-
Status:
Researcher
-
Institution of origin:
Météo France Grenoble
-
Dates:
October 9-12
-
Context of the visit:
Assessment of the compatibility of the snow (continuous and numerical) models with thermodynamics.
-
Mobility program/type of mobility:
Research stay in the framework of the IMPT S-NOW project; cf. § 8.4.3.
Alexandre Ern
-
Status:
Professor
-
Institution of origin:
École des Ponts ParisTech
-
Dates:
November 3
-
Context of the visit:
A posteriori error estimates for time-dependent wave propagation problems.
-
Mobility program/type of mobility:
Funded by the "Action exploratoire" AEx POPEG; see § 8.4.4.
8.2.3 Visits to international teams
T. Chaumont-Frelet
-
Visited institution:
University of Zurich
-
Country:
Switzerland
-
Dates:
October 9-13
-
Context of the visit:
Visited Stefan Sauter to work on the finite element discretization of time-harmonic wave propagation problems.
-
Mobility program/type of mobility:
Research stay funded by Univ. Zurich.
T. Chaumont-Frelet
-
Visited institution:
University of Bath
-
Country:
UK
-
Dates:
October 16-19
-
Context of the visit:
Visited Euan Spence to work on the finite element discretization of time-harmonic wave propagation problems.
-
Mobility program/type of mobility:
Research stay funded by AEx POPEG; see § 8.4.4.
T. Chaumont-Frelet
-
Visited institution:
TU Vienna
-
Country:
Austria
-
Dates:
November 27 - December 1
-
Context of the visit:
Visited Markus Melenk to work on the finite element discretization of time-harmonic wave propagation problems.
-
Mobility program/type of mobility:
Research stay funded by AEx POPEG; see § 8.4.4.
8.3 European initiatives
8.3.1 H2020 projects
C. Cancès, C. Chainais-Hillairet, B. Merlet and J. Venel are involved in the H2020 project EURAD (EUropean Joint Programme on RADioactive Waste Management). Inside EURAD, the DONUT work-package is concerned with the development and improvement of numerical methods and tools for modelling coupled processes. The task of the RAPSODI project-team inside EURAD/DONUT is to establish an energetic formulation of the Diffusion Poisson Coupled Model leading to new long-time robust numerical methods for the simulation of the corrosion processes in an underground repository. The project started in 2019, and the RAPSODI project-team received a grant of 138 750 euros. The final technical report (2023) is available 46.
8.4 National initiatives
8.4.1 ANR projects
C. Cancès has been a member of the ANR JCJC project COMODO. This project focuses on the mathematical and numerical study of cross-diffusion systems in moving domains. The targeted application is the simulation of the production of photovoltaic devices by a vapor deposition process.
- Title: CrOss-diffusion equations in MOving DOmains
- Type: JCJC
- ANR committee: Modèles numériques, simulation, applications (CE46) - 2019
- ANR reference: ANR-19-CE46-0002
- Duration: January 2020 - December 2023
- Budget: 213 810 euros
- Coordinator: Virginie Ehrlacher (ENPC & Inria Paris)
C. Cancès and M. Herda are members of the ANR JCJC project MICMOV. This project aims at gathering PDE analysts, probability theorists, and theoretical physicists to work on the derivation of macroscopic properties of physical systems from their microscopic description. The rigorous microscopic description of moving interfaces, the understanding of macroscopic nonlocal effects, and the mathematical apprehension of the underlying atomic mechanisms, are particularly important matters of this project.
- Title: MICroscopic description of MOVing interfaces
- Type: JCJC
- ANR committee: Mathématiques (CE40) - 2019
- ANR reference: ANR-19-CE40-0012
- Duration: March 2020 - October 2024
- Budget: 132 256 euros
- Coordinator: Marielle Simon (Université Lyon 1)
T. Chaumont-Frelet is the PI of the ANR JCJC project APOWA, funded in the 2023 generic call. The APOWA project aims at the development, analysis and implementation of a posteriori error estimators and adaptive finite element schemes for time-dependent wave propagation problems.
- Title: APOsteriori error estimates for WAve equations
- Type: JCJC
- ANR committee: Mathématiques (CE40) - 2023
- ANR reference: ANR-23-CE40-0019
- Duration: January 2024 - December 2027 (48 months)
- Budget: 266 725 euros
- Coordinator: T. Chaumont-Frelet
S. Lemaire is the PI of the ANR PRCE project HIPOTHEC, funded in the 2023 generic call. This project aims at developing accurate and flexible numerical solvers for eddy current testing simulations, based on high-order polyhedral methods. The target application, of industrial interest, is the non-invasive detection of flaws within steam generator tubes in nuclear plants.
- Title: HIgh-order POlyhedral meTHods for Eddy Current testing simulations
- Type: PRCE, in partnership with EDF R&D
- ANR committee: Modèles numériques, simulation, applications (CE46) - 2023
- ANR reference: ANR-23-CE46-0013
- Duration: January 2024 - December 2028 (60 months)
- Budget: 604 193 euros (in total), with 143 464 euros for Inria (Lille)
- Coordinator: S. Lemaire
- Consortium: Inria (Lille), UPHF (Valenciennes) - EDF (Palaiseau) - Université de Montpellier, Université Côte d'Azur (Nice)
8.4.2 LabEx CEMPI
Through their affiliation to the Laboratoire Paul Painlevé of Université de Lille, RAPSODI team members benefit from the support of the LabEx CEMPI.
- Title: Centre Européen pour les Mathématiques, la Physique et leurs Interactions
- Partners: Laboratoire Paul Painlevé (LPP) and Laser Physics department (PhLAM), Université de Lille
- ANR reference: 11-LABX-0007
- Duration: February 2012 - December 2024 (the project has been renewed in 2019)
- Budget: 6 960 395 euros
- Coordinator: Emmanuel Fricain (LPP, Université de Lille)
The "Laboratoire d'Excellence" CEMPI (Centre Européen pour les Mathématiques, la Physique et leurs Interactions), a project of the Laboratoire de mathématiques Paul Painlevé (LPP) and the laboratoire de Physique des Lasers, Atomes et Molécules (PhLAM), was created in the context of the "Programme d'Investissements d'Avenir" in February 2012. The association Painlevé-PhLAM creates in Lille a research unit for fundamental and applied research and for training and technological development that covers a wide spectrum of knowledge stretching from pure and applied mathematics to experimental and applied physics. The CEMPI research is at the interface between mathematics and physics. It is concerned with key problems coming from the study of complex behaviors in cold atoms physics and nonlinear optics, in particular fiber optics. It deals with fields of mathematics such as algebraic geometry, modular forms, operator algebras, harmonic analysis, and quantum groups, that have promising interactions with several branches of theoretical physics.
8.4.3 Mathematical Institute for Planet Earth (IMPT)
C. Cancès is the co-PI, together with Kévin Fourteau (Météo France Grenoble), of the S-NOW project (2023-2024) funded (15k€) by the Mathematical Institute for Planet Earth (IMPT). The goal of the S-NOW project is to assess the compatibility of the models used to described snow with thermodynamics, and introduce as minor as possible corrections if needed.
A. Natale is leading with Gaël Beaunée (INRAE) the project “Calibration of epidemic models on graphs with Optimal Transport and derivative-free optimization" (2023-2024) financed (55k€) by the Mathematical Institute for Planet Earth (IMPT). The project deals with the design of inference methods for epidemiological models on graphs. State-of-the-art inference methods to determine unknown parameters in this context often rely on extensive manipulations of the model outputs to match simulated results with measurements, which limits their robustness and reliability. This project aims at developing optimal transport metrics to compare epidemic scenarios, and use these to construct more robust calibration techniques via minimum discrepancy estimators. The post-doc position of C. Sarrazin is funded in the framework of this project.
8.4.4 Exploratory Actions (AEx)
T. Chaumont-Frelet is the PI of the "Action exploratoire" AEx POPEG funded by Inria. The aim of the POPEG project is to develop innovative Galerkin methods for high-frequency wave propagation problems. Specifically, the objective is to use Gaussian coherent state basis functions in order to drastically reduce the number of degrees of freedom compared to finite element basis functions for the same accuracy when the frequency is high. The PhD position of Florentin Proust is supported by this project.
8.4.5 SMAI BOUM
M. Pegon is the PI of a SMAI BOUM 2023 project aiming at funding ( 1k€) the participation of young researchers to the conference "Calculus of Variations in Lille - 4th edition" which will take place in Lille in June 2024.
8.5 Regional initiatives
8.5.1 Technological Development Actions (ADT)
S. Lemaire is the coordinator of the ADT project ParaSkel++, funded by Inria and the Hauts-de-France region, which started in February 2020 and was renewed for two more years in 2022. The aim of the project is to develop an optimized parallel C++ platform for the arbitrary-order numerical approximation of PDEs on general polytopal meshes (more details can be found in Section 5.1.1). T. Zoto was hired in December 2022 for 2 years as the new lead developer of the platform.
8.5.2 CPER WaveTech
The regional initiative CPER WaveTech "Ondes et Matière pour la Deep Tech" aims at investigating, in relation with the regional industrial and socio-economical spheres, advanced subjects in photonics, TeraHertz, and quantum mechanics. The post-doc of P. Gervais, supervised by M. Herda in the framework of a collaboration with the PhLAM laboratory, is funded by the CPER WaveTech.
9 Dissemination
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
C. Calgaro was part of the organizing committee of the Colloque Analyse Appliquée et Modélisation held on November 15-17 2023 in Monastir (Tunisia). The aim of this conference was to bring together researchers specialising in modelling and analysis, both theoretical and numerical, in memory of Ezzeddine Zahrouni, who passed away in 2018. The main aspects covered were the analysis of nonlinear partial differential equations, numerical schemes for partial differential equations, and dispersive equations.
C. Cancès, C. Chainais-Hillairet, M. Herda, M. Pegon, and T. Rey co-organized the 5th edition of the conference "Asymptotic Behaviors of systems of PDEs arising in physics and biology" (ABPDE V), that was held in Lille (at Polytech Lille engineering school) from June 5 to June 9, 2023. The event gathered around 70 participants and featured 10 plenary talks, 21 contributed talks, and 10 posters.
9.1.2 Member of the conference program committees
C. Chainais-Hillairet was a member of the scientific committee of the international conference FVCA X held in Strasbourg from October 30 to November 3.
As members of the scientific committee of the GdR MaNu, C. Cancès and C. Chainais-Hillairet served in the scientific committee of the Scientific Days of the GdR, which were held in Le Croisic on October 23-27.
9.1.3 Member of the editorial boards
C. Chainais-Hillairet is editor-in-chief of the book series Mathématiques et Applications and member of the editorial boards of ESAIM: Mathematical Modelling and Numerical Analysis and of the North-Western European Journal of Mathematics.
9.1.4 Reviewer - reviewing activities
RAPSODI permanent team members are regular reviewers for all the main international journals in PDEs, calculus of variations, numerical analysis, and scientific computing.
9.1.5 Scientific communications
C. Cancès gave invited talks at the KWIM Conference 2023: Cross-Diffusion Systems: Analysis and Stochastics held in Konstanz (Germany) from February 27 to March 3, and at the FVCA X conference held in Strasbourg from October 30 to November 3 where he was a plenary speaker. He also gave talks in mini-symposia at the SIAM Geosciences congress (Bergen, Norway, June 19-22) and at the ENUMATH 2023 congress (Lisbon, Portugal, September 4-8). He finally gave a seminar at the CERAMATHS laboratory (Université Polytechnique des Hauts-de-France, Valenciennes) on March 30.
J. Candau-Tilh gave a short talk during the SHAPO ANR project closure meeting held in Paris in April 2023.
C. Chainais-Hillairet presented a poster at the FVCA X conference held in Strasbourg from October 30 to November 3.
T. Chaumont-Frelet gave a seminar at the Zurich Colloquium in Applied and Computational Mathematics of ETHZ on October 11.
M. Herda gave several seminar talks, in Université de Nantes in January 2023, in Université de Lyon and Université de Toulouse in May 2023, and in UTC (Compiègne) in November 2023.
M. Jonval presented a poster at the ABPDE V conference held in Lille on June 5-9. He also gave contributed talks at the SIAM Geosciences congress held in Bergen (Norway) on June 19-22 and at the Scientific Days of the GdR MaNu that were held in Le Croisic on October 23-27.
T. Laidin gave a talk at the MAFRAN DAYS 2023 held at King's College in Cambridge from February 27 to March 2. He also gave talks at the APBDE V conference in Lille and at the FVCA X conference in Strasbourg.
S. Lemaire gave a talk at the SIAM Conference on Computational Science and Engineering (CSE23) held in Amsterdam (The Netherlands) on February 27-March 3. He also gave a talk during the workshop on "StrUcture-PREserving NUmerical Methods for Partial Differential Equations" (SUPRENUMPDE 2023) that was held in Lausanne (Switzerland) on July 3-7, as well as during the 17th US National Congress on Computational Mechanics (USNCCM XVII) held in Albuquerque (NM, USA) on July 23-27. Lastly, S. Lemaire attended the "Assyr Abdulle's Memorial Conference" organized in Lausanne (Switzerland) on February 2, as well as the 5th Conference on Asymptotic Behaviors of systems of PDEs arising in physics and biology (ABPDE V) held in Lille on June 5-9.
B. Merlet gave a talk at the workshop "Topological and geometrical aspects in complex materials". He also gave an online talk at the conference "Compensated compactness and applications to materials" held from April 3 to April 7 at the Banff International Research Station.
J. Moatti gave a talk at the ABPDE V conference held in Lille on June 5-9. He also gave a talk at the FVCA X conference held in Strasbourg from October 30 to November 3.
A. Natale gave a talk in the workshop "Optimal Transport Theory and Applications to Physics" which was held at Les Houches School of Physics on March 13-17. He also gave a talk at the ENUMATH 2023 congress held in Lisbon (Portugal) on September 4-8 within the mini-symposium "Entropy/energy-stable methods for time evolution problems". He also gave a talk at the workshop Firedrake `23 which took place in Great Missenden (UK) on September 13-15. He finally gave a seminar at Université Paris-Saclay (January 23).
T. Rey gave several seminars, in Université Côte d'Azur (Nice), École Centrale de Lyon, and K.U. Leuven.
T. Zoto attended the 5-day long CEA-EDF-Inria Summer School in Numerical Analysis on "Robust polyhedral discretizations for computational mechanics", that was organized at the EDF Lab (Palaiseau) on June 26-30. It consisted mostly of lectures during the day, and practical sessions in the evenings. T. Zoto also attended the 5-day long ACM Europe Summer School on "HPC Computer Architectures for AI and Dedicated Applications" at the Barcelona Supercomputing Center in Barcelona (Spain) on July 3-7. It consisted of lectures, and of practicals on HPC computer architectures and AI applications.
9.1.6 Leadership within the scientific community
C. Cancès is the leader of the task "Numerical methods for high-performance computing of coupled processes" in the DONUT work-package on the development and improvement of numerical methods and tools for modelling coupled processes within the H2020 EJP EURAD project on the management of nuclear waste at the European level (see Section 8.3.1).
9.1.7 Scientific expertise
C. Chainais-Hillairet was part of the selection committee for junior researchers (CR and ISFP) of the Inria Center at the University of Lille, as well as of the selection committees for full professor (PR) positions at Université Rennes 1 and Université de Rouen-Normandie and for a tenured assistant professor (MCF) position at Université Paris-Dauphine. She is also a member of the Section 26 - "Mathématiques appliquées et applications des mathématiques" of the Conseil National des Universités. She was finally a member of the HCERES committee for the evaluation of the Laboratoire Jacques-Louis Lions in November 2023.
T. Rey was part of the hiring committee for a tenured assistant professor (MCF) position at Université Paris-Dauphine.
9.1.8 Research administration
C. Calgaro is a member of the management team of the Faculté des Sciences et Technologies at Université de Lille.
J. Candau-Tilh is a member of the Commission Égalité of the Laboratoire Paul Painlevé.
C. Cancès is a member of the council of the graduate school MADIS, of the Conseil d’Administration of the SMAI, and of the Bureau Scientifique de Centre (BSC) of the Inria Center at the University of Lille.
C. Cancès and C. Chainais-Hillairet are members of the scientific committee of the GdR MaNu, a research network on mathematics for nuclear energy.
C. Chainais-Hillairet is vice-director of the Laboratoire Paul Painlevé, in charge of human resources for researchers, professors and assistant professors.
M. Herda is an elected member of the Conseil de Laboratoire and of the Commission Mixte related to the math laboratory and the math department respectively. M. Herda is also substitute member of the Inria Lille Comité de Centre and nominated member of the Commission des Utilisateurs des Moyens Informatiques (CUMI) at Inria Lille.
M. Jonval is the PhD students representative at the MADIS doctoral school council.
T. Laidin is a member of the Commission Mixte of the Laboratoire Paul Painlevé.
Since 2022, S. Lemaire is responsible for the Inria Lille research center (15 research teams) of the coordination of the yearly campaign of activity reports. He was also a member, until August 2023, of the Commission de Développement Technologique (CDT) of the Inria Lille research center in charge of the recruitment of engineers. Finally, he is the webmaster of the RAPSODI website.
B. Merlet is an elected member of the council of the Faculté des Sciences et Technologies at Université de Lille. He is also a designated member of the Commission Mixte of the Laboratoire Paul Painlevé.
A. Natale has been the co-organizer of the Numerical Analysis and PDEs (ANEDP) seminar of the Laboratoire Paul Painlevé since September 2022.
T. Rey was in charge until August 2023 of the evaluation and communication on the environmental footprint of the activities of the Laboratoire Paul Painlevé.
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
RAPSODI team members are strongly involved in teaching at Université de Lille and Université Polytechnique des Hauts-de-France (UPHF, Valenciennes), as well as in the engineering schools Centrale Lille and Polytech Lille, and in SKEMA Business School.
Faculty members of the project-team ensure their teaching duties (192h yearly), as well as important administrative tasks in the math departments. E. Creusé is the head of the mathematics department of the CERAMATHS laboratory at UPHF. T. Rey was in charge of the M2 Scientific Computing until August 2023. C. Calgaro is a member of the Conseil de Département de Mathématiques at Université de Lille. M. Pegon is in charge of the students' recruitment for a departement of the engineering school Polytech Lille.
Inria members of the project-team also take an important part in teaching activities. C. Cancès was in charge of the course "Scientific computing" (24h) for 1st year (L3) students in Centrale Lille, as well as of the course "Nonlinear PDEs" (48h) of the M2 Recherche and of the course "Mathematical tools for simulation - Hyperbolic PDEs" (18h) of the M2 Scientific Computing at Université de Lille. A. Natale taught the course "Refresher in mathematics" (20h) in the framework of the M2 Data Science of Université de Lille and Centrale Lille. He also taught the course "Numerical solution of nonlinear problems" (49h) in the framework of the M1 Scientific Computing at Université de Lille. S. Lemaire taught the course "Mathematical tools for simulation - Elliptic & Parabolic PDEs" (34h) in the framework of the M2 Scientific Computing at Université de Lille. M. Herda taught part (15h) of the M2 Scientific Computing refresher course "Modeling" in September.
Finally, PhD students and post-docs also contribute in the teaching activities (up to 64h yearly), either at Université de Lille (J. Candau-Tilh, P. Gervais, T. Laidin, J. Moatti) or in SKEMA Business School and Centrale Lille (M. Jonval).
In the framework of the Journées scientifiques du GdR MaNu, C. Chainais-Hillairet gave a 3-hour lecture on corrosion models. S. Lemaire also gave a short lecture in the framework of the CEA-EDF-Inria Summer School in Numerical Analysis on "Robust polyhedral discretizations for computational mechanics", that was organized at the EDF Lab (Palaiseau) on June 26-30.
9.2.2 Supervision
Post-docs
- Post-doc of C. Sarrazin (Inria): Calibration of epidemic models on graphs with Optimal Transport and derivative-free optimization, co-supervised by A. Natale and Gaël Beaunée (INRAE), since November 2023, funded by the Mathematical Institute for Planet Earth (IMPT).
- Post-doc of P. Gervais (CNRS): Self-consistent Vlasov-Fokker-Planck equations, and application to the modeling of electron beams, advised by M. Herda, since September 2023, funded by the CPER WaveTech (CNRS).
- Post-doc of S. Pitassi (Inria/EDF): High-order polyhedral methods for eddy current testing simulation, co-supervised by S. Lemaire and Jérémy Dalphin & Jean-Pierre Ducreux (EDF), since October 2022, funded through the research collaboration contract between RAPSODI and EDF R&D in the framework of the France Relance funding plan.
- Post-doc of E. Facca (Inria): Locally conservative methods for the approximation of dynamical transport on unstructured meshes, advised by A. Natale, until March 2023, funded by Inria.
PhD students
- PhD of A. Dupouy (Inria): Mathematical and numerical analysis of dissipative problems with free boundaries, co-supervised by C. Cancès and C. Chainais-Hillairet, since October 2023, co-funded by Inria and the Hauts-de-France region.
- PhD of R. Colombier (UPHF, Valenciennes): Numerical schemes for solving the macroscopic quantum hydrodynamics equations, co-supervised by E. Creusé (UPHF) and C. Calgaro, since November 2022, co-funded by UPHF and the Hauts-de-France region.
- PhD of M. Jonval (Inria/IFPEn): Advanced numerical methods for stiff problems in the context of reactive transport, co-supervised by C. Cancès and Ibtihel Ben Gharbia & Thibault Faney & Quang-Huy Tran (IFPEn), since October 2021, co-funded by Inria and IFPEn in the framework of the bilateral contract.
- PhD of T. Laidin (Université de Lille): Hybrid kinetic/fluid numerical methods and discrete hypocoercivity for the Boltzmann equation for semi-conductors, co-supervised by T. Rey and Marianne Bessemoulin-Chatard (CNRS & Université de Nantes), since October 2021, co-funded by the LabEx CEMPI and the Hauts-de-France region.
- PhD of J. Candau-Tilh (Université de Lille): Isoperimetric problems with Wasserstein interactions, co-supervised by B. Merlet and Michael Goldman (CMAP, École Polytechnique), since September 2021, funded by an ENS fellowship.
- PhD of J. Moatti (Inria): Development and numerical analysis of high-order schemes for convection-diffusion models, study of their long-time behaviour, co-supervised by C. Chainais-Hillairet, M. Herda and S. Lemaire, defended on September 26 2023, funded by Inria.
Engineers
- Software engineer position of T. Zoto (Inria) on the development of the ParaSkel++ platform: supervised by S. Lemaire, since December 2022, funded by Inria and the Hauts-de-France region (ADT ParaSkel++).
Interns
- M2 internship of S. Dossin (MSc Scientific Computing, Université de Lille): Design of a mathematical model of infection by arboviruses describing the within-vector dynamics, supervised by M. Herda and A. Natale, April-September 2023, funded by the MIIDIVEC INRAE project of Gaël Beaunée (INRAE).
- M1 internship of A. A. Diallo (MSc Scientific Computing, Université de Lille): Study and implementation of a reaction-advection-diffusion population dynamics model, supervised by C. Calgaro and Olivier Goubet (ULille), May-July 2023, funded by Inria.
- M1 internship of I. Tagliaferro de Oliveira Tezoto (MSc Scientific Computing, Université de Lille): Analysis and simulations of an epidemiological model with transmission via neighborhood contacts, supervised by M. Herda and A. Natale, May-July 2023, funded by Inria.
- M1 internship of A. El Hajj (MSc Scientific Computing, Université de Lille): Spectral moment method for a linear Vlasov equation, supervised by T. Rey, May-July 2023.
9.2.3 Juries
Habilitation à Diriger des Recherches (HDR)
- C. Chainais-Hillairet chaired the Habilitation defense committee of T. Rey (Université de Lille) on February 17. Title: Contributions to the Mathematical and Numerical Analysis of Multiscale Kinetic Equations41.
- C. Chainais-Hillairet reported on the Habilitation manuscript and was a member of the Habilitation defense committee of Benjamin Boutin (Université Rennes 1) on July 3. Title: Finite difference methods for hyperbolic problems with boundaries: stability and multiscale analysis.
- C. Cancès was a member of the Habilitation defense committee of Marianne Bessemoulin-Chatard (CNRS & Université de Nantes) on July 12. Title: Construction et analyse de schémas numériques pour des modèles issus de la physique.
- C. Chainais-Hillairet was a member of the Habilitation defense committee of Caroline Bauzet (Aix-Marseille Université) on December 18. Title: Stochastic PDEs, finite-volume schemes and applications in mechanics.
PhD defense
- C. Chainais-Hillairet was a member of the PhD defense committee of Ali Toufaili (Aix-Marseille Université) on March 14. Title: Modélisation de la turbulence compressible pour l'explosion.
- C. Chainais-Hillairet was a referee of the thesis manuscript and a member of the PhD defense committee of Massimiliano Montone (Université Côte d’Azur) on March 30. Title: Full-wave discontinuous Galerkin time-domain methods for semiconductor device simulation.
- C. Chainais-Hillairet, M. Herda and S. Lemaire were members of the PhD defense committee of J. Moatti (Inria RAPSODI, Université de Lille) on September 26. Title: Development and numerical analysis of high-order schemes for convection-diffusion models, study of their long-time behaviour40.
- B. Merlet chaired the PhD defense committee of Élise Bonhomme (Université Paris-Saclay) on November 8. Title: Variational methods applied to discrete and evolutionary brittle damage models.
9.3 Popularization
9.3.1 Organization of popularization events
M. Herda co-organized the opening event of the photo exhibition "Mathématiques, informatique... avec elles !" at Université de Lille. This half-day event gathered students, teachers, and university staff to exchange on the place of women in jobs related to mathematics. The event consisted of a conference by an historian of mathematics, a round table with testimonies from women working in math related jobs (academic and private), and closed with the opening of the photo exhibition.
9.3.2 Internal or external Inria responsibilities
Since September 2023, S. Lemaire is part of the mediation team at the Inria Lille research center, co-responsible of the organization of the monthly internal scientific outreach event "30 MIN. de sciences".
9.3.3 Education
C. Calgaro spent 3 half-days with middle and high school students visiting the University. She introduced them to the research world in mathematical fluid dynamics.
M. Jonval welcomed a schoolgirl (3ème) for a day to introduce her to the research world.
B. Merlet supervised a group of PhD students during the Mathematics-Enterprises week (SEME) that took place in Lille from April 17 to April 21. The aim of a SEME is to create exchanges between industry and academia through a week-long work session on problems posed by the industry and requiring innovative mathematical approaches.
9.3.4 Interventions
M. Pegon co-animated a workshop for highschool students titled "First contact with the research in mathematics" for the initiative "Les cordées de la réussite".
S. Lemaire realized two interventions in the framework of the national scientific outreach program "1 scientifique, 1 classe / Chiche !" in two (2nde) classes of the high schools César Baggio (Lille) and Jean Moulin (Roubaix) in February and March.
T. Laidin gave a talk at the "13:45" popularization seminar of the Inria Center at the University of Lille.
10 Scientific production
10.1 Major publications
- 1 articleExponential decay of a finite volume scheme to the thermal equilibrium for drift--diffusion systems.Journal of Numerical Mathematics2532017, 147-168HALDOI
- 2 articleHypocoercivity and diffusion limit of a finite volume scheme for linear kinetic equations.Mathematics of Computation89January 2020, 1093-1133HALDOIback to text
- 3 articleImproving Newton's method performance by parametrization: the case of Richards equation.SIAM Journal on Numerical Analysis5542017, 1760--1785HALback to text
- 4 articleIncompressible immiscible multiphase flows in porous media: a variational approach.Analysis & PDE1082017, 1845--1876HALDOIback to text
- 5 articleNumerical analysis of a robust free energy diminishing Finite Volume scheme for parabolic equations with gradient structure.Foundations of Computational Mathematics1762017, 1525-1584HALback to text
- 6 articleLarge-time behaviour of a family of finite volume schemes for boundary-driven convection-diffusion equations.IMA Journal of Numerical Analysis404October 2020, 2473-2505HALDOIback to text
- 7 articlep-robust equilibrated flux reconstruction in H(curl) based on local minimizations. Application to a posteriori analysis of the curl-curl problem.SIAM Journal on Numerical Analysis6142023, 1783--1818HALDOI
- 8 articleA discrete Weber inequality on three-dimensional hybrid spaces with application to the HHO approximation of magnetostatics.Mathematical Models and Methods in Applied Sciences3212022, 175-207HALDOI
- 9 articleAn arbitrary-order and compact-stencil discretization of diffusion on general meshes based on local reconstruction operators.Computational Methods in Applied Mathematics144June 2014, 461-472HALDOIback to text
- 10 articleAn efficient numerical method for solving the Boltzmann equation in multidimensions.Journal of Computational Physics3532018, 46-81HALDOIback to text
- 11 articleGeneralized compressible flows and solutions of the H(div) geodesic problem.Archive for Rational Mechanics and Analysis2020HALDOI
- 12 articleA highly anisotropic nonlinear elasticity model for vesicles I. Eulerian formulation, rigidity estimates and vanishing energy limit.Arch. Ration. Mech. Anal.21722015, 651--680HALDOI
10.2 Publications of the year
International journals
International peer-reviewed conferences
Doctoral dissertations and habilitation theses
Reports & preprints
10.3 Cited publications
- 63 articleAn optimization-based numerical method for diffusion problems with sign-changing coefficients.Comptes Rendus. Mathématique35542017, 472--478DOIback to text
- 64 articleNumerical analysis of a nonlinearly stable and positive Control Volume Finite Element scheme for Richards equation with anisotropy.ESAIM: Mathematical Modelling and Numerical Analysis5242018, 1532-1567HALDOIback to text
- 65 articleConvergence of a positive nonlinear control volume finite element scheme for an anisotropic seawater intrusion model with sharp interfaces.Numerical Methods for Partial Differential Equations3612020, 133-153HALDOIback to text
- 66 articleNumerical analysis of a finite volume scheme for a seawater intrusion model with cross-diffusion in an unconfined aquifer.Numerical Methods for Partial Differential EquationsMay 2018HALDOIback to text
- 67 bookGradient flows: in metric spaces and in the space of probability measures.Springer Science & Business Media2005back to text
- 68 articleMultiscale Hybrid-Mixed method.SIAM J. Numer. Anal.5162013, 3505--3531back to text
- 69 articleOn convex Sobolev inequalities and the rate of convergence to equilibrium for Fokker-Planck type equations.Comm. Partial Differential Equations261-22001, 43-100URL: http://dx.doi.org/10.1081/PDE-100002246DOIback to text
- 70 bookMathematical foundations of computational electromagnetism.198Applied Mathematical SciencesSpringer, Cham2018, ix+458URL: https://doi.org/10.1007/978-3-319-70842-3DOIback to text
- 71 articleA note on hypocoercivity for kinetic equations with heavy-tailed equilibrium.Comptes Rendus. Mathématique3583July 2020, 333-340HALDOIback to text
- 72 articleProjective and Telescopic Projective Integration for Non-Linear Kinetic Mixtures.Journal of Computational Physics45836 pages, 16 figures, 3 tablesJune 2022, 111082HALDOIback to text
- 73 articleOn several numerical strategies to solve Richards' equation in heterogeneous media with Finite Volumes.Computational Geosciences262022, 1297--1322HALDOIback to text
- 74 inproceedingsRobust Newton solver based on variable switch for a finite volume discretization of Richards equation.Finite Volumes for Complex Applications IXBergen, NorwayJune 2020HALback to text
- 75 articleCorrosion modelling of iron based alloy in nuclear waste repository.Electrochim. Acta55152010, 4451--4467back to textback to textback to textback to text
- 76 bookIntroduction to modeling of transport phenomena in porous media.4Springer1990back to text
- 77 softwareParaSkel++: a C++ platform for the high-performance, arbitrary-order, 2/3D numerical approximation of PDEs on general polytopal meshes using skeletal Galerkin methods.v1August 2021 lic: GNU Lesser General Public License v3.0 only.HALSoftware HeritageVCSback to text
- 78 articleBasic principles of virtual element methods.Math. Models Methods Appl. Sci. (M3AS)2312013, 199--214back to text
- 79 incollectionVariational mean field games.Active Particles, Volume 1Springer2017, 141--171back to text
- 80 articleA relaxation scheme for the nonlinear Schrödinger equation.4232004, 934--952back to text
- 81 articleExponential decay of a finite volume scheme to the thermal equilibrium for drift--diffusion systems.Journal of Numerical Mathematics253https://arxiv.org/abs/1601.00813September 2017, 147-168HALDOIback to text
- 82 articleStudy of a finite volume scheme for the drift-diffusion system. Asymptotic behavior in the quasi-neutral limit.SIAM J. Numer. Anal.5242014, 1666--1691URL: http://dx.doi.org/10.1137/130913432DOIback to text
- 83 articleWeitere Studien über das Wärmegleichgewicht unter Gasmolekl̎en.Wiener Berichte661872, 275--370back to text
- 84 articleDécomposition polaire et réarrangement monotone des champs de vecteurs.CR Acad. Sci. Paris Sér. I Math.3051987, 805--808back to text
- 85 articleImproving Newton's Method Performance by Parametrization: The Case of the Richards Equation.SIAM J. Numer. Anal.5542017, 1760-1785back to text
- 86 articleCollective learning modeling based on the kinetic theory of active particles.Phys. Life Rev.162016, 123--139back to text
- 87 articleLinear theory of microwave instability in electron storage rings.Physical Review Special Topics-Accelerators and Beams1462011, 061002back to textback to text
- 88 articleTwo classes of linearly implicit local energy-preserving approach for general multi-symplectic Hamiltonian PDEs.4012020, 108975back to text
- 89 articleA combined finite volume-finite element scheme for a low-Mach system involving a Joule term.AIMS Math.512020, 311--331URL: https://doi.org/10.3934/math.2020021DOIback to text
- 90 articleA numerical analysis focused comparison of several Finite Volume schemes for an Unipolar Degenerated Drift-Diffusion Model.IMA Journal of Numerical Analysis4112021, 271-314HALDOIback to text
- 91 articleConvergence of a Finite-Volume Scheme for a Degenerate Cross-Diffusion Model for Ion Transport.Numerical Methods for Partial Differential Equations352https://arxiv.org/abs/1801.094082019, 545-575HALDOIback to text
- 92 articleLarge time behavior of nonlinear finite volume schemes for convection-diffusion equations.SIAM Journal on Numerical Analysis585September 2020, 2544-2571HALDOIback to text
- 93 articleNumerical analysis of a nonlinear free-energy diminishing Discrete Duality Finite Volume scheme for convection diffusion equations.Computational Methods in Applied Mathematics183https://arxiv.org/abs/1705.10558 - Special issue on ''Advanced numerical methods: recent developments, analysis and application''2018, 407-432HALDOIback to text
- 94 articleSimulation of multiphase porous media flows with minimizing movement and finite volume schemes.European Journal of Applied Mathematics3062019, 1123-1152HALDOIback to text
- 95 articleA variational finite volume scheme for Wasserstein gradient flows.Numerische Mathematik14632020, pp 437 - 480HALDOIback to text
- 96 articleA convergent entropy diminishing finite volume scheme for a cross-diffusion system.SIAM Journal on Numerical Analysis585https://arxiv.org/abs/2001.112222020, pp. 2784-2710HALDOIback to text
- 97 articleA two-phase two-fluxes degenerate Cahn--Hilliard model as constrained Wasserstein gradient flow.Arch. Ration. Mech. Anal.23322019, 837--866back to text
- 98 articleFinite Volume approximation of a two-phase two fluxes degenerate Cahn-Hilliard model.ESAIM: Mathematical Modelling and Numerical Analysis5532021, 969--1003HALDOIback to text
- 99 articleConvergence and a posteriori error analysis for energy-stable finite element approximations of degenerate parabolic equations.Mathematics of Computation903282021, 517-563HALDOIback to text
- 100 articleA convergent finite volume scheme for dissipation driven models with volume filling constraint.Numerische Mathematik1512022, 279--328HALDOIback to textback to text
- 101 incollectionRecent development in kinetic theory of granular materials: analysis and numerical methods.Trails in Kinetic TheorySEMA SIMAI Springer Serieshttps://arxiv.org/abs/2001.11206 - 36 pages, 5 figuresSpringerFebruary 2021, 1-36HALDOIback to text
- 102 articleEntropy dissipation methods for degenerate parabolic problems and generalized Sobolev inequalities.Monatsh. Math.13312001, 1--82URL: http://dx.doi.org/10.1007/s006050170032DOIback to text
- 103 articleAsymptotic behaviour of a finite-volume scheme for the transient drift-diffusion model.IMA J. Numer. Anal.2742007, 689--716URL: http://dx.doi.org/10.1093/imanum/drl045DOIback to text
- 104 articleLong-time behaviour of hybrid finite volume schemes for advection-diffusion equations: linear and nonlinear approaches.Numerische Mathematik1512022, 963-1016HALDOIback to textback to textback to text
- 105 articleEntropy-dissipative discretization of nonlinear diffusion equations and discrete Beckner inequalities.Modelisation Mathématique et Analyse Numérique5012016, 135-162HALback to text
- 106 articleConvergence of a finite volume scheme for a parabolic system with a free boundary modeling concrete carbonation.ESAIM: Mathematical Modelling and Numerical Analysis5222018, 457-480HALDOIback to text
- 107 articleBridging the Multiscale Hybrid-Mixed and Multiscale Hybrid High-Order methods.ESAIM: Mathematical Modelling and Numerical Analysis5612022, 261-285HALDOIback to text
- 108 articleA discrete Weber inequality on three-dimensional hybrid spaces with application to the HHO approximation of magnetostatics.Mathematical Models and Methods in Applied Sciences3212022, 175-207HALDOIback to text
- 109 articleA Hybrid High-Order method for highly oscillatory elliptic problems.Computational Methods in Applied Mathematics1942019, 723-748HALDOIback to text
- 110 articleUnified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second-order elliptic problems.SIAM J. Numer. Anal.4722009, 1319--1365back to text
- 111 bookPoromechanics.John Wiley & Sons2004back to text
- 112 inproceedingsSinkhorn Distances: Lightspeed Computation of Optimal Transport.Proceedings of the 26th International Conference on Neural Information Processing Systems - Volume 2NIPS'13Red Hook, NY, USALake Tahoe, NevadaCurran Associates Inc.2013, 2292–2300back to text
- 113 articleA Hybrid High-Order locking-free method for linear elasticity on general meshes.Comput. Methods Appl. Mech. Engrg.2832015, 1--21back to text
- 114 articleStatistical mechanics of money.The European Physical Journal B-Condensed Matter and Complex Systems1742000, 723--729back to text
- 115 articleFinite volume schemes for diffusion equations: introduction to and review of modern methods.Math. Models Methods Appl. Sci.2482014, 1575-1620back to text
- 116 articleStable coherent terahertz synchrotron radiation from controlled relativistic electron bunches.Nature Physics1572019, 635--639back to text
- 117 articleTP or not TP, that is the question.Comput. Geosci.182014, 285--296back to text
- 118 articleConvergence of a Lagrangian discretization for barotropic fluids and porous media flow.SIAM Journal on Mathematical Analysis5432022HALDOIback to text
- 119 inproceedingsWhy Do We Need Voronoi Cells and Delaunay Meshes?Numerical Geometry, Grid Generation and Scientific ComputingLecture Notes in Computational Science and EngineeringChamSpringer International Publishing2019, 45--60DOIback to text
- 120 articleEntropy and convergence analysis for two finite volume schemes for a Nernst-Planck-Poisson system with ion volume constraints.Numerische Mathematik1511April 2022, 99-149HALDOIback to text
- 121 articleProjective methods for stiff differential equations: problems with gaps in their eigenvalue spectrum.SIAM J. Sci. Comput.2442003, 1091--1106back to text
- 122 articleStrong stability-preserving high-order time discretization methods.SIAM Rev.4312001, 89--112URL: https://doi.org/10.1137/S003614450036757Xback to text
- 123 articleAnisotropic Boltzmann-Gibbs dynamics of strongly magnetized Vlasov-Fokker-Planck equations.Kinetic and Related Models 123https://arxiv.org/abs/1610.051382019, 593-636HALDOIback to text
- 124 articleHydrodynamic limit of granular gases to pressureless Euler in dimension 1.Quarterly of Applied Mathematics75https://arxiv.org/abs/1602.09103 - 26 pages, 1 figure2017, 155-179HALDOIback to text
- 125 articleThe variational formulation of the Fokker-Planck equation.SIAM J. Math. Anal.2911998, 1--17back to text
- 126 articleOn the translocation of masses.C. R. (Dokl.) Acad. Sci. URSS, n. Ser.371942, 199--201back to text
- 127 articleMsFEM à la Crouzeix--Raviart for highly oscillatory elliptic problems.Chinese Annals of Mathematics, Series B3412013, 113--138back to text
- 128 articleAsymptotic-preserving Projective Integration Schemes for Kinetic Equations in the Diffusion Limit.3422012, A579–-A602back to textback to text
- 129 articleAn overview of computational methods for chemical equilibrium and kinetic calculations for geochemical and reactive transport modeling.Pure Appl. Chem.8952017, 597--643back to text
- 130 articleBridging the hybrid high-order and virtual element methods.IMA J. Numer. Anal.4112021, 549--593DOIback to text
- 131 articleA variational formulation of the BDF2 method for metric gradient flows.ESAIM: M2AN5312019, 145-172back to text
- 132 inproceedingsProjective integration for nonlinear BGK kinetic equations.Finite Volumes for Complex Applications VIII200Hyperbolic, Elliptic and Parabolic ProblemsProceedings FVCA 8Lille, FranceSpringer International PublishingJune 2017, 155-162HALDOIback to text
- 133 articleA gradient structure for reaction-diffusion systems and for energy-drift-diffusion systems.Nonlinearity2442011, 1329--1346URL: http://dx.doi.org/10.1088/0951-7715/24/4/016DOIback to text
- 134 softwareversionKINEBEC - Numerical simulation of Boltzmann-Norheim equation.1.0December 2021 lic: GNU General Public License v3.0 only.HALSoftware Heritageback to text
- 135 articleLongitudinal wake field for an electron moving on a circular orbit.Part. Accel.57BNL-630901996, 9--64back to text
- 136 articleA mixed finite element discretization of dynamical optimal transport.Journal of Scientific Computing9122022, 1--26back to text
- 137 articleComputation of optimal transport with finite volumes.ESAIM: Mathematical Modelling and Numerical Analysis555September 2021, 1847-1871HALDOIback to textback to text
- 138 inproceedingsTPFA finite volume approximation of Wasserstein gradient flows.International Conference on Finite Volumes for Complex ApplicationsSpringer2020, 193--201back to text
- 139 articleReciprocal relations in irreversible processes. II..Physical Review381931, 2265--2279back to text
- 140 articleMoment preserving Fourier-Galerkin spectral methods and application to the Boltzmann equation.SIAM Journal on Numerical Analysis606December 2022, 3216-3240HALDOIback to text
- 141 articleOn the stability of equilibrium preserving spectral methods for the homogeneous Boltzmann equation.Applied Mathematics Letters120https://arxiv.org/abs/2011.05811November 2021, 107187HALback to text
- 142 articlePartial Localization, Lipid Bilayers, and the Elastica Functional.1933September 2009, 475--537DOIback to text
- 143 unpublishedVariational Modelling: Energies, gradient flows, and large deviations.2014, arXiv:1402.1990back to text
- 144 articleComputational optimal transport.Center for Research in Economics and Statistics Working Papers2017-862017back to text
- 145 phdthesisSpatio-temporal dynamics of relativistic electron bunches during the microbunching instability : study of the Synchrotron SOLEIL and UVSOR storage rings.Université Lille1 - Sciences et TechnologiesSeptember 2014HALback to text
- 146 bookOptimal transport for applied mathematicians.Birkäuser, NY5558-63Springer2015, 94back to text
- 147 articleDirectional persistence of chemotactic bacteria in a traveling concentration wave.Proceedings of the National Academy of Sciences108392011, 16235--16240back to text
- 148 articleMulti-Component Multiphase Flow Through a Poroelastic Medium.J. Elasticity1352019, 485-507back to text
- 149 articleMulti-component Multiphase Porous Flow.Arch. Ration. Mech. Anal.2352020, 2171-2196URL: https://doi.org/10.1007/s00205-019-01473-7back to text
- 150 articleA universal model for mobility and migration patterns.Nature48473922012, 96--100back to text
- 151 unpublishedA thermodynamic formulation for multiphase compositional flows in porous media.2020, HAL: hal-02925433back to text

