2023Activity reportProject-TeamSERENA

7.1.1 DiSk++

• Name:
  Discontinuous Skeletal C++ Library
• Keywords:
  High order methods, Polyhedral meshes, C++
• Scientific Description:
  Discontinuous Skeletal methods approximate the solution of boundary-value problems by attaching discrete unknowns to mesh faces (hence the term skeletal) while allowing these discrete unknowns to be chosen independently on each mesh face (hence the term discontinuous). Cell-based unknowns, which can be eliminated locally by a Schur complement technique (also known as static condensation), are also used in the formulation. Salient examples of high-order Discontinuous Skeletal methods are Hybridizable Discontinuous Galerkin methods and the recently-devised Hybrid High-Order methods. Some major benefits of Discontinuous Skeletal methods are that their construction is dimension-independent and that they offer the possibility to use general meshes with polytopal cells and non-matching interfaces. The mathematical flexibility of Discontinuous Skeletal methods can be efficiently replicated in a numerical software: by using generic programming, the DiSk++ library offers an environment to allow a programmer to code mathematical problems in a way completely decoupled from the mesh dimension and the cell shape.
• Functional Description:
  The software provides a numerical core to discretize partial differential equations arising from the engineering sciences (mechanical, thermal, diffusion). The discretization is based on the "Hybrid high-order" or "Discontinuous Skeletal" methods, which use as principal unknowns polynomials of arbitrary degree on each face of the mesh. An important feature of these methods is that they make it possible to treat general meshes composed of polyhedral cells. The DiSk ++ library, using generic programming techniques, makes it possible to write a code for a mathematical problem independently of the mesh. When a user writes the code for his problem using the basic operations offered by DiSk ++, that code can be executed without modifications on all types of mesh already supported by the library and those that will be added in the future.
• URL:
  https://­github.­com/­wareHHOuse/­diskpp
• Publication:
  hal-01429292
• Author:
  Matteo Cicuttin
• Contact:
  Matteo Cicuttin
• Partner:
  CERMICS

7.1.2 APS-MG

• Name:
  A-Posteriori-Steered MultiGrid
• Keywords:
  Finite element modelling, Linear system, A posteriori error estimates, Multigrid methods, P-robustness
• Scientific Description:
  APS-MG (a-posteriori-steered multigrid) is a geometric-type multigrid solver whose execution is steered by the associated a posteriori estimate of the algebraic error. In particular, the descent direction and the level-wise step sizes are adaptively optimized. APS-MG corresponds to a V-cycle geometric multigrid with zero pre- and solely one post-smoothing step, via block-Jacobi (overlapping additive Schwarz/local patchwise problems). Its particularity is that it is robust with respect to the polynomial degree p of the underlying finite element discretization, i.e., APS-MG contracts the error on each iteration by a factor that is independent of p. APS-MG is the implementation of the solver developed in https://hal.science/hal-02070981 and https://hal.science/hal-02494538.
• Functional Description:
  APS-MG (a-posteriori-steered multigrid) is an iterative linear solver implemented in MATLAB. It can treat systems of linear algebraic equations arising from order p conforming finite element discretization of second-order elliptic diffusion problems. APS-MG is a geometric-type multigrid method and uses a hierarchy of nested meshes. It corresponds to a V-cycle geometric multigrid solver with zero pre- and one post-smoothing step via block-Jacobi (overlapping additive Schwarz/local patchwise problems). A salient feature is the choice of the optimal step size for the descent direction on each mesh level.
• URL:
  https://­github.­com/­JanPapez/­APS-MG
• Publications:
  hal-02070981, hal-02494538, hal-02498247
• Contact:
  Jan Papez

7.1.3 FEMLAB

• Name:
  FEMLAB
• Keywords:
  High order finite elements, Discontinuous Galerkin, Hybrid high-order methods, Adaptive algorithms, Finite element modelling
• Functional Description:
  FEMLAB is a Matlab library for different classes of FEM code. This library is designed to use a parallel computing toolbox in Matlab to accelerate the time for assembling the linear systems. It has been tested on 48 parallel processors of the HPC nodes. Another critical point is that different FEM codes in this library are designed to support arbitrary order of the basis functions and support the adaptive mesh refinement algorithm.
• Release Contributions:
  FEMLAB is updated in 2023 to support the adaptive algorithm.
• URL:
  https://­gitlab.­inria.­fr/­zdong/­FEMLAB
• Publications:
  hal-03109470, hal-03109548, hal-03322267, hal-03513280, hal-03185683, hal-03315088, hal-03695484, hal-03753221, hal-03889072
• Contact:
  Zhaonan Dong

7.1.4 Skwer

• Keywords:
  Differential equations, State-oriented simulation
• Scientific Description:
  Unlike classical approaches which discretize time a priori to determine the state, the State-Oriented Simulation (SOS) method discretizes the state to determine durations, thus following ideas from the Quantized State Systems (QSS) methods. The aim is to give rigorous interpretation of idealized or hybrid physical models, and of cosimulation. The aspect that most distinguishes us from other approaches is that we do not make use of differential-algebraic equations (DAEs). We rather solve more general multiscale numerical stiffness problems based on nonstandard ODE formulations.
• Functional Description:
  Skwer aims at solving differential equations inherent to 0D physical modeling. This includes in particular standard ODEs but also differential equations with conditionals and "idealized behavior" resulting from passing to the limit over some parameters.
• News of the Year:
  We have developed the necessary machinery to desynchronize elementary integrators making the approach fully asynchronous event in dense cases (contrary to the QSS approach, which requires synchronization of internal states in case of direct variable-equation dependency between integrators). We have finalized system rewriting aspects (various enhancement of data structures as well as algorithms). We have developed a variable order scheme where each state variable may have its own order (independent of others) thanks to the use of a formula-based technique to produce guaranteed a priori error bounds for the individual approximations. We have finally dropped the Maclaurin series code in favor of a more specialized (and lighter) approach based on direct generation of exponential terms. We have tested the final algorithm over various systems of differential equations to validate the approach.
• URL:
  https://­gitlab.­inria.­fr/­skwer/­skwer
• Publication:
  hal-01636392
• Contact:
  Sebastien Furic
• Participants:
  Sebastien Furic, François Clement, Geraldine Pichot

7.1.5 coq-num-analysis

• Name:
  Numerical analysis Coq library
• Keywords:
  Coq, Numerical analysis, Real analysis
• Scientific Description:
  These Coq developments are based on the Coquelicot library for real analysis. Version 1.0 includes the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
• Functional Description:
  Formal developments and proofs in Coq of numerical analysis problems. The current long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
• News of the Year:

  The formalization in Coq of simplicial Lagrange finite elements is almost complete. This include the formalizations of the definitions and main properties of monomials, their representation using multi-indices, Lagrange polynomials, the vector space of polynomials of given maximum degree (about 6 kloc). This also includes algebraic complements on the formalization of the definitions and main properties of operators on finite families of any type, the specific cases of abelian monoids (sum), vector spaces (linear combination), and affine spaces (affine combination, barycenter, affine mapping), sub-algebraic structures, and basics of finite dimension linear algebra (about 22 kloc). A new version (2.0) of the opam package will be available soon, and a paper will follow.

  We have also contributed to the Coquelicot library by adding the algebraic structure of abelian monoid, which is now the base of the hierarchy of canonical structures of the library.

• URL:
  https://­lipn.­univ-paris13.­fr/­coq-num-analysis/
• Publications:
  hal-01344090, hal-01391578, hal-03105815, hal-03471095, hal-03516749, hal-03889276
• Contact:
  Sylvie Boldo
• Participants:
  Sylvie Boldo, François Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
• Partners:
  LIPN (Laboratoire d'Informatique de l'Université Paris Nord), LMAC (Laboratoire de Mathématiques Appliquées de Compiègne)

7.1.6 MODFRAC

• Name:
  MODFRAC
• Keywords:
  Meshing, Fracture network, Ellipses, Polygons, Mesher, Mesh
• Scientific Description:
  The meshing methodology is based on a combined frontal-Delaunay approach in a Riemannian context.
• Functional Description:
  The MODFRAC software automatically builds meshes of fracture networks. As an input, it takes a DFN (Discrete Fracture Network) geometric model consisting of ellipses or polygons that have been randomly generated in the tridimensional space while following experimental statistics. It completes this model by first calculating the intersections between fractures, that are straight segments. On each fracture, it computes in turn the intersections between these straight segments, subdividing them into subsegments. It then creates a conforming set of these subsegments, and selects the necessary fractures using a graph structure. It transmits this information to an “indirect” surface mesher, where the tridimensional mesh results from the construction of planar meshes of the parametric domains.
• News of the Year:
  APP deposit, january 2023. Addition of OpenMP parallelism.
• Publications:
  hal-03480570, hal-02102811
• Contact:
  Geraldine Pichot
• Participants:
  Patrick Laug, Houman Borouchaki, Geraldine Pichot
• Partner:
  Université de Technologie de Troyes

7.1.7 nef-flow-fpm

• Keywords:
  2D, 3D, Porous media, Fracture network, Geophysical flows
• Scientific Description:

  The code is based on the implementation of the mixed hybrid finite element method as detailed in: An efficient numerical model for incompressible two-phase flow in fractured media Hussein Hoteit, Abbas Firoozabadi, Advances in Water Resources 31, 891–905, 2008. https://doi.org/10.1016/j.advwatres.2008.02.004

  The model of fractures and the coupling between the porous flow and the flow in the network of fractures is described in: : Modeling Fractures and Barriers as Interfaces for Flow in Porous Media V. Martin, J. Jaffré, J. E. Roberts, SIAM Journal on Scientific Computing, 2005. https://doi.org/10.1137/S1064827503429363

  Validation benchmark test from the publication: Inga Berre, et al., Verification benchmarks for single-phase flow in three-dimensional fractured porous media, Advances in Water Resources, Volume 147, 2021. https://doi.org/10.1016/j.advwatres.2020.103759.

• Functional Description:
  nef-flow-fpm is a Matlab code to simulate flows in fractured porous media with the mixed-hybrid finite element methods (RT0).
• Release Contributions:
  Implementation of the mixed hybrid method for 3D porous flows, Discrete fracture Networks (DFN) flows and the coupling between DFN and porous flows.
• News of the Year:
  Call metis to perform the mesh partitionning. Generate data per subdomain for HPDDM solver (Neumann matrices, local sizes and indices, local second member). Simulations with PETSC/HPDDM, the largest networks contains 378k fractures.
• URL:
  https://­gitlab.­inria.­fr/­nef/­nef-flow-fpm
• Contact:
  Geraldine Pichot
• Participants:
  Geraldine Pichot, Daniel Zegarra Vasquez, Michel Kern, Raphael Zanella

7.1.8 nef-transport-fpm

• Keywords:
  3D, Porous media, Incompressible flows, Transport model
• Scientific Description:
  The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit.
• Functional Description:
  nef-transport-fpm is a Matlab code for simulating transport by advection diffusion in porous-fractured media.
• News of the Year:
  Add transport in a network of fractures with the proper handling of the coupling conditions at the fractures intersections.
• Contact:
  Geraldine Pichot
• Participants:
  Geraldine Pichot, Michel Kern, Daniel Zegarra Vasquez, Alessandra Marelli, Dania Khiralla

7.1.9 ParaCirce

• Name:
  Parallel Circulant Embedding
• Keywords:
  2D, 3D, Hydrogeology, Gaussian random fields, MPI
• Scientific Description:
  ParaCirce implements the algorithm proposed by [C. R. Dietrich and G. N. Newsam. A fast and exact method for multidimensional gaussian stochastic simulations. Water Resources Research, 29(8):2861-2869, 1993] as well as an algorithm to accelerate the padding estimation [Pichot et al. SMAI Journal of Computational Mathematics, 8, pp.21, 2022].
• Functional Description:
  ParaCirce implements a parallel Circulant Embedding method for the generation in parallel of 2D or 3D Gaussian Random Fields (second order stationary).
• Release Contributions:
  A new GRF type has been introduced to wrap the std::vector initially returned from generate(). It contains all the characteristics of the GRF. Add API for the FFTW to select the planning strategy.
• News of the Year:
  A new GRF type has been introduced to wrap the std::vector initially returned from generate(). It contains all the characteristics of the GRF. Add API for the FFTW to select the planning strategy.
• URL:
  https://­gitlab.­inria.­fr/­slegrand/­paracirce
• Publication:
  hal-03190252
• Contact:
  Geraldine Pichot
• Participants:
  Geraldine Pichot, Simon Legrand

7.1.10 Pruners

• Name:
  Pruners
• Keywords:
  Combinatorics, Parameter studies, Automation
• Functional Description:
  Pruners is a language aimed at automating parameter studies. It allows the specification of parameter combinations, and make them available via environment variables. Those can then be used by any specified command as input parameters.
• Release Contributions:
  - Parameter space specification - Launching commands with each combination as parameter - File system interaction with read/write functions and Json format
• News of the Year:
  Open source licence GPL and opening of the repository. Add skip and keep options to select particular combinations of parameters. Add configure option to replace pruners script variables into a templated file. Add asynchronous execution of combinations.
• URL:
  https://­team.­inria.­fr/­serena/­en/­research/­software/­pruners/
• Authors:
  Thierry Martinez, Simon Legrand, Geraldine Pichot
• Contact:
  Thierry Martinez

Invariant-domain time-stepping for compressible flows

Participants: Alexandre Ern, Jean-Luc Guermond, Zuodong Wang.

Compressible Navier–Stokes simulation at $Re=1000$

In 2022, the authors laid the foundations of a new paradigm for invariant-domain time-stepping applied to hyperbolic problems using high-order Runge–Kutta methods. The key result achieved this year is the extension to implicit-explicit (IMEX) time-stepping and the application to the compressible Navier–Stokes equations, as described in 26. The decisive step-forward is the satisfaction of physical bounds on the density and energy while allowing for a high-order discretization in space and in time. An example of application to the compressible Navier–Stokes equations at Reynolds $Re=1000$ is displayed in Figure 1. This is a very challenging problem owing to the interactions between shocks and walls and the development of multiscale vortical structures. Moreover, in 49, we considered a scalar conservation law with a stiff source term having multiple equilibrium points. For this quite challenging situation, we proposed a scheme that can be asymptotic-preserving.

Polytopal discretization methods

Participants: Zhaonan Dong, Alexandre Ern, Jean-Luc Guermond, Stefano Piccardo, Morgane Steins, Zuodong Wang.

Further progress has been accomplished in the development and analysis of hybrid high-order (HHO) methods. Three topics were investigated. First, $C^0$-HHO methods for the biharmonic problem in 22 leading to a competitive method in terms of error vs. computational effort with respect to estabished methods such as the $C^0$-interior penalty discontinuous Galerkin method. Second, within the framework of the PhD Thesis of Morgane Steins (38,defended this year), HHO methods for the wave equation using a leapfrong scheme for time discretization were studied. The contributions include a convergence analysis 50 and a time-explicit marching scheme 35. Finally, HHO methods were used to study surface tension effects between two immiscible Stokes fluids within the PhD Thesis of Stefano Piccardo (37, defended this year) 34.

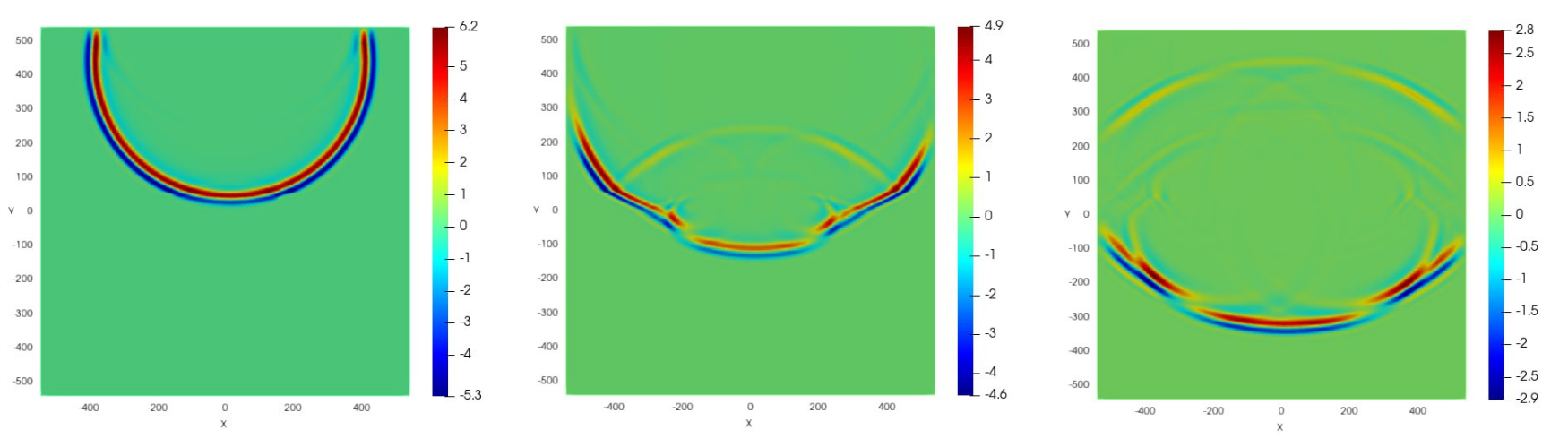
Error control with quality uniform in polynomial degree for the curl–curl (simplified Maxwell) problem

Participants: Martin Vohralík.

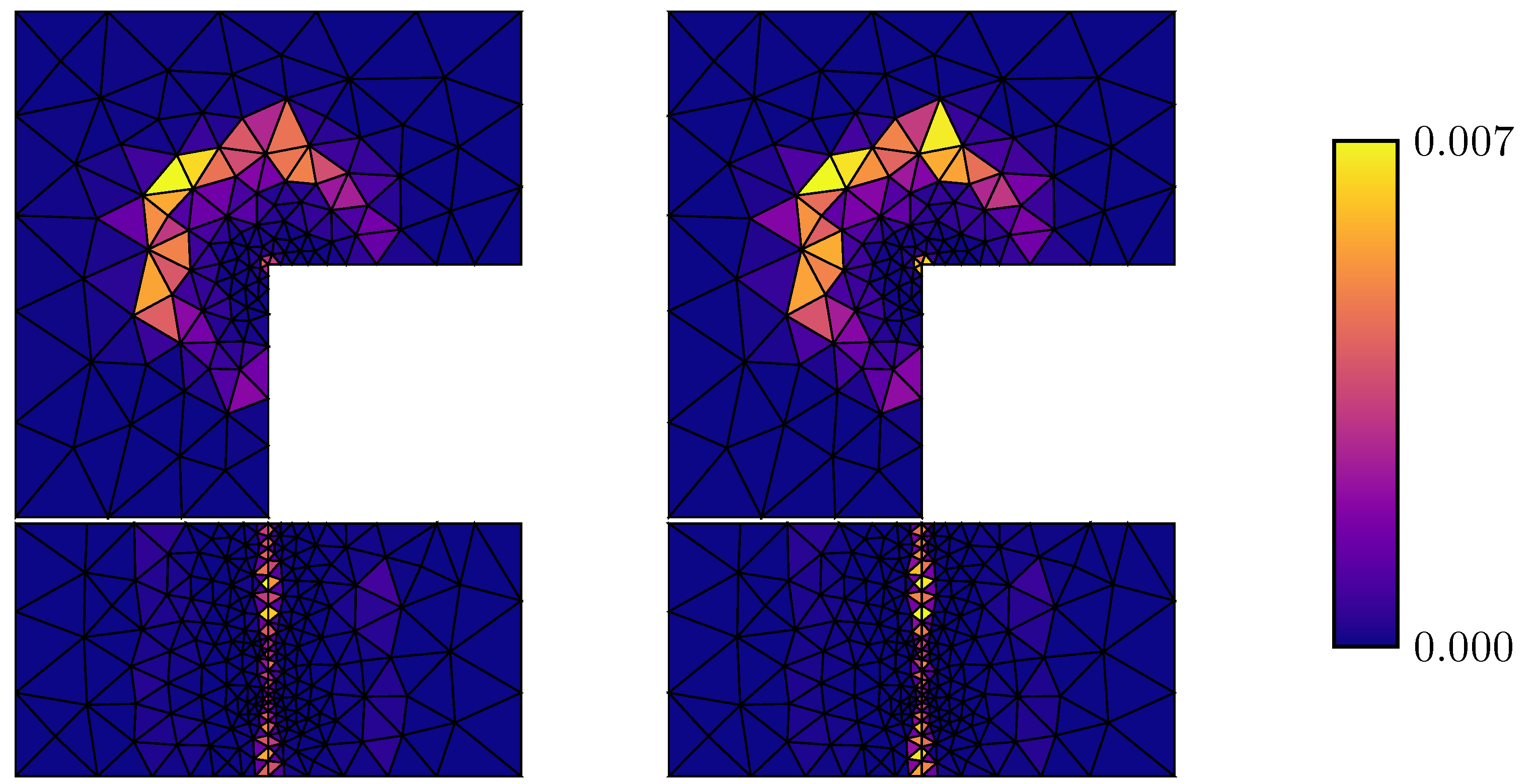
A posteriori estimates for the curl–curl problem

In 20, we present a local construction of $𝐇\left(\mathrm{curl}\right)$-conforming piecewise polynomials satisfying a prescribed curl constraint. We start from a piecewise polynomial not contained in the $𝐇\left(\mathrm{curl}\right)$ space but satisfying a suitable orthogonality property. The procedure employs minimizations in vertex patches and the outcome is, up to a generic constant independent of the underlying polynomial degree, as accurate as the best-approximations over the entire local versions of $𝐇\left(\mathrm{curl}\right)$. This allows to design guaranteed, fully computable, constant-free, and polynomial-degree-robust a posteriori error estimates of the Prager–Synge type for Nédélec's finite element approximations of the curl–curl problem. A divergence-free decomposition of a divergence-free $𝐇\left(\mathrm{div}\right)$-conforming piecewise polynomial, relying on over-constrained minimizations in Raviart–Thomas' spaces, is the key ingredient. Numerical results confirm the theoretical developments, see Figure 2 for an illustration.

Error control with quality uniform in spline degree for isogeometric analysis

Participants: Gregor Gantner, Martin Vohralík.

In 29, we consider spline/isogeometric analysis discretizations of the Poisson model problem, focusing on high polynomial degrees and strong hierarchical refinements. We derive a posteriori error estimates by equilibrated fluxes, i.e., vector-valued mapped piecewise polynomials lying in the $𝐇\left(\mathrm{div}\right)$ space which appropriately approximate the desired divergence constraint. Our estimates are constant-free in the leading term, locally efficient, and robust with respect to the polynomial degree. They are also robust with respect to the number of hanging nodes arising in adaptive mesh refinement employing hierarchical B-splines. Two partitions of unity are designed, one with larger supports corresponding to the mapped splines, and one with small supports corresponding to mapped piecewise multilinear finite element hat basis functions. The equilibration is only performed on the small supports, avoiding the higher computational price of equilibration on the large supports or even the solution of a global system. Thus, the derived estimates are also as inexpensive as possible. An abstract framework for such a setting is developed, whose application to a specific situation only requests a verification of a few clearly identified assumptions. Numerical experiments illustrate the theoretical developments and even indicate, though not rigorougsly proved, robustness with respect to the smoothness of the splines.

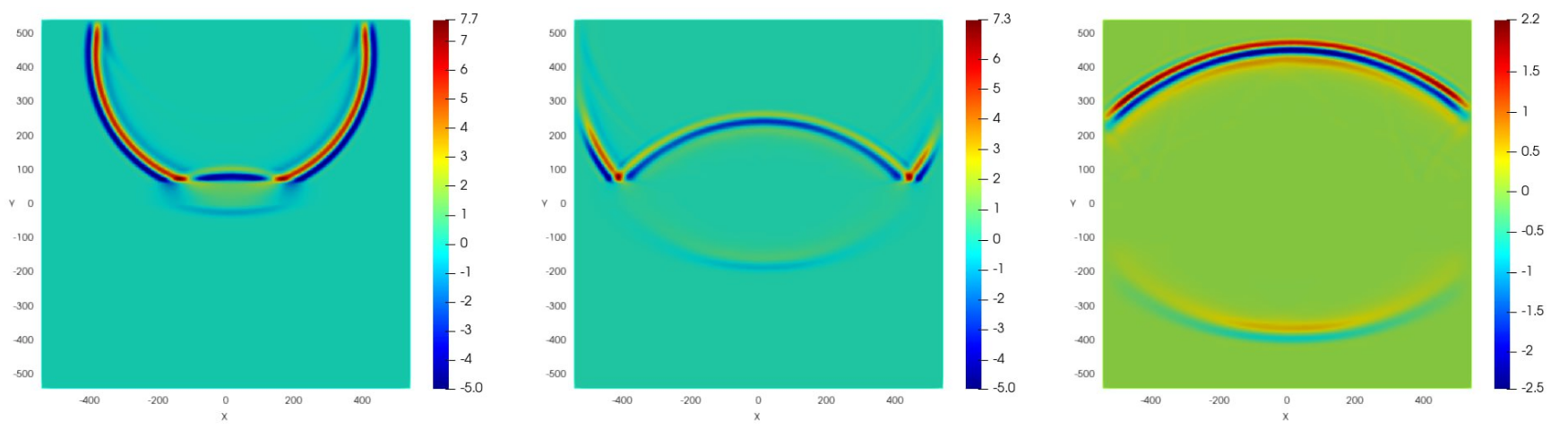
Adaptive regularization, discretization, and linearization for nonsmooth problems

Participants: André Harnist, Ari Rappaport, Martin Vohralík.

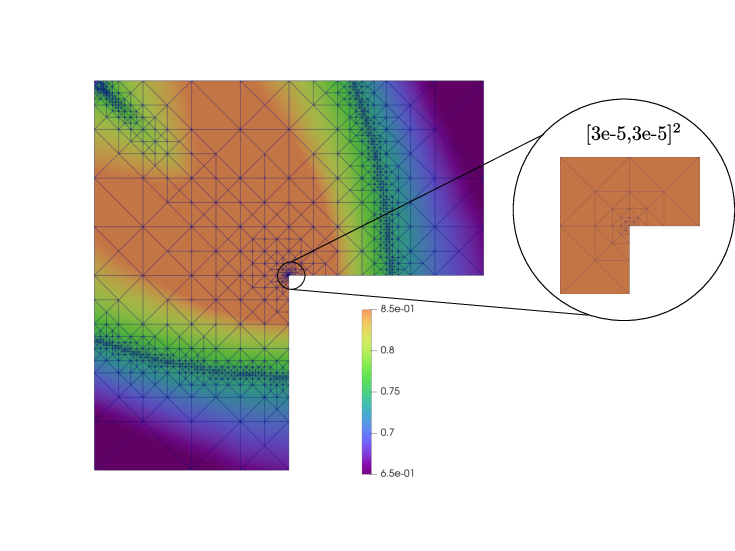
Adaptive regularization and adaptive mesh refinement for nonsmooth nonlinearity

In 28, we consider nonsmooth partial differential equations associated with a minimization of an energy functional. We adaptively regularize the nonsmooth nonlinearity so as to be able to apply the usual Newton linearization, which is not always possible otherwise. We apply the finite element method as a discretization. We focus on the choice of the regularization parameter and adjust it on the basis of an a posteriori error estimate for the difference of energies of the exact and approximate solutions. We prove guaranteed upper bounds for the energy difference, identify the individual error components, and design an adaptive algorithm with both adaptive regularization and adaptive mesh refinement. Effeciency and robustness of the estimates with respect to the magnitude of the nonlinearity is addressed in 52. Numerical results confirm the theoretical developments, see Figure 3 for an illustration.

Functional software

Participants: Sébastien Furic.

See the "News of the Year" about software Skwer (Section 7.1.4).

Coq formalizations

Participants: François Clément, Houda Mouhcine.

In 36, we describe the formal definition and proof in Coq of product $\sigma$-algebras, product measures and their uniqueness, the construction of iterated integrals, up to Tonelli's theorem. We also advertise the Lebesgue induction principle provided by an original inductive type for nonnegative measurable functions.

See also the "News of the Year" about software coq-num-analysis (Section 7.1.5).

Flow through fractured and fractured porous media

Participants: Michel Kern, Simon Legrand, Alessandra Marelli, Géraldine Pichot, Martin Vohralík, Raphaël Zanella, Daniel Zegarra Vasquez.

We have experimented with the domain decomposition preconditioner HPDDM, developped by the Alpines team  55, 56 to solve the linear system obtained from nef-flow-fpm. The improvement over the more classical preconditioners used until then (mainly algebraic multigrid) are significant as can be seen on Figure 4.

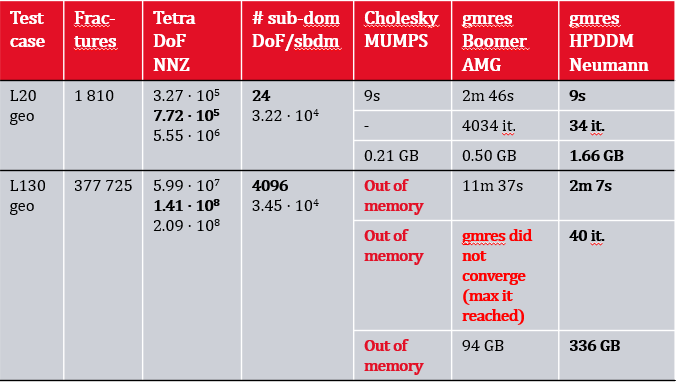
Performances of the domain decomposition preconditioner HPDDM

Thanks to the gmres solver and the HPDDM preconditioner, we are now able to solve flow problem in large scale fractured porous media that are out of reach with direct solvers like MUMPS Cholesky or with gmres preconditioned by multigrid like BoomerAMG. As example, solving the linear system of size $1.41\times {10}^8$ for a network containing 378k fractures takes in parallel, with gmres preconditioned with HPDDM, only 2 minutes and 40 iterations with 4096 MPI processes.

Another goal is to simulate the transport by advection of an inert tracer. The transport is described by the conservation of mass and gives rise to an equation with partial derivatives of the first order in which the velocity, computed with the software nef-flow-fpm, is heterogeneous. The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit.

As part of Alessandra Marelli's internship, we were able to simulate the transport in a network of fractures. The main challenge was the correct handling of the coupling conditions at the fracture intersections. An example is shown in Figure 5. The method is implemented in nef-transport-fpm.

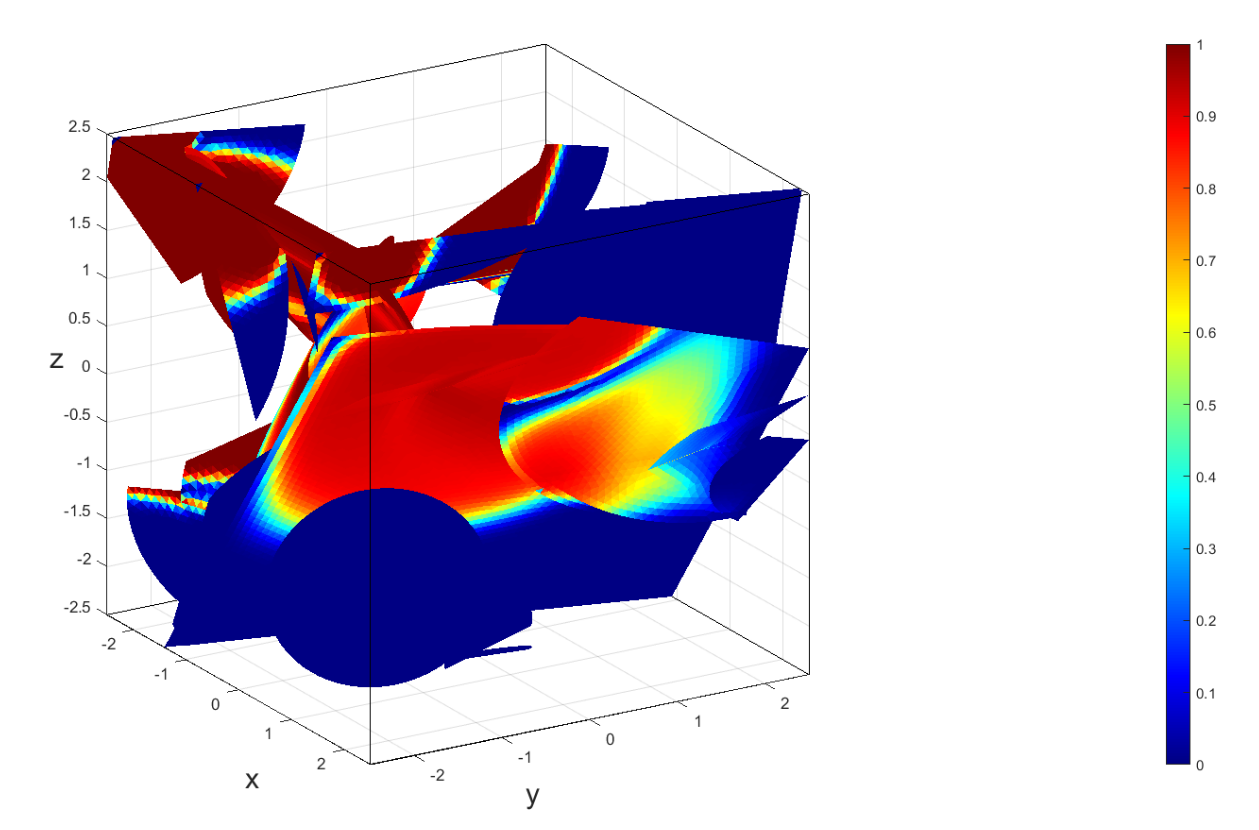
Concentration in a discrete fracture network with 28 fractures

Multiphase reactive flow

Participants: Michel Kern.

Michel Kern was part of a group with Etienne Ahusborde, Brahim Amaziane (University of Pau), Stephen de Hoop and Denis Voskov (Delft University of Technology) that proposed a benchmark targeted towards the simulation of reactive two-phase flow. Six teams participated in the benchmark. The results showed good agreements between most groups on the simpler test cases, but also that the interaction between complex chemistry and two-phase flow with phase exchanges still remains a challenge for simulation software. The model is presented in 30, while the results are presented in 14, see Figure 6.

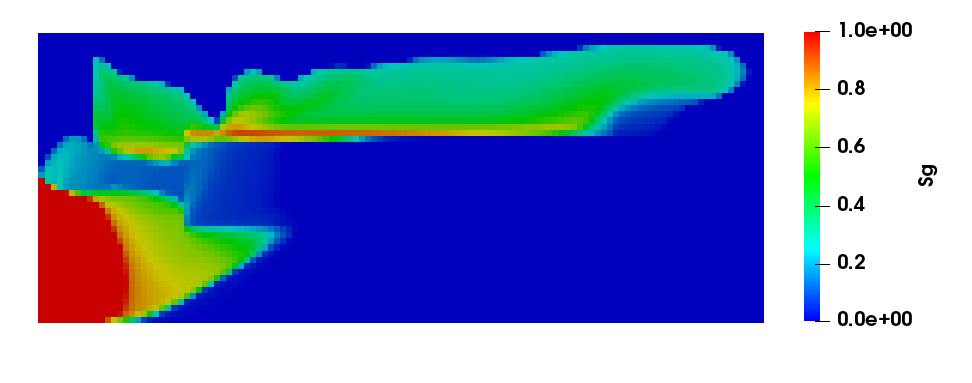
Evolution of the gas saturation

Evolution of the gas saturation

Wave propagation in geophysical media

Participants: Alexandre Ern, Michel Kern, Clément Maradei, Romain Mottier.

As part of the internship of Clément Maradei, we studied a model for the wave equations that includes both a diffusive (first order derivative in time) and a so-called "viscous" term (first order time derivative of the Laplacian). The model has been proposed to represent frequency-dependent attenuation. Thanks to finite element simulations (using FreeFeem++), we were able to compare the respective contributions of the two terms, and use a scaling analysis to better understand the influence of the two parameters. The results have been presented at the 15th FreeFem Days.

Comparison of the wavefield for the diffusive and viscous damping

Comparison of the wavefield for the diffusive and viscous damping

Within the PhD Thesis of Romain Mottier, we developed HHO methods to simulate coupled acoustic-elastodynamic waves in geophysical media. One goal is to highlight the role of sedimentary bassins in energy transfer from the bedrock to the atmosphere.

Data assimilation

Participants: Alexandre Ern.

Our work on data assimilation was pursued this year by addressing the heat equation. Our first contribution is on the theoretical side and concerns a Carleman estimate 17. The second contribution deals with the devising and numerical analysis of a high-order method (based on a dG method in time and a hybrid dG method in space) 18.

A stable local commuting projector and optimal $hp$ approximation estimates in $𝐇\left(\mathrm{curl}\right)$

Participants: Théophile Chaumont-Frelet, Martin Vohralík.

We design an operator from the infinite-dimensional Sobolev space $𝐇\left(\mathrm{curl}\right)$ to its finite-dimensional subspace formed by the Nédélec piecewise polynomials on a tetrahedral mesh that has the following properties: 1) it is defined over the entire $𝐇\left(\mathrm{curl}\right)$, including boundary conditions imposed on a part of the boundary; 2) it is defined locally in a neighborhood of each mesh element; 3) it is based on simple piecewise polynomial projections; 4) it is stable in the ${𝐋}^2$-norm, up to data oscillation; 5) it has optimal (local-best) approximation properties; 6) it satisfies the commuting property with its sibling operator on $𝐇\left(\mathrm{div}\right)$; 7) it is a projector, i.e., it leaves intact objects that are already in the Nédélec piecewise polynomial space. This operator can be used in various parts of numerical analysis related to the $𝐇\left(\mathrm{curl}\right)$ space. We in particular employ it here to establish the two following results: i) equivalence of global-best, tangential-trace- and curl-constrained, and local-best, unconstrained approximations in $𝐇\left(\mathrm{curl}\right)$ including data oscillation terms; and ii) fully $h$- and $p$- (mesh-size- and polynomial-degree-) optimal approximation bounds valid under the minimal Sobolev regularity only requested elementwise.

Some novel results concerning Maxwell's equations

Participants: Alexandre Ern, Jean-Luc Guermond.

In 43, we established the asymptotic optimality of the edge finite element approximation of the time-harmonic Maxwell's equations. This fundamental result, which is the counterpart of a known result concering the Helmholtz equation and conforming finite elements, was still lacking in the litterature. A second novel result, that was also lacking in the literature, concerns the spectral correctness (no spurious eigenvalues) of the dG approximation of Maxwell's equations in first-order form (the result was known for Maxwell's equations in second-order form), thereby confirming numerical observations by various authors made over the last two decades. We proved this result first with constant coefficients 27 and then in the more challenging case of discontinuous coefficients 48.

Solutions to 1D advection-diffusion problems with discontinuous coefficients

Participants: Géraldine Pichot.

Diffusive transport in media with discontinuous properties is a challenging problem that arises in many applications. In 39, wefocus on one-dimensional discontinuous media with generalized permeable boundary conditions at the discontinuity interface. The paper presents novel analytical expressions from the method of images to simulate diffusive processes, such as mass or thermal transport. The analytical expressions are used to formulate a generalization of the existing Skew Brownian Motion, HYMLA and Uffink's method, here named as GSBM, GHYMLA and GUM respectively, to handle generic interface conditions. The algorithms rely upon the random walk method and are tested by simulating transport in a bimaterial and in a multilayered medium with piece-wise constant properties. The results indicate that the GUM algorithm provides the best performance in terms of accuracy and computational cost. The methods proposed can be applied for simulation of a wide range of differential problems, like heat transport problem 40.

Model-order reduction

Participants: Alexandre Ern, Abbas Kabalan.

One important topic has been the development of reduced-order methods to handle variational inequalities such as those encountered when studying contact problems (with friction) in computational mechanics. In 33, we introduce an efficient algorithm to guarantee inf-sup stability for saddle-point problems with parameter-dependent constraints. In 54, we pursued a different, and complementary, approach, where the constraints are taken into account by a nonlinaer Nitsche's method, thereby allowing one to use a primal formulation. Finally, within the PhD Thesis of Abbas Kabalan, we are investigating shape variability within the context of reduced-order models.

Best-approximation errors for fields with low regularity

Participants: Zhaonan Dong, Alexandre Ern, Jean-Luc Guermond.

In 23, we established optimal decay rates on the best-approximation errors using vector-valued finite elements (of Nédélec or Raviart–Thomas type) for fields with low regularity but having an integrable curl or divergence.

$hp$-optimal error estimates of dG methods

Participants: Zhaonan Dong.

In 25, we derived $hp$-optimal error estimates for dG methods for the biharmonic problem with homogeneous essential boundary conditions, which removed the $1.5$ suboptimal rate in term of $p$ in the classical error analysis of dG methods. The main ingredient in the analysis is the construction of a global $H^2$ piecewise polynomial approximants with $hp$-optimal approximation properties over the meshes. Moreover recently, we derived $hp$-optimal error estimates for the upwind dG method when approximating solutions to first-order hyperbolic problems with constant convection fields in the $L_2$ and DG norms in 47. The main novelty in the analysis are novel $hp$-optimal approximation properties of the special projector introduced in [Cockburn, Dong, Guzman, SINUM, 2008].

These works were performed in collaboration with L. Mascotto.

10.1.1 Visits of international scientists

10.1.2 Visits to international teams

10.2.1 H2020 projects

11.1.1 Scientific events: organisation

11.1.2 Scientific events: selection

11.1.3 Journal

11.1.4 Invited talks

Zhaonan Dong and Géraldine Pichot were invited to organize a mini-tutorial at the SIAM Conference on Mathematical & Computational Issues in the Geosciences 2023, Bergen, Norway, June 2023.

Alexandre Ern gave a plenary lecture at the ECCOMAS Meeting on Modern Finite Element Technologies, Mühlheim an der Ruhr, Germany, August, 2023.

Alexandre Ern gave an invited lecture within the special activity organized by IIT Roorkee, India on Differential equations: analysis, computation and applications.

Géraldine Pichot gave a plenary lecture at the Large-Scale Scientific Computations international conference LSSC23, Sozopol, Bugaria, June 2023.

Martin Vohralík gave an plenary talk at the SIAM Conference on Mathematical and Computational Issues in the Geosciences Bergen, Norway (June 2023), a plenary talk at Congrès international sur l’analyse numérique des EDP, Meknès, Morocco (October 2023), and an invited talk at HOFEIM 2023, Larnaca, Cyprus (May 2023).

11.1.5 Leadership within the scientific community

Alexandre Ern served within the Administration Board of SMAI and was Vice-President in charge of relations with industry.

Michel Kern is a member of

• the Scientific Board of ORAP, Organisation Associative du Parallélisme;
• the board of École Doctorale Galilée at University Sorbonne Paris-Nord;
• the steering committee of GDR HydroGEMM
• Martin Vohralík served as the president/member of the scientific committee of Summer schools CEA–EDF–INRIA.
• Martin Vohralík served as a member of the scientific board of the IFP Energies Nouvelles – Inria joint strategic partnership laboratory.

11.1.6 Scientific expertise

Michel Kern is a reviewer for the Allocation of Computing Time located at the Juelich Supercomputing Centre in Germany.

11.1.7 Research administration

François Clément is a member of the Commission des usagers de la rue Barrault (CURB) for the next relocation of the Inria Paris Center.

Michel Kern is the chair of the Comission de Développement Technologique of the Inria Paris Center.

Géraldine Pichot is the president of the Commission des utilisateurs des moyens informatiques de Paris (CUMI Paris).

Géraldine Pichot is a member of the Comité de Suivi Doctoral de Paris (CSD).

Géraldine Pichot is the contact person at Inria Paris for the Agence pour les Mathématiques en Interaction avec l'Entreprise et la Société (AMIES).

11.2.1 Teaching

• Master : Alexandre Ern, Discontinuous Galerkin methods, 20h, M2, Sorbonne University, France.
• Master: Alexandre Ern, Finite Elements, 15h, M1, ENPC, France.
• Master: Alexandre Ern, Hyperbolic equations, 6h, M2, Sorbonne University, France.
• Master: Michel Kern, Models and numerical methods for subsurface flow, 30h, M2, Université Paris Saclay, France.
• Master: Michel Kern, Advanced numerical analysis, 30h, M1, Institut Galilée, Université Paris-Nord, France.
• Master: Martin Vohralík, Advanced finite elements, 21h, M1, ENSTA (Ecole nationale supérieure de techniques avancées), Paris, France.

11.2.2 Supervision

• PhD defended: Stefano Piccardo, Simulation of two-fluid immiscible Stokes flows using hybrid nonconforming methods and geometrically unfitted meshes, 04 December 2023, Alexandre Ern and Antonio Huerta (UPC Barcelone), 37.
• PhD defended: Morgane Steins, An explicit hybrid high-order method for structural dynamics, 05 December 2023, Alexandre Ern and Olivier Jamond (CEA), 38.
• PhD in progress: Nicolas Hugot, A posteriori error estimates for the wave equation, started November 2023, Martin Vohralík.
• PhD in progress: Abbas Kabalan, Model order reduction for nonparametrized geometrical variability, started October 2022, Virginie Ehrlacher (Matherials) and Alexandre Ern.
• PhD in progress: Clément Maradei, Parallel adaptive $hp$-FEM, started October 2023, Zhaonan Dong and Martin Vohralík.
• PhD in progress: Romain Mottier, Unfitted hybrid high-order methods for geophysical wave propagation, started October 2021, Alexandre Ern and Laurent Guillot (CEA).
• PhD in progress: Houda Mouhcine, Formal proofs in applied mathematics: verification of a generator for quadrature formulas, started October 2021, Sylvie Boldo (Toccata), François Clément, and Micaela Mayero (LIPN).
• PhD in progress: Ari Rappaport, A posteriori error estimates and adaptivity in numerical approximation of PDEs: regularization, linearization, discretization, and floating point precision, started January 2021, Martin Vohralík.
• PhD in progress: Daniel Zegarra Vasquez, High-performance simulation of single-phase flows in a fractured porous medium, started October 2021, Géraldine Pichot, Michel Kern, and Martin Vohralík.
• PhD in progress: Zuodong Wang, Finite element methods for hyperbolic and degenerate parabolic problems, started October 2021, Zhaonan Dong and Alexandre Ern.
• Internship: Nicolas Hugot (ENSTA), Flux reconstruction for the wave equation, April-September 2023, Martin Vohralík.
• Internship: Clément Maradei (Sup Galilée), Finite element simulation of the viscous wave equation, February-March 2023, Michel Kern.
• Internship: Clément Maradei (Sup Galilée), Parallel adaptive $hp$-FEM, April-September 2023, Zhaonan Dong and Martin Vohralík.
• Internship: Alessandra Marelli (Politecnico di Milano), Simulation of advective transport in fracture networks, April-September 2023, Géraldine Pichot and Michel Kern.

11.2.3 Juries

• Alexandre Ern was external reviewer for the PhD of Matthieu Barré (IPP), Simon Le Berre (CEA Cadarache and Mines ParisTech), and Kenneth Assogba (IPP) and committee member for the HDR of Laurent Monasse (Cote d'Azur University) and for the PhD of Julien Moatti (Lille University).
• Martin Vohralík was a referee and committee president for the PhD thesis of Hussein Albazzal (Université de Bourgogne Franche-Comté), committee president for the PhD thesis of Georges Seeman (Université Saint-Joseph de Beyrouth), and committee member for the PhD thesis of Sarah Perez (Université de Pau et des Pays Adour) and Yipeng Wang (Sorbonne Université).

11.3.1 Internal or external Inria responsibilities

Martin Vohralík served in the scientific committee of Summer schools CEA–EDF–INRIA.

11.3.2 Interventions

Michel Kern gave a presentation on "Modeling and simulation: applications to subsurface water" to a "classe de seconde" at Lycée Lucie Aubrac (Courbevoie) as part of the 1 scientifique, 1 classe : chiche ! project.

International journals

• 14 articleE.Etienne Ahusborde, B.Brahim Amaziane, S.Stephan de Hoop, M.Mustapha El Ossmani, E.Eric Flauraud, F. P.François P. Hamon, M.Michel Kern, A.Adrien Socié, D.Danyang Su, K. U.K. Ulrich Mayer, M.Michal Tóth and D.Denis Voskov. A benchmark study on reactive two-phase flow in porous media: Part II -results and discussion.Computational Geosciences2023HALback to text
• 15 articleI.Ibtihel Ben Gharbia, J.Joëlle Ferzly, M.Martin Vohralík and S.Soleiman Yousef. Adaptive inexact smoothing Newton method for a nonconforming discretization of a variational inequality.Computers & Mathematics with Applications1332023, 12-29HALDOI
• 16 articleI.Ibtihel Ben Gharbia, J.Joëlle Ferzly, M.Martin Vohralík and S.Soleiman Yousef. Semismooth and smoothing Newton methods for nonlinear systems with complementarity constraints: Adaptivity and inexact resolution.Journal of Computational and Applied Mathematics4202023, 114765HALDOI
• 17 articleE.Erik Burman, G.Guillaume Delay, A.Alexandre Ern and L.Lauri Oksanen. A stability estimate for data assimilation subject to the heat equation with initial datum.Comptes Rendus. Mathématique2024HALback to text
• 18 articleE.Erik Burman, G.Guillaume Delay and A.Alexandre Ern. The unique continuation problem for the heat equation discretized with a high-order space-time nonconforming method.SIAM Journal on Numerical Analysis6152023, 2534-2557HALback to text
• 19 articleA.Andrea Cangiani, Z.Zhaonan Dong and E. H.Emmanuil H Georgoulis. A posteriori error estimates for discontinuous Galerkin methods on polygonal and polyhedral meshes.SIAM Journal on Numerical Analysis6152023, 2352--2380HALDOI
• 20 articleT.Théophile Chaumont-Frelet and M.Martin Vohralík. p-robust equilibrated flux reconstruction in H(curl) based on local minimizations. Application to a posteriori analysis of the curl-curl problem.SIAM Journal on Numerical Analysis614July 2023, 1783--1818HALDOIback to textback to text
• 21 articleP.Patrik Daniel and M.Martin Vohralík. Guaranteed contraction of adaptive inexact $hp$-refinement strategies with realistic stopping criteria.ESAIM: Mathematical Modelling and Numerical Analysis571February 2023, 329 - 366HALDOI
• 22 articleZ.Zhaonan Dong and A.Alexandre Ern. $C^0$-hybrid high-order methods for biharmonic problems.IMA Journal of Numerical Analysis441February 2024, 24–57HALDOIback to text
• 23 articleZ.Zhaonan Dong, A.Alexandre Ern and J.-L.Jean-Luc Guermond. Local decay rates of best-approximation errors using vector-valued finite elements for fields with low regularity and integrable curl or divergence.Comptes Rendus. Mathématique361May 2023, 723-736HALDOIback to text
• 24 articleZ.Zhaonan Dong, M.Moritz Hauck and R.Roland Maier. An improved high-order method for elliptic multiscale problems.SIAM Journal on Numerical Analysis6142023, 1918-1937HALDOI
• 25 articleZ.Zhaonan Dong and L.Lorenzo Mascotto. hp-optimal interior penalty discontinuous Galerkin methods for the biharmonic problem.Journal of Scientific Computing9630May 2023HALDOIback to text
• 26 articleA.Alexandre Ern and J.-L.Jean-Luc Guermond. Invariant-domain preserving high-order time stepping: II. IMEX schemes *.SIAM Journal on Scientific Computing4552023, A2511-A2538HALback to textback to text
• 27 articleA.Alexandre Ern and J.-L.Jean-Luc Guermond. The discontinuous Galerkin approximation of the grad-div and curl-curl operators in first-order form is involution-preserving and spectrally correct.SIAM Journal on Numerical Analysis2024HALback to text
• 28 articleF.François Févotte, A.Ari Rappaport and M.Martin Vohralík. Adaptive regularization, discretization, and linearization for nonsmooth problems based on primal-dual gap estimators.Computer Methods in Applied Mechanics and Engineering418May 2023, 116558HALDOIback to textback to text
• 29 articleG.Gregor Gantner and M.Martin Vohralík. Inexpensive polynomial-degree-robust equilibrated flux a posteriori estimates for isogeometric analysis.Mathematical Models and Methods in Applied Sciences2023, 1-46HALDOIback to text
• 30 articleS.Stephan de Hoop, D.Denis Voskov, E.Etienne Ahusborde, B.Brahim Amaziane and M.Michel Kern. A benchmark study on reactive two-phase flow in porous media: Part I -model description.Computational Geosciences2023HALback to text
• 31 articleM.Manu Jayadharan, M.Michel Kern, M.Martin Vohralík and I.Ivan Yotov. A space-time multiscale mortar mixed finite element method for parabolic equations.SIAM Journal on Numerical Analysis612April 2023, 675 - 706HALDOI
• 32 articleK.Koondanibha Mitra and M.Martin Vohralík. A posteriori error estimates for the Richards equation.Mathematics of ComputationDecember 2023HAL
• 33 articleI.Idrissa Niakh, G.Guillaume Drouet, V.Virginie Ehrlacher and A.Alexandre Ern. Stable model reduction for linear variational inequalities with parameter-dependent constraints.ESAIM: Mathematical Modelling and Numerical Analysis5712023, 167--189HALback to text
• 34 articleS.Stefano Piccardo and A.Alexandre Ern. Surface tension effects between two immiscible Stokes fluids: a computational study using unfitted hybrid high-order methods and a level-set scheme.SMAI Journal of Computational Mathematics92023, 257-283HALback to text
• 35 articleM.Morgane Steins, A.Alexandre Ern, O.Olivier Jamond and F.Florence Drui. Time-explicit Hybrid High-Order method for the nonlinear acoustic wave equation.ESAIM: Mathematical Modelling and Numerical Analysis5752023, 2977-3006HALback to text

International peer-reviewed conferences

• 36 inproceedingsS.Sylvie Boldo, F.François Clément, V.Vincent Martin, M.Micaela Mayero and H.Houda Mouhcine. A Coq Formalization of Lebesgue Induction Principle and Tonelli's Theorem.Proceedings of the 25th International Symposium on Formal Methods25th International Symposium on Formal Methods (FM 2023)14000Lecture Notes in Computer ScienceLübeck, GermanyMarch 2023, 39--55HALDOIback to text

Doctoral dissertations and habilitation theses

• 37 thesisS.Stefano Piccardo. Simulation of two-fluid immiscible Stokes flows using hybrid nonconforming methods and geometrically unfitted meshes.Ecole des Ponts ParisTech; Universitat Politècnica de Catalunya, Barcelona (Spain)December 2023HALback to textback to text
• 38 thesisM.Morgane Steins. An explicit hybrid high-order method for structural dynamics.ENPC - École des Ponts ParisTechDecember 2023HALback to textback to text

Reports & preprints

• 39 miscE.Elisa Baioni, A.Antoine Lejay, G.Géraldine Pichot and G. M.Giovanni Michele Porta. Modeling diffusion in discontinuous media under generalized interface conditions: theory and algorithms.July 2023HALback to text
• 40 miscE.Elisa Baioni, A.Antoine Lejay, G.Géraldine Pichot and G. M.Giovanni Michele Porta. Random walk modeling of conductive heat transport in discontinuous media.July 2023HALback to text
• 41 reportS.Sylvie Boldo, F.François Clément, V.Vincent Martin, M.Micaela Mayero and H.Houda Mouhcine. Lebesgue Induction and Tonelli's Theorem in Coq.RR-9457Institut National de Recherche en Informatique et en Automatique (INRIA)January 2023, 17HAL
• 42 miscA.Annalisa Buffa, O.Ondine Chanon, D.Denise Grappein, R.Rafael Vázquez and M.Martin Vohralík. An equilibrated flux a posteriori error estimator for defeaturing problems.December 2023HAL
• 43 miscT.Théophile Chaumont-Frelet and A.Alexandre Ern. Asymptotic optimality of the edge finite element approximation of the time-harmonic Maxwell's equations.September 2023HALback to text
• 44 miscT.Théophile Chaumont-Frelet and M.Martin Vohralík. A stable local commuting projector and optimal hp approximation estimates in H(curl).December 2023HAL
• 45 miscT.Théophile Chaumont-Frelet and M.Martin Vohralík. Constrained and unconstrained stable discrete minimizations for p-robust local reconstructions in vertex patches in the De Rham complex.May 2023HAL
• 46 miscZ.Zhaonan Dong, E. H.Emmanuil H Georgoulis and P. J.Philip J. Herbert. A hypocoercivity-exploiting stabilised finite element method for Kolmogorov equation.January 2024HAL
• 47 miscZ.Zhaonan Dong and L.Lorenzo Mascotto. $hp$-optimal convergence of the original DG method for linear hyperbolic problems on special simplicial meshes.November 2023HALback to text
• 48 miscA.Alexandre Ern and J.-L.Jean-Luc Guermond. Spectral correctness of the discontinuous Galerkin approximation of the first-order form of Maxwell's equations with discontinuous coefficients.June 2023HALback to text
• 49 miscA.Alexandre Ern, J.-L.Jean-Luc Guermond and Z.Zuodong Wang. Asymptotic and invariant-domain preserving schemes for scalar conservation equations with stiff source terms and multiple equilibrium points.December 2023HALback to text
• 50 miscA.Alexandre Ern and M.Morgane Steins. Convergence analysis for the wave equation discretized with hybrid methods in space (HHO, HDG and WG) and the leapfrog scheme in time.September 2023HALback to text
• 51 miscF.François Févotte, A.Ari Rappaport and M.Martin Vohralík. Adaptive regularization for the Richards equation.October 2023HAL
• 52 miscA.André Harnist, K.Koondanibha Mitra, A.Ari Rappaport and M.Martin Vohralík. Robust energy a posteriori estimates for nonlinear elliptic problems.March 2023HALback to text
• 53 miscK.Koondanibha Mitra and M.Martin Vohralík. Guaranteed, locally efficient, and robust a posteriori estimates for nonlinear elliptic problems in iteration-dependent norms. An orthogonal decomposition result based on iterative linearization.July 2023HAL
• 54 miscI.Idrissa Niakh, G.Guillaume Drouet, V.Virginie Ehrlacher and A.Alexandre Ern. A reduced basis method for frictional contact problems formulated with Nitsche's method.July 2023HALback to text