2023Activity reportProject-TeamVALSE
RNSR: 201923115X- Research center Inria Centre at the University of Lille
- In partnership with:Ecole Centrale de Lille, Université de Lille
- Team name: Finite-time control and estimation for distributed systems
- In collaboration with:Centre de Recherche en Informatique, Signal et Automatique de Lille
- Domain:Applied Mathematics, Computation and Simulation
- Theme:Optimization and control of dynamic systems
Keywords
Computer Science and Digital Science
- A5.9.2. Estimation, modeling
- A6.4.1. Deterministic control
- A6.4.4. Stability and Stabilization
- A6.4.5. Control of distributed parameter systems
- A9.5. Robotics
Other Research Topics and Application Domains
- B1.1.8. Mathematical biology
- B2.1. Well being
- B5.6. Robotic systems
- B7.2.1. Smart vehicles
1 Team members, visitors, external collaborators
Research Scientists
- Denis Efimov [Team leader, INRIA, Senior Researcher, HDR]
- Jin Gyu Lee [INRIA, ISFP]
- Andrey Polyakov [INRIA, Researcher, HDR]
- Rosane Ushirobira [INRIA, Researcher, HDR]
Post-Doctoral Fellow
- Jesus Mendoza Avila [INRIA, until Nov 2023]
PhD Students
- Mohamed Yassine Arkhis [INRIA, from Oct 2023]
- Mericel Ayamou [UNIV LILLE]
- Mahugnon Dadjo [INRAE]
- Min Li [CSC Scholarship]
- Danilo Rodrigues De Lima [INRIA]
- Yu Zhou [CSC Scholarship]
Technical Staff
- Gerald Dherbomez [CNRS, Engineer]
Administrative Assistant
- Lucille Leclercq [INRIA, from Feb 2023]
Visiting Scientists
- Leonid Fridman [UNAM, until Jan 2023]
- Ariana Gutierrez [IT Laguna, from Aug 2023 until Oct 2023]
- Ankit Kumar [IIT Delhi, from Mar 2023 until May 2023]
- Manuel Mera [Instituto Politécnico Nacional, from Aug 2023 until Sep 2023]
- Jose Antonio Ortega [UNAM, from Aug 2023 until Oct 2023]
- Hector Rios Barajas [IT Laguna, from Aug 2023 until Sep 2023]
2 Overall objectives
The Valse team studies the estimation and control problems arising in the analysis and the design of distributed, uncertain, and interconnected dynamical systems:
- Using the concepts of finite-time/fixed-time/hyperexponential convergence and stability, the main idea is to separate and hierarchize in time the control and estimation processes, which are distributed in space. This greatly simplifies their analysis and the design for large-scale solutions.
- The main areas of investigation and application are the Internet of Things (IoT) and Cyber-Physical Systems (CPS).
- The team aims to draw up algorithms for decentralized finite-time control and estimation. The methodology to be developed includes extensions of the theory of homogeneous systems and of finite-time/fixed-time/hyperexponential convergence and stability notions. Particular attention is given to applications in real-world scenarios.
- It is a joint proposal with the CNRS CRIStAL UMR 9189.
3 Research program
The Valse team works in the domains of control science: dynamical systems, stability analysis, estimation, and automatic control. Our developments are focused on the theoretical and applied aspects related to the control and estimation of large-scale multi-sensor and multi-actuator systems based on the use of the theories of finite-time/fixed-time/hyperexponential convergence and homogeneous systems. The Lyapunov function method and other methods of analysis of dynamical systems form a basis for the studies in the Valse team.
The key idea of the research program for the team is that a fast (non-asymptotic) convergence of the regulation and estimation errors increases the reliability of intelligent distributed actuators and sensors in complex scenarios, such as interconnected cyber-physical systems (CPSs).
The expertise of Valse's members in theoretical developments of control and estimation theory (finite-time control and estimation algorithms in centralized context 84, 70, 81, 80, 77, homogeneity framework for differential equations 85, 72, 71, 73, 75, 86, 82, time-delay systems 74, 76, 89, distributed systems 83 and algebraic-based methods for estimation 87, 88) is an essential ingredient to achieve our objective.
The generic chart of different goals and tasks included in the scientific work program of Valse and interrelations between them are presented in Fig. 1. We have selected three main objectives to pursue with the related tasks to fulfill:
- The first objective is to design control and estimation solutions for CPS and IoT, which is the principal aim of Valse. It will contain the main outcomes of our research.
- The second objective is more theoretical and needed to make the basement for our design and analysis parts in the last goal.
- The third objective deals with applications, which will drive the team and motivate the theoretical studies and selected design performances.
All these objectives are interconnected: from a particular problem in an IoT application, it is planned to design control or estimation algorithms, leading to the development of theoretical tools; and vice versa, a new theoretical advance can provide a possibility for the development of novel tools which can be used in applications.
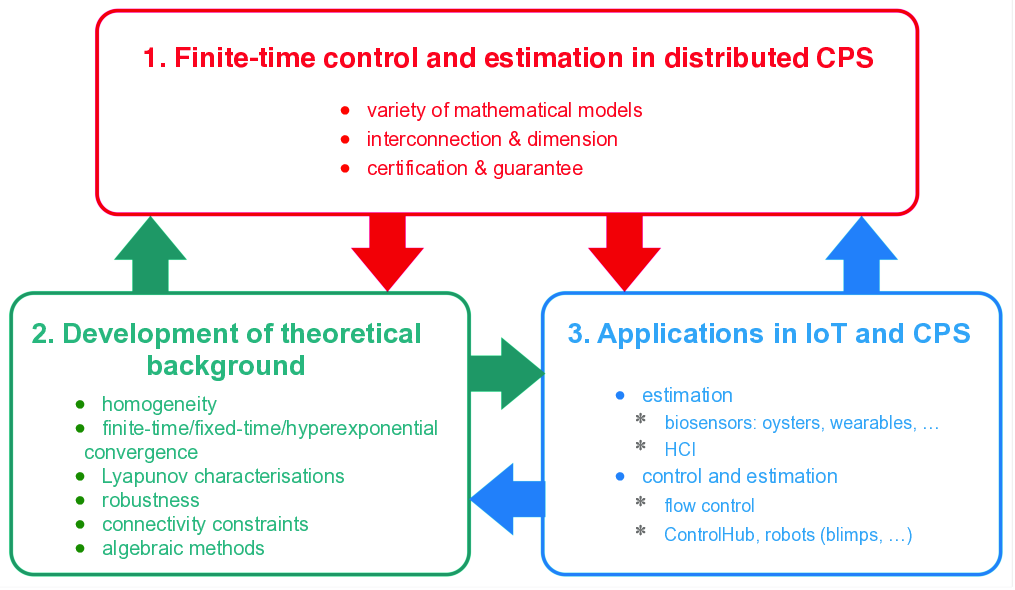
Graphical presentation of objectives given in the text
Structure of the objectives and tasks treated in Valse
To explain our motivation: why use finite time? Applying any method for control/estimation has a price in terms of its advantages and disadvantages. There is no universal framework that is the best always and everywhere. Finite-time may appear as a luxurious property for a physical system, requiring nonlinear tools. Of course, if an asymptotic convergence and a linear model are enough for solving a given problem, then there is no reason to develop something else. However, most of the present problems in CPS and IoT are nonlinear (i.e., they have various local behaviors that cannot be collected in only one linear model). Design and analysis of various local linearized models and solutions are luxurious, too. The theory of homogeneity can go beyond linearity, offering many new features while not appearing as severe as other nonlinear tools and having almost all hints of the linear framework. Suppose that, thanks to the homogeneity theory, finite-time/fixed-time can be obtained with little difficulty while adding the bonuses of stronger robustness and faster convergence compared to the linear case? We are convinced that the price of going beyond linear control and estimation can be strongly dropped by maturing the theory of homogeneity and finite/fixed-time convergence. We are also convinced that it will be compensated in terms of robustness and speed, which can be demanded in the new areas of application such as IoT for example.
4 Application domains
An objective of the team is the application of the developed control and estimation algorithms for different scenarios in IoT or CPSs. Participation in various potential applications allows the Valse team to better understand the features of CPSs and their required performances, and to properly formulate the control and estimation problems that must be solved. Here is a list of ongoing, past and potential applications addressed by the team:
- smart bivalve-based biosensor for water quality monitoring (ANR project
WaQMoS, the developed
sensor is shown in Fig. 2): in living beings,
the presence of persistent external perturbations may be difficult
to measure, and important model uncertainties render the application
of conventional techniques complicated; another issue for estimation
is the consensus-seeking between animals for contamination detection 68;

Underwater photo of bivalves connected to computer
Figure2: The valvometer used in the ANR project WaQMoS
- control and estimation for flying vehicles, e.g. quadrotors
or blimps given in Fig. 3: the nonlinearity of the model and its
uncertainty coupled with important aerodynamic perturbations have
to be compensated by fast (finite- or fixed-time) and robust control
and estimation algorithms;


1) Photo of blimp robot, big ball with helium with a small computer at the bottom. 2) S. Wang placing a bottle of water on the flying drone
1) Photo of blimp robot, big ball with helium with a small computer at the bottom. 2) S. Wang placing a bottle of water on the flying drone
Figure3: Blimp and quadrotor robots
- human behavior modeling and identification with the posterior design of algorithms for human-computer interaction (HCI, with the Inria team LOKI): robust finite-time differentiators demonstrate good estimation capabilities needed for prediction in this application 88, 69;
- human physiological characteristics estimation (like emotion detection, galvanic skin response filtering, fatigue evaluation in collaborations with Neotrope and Ellcie Healthy): intelligent robust filtering and finite-time distributed estimation are key features in these scenarios;
- path planning for autonomous vehicles taking into account the behavior of humans (with the Inria team SCOOL): application of interval and finite-time adaptive estimation and prediction techniques allows for treating the uncertainty of the environment by reducing the computational complexity of reinforcement learning 791;
- flow control 78: the case of control and
estimation of a distributed-parameter system with very fast and uncertain
dynamics, where finite-time solutions developed by Valse are necessary (an example of results is given in Fig. 4);
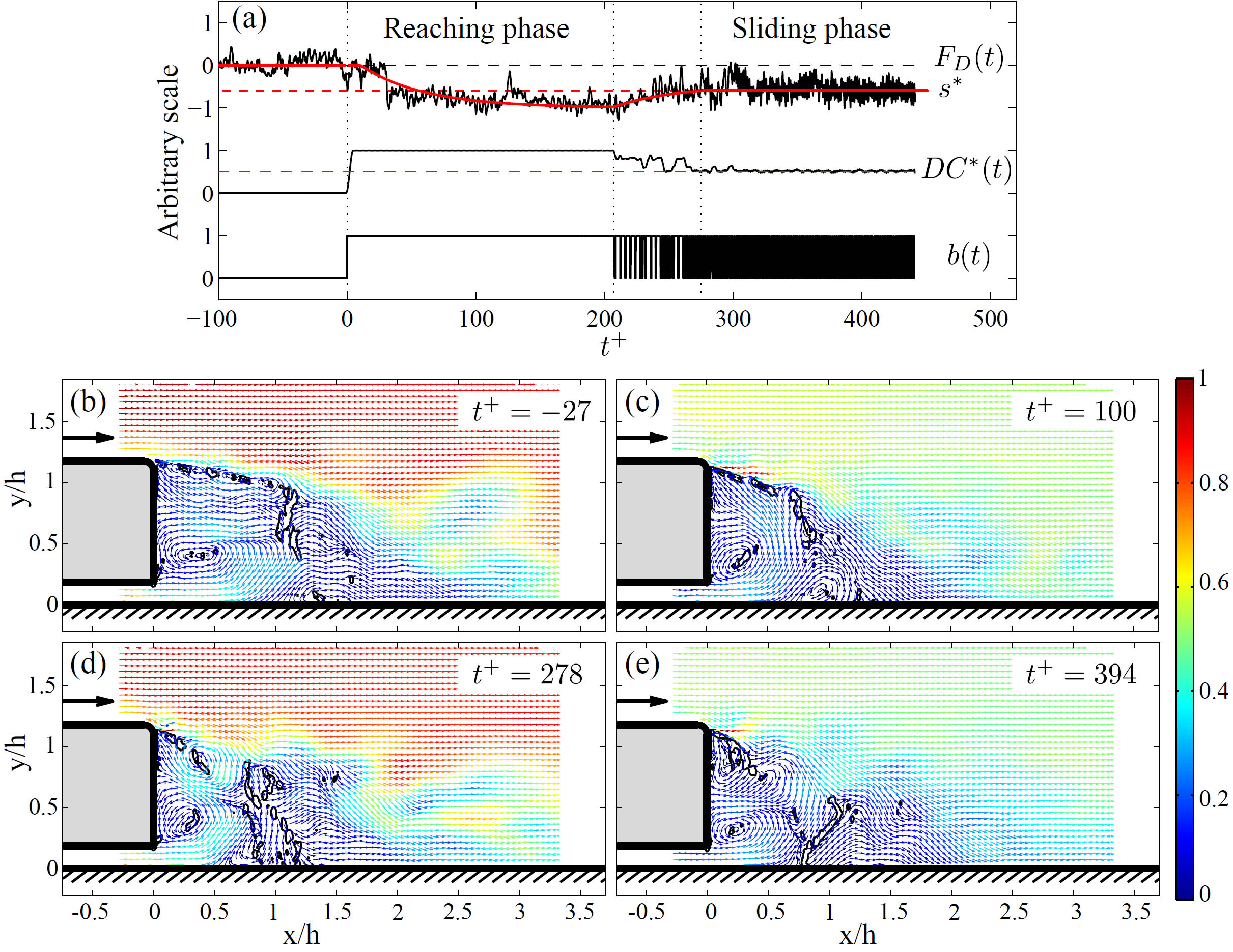
Different graphics demonstrating flow behavior and the control input
Figure4: Particle Image Velocimetry on flow control for an Ahmed body (LAMIH wind tunnel)
- control of bioreactors (in the framework of IPL COSY): here again, the problem is an important uncertainty of the model, which can be handled by robust sliding mode control algorithms, or by applying adaptive finite-time estimation and identification tools;
It is worth highlighting a widespread distribution of various scientific domains in the list of applications for the team given above. Such interdisciplinarity for Valse is unsurprising since control theory is a science of systems whose interest today is, by nature, to interface with other disciplines and their fields of application. This is also well aligned with the domain of CPSs, which by its origin requires multidisciplinary competencies.
5 Social and environmental responsibility
Activities of the team related with social responsibility:
- Engaging in outreach programs to promote mathematics education and awareness in local communities: Rosane Ushirobira participes in the work of CIMPA
- Collaborating with educational institutions to support the development of math skills for young generation: Rosane Ushirobira made several CHICHE sessions in high schools of Lille and metropolitan area
- Participating in mentorship programs to encourage underrepresented groups to pursue careers in mathematics and related fields: Rosane Ushirobira organized the days of young girls in informatics and mathematics (RJMI)
- Contributing to interdisciplinary research that addresses societal challenges, such as healthcare, by applying mathematical modeling and analysis: a new ANR project NOCIME has been accepted with participation of the team on analysis of epidimiological models, in addition, there are publications on this subject
- Mentoring and supporting early-career researchers to foster a diverse and inclusive research community
Activities of the team related with environmental responsibility:
- Developing mathematical models and the methods for their design and analysis to support sustainable energy systems: ANR project SyNPiD devoted to this issue
- Collaborating with environmental scientists, engineers, and policymakers to provide mathematical insights and solutions for environmental challenges and their mitigations: a PhD student is supervised with INRAE on the waste water treatment problems
Overall, social and environmental responsibility for researchers in the team involves using mathematical expertise to address societal issues, promote inclusivity, and contribute to environmental sustainability through research, collaboration, and outreach efforts.
6 Highlights of the year
- ANR Project NOCIME has been accepted
- Regional project STARS of Jin Gyu Lee has been accepted
- Almost all members of the team visited IEEE CDC in Singapore, where our team kept of the total number of accepted publications
- Among 28 journal publications of the team this year, 7 are in Automatica and 10 in IEEE TAC (the top journals in the domain of the theory of control), which is of scientific production
7 New software, platforms, open data
7.1 New software
7.1.1 HCS Toolbox
-
Name:
Homogeneous Systems Control Toolbox (HSC Toolbox) for MATLAB
-
Keywords:
Control design, Matlab, Homogeneity
-
Functional Description:
Homogeneous Systems Control Toolbox (HCS Toolbox) for MATLAB is a collection of functions for design and tuning of control systems with improved control quality (faster convergences, better robustness, smaller overshoots, etc) based on the concept of a dilation symmetry (homogeneity). Homogeneous controllers/observers design well as procedures for upgrading of existing linear controllers/observers to nonlinear (homogeneous) ones are developed for both Single-Input Single-Output (SISO) and Multiply-Input Multiply-Output (MIMO) systems.
-
Release Contributions:
HCS Toolbox for MATLAB ver. 0.1
This is the first release of HCS Toolbox for MATLAB. The list of MATLAB functions provided for homogeneous control systems design: (Homogeneous Objects) hnorm - computation of homogeneous norm hproj - computation of homogeneous projection hcurve - generation of points of a homogeneous curve hsphere - generation of a random grid on a homogeneous sphere (Homogeneous Control Design) hpc_design - Homogeneous Proportional Control (HPC) design hpci_design - Homogeneous Proportional-Integral Control (HPIC) design hsmc_design - Homogeneous Sliding Mode Controller (HSMC) design hsmci_design - design of HSMC with Integral action fhpc_design - Fixed-time HPC design fhpic_design - Fixed-time HPIC design lpc2hpc - upgrading Linear Proportional Control (LPC) to HPC lpic2hpc - upgrading Linear PI control (LPIC) to HPIC (Discretization of Homogeneous Control) e_hpc - explicit discretization of HPC e_hpc - semi-implicit discretization of HPC c_hpc - consistent discretization of HPC e_hpic - explicit discretization of HPIC e_hsmc - explicit discretization of HSMC si_hsmc - semi-implicit explicit discretization of HSMC e_hsmci - explicit discretization of HSMC with Integral action e_fhpc - explicit discretization of Fixed-time HPC si_fhpc - semi-implicit discretization of Fixed-time HPC e_fhpic - explicit discretization of Fixed-time HPIC (Homogeneous Observer Design) ho_design - Homogeneous Observer (HO) design fho_design - Fixed-time HO design lo2ho - upgrading Linear Observer (LO) to HO (Discretization of Homogeneous Observer) e_ho - explicit Euler discretization of HO e_fho - explicit Euler discretization of FHO si_ho - semi-implicit discretization of HO si_fho - semi-implicit discretization of FHO (Block forms ) block_con - transformation to block controlability form bloc_obs - transformation to block bservability form trans_con - transformation to partial block controlability form trans_con - transformation to partial block observability form output_form - transformation to reduced order output control system (Examples) demo_hnorm - demo of computation of a homogeneous norm demo_hsphere - plot of homogeneous balls in 2D demo_hpc - demo of HPC design and simulation demo_hpic - demo of HPIC design and simulation demo_hsmc - demo of HSMC design and simulation demo_hsmci - demo of HSMCI design and simulation demo_fhpc - demo of FHPC design and simulation demo_fhpic - demo of FHPIC design and simulation demo_lpc2hpc - demo of upgrading LPC to HPC/FHPC demo_lpic2hpic - demo of upgrading LPIC to HPIC/FHPIC demo_ho - demo of HO design and simulation demo_fho - demo of FHO design and simulation demo_lo2ho - demo of upgrading LO to HO/FHO For more details please read the documentation: HCS_doc.pdf
- URL:
-
Author:
Andrey Polyakov
-
Contact:
Andrey Polyakov
8 New results
8.1 Analysis and design of homogeneous and finite-time stable systems
Participants: Denis Efimov, Andrey Polyakov.
Input-to-state stability (ISS) is one of the most utilizable robust stability properties for nonlinear dynamical systems, while (nearly) fixed-time convergence is a kind of decay for trajectories of disturbance-free systems that is independent in initial conditions. The presence of both these features for a system can be checked by existence of a proper Lyapunov function. The objective of 10 was to provide the conditions for a converse result that (nearly) fixed-time input-to-state stable systems admit a respective Lyapunov function. Similar auxiliary results for uniform finite-time stability and uniform (nearly) fixed-time stability are obtained.
Usually, singularly perturbed models are used to justify the decomposition of the interconnected systems into the Main Dynamics (MD) and the Parasitic Dynamics (PD). In 20, the effect of a homogeneous PD on the stability of a homogeneous MD, when homogeneity degrees are possibly different, is studied via ISS approach in the framework of singular perturbations. Proposed analysis discovers three kinds of stability in the behavior of such an interconnection by assuming that both, regulated MD and unforced PD, are globally asymptotically stable.
The paper 33 develops control algorithms for a class of affine nonlinear systems using the so-called canonical homogeneous representation. It is demonstrated that such a representation exists for any homogeneous vector field bounded on the unit sphere. It is shown that canonical homogeneous representation is useful for LMI-based control design and stability analysis of nonlinear systems.
Non-overshooting stabilization is a form of safe control where the setpoint chosen by the user is at the boundary of the safe set. Exponential non-overshooting stabilization, including suitable extensions to systems with deterministic and stochastic disturbances, has been solved previously. In 25, we develop homogeneous feedback laws for fixed-time nonovershooting stabilization of nonlinear systems that are input-output linearizable with a full relative degree, i.e., for systems that are diffeomorphically equivalent to the chain of integrators. These homogeneous feedback laws can also assume the secondary role of 'fixed-time safety filters' (FxTSf filters) which keep the system within the closed safe set for all time but, in the case where the user's nominal control commands approach to the unsafe set, allow the system to reach the boundary of the safe set no later than a desired time that is independent of nominal control and independent of the value of the state at the time the nominal control begins to be overridden.
The problem of finite-time stabilization of a linear plant with an optimization of both a settling time and an averaged/weighted control energy is studied using the concept of generalized homogeneity in 23. It is shown that the optimal finite-time stabilizing control in this case can be designed by means of solving a simple linear algebraic equation. Robustness of the obtained control law is studied.
The paper 11 addresses the problem of input-to-state stabilization for heat equation with external input via boundary control strategy. Following our previous results, based on the backstepping approach, a switching boundary control law depending on the system state is designed. By estimating the upper bound of kernel functions, switching levels are determined and commutation law is further constructed. For the chosen switched control, the well-posedness property is verified. It is proved that the resulting system is ISS, and the solutions of the system will not exceed the highest admissible level dependent on the disturbance amplitude. Meanwhile, a stronger result is also obtained, that is the finite-time stability for the disturbance-free system.
8.2 Analysis and design for time-delay systems
Participants: Denis Efimov.
For a class of nonlinear systems with homogeneous right-hand sides of non-zero degree and distributed delays, the problem of stability robustness of the zero solution with respect to time-varying perturbations multiplied by a nonlinear functional gain is studied in 7. It is assumed that the disturbance-free and delay-free system (that results after substitution of non-delayed state for the delayed one) is globally asymptotically stable. First, it is demonstrated that in the disturbance-free case the zero solution is either locally asymptotically stable or practically globally asymptotically stable, depending on the homogeneity degree of the delay-free counterpart. Second, using averaging tools several variants of the time-varying perturbations are considered and the respective conditions are derived evaluating the stability margins in the system. The results are obtained by a careful choice and comparison of Lyapunov-Krasovskii and Lyapunov-Razumikhin approaches. Finally, the obtained theoretical findings are illustrated on two mechanical systems.
For input-affine nonlinear dynamical systems, an ISS analysis with respect to (weighted) average values of exogenous perturbations is proposed in 9. The time-delay method is used to represent the system in a suitable form for investigation: a kind of neutral-type differential equation. The introduced approach allows the asymptotic gains with respect to zero-mean periodic signals to be evaluated for nonlinear systems (an analogue of Bode magnitude plot), as well as for integral ISS (iISS) systems with periodic inputs. The results are illustrated on the class of homogeneous systems.
8.3 Discretisation of homogeneous systems
Participants: Denis Efimov, Andrey Polyakov.
The paper 22 proposes a discretization (sampled-time implementation) algorithm for a class of homogeneous controllers for linear time-invariant systems preserving the finite-time and nearly fixed-time stability properties. The sampling period is assumed to be constant. Both single-input and multiple-input cases are considered. The robustness (ISS) of the obtained sampled-time control system is studied as well.
The paper 21 is dedicated to the experimental analysis of discrete-time differentiators implemented in closed-loop control systems. To this end, two laboratory setups, namely an electro-pneumatic system and a rotary inverted pendulum have been used to implement 25 different differentiators. Since the selected laboratory setups behave differently in the case of dynamic response and noise characteristics, it is expected that the results remain valid for a wide range of control applications. The validity of several theoretical results, which have been already reported in the literature using mathematical analysis and numerical simulations, has been investigated, and several comments are provided to allow one to select an appropriate differentiation scheme in practical closed-loop control systems.
8.4 Homogenization through controls
Participants: Andrey Polyakov.
In 18, the leader-following consensus problem for multi-agent systems is considered. Each agent is assumed to be modeled by a linear multi-input system. A novel (generalized homogeneous) consensus control protocol is designed under the assumption that there are some uncertainties in the dynamic of the leader. Some LMIs are derived to select the control parameters in order to ensure the ISS and global finite-time stability of the consensus errors with desired homogeneity degrees.
The methodology of the unit sliding mode control design (known since 1970s) for linear systems is revised based on the concept of the generalized homogeneity in 24. The restriction about a consistency of the number of control inputs with the dimension of the sliding surface is eliminated. A simple procedure of control tuning based on a known maximal magnitude of matched perturbations is developed. To deal with perturbations of unknown magnitude, a homogeneous sliding mode control with integral action is designed as well.
A generalized homogeneous control with integral action for a multiple-input plant operating under uncertainty conditions is designed in 31. The stability analysis is essentially based on a special version of the non-smooth Lyapunov function theorem for differential equations with discontinuous right-hand sides. A Lyapunov function for analysis of the closed-loop system is presented. For negative homogeneity degree, this Lyapunov function becomes a strict Lyapunov function allowing an advanced analysis to be provided. In particular, the maximum control magnitude and the settling-time of the closed-loop system are estimated and a class of disturbances to be rejected by the control law is characterized. The control parameters are tuned by solving a system of LMIs, whose feasibility is proved at least for small (close to zero) homogeneity degrees.
8.5 Control and estimation for Persidskii systems
Participants: Denis Efimov, Rosane Ushirobira.
Generalized Persidskii systems (or Lur'e systems) represent the dynamics described by the superposition of a linear part with multiple sector nonlinearities and exogenous perturbations. They can be used to model many physical and engineering phenomena.
The paper 19 studies the trajectory behavior evaluation for generalized Persidskii systems with an essentially bounded input on a finite time interval. Also, the notions of annular settling and output annular settling for general nonlinear systems are introduced, and the respective stability conditions are porposed. These conditions are based on the verification of linear matrix inequalities. An application to recurrent neural networks illustrates the usefulness of the proposed notions and conditions.
The paper 12 considers the state estimation problem for a class of non-autonomous nonlinear systems. We propose conditions on the existence and stability of a nonlinear observer based on the invariant manifold approach in both continuous and discrete-time scenarios. The requirements are formulated using linear matrix equalities and LMIs. We present two possible applications of the result: a reduced-order observer (e.g., an observer for unmeasured states) and regression in linear and nonlinear, continuous-and discretetime settings. With nonlinear regression being a sophisticated case, the parameter estimation problem for a particular output equation (when the fusion of linear and nonlinear sensors is weighted) is investigated.
The article 27 deals with the problem of time-varying parameter identification in dynamical regression models affected by disturbances. The disturbances comprise time-dependent external perturbations and nonlinear unmodeled dynamics. With this aim in mind, we propose a robust nonlinear adaptive observer. The algorithm ensures the asymptotic convergence of the parameter identification error to an acceptably small region around the origin in the presence of disturbances. The synthesis of the adaptive observer is given in terms of linear matrix inequalities since the error dynamics is reduced to Persidskii form, providing a constructive design method.
8.6 Control of robotic systems
Participants: Andrey Polyakov.
The paper 32 deals with the tracking problem for the unicycle mobile robot with slippage effects. A homogeneous controller is developed based on a particular cascade control strategy. The robustness of the closed-loop system is studied. The design is essentially based on the canonical homogeneous norm being a Lyapunov function of the system. The (finite-time or exponential) convergence rate of the homogeneous controller can be tuned by a proper selection of the so-called homogeneity degree. Some experimental results illustrate the performance of the proposed homogeneous control in the UMR QBot2 by Quanser.
The paper 28 contributes to the design of a second order sliding-mode controller for the trajectory tracking problem in perturbed unicycle mobile robots. The proposed strategy takes into account the design of two particular sliding variables, which ensure the convergence of the tracking error to the origin in a finite time despite the effect of some external perturbations. The straightforward structure of the controller is simple to tune and implement. The global, uniform and finite-time stability of the closed-loop tracking error dynamics is demonstrated by means of Lyapunov functions. Furthermore, the performance of the proposed approach is validated through some experiments using a QBot2 unicycle mobile robot.
8.7 Estimation under communication constraints
Participants: Denis Efimov.
In the paper 30, an approach is proposed for the remote observation of a dynamical system through a data-rate constrained communication channel. The focus is put on discrete-time systems with a Lipschitz nonlinearity, driven by an external signal, and subject to bounded state perturbation and measurement error. The problem at hand is providing estimates of system's state at a remote location, which is connected via a channel, which can only sent limited numbers of bits per unit of time. A solution, named observation scheme, is proposed in the form of several interacting agents. This solution is designed such that the maximum observation error is upper-bounded by a computable quantity dependent on system constants and selectable parameters. The scheme is designed in an event-triggered fashion, such that the actual communication rate is sometimes much lower than the theoretically evaluated maximum one.
8.8 Synchronization and multistability
Participants: Denis Efimov, Rosane Ushirobira, Jin Gyu Lee.
We present new results for global boundedness of state periodic systems in 29. Thereby, we address both the case of systems, whose dynamics is periodic with respect to a part of the state vector and the case of systems, whose dynamics is periodic with respect to all state variables. Both classes of systems are of high relevance in diverse and timely applications. To derive the results the notion of strong Leonov functions is refined. The main results are complemented by a number of relaxations based on the concpet of weak Leonov functions.
In the paper 8, we study the problem of robust stabilization of affine nonlinear multistable systems in the presence of exogenous disturbances. The results are based on the theory of ISS and iISS for systems with multiple invariant sets. The notions of ISS and iISS control Lyapunov functions (CLFs) and the small control property are extended within the multistability framework. Such properties are also complemented by the concept of a weak iISS CLF and corresponding small control property. It is verified that the universal control formula can be applied to yield the ISS (iISS) property for the closed-loop system. The efficiency of the extended CLF framework in the multistable sense is illustrated for a Duffing system and in application to a noise-induced transition in a semiconductor-gas-discharge gap system.
When a group of heterogeneous node dynamics are diffusively coupled with a high coupling gain, the group exhibits a collective emergent behavior which is governed by a simple algebraic average of the node dynamics called the blended ones. This finding has been utilized for designing heterogeneous multi-agent systems by building the desired blended dynamics first and then splitting it into the node dynamics. However, to compute the magnitude of the coupling gain, each agent needs to know global information such as the number of participating nodes, the graph structure, and so on, which prevents a fully decentralized design of the node dynamics in conjunction with the coupling laws. To resolve this issue, the idea of funnel control, which is a method for adaptive gain selection, was exploited in 16.
A discrete-time version of the blended dynamics theorem is proposed in 13 that can be used for design of distributed computation algorithms. The blended dynamics theorem enables to predict the behavior of heterogeneous multi-agent systems. Therefore, once we get a blended dynamics for a particular computational task, design idea of node dynamics for individual heterogeneous agents can easily occur. In the continuous-time case, prediction by blended dynamics was enabled by high coupling gain among neighboring agents. In the discrete-time case, we propose an equivalent action.
The paper 17 examines how weak synaptic coupling can achieve rapid synchronization in heterogeneous networks. The assumptions aim at capturing the key mathematical properties that make this possible for biophysical networks. In particular, the combination of nodal excitability and synaptic coupling are shown to be essential to the phenomenon.
The paper 15 investigates the finite-time stability and nearly fixed-time stability of nonlinear impulsive systems with destabilizing impulses. A Lyapunov inequality with linear terms has been used to derive sufficient conditions based on the dwell time (DT) and average dwell time (ADT) properties of impulsive sequences to ensure stability of the system. The main results of this paper are applied to the synchronization problem of impulsive neural networks with destablizing impulses.
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
Participants: Denis Efimov, Rosane Ushirobira.
- 52 Hertz is a startup (Brest, France) that develops an underwater communication device for divers. The goal of this contract was to develop an intelligent filtering algorithm that compensates for the voice deformation during underwater vocal communication through the device. The code for the filter was written in Matlab, with further help for its adaptation in Python and C.
10 Partnerships and cooperations
10.1 International initiatives
10.1.1 Participation in other International Programs
ECOS-Nord, Mexico
Participants: Denis Efimov, Andrey Polyakov, Rosane Ushirobira.
-
Title:
Artificial Intelligence-based Control Approaches for Multiple Mobile Robots
-
Partner Institution(s):
- IT Laguna, Mexico
- Instituto Politécnico Nacional, Mexico
-
Date/Duration:
2021–2023
-
Additionnal info/keywords:
This project was focused on studying several tracking tasks for autonomous mobile robot systems, particularly unmanned aerial vehicles and wheeled mobile robots. This project aimed to develop robust control and navigation schemes by combining the methods of artificial intelligence and control theory.
PHC Aurora
Participants: Denis Efimov, Andrey Polyakov, Rosane Ushirobira, Jin Gyu Lee.
-
Title:
Equivalent nonlinear control methods for digitalization in robotics and autonomous systems
-
Partner Institution(s):
- University of Agder, Norway
-
Date/Duration:
2023-2024
-
Additionnal info/keywords:
The robotic and autonomous systems rely heavily on the complex, often distributed, and hierarchical control systems, which ensure main functionalities with a flexible and safe operation. The classical automatic controllers with feedback from the acquisition and perception devices continue to experience the new challenges coming from an increasing complexity in the dynamic behavior of the systems to be controlled on the one hand, and from the digitalization and associated transformations of data, their spatial availability and communication time delays on the other hand. To propose the advanced nonlinear control methods which, however, would be equivalent (in terms of simplicity of tuning and implementation) to the widely accepted standard linear controls (such as PID), and in this way would be more accessible for future applications, is the scientific scope of this project.
10.2 International research visitors
10.2.1 Visits of international scientists
Inria International Chair
Participants: Denis Efimov, Andrey Polyakov, Rosane Ushirobira, Jin Gyu Lee.
Leonid Fridman, UNAM, until Jan 2023
Other international visits to the team
Ariana Gutierrez
-
Status:
PhD
-
Institution of origin:
IT Laguna
-
Country:
Mexico
-
Dates:
from Aug 2023 until Oct 2023
-
Context of the visit:
ECOS Nord
-
Mobility program/type of mobility:
research stay
Jose Antonio Ortega
-
Status:
PhD
-
Institution of origin:
UNAM
-
Country:
Mexico
-
Dates:
from May 2023 until Jun 2023
-
Context of the visit:
Consyt grant
-
Mobility program/type of mobility:
research stay
Hector Rios Barajas
-
Status:
researcher
-
Institution of origin:
IT Laguna
-
Country:
Mexico
-
Dates:
from Aug 2023 until Sep 2023
-
Context of the visit:
ECOS Nord
-
Mobility program/type of mobility:
research stay
Manuel Mera
-
Status:
researcher
-
Institution of origin:
Instituto Politécnico Nacional
-
Country:
Mexico
-
Dates:
from Aug 2023 until Sep 2023
-
Context of the visit:
Inria invited professor
-
Mobility program/type of mobility:
research stay
Ankit Kumar
-
Status:
PhD
-
Institution of origin:
IIT Delhi
-
Country:
India
-
Dates:
from Mar 2023 until May 2023
-
Context of the visit:
CEFIPRA mobility grant
-
Mobility program/type of mobility:
research stay
10.3 National initiatives
10.3.1 ANR
- NOCIME (New Observation and Control Issues Motivated by Epidemiology), coordinator Pierre-Alexandre Bliman (Inria, Paris)
- SyNPiD (Synchronization in power networks with periodic dynamics), coordinators Denis Efimov (Inria, France) and J. Schiffer (Brandenburg University of Technology Cottbus-Senftenberg, Germany)
10.4 Regional initiatives
- Project STARS "Practical design for interconnected CPSs by synchronization enforcement" of Jin Gyu Lee
11 Dissemination
The members of the team serve as reviewers for major journals and conferences in the field of the theory of control and automation.
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
Member of the conference program committees
- Denis Efimov , IFAC World Congress, Yokohama, Japan
11.1.2 Journal
Member of the editorial boards
- Denis Efimov , Associate editor, IFAC Journal on Nonlinear Analysis: Hybrid Systems
- Denis Efimov , Associate editor, IEEE Transactions on Automatic Control
- Denis Efimov , Associate editor, Automatica
- Rosane Ushirobira , Associate editor, Asian Journal of Control
- Rosane Ushirobira , Associate editor, Trends in Computational and Applied Mathematics (TEMA)
11.1.3 Invited talks
- Denis Efimov , Hangzhou Dianzi University, China
- Denis Efimov , Xidian University, Xi'an, China
- Andrey Polyakov , Xidian University, Xi'an, China
11.1.4 Leadership within the scientific community
- Denis Efimov , Senior member IEEE
- Denis Efimov , Member of IFAC TC 1.2. Adaptive and Learning Systems
- Denis Efimov , Publication vice-chair of IFAC TC 9.2. Systems and Control for Societal Impact
- Denis Efimov , Executive committee member, IEEE CSS Technical Committee on Variable Structure and Sliding Mode Control
- Denis Efimov , Co-chair of European PhD Award on Control for Complex and Heterogeneous Systems
- Rosane Ushirobira , Scientific Officer at CIMPA (Centre International de Mathématiques Pures et Appliquées)
11.1.5 Research administration
- Rosane Ushirobira , Elected member of the CE Inria
- Rosane Ushirobira , President of the CER (Commission des emplois de recherche) Inria Lille
- Andrey Polyakov, Jury member of the CRCN/ISFP Inria Lille
- Rosane Ushirobira, Jury member of the CRCN/ISFP Inria Lyon; CoS MCF CNU 61 IUT Lille
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Licence: Rosane Ushirobira , Basic courses in Linear algebra and Calculus, 71h, L3, Polytech Lille
- Master: Jin Gyu Lee , Dynamical systems, 17h, M2, Université de Lille
11.2.2 Juries
The members of the team participated in numerous juries for Ph.D. defense.
11.3 Popularization
11.3.1 Internal or external Inria responsibilities
- Denis Efimov , Member of IES comittee
- Rosane Ushirobira , Scientific Officer for Scientific Popularization
- Rosane Ushirobira , Organizer of 30 min. of science (monthly seminar for scientists in the center)
11.3.2 Interventions
- Rosane Ushirobira , Organizer of CHICHE sessions in Lille Academy, gave 13 talks to high-school students within this framework
- Rosane Ushirobira , Organizer of the 3rd Rendez-vous des Jeunes Mathématiciennes et Informaticiennes (RJMI) Inria Lille
12 Scientific production
12.1 Major publications
- 1 articleDesign of Finite/Fixed-time ISS-Lyapunov Functions for Mechanical Systems.Mathematics of Control, Signals, and Systems2022HAL
- 2 articleAccelerated convergence with improved robustness for discrete-time parameter estimation.Systems and Control Letters5512October 2022, 324-329HALDOI
- 3 articleOn Computer Mouse Pointing Model Online Identification and Endpoint Prediction.IEEE Transactions on Human-Machine Systems525October 2022HAL
- 4 articleHyperexponential and fixed-time stability of time-delay systems: Lyapunov-Razumikhin method.IEEE Transactions on Automatic Control2022HALDOI
- 5 articleQuadrotor stabilization under time and space constraints using implicit PID controller.Journal of The Franklin InstituteJanuary 2022HAL
12.2 Publications of the year
International journals
International peer-reviewed conferences
Scientific book chapters
Reports & preprints
12.3 Cited publications
- 68 articleVelocity estimation of valve movement in oysters for water quality surveillance.IFAC-PapersOnLine482015, 333--338back to text
- 69 conferenceFrequency Domain Forecasting Approach for Latency Reduction in Direct Human-Computer Interaction.Proc. 56th IEEE Conference on Decision and Control (CDC)Melbourne2017back to text
- 70 articleRobust finite-time output feedback stabilization of the double integrator.International Journal of Control8832015, 451--460back to text
- 71 articleOn Homogeneity and Its Application in Sliding Mode.Int. J. Franklin Institute35142014, 1866--1901back to text
- 72 articleVerification of ISS, iISS and IOSS properties applying weighted homogeneity.Systems & Control Letters622013, 1159--1167back to text
- 73 articleOn conditions of oscillations and multi-homogeneity.Mathematics of Control, Signals, and Systems2812015, 1--37URL: http://dx.doi.org/10.1007/s00498-015-0157-yback to text
- 74 articleDevelopment of Homogeneity Concept For Time-Delay Systems.SIAM Journal on Optimization and Control5232014, 1403--1808back to text
- 75 articleRealization and Discretization of Asymptotically Stable Homogeneous Systems.IEEE Trans. Automatic Control62112017, 5962--5969back to text
- 76 articleWeighted Homogeneity for Time-Delay Systems: Finite-Time and Independent of Delay Stability.IEEE Trans. Automatic Control6112016, 210--215back to text
- 77 articleBoundary time-varying feedbacks for fixed-time stabilization of constant-parameter reaction-diffusion systems.Automatica1032019, 398--407URL: https://doi.org/10.1016/j.automatica.2019.02.013back to text
- 78 articleSISO model-based control of separated flows: Sliding mode and optimal control approaches.International Journal of Robust and Nonlinear Control27182017, 5008-5027back to text
- 79 conferenceInterval Prediction for Continuous-Time Systems with Parametric Uncertainties.Proc. 58th IEEE Conference on Decision and Control (CDC)Nice2019back to text
- 80 articleFinite-time and Fixed-time Observer Design: Implicit Lyapunov function approach.Automatica8712018, 52-60back to text
- 81 articleOn Homogeneous Finite-Time Control for Linear Evolution Equation in Hilbert Space.IEEE Transactions on Automatic Control2018back to text
- 82 articleConsistent Discretization of Finite-time and Fixed-time Stable Systems.SIAM Journal on Optimization and Control5712019, 78--103back to text
- 83 articleOn Homogeneous Distributed Parameter Systems.IEEE Trans. Automatic Control61112016, 3657--3662back to text
- 84 articleFinite-time and fixed-time stabilization: Implicit Lyapunov function approach.Automatica512015, 332-340back to text
- 85 articleNonlinear feedback design for fixed-time stabilization of linear control systems.IEEE Transactions on Automatic Control57(8)2012, 2106-2110back to text
- 86 articleTime-Varying Parameter Identification Algorithms: Finite and Fixed-Time Convergence.IEEE Transactions on Automatic Control6272017, 3671--3678URL: https://dx.doi.org/10.1109/TAC.2017.2673413back to text
- 87 conferenceEstimating the infection rate of a SIR epidemic model via differential elimination.Proceedings of ECCNaples2019back to text
- 88 conferenceA forecasting algorithm for latency compensation in indirect human-computer interactions.Proceedings of ECCAlborg2016, 1081--1086back to textback to text
- 89 articleA note on delay robustness for homogeneous systems with negative degree.Automatica7952017, 178--184back to text

