2.1 Scientific grounds

Mesh generation is a notoriously difficult task. A quick search on the NSF grant web page with “mesh generation AND finite element” keywords returns more than 30 currently active grants for a total of $8 million. NASA indicates mesh generation as one of the major challenges for 2030  45, and estimates that it costs 80% of time and effort in numerical simulation. This is due to the need for constructing supports that match both the geometry and the physics of the system to be modeled. In our team we pay a particular attention to scientific computing, because we believe it has a world changing impact.

It is very unsatisfactory that meshing, i.e. just “preparing the data” for the simulation, eats up the major part of the time and effort. Our goal is to change the situation, by studying the influence of shapes and discretizations, and inventing new algorithms to automatically generate meshes that can be directly used in scientific computing. This goal is a result of our progressive shift from pure graphics (“Geometry and Lighting”) to real-world problems (“Shape Fidelity”).

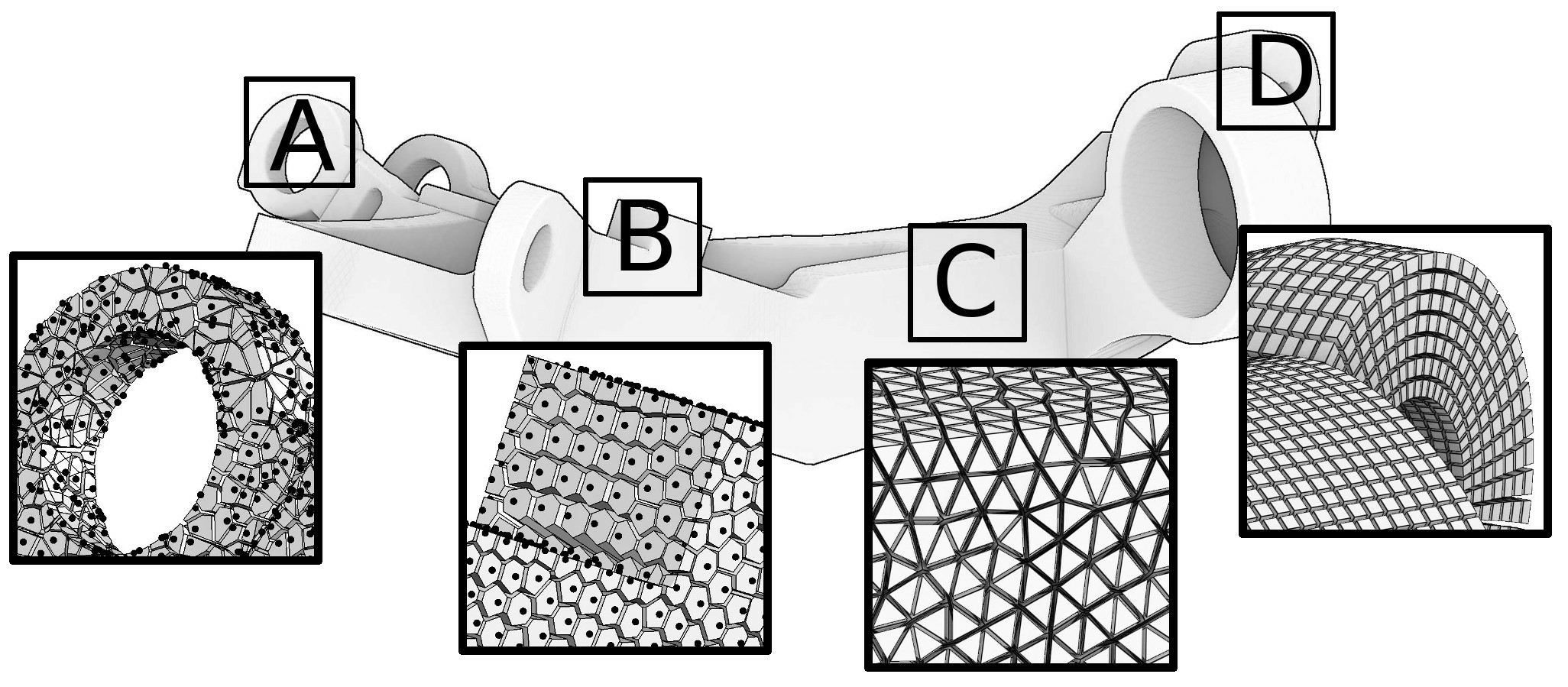
Meshing is central in geometric modeling because it provides a way to represent functions on the objects being studied (texture coordinates, temperature, pressure, speed, etc.). There are numerous ways to represent functions, but if we suppose that the functions are piecewise smooth, the most versatile way is to discretize the domain of interest. Ways to discretize a domain range from point clouds to hexahedral meshes; let us list a few of them sorted by the amount of structure each representation has to offer (refer to Figure 1).

• At one end of the spectrum there are point clouds: they exhibit no structure at all (white noise point samples) or very little (blue noise point samples). Recent explosive development of acquisition techniques (e.g. scanning or photogrammetry) provides an easy way to build 3D models of real-world objects that range from figurines and cultural heritage objects to geological outcrops and entire city scans. These technologies produce massive, unstructured data (billions of 3D points per scene) that can be directly used for visualization purposes, but this data is not suitable for high-level geometry processing algorithms and numerical simulations that usually expect meshes. Therefore, at the very beginning of the acquisition-modeling-simulation-analysis pipeline, powerful scan-to-mesh algorithms are required.

  During the last decade, many solutions have already been proposed  40, 19, 35, 34, 23, but the problem of building a good mesh from scattered 3D points is far from being solved. Beside the fact that the data is unusually large, the existing algorithms are challenged also by the extreme variation of data quality. Raw point clouds have many defects, they are often corrupted with noise, redundant, incomplete (due to occlusions): they all are uncertain.

• Triangulated surfaces are ubiquitous, they are the most widely used representation for 3D objects. Some applications like 3D printing do not impose heavy requirements on the surface: typically it has to be watertight, but triangles can have an arbitrary shape. Other applications like texturing require very regular meshes, because they suffer from elongated triangles with large angles.

  While being a common solution for many problems, triangle mesh generation is still an active topic of research. The diversity of representations (meshes, NURBS, ...) and file formats often results in a “Babel” problem when one has to exchange data. The only common representation is often the mesh used for visualization, that has in most cases many defects, such as overlaps, gaps or skinny triangles. Re-injecting this solution into the modeling-analysis loop is non-trivial, since again this representation is not well adapted to analysis.

• Tetrahedral meshes are the volumic equivalent of triangle meshes, they are very common in the scientific computing community. Tetrahedral meshing is now a mature technology. It is remarkable that still today all the existing software used in the industry is built on top of a handful of kernels, all written by a small number of individuals 25, 43, 50, 29, 41, 44, 26, 55.

  Meshing requires a long-term, focused, dedicated research effort that combines deep theoretical studies with advanced software development. We have the ambition to bring this kind of maturity to a different type of mesh (structured, with hexahedra), which is highly desirable for some simulations, and for which, unlike tetrahedra, no satisfying automatic solution exists. In the light of recent contributions, we believe that the domain is ready to overcome the principal difficulties.

• Finally, at the most structured end of the spectrum there are hexahedral meshes composed of deformed cubes (hexahedra). They are preferred for certain physics simulations (deformation mechanics, fluid dynamics ...) because they can significantly improve both speed and accuracy. This is because (1) they contain a smaller number of elements (5-6 tetrahedra for a single hexahedron), (2) the associated tri-linear function basis has cubic terms that can better capture higher-order variations, (3) they avoid the locking phenomena encountered with tetrahedra 16, (4) hexahedral meshes exploit inherent tensor product structure and (5) hexahedral meshes are superior in direction dominated physical simulations (boundary layer, shock waves, etc). Being extremely regular, hexahedral meshes are often claimed to be The Holy Grail for many finite element methods  17, outperforming tetrahedral meshes both in terms of computational speed and accuracy.

  Despite 30 years of research efforts and important advances, mainly by the Lawrence Livermore National Labs in the U.S. 49, 47, hexahedral meshing still requires considerable manual intervention in most cases (days, weeks and even months for the most complicated domains). Some automatic methods exist 33, 53, that constrain the boundary into a regular grid, but they are not fully satisfactory either, since the grid is not aligned with the boundary. The advancing front method 14 does not have this problem, but generates irregular elements on the medial axis, where the fronts collide. Thus, there is no fully automatic algorithm that results in satisfactory boundary alignment.

3.1 Point clouds

Currently, transforming the raw point cloud into a triangular mesh is a long pipeline involving disparate geometry processing algorithms:

• Point pre-processing: colorization, filtering to remove unwanted background, first noise reduction along acquisition viewpoint;
• Registration: cloud-to-cloud alignment, filtering of remaining noise, registration refinement;
• Mesh generation: triangular mesh from the complete point cloud, re-meshing, smoothing.

The output of this pipeline is a locally-structured model which is used in downstream mesh analysis methods such as feature extraction, segmentation in meaningful parts or building Computer-Aided Design (CAD) models.

It is well known that point cloud data contains measurement errors due to factors related to the external environment and to the measurement system itself  46, 39, 21. These errors propagate through all processing steps: pre-processing, registration and mesh generation. Even worse, the heterogeneous nature of different processing steps makes it extremely difficult to know how these errors propagate through the pipeline. To give an example, for cloud-to-cloud alignment it is necessary to estimate normals. However, the normals are forgotten in the point cloud produced by the registration stage. Later on, when triangulating the cloud, the normals are re-estimated on the modified data, thus introducing uncontrollable errors.

We plan to develop new reconstruction, meshing and re-meshing algorithms, with a specific focus on the accuracy and resistance to all defects present in the input raw data. We think that pervasive treatment of uncertainty is the missing ingredient to achieve this goal. We plan to rethink the pipeline with the position uncertainty maintained during the whole process. Input points can be considered either as error ellipsoids  51 or as probability measures  31. In a nutshell, our idea is to start by computing an error ellipsoid  54, 36 for each point of the raw data, and then to cumulate the errors (approximations) made at each step of the processing pipeline while building the mesh. In this way, the final users will be able to take the knowledge of the uncertainty into account and rely on this confidence measure for further analysis and simulations. Quantifying uncertainties for reconstruction algorithms, and propagating them from input data to high-level geometry processing algorithms has never been considered before, possibly due to the very different methodologies of the approaches involved. At the very beginning we will re-implement the entire pipeline, and then attack the weak links through all three reconstruction stages.

3.2 Parameterizations

One of the favorite tools we use in our team are parameterizations, and we have major contributions to the field: we have solved a fundamental problem formulated more than 60 years ago 1. Parameterizations provide a very powerful way to reveal structures on objects. The most omnipresent application of parameterizations is texture mapping: texture maps provide a way to represent in 2D (on the map) information related to a surface. Once the surface is equipped with a map, we can do much more than a mere coloring of the surface: we can approximate geodesics, edit the mesh directly in 2D or transfer information from one mesh to another.

Parameterizations constitute a family of methods that involve optimizing an objective function, subject to a set of constraints (equality, inequality, being integer, etc.). Computing the exact solution to such problems is beyond any hope, therefore approximations are the only resort. This raises a number of problems, such as the minimization of highly nonlinear functions and the definition of direction fields topology, without forgetting the robustness of the software that puts all this into practice.

Show image description

 

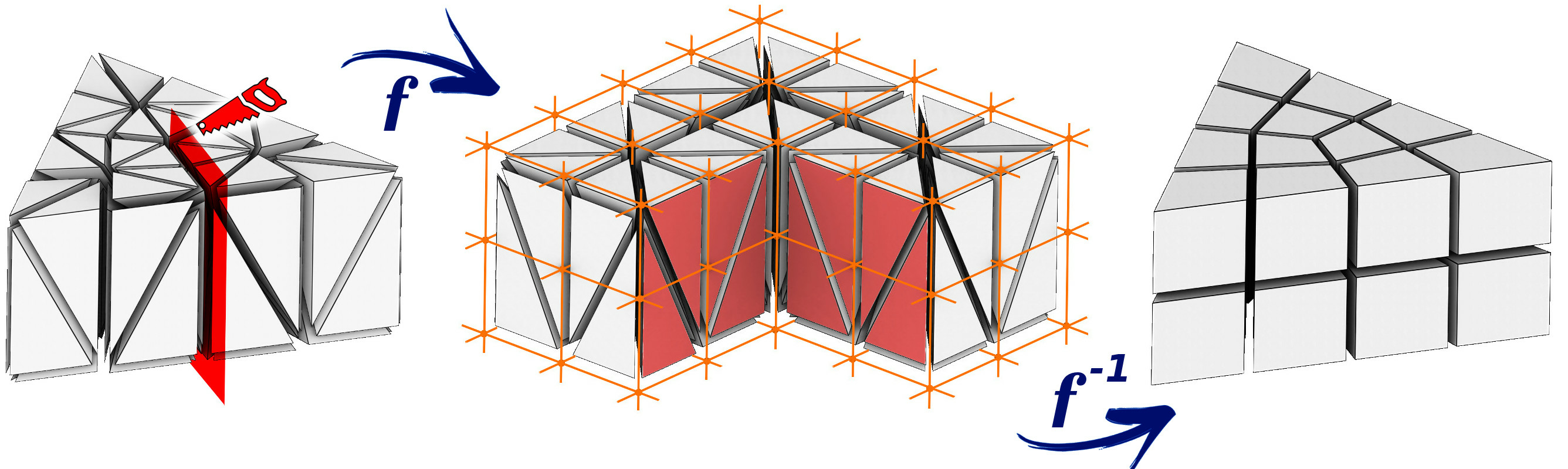
We are particularly interested in a specific instance of parameterization: hexahedral meshing. The idea 3, 2 is to build a transformation $f$ from the domain to a parametric space, where the distorted domain can be meshed by a regular grid. The inverse transformation $f^{-1}$ applied to this grid produces the hexahedral mesh of the domain, aligned with the boundary of the object. The strength of this approach is that the transformation may admit some discontinuities. Let us show an example: we start from a tetrahedral mesh (Figure 2, left) and we want to deform it in a way that its boundary is aligned with the integer grid. To allow for a singular edge in the output (the valency 3 edge, Figure 2, right), the input mesh is cut open along the highlighted faces and the central edge is mapped onto an integer grid line (Figure 2, middle). The regular integer grid then induces the hexahedral mesh with the desired topology.

Current global parameterizations allow grids to be positioned inside geometrically simple objects whose internal structure (the singularity graph) can be relatively basic. We wish to be able to handle more configurations by improving three aspects of current methods:

• Local grid orientation is usually prescribed by minimizing the curvature of a 3D steering field. Unfortunately, this heuristic does not always provide singularity curves that can be integrated by the parameterization. We plan to explore how to embed integrability constraints in the generation of the direction fields. To address the problem, we already identified necessary validity criteria: for example, the permutation of axes along elementary cycles that go around a singularity must preserve one of the axes (the one tangent to the singularity). The first step to enforce this (necessary) condition will be to split the frame field generation into two parts: first we will define a locally stable vector field, followed by the definition of the other two axes by a 2.5D directional field (2D advected by the stable vector field).
• The grid combinatorial information is characterized by a set of integer coefficients whose values are currently determined through numerical optimization of a geometric criterion: the shape of the hexahedra must be as close as possible to the steering direction field. Thus, the number of layers of hexahedra between two surfaces is determined solely by the size of the hexahedra that one wishes to generate. In these settings, degenerate configurations arise easily, and we want to avoid them. In practice, mixed integer solvers often choose to allocate a negative or zero number of layers of hexahedra between two constrained sheets (boundaries of the object, internal constraints or singularities). We will study how to inject strict positivity constraints into these cases, which is a very complex problem because of the subtle interplay between different degrees of freedom of the system. Our first results for quad-meshing of surfaces give promising leads, notably thanks to motorcycle graphs  22, a notion we wish to extend to volumes.
• Optimization for the geometric criterion makes it possible to control the average size of the hexahedra, but it does not ensure the bijectivity (even locally) of the resulting parameterizations. Considering other criteria, as we did in 2D  30, would probably improve the robustness of the process. Our idea is to keep the geometry criterion to find the global topology, but try other criteria to improve the geometry.

3.3 Hexahedral-dominant meshing

All global parameterization approaches are decomposed into three steps: frame field generation, field integration to get a global parameterization, and final mesh extraction. Getting a full hexahedral mesh from a global parameterization means that it has positive Jacobian everywhere except on the frame field singularity graph. To our knowledge, there is no solution to ensure this property, but some efforts are done to limit the proportion of failure cases. An alternative is to produce hexahedral dominant meshes. Our position is in between those two points of view:

1. We want to produce full hexahedral meshes;
2. We consider as pragmatic to keep hexahedral dominant meshes as a fallback solution.

The global parameterization approach yields impressive results on some geometric objects, which is encouraging, but not yet sufficient for numerical analysis. Note that while we attack the remeshing with our parameterizations toolset, the wish to improve the tool itself (as described above) is orthogonal to the effort we put into making the results usable by the industry. To go further, our idea (as opposed to  37, 24) is that the global parameterization should not handle all the remeshing, but merely act as a guide to fill a large proportion of the domain with a simple structure; it must cooperate with other remeshing bricks, especially if we want to take final application constraints into account.

For each application we will take as an input domains, sets of constraints and, eventually, fields (e.g. the magnetic field in a tokamak). Having established the criteria of mesh quality (per application!) we will incorporate this input into the mesh generation process, and then validate the mesh by a numerical simulation software.

4.1 Geometric Tools for Simulating Physics with a Computer

Numerical simulation is the main targeted application domain for the geometry processing tools that we develop. Our mesh generation tools will be tested and evaluated within the context of our cooperation with Hutchinson, experts in vibration control, fluid management and sealing system technologies. We think that the hex-dominant meshes that we generate have geometrical properties that make them suitable for some finite element analyses, especially for simulations with large deformations.

We also have a tight collaboration with a geophysical modeling specialists via the RING consortium. In particular, we produce hexahedral-dominant meshes for geomechanical simulations of gas and oil reservoirs. From a scientific point of view, this use case introduces new types of constraints (alignments with faults and horizons), and allows certain types of nonconformities that we did not consider until now.

Our cooperation with RhinoTerrain pursues the same goal: reconstruction of buildings from point cloud scans allows to perform 3D analysis and studies on insolation, floods and wave propagation, wind and noise simulations necessary for urban planification.

6.1 New software

7.1 Lowest distortion mapping

Mapping is one of the longest standing problems in computational mathematics. In many applications, like in navigation, it is much simpler to work in a map than to directly manipulate the object itself. This makes mapping 3D surfaces to 2D space (or solid domains to 3D space) one of the most important problems in geometry processing. Nowadays applied to a broad variety of domains, mapping takes its origins in the geography. We can trace the interest of mathematicians in maps to the earliest of time. Claudius Ptolemy (circa 100–170 AD), in his treatise “Sphœrœ a planetis projectio in planum”, was already working on mathematical tools to represent these surfaces, in this case the Earth, on the plane. It is indeed a challenge to represent faithfully the surface of the Earth, with its curvature, on the flat plane.

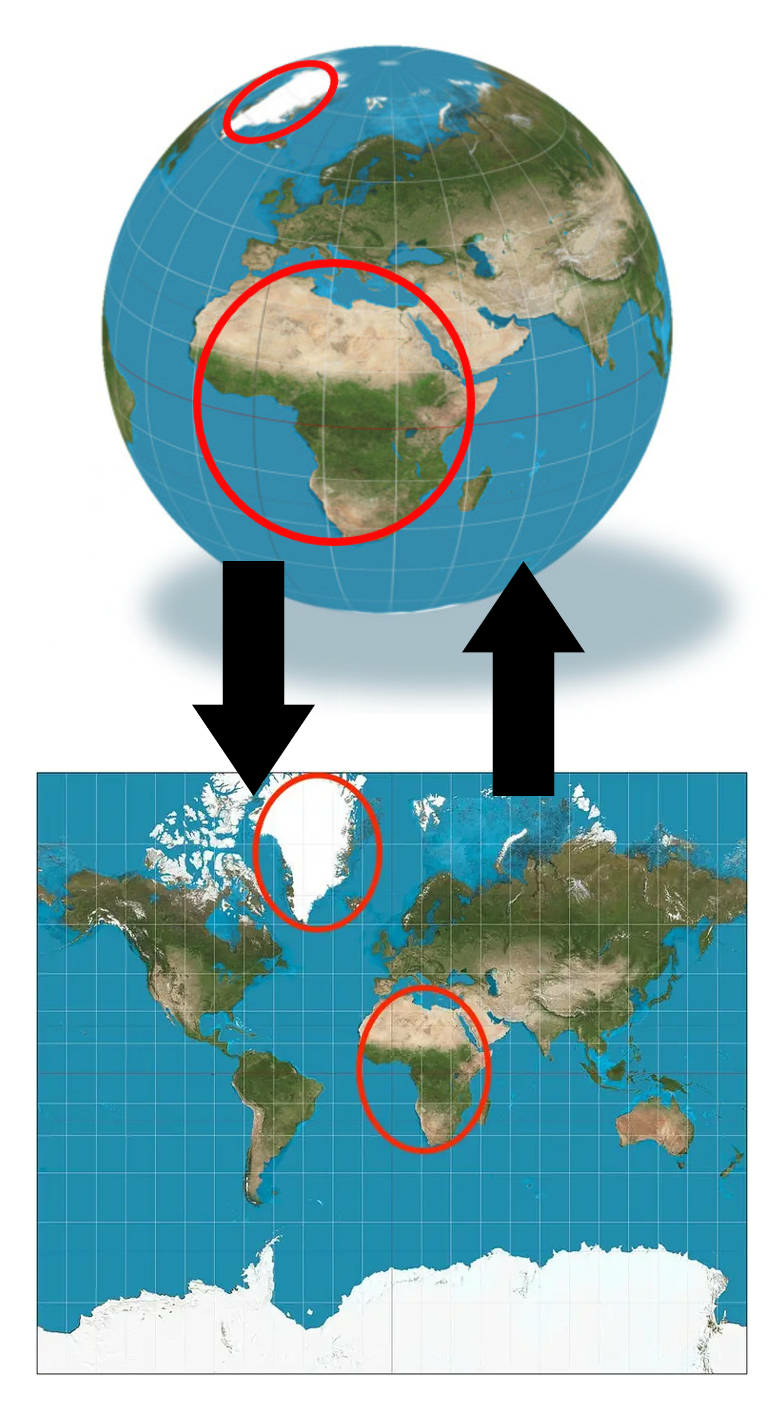
We can distinguish two fundamental properties necessary for a “good” map:

1. Invertibility: the very idea of computing a map is to be able to go back and forth between the object itself and its image without ambiguities. If it is the case, we say that the map is invertible.
2. Quality: a truly good map must be as little distorted as possible. For example, it is very challenging to measure distances in the Mercator projection of the Earth: in this map Greenland has the size of Africa, while in reality Greenland is 14 times smaller!

Both proprieties have been the subject of extensive research, from Ptolemy in his seminal work “Sphœrœ a planetis projectio in planum” to numerous modern papers. In collaboration with our colleagues from Moscow Institute of Physics and Technology, we set a new bar for mapping algorithms. Few years ago we achieved 1 the biggest leap in guarantees on invertibility since 1963 and now we furthermore extend 5 this leap by providing the best guarantees on the distortion bounds since 1856.

Working directly on distortion of lengths in maps is crazy difficult, and we follow the path set by many others, by solving a proxy problem instead. Imagine that the domain of interest is made of some elastic material, then a deformation with least stored energy must be a good map! It is a sensible approach, since mathematical elasticity minimizes the deviation from the isometric deformation state on average. So, it is pretty common to minimize $\int f$, where $f$ stands for the energy density. By choosing $f$, we choose the material and can control the output. This approach is time-tested and produces good results. The problem, however, is that by minimizing the stored energy, we optimize the distortion on average, while in some points the distortion can grow without limits.

Show image description

 

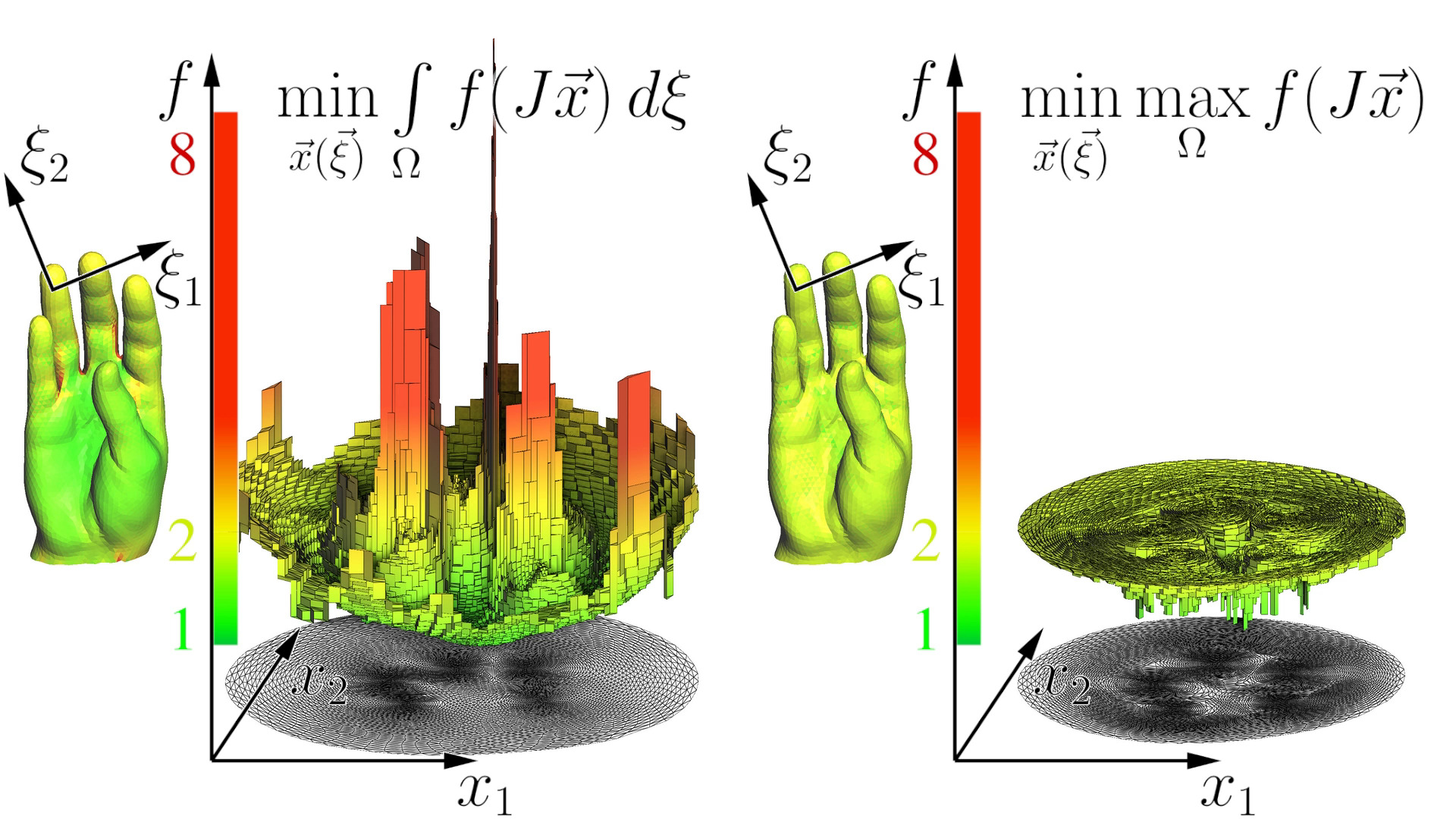
Figure 4 provides the illustration. On the left you can see the map that minimizes the distortion on average, and, thanks to our prior work 1, 9, we can reliably build such maps. In this case most of the cells have little deformation, but several triangles are badly distorted. The problem is that even a single badly distorted element can drastically increase the computational cost when used in a numerical simulation. We can improve the quality of these triangles by sacrificing the quality of some other. In this work we are interested in minimizing the worst distortion, we want to know how to solve the much more difficult problem on the right.

Surprisingly, these two problems are very closely connected, and exposing this connection is an important contribution. We have shown that despite being quite different problems, foldover-free and bounded distortion mapping problems can be solved with very similar approaches. Our very simple approach (150 lines of C++!) allows us to reliably build 2D and 3D mesh deformations with smallest known distortion estimates.

7.2 Curvature-Driven Conformal Deformations

Show image description

 

    

Immersion of a combinatorial Ricci flow toward a cone metric. Blue spheres highlights $-\pi /2$ cones and red spheres $\pi /2$ cones.Show image description

 

Show image description

 

Show image description

 

Curvature flows stand as indispensable tools in computer graphics for surface manipulation. They iteratively deform surfaces by minimizing an energy while complying with given constraints, such as area or volume preservation, positional constraints. They essentially define surfaces as the minimizers of specific energies. Computer graphics is usually concerned with two types of curvature-based flows: fairing flows, aimed at surface smoothing, and intrinsic flows, for which computing an embedded representation is often unnecessary.

The first category, fairing flows, progressively molds surfaces to make it as round as possible by minimizing the surface bending. This is quantified by the p-norm of the shape operator, encapsulating the variations in surface normals across all directions. Fairing flows for various p are shown by Figure 5.

The second category: the intrinsic flows, is commonly used in the computer graphics community to “flatten” the surface not visually but from the intrinsic perspective of an “observerliving” on the geometry. In computer graphics, these flows naturally arise when computing texture atlases 42, cone parametrization for quad remeshing 15, or surface approximation using developable patches for manufacturing 52. Here, the focus is on modifying the Gaussian curvature, i.e., the determinant of the shape operator.

These two geometrical flows are of very different nature and were, until now, not treated by the same algorithm.

Furthermore, ensuring a geometric realization of the flow involves formulating these energies in terms of vertex displacement or Jacobian matrices. However, evaluating curvature, a second-order derivative of point positions, on a discrete mesh introduces considerable numerical instability.

In this work 4, we were concerned with unifying the treatment of geometrical flows and improving their numerical instability. To do so, we propose focus on conformal deformation: deformation preserving local angles but allowing large area deformations. This allows us to perform a change of variables to directly operate with scale factors and shape operators. These new variables offer two significant advantages: improving long term stability of the flow and simplifying manipulations of curvature-based energies. Having access to the complete curvature tensor enables us to handle a wide range of energies, including fairing (Figure 5) and “intrinsic" energies (Figure 5). This is made possible by the discovery of a previously unknown necessary and sufficient integrability condition for topological spheres describing when the curvature tensor and the scale factor define a valid conformal deformation.

7.3 Deformation Recovery

Show image description

 

Estimating meaningful deformations of surfaces is a classical problem in computer graphics, with applications in several downstream tasks such as surface mapping and registration, character reposing, and handle-based editing. Due to its broad applicability, numerous techniques have been developed to address this task 18.

While early approaches relied on numerical techniques 18, recent methods, following this trend, leverage structured data-driven priors to estimate plausible deformations 28, 48, 13, 20. Despite significant ongoing efforts, this problem remains challenging. A key difficulty with most existing data-driven methods lies in constructing a feasible latent space 32. This typically requires amassing a collection comprising all plausible deformations 27, 13, thus necessitating a significant amount of training data. Furthermore, even when such data is available, representing shapes using a global encoding typically ties existing approaches to specific shape categories, and thus requires extensive re-training for cross-category generalization.

In this work 7 (also refer to Figure 6), instead of relying on a global shape encoding, we condition our predictions on a coarse, local deformation input signal. This choice is motivated by the observation that, in specific scenarios, constructing an appropriate local input signal is sufficient to learn category-agnostic high-quality deformations. Building on the recent success of Jacobian fields as learnable deformation representation 13, we design a network that predicts Jacobian matrices per triangles. The input to our network is thus a field of Jacobian matrices, averaged to vertices around a one-ring neighborhood, representing a coarse deformation. Our network comprises a series of MLPs coupled with a smoothing operator, which takes coarse Jacobians as input and produces detailed Jacobians. Our network has fully shared weights and is applied independently at each triangle.

Our network prediction is trained by supervising Jacobians corresponding to the detailed mesh, mesh vertex positions, and an integrability loss on Jacobians. Due to the purely local and fully shared nature of our networks, they can be trained using a handful of shapes, as each triangle becomes a training instance.

We consider two general scenarios: shape correspondence and shape editing. For map refinement and shape correspondence, given a fixed source shape and a target shape representing a coarse deformation of the source, we first express the coordinate function of the target shape using the low-frequency eigenfunctions of its Laplace-Beltrami operator to obtain a smooth approximation of its geometry, referred to as the spectrally projected shape. This is a natural representation supported by shape correspondence methods that use the functional map framework 38. We then define the Jacobians from the source shape to the spectrally projected target shape as the coarse deformation signal, which forms the input to our network. For shape editing, we use the rotation matrices at each face, averaged to the incident vertex, as the input signal to produce Jacobians corresponding to a valid shape. The network, training data, and supervision remain consistent across all input signals.

7.4 2.5D Hexahedral meshing for reservoir simulations

Show image description

 

In collaboration with the startup TESSAEL stemmed from the team and TotalEnergies, we presented a new method 6 for generating pure hexahedral meshes for reservoir simulations. The grid is obtained by extruding a quadrangular mesh, using ideas from the latest advances in computational geometry, specifically the generation of semi-structured quadrangular meshes based on global parameterization.

Hexahedral elements are automatically constructed to smoothly honor input features' geometry (domain boundaries, faults, and horizons), thus, making it possible to be used for multiple types of physical simulations on the same mesh.

Main contributions are: the introduction of a new semi-structured hexahedral meshing workflow producing high-quality meshes for a wide range of fault systems, and the study and definition of weak verticality on triangulated surface meshes. This allows us to design better and more robust algorithms during the extrusion phase along non-vertical faults.

We demonstrate 1) the simplicity of using such hexahedral meshes generated using the proposed method for coupled flow-geomechanics simulations with state-of-the-art simulators for reservoir studies, and 2) the possibility of using such semi-structured hexahedral meshes in commercial structured flow simulators, offering an alternative gridding approach to handle a wider family of fault networks without recourse to the stair-step fault approximation.

8.1 Bilateral contracts with industry

Company: TotalEnergies

Duration: 01/10/2020 – 30/03/2024

Participants: Dmitry Sokolov, Nicolas Ray and David Desobry

Abstract: The goal of this project is to improve the accuracy of rubber behavior simulations for certain parts produced by TotalEnergies, notably gaskets. To do this, both parties need to develop meshing methods adapted to the simulation of large deformations in non-linear mechanics. The Pixel team has a strong expertise in hex-dominant meshing, TotalEnergies has a strong background in numerical simulation within an industrial context. This collaborative project aims to take advantage of both expertises.

9.1 International initiatives

Participants: Étienne Corman.

10.1 Promoting scientific activities

Dmitry Sokolov is an elected member of the executive board of the Association Française d'Informatique Graphique. AFIG is a non-profit scientific association, its aim is to federate and animate the scientific community in fields related to Computer Graphics, to disseminate information and events in the field, and to facilitate networking and interaction between researchers, as well as between industry and research.

10.1.1 Scientific events: organisation

General chair, scientific chair

  This year the team has organised the 64th edition of the CEA–EDF–Inria summer school, 43 participants attended to the school (Fig. 8) which took place from June 10 to June 14 at the Centre Inria of the University of Lorraine.

The aim of this summer school was to provide an overview of the automatic and semi-automatic methods currently used to generate hexahedral meshes for academic and industrial purposes. Starting from CAD-like geometric models as input data, recently developed practical and theoretical methods for generating and manipulating hexahedral meshes were presented. In particular, the following points were addressed:

• An overview of existing (semi-)automatic methods for generating hexahedral meshes with associated quality criteria;
• A focus on different representations and methods for generating orientation fields;
• Notions of global parametrizations and their use in meshing;
• Polycube methods;
• Grid intersection methods.

An important part of the course was be devoted to computer-based practical exercises to manipulate these concepts using various software packages, ranging from understanding concepts such as orientation fields to interactive generation of block-structured meshes, via mesh quality assessment.

Show image description

 

Reviewer

  Members of the team were reviewers for Eurographics, SIGGRAPH, SIGGRAPH Asia, ISVC, Pacific Graphics, and SPM.

10.2 Teaching - Supervision - Juries

11.1 Major publications

• 1 articleV.Vladimir Garanzha, I.Igor Kaporin, L.Liudmila Kudryavtseva, F.François Protais, N.Nicolas Ray and D.Dmitry Sokolov. Foldover-free maps in 50 lines of code.ACM Transactions on GraphicsVolume 40issue 4July 2021, Article No.102, pp 1–16HALDOIback to textback to textback to text
• 2 articleN.Nicolas Ray, D.Dmitry Sokolov and B.Bruno Lévy. Practical 3D Frame Field Generation.ACM Trans. Graph.356November 2016, 233:1--233:9URL: http://doi.acm.org/10.1145/2980179.2982408DOIback to text
• 3 articleD.Dmitry Sokolov, N.Nicolas Ray, L.Lionel Untereiner and B.Bruno Lévy. Hexahedral-Dominant Meshing.ACM Transactions on Graphics3552016, 1 - 23HALDOIback to text

11.2 Publications of the year

11.3 Cited publications

• 13 articleN.Noam Aigerman, K.Kunal Gupta, V. G.Vladimir G Kim, S.Siddhartha Chaudhuri, J.Jun Saito and T.Thibault Groueix. Neural Jacobian Fields: Learning Intrinsic Mappings of Arbitrary Meshes.SIGGRAPH2022back to textback to textback to text
• 14 articleT. C.Tristan Carrier Baudouin, J.-F.Jean-François Remacle, E.Emilie Marchandise, F.François Henrotte and C.Christophe Geuzaine. A frontal approach to hex-dominant mesh generation.Adv. Model. and Simul. in Eng. Sciences112014, 8:1--8:30URL: https://doi.org/10.1186/2213-7467-1-8DOIback to text
• 15 inproceedingsM.Mirela Ben-Chen, C.Craig Gotsman and G.Guy Bunin. Conformal flattening by curvature prescription and metric scaling.Computer Graphics Forum272Wiley Online Library2008, 449--458back to text
• 16 inproceedingsS. E.Steven E. Benzley, K.Karl Ernest Perry, B. C.Brett Clark Merkley and G.Greg Sjaardema. A Comparison of All-Hexahedral and All-Tetrahedral Finite Element Meshes for Elastic and Elasto-Plastic Analysis.International Meshing Roundtable conf. proc.1995back to text
• 17 inproceedingsT.Ted Blacker. Meeting the Challenge for Automated Conformal Hexahedral Meshing.9th International Meshing Roundtable2000, 11--20back to text
• 18 articleM.Mario Botsch and O.Olga Sorkine. On Linear Variational Surface Deformation Methods.IEEE Transactions on Visualization and Computer Graphics1412008, 213-230DOIback to textback to text
• 19 miscCloud Compare.http://www.danielgm.net/cc/release/back to text
• 20 articleA.Ana Dodik, O.Oded Stein, V.Vincent Sitzmann and J.Justin Solomon. Variational Barycentric Coordinates.ACM Transactions on Graphics426December 2023, 1–16URL: http://dx.doi.org/10.1145/3618403DOIback to text
• 21 articleZ.Zhengchun Du, M.Mengrui Zhu, Z.Zhaoyong Wu and J.Jianguo Yang. Measurement uncertainty on the circular features in coordinate measurement system based on the error ellipse and Monte Carlo methods.Measurement Science and Technology27122016, 125016URL: http://stacks.iop.org/0957-0233/27/i=12/a=125016back to text
• 22 inproceedingsD.David Eppstein, M. T.Michael T. Goodrich, E.Ethan Kim and R.Rasmus Tamstorf. Motorcycle Graphs: Canonical Quad Mesh Partitioning.Proceedings of the Symposium on Geometry ProcessingSGP '08Aire-la-Ville, Switzerland, SwitzerlandCopenhagen, DenmarkEurographics Association2008, 1477--1486URL: http://dl.acm.org/citation.cfm?id=1731309.1731334back to text
• 23 miscGRAPHITE.http://alice.loria.fr/software/graphite/doc/html/back to text
• 24 articleX.Xifeng Gao, W.Wenzel Jakob, M.Marco Tarini and D.Daniele Panozzo. Robust Hex-Dominant Mesh Generation using Field-Guided Polyhedral Agglomeration.ACM Transactions on Graphics (Proceedings of SIGGRAPH)364July 2017DOIback to text
• 25 articleP. L.P. L. George, F.F. Hecht and E.E. Saltel. Fully Automatic Mesh Generator for 3D Domains of Any Shape.IMPACT Comput. Sci. Eng.23December 1990, 187--218URL: http://dx.doi.org/10.1016/0899-8248(90)90012-YDOIback to text
• 26 articleC.C. Geuzaine and J.-F.J.-F. Remacle. Gmsh: a three-dimensional finite element mesh generator.International Journal for Numerical Methods in Engineering79112009, 1309-1331back to text
• 27 inproceedingsT.Thibault Groueix, M.Matthew Fisher, V. G.Vladimir G Kim, B. C.Bryan C Russell and M.Mathieu Aubry. 3d-coded: 3d correspondences by deep deformation.Proceedings of the European Conference on Computer Vision (ECCV)2018, 230--246back to text
• 28 inproceedingsT.Thibault Groueix, M.Matthew Fisher, V. G.Vladimir G. Kim, B.Bryan Russell and M.Mathieu Aubry. AtlasNet: A Papier-Mâché Approach to Learning 3D Surface Generation.Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR)2018back to text
• 29 inproceedingsY.Yasushi Ito, A. M.Alan M. Shih and B. K.Bharat K. Soni. Reliable Isotropic Tetrahedral Mesh Generation Based on an Advancing Front Method.International Meshing Roundtable conf. proc.2004back to text
• 30 inproceedingsB.Bruno Lévy, S.Sylvain Petitjean, N.Nicolas Ray and J.Jérome Maillot. Least squares conformal maps for automatic texture atlas generation.ACM transactions on graphics (TOG)21ACM2002, 362--371back to text
• 31 articleB.B. Lévy and E.E. Schwindt. Notions of Optimal Transport theory and how to implement them on a computer.Computer and Graphics2018back to text
• 32 articleA.Arman Maesumi, P.Paul Guerrero, V. G.Vladimir G. Kim, M.Matthew Fisher, S.Siddhartha Chaudhuri, N.Noam Aigerman and D.Daniel Ritchie. Explorable Mesh Deformation Subspaces from Unstructured Generative Models.2023DOIback to text
• 33 inproceedingsL.Loïc Maréchal. A New Approach to Octree-Based Hexahedral Meshing.International Meshing Roundtable conf. proc.2001back to text
• 34 miscMeshMixer.http://www.meshmixer.com/back to text
• 35 miscMeshlab.http://www.meshlab.net/back to text
• 36 inproceedingsC.C. Mezian, B.Bruno Vallet, B.Bahman Soheilian and N.Nicolas Paparoditis. Uncertainty Propagation for Terrestrial Mobile Laser Scanner.SPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences2016back to text
• 37 articleM.M. Nieser, U.U. Reitebuch and K.K. Polthier. CubeCover - Parameterization of 3D Volumes.Computer Graphics Forum3052011, 1397-1406URL: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-8659.2011.02014.xDOIback to text
• 38 articleM.Maks Ovsjanikov, M.Mirela Ben-Chen, J.Justin Solomon, A.Adrian Butscher and L.Leonidas Guibas. Functional maps: a flexible representation of maps between shapes.ACM Transactions on Graphics (ToG)3142012, 1--11back to text
• 39 miscJ.-H.Jae-Han Park, Y.-D.Yong-Deuk Shin, J.-H.Ji-Hun Bae and M.-H.Moon-Hong Baeg. Spatial Uncertainty Model for Visual Features Using a Kinect Sensor.2012back to text
• 40 miscPoint Cloud Library.http://www.pointclouds.org/downloads/back to text
• 41 articleSchöberl. NETGEN An advancing front 2D/3D-mesh generator based on abstract rules.Computing and visualization in science111997back to text
• 42 articleA.Alla Sheffer, E.Emil Praun, K.Kenneth Rose and others. Mesh parameterization methods and their applications.Foundations and Trends®222007, 105--171back to text
• 43 articleM.Mark Shephard and M.Marcel Georges. Automatic three-dimensional mesh generation by the finite octree technique.International Journal for Numerical Methods in Engineering3241991back to text
• 44 articleH.Hang Si. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator.ACM Trans. on Mathematical Software4122015back to text
• 45 techreportJ.J. Slotnick, A.A. Khodadoust, J.J. Alonso, D.D. Darmofal, G.G. William, L.L. Elizabeth and D.D. Mavriplis. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences.NASA/CR-2014-218178, NF1676L-183322014back to text
• 46 articleS.Sylvie Soudarissanane, R.Roderik Lindenbergh, M.Massimo Menenti and P.Peter Teunissen. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points.ISPRS Journal of Photogrammetry and Remote Sensing6642011, 389 - 399URL: http://www.sciencedirect.com/science/article/pii/S0924271611000098DOIback to text
• 47 inproceedingsM. L.Matthew L. Staten, S. J.Steven J. Owen and T.Ted Blacker. Unconstrained Paving & Plastering: A New Idea for All Hexahedral Mesh Generation.International Meshing Roundtable conf. proc.2005back to text
• 48 articleR.Ramana Sundararaman, R.Riccardo Marin, E.Emanuele Rodola and M.Maks Ovsjanikov. Reduced Representation of Deformation Fields for Effective Non-rigid Shape Matching.Advances in Neural Information Processing Systems352022back to text
• 49 articleT. J.Timothy J. Tautges, T.Ted Blacker and S. A.Scott A. Mitchell. The whisker weaving algorithm.International Journal of Numerical Methods in Engineering1996back to text
• 50 articleN. P.N. P. Weatherill and O.O. Hassan. Efficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints.International Journal for Numerical Methods in Engineering37121994, 2005--2039URL: http://dx.doi.org/10.1002/nme.1620371203DOIback to text
• 51 inproceedingsM.Markus Ylimäki, J.Juho Kannala and J.Janne Heikkilä. Robust and Practical Depth Map Fusion for Time-of-Flight Cameras.Image AnalysisChamSpringer International Publishing2017, 122--134back to text
• 52 articleC.Chao Yuan, N.Nan Cao and Y.Yang Shi. A Survey of Developable Surfaces: From Shape Modeling to Manufacturing.arXiv preprint arXiv:2304.095872023back to text
• 53 inproceedingsY.Yongjie Zhang and C.Chandrajit Bajaj. Adaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data.International Meshing Roundtable conf. proc.2004back to text
• 54 articleD.Du Zhengchun, W.Wu Zhaoyong and Y.Yang Jianguo. Point cloud uncertainty analysis for laser radar measurement system based on error ellipsoid model.Optics and Lasers in Engineering792016, 78 - 84URL: http://www.sciencedirect.com/science/article/pii/S0143816615002675DOIback to text
• 55 miscCgal, Computational Geometry Algorithms Library.http://www.cgal.orgback to text