Section: New Results
Modeling and Animation
Participants : Georges-Pierre Bonneau, Alexandre Derouet-Jourdan, Nicolas Holzschuch, Nassim Jibai, Cyril Soler, Joëlle Thollot.
Multiscale Feature-Preserving Smoothing of Tomographic Data
Participants : Nassim Jibai, Nicolas Holzschuch, Cyril Soler.
|
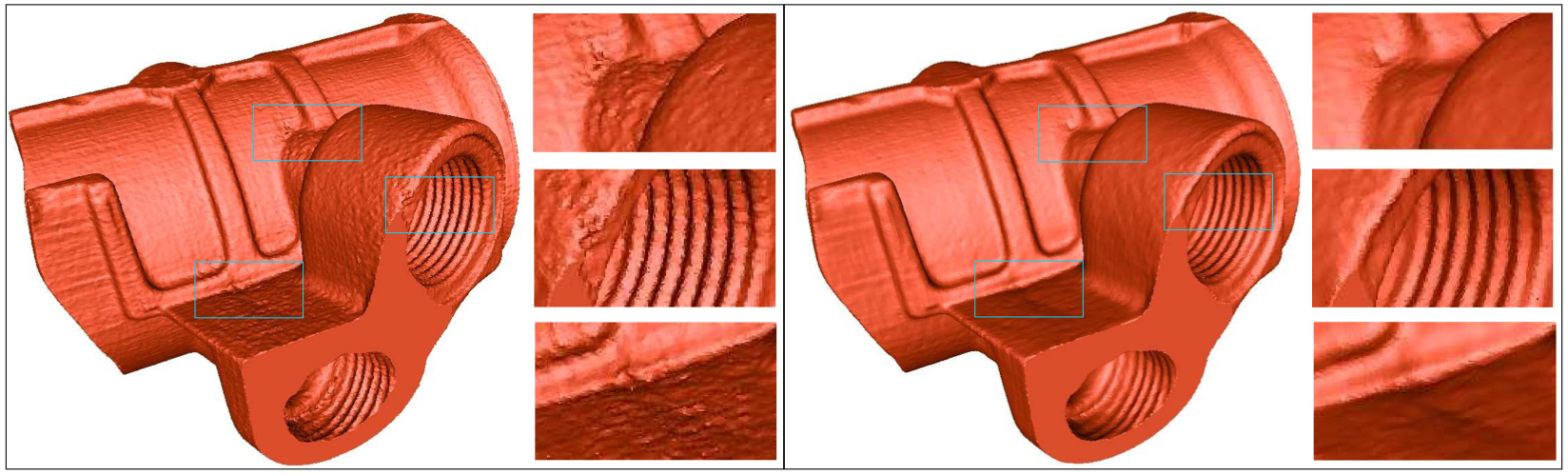
Computer tomography (CT) has wide application in medical imaging and reverse engineering. Due to the limited number of projections used in reconstructing the volume, the resulting 3D data is typically noisy. Contouring such data, for surface extraction, yields surfaces with localised artifacts of complex topology. To avoid such artifacts, we propose a method for feature-preserving smoothing of CT data, illustrated in Figure 10 . The smoothing is based on anisotropic diffusion, with a diffusion tensor designed to smooth noise up to a given scale, while preserving features. We compute these diffusion kernels from the directional histograms of gradients around each voxel, using a fast GPU implementation. This work has been published as a Siggraph'2011 Poster [26] .
3D Inverse Dynamic Modeling of Strands
Participants : Alexandre Derouet-Jourdan, Joëlle Thollot.
|
In this work, we propose a new method to automatically and consistently convert 3D splines into dynamic rods at rest under gravity, bridging the gap between the modeling of 3D strands (such as hair, plants) and their physics-based animation. An illustration is given in Figure 11 . This work is done in collaboration with F. Bertails from the BIPOP team-project. It has been published in a Siggraph'2011 poster [25] .
Lagrangian Texture Advection: Preserving both Spectrum and Velocity Field
Participants : Eric Bruneton, Nicolas Holzschuch, Fabrice Neyret.
Texturing an animated fluid is a useful way to augment the visual complexity of pictures without increasing the simulation time. But texturing flowing fluids is a complex issue, as it creates conflicting requirements: we want to keep the key texture properties (features, spectrum) while advecting the texture with the underlying flow — which distorts it. In this context we present a new, Lagrangian, method for advecting textures: the advected texture is computed only locally and follows the velocity field at each pixel (see Figure 12 ). The texture retains its local properties, including its Fourier spectrum, even though it is accurately advected. Due to its Lagrangian nature, our algorithm can perform on very large, potentially infinite scenes in real time. Our experiments show that it is well suited for a wide range of input textures, including, but not limited to, noise textures. This work has been published in the IEEE Transactions on Visualization and Computer Graphics (TVCG) [18] .
|
Feature-Based Vector Simulation of Water Waves
Participant : Fabrice Neyret.
We have developed a method for simulating local water waves caused by obstacles in water streams for real-time graphics applications. Given a low-resolution water surface and velocity field, our method is able to decorate the input water surface with high resolution detail for the animated waves around obstacles. We construct and animate a vector representation of the waves. It is then converted to feature-aligned meshes for capturing the surfaces of the waves (see Figure 13 ). Results demonstrate that our method has the benefits of real-time performance and easy controllability. The method also fits well into a state-of-the-art river animation system. This work has been published in the Journal of Computer Animation and Virtual Worlds [19] .
|
Volume-preserving FFD for Programmable Graphics Hardware
Participant : Georges-Pierre Bonneau.
|
This work is the result of a collaboration with S. Hahmann from the EVASION team-project, Prof. Gershon Elber from Technion and Prof. Hans Hagen from the University of Kaiserslautern.
Free Form Deformation (FFD) is a well established technique for deforming arbitrary object shapes in space. Although more recent deformation techniques have been introduced, amongst them skeleton-based deformation and cage based deformation, the simple and versatile nature of FFD is a strong advantage, and justifies its presence in nowadays leading commercial geometric modeling and animation software systems. Since its introduction in the late 80's, many improvements have been proposed to the FFD paradigm, including control lattices of arbitrary topology, direct shape manipulation and GPU implementation. Several authors have addressed the problem of volume preserving FFD. These previous approaches either make use of expensive non-linear optimization techniques, or resort to first order approximation suitable only for small-scale deformations. In this work we take advantage from the multi-linear nature of the volume constraint in order to derive a simple, exact and explicit solution to the problem of volume preserving FFD (see Figure 14 ). Two variants of the algorithm are given, without and with direct shape manipulation. Moreover, the linearity of our solution enables to implement it efficiently on GPU. The results have been published in a Visual Computer journal paper [17] .