Section: Application Domains
Viscoelastic flows
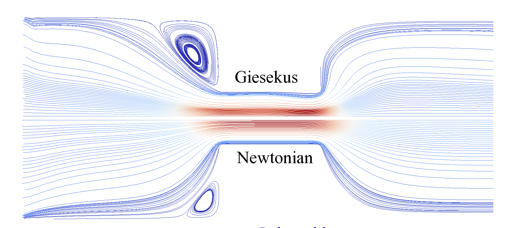
Polymeric fluids are, from a rheological point of view, viscoelastic non-Newtonian fluids, see Figure 3 . Their specific behavior can be observed in a variety of physical phenomena, which are unseen with Newtonian liquids and which cannot be predicted by the Navier-Stokes equations. The better known examples include the rod climbing Weissenberg effect, die swell and extrusion instabilities (cf. fig. 1). The rheological behavior of polymers is so complex that many different constitutive equations have been proposed in the literature in order to describe these phenomena, see for instance [72] . The choice of an appropriate constitutive law is still a central problem. We consider realistic constitutive equations such as the Giesekus model. In comparison to the classical models used in CFD, such as UCM or Oldroyd B fluids, the Giesekus model is characterized by a quadratic stress term. It is important to understand the theoretical properties of the Giesekus model. As outlined above, energy estimates are crucial for the development of robust numerical schemes, see also the recent work on similar questions in the EPI MICMAC [51] , [64] .
Our aim is to develop new algorithms for the discretization of polymer models, which should be efficient and robust for . For this purpose, we will develop a mathematical approach based on recent ideas on discretizations preserving the positivity of the conformation tensor. This property is believed to be crucial in order to avoid numerical instabilities associated with large Weissenberg numbers. In order to develop monotone numerical schemes, we use recent discretization techniques such as stabilized finite element and discontinuous Galerkin methods. We have validated our code at hand of academic benchmark problems in comparison with the commercial code PolyFlow®.
|
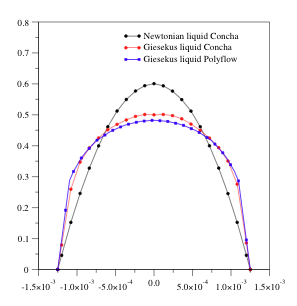
The result of a computation of a 4:1-contraction, comparing Newtonian flow with Giesekus model, is shown in Figure 4 . In the same figure, a comparison of the computed profile in the channel with the one obtained by the PolyFlow®, both on a relatively coarse mesh, is shown. A precise study shows that the results are in good agreement for moderate Weissenberg numbers ; the computation time is by a factor of two smaller for the preliminary version of our code based on triangular meshes. For , we were not able to get a converged solution with the commercial code, whereas our program yields stationary solutions up to .
Further improvements are expected from the use of adaptivity, as well as from the implementation of adequate iterative solvers. The long-term goal is to successively build up robust and efficient software tools in order to tackle design problems, such as the design of mixing devices.