Section: New Results
Discretization of Euler's equations
Participants : Roland Becker, Kossivi Gopki, Eric Schall, David Trujillo.
Over the past years, significant advances have been made in developing discontinuous Galerkin finite element methods (DGFEM) for applications in fluid flow and heat transfer. Certain features of the method have made it attractive as an alternative to other popular methods such as finite volume and more convenient finite element methods in thermal fluid engineering analyses. The DGFEM has been used successfully to solve hyperbolic systems of conservation laws. It makes use of the same local function space as the continuous method, but with relaxed continuity at inter-element boundaries. Since it uses discontinuous piecewise polynomial bases, the discretization is locally conservative and in the considered lowest-order case, the method preserves the maximum principle for scalar equations.
One of the challenges in Computational Fluid Dynamic (CFD) is to obtain as accurate as possible the solution of the problem under consideration at very low cost in terms of computational time. So our principal work is to find some relevant and robust strategies and technics of meshes adaptation in order to concentrate just the calculation where there are physical phenomena to capture. From Industrial point of view, the aim is to get the stationary solution as quick as possible with as much accuracy as possible. The main limitation of these results in CFD concern the underlying models: for example, nearly nothing seems to be known for (even linear) first-order systems or for realistic nonlinear equations. We therefore have developed different modern techniques, especially adaptive methods, to tackle this kind of problems in compressible CFD. The strategy is to iteratively improve the quality of the approximate solutions based on computed information (a posteriori error analysis). In this way, a sequence of locally refined meshes is constructed, which allows for better efficiency as compared to more classical approaches in the presence of different kind of singularities. The main goal is to improve the aerodynamical design process for complex configurations by significantly reducing the time from geometry to solution at engineering-required accuracy using high-order adaptive methods.
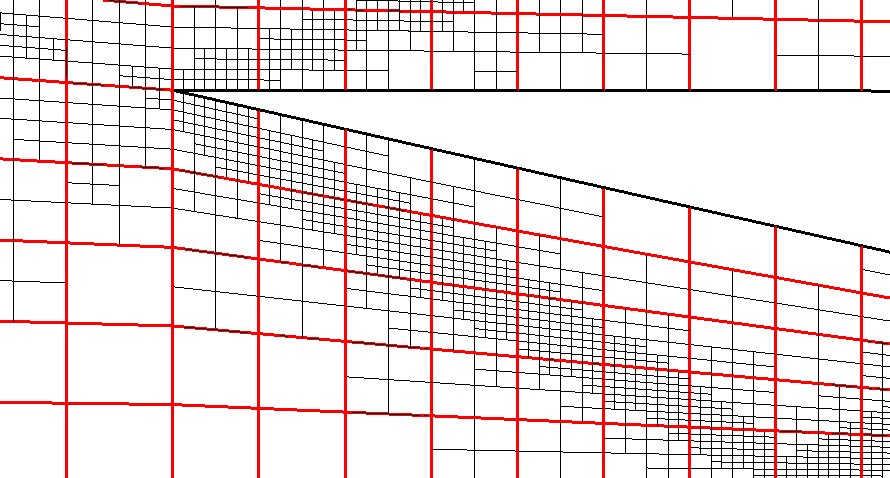
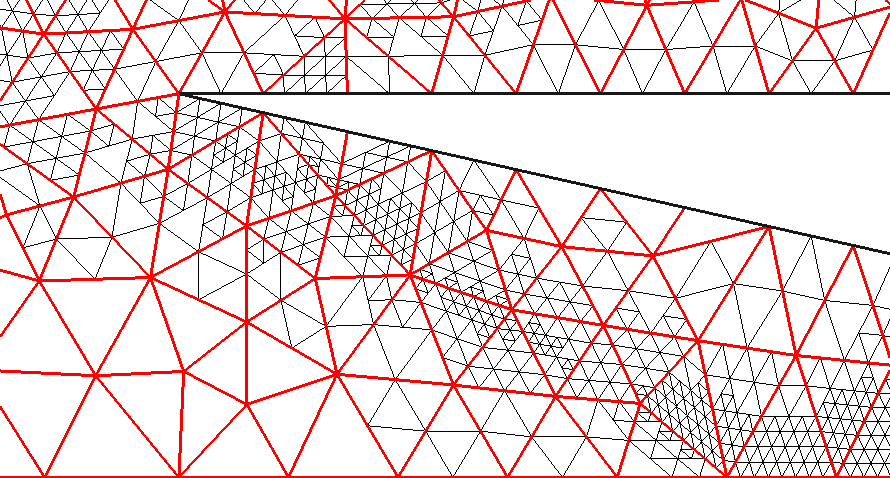
One of our strategies of refinement is based on the creation of hanging nodes commonly called non-conforming refinement. The figures 15 show superposition of two kinds of meshes. One is a non-conforming refined mesh (black color) and the other one is the initial grid (red color) on which the refinement has been performed. It shows the technic of cutting the cells where singularities occur in the scramjet inlet.
|
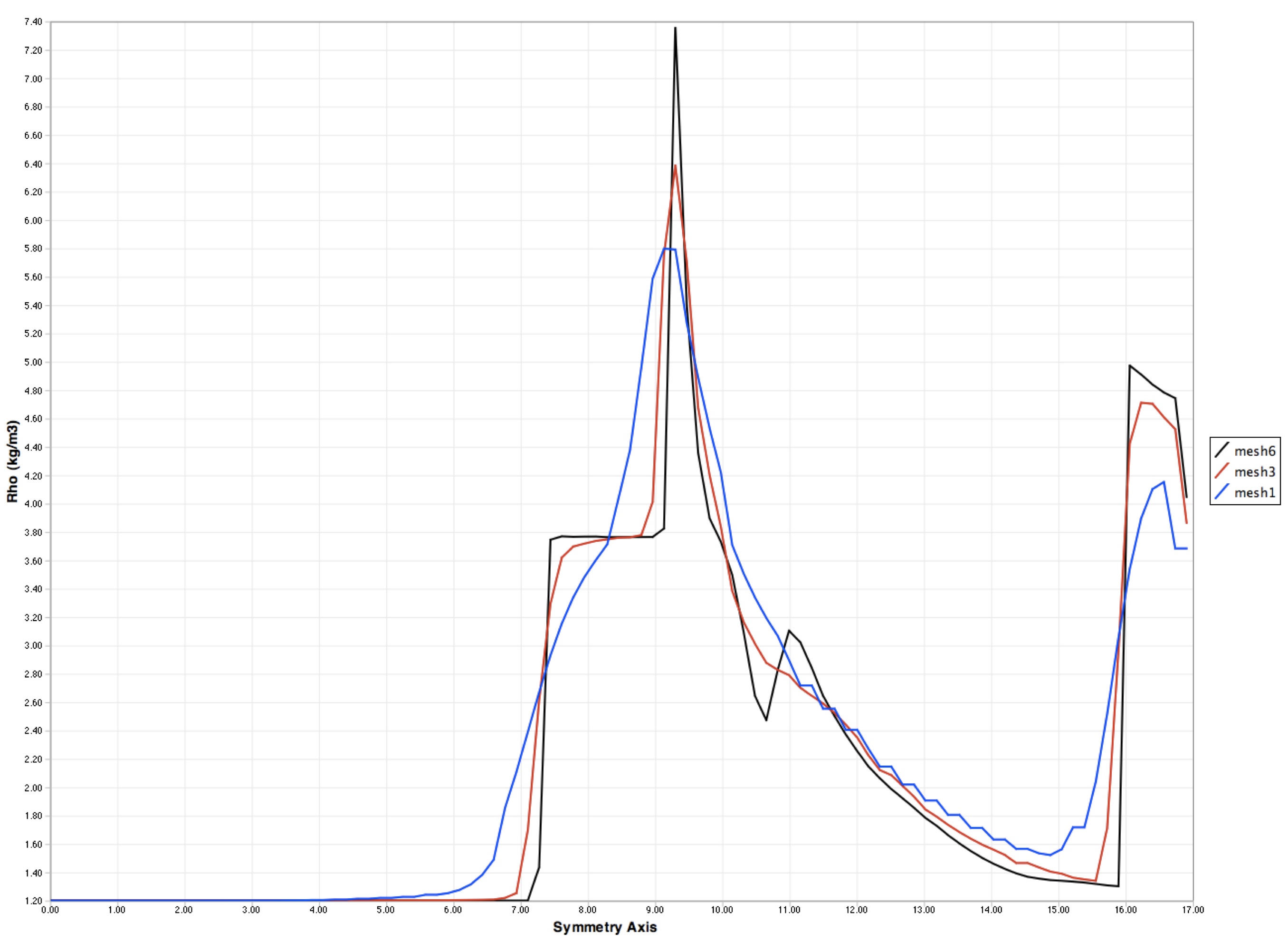
The mesh adaptation is designed using some criteria as a posteriori error estimates. We have designed criteria based on the calculation of the jump of physical quantities like density, pressure, entropy, temperature and mach number at the inter-element. This criteria seems to be a very good indicator for the mesh adaptation. Figure 16 is the comparison of isoline of the density in scramjet internal flow at mach 3 of the initial mesh, the third and the sixth mesh after refinement.The indicator used is the density jump. It shows the impact and the accuracy of the solution obtained after the sixth iteration of the refinement.
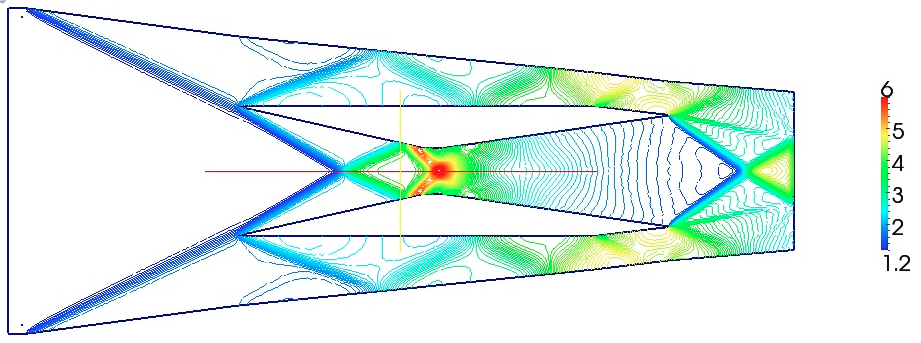
The figure 17 shows the streamlines of the density in the scramjet inlet after the seventh iteration. This shows how the adaptation depicts almost clearly and accurately the shock waves and the expansion waves and their interactions in the domain.
|
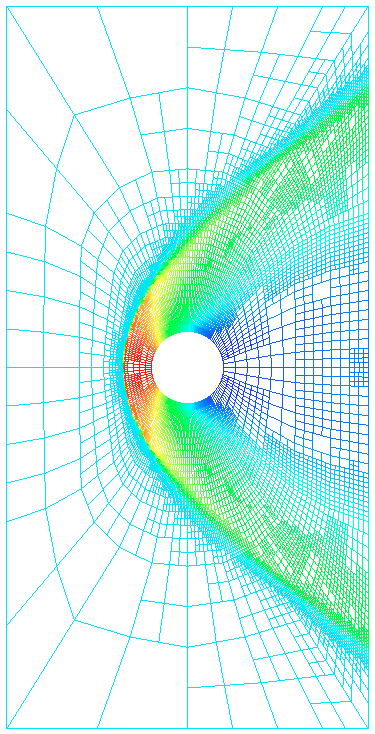
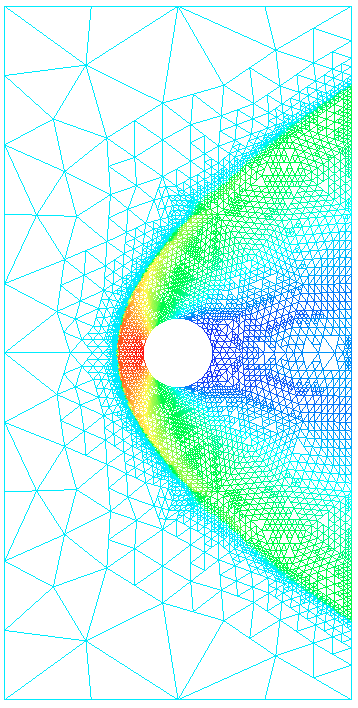
Figure 18 represent the density isolines of a flow past cylinder test case using the non-conforming mesh adaptation with quadrangular an triangular girds.
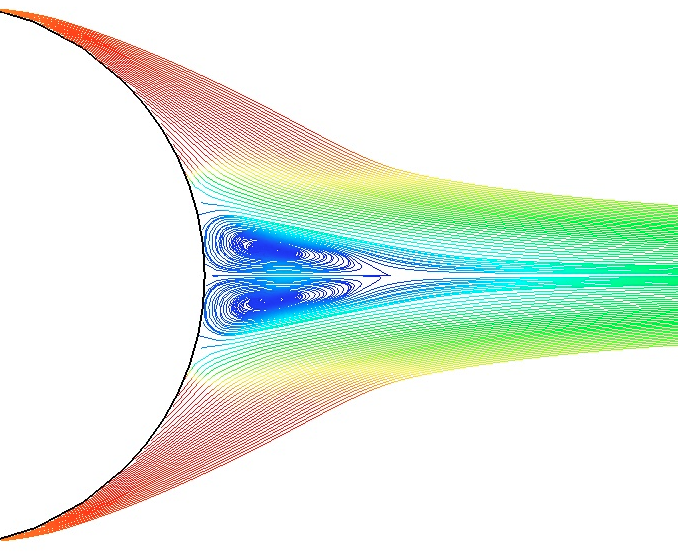
We have also settled another indication which is hierarchical. It measures the difference of with the physical quantity obtained by computation on a globally refined mesh . This allows us the make comparison with the previous indicator. The case test considered for this comparison is an external flows past a cylinder airfoil at fixed free stream conditions : . The result is quite surprising the way one type of indicator can capture phenomenon that are not capture by the another one. In fact the hierarchical indicator seems to capture recirculation downstream to the obstacle which was not capture by the jump indicator (see figure 19 )
|
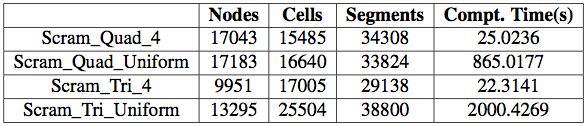
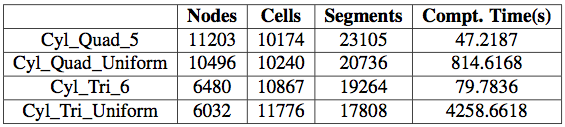
We compare the computational time between a non-conforming mesh refinement and a globally mesh refined with nearly the same amount of cells. The meshes contain quadrangles or triangles. We can observe trough the following tables that the adapted meshes wether triangular or quadrangular meshes allow to save 20 to 90 times the computational time than the normal globally refined mesh. (see tables 1 and 2)
|
In table 1, the gain in time is 35 times in quadrangular grid case and 90 times triangular ones and in table 2, the gain in time: 18 times in quadrangular grid case and 58 times triangular ones. So one can say that the adaptive mesh with the strategies and technics we have settled are efficient and robust in capturing physical phenomenon at a very reasonable low cost.
In concluding, the procedure of refinement permit to save computational time and have good accuracy of the approximated solution computed. Our focus is to continue the improve our methods and strategies in order to meet the requirement of accuracy, robustness and efficiency. Many other works are in hand such as slope limiters for high-order Discontinous Galerkin, low mach number computation with some remarkable approaches.