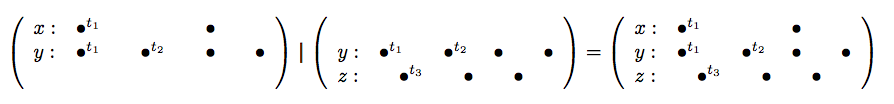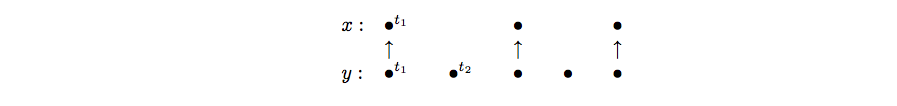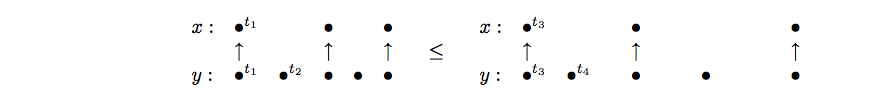Accessibility setting

Section: Scientific Foundations

Introduction

Embedded systems are not new, but their pervasive introduction in ordinary-life objects (cars, telephone, home appliances) brought a new focus onto design methods for such systems. New development techniques are needed to meet the challenges of productivity in a competitive environment. Synchronous languages rely on the synchronous hypothesis, which lets computations and behaviors be divided into a discrete sequence of computation steps which are equivalently called reactions or execution instants. In itself this assumption is rather common in practical embedded system design.

But the synchronous hypothesis adds to this the fact that, inside each instant, the behavioral propagation is well-behaved (causal), so that the status of every signal or variable is established and defined prior to being tested or used. This criterion, which may be seen at first as an isolated technical requirement, is in fact the key point of the approach. It ensures strong semantic soundness by allowing universally recognized mathematical models to be used as supporting foundations. In turn, these models give access to a large corpus of efficient optimization, compilation, and formal verification techniques. The synchronous hypothesis also guarantees full equivalence between various levels of representation, thereby avoiding altogether the pitfalls of non-synthesizability of other similar formalisms. In that sense the synchronous hypothesis is, in our view, a major contribution to the goal of model-based design of embedded systems.

We shall describe the synchronous hypothesis and its mathematical background, together with a range of design techniques enpowered by the approach. Declarative formalisms implementing the synchronous hypothesis can be cast into a model of computation [11] consisting of a domain of traces or behaviors and of semi-lattice structure that renders the synchronous hypothesis using a timing equivalence relation: clock equivalence. Asynchrony can be superimposed on this model by considering a flow equivalence relation as well as heterogeneous systems  [33] by parameterizing composition with arbitrary timing relations.

A synchronous model of computation

We consider a partially-ordered set of tags $t$ to denote instants seen as symbolic periods in time during which a reaction takes place. The relation $t_1\le t_2$ says that $t_1$ occurs before $t_2$. Its minimum is noted 0. A totally ordered set of tags $C$ is called a chain and denotes the sampling of a possibly continuous or dense signal over a countable series of causally related tags. Events, signals, behaviors and processes are defined as follows:

• an event $e$ is a pair consisting of a value $v$ and a tag $t$,

• a signal $s$ is a function from a chain of tags to a set of values,

• a behavior $b$ is a function from a set of names $x$ to signals,

• a process $p$ is a set of behaviors that have the same domain.

In the remainder, we write $\mathrm{tags}\left(s\right)$ for the tags of a signal $s$, $\mathrm{vars}\left(b\right)$ for the domain of $b$, ${b|}_X$ for the projection of a behavior $b$ on a set of names $X$ and $b/X$ for its complementary.

Figure 1 depicts a behavior $b$ over three signals named $x$, $y$ and $z$. Two frames depict timing domains formalized by chains of tags. Signals $x$ and $y$ belong to the same timing domain: $x$ is a down-sampling of $y$. Its events are synchronous to odd occurrences of events along $y$ and share the same tags, e.g. $t_1$. Even tags of $y$, e.g. $t_2$, are ordered along its chain, e.g. $t_1<t_2$, but absent from $x$. Signal $z$ belongs to a different timing domain. Its tags are not ordered with respect to the chain of $y$.

Figure 1. Behavior $b$ over three signals $x$, $y$ and $z$ in two clock domains

Composition

Synchronous composition is noted $p\left|\right|q$ and defined by the union $b\cup c$ of all behaviors $b$ (from $p$) and $c$ (from $q$) which hold the same values at the same tags ${b|}_I{=c|}_I$ for all signal $x\in I=\mathrm{vars}\left(b\right)\cap \mathrm{vars}\left(c\right)$ they share. Figure 2 depicts the synchronous composition (Figure 2 , right) of the behaviors $b$ (Figure 2 , left) and the behavior $c$ (Figure 2 , middle). The signal $y$, shared by $b$ and $c$, carries the same tags and the same values in both $b$ and $c$. Hence, $b\cup c$ defines the synchronous composition of $b$ and $c$.

Figure 2. Synchronous composition of $b\in p$ and $c\in q$

Scheduling

A scheduling structure is defined to schedule the occurrence of events along signals during an instant $t$. A scheduling $\to$ is a pre-order relation between dates $x_t$ where $t$ represents the time and $x$ the location of the event. Figure 3 depicts such a relation superimposed to the signals $x$ and $y$ of Figure 1 . The relation $y_{t_1}\to x_{t_1}$, for instance, requires $y$ to be calculated before $x$ at the instant $t_1$. Naturally, scheduling is contained in time: if $t<t^{\text{'}}$ then $x_t{\to }^b{x}_{t^{\text{'}}}$ for any $x$ and $b$ and if $x_t{\to }^b{x}_{t^{\text{'}}}$ then $t^{\text{'}}\neg <t$.

Figure 3. Scheduling relations between simultaneous events

Structure

A synchronous structure is defined by a semi-lattice structure to denote behaviors that have the same timing structure. The intuition behind this relation is depicted in Figure 4 . It is to consider a signal as an elastic with ordered marks on it (tags). If the elastic is stretched, marks remain in the same relative (partial) order but have more space (time) between each other. The same holds for a set of elastics: a behavior. If elastics are equally stretched, the order between marks is unchanged.

In Figure 4 , the time scale of $x$ and $y$ changes but the partial timing and scheduling relations are preserved. Stretching is a partial-order relation which defines clock equivalence. Formally, a behavior $c$ is a stretching of $b$ of same domain, written $b\le c$, iff there exists an increasing bijection on tags $f$ that preserves the timing and scheduling relations. If so, $c$ is the image of $b$ by $f$. Last, the behaviors $b$ and $c$ are said clock-equivalent, written $b\sim c$, iff there exists a behavior $d$ s.t. $d\le b$ and $d\le c$.

Figure 4. Relating synchronous behaviors by stretching.

A declarative design language

Signal [6] is a declarative design language expressed within the polychronous model of computation. In Signal, a process $P$ is an infinite loop that consists of the synchronous composition $P\left|\right|Q$ of simultaneous equations $x=yfz$ over signals named $x,y,z$. The restriction of a signal name $x$ to a process $P$ is noted $P/x$.

Equations $x=yfz$ in Signal more generally denote processes that define timing relations between input and output signals. There are four primitive combinators in Signal:

• delay $x=y\$\mathrm{𝚒𝚗𝚒𝚝}v$, initially defines the signal $x$ by the value $v$ and then by the previous value of the signal $y$. The signal $y$ and its delayed copy $x=y\$\mathrm{𝚒𝚗𝚒𝚝}v$ are synchronous: they share the same set of tags $t_1,t_2,\cdots$. Initially, at $t_1$, the signal $x$ takes the declared value $v$ and then, at tag $t_n$, the value of $y$ at tag $t_{n-1}$.

  $\begin{array}{ccccc}\hfill y& {•}^{t_1,v_1}\hfill & {•}^{t_2,v_2}\hfill & {•}^{t_3,v_3}\hfill & \cdots \hfill \\ \hfill y\$\mathrm{𝚒𝚗𝚒𝚝}v& {•}^{t_1,v}\hfill & {•}^{t_2,v_1}\hfill & {•}^{t_3,v_2}\hfill & \cdots \hfill \end{array}$

• sampling $x=y\mathrm{𝚠𝚑𝚎𝚗}z$, defines $x$ by $y$ when $z$ is true (and both $y$ and $z$ are present); $x$ is present with the value $v_2$ at $t_2$ only if $y$ is present with $v_2$ at $t_2$ and if $z$ is present at $t_2$ with the value true. When this is the case, one needs to schedule the calculation of $y$ and $z$ before $x$, as depicted by $y_{t_2}\to x_{t_2}\leftarrow z_{t_2}$.

• merge $x=y\mathrm{𝚍𝚎𝚏𝚊𝚞𝚕𝚝}z$, defines $x$ by $y$ when $y$ is present and by $z$ otherwise. If $y$ is absent and $z$ present with $v_1$ at $t_1$ then $x$ holds $(t_1,v_1)$. If $y$ is present (at $t_2$ or $t_3$) then $x$ holds its value whether $z$ is present (at $t_2$) or not (at $t_3$).

  $\begin{array}{ccccc}\hfill y& & •\hfill & {•}^{t_2,v_2}\hfill & \cdots \hfill \\ & & & \downarrow \hfill \\ \hfill y\mathrm{𝚠𝚑𝚎𝚗}z& & & {•}^{t_2,v_2}\hfill & \cdots \hfill \\ & & & \uparrow \hfill \\ \hfill z& •\hfill & {•}^{t_1,0}\hfill & {•}^{t_2,1}\hfill & \cdots \hfill \end{array}\begin{array}{ccccc}\hfill y& & {•}^{t_2,v_2}\hfill & {•}^{t_3,v_3}\hfill & \cdots \hfill \\ & & \downarrow \hfill & \downarrow \hfill \\ \hfill y\mathrm{𝚍𝚎𝚏𝚊𝚞𝚕𝚝}z& {•}^{t_1,v_1}\hfill & {•}^{t_2,v_2}\hfill & {•}^{t_3,v_3}\hfill & \cdots \hfill \\ & \uparrow \hfill \\ \hfill z& {•}^{t_1,v_1}\hfill & & •\hfill & \cdots \hfill \end{array}$

The structuring element of a Signal specification is a process. A process accepts input signals originating from possibly different clock domains to produce output signals when needed. This allows, for instance, to specify a counter where the inputs tick and reset and the output value have independent clocks. The body of counter consists of one equation that defines the output signal value . Upon the event reset , it sets the count to 0. Otherwise, upon a tick event, it increments the count by referring to the previous value of value and adding 1 to it. Otherwise, if the count is solicited in the context of the counter process (meaning that its clock is active), the counter just returns the previous count without having to obtain a value from the tick and reset signals.

    process counter = (? event tick, reset ! integer value)

        (| value := (0 when reset)

            default ((value$ init 0 + 1) when tick)

            default (value$ init 0)

        |);

A Signal process is a structuring element akin to a hierarchical block diagram. A process may structurally contain sub-processes. A process is a generic structuring element that can be specialized to the timing context of its call. For instance, the definition of a synchronized counter starting from the previous specification consists of its refinement with synchronization. The input tick and reset clocks expected by the process counter are sampled from the boolean input signals tick and reset by using the when tick and when reset †expressions. The count is then synchronized to the inputs by the equation reset ^= tick ^= count .

    process synccounter = (? boolean tick, reset ! integer value)

        (| value := counter (when tick, when reset)

         | reset ^= tick ^= value

         |);

Compilation of Signal

Sequential code generation starting from a Signal specification starts with an analysis of its implicit synchronization and scheduling relations. This analysis yields the control and data flow graphs that define the class of sequentially executable specifications and allow to generate code.

Synchronization and scheduling specifications

In Signal, the clock $\widehat{}x$ of a signal $x$ denotes the set of instants at which the signal $x$ is present. It is represented by a signal that is true when $x$ is present and that is absent otherwise. Clock expressions represent control. The clock $\mathrm{𝚠𝚑𝚎𝚗}x$ (resp. $\mathrm{𝚠𝚑𝚎𝚗}\mathrm{𝚗𝚘𝚝}x$) represents the time tags at which a boolean signal $x$ is present and true (resp. false).

The empty clock is written 0 and clock expressions $e$ combined using conjunction, disjunction and symmetric difference. Clock equations $E$ are Signal processes: the equation $e\widehat{}=e^{\text{'}}$ synchronizes the clocks $e$ and $e^{\text{'}}$ while $e\widehat{}<e^{\text{'}}$ specifies the containment of $e$ in $e^{\text{'}}$. Explicit scheduling relations $x\to y\mathrm{𝚠𝚑𝚎𝚗}e$ allow to schedule the calculation of signals (e.g. $x$ after $y$ at the clock $e$).

Synchronization and scheduling analysis

A Signal process $P$ corresponds to a system of clock and scheduling relations $E$ that denotes its timing structure. It can be defined by induction on the structure of $P$ using the inference system $P:E$ of Figure 5 .

    x := y$ init v   : ^x ^= ^y

    x := y when z    : ^x ^= ^y when z | y -> x when z

    x := y default z : ^x ^= ^y default ^z | y -> x when ^y | z -> x when ^z ^- ^y

Hierarchization

The clock and scheduling relations $E$ of a process $P$ define the control-flow and data-flow graphs that hold all necessary information to compile a Signal specification upon satisfaction of the property of endochrony. A process is said endochronous iff, given a set of input signals and flow-equivalent input behaviors, it has the capability to reconstruct a unique synchronous behavior up to clock-equivalence: the input and output signals are ordered in clock-equivalent ways.

Figure 6. Hierarchization of clocks