Section: New Results

Development of New Methods for Data Assimilation

Variational Data Assimilation with Control of Model Error

Participants : Bénédicte Lemieux-Dudon, Arthur Vidard.

One of the main limitation of the current operational variational data assimilation techniques is that they assume the model to be perfect mainly because of computing cost issues. Numerous researches have been carried out to reduce the cost of controlling model errors by controlling the correction term only in certain privileged directions or by controlling only the systematic and time correlated part of the error.

Both the above methods consider the model errors as a forcing term in the model equations. Trémolet (2006) describes another approach where the full state vector (4D field: 3D spatial + time) is controlled. Because of computing cost one cannot obviously control the model state at each time step. Therefore, the assimilation window is split into sub-windows, and only the initial conditions of each sub-window are controlled, the junctions between each sub-window being penalized. One interesting property is that, in this case, the computation of the gradients, for the different sub-windows, are independent and therefore can be done in parallel.

We are implementing this method in a realistic Oceanic framework using OPAVAR/ NEMOVAR as part of the VODA ANR project. An extensive documentation is being produced and should be available along with a first prototype early 2012.

Variational Data Assimilation and Control of the Boundary Conditions

Participant : Eugène Kazantsev.

A variational data assimilation technique applied to the identification of the optimal discretization of interpolation operators and derivatives in the nodes adjacent to the boundary of the domain is discussed in the context of the shallow water model. It was shown in [8] that control of approximation of boundary derivatives and interpolations can increase the model's accuracy in boundary regions and improve the solution in general. On the other hand, optimal schemes obtained in this way may not approximate derivatives in a common sense. This may lead to another model physics, violating, for example, impermeability boundary condition.

Experiments with a full non-linear shallow water model in [7] show that controlling the discretization of operators near a rigid boundary can bring the model solution close to observations as in the assimilation window and beyond the window. This type of control allows also to improve climatic variability of the model. These properties have been studied in two different configurations: an academic case of assimilation of artificially generated observational data in a square box configuration and assimilation of real observations in a model of the Black sea [30] .

The sensitivity of the shallow water model in the previously described configurations has been studied in detail in [9] . It is shown in both experiments that the boundary conditions near a rigid boundary influence the solution higher than the initial conditions. This fact points out the necessity to identify optimal boundary approximation during a model development.

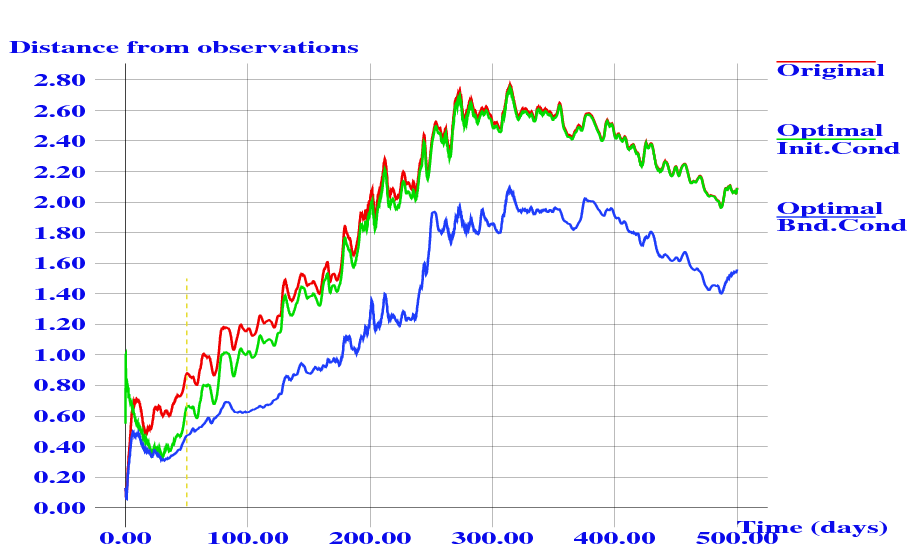
In order to illustrate the influence of optimal discretization of operators near the boundary we compare this influence with now classical data assimilation for identification of the optimal initial conditions of the model. The norm of the difference between the model solution and real observational data is plotted in figure 3 . Observed sea surface elevation of the Black sea was assimilated during 50 days (May–Juin 1992) to identify optimal initial and boundary conditions. After that, models have been integrated forward for 500 days and their solutions have been compared with data. One can see that, starting from optimal initial point, the model remains close to observations during less than 100 days while optimal optimal discretization of operators allows the model to be always closer than the model with default parameters.

Adjoint models, necessary to variational data assimilation have been produced by the TAPENADE software, developed by the TROPICS team.

Figure 3. Evolution of the difference "model–observations".

A Nudging-Based Data Assimilation Method: the Back and Forth Nudging

Participants : Didier Auroux, Jacques Blum, Maëlle Nodet.

The Back and Forth Nudging (BFN) algorithm (see [63] ) has been recently introduced for simplicity reasons, as it does not require any linearization, nor adjoint equation, or minimization process in comparison with variational schemes. Nevertheless it provides a new estimation of the initial condition at each iteration.

Previous theoretical results [65] showed that BFN was often ill-posed for viscous partial differential equations. To overcome this problem, we proposed a new version of the algorithm, which we called the Diffusive BFN [2] , and which showed very promising results on one-dimensional viscous equations. Experiments on more sophisticated geophysical models, such as Shallow-Water equations and NEMO ocean model are still in progress, in collaboration with University of Nice.

Variational Data Assimilation for locally nested models.

Participants : Eric Blayo, Laurent Debreu, François-Xavier Le Dimet, Emilie Neveu.

The objectives are to study the mathematical formulation of variational data assimilation for locally nested models and to conduct numerical experiments for validation.

The state equations of the optimality system have been written for the general case of two embedded grids, for which several kinds of control (initial conditions, boundary conditions) have been proposed. Both one way and two way interactions have been studied. This last year, we worked on integration of non linear grid interactions in the algorithm. Additionally, the problem of specification of background error covariances matrices has been studied (see [85] ).

In the ANR MSDAG project and Emilie Neveu's PhD, we continue to work on the subject. Our main interest is on the use of multiscale optimization methods for data assimilation. The idea is to apply a multigrid algorithm to the solution of the optimization problem. The work includes the analysis of the ellipticity of the optimization problem [12] , the comparison of different multigrid methods (Gauss-Newton multigrid method and Full Approximation Scheme) and specific developments for highly non linear problems. To extend previous work on Burgers equation, the Full Approximation Scheme (FAS) and the Newton Multigrid algorithm have been compared in a more complex shallow water model. The results shows good performance of the FAS and also put more interest in the design of the background error covariance matrix.