Section: Scientific Foundations
Proof of Imperative and Object-Oriented programs
Participants : Romain Bardou, François Bobot, Sylvie Boldo, Jean-Christophe Filliâtre, Claude Marché, Tuyen Nguyen, Andrei Paskevich, Christine Paulin-Mohring, Asma Tafat, Wendi Urribarrí.
A foundation step of the project is the PhD thesis of Jean-Christophe Filliâtre [6] that proposes to establish soundness of a program with imperative features (assignments, while loops, but also exceptions and exception handlers) by means of a translation into an equivalent purely functional program with logical annotations. Such an annotated functional program is very well-suited to be expressed in Coq's type theory, hence this approach allowed for the first time to prove imperative programs with Coq [68] .
Following this thesis, a new tool called Why was developed. It takes as input an imperative program and a specification that this program is expected to fulfil. It produces on one hand a set of verification conditions (VCs): logical formulas which have to be proved in the Coq system ; and on the other hand a Coq-term which contains a functional translation of the imperative program and a proof of correctness of this program based on the VCs. It was early remarked that this tool was independent of Coq, because the VCs can be validated in other interactive tools or with automatic provers. This multi-prover architecture is a powerful feature of Why: it spreads this technology well beyond the Coq community.
The Why platform
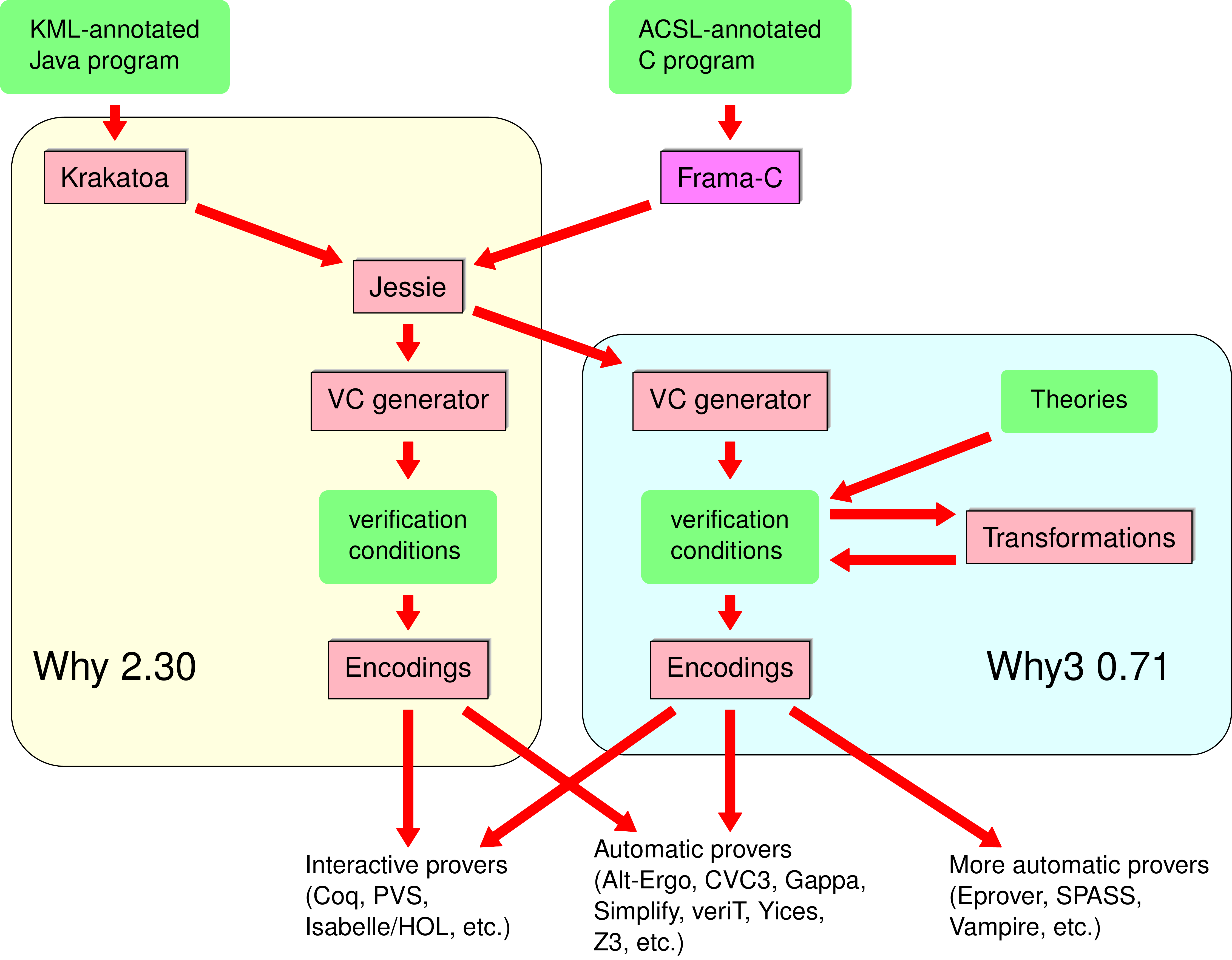
Since 2002, we tackle programs written in mainstream programming languages. We first considered Java source code annotated with JML (Java Modeling Language). This method was implemented in a new tool called Krakatoa [10] . The approach is based on a translation from annotated Java programs into the specific language of Why, we then can reuse Why's VCG mechanism and choose between different provers for establishing these VCs. From 2003, we followed the same approach for programs written in ANSI C [7] .
The combination of the Why VC generator and the front-ends dealing with C or Java form a tool box for program verification, called the Why platform. Its overall architecture is shown on Figure 1 . Nowadays, the front-end for C is in fact integrated in the Frama-C environment for static analysis of C programs (http://www.frama-c.cea.fr/ ), which was developed by the CEA-List in collaboration with us. Frama-C has an open architecture, structured as plugins around a shared kernel, and deductive verification of C code can be done using Why via the Jessie plugin. The annotation language for C source is also designed in collaboration with CEA, and called ACSL [54] .
The central issue for the design of our platform is the modeling of memory heap for Java and C programs, handling possible aliasing (two different pointer or object expressions representing the same memory location): the Why VC generator does not handle aliasing by itself, indeed it does not support any form of complex data structures like objects, structures, pointers. On the other hand, it supports declaration of a kind of algebraic specifications: abstract data types specified by first-order functions, predicates and axioms. As a consequence, there is a general approach for using Why as a target language for programming the semantics of higher-level programming languages [85] . The Krakatoa and the Jessie memory models are inspired by the `component-as-array' representation due to Bornat, following an old idea from Burstall, and commonly used to verify pointers programs [58] . Each field declaration in a Java class or a C structure introduces a Why variable in the model, which is a map (or an array) indexed by addresses. We extended this idea to handle Java arrays and JML annotations [10] and pointer arithmetic in C [7] .
An important difficulty with programs handling pointers is to specify side-effects of a function or a method. The annotation languages offer the assigns clauses in specifications in order to delimitate the part of memory which is modified by a function or a method. We proposed an original modeling for such clauses [82] [7] .
This kind of memory model does not scale up well for large programs. We designed an improved modeling of memory heap incorporating ideas from static analysis of memory separation, and from Reynolds' separation logic. Experiments on a C code proposed by Dassault Aviation were successful [74] , [73] .
The use of Why as intermediate language opens interesting new approaches for reasoning on programs. We studied the specification of global properties, by reuse of the validation term of Why in order to define a model of each function, and then express and prove properties of functions composition. Such an approach was investigated by J. Andronick in the framework of proofs of security properties on smart cards [47] , [46] . We also proposed a way to handle the Java Card transaction mechanism (a specificity of Java Card memory with both persistent and volatile parts), by indeed generating a Why model on-the-fly for each Java Card applet [83] , thanks again to the flexibility of the approach using Why as an intermediate language.
Applications and case studies
The techniques we are developing can be naturally applied in domains which require to develop critical software for which there is a high need of certification.
The Krakatoa tool was successfully used for the formal verification of a commercial smart card applet [75] proposed by Gemalto. This case study have been conducted in collaboration with LOOP and Jive groups. Banking applications are concerned with security problems that can be the confidentiality and protection of data, authentication, etc. The translation of such specifications into assertions in the source code of the program is an essential problem. We have been working on a Java Card applet for an electronic purse Demoney [59] developed by the company Trusted Logic for experimental purpose. Other Java Card case studies have been conducted in collaboration with Gemalto by J. Andronick and N. Rousset, in particular on global properties and Java Card transactions [47] , [83] .
To illustrate the effectiveness of the approach on C programs, T. Hubert and C. Marché performed a full verification of a C implementation of the Schorr-Waite algorithm [8] , using Coq for the proofs. This is an allocation-free graph-marking algorithm used in garbage collectors, which is considered as a benchmark for verification tools. Other industrial case studies have been investigated by T. Hubert (with Dassault Aviation) [73] and by Y. Moy (with France Telecom) [88] , [87] .
Since the beginning of 2011, we propose on the web a Gallery of Verified programs (http://proval.lri.fr/gallery/index.en.html ) which provides a large set of examples of programs that we proved correct, using various techniques. The gallery can be browsed using different criteria: by topics, by reference to benchmarks, by tools.