Section: Application Domains
Design of complex systems
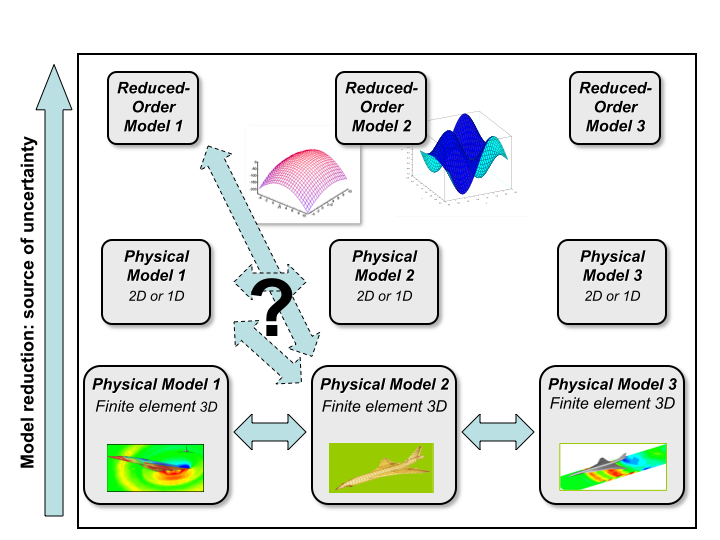
The design of a complex (mechanical) system such as aircraft, automobile or nuclear plant involves numerical simulation of several interacting physical phenomena: CFD and structural dynamics, thermal evolution of a fluid circulation, ... For instance, they can represent the resolution of coupled partial differential equations using finite element method. In the framework of uncertainty treatment, the studied “phenomenological model" is a chaining of different models representing the various involved physical phenomena. As an example, the pressure field on an aircraft wing is the result of both aerodynamic and structural mechanical phenomena. Let us consider the particular case of two models of partial differential equations coupled by limit conditions. The direct propagation of uncertainties is impossible since it requires an exploration and then, many calls to costly models. As a solution, engineers use to build reduced-order models: the complex high-fidelity model is substituted with a CPU less costly model. The uncertainty propagation is then realized through the simplified model, taking into account the approximation error (see [46] ).
Interactions between the various models are usually explicited at the finest level (cf. Fig. 3 ). How may this coupling be formulated when the fine structures of exchange have disappeared during model reduction? How can be expressed the interactions between models at different levels (in a multi-level modeling)? The ultimate question would be: how to choose the right level of modeling with respect to performance requirements?
In the multi-physical numerical simulation, two kinds of uncertainties then coexist: the uncertainty due to substitution of high-fidelity models with approximated reduced-order models, and the uncertainty due to the new coupling structure between reduced-order models.
According to the previous discussion, the uncertainty treatment in a multi-physical and multi-level modeling implies a large range of issues, for instance numerical resolutions of PDE (which do not enter into the research topics of Regularity ). Our goal is to contribute to the theoretical arsenal that allows to fly among the different levels of modeling (and then, among the existing numerical simulations). We will focus on the following three axes:
-
In the case of a phenomenon represented by two coupled partial differential equations whose resolution is represented by reduced-order models, how to define a probabilistic model of the coupling errors? In connection with our theoretical development, we plan to characterize the regularity of this error in order to quantify its distribution. This research axis is supported by an ANR grant (OPUS project).
-
The multi-level modeling assumes the ability to choose the right level of details for the models in adequacy to the goals of the study. In order to do that, a rigorous mathematical definition of the notion of model fineness/granularity would be very helpful. Again, a precise analysis of the fine regularity of stochastic models is expected to give elements toward a precise definition of granularity. This research axis is supported by a a Pôle SYSTEM@TIC grant (EHPOC project), and also by a collaboration with EADS.
-
Some fine characteristics of the phenomenological model may be used to define the probabilistic behaviour of its variability. The action of modeling a phenomena can be seen as an interpolation issue between given observations. This interpolation can be driven by physical evolution equations or fine analytical description of the physical quantities. We are convinced that Hölder regularity is an essential parameter in that context, since it captures how variations at a given point induce variations at its neighbors. Stochastic processes with prescribed regularity (see section 3.3 ) have already been used to represent various fluctuating phenomena: Internet traffic, financial data, ocean floor. We believe that these models should be relevant to describe solutions of PDE perturbed by uncertain (random) coefficients or limit conditions. This research axis is supported by a Pôle SYSTEM@TIC grant (CSDL project).