Section: Scientific Foundations
Adaptivity
|
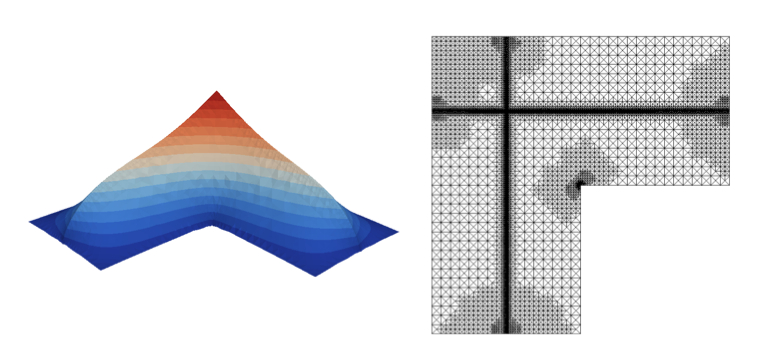
Adaptive finite element methods are becoming a standard tool in numerical simulations, and their application in CFD is one of the main topics of Concha. Such methods are based on a posteriori error estimates of the discretization error avoiding explicit knowledge of properties of the solution, in contrast to a priori error estimates. The estimator is used in an adaptive loop by means of a local mesh refinement algorithm. The mathematical theory of these algorithms has for a long time been bounded to the proof of upper and lower bounds, but has made important improvements in recent years. For illustration, a typical sequence of adaptively refined meshes on an -shaped domain is shown in Figure 2 .
The theoretical analysis of mesh-adaptive methods, even in the most standard case of the Poisson problem, is in its infancy. The first important results in this direction concern the convergence of the sequence of solution generated by the algorithm (the standard a priori error analysis does not apply since the global mesh-size does not necessarily go to zero). In order to prove convergence, an unavoidable data approximation term has to be treated in addition to the error estimator [69] . These result do not say anything about the convergence speed, that is the number of unknowns required to achieve a given accuracy. Such complexity estimates are the subject of active research, the first fundamental result in this direction is [54] .
Our first contribution [23] to this field has been the introduction of a new adaptive algorithm which makes use of an adaptive marking strategy, which refines according to the data oscillations only if they are by a certain factor larger then the estimator. This algorithm allowed us to prove geometric convergence and quasi-optimal complexity, avoiding additional iteration as used before [71] . We have extended our results to conforming FE without inner node refinement [51] and to mixed FE [50] . In this case, a major additional difficulty arises from the fact that, due to the saddle-point formulation, the orthogonality relation known from continuous FEM does not hold. In addition, we have considered the case of incomplete solution of the discrete systems. To this end, we have developed a simple adaptive stopping criterion based on comparison of the iteration error with the discretization error estimator, see also [49] .
Goal-oriented error estimation has been introduced in [52] . It allows to error control and adaptivity directly oriented to the computation of physical quantities, such as the drag and lift coefficient, the Nusselt number, and other physical quantities.