Section: New Results

Mesh Generation and Geometry Processing

New bounds on the size of optimal meshes

Participant : Donald Sheehy.

The theory of optimal size meshes gives a method for analyzing the output size (number of simplices) of a Delaunay refinement mesh in terms of the integral of a sizing function over the input domain. The input points define a maximal such sizing function called the feature size. This work aims to find a way to bound the feature size integral in terms of an easy to compute property of a suitable ordering of the point set. The key idea is to consider the pacing of an ordered point set, a measure of the rate of change in the feature size as points are added one at a time. In previous work, Miller et al. showed that if an ordered point set has pacing $\phi$, then the number of vertices in an optimal mesh will be $O\left({\phi }^{d}n\right)$, where $d$ is the input dimension. We give a new analysis of this integral showing that the output size is only $\Theta (n+nlog\phi )$. The new analysis tightens bounds from several previous results and provides matching lower bounds. Moreover, it precisely characterizes inputs that yield outputs of size $O\left(n\right)$ [20] .

State of the art in quad meshing

Participant : David Bommes.

Triangle meshes have been nearly ubiquitous in computer graphics, and a large body of data structures and geometry processing algorithms based on them has been developed in the literature. At the same time, quadrilateral meshes, especially semi-regular ones, have advantages for many applications, and significant progress was made in quadrilateral mesh generation and processing during the last several years. In this work, we discuss the advantages and problems of techniques operating on quadrilateral meshes, including surface analysis and mesh quality, simplification, adaptive refinement, alignment with features, parametrization, and remeshing [23] .

Meshing the hyperbolic octagon

Participants : Mathieu Schmitt, Monique Teillaud.

We propose a practical method to compute a mesh of the octagon, in the Poincaré disk, that respects its symmetries. This is obtained by meshing the Schwartz triangle $T(8,3,2)$ and applying relevant hyperbolic symmetries (ie., Euclidean reflexions or inversions). The implementation is based on cgal 2D meshes and on the ongoing implementation on cgal hyperbolic Delaunay triangulations [44] . Further work will include solving robutsness issues and generalizing the method to any Schwartz triangle [62] .

Index-based data structure for 3D polytopal complexes

Participant : David Bommes.

OpenVolumeMesh is a data structure which is able to represent heterogeneous 3-dimensional polytopal cell complexes and is general enough to also represent non-manifolds without incurring undue overhead [30] . Extending the idea of half-edge based data structures for two-manifold surface meshes, all faces, i.e. the two-dimensional entities of a mesh, are represented by a pair of oriented half-faces. The concept of using directed half-entities enables inducing an orientation to the meshes in an intuitive and easy to use manner. We pursue the idea of encoding connectivity by storing first-order top-down incidence relations per entity, i.e. for each entity of dimension d, a list of links to the respective incident entities is stored. For instance, each half-face as well as its orientation is uniquely determined by a tuple of links to its incident half-edges or each 3D cell by the set of incident half-faces. This representation allows for handling non-manifolds as well as mixed-dimensional mesh configurations. No entity is duplicated according to its valence, instead, it is shared by all incident entities in order to reduce memory consumption. Furthermore, an array-based storage layout is used in combination with direct index-based access. This guarantees constant access time to the entities of a mesh. Although bottom-up incidence relations are implied by the top-down incidences, our data structure provides the option to explicitly generate and cache them in a transparent manner. This allows for accelerated navigation in the local neighbor- hood of an entity. We provide an open-source and platform-independent implementation of the proposed data structure written in C++ using dynamic typing paradigms. The library is equipped with a set of STL compliant iterators, a generic property system to dynamically attach properties to all entities at run-time, and a serializer/deserializer supporting a simple file format. Due to its similarity to the OpenMesh data structure, it is easy to use, in particular for those familiar with OpenMesh. Since the presented data structure is compact, intuitive, and efficient, it is suitable for a variety of applications, such as meshing, visualization, and numerical analysis. OpenVolumeMesh is open-source software licensed under the terms of the LGPL [29] .

Editable SQuad representation for triangle meshes

Participant : Olivier Devillers.

In collaboration with Luca Castelli Aleardi (LIX, Palaiseau) and Jarek Rossignac (Georgia Tech).

We consider the problem of designing space efficient solutions for representing the connectivity information of manifold triangle meshes. Most mesh data structures are quite redundant, storing a large amount of information in order to efficiently support mesh traversal operators. Several compact data structures have been proposed to reduce storage cost while supporting constant-time mesh traversal. Some recent solutions are based on a global re-ordering approach, which allows to implicitly encode a map between vertices and faces. Unfortunately, these compact representations do not support efficient updates, because local connectivity changes (such as edge-contractions, edge-flips or vertex insertions) require re-ordering the entire mesh. Our main contribution is to propose a new way of designing compact data structures which can be dynamically maintained. In our solution, we push further the limits of the re-ordering approaches: the main novelty is to allow to re-order vertex data (such as vertex coordinates), and to exploit this vertex permutation to easily maintain the connectivity under local changes. We describe a new class of data structures, called Editable SQuad (ESQ), offering the same navigational and storage performance as previous works, while supporting local editing in amortized constant time. As far as we know, our solution provides the most compact dynamic data structure for triangle meshes. We propose a linear-time and linear-space construction algorithm, and provide worst-case bounds for storage and time cost [25] .

Surface reconstruction through point set structuring

Participants : Pierre Alliez, Florent Lafarge.

We present a method for reconstructing surfaces from point sets. The main novelty lies into a structure-preserving approach where the input point set is first consolidated by structuring and resampling the planar components, before reconstructing the surface from both the consolidated components and the unstructured points. The final surface is obtained through solving a graph-cut problem formulated on the 3D Delaunay triangulation of the structured point set where the tetrahedra are labeled as inside or outside cells. Structuring facilitates the surface reconstruction as the point set is substantially reduced and the points are enriched with structural meaning related to adjacency between primitives. Our approach departs from the common dichotomy between smooth/piecewise-smooth and primitive-based representations by gracefully combining canonical parts from detected primitives and free-form parts of the inferred shape. Our experiments on a variety of inputs illustrate the potential of our approach in terms of robustness, flexibility and efficiency [59] .

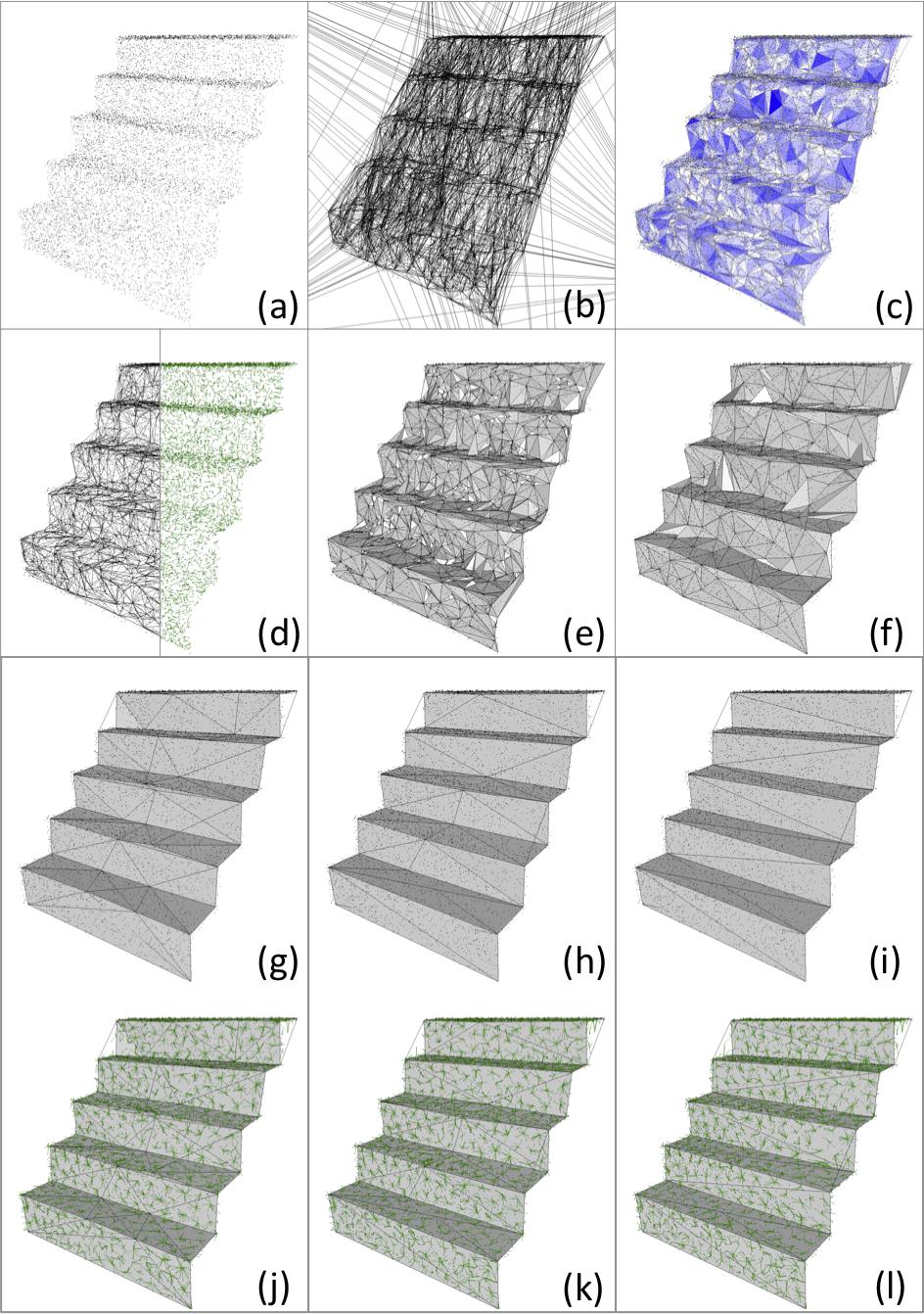
Feature-preserving surface reconstruction and simplification from defect-laden point sets

Participants : Pierre Alliez, David Cohen-Steiner, Julie Digne.

In collaboration with Fernando de Goes and Mathieu Desbrun from Caltech.

We introduce a robust and feature-capturing surface reconstruction and simplification method that turns an input point set into a low triangle-count simplicial complex. Our approach starts with a (possibly non-manifold) simplicial complex filtered from a 3D Delaunay triangulation of the input points. This initial approximation is iteratively simplified based on an error metric that measures, through optimal transport, the distance between the input points and the current simplicial complex, both seen as mass distributions. Our approach is shown to exhibit both robustness to noise and outliers, as well as preservation of sharp features and boundaries (Figure 1 ). Our new feature-sensitive metric between point sets and triangle meshes can also be used as a post-processing tool that, from the smooth output of a reconstruction method, recovers sharp features and boundaries present in the initial point set [58] .

Similarity based filtering of point clouds

Participant : Julie Digne.

Denoising surfaces is a crucial step in the surface processing pipeline. This is even more challenging when no underlying structure of the surface is known, that is when the surface is represented as a set of unorganized points. We introduce a denoising method based on local similarities. The contributions are threefold: first, we do not denoise directly the point positions but use a low/high frequency decomposition and denoise only the high frequency. Second, we introduce a local surface parameterization which is proved stable. Finally, this method works directly on point clouds, thus avoiding building a mesh of a noisy surface which is a difficult problem. Our approach is based on denoising a height vector field by comparing the neighborhood of the point with neighborhoods of other points on the surface (Figure 2 ). It falls into the non-local denoising framework that has been extensively used in image processing, but extends it to unorganized point clouds [26] .

Progressive compression of manifold polygon meshes

Participant : Pierre Alliez.

In collaboration with Adrien Maglo, Clément Courbet and Céline Hudelot from Ecole Centrale Paris.

We present a new algorithm for the progressive compression of surface polygon meshes. The input surface is decimated by several traversals that generate successive levels of detail through a specific patch decimation operator which combines vertex removal and local remeshing. This operator encodes the mesh connectivity through a transformation that generates two lists of Boolean symbols during face and edge removals. The geometry is encoded with a barycentric error prediction of the removed vertex coordinates. In order to further reduce the size of the geometry and connectivity data, we propose a curvature prediction method and a connectivity prediction scheme based on the mesh geometry. We also include two methods that improve the rate-distortion performance: a wavelet formulation with a lifting scheme and an adaptive quantization technique. Experimental results demonstrate the effectiveness of our approach in terms of compression rates and rate-distortion performance. Our approach compares favorably to compression schemes specialized to triangle meshes [31] .