Section: New Results

Mathematical Modelling of the Ocean Dynamics

Beyond the traditional approximation on the Coriolis force

Participant : Antoine Rousseau.

Formerly, A. Rousseau has performed some theoretical and numerical studies around the derivation of quasi-hydrostatic models. With C. Lucas, he proved that it is sometimes necessary to take into account the cosine part of the Coriolis force (which is usually neglected, leading to the so-called Traditional Approximation).

They have also shown that the non-traditional terms do not raise any additional mathematical difficulty in the primitive equations: well-posedness for both weak and strong solutions.

A. Rousseau and J. McWilliams (UCLA) proposed a mathematical justification of the tilt of convective plumes in the quasi-geostrophic regime, thanks to the account of the complete Coriolis force in the so-called quasi-hydrostatic quasi-geostrophic (QHQG) model. The new model has been presented in international conferences [59] and [60] .

Coupling Methods for Oceanic and Atmospheric Models

Participants : Eric Blayo, David Cherel, Laurent Debreu, Antoine Rousseau, Manel Tayachi.

Interface conditions for coupling ocean models

Many physical situations require coupling two models with not only different resolutions, but also different physics. Such a coupling can be studied within the framework of global-in-time Schwarz methods. However, the efficiency of these iterative algorithms is strongly dependent on interface conditions. As a first step towards coupling a regional scale primitive equations ocean model with a local Navier-Stokes model, a study on the derivation of interface conditions for 2-D $x-z$ Navier-Stokes equations has been performed in D. Cherel PhD thesis. It has been shown theoretically that several usual conditions lead to divergent algorithms, and that a convergent algorithm is obtained when using transmission conditions given by a variational calculation.

D. Cherel has implemented a Schwarz-based domain decomposition method, for which he developed optimized absorbing boundary conditions that mix the velocity and pressure variables on an Arakawa-C grid. The numerical results confirm the rate of convergence that has been obtained theoretically, thanks to a Fourier analysis of the semi-discretized problem.

A first step towards the coupling between Navier-Stokes and primitive equations has been made in 2012. Starting from the optimized boundary conditions obtained for the Navier-Stokes equations, we performed an asymptotic analysis in order to obtain boundary conditions that should supplement the hydrostatic Navier-Stokes equations. These results have been presented in national and international conferences [47] , [46] , a paper is in preparation. David Cherel defended his PhD on Dec. 12th, 2012.

Coupling dimensionally heterogeneous models

The coupling of different types of models is gaining more and more attention recently. This is due, in particular, to the needs of more global models encompassing different disciplines (e.g. multi-physics) and different approaches (e.g. multi-scale, nesting). Also, the possibility to assemble different modeling units inside a friendly modelling software platform is an attractive solution compared to developing more and more global complex models. More specifically one may want to couple 1D to 2D or 3D models, such as Shallow Water and Navier Stokes models: this is the framework of our partnership with EDF in the project MECSICO. In her PhD, M. Tayachi is aimed to build a theoretical and numerical framework to couple 1D, 2D and 3D models for river flows.

In [65] , we propose and analyze an efficient iterative coupling method for a dimensionally heterogeneous problem. We consider the case of a 2-D Laplace equation with non symmetric boundary conditions with a corresponding 1-D Laplace equation. We first show how to obtain the 1-D model from the 2-D one by integration along one direction, by analogy with the link between shallow water equations and the Navier-Stokes system. Then we focus on the design of a Schwarz-like iterative coupling method. We discuss the choice of boundary conditions at coupling interfaces. We prove the convergence of such algorithms and give some theoretical results related to the choice of the location of the coupling interface, and to the control of the difference between a global 2-D reference solution and the 2-D coupled one. These theoretical results are illustrated numerically. The extension of this work to shallow0water equations and primitive equations has been started recently.

Numerical schemes for ocean modelling

Participants : Laurent Debreu, Jérémie Demange.

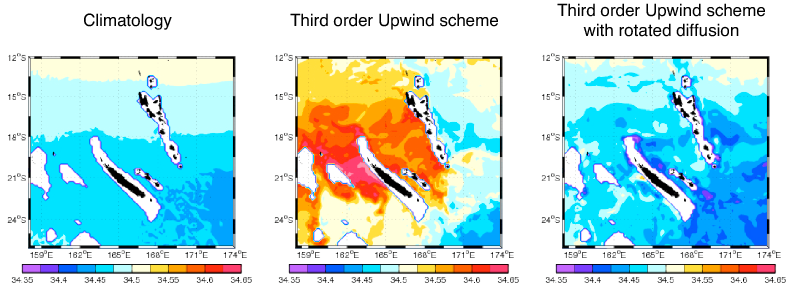
Reducing the traditional errors in terrain-following vertical coordinate ocean models (or sigma models) has been a focus of interest for the last two decades. The objective is to use this class of model in regional domains which include not only the continental shelf, but the slope and deep ocean as well. Two general types of error have been identified: 1) the pressure-gradient error and 2) spurious diapycnal diffusion associated with steepness of the vertical coordinate. In a recent paper [87] , we have studied the problem of diapycnal mixing. The solution to this problem requires a specifically designed advection scheme. We propose and validate a new scheme, where diffusion is split from advection and is represented by a rotated biharmonic diffusion scheme with flow-dependent hyperdiffusivity satisfying the Peclet constraint.

In 2012, in collaboration with F. Lemarié at UCLA, this work has been extended in order to render the biharmonic diffusion operator scheme unconditionally stable [17] . This is particularly needed when the slopes between coordinates lines and isopycnal surfaces are important so that the rotation of the biharmonic leads to strong stability condition along the vertical coordinate where the grid size is relatively small. This work also extends more classical results on the stability of laplacian diffusion with mixed derivatives.

In his PhD, Jérémie Demange begins a work on advection-diffusion schemes for ocean models (Supervisors : L. Debreu, P. Marchesiello (IRD)). His work will focus on the link between tracers (temperature and salinity) and momentum advection and diffusion in the non hyperbolic system of equations typically used in ocean models (the so called primitive equations with hydrostatic and Boussinesq assumptions). We also investigated the use of a depth dependent barotropic mode in free surface ocean models. When most ocean models assume that this mode is vertically constant, we have shown that the use of the true barotropic mode, derived from a normal mode decomposition, allows more stability and accuracy in the representation of external gravity waves [49] , [48] .

Salinity at 1000 m in the Southwest Pacific ocean is shown in figure 1 . The use of traditional upwind biased schemes (middle) exhibits a strong drift in the salinity field in comparison with climatology (left). The introduction of high order diffusion rotated along geopotential surfaces prevents this drift while maintaining high resolution features (right).

Figure 1. Salinity at 1000m in the Southwest Pacific ocean.