Section: Scientific Foundations
Adaptive Cartesian mechanics
In order to focus computations on a specific set of atoms, when performing quasi-static simulations (minimizations), we have developed an adaptive Cartesian mechanics algorithm, which decides which atoms should move at each time step.
In the simplest approach, we simply examine the force applied on each atom. When the norm of the force is above a user-defined threshold, the atom is active. Else the atom position is frozen. A slightly more elaborate version consists in defining the threshold automatically based on the system state (it might be e.g., the average applied force, a percentage of the maximum norm, etc.).
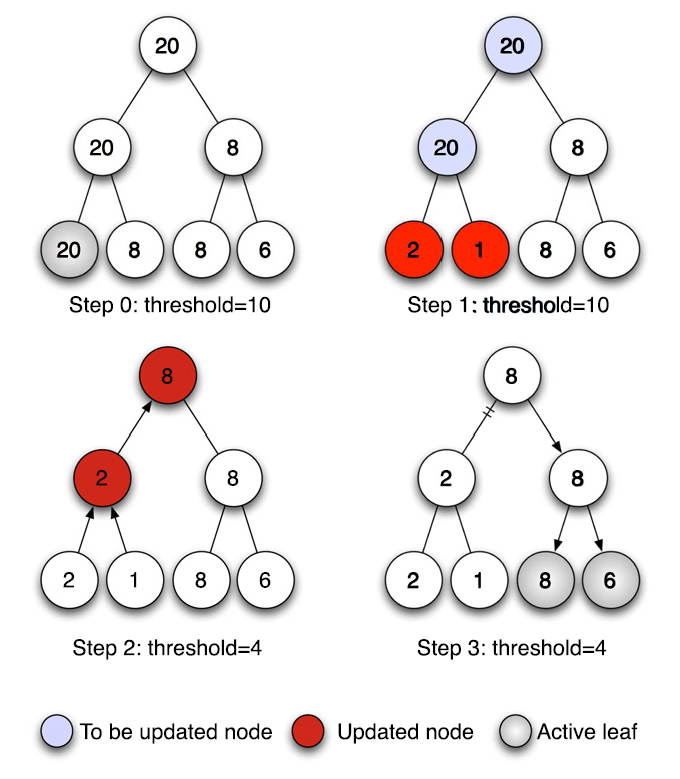
In order to avoid the linear cost of determining the set of active atoms at each time step, a binary tree is used to represent the system. Each leaf node represents an individual atom, while each internal node represents a set of atoms. Each leaf node stores the norm of the force applied to the corresponding atom. Each non-leaf node stores the maximum of the two force norms of its children, as illustrated in Figure 2 . We use two tree passes in order to update tree nodes' values and to determine the new active atoms. In the first, bottom-up pass, force norms are updated in a sub-tree of the binary tree (only some atoms have moved since the previous time step, so only some forces have been updated), starting from the leaves with modified norms, in times where is the number of active atoms and the total number of atoms. In the second, top-down pass, the new active atoms (i.e., the atoms with the force norms which are now the largest), are determined in times where is the new number of active atoms. This process is illustrated in Figure 2 as well.
Precisely, Figure 2 illustrates the procedure to determine the active zone, when the threshold is automatically set to half the largest atomic force norm. In this example, the four leaves correspond to atoms 1 to 4. The value indicated in each leaf node is the norm of the force applied to its corresponding atom. For internal nodes, this value is the maximum of the norms of the forces applied to atoms in the corresponding group. In step 0, the threshold is automatically set to 10. As a result, only atom 1 moves. In step 1, the potential is incrementally updated, and the norms of the forces applied to atoms 1 and 2 are updated. In step 2, the values associated to the tree nodes are incrementally updated through a bottom-up pass that starts from the modified leaf nodes values. Because of this bottom-up update, the adaptive threshold becomes equal to 4. In step 3, the new active atoms are determined through a top-down pass, by visiting only the nodes that have a value larger than the adaptive threshold.