Section: Overall Objectives
Introduction
The general objective of the Toccata project is to promote formal specification and computer-assisted proof in the development of software that requires a high assurance of its safety and its correctness with respect to its intended behavior.
State of the Art of Program Verification
The importance of software in critical systems increased a lot in the last decade. Such a software appears in various application domains like transportation (e.g. airplanes, railway), communication (e.g. smart phones) or banking. The set of available features is quickly increasing, together with the number of lines of codes involved. Given the need of high assurance of safety in the functional behavior of such applications, the need for automated (i.e. computer-assisted) methods and techniques to bring guarantee of safety became a major challenge. In the past, the main process to check safety of a software was to apply heavy test campaigns, which take a large part of the costs of software development.
This is why static analysis techniques were invented to complement tests. The general aim is to analyze a program code without executing it, to get as much guarantees as possible on all possible executions at once. The main classes of static analysis techniques are:
Abstract Interpretation: it approximates program execution by abstracting program states into well-chosen abstraction domains. The reachable abstract states are then analyzed in order to detect possible mistakes, corresponding to abstract states that should not occur. The efficiency of this approach relies on the quality of the approximation: if it is too coarse, false positives will appear, which the user needs to analyze manually to determine if the error is real or not. A major success of this kind of approach is the verification of absence of run-time errors in the control-command software of the Airbus A380 by the tool Astrée [77] .
Model-checking: it denotes a class of approaches that got a great success in industry, e.g. the quality of device drivers of Microsoft's Windows operating system increased a lot by systematic application of such an approach [76] . A program is abstracted into a finite graph representing an approximation of its execution. Functional properties expected for the execution can be expressed using formal logic (typically temporal logic) that can be checked valid by an exploration of the graph. The major issue of model-checking is that the size of the graph can get very large. Moreover, to get less coarse approximations, one may be interested in abstracting a program into an infinite graph. In that case, extensions of model-checking are proposed: bounded model-checking, symbolic model-checking, etc. Predicate Abstraction is also a rather successful kind of model-checking approach because of its ability of getting iteratively refined to suppress false positives [48] .
Deductive verification: it differs from the other approaches in that it does not approximate program execution. It originates from the well-known Hoare logic approach. Programs are formally specified using expressive logic languages, and mathematical methods are applied to formally prove that a program meets its specification.
The Toccata project is mainly interested in exploring the deductive verification approach, although we believe that the class of approaches above are compatible. We indeed have studied some way to combine approaches in the past [10] [87] [24] .
Deductive Program Verification nowadays
In the past decade, there have been significant progress made in the domain of deductive program verification. They are emphasized by some success stories of application of these techniques on industrial-scale software, e.g. the Atelier B system was used to develop part of the embedded software of the Paris metro line 14 [56] and other railroad-related systems, a formally proved C compiler was developed using the Coq proof assistant [92] , Microsoft's hypervisor for highly secure virtualization was verified using VCC [78] and the Z3 prover [110] , the L4-verified project developed a formally verified micro-kernel with high security guarantees, using analysis tools on top of the Isabelle/HOL proof assistant [89] . Another sign of recent progress is the emergence of deductive verification competitions.
In the deductive verification context, there are two main families of approaches. Methods in the first family build on top of mathematical proof assistants (e.g. Coq, Isabelle) in which both the models and the programs are encoded, and the proofs that a program meets its specification is typically conducted in an interactive way using the underlying proof construction engine. Methods from the second family proceed by the design of standalone tools taking as input a program in a particular programming language (e.g. C, Java) specified with a dedicated annotation language (e.g. ACSL [55] , JML [67] ) and automatically producing a set of mathematical formulas (the verification conditions) which are typically proved using automatic provers (e.g. Z3, Alt-Ergo [57] , CVC3 [53] ). The first family of approaches usually offers a higher level of assurance than the second, but also demands more work to perform the proofs (because of their interactive nature) and makes them less easy to adopt by industry. Moreover they do not allow to directly analyze a program written in a mainstream programming language like Java or C. The second kind of approaches has benefited in the past years from the tremendous progresses made in SAT and SMT solving techniques, allowing more impact on industrial practices, but suffers from a lower level of trust: in all parts of the proof chain (the model of the input programming language, the VC generator, the back-end automatic prover) potential errors may appear, compromising the guarantee offered. They can be applied to mainstream languages, but usually only a subset of them is supported. Finally, recent trends in the industrial practice for development of critical software is to require more and more guarantees of safety, e.g. the upcoming DO-178C standard for developing avionics software adds to the former DO-178B the use of formal models and formal methods. It also emphasizes the need for certification of the analysis tools involved in the process.
Overview of our Former Contributions
To illustrate our past contributions in the domain of deductive verification, we provide below a set of reference publications of our former scientific results, published in the past 4 years.
Concerning Automated Deduction, our references publications are: a TACAS'2011 paper [6] on an SMT decision procedure for associativity and commutativity, an IJCAR'2012 paper [20] about an original contribution to decision procedures for arithmetic, a CAV'2012 paper [24] presenting a SMT-based model checker, a FroCos'2011 paper [2] presenting an new approach for encoding polymorphic theories into monomorphic ones.
Regarding deductive program verification in general, a first reference publication is the habilitation thesis of Filliâtre [8] which provides a very good survey of our recent contributions. A shorter version appears in the STTT journal [82] . The ABZ'2012 paper [29] is a representative publication presenting an application of our Why3 system to solving proof obligations coming from Atelier B. The VSTTE'2012 paper [27] is a reference case study publication: proof of a program solving the -queens problem, that uses bitwise operations for efficiency.
In industrial applications, numerical calculations are very common (e.g. control software in transportation). Typically they involve floating-point numbers. Concerning the analysis of numerical programs, our representative publications are: a paper in the MCS journal in 2011 [4] presenting on various examples our approach of proving behavioral properties of numerical C programs using Frama-C/Jessie, a paper in the TC journal in 2010 [109] presenting the use of the Gappa solver for proving numerical algorithms, a paper in the ISSE journal in 2011 [66] together with a paper at the CPP'2011 conference [102] presenting how we can take architectures and compilers into account when dealing with floating-point programs. We also contributed to the Handbook of Floating-Point Arithmetic in 2009 [101] . A representative case study is the analysis and the proof of both the method error and the rounding error of a numerical analysis program solving the one-dimension acoustic wave equation, presented in part at ITP'2010 [61] and in another part at ICALP'2009 [3] and fully in a paper in the JAR journal [14] .
Finally, about the theme of certification of analysis tools, the reference papers are: a PEPM'2010 [75] and a RTA'2011 paper [7] on certified proofs of termination and other related properties of rewriting systems, and a VSTTE'2012 paper [28] presenting a certified VC generator.
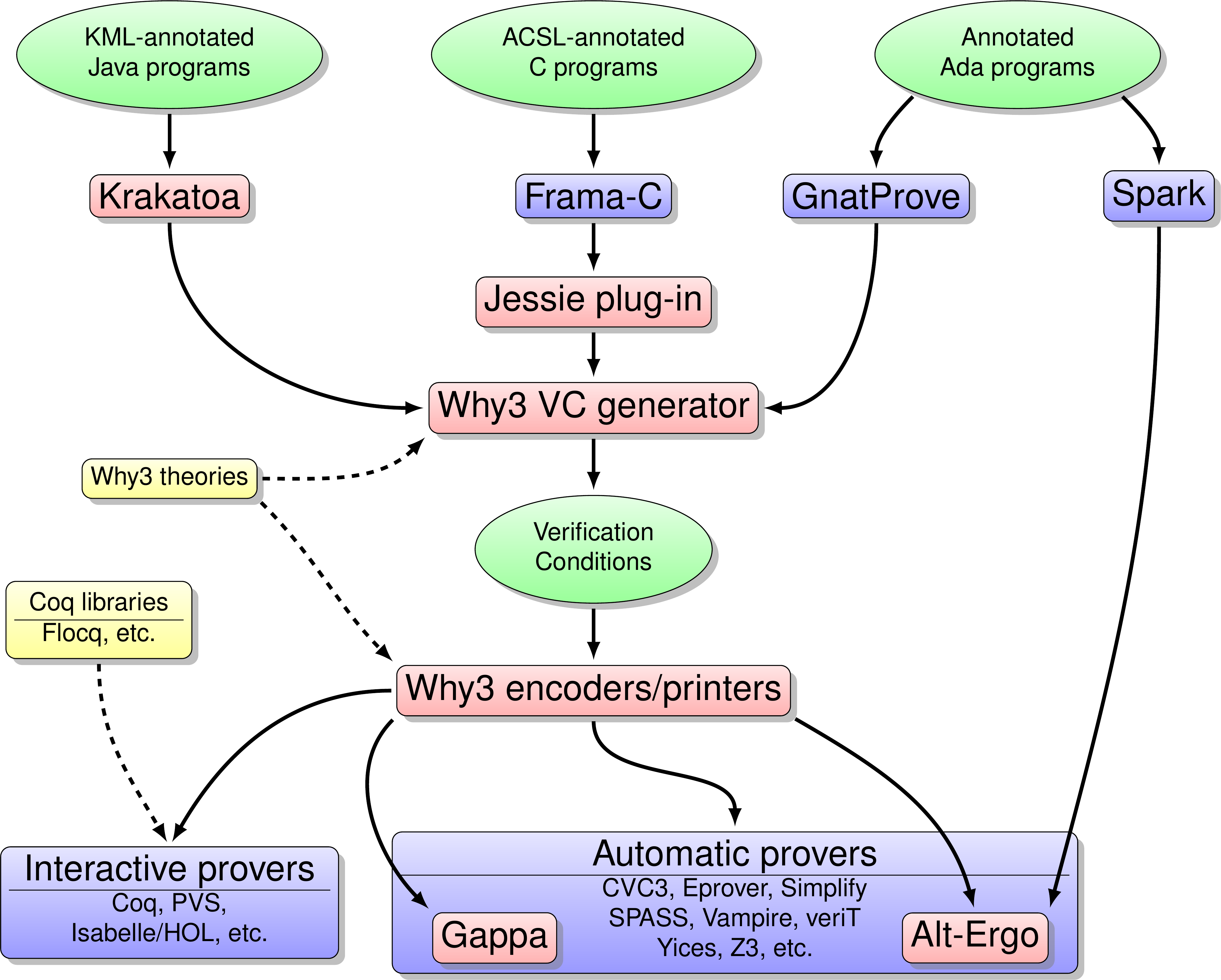
The diagram of Figure 1 details how our tools interact with each other and with other tools. The tools in pink boxes are designed by us, while those in blue boxes are designed by partners. The central tool is Why3 [1] [17] , which includes both a Verification Condition generator and a set of encoders and printers. The VC generator reads source programs in a dedicated input language that includes both specifications and code. It produces verification conditions that are encoded and printed into various formats and syntax so that a large set of interactive or automatic provers can be used to discharge the verification conditions.
Among automated provers, our own tool Alt-Ergo [57] is an SMT solver that is able to deal with quantifiers, arithmetic in integers or real numbers, and a few other theories. Gappa [9] is a prover designed to support arithmetic on real numbers and floating-point rounding. As front-ends, our tool Krakatoa [94] reads annotated Java source code and produces Why3 code. The tool Jessie [100] [10] is a plug-in for the Frama-C environment (which we designed in collaboration with CEA-List); it does the same for annotated C code. The GnatProve tool is a prototype developed by Adacore company; it reads annotated Ada code and also produces Why3 code. Spark is an ancestor of GnatProve developed by Altran-Praxis company; it has a dedicated prover but it was recently modified so as to produce verification conditions in a suitable format for Alt-Ergo.
Last but not least, the modeling of programs semantics and the specification of their expected behaviors is based on some libraries of mathematical theories that we develop, either in the logic language of Why3 or in Coq. These are the yellow boxes of the diagram. For example, we developed in Coq the Flocq library for the formalization of floating-point computations [5] .