Section: Research Program

Multiscale propagation phenomena in biology

Project team positioning

The originality of our work is the quantitative description of propagation phenomena for some models including several scales. We are able to compute the speed of propagation and the distribution with respect to the microscopic variable at relevant locations (e.g. the edge and the back of the front) in a wide variety of models.

Multiscale modeling of propagation phenomena raises a lot of interest in several fields of application. This ranges from shock waves in kinetic equations (Boltzmann, BGK, etc...), bacterial chemotactic waves, selection-mutation models with spatial heterogeneities, age-structured models for epidemiology or subdiffusive processes.

Earlier works generally focused on numerical simulations, hydrodynamic limits to average over the microscopic variable, or specific models with only local features, not suitable for most of the relevant models. Our contribution enables to derive the relevant features of propagation analytically, and far from the hydrodynamic regime for a wide range of models including nonlocal interaction terms.

We emphasize that accurate modeling of bacterial chemotactic waves (described in Adler 1966) was still not achieved. Combination of massive tracking experiments together with a well-parametrized multiscale kinetic model enabled the first accurate description of such waves (Saragosti et al, PNAS 2011).

Our recent understanding is closely related to the analysis of large deviations in multiscale dispersion equations, for which we give important contributions too.

These advances are linked to the work of other Inria teams (BANG, DRACULA, BEAGLE), and collaborators in mathematics, physics and theoretical biology in France, Austria and UK.

Recent results

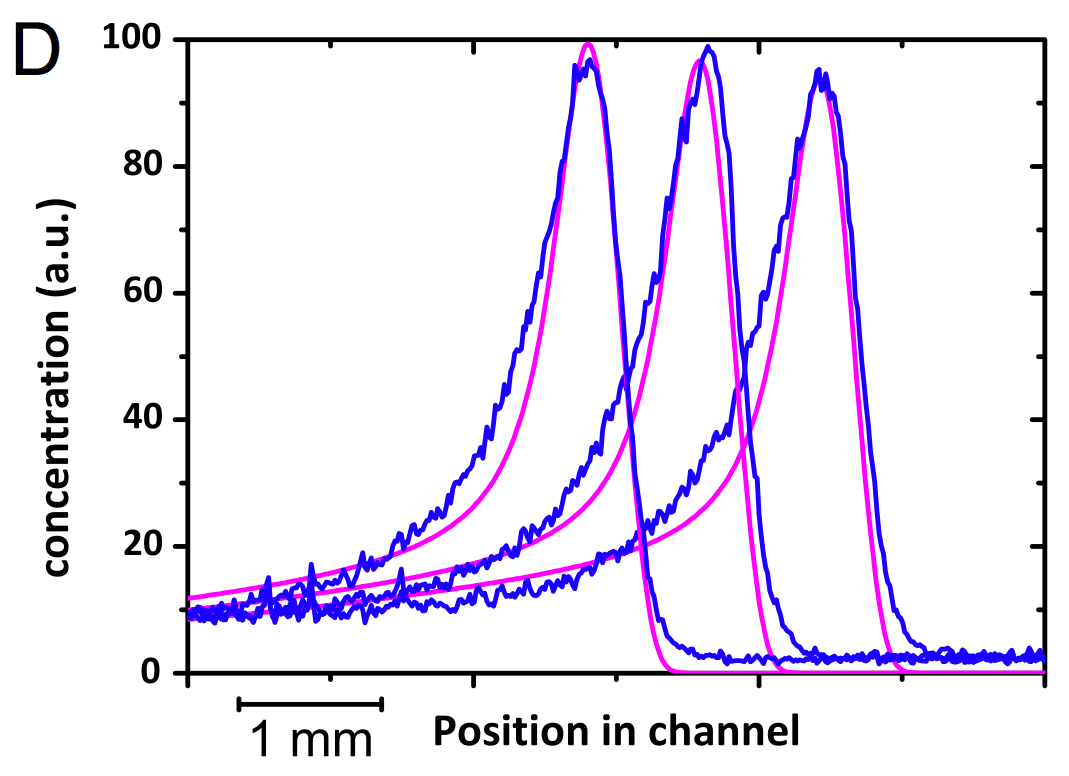
We began with the mathematical description of bacterial chemotactic waves (Saragosti et al 2010). We demonstrated that such waves are better described using a kinetic model for the run-tumble process in the phase space position/velocity (Saragosti et al, PNAS 2011). Taking into account local velocity heterogeneity of the bacterial population is now tractable both experimentally (massive tracking experiments) and mathematically (decorrelation of the asymptotic space decay and the distribution w.r.t. the microscopic variable at the edge of the front). This gave excellent matches in 1D (wave in a straight microchannel), see Figure 1 for the evolution of the spatial density profile.

We emphasize that Filbet and Yang (Univ. Lyon 1) have computed numerically very good predictions of bacterial waves in two-dimensional curved geometries using our model (results not shown).

Next we investigated the analytical computation of the relevant features of the wave (speed, velocity distribution), first in the hydrodynamic regime, then in the full kinetic model.

This work motivated the analysis of reaction-diffusion traveling waves, where diffusion is replaced by a transport-scattering operator. By analogy with the Fisher-KPP equation we proved existence and stability of traveling waves, and spreading properties of the model (Bouin-Calvez-Nadin 2013, Bouin-Calvez-Nadin 2013). A key assumption is the boundedness of the velocity set. Under this assumption we can perform the large deviation limit of the kinetic equation, leading to a new eikonal equation (Bouin-Calvez 2012). Spreading in the case of arbitrarily large speeds (even if they are arbitrarily rare) shows very unexpected properties. For this purpose we currently investigate the large deviation limit of the kinetic BGK model with a Gaussian redistribution of velocities, leading to a new kind of Hamilton-Jacobi equation with constraints (Bouin-Calvez-Grenier-Nadin, in progress). This yields accelerating waves in the corresponding transport-reaction model.

In parallel, we have investigated a selection-mutation model with spatial heterogeneities which combines ecological scales (propagation of invasive species) and evolutionary scales (selection of more motile individuals). This applies to the current invasion of cane toads in Northern Australia. (We emphasize that, just as for kinetic models, the microscopic variable (trait = ability to move) acts on the spatial operator (here, diffusion).). Again we are able to compute the speed of the wave and the diversity of the population at the edge in the case of bounded phenotypical trait (Bénichou et al 2012, Bouin et al 2012). In the case where it is unbounded we observe accelerating waves, due to continual sorting of more motile individuals at the edge of the front (Bouin et al 2012), just as it is observed in Australia. We also derive formally the limit of adaptive dynamics of this multiscale model (only one trait is selected at each location)(This leads to a Burgers equation with source term, due to sorting effects at the edge of the front.).

This work has already been cited in the context of tumor progression, taking into account heterogeneity and local competition (Orlando et al, Frontiers in Oncology 2013).

Collaborations

• Mathematical description of bacterial chemotactic waves:

  • N. Bournaveas (Univ. Edinburgh), V. Calvez (ENS de Lyon, Inria NUMED) B. Perthame (Univ. Paris 6, Inria BANG), Ch. Schmeiser (Univ. Vienna), N. Vauchelet: design of the model, analysis of traveling waves, analysis of optimal strategies for bacterial foraging.

  • J. Saragosti, V. Calvez (ENS de Lyon, Inria NUMED), A. Buguin, P. Silberzan (Institut Curie, Paris): experiments, design of the model, identification of parameters.

  • F. Filbet, C. Yang (Univ. Lyon 1): numerical simulations in 2D in curved geometries.

• Transport-reaction waves and large deviations:

  • E. Bouin, V. Calvez (ENS de Lyon, Inria NUMED), E. Grenier (ENS de Lyon, Inria NUMED), G. Nadin (Univ. Paris 6)

• Selection-mutation models of invasive species:

  • E. Bouin (ENS de Lyon, Inria NUMED), V. Calvez (ENS de Lyon, Inria NUMED), S. Mirrahimi (Inst. Math. Toulouse): construction of traveling waves, asymptotic propagation of fronts,

  • E. Bouin (ENS de Lyon, Inria NUMED), V. Calvez (ENS de Lyon, Inria NUMED), N. Meunier, (Univ. Paris 5), B. Perthame (Univ. Paris 6, Inria Bang), G. Raoul (CEFE, Montpellier), R. Voituriez (Univ. Paris 6): formal analysis, derivation of various asymptotic regimes.

• Age-structured equations for subdiffusive processes (just starting)

  • H. Berry (Inria BEAGLE), V. Calvez (ENS de Lyon, Inria NUMED), Th. Lepoutre (Inria DRACULA), P. Gabriel (Univ. UVSQ)

This work is also supportet by a PEPS project (CNRS) "Physique Théorique et ses Interfaces", led by N. Vauchelet (Univ. Paris 6).