Section: New Results
Optimum design in structural mechanics
Shape Optimization in Multidisciplinary Non-Linear Mechanics
Participants : Aalae Benki, Jean-Antoine Désidéri, Abderrahmane Habbal, Gael Mathis [ArcelorMittal, CRAA] .
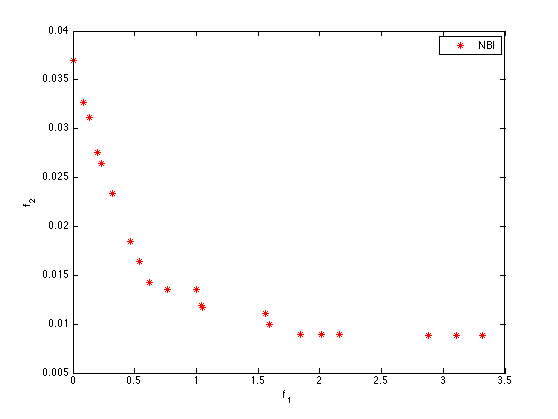
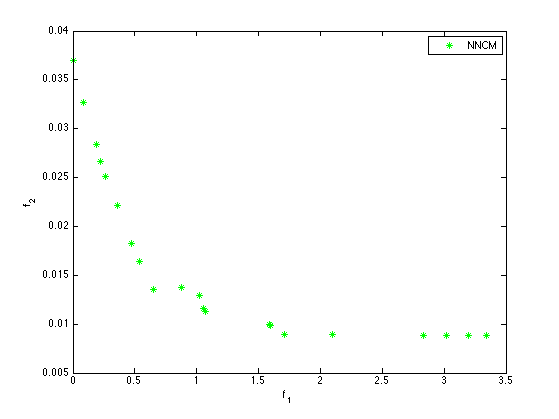
In collaboration with the ArcelorMittal's Center for Research in Automotive and Applications (CRAA), we study the multidisciplinary shape and parameter design of highly non linear mechanical 2D and 3D structures. We have developed methods adapted to the approximation of Pareto Fronts such as Normal Boundary Intersection NBI and Normalized Normal Constraint Method NNCM. Due to the time consuming cost evaluation, the use of cheap to evaluate surrogate models is mandatory. We have studied the consistency of the approach NBI or NNCM plus surrogates, which turned out to be successful for a broad panel of standard mathematical benchmarks. The coupling is successfully applied to a small scale industrial case, namely the shape optimization of a can bottom vis à vis dome reversal pressure and dome growth criteria. We have then defined a Nash game between criteria where the latter are approximated by the RBF metamodels. First, we validated the computation of a Nash equilibrium for mathematical functions, then we computed Nash equilibria for the small scale industrial case of the shape optimization of the can bottom.
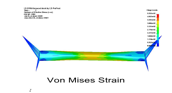
Then, we considered the 3D problem of an automotive twist beam. In this 3D case, we aim to Pareto-optimal shapes for two objectives, the first being to minimize the Von-Mises strain to guarantee the formability of the twist beam, and the second being to maximize the stiffness. For solution with higher stiffness than the initial one, we could decrease the thickness to obtain a mass reduction with the same end-user properties.
We also introduced, to our knowledge for the first time in the structural optimization area, the notion of Kalai-Smorodinky equilibria which is aimed at the selection of equilibria among Pareto-optimal solutions. We applied this notion of equilibria to both industrial cases, and compared the results to Nash equilibria. [56] [64]
|
Optimization of Addendum Surfaces in Stamping
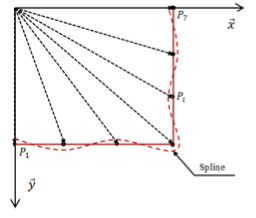
Participants : Fatima Zahra Oujebbour, Rachid Ellaia, Abderrahmane Habbal, Ziheng Zhao.
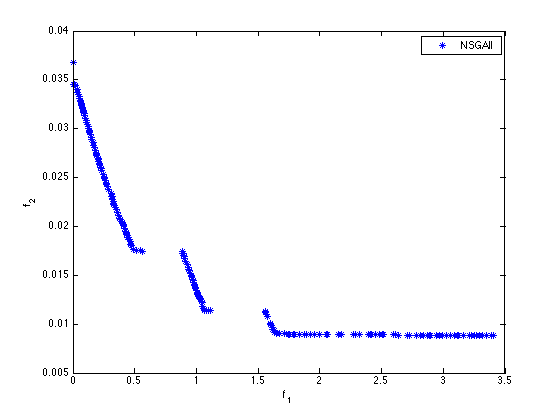
Within the OASIS Consortium (ArcelorMittal, ErDF, Inria, UTC, EURODECISION, ESILV, NECS, DeltaCAD, SCILAB-DIGITEO), the Opale project-team leads the Optimization task. Our aim is to develop decentralized decision-making algorithms dedicated to find efficient solutions (Pareto optimal) in a complex multidisciplinary framework (forming, stamping, welding non-linear processes, spring-back, vibration, in-function linear processes, crash and fatigue non linear and non differentiable processes) for several (between three and five) criteria. An important difficulty when trying to identify the Pareto Front, even when using adapted methods such the Normal Boundary Intersection, is that the criteria involved (thanks to the high nonlinearity in the mechanical models) exhibit many local optima. So one must use global optimization methods. We have studied the hybrid approach Simulated Annealing with Simultaneous Perturbation SASP for a suite of mathematical test-cases. To envisage the application of our method to the complex CPU time consuming stamping process, we lead an intermediate phase dedicated to the validation of the SASP method for the minimization of the spring-back that follows the stamping of a metal sheet, the design variable being the process parameters (two then four parameters). Then, we considered the more complex shape design of the initial blank. The initial blank design is a critical step in stamping design procedure, therefore it should be optimally designed. Our aim is to find the optimal initial blank shape that avoids or at least minimizes the springback and failure flaws. For this study, the geometry of the blank contour is described by parametric spline curves. Seven control points (P1,...,P7) are used to define the spline curves in order to have a wide variety of geometries. The exact computational evaluation of our criteria, springback and failure, is very expensive (the FE model request around 45 min to predict these two criteria) and the design space is of quite high dimension. Therefore, we considered the recourse to the sparse grid interpolation. Optimization process based on sparse grid interpolation is an optimal alternative in which criteria can be approximated with a suitable interpolation formula that needs significantly less points than the full grid. the obtained metamodel using sparse grid interpolation needs less than 1s to predict springback and failure on the same computation machine. To find the optimal initial blank shape, it was decided to perform the optimization process using the obtained metamodel. The construction of the sparse grid interpolant was based on the Chebyshev Gauss-Lobatto grid type and using the polynomial basis functions. This technique achieves a good accuracy with a competitive number of grid points. The comparison of the obtained fronts shows that we can capture Pareto solutions by NBI and NNCM with fewer points than NSGAII which requires a large number of populations and several generations to obtain the Pareto front. [60] [61] [63] [77]
|