Section: New Results

Time domain wave propagation problems

Numerical methods in electromagnetism

Participant : Gary Cohen.

In the framework of contract GREAT, we implemented and compared two discontinuous Galerkin methods to solve Maxwell's equations for time dependent problems, the first using tetrahedral meshes (first used by Hesthaven), the second using hexahedral meshes with mass lumping. This comparison showed the undeniable superiority of the second method, 4-7 times faster (for orders from 2 to 4) for the same accuracy.

The ultimate goal of this program was the hybridization of those two types of meshes because the construction of purely hexahedral mesh for complex geometries is often difficult or almost impossible. A first approach was studied in the thesis Morgane Bergot, where the transition between the two grids was performed by the use of pyramids. The implementation of such elements is difficult and costly, we were interested in a transition mortars elements capable of hybridizing directly tetrahedra with flat faces and hexahedral with non-planar faces. This approach is promising and should lead to a rapid and efficient method. A theoretical study of the error and stability is conducted in collaboration with Eric Chung of CUHK (Chinese University of Hong Kong).

Moreover, always with E. Chung, we became interested in the construction of a discontinuous Galerkin method on hexahedral meshes offset for solving Maxwell's equations. This approach has two advantages : firstly, the shift naturally removes the spurious waves which appear with other approaches (which usually requires the introduction of a dissipative term to remove them). On the other hand, a phenomenon of super-convergence appears which should lead to a substantial time saving. A first study of the dispersion of this method led to a publication.

Solving the Homogeneous Isotropic Linear Elastodynamics Equations Using Potentials and Finite Elements.

Participants : Aliénor Burel, Patrick Joly.

The aim of this subject, investigated in collaboration with Marc Duruflé (Inria Bordeaux) and Sébastien Imperiale (Inria Saclay), is to use the classical theoretical decomposition of the elastodynamic displacement into two potentials referring to the pressure wave and the shear wave, and use it in a numerical framework. During the past two years, a method has been proposed for solving the Dirichlet problem (clamped boundary), successfully analysed and implemented, and for the free boundary conditions, we proposed an original method considering these boundary conditions as a perturbation of the Dirichlet conditions. This approach performs successfully in the time-harmonic regime but appears to give rise to severe instabilities in the time-dependent case after space and time discretization. Our investigations seem to prove that this instability is already present in the semi-discrete problem in space, but we are still looking for an explanation of this phenomenon.

Limiting amplitude principle in a two-layered medium composed of a dielectric and a metamaterial

Participants : Maxence Cassier, Christophe Hazard, Patrick Joly, Valentin Vinoles.

We are investigating this problem from both theoretical and numerical points of view. This is also the object of a collaboration with B. Gralak from the Institut Fresnel in Marseille.

This work is the time-domain counterpart of the research done at Poems about frequency domain analysis of metamaterials in electromagnetism, in the framework of the ANR Project METAMATH. One fundamental question is the link between the evolution / time harmonic problems via the limiting amplitude principle, in particular in the cases where the time harmonic problem fails to be well posed. This occurs, at certain frequencies, when one considers a transmission problem between a standard dielectric material and a dispersive material obeying for instance to the Drude model (other models as Lorentz materials or their generalization also give rise to the same results). Indeed, for well-chosen coefficients (which we refer as the critical case), there exist critical frequencies (only one frequency ${\omega }_c$ for the Drude model) for which the metamaterial behaves as a material whose equivalent electric permittivity and magnetic permeability are negative and precisely opposite to the ones of the dielectric medium : in such a situation, in the case of a plane interface, it is known that the time harmonic transmission problem is strongly ill-posed.

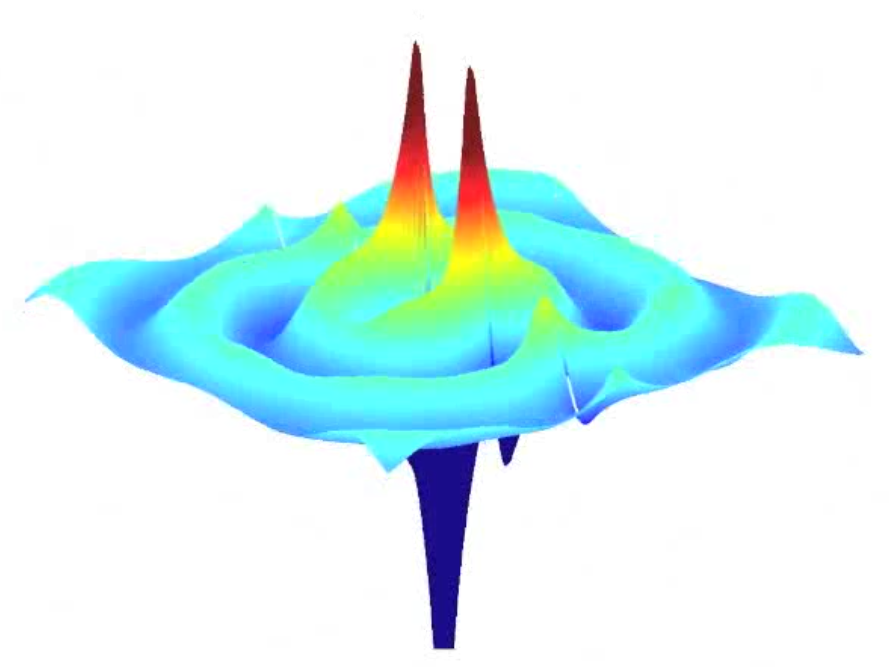
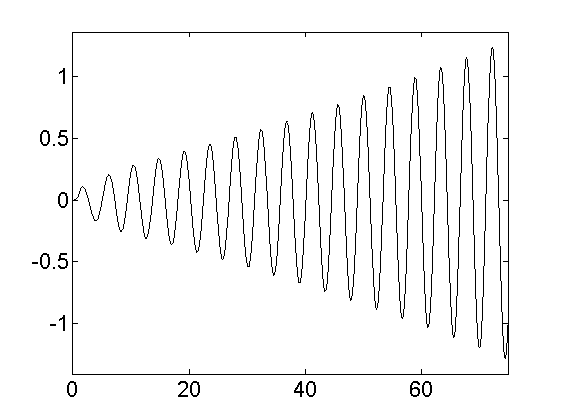
We have considered the evolution problem in a two-layered medium, when we consider a source term $f\left(x\right)e^{i\omega t}$ with frequency $\omega >0$. In the non critical case, the limiting amplitude principle holds : for large times, the solution $u(x,t)$ of the evolution problem "converges" to a time harmonic solution of the form $u^{\infty }\left(x\right)e^{i\omega t}$. In the critical case, the limiting amplitude principle no longer holds. If $\omega \ne {\omega }_c$, the solution of the evolution problem behaves when $t\to +\infty$ to a "double frequency" solution of the form

If $\omega ={\omega }_c$, the solution blows up linearly at infinity :

where the function $u_c^{\infty }\left(x\right)$ is "concentrated" near the interface : this can be interpreted as an "interface resonance" phenomenon. We have performed various numerical experiments (using in particular the stabilized PMLs evoked in section 6.3.2 ) that illustrate this resonance phenomenon (cf figure 1 ).

From the mathematical point of view, the method we have used consists in rewriting the original problem as an abstract Schrödinger equation

where $A$ is a self-adjoint operator in an appropriate Hilbert space $H$. The key of the analysis is the spectral theory of the operator A. This permits a quasi-explicit representation of the solution via the (generalized) diagonalization of $A$. This is achieved by combining a partial Fourier transform along the interface with Sturm-Liouville type techniques in the orthogonal direction. In the critical case, the resonance phenomenon appears to be linked to the fact that $A$ admits a (single) eigenvalue of infinite multiplicity.

Finite differences method for nonlinear acoustic waves with fractional derivatives

Participant : Jean-François Mercier.

This subject is developed in collaboration with Bruno Lombard from LMA.

We develop a numerical method to study the wave propagation in a 1-D guide with an array of Helmholtz resonators, considering large amplitude waves and viscous boundary layers. The model consists in two coupled equations: a nonlinear PDE for the velocity in the tube (Burgers like equation) and a linear ODE describing the pressure oscillations in the Helmholtz resonators. The dissipative and dispersive effects in the tube and in the necks of the resonators are modelled by fractional derivatives expressed as convolution products with singular kernels. Based on a diffusive representation, the convolution kernels of the fractional derivatives are replaced by a finite number of memory variables that satisfy local ordinary differential equations. The procedure to compute weights and nodes of the diffusive representation of fractional derivatives is optimized. Moreover an adequate coupling between the PDE and the ODE is introduced to be sure that the discrete energy is decreasing. A splitting strategy is then applied to the evolution equations to obtain a stable scheme under the optimal CFL condition: the propagative part is solved by a standard TVD scheme for hyperbolic equations, whereas the diffusive part is solved exactly. This approach is validated by comparisons with exact solutions. The properties of the full nonlinear solutions are investigated numerically. In particular, the existence of acoustic solitary waves, due to the competition between dispersion and nonlinear effects, is confirmed.