Section: New Results
Applications in deterministic optimal control
Contrast imaging problem in nuclear magnetic resonance
Participant : Pierre Martinon.
In collaboration with team McTAO (Sophia), we started in 2013 to study the contrast imaging problem in nuclear magnetic resonance, modeled as Mayer problem in optimal control ( [58] ). Using tools from the Maximum Principle and geometric control, we obtained a first synthesis of locally optimal solutions is given in the single-input case, as well as preliminary results in the bi-input case. This analysis was supported by comprehensive numerical investigations using a combination of indirect shooting (HamPath software) and direct method (Bocop ), with a moment-based (LMI ) technique to estimate the global optimum.
These results have been extended in 2014, on the theoretical side with the classification of singular extremals ([35] ), and on the numerical side with the study of a large number of spins particles subject to spatial inhomogeneities in the magnetic field.
Optimal strokes and design for N-link microswimmer
Participant : Pierre Martinon.
Following [71] , we pursued the study of the N-link swimmer, a generalization of the classical Purcell swimmer. We use the model of the Resistive Force Theory to derive the motion equation for the swimmer in a fluid with a low Reynolds number. This allows use to study and solve the optimal swimming problem in the framework of optimal control. We extend our previous study of the optimal strokes by moving to the optimal design of the swimmer. In [72] we provide an estimate of the optimal link ratio for maximal displacement, based on an expansion for small amplitudes. This theoretical result is supported by numerical simulations, that also give some insight on the type of optimal strokes depending on the constraints on the amplitude and deformation speed.
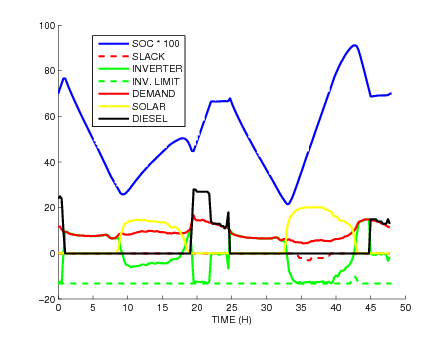
Energy management for a micro-grid
Participants : Frédéric Bonnans, Daphné Giorgi, Benjamin Heymann, Stéphan Maindrault, Pierre Martinon.
We study the energy management problem for a microgrid including a diesel generator and a photovoltaic plant with a battery storage system. The objective is to minimize the total operational cost over a certain timeframe, primarily the diesel consumption, while satisfying a prescribed power load. After reformulation, the decision variables can be reduced to the charging/discharging power for the battery system. We take into account the switching cost for the diesel generator, the non-convex objective, and the long-term aging of the batteries. We solve this problem using a continuous optimal control framework, with both a direct transcription method (time discretization) and a Dynamic Programming method (Hamilton Jacobi Bellman). This project is a collaboration between team COMMANDS (Inria Saclay, France) and Centro de Energia (Universidad de Chile, Chile). A first paper is currently in preparation, while ongoing studies include comparison with the existing MILP approach, more refined battery aging models, and modeling the stochastic nature of the photovoltaic power and power load.