Section: New Results
Optimum design and control in fluid dynamics and its couplings
In computational sciences for physics and engineering, Computational Fluid Dynamics (CFD) are playing one of the major roles in the scientific community to foster innovative developments of numerical methodologies. Very naturally, our expertise in compressible CFD has led us to give our research on numerical strategies for optimum design a particular, but not exclusive focus on fluids.
The framework of our research aims to contribute to numerical strategies for PDE-constrained multi-objective optimization, with a particular emphasis on CPU-demanding computational applications in which the different criteria to be minimized (or reduced) originate from different physical disciplines that share the same set of design variables. These disciplines are often fluids, as a primary focus, coupled with some other disciplines, such as structural mechanics.
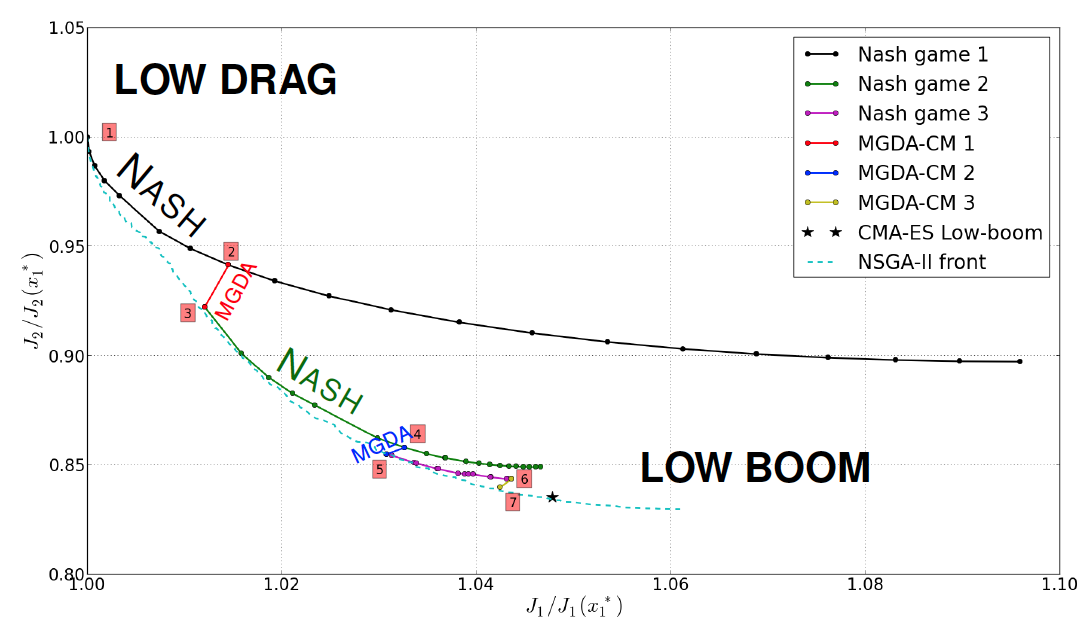
Our approach to competitive optimization is focused on the two-discipline problem. It is based on a particular construction of Nash games, relying on a split of territory in the assignment of individual strategies. A methodology has been proposed for the treatment of two-discipline optimization problems in which one discipline, the primary discipline, is preponderant, or fragile. Then, it is recommended to identify, in a first step, the optimum of this discipline alone using the whole set of design variables. Then, an orthogonal basis is constructed based on the evaluation at convergence of the Hessian matrix of the primary criterion and constraint gradients. This basis is used to split the working design space into two supplementary subspaces to be assigned, in a second step, to two virtual players in competition in an adapted Nash game, devised to reduce a secondary criterion while causing the least degradation to the first. The formulation has been proved to potentially provide a set of Nash equilibrium solutions originating from the original single-discipline optimum point by smooth continuation, thus introducing competition gradually [65] (see also subsectionsubsect:helico).
Our approach to cooperative optimization, in theory, is not limited in number of objective functions. It is based on a result of convex analysis established for a general unconstrained multiobjective problem in which all the gradients are assumed to be known. The theorem [66] states that in the convex hull of the gradients, there exists a unique vector of minimal norm, ; if it is nonzero, the vector is a descent direction common to all criteria; otherwise, the current design point is Pareto-stationary. This result led us to generalize the classical steepest-descent algorithm by using the vector as search direction. We refer to the new algorithm as the multiple-gradient descent algorithm (MGDA). The MGDA yields to a Pareto-stationary point, and in practice actual Pareto-optimality is verified a posteriori.
The two approaches have been combined to explore the Pareto front segment-wise as illustrated on Figure 2 .
|
Multiple-Gradient Descent Algorithm (MGDA)
Participants : Jean-Antoine Désidéri, Régis Duvigneau, Camilla Fiorini, Matteo Giacomini, Abderrahmane Habbal, Adrien Zerbinati.
Theory and numerical experimentation of the MGDA construction
In multi-objective optimization, the knowledge of the Pareto set provides valuable information on the reachable optimal performance. A number of evolutionary strategies (PAES, NSGA-II, etc), have been proposed in the literature and proved to be successful to identify the Pareto set. However, these derivative-free algorithms are very demanding in terms of computational time. Today, in many areas of computational sciences, codes are developed that include the calculation of the gradient, cautiously validated and calibrated [66] .
The notion of Pareto-stationarity, originally established to be a necessary condition of optimality in differentiable multi-objective optimization of unconstrained problems, has been extended to problems subject to equality constraints. On this basis, we were able to establish that by augmenting, in a classical manner, the objective-functions of a penalty term equal to the square of the constraint violation, and applying the standard MGDA to it, would result in converged solutions that are Pareto-stationary in the extended sense. Numerical experimentation on this is on-going.
Meta-model-assisted CFD optimization by MGDA
Using MGDA in a multi objective optimization problem requires the evaluation of a large number of points with regard to criteria, and their gradients. In the particular case of a CFD problems, each point evaluation is very costly since it involves a flow computation, possibly the solution of an adjoint-equation. To alleviate this difficulty, we have proposed to construct meta-models of the functionals of interest (lift, drag, etc) and to calculate approximate gradients by local finite differences. These meta-models are updated throughout the convergence process to the evaluation of the new design points by the high-fidelity model, here the 3D compressible Euler equations.
This variant of MGDA has been tested successfully over several aerodynamic shape optimization problems : lift concurrently with drag optimization for transonic aircraft; drag (under lift constraint) concurrently with sonic boom reduction for 3D supersonic configuration (at ONERA); drag (under lift constraint) concurrently with mass reduction for transport aircraft (at ONERA) [56] .
Exact shape gradients
MGDA has successfully been tested over a two-objective optimization problem governed by two-dimensional elasticity. The deformation of a plate is calculated using an isogeometric approximation and compliance derived from it. The exact parametric shape gradient is calculated, yielding the gradient of the objective function in two antagonistic situations differing by the loading. Pareto-fronts are thus identified [68] .
Optimization of an unsteady system using a multiobjective formulation
An approach has been developed to solve optimization problems in which the functional that has to be minimized is time dependent. In the literature, the most common approach when dealing with unsteady problems, is to consider a time-average criterion. However, this approach is limited since the dynamical nature of the state is neglected. Our alternative consists in building a set of cost functionals by evaluating a single criterion at different sampling times. In this way, the optimization of the unsteady system is formulated as a multi-objective optimization problem, solved using an appropriate descent algorithm (MGDA). Moreover, we also consider a hybrid approach in which the set of cost functionals is built by doing a time-average operation over multiple intervals. These strategies have been illustrated and applied to a non-linear unsteady system governed by a one-dimensional convection-diffusion-reaction partial differential equation [67] .
Perspectives
MGDA offers the possibility to handle in a rational way several objective-functions for which gradients are known or approximated concurrently. This potential opens methodological paths to several themes of interest in high-fidelity simulation-based optimization: optimization of complex systems whose performance is evaluated w.r.t. several criteria originating from different, coupled disciplines; optimization under uncertainties, by introducing sensitivities as additional objectives; optimization of time-dependent systems, such as optimization of flow-control devices that generate a periodic flow (see next subsection), by converting the problem into a multipoint problem by time-discretization of the time and parameter-dependent functional (as above); etc.
Flow control
Participants : Régis Duvigneau, Jérémie Labroquère, Emmanuel Guilmineau [Ecole Centrale de Nantes] .
Shape optimization methods are not efficient to improve the performance of fluid systems, when the flow is characterized by a strong unsteadiness related to a massive detachment. This is typically the case for the flow around an automotive body or a wing in stall condition. To overcome this difficulty, flow control strategies are developed, that aim at manipulating vortex dynamics by introducing some active actuators, such as periodic blowing/suction jets. In this context, the choice of the control parameters (location, amplitude, frequency) is critical and not straightforward. Therefore, we develop a methodology to determine optimal control parameters by coupling the simulation of unsteady actuated flows with optimization algorithms. Two research axes have been considered :
-
the resolution of the unsteady sensitivity equations derived from the state equations, to exhibit the dependency of the flow dynamics with respect to the control and apply an unsteady gradient-based approach[67] ;
-
the optimization of control parameters using a statistical metamodel-based strategy [39] .
In this perspective, unsteady Reynolds Averaged Navier-Stokes equations are solved, with some turbulence closures. Different models for synthetic jet have been implemented to simulate the actuation, and then validated for different turbulence closures .
Specific developments have be carried out in the metamodel-based optimizer to include a noise term into Gaussian Process model, which is used to filter errors arising from unsteady simulations. A systematic assessment of modeling and numerical errors has been archived for a backward facing step test-case, with the objective of controlling the re-attachment point location[46] , [58] .
This activity is conducted in collaboration with the CFD team of Ecole Centrale de Nantes.
Adjoint-based mesh quality control
Participants : Jean-Antoine Desideri, Maxime Nguyen-Dinh [ONERA doctoral student] , Jacques Peter [Research Engineer, ONERA/DSNA] , Renaud Sauvage [Airbus France] , Mathieu Meaux [EADS IW] .
In his doctoral thesis [29] , Nguyen Dinh has studied mesh adaptation methods based on the total derivatives of aerodynamic outputs with respect to mesh coordinates by the discrete adjoint method. Firstly, mesh adaptation methods have been devised for Eulerian flows. Zones to be refined are detected using a sensor based on the total derivative, and numerical experiments confirmed the adequacy of the approach. Secondly, the method was extended to the Reynolds-averaged Navier equations (RANS) and thirdly demonstrated for 3D industrial configurations [53] .
Helicopter rotor blade optimization in both situations of hovering and forward flight
Participants : David Alfano [Airbus Helicopter] , Michel Costes [Research Engineer, ONERA/DAAP] , Jean-Antoine Désideri, Arnaud Le Pape [Research Engineer, ONERA/DAAP] , Enric Roca Leon.
E. Roca Leon has conducted a CIFRE thesis at ONERA DAAP supported by Airbus Helicopter (Marignane) [34] . This thesis follows the doctoral thesis of A. Dumont in which the adjoint-equation approach was used to optimize a rotor blade in hovering flight. The goal of this new thesis is to solve a two-objective optimization problem in which the hovering-flight criterion is considered preponderant, but a new criterion that takes into account the forward-flight situation is also introduced, concurrently. The second criterion is the power necessary to maintain the forward motion. The first phase of thesis work has been devoted to the set up of a hierarchy of models from low to high fidelity, in order to calibrate appropriate functional criteria. Then, actual two-objective optimizations are conducted via our Nash game approach to competitive optimization with territory splitting based on reduced Hessian diagonalization. Successful optimization has been realized involving 16 geometrical parameters to reduce the power in forward motion while maintaining sub-optimality of the drag in hover [55] [64] [65] .