Section: New Results

Generalized Solution of Euler

Minimal geodesics along volume preserving maps, through semi-discrete optimal transport

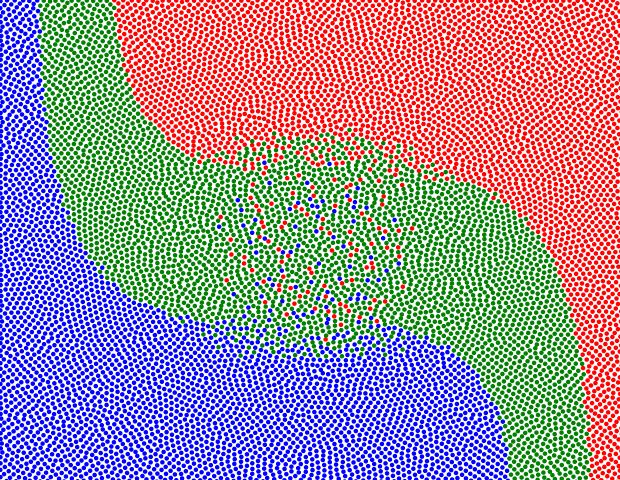
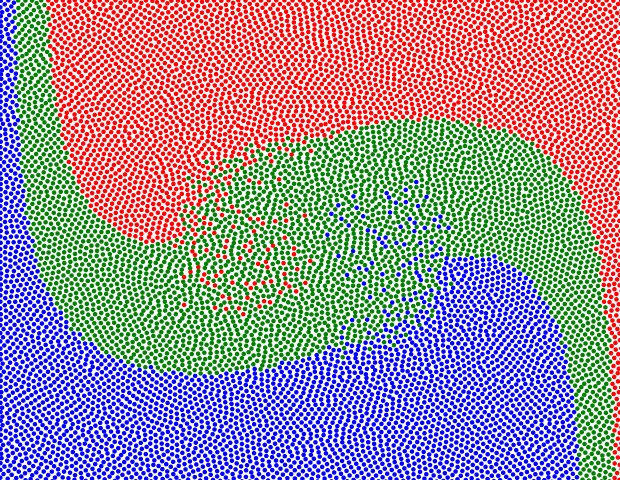
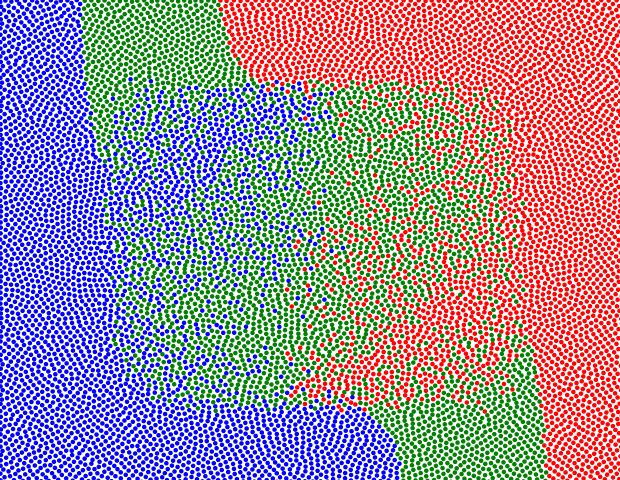
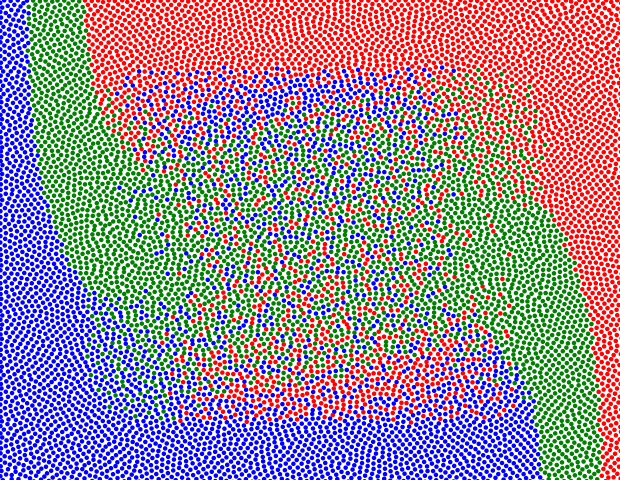
Q. Mérigot and J.-M. Mirebeau introduced a numerical method for extracting minimal geodesics along the group of volume preserving maps, equipped with the ${\mathrm{L}}^2$ metric, which as observed by Arnold solve Euler's equations of inviscid incompressible fluids. The method relies on the generalized polar decomposition of Brenier, numerically implemented through semi-discrete optimal transport. It is robust enough to extract non-classical, multi-valued solutions of Euler's equations, for which the dimension of the support of the flow is higher than the dimension of the domain, a striking and unavoidable consequence of this model. Our convergence results encompass this generalized model, and our numerical experiments illustrate it for the first time in two space dimensions (see Figure 14 ).

Figure 14. (First row) Beltrami flow in the unit square at various timesteps, a classical solution to Euler's equation. The color of the particles depend on their initial position. (Second to fifth row) Generalized fluid flows that are reconstructed by our algorithm, using boundary conditions displayed in the first and last column. When $t_{\max }<1$ we recover the classical flow, while for $t_{\max }\ge 1$ the solution is not classical any more and includes some mixing.